2. 烟台大学,山东 烟台 264005
2. Yantai University, Yantai 264005, China
海上环境具有很大的不确定性,使得船舶在海上遇到危险的可能性很大。为保证安全,船舶必须随时与外部世界保持联络。因此,在船舶和岸台之间进行信息交互是十分必要的。当前,为了达到点对点的传输,一般采用虚拟网进行数据交换。最关键的是数据交互的精确性和时效性。前者是指在传输过程中,数据的完整性,主要由数据的加密来完成。目前,随着信息技术的飞速发展,数据加密技术已经相当成熟,可以有效地保护信息的安全。随着物联网、云计算、无线通信等技术的飞速发展,数据处理技术占有举足轻重的地位。如何充分发挥大数据的作用,已经引起了广泛的关注。将会大力推进大规模的技术研究,以获取、存储、管理大数据,进而实现最大化的共享,从而提升科学、教育和安全的能力[1-3]。
1 正则化方法由于病态逆问题在地球物理、生命科学、模式识别等诸多领域中产生,因此,病态逆解的数值求解技术也随之发展起来,这些都被称为“正规化”。目前最成熟和使用最多的是 TSVD (TSVD)和 Tikhonov规律化(TRM)。为了降低船舶磁场模型中的病态反演问题,本文利用 TSVD与 TRM正则化相结合的方法,对船舶磁场进行反演。
1.1 TSVD| $ {\boldsymbol{A}} = {\boldsymbol{U}}\Lambda {{\boldsymbol{V}}^{\rm{T}}} = \sum\limits_{{i} = 1}^{{r}} {{{{u}}_{i}}} {\sigma _{i}}{v}_{i}^{\rm{T}} \text{,} $ |
式中:U=[U1...UM]和V=[v1...vn]都为正交矩阵;对交的矩阵有Λ=diag(σ1...σr...0)且σ1≥σ1≥...σr≥0;r为系数矩阵的秩。
| $ \chi = \sum\limits_{{\text{i}} = 1}^{r} {\frac{{{{u}_{i}}{b}}}{{{\sigma _{i}}}}{\nu _{i}}} \text{,} $ |
将上式中的系数矩阵A进行奇异值分解有
A=UAvT-uov。在i=1公式中,U=[u… um]及y均是正交矩阵:对角矩阵1= diag (a,0,...o),并且O≥O,≥ O,≤0;r表示系数矩阵的秩。对于反欠问题的最小模型解,可以为x=>iov.i=1Oi,可以很容易地看出,系数矩阵的小奇异值可以被放大。为了改善求解的稳定性,TSVD的基本思路是通过对求解引起干扰的小奇异值进行截断,也就是:
| $ {\chi _{TSVD}} = \sum\limits_{{\text{i}} = 1}^{k} {\frac{{{{u}_{i}}{b}}}{{{\sigma _{i}}}}{\nu _{i}}} \text{。} $ |
式中:k为截断项数,且k<r。
1.2 移动目标轨迹数据运动物体的轨迹是指运动物体在给定时间段内的轨迹,可以用二维、三维甚至更高维的时间序列来表示。目前,在轨道聚类、热路径分析、相似性度量等领域有许多研究成果,但这些研究主要针对车辆轨道的分析[4-6]。在飞机网络(如道路网络)中,只需提取一个固定点或方向点,以减少数据的维数,并且不能用于分析飞机和船舶的轨迹。在此基础上,提出一种基于运动对象的搜索算法,并利用现有的复杂聚类算法对搜索范围进行分类。结合基于大数据表达和感知的相关算法,从热点区域提取和运动轨迹相似性2个方面详细分析运动目标的运动轨迹数据。移动目标轨迹数据处理如图1所示。

|
图 1 移动目标轨迹数据处理 Fig. 1 Move the target trajectory data processing |
首先,通过大量的历史记录资料,对移动对象经常访问的热点区域进行降级,能够反映出移动对象的单个或多个移动对象的运动规律,从而为对方的判断提供依据。将移动空间分为不同的不交迭单元,将移动目标的轨迹转化为经过的单位,从而提高了运算效率。根据存取次数,可以找出若干邻近单元的关联数据。由于只涉及到单位的数量,因此大大降低了计算量。该方法适用于实时子轨道,仅需要对对应单元的访问频率进行更新。
1.3 数据的表示高维数据存在着大量的冗余和噪声,其基本维数较低,因此必须将高维数据降维,将高维数据在低维空间中的表现出来。采用传统的线性降维方法,如主成分分析(princi-pal component analysis,PCA)、线性判别分析(linear discriminant analysis,LDA)等,线性结构分布数据的降维可以使计算简单易懂。然而,实际数据通常表现出结构非线性或属性的强相关性,因此不能使用线性方法。多学习降维算法是近年来发展起来的一种非线性降维算法。它假设高维观测数据被收集到低维流形中,然后使用一些显式或隐式映射关系来获得假设流形,接着将其投影到低维嵌入空间中,以反映数据的基本属性。
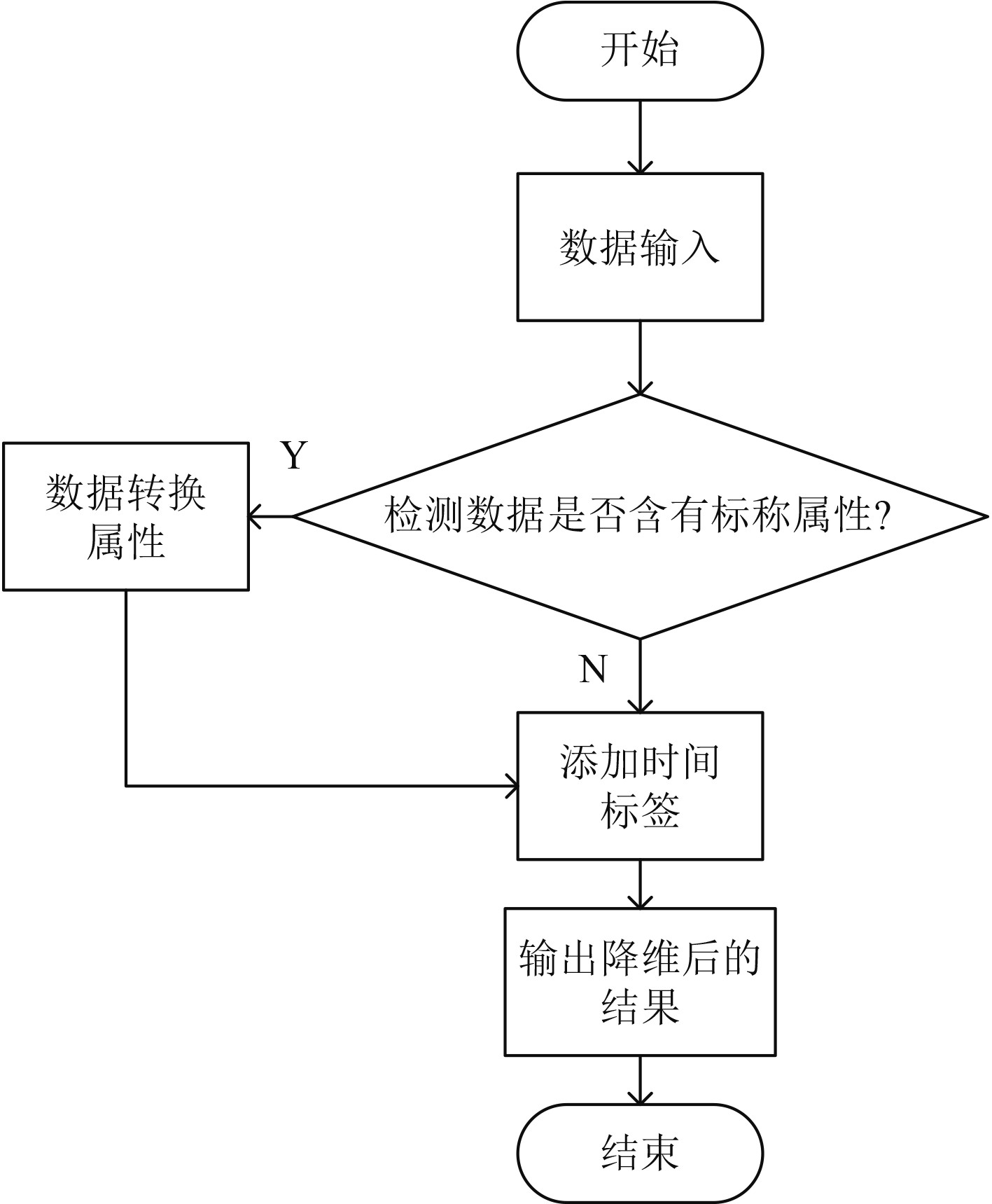
2 多维关联数据动态降维船舶网络数据库中的数据量很大,数据的维数也不一致。如果资料维数过高,有些资料特性会被覆写。采用主分量分析方法对数据进行降维处理。动态降维流程图如图2所示。
|
图 2 动态降维流程图 Fig. 2 Dynamic dimensionality reduction flow chart |
首先,如果只有数字属性,则对噪声自动编码器的输出数据进行评估和处理;然后将时间戳添加到数据中。同时,时间戳被视为滑动窗口大小。在此基础上,通过求解窗口间的相关系数来确定每个参数矩阵的性质和特征向量。根据属性值的降序,接收相应的数据贡献。在此基础上,根据主成分的贡献系数选择主成分决策矩阵向下滑动窗口。
2.1 数据降维采用流形学习中的局部线性嵌入法(lo-cally linear embedding bedding edding,LLE)进行数据降维。给定轨迹数据集Tr,其中Tri∈RD,I=1,…,N,其中N为样本总数,D为原始空间维数,在每个样本的邻域{Tri(1),…,Tri(k)},Tri(k)∈Tr,然后来计算得到最小的特征重构权值。
| $ \varphi (W)=\left|\right|Tr^i-{\displaystyle \sum _{}{}_{j=1}^k}{W}_{ij}T{r}^{i}(j)|{|}^{2} \text{。} $ |
在此基础上,通过引入一小正则化因子,保证了线性系统系数矩阵的非奇性。通过对重构加权的计算,可以利用重构的加权来构建稀疏矩阵。
2.2 特征提取同时,压缩感知提取特征可以有效地降低数据的维数。在此基础上,使用稀疏子域聚类(SSC)算法离散子群方法来解决特征值提取最小化的问题。因此,通过使用L1标准表示信号中每个元素的绝对值之和,并使用凸优化方法解决上述问题。利用L1范数方法,将约束条件转化为罚周期,得到无约束最优解。
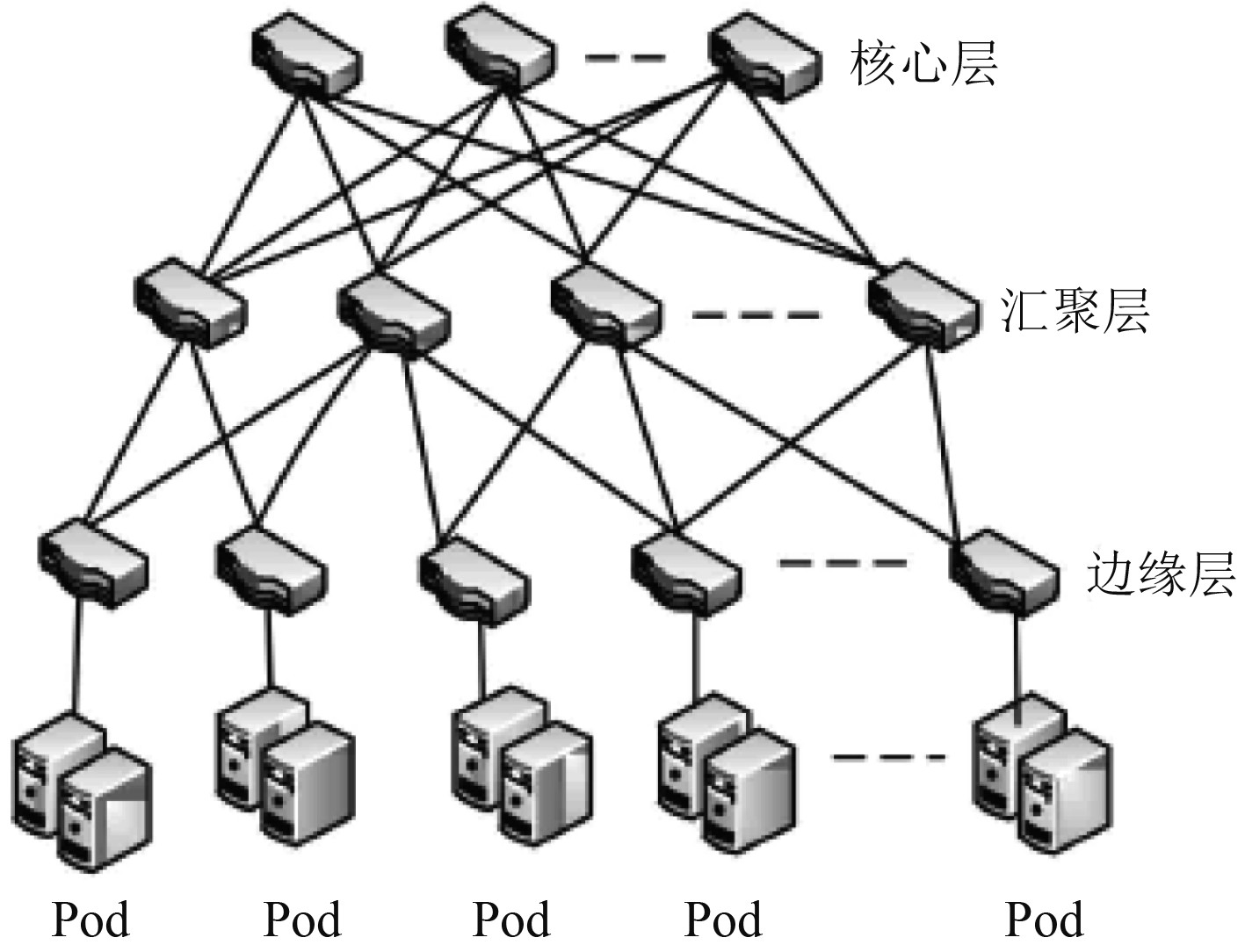
2.3 船舶多维通信虚拟模型要在虚拟网中进行动态的数据交互,必须对其节点的布置有一定的认识。典型的船舶网络拓扑结构包括核心层、汇聚层和边缘层3个层次,船舶虚拟图如图3所示。
|
图 3 船舶虚拟图 Fig. 3 Ship virtual diagram |
目标函数是为了实现研究的总体目标,其数学描述是基于目标+约束的基本模型。在此基础上,我们设计了一个目标函数,将实际交互延迟与数据平均延迟之差作为目标函数,其基本表达式如下:
| $ {\rm min}F(x)={\displaystyle \sum _{\text{r}\in R}(|{D}_{\text{r}}-\overline{D}|)} \text{。} $ |
式中:Dr为所有数据包的平均延迟;x为数据包的实际延迟。目标函数的求解必须在强制性条件下进行,因此,除了目标函数要达到的目的外,还必须给出相应的强制性条件,这两者都是不可或缺的。因此,给出目标函数的几个局限性。
1)限制1
所有数据包的传输速率之和应大于或等于数据传输通道的容量。
| $ \sum\limits_{{\text{r}} \in R} {{\chi _{\text{r}}} \geqslant R} \text{,} $ |
其中,R为数据交互通道的容量。
2) 限制2
虚拟机网络节点的数据传输请求对应于它作为起点与之交互的数据量。流程如下:ei(e),j(e)xetethutt。式中,通过描述一条单程通路,可以获取一条通路的开始与结束状态,还能获得各节点间的数据流的通讯信道总和,从而满足资料交换要求。
流量极限,也就是说,当通讯通道e为最短的数据互动时,它的传送业务与全部通道的平均负荷相等;不然,通讯频道就无法和资料进行互动。这个公式是这样的:
3)极限3
流量极限,也就是说,当通信通道e为最短的数据互动时,它的传送业务与全部通道的平均负荷相等。不然,通信频道就无法和资料进行互动。这个公式是这样的:
| $ 0\leqslant {y}_{\text{i}(e)t}-{\chi }_{\text{et}}\leqslant (1-{\text{u}}_{et}){\displaystyle \sum _{v}{\text{h}}_{vt}} \text{,} $ |
| $ {\chi _{{\text{et}}}} \leqslant {\chi _{{\text{et}}}}\sum\limits_{n} {{{\text{h}}_{{vt}}}} \text{。} $ |
式中:hvt为最短的所有传输路径。
| $ {\displaystyle \sum _{\text{r}\in R}{\chi }_{\text{r}}\leqslant {\text{v}}_{e}}(k)\text{,}{\forall }_{\text{e}} \text{。} $ |
式中:Ve(k)为描述信道e的传输速率;k为在信道e上数据包被成功交互的概率。由于海洋环境的恶劣,使得船舶在海上航行时,存在着诸多危险因素,严重地威胁着船舶的安全。为保证船只的航行安全,船舶与地面基地台间的即时通信十分关键。为改善虚拟船舶网络的动态数据交互能力,本文所提出的优化方法主要是求出最优的目标函数,以求出最佳的数据交互方式,最佳数据交互波形图如图4所示。实验结果显示,使用这种算法可以降低网络的平均延迟和分组丢失,从而提高网络的交互性。

|
图 4 最佳数据交互波形图 Fig. 4 Best Data Interaction Waveform |
本文主要研究船舶通信中多维相关数据的相关性,并采用正则化方法解决船舶多维相关数据计算问题。通过对船舶通信多维相关数据的实例分析,表明正则化算法可以有效地减少船舶通信多维相关性数据的降维计算,提高船舶导航问题的精度和稳定性。
根据实际情况,通过对大量包含有重要信息的运动物体的航迹数据进行收集,结合多维相关数据表达与感知的相关算法,给出了一种基于海洋环境下的热点区域提取方法。在此基础上,对多个运动对象进行大量的访问,并对其进行仿真,减少数据的维数,提高了运算速度,具有较强的实用价值。利用更高级的大数据技术,能够持续地对运动物体的运动轨迹进行聚类、分类、预测、其他的分析和处理,并提供更多的潜在和有用的信息。船舶通信中有关多维的数据,在信息提取、处理、网络安全和监控、作战指挥等领域,已经成为一种新的研究热点。本文着重介绍了大量数据的正则化分析、数据可视化等关键技术。
| [1] |
王宪保, 陈诗文, 姚明海. 基于正则化的半监督等距映射数据降维方法[J]. 电子与信息学报, 2016, 38(1): 5. WANG Xian-bao, CHEN Shi-wen, YAO Ming-hai. Dimensionality reduction method for semi-supervised isometric mapping data based on regularization[J]. Journal of Electronics and Information, 2016, 38(1): 5. |
| [2] |
周兴林, 王明石. 多维力传感器动态力反演正则化求解仿真[J]. 计算机仿真, 2020(037-011). ZHOU Xing-lin, WANG Ming-shi. Simulation of dynamic force inversion regularization for multi-dimensional force sensor [J]. Computer Simulation, 2020(037-011). |
| [3] |
彭艳斌, 苏先创, 邱薇薇, 等. 基于流形正则化非负矩阵分解的高光谱数据降维[J]. 光电子. 激光, 2018, 29(2): 5. PENG Yan-bin, SU Xian-chuang, QIU Wei-wei, et al. Dimensionality reduction of hyperspectral data based on manifold regularized non-negative matrix factorization[J]. Optoelectronics. Laser, 2018, 29(2): 5. |
| [4] |
朱劲夫, 刘明哲, 赵成强, 等. 正则化在逻辑回归与神经网络中的应用研究[J]. 信息技术, 2016, 40(7): 5. ZHU Jin-fu, LIU Ming-zhe, ZHAO Cheng-qiang, et al. Application of regularization in logistic regression and neural network[J]. Information Technology, 2016, 40(7): 5. DOI:10.13274/j.cnki.hdzj.2016.07.001 |
| [5] |
高云龙, 潘金艳, 陈福兴. 基于判别正则化局部保留投影的图像数据降维方法及系统: , CN111553417A[P]. 2020. GAO Yun-long, PAN Jin-yan, CHEN Fu-xing. Dimensionality Reduction Method and System for Image Data Based on Discriminant Regularization Local Preserving Projection: CN111553417A[P]. 2020. |
| [6] |
王丽艳, 李伟生. 基于判别性降维的字典学习在光照变化人脸识别中的应用[J]. 科学技术与工程, 2014(8): 7. WANG Li-yan, LI Wei-sheng. The application of dictionary learning based on discriminative dimension reduction in face recognition with illumination changes[J]. Science Technology and Engineering, 2014(8): 7. DOI:10.3969/j.issn.1671-1815.2014.08.009 |
 2022, Vol. 44
2022, Vol. 44
