0 引　言

舰船在航行过程中，需要根据自身所处的复杂环境情况，结合多源信息规划出一条无碰撞、安全的路径，以此来保障舰船航行的安全性。但是，在实际航行过程中，所处环境呈现动态变化，相关信息也是实时变动的，产生的数据体量较大，为路径规划带来了极大的困难与挑战，成为制约舰船发展与应用的关键问题。本文提出基于大数据分析的复杂环境舰船导航方法，通过大数据分析技术的应用，提升舰船导航的实时性与精确性。

1 复杂环境舰船导航方法 1.1 复杂环境模型构建

复杂环境模型构建是舰船导航进行之前必要的基础与前提，是影响舰船路径规划效率与精度的关键因素。利用舰船自身搭载的多种传感器(激光雷达、毫米波雷达、GPS、加速度器、陀螺仪、电子罗盘等)获取舰船周围环境信息，利用栅格法构建复杂环境模型，为后续舰船导航定位与路径规划奠定坚实的基础。栅格法将舰船所处的复杂环境抽象为二维静态空间，并将其划分为多个尺寸一致的正方形栅格形式，以颜色表示栅格区域是否能够通过。当正方形栅格显示为黑色，表明该栅格区域无法通过；当正方形栅格显示为白色，表明该栅格区域可以通过。栅格排序规则为：从左至右，从上至下^[3]。设置栅格行、列号为 $x$ 、 $y$ ，序号为 ${\delta _x}$ ，两者之间的转换关系如下式：

$\left\{ {\begin{array}{*{20}{c}} {x = \bmod \left[ {{\delta _x},n} \right]}，\\ {y = ceil\left[ {{\delta _x},n} \right]}。\end{array}} \right.$

(1)

式中：mod[]是取余运算函数； $n$ 为栅格行、列号的最大值；ceil[]是向上取整运算函数。

依据栅格区域能否通过，对栅格序号进行赋值，其规则如下式：

${\delta }_{x}=\left\{\begin{array}{cc}0，& 可通行，\\ 1，& 不可通行。\end{array}\right.$

(2)

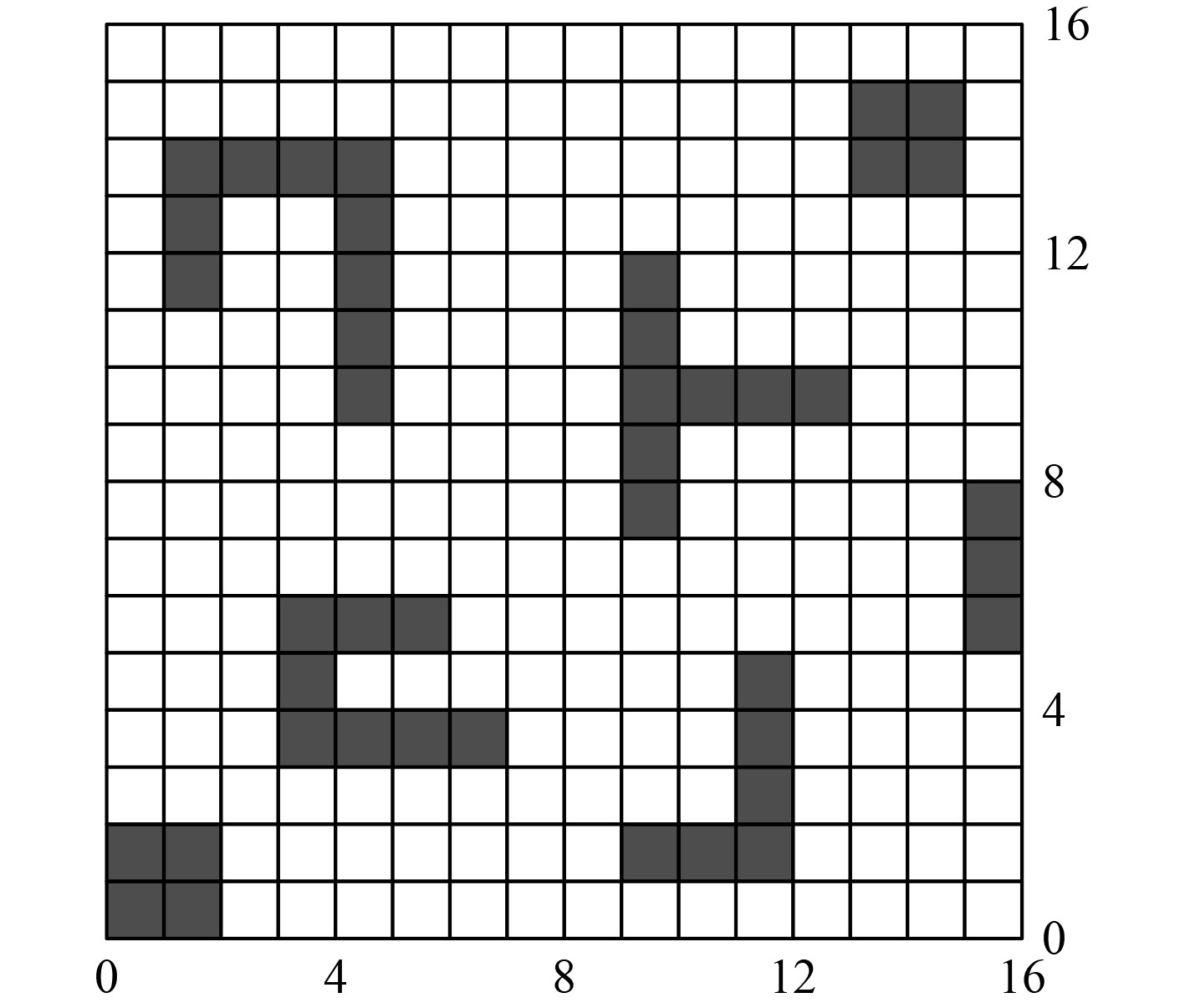
依据上述描述构建复杂环境栅格模型，具体如图1所示。

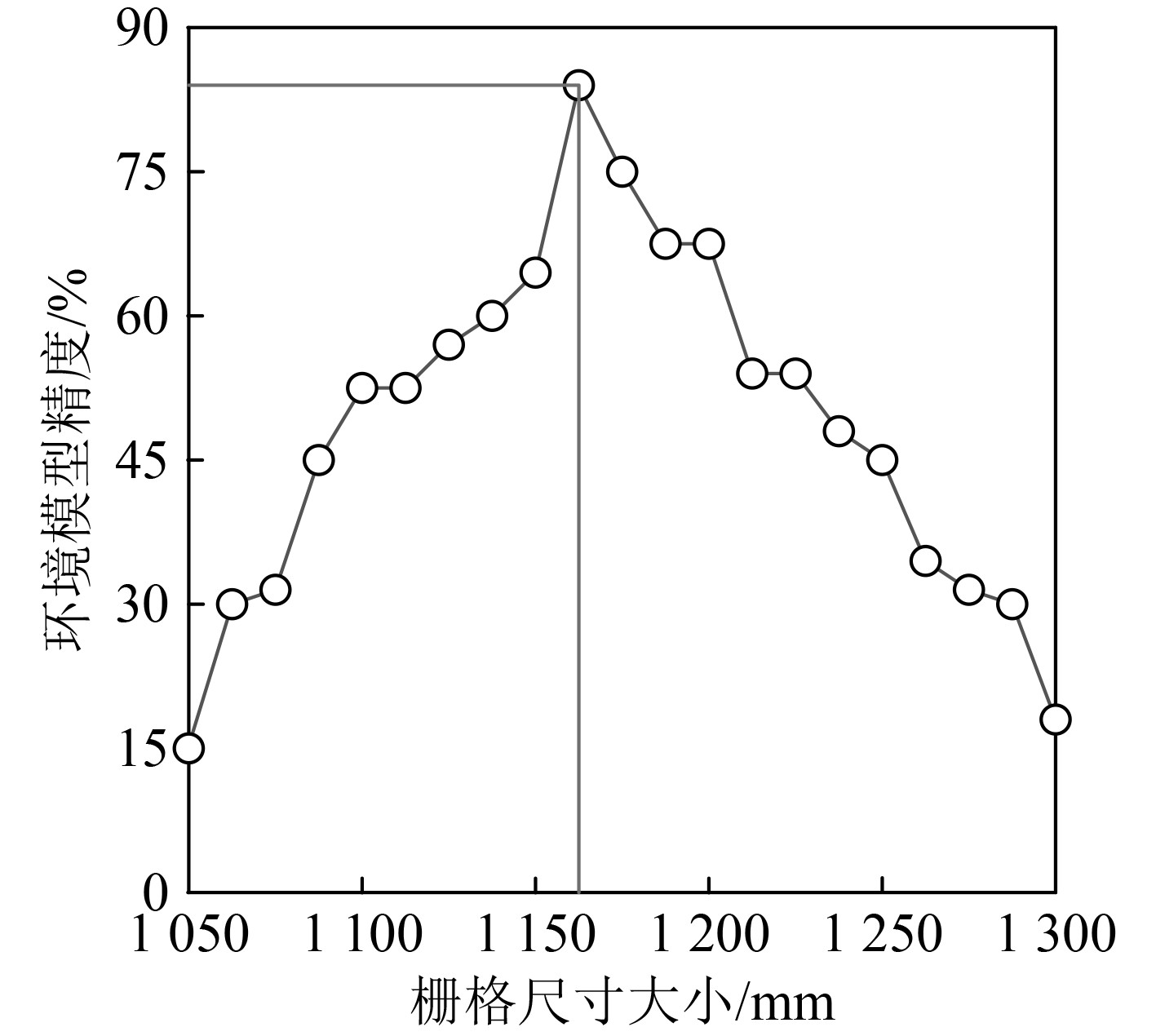
复杂环境栅格模型示例图规格为16×16，黑色栅格区域舰船无法通过，白色栅格区域舰船能够通过。在栅格模型构建过程中，栅格尺寸大小选取也是一个关键的问题，涉及到多个方面，例如环境模型精度、舰船尺寸、水域范围等^[4]。若是栅格尺寸大小设置过大，环境模型分辨率较低，很难清晰地反映舰船所处的环境信息；若是栅格尺寸大小设置过小，环境模型抗干扰性能较差，容错率较低，影响后续舰船路径规划的效率^[5]。通过测试获得栅格尺寸大小与环境模型精度之间的关系如图2所示。随着栅格尺寸大小的增加，环境模型精度呈现先上升后下降的趋势^[6]。当栅格尺寸大小取值为1162.5×1162.5 mm时，环境模型精度达到最大值84%。因此，确定最佳栅格尺寸大小为1162.5×1162.5 mm。

1.2 舰船导航数据预处理

舰船导航数据来自于多个监测设备，并且数据体量巨大，故采用大数据分析技术对其进行预处理，主要为舰船导航数据时间归一化处理、误差改正处理与野值剔除处理。舰船导航数据时间归一化处理是将全部数据归算到同一采样周期 ${T^o}$ 内，方便后续导航数据的应用，表达式为：

${t'_i} = \frac{{{t_i} - {t_{\min }}}}{{{t_{\max }} - {t_{\min }}}}。$

(3)

式中： ${t_i}$ 与 ${t'_i}$ 是归一化前、后的导航数据时间； ${t_{\min }}$ 与 ${t_{\max }}$ 是导航数据时间的最小值与最大值。需要注意的是，归一化处理后的导航数据时间 ${t'_i}$ 必须在采样周期 ${T^o}$ 内。

由于监测设备的自身缺陷，获取的舰船导航数据存在着一定的系统误差，其会对导航性能产生不利的影响^[7]。因此，此研究利用预存改正量对数据误差进行相应的改正处理。以航向角数据为例，其误差改正处理表达式为：

$\varphi ' = \varphi + \Delta \varphi。$

(4)

式中： $\varphi$ 与 $\varphi '$ 是原始航向角数据与误差改正后的航向角数据； $\Delta \varphi$ 是航向角数据对应的预存改正量。

导航数据中无可避免会存在少数的野值(反常值与坏值)，容易造成导航路径的错误，威胁舰船的航行安全，故应用卡尔曼滤波判定野值，并对其进行剔除处理^[8]。野值判定规则如下：

$\left\{\begin{array}{c}\varepsilon \left({t}_{i}\right)=Y\left({t}_{i}\right)-\left[h\left({t}_{i}\right)X\left({t}_{i},{t}_{i-1}\right)\right]，\\ \begin{array}{cc}\left|\varepsilon \left({t}_{i}\right)\right| > {\alpha }^{\ast }，& 野值，\\ \left|\varepsilon \left({t}_{i}\right)\right|\leqslant {\alpha }^{\ast }，& 正常值。\end{array}\end{array}\right.$

(5)

式中： $Y\left( {{t_i}} \right)$ 为采集导航数据； $h\left( {{t_i}} \right)X\left( {{t_i},{t_{i - 1}}} \right)$ 为预测导航数据； $\varepsilon \left( {{t_i}} \right)$ 为采集导航数据 $Y\left( {{t_i}} \right)$ 与预测导航数据 $h\left( {{t_i}} \right)X\left( {{t_i},{t_{i - 1}}} \right)$ 的差值； ${\alpha ^ * }$ 为野值判定阈值，需要根据舰船导航数据具体情况进行设置。

上述过程应用多种大数据分析技术预处理舰船导航数据，统一采样时间周期，改正系统误差，剔除了野值，提升了导航数据的精度，为后续舰船导航定位的实现提供依据支撑。

1.3 舰船导航定位

以预处理后的舰船导航数据为基础，以复杂环境模型为背景，融合GPS与IMU数据，确定舰船导航当前的绝对位置，为舰船路径规划做好充足的准备。IMU数据与舰船导航数据隶属于二维直角坐标系中，而GPS输出数据为地球坐标系背景下的经纬度信息，无法对其进行融合应用，故先对GPS数据进行坐标系转换，表达式为：

$\begin{aligned}\begin{cases} {\beta = {\beta _0} + {\gamma _0}V\left( {\eta + \left( {1 - \kappa + \lambda } \right)\dfrac{{{\eta ^3}}}{6} + \left( {5 - 18\kappa + {\kappa ^2}} \right)\dfrac{{{\eta ^5}}}{{120}}} \right)}，\\ \chi = {\chi _0} + {\gamma _0}V\left( \mu + V\tan \left( \dfrac{{{\eta ^2}}}{2} + \left( {5 - \kappa + 9\lambda + 4{\lambda ^2}} \right)\dfrac{{{\eta ^4}}}{{24}} + \right.\right.\\ \quad \;\; \left.\left.\left( {61 - 58\kappa + {\kappa ^2}} \right)\dfrac{{{\eta ^2}}}{{720}} \right) \right) 。\end{cases}\end{aligned}$

(6)

式中： $\left( {\beta ,\chi } \right)$ 为二维直角坐标数据； $\left( {{\beta _0},{\chi _0}} \right)$ 为二维直角坐标系原点； ${\gamma _0}$ 为随机常数，由坐标系转换具体情况确定； $V$ ， $\eta$ ， $\kappa$ ， $\lambda$ 与 $\mu$ 为坐标系转换参数，由地球坐标信息 $\left( {\tau ,\upsilon } \right)$ 计算获取，表达式为：

$\begin{split}\begin{cases} {V = \dfrac{1}{{\sqrt {1 - {e^2}{{\sin }^2}\upsilon } }}}，\\ {\eta = \left( {\tau - {\tau _0}} \right)\cos \upsilon }，\\ {\kappa = {{\tan }^2}\upsilon }，\\ {\lambda = {{\cos }^2}\upsilon \times \dfrac{{{e^2}}}{{1 - {e^2}}}}，\\ {\mu = \sin 6\upsilon \times \dfrac{{35{e^6}}}{{3072}}} 。\end{cases}\end{split}$

(7)

式中， ${\tau _0}$ 为地球坐标系中原点经度信息。

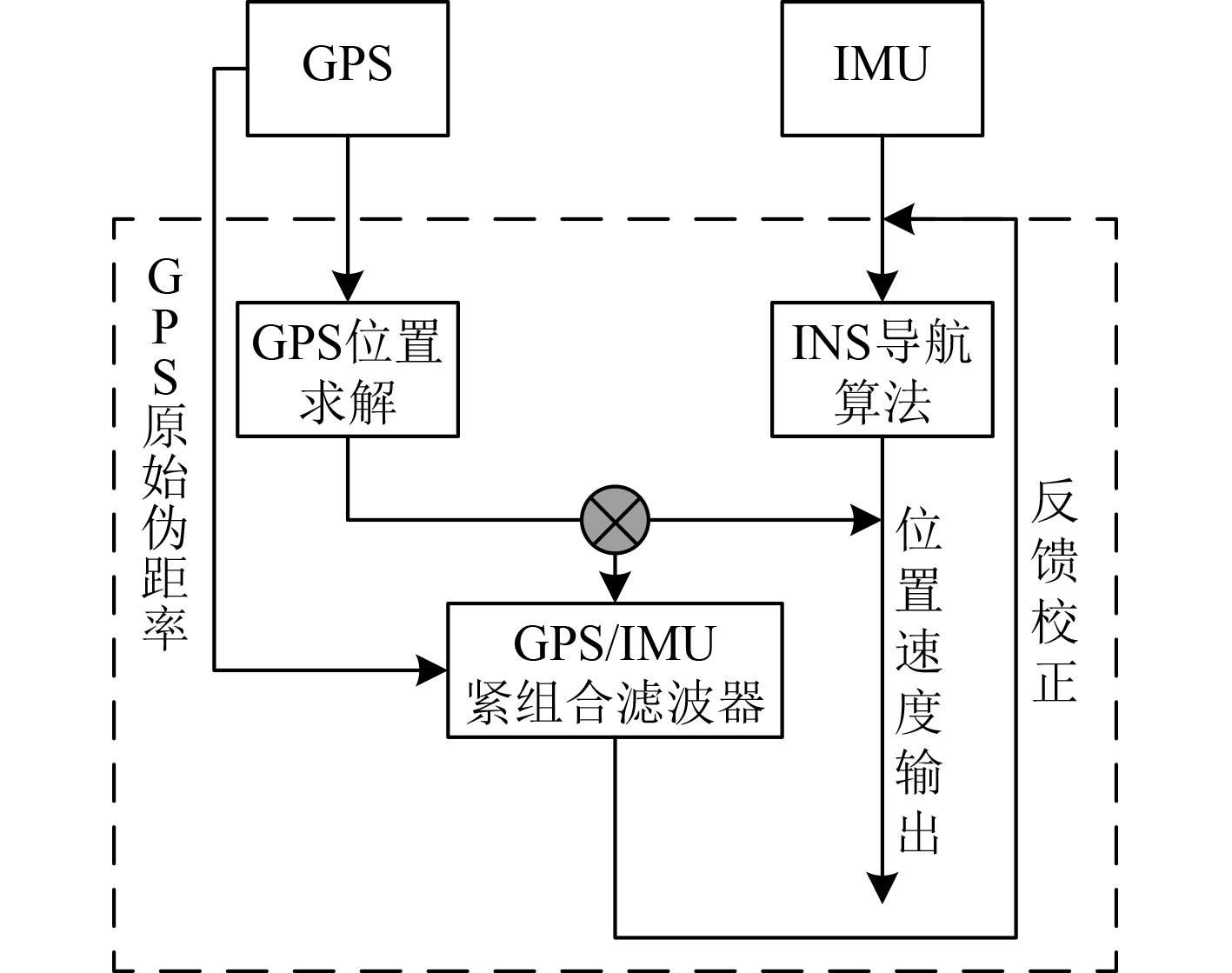
将式(7)计算结果输入至式(6)即可获得地球坐标系 $\left( {\tau ,\upsilon } \right)$ →二维直角坐标系 $\left( {\beta ,\chi } \right)$ 的转换规则，以此为基础，对全部GPS数据进行坐标系转换处理，采用紧组合原理将GPS数据与IMU数据进行融合，即可获得当前时刻舰船导航的绝对位置信息，为后续的舰船导航实现提供支撑。舰船导航位置确定框架如图3所示。依据图3所示框架获得当前时刻舰船导航的绝对位置信息，为舰船路径规划提供便利。

1.4 舰船路径规划

以舰船导航定位结果为基础，应用遗传算法获取最佳舰船路径，从而实现复杂环境背景下舰船导航，保障航行的安全与稳定。

基于遗传算法的最佳舰船路径获取步骤如下：

1) 构建复杂环境栅格模型，并获取障碍物位置、属性等信息；

2) 初始化信息熵遗传算法，制定迭代终止条件；

3) 构造适应度函数，为舰船路径寻优做准备，表达式为：

$\left\{ {\begin{array}{*{20}{c}} {F\left( g \right) = \dfrac{{1000}}{{10 \times d\left( g \right) + \dfrac{{\varPsi \left( g \right)}}{\psi } \times m \times 2 + {\sigma _\theta }}}}，\\ {H\left( g \right) = F\left( g \right) - \omega * {N_p}}。\end{array}} \right.$

(8)

式中：F(g)与H(g)是可行路径与不可行路径的适应度函数；d(g)是路径长度； $\varPsi \left( g \right)$ 是平滑度； $\psi$ 是平滑度总和； $m$ 是种群规模； ${\sigma _\theta }$ 是大角度转弯点的数量； $\omega$ 是权重系数；N_p是路径穿过障碍物的线段数量。

4) 通过交叉算子、变异算子对个体进行更新，并重新计算适应度数值。当未满足迭代终止条件时，转至步骤3进行重复迭代；当满足迭代终止条件时，输出个体对应的舰船路径。

通过上述过程即可获得最佳舰船路径，实现了舰船导航功能，为舰船作业、航行等提供有效的帮助，保障舰船自身安全。

2 仿真实验

选取海洋气象环境影响下的复杂水域船舶路径规划与复杂开放水域下智能船舶路径规划与避障方法作为对比方法，分别称之为对比方法1和对比方法2，以验证本文方法的优越。

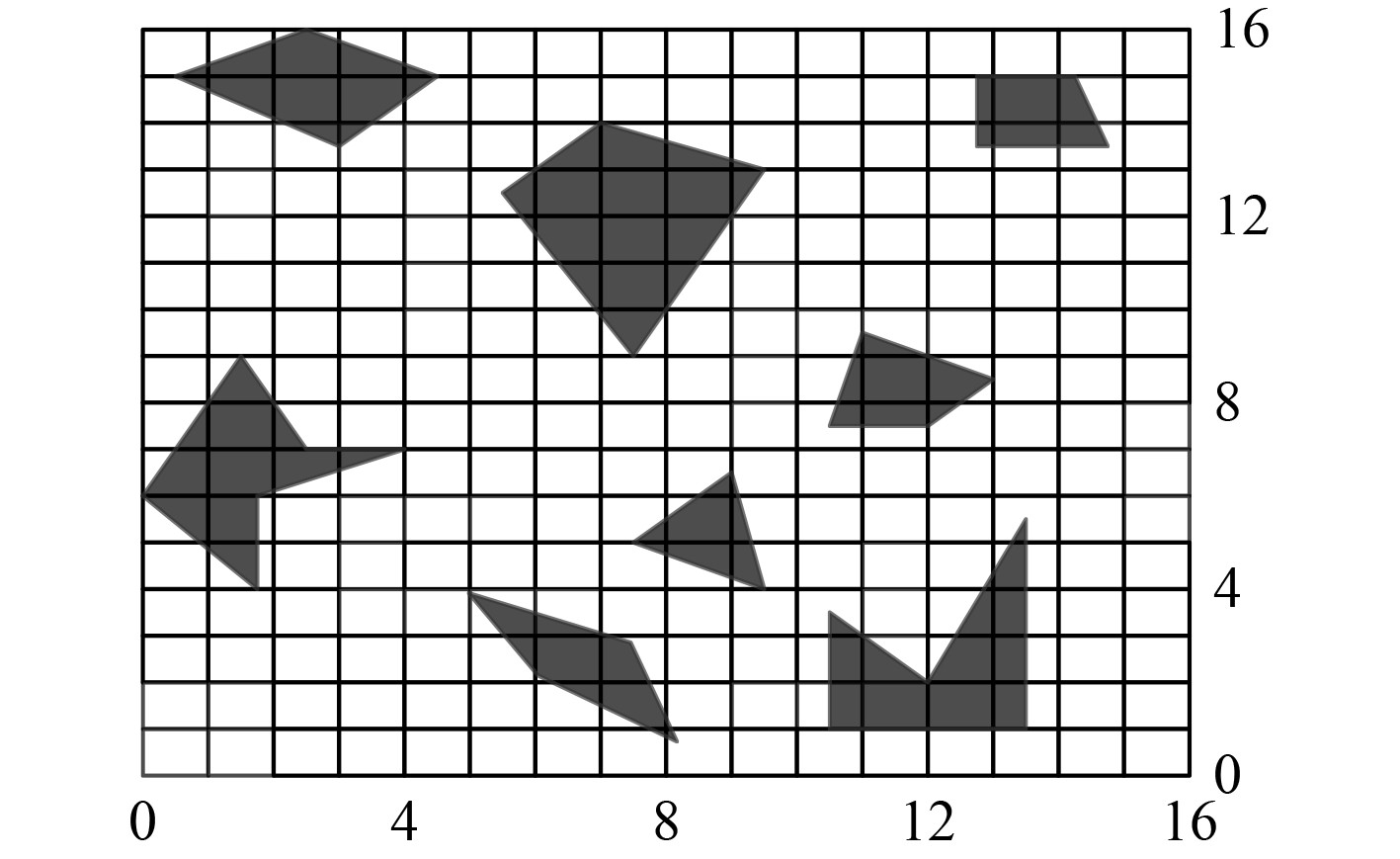
2.1 实验环境段

选取实验水域，通过传感器获取实验水域的障碍物位置、属性信息，构建复杂环境栅格模型，具体如图4所示。实验水域障碍物分布无规律，尺寸大小、形状等也存在着较大的差异，符合提应用性能测试需求。

舰船航行状态的确定也是保障实验顺利进行的关键所在。实验以航向、速度与船位作为舰船航行状态变量，则舰船航行状态方程表达式为：

$\left\{ {\begin{array}{*{20}{c}} {J = {V_N} + Q\cos \vartheta }，\\ {W = {V_E} + Q\sin \vartheta } 。\end{array}} \right.$

(9)

式中： $J$ 与 $W$ 是纬度与经度弧长； ${V_N}$ 与 ${V_E}$ 是北与东向的海流速度； $Q$ 是舰船相对海流速度； $\vartheta$ 是舰船航向。

在实际舰船航行过程中，航向、速度与船位会存在偏差，式(9)无法精确的表示舰船航行状态，故对其进行修正，获得最终舰船航行状态方程，表达式为：

$\left\{ {\begin{array}{*{20}{c}} {\left( {J + \Delta J} \right) = \left( {{V_N} + \Delta {V_N}} \right) + \left( {Q + \Delta Q} \right)\cos \left( {\vartheta + \Delta \vartheta } \right)} ，\\ {\left( {W + \Delta W} \right) = \left( {{V_E} + \Delta {V_E}} \right) + \left( {Q + \Delta Q} \right)\sin \left( {\vartheta + \Delta \vartheta } \right)}。\end{array}} \right.$

(10)

式中， $\Delta$ 是偏差量符号。

上述过程完成了实验水域复杂环境栅格模型的构建，确定了舰船航行状态方程。

2.2 实验结果分析

定位是舰船导航实现的关键环节，其定位是否精准直接关系着舰船导航路径的合理性与科学性。通过实验获得舰船导航定位误差如表1所示。相较于2种对比方法来看，应用本文方法获得的舰船导航定位误差数值较小，最小值为0.12%，表明本文方法舰船导航定位精度更高。

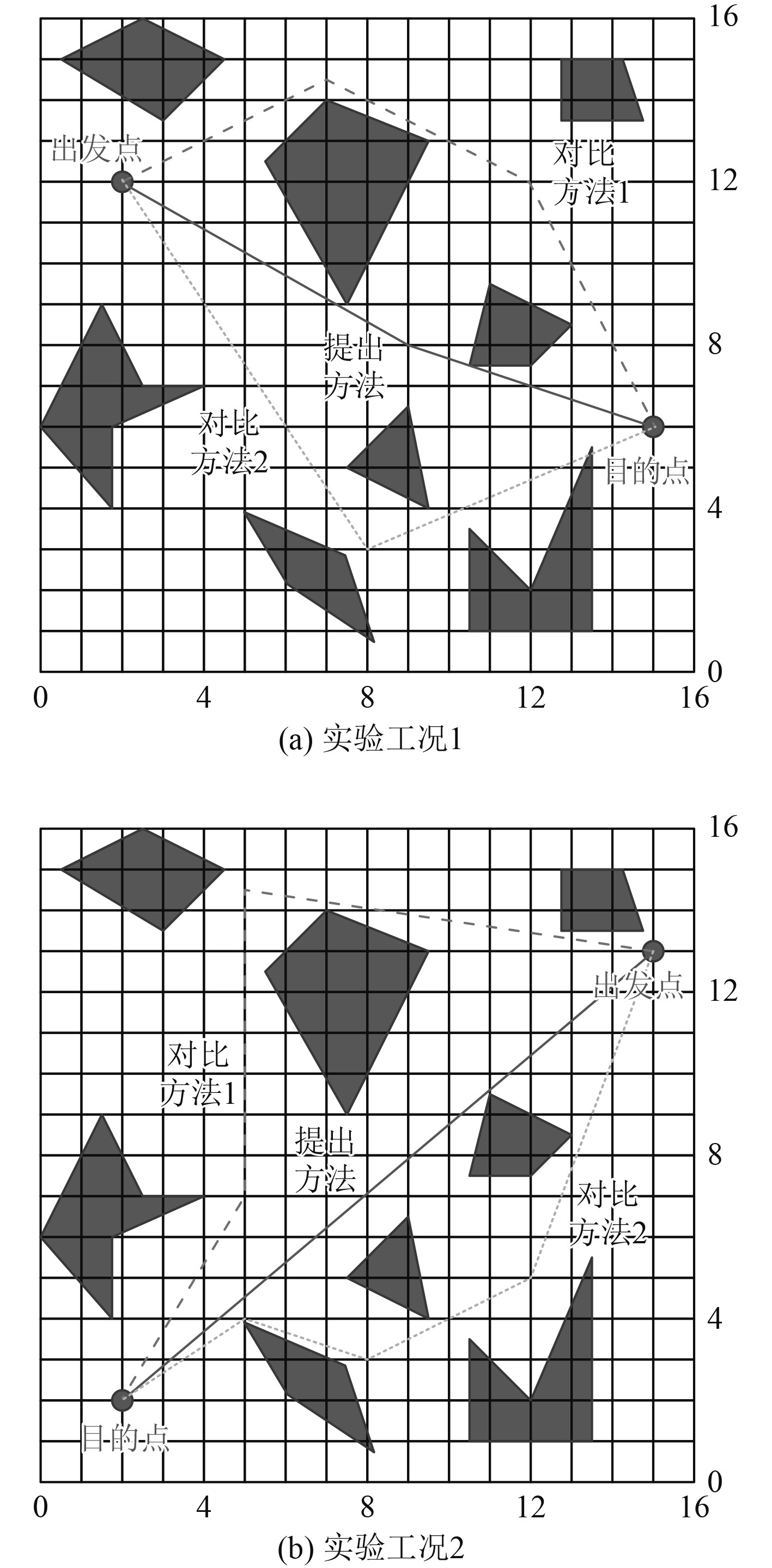
为了提升实验结论的精准性，设置2组出发点与目的点。通过实验获得舰船导航路径如图5所示。相较于2种对比方法来看，应用本文方法获得的舰船导航路径长度更短，更为平滑，能够保障舰船航行的稳定性。

3 结　语

本文提出基于大数据分析的复杂环境舰船导航方法。实验数据表明：本文方法大幅度降低舰船导航定位误差与舰船导航路径长度，提升了舰船导航路径的平滑性。