2. 北京电子科技职业学院,北京 100176
2. Beijing Polytechnic, Beijing 100176, China
在舰船技术发展今天,采用机器人进行舰船自主航行已成为必然趋势。为此,舰船导航机器人应运而生,并在海洋航行领域得到了广泛的应用。在移动机器人自动驾驶中,导航技术是核心技术。当前,导航机器人主要采用磁力导航,存在灵活性低、扩展路线复杂、维修难度大等问题。视觉导航技术是近几年来的一个研究热点,为了使机器人能够在预先设定路线上稳定、实时地进行巡视,提高机器人反应速度和轨迹准确性是机器人需要解决的问题。文献[1]提出了基于深度强化学习的控制方法,该方法通过构建深度学习模型,结合神经网络在同一任务场景下,实时控制机器人导航系统。文献[2]提出了基于RTK与Lidar组合的控制方法,采用 RTK算法对大范围场景进行精确定位,利用RTK算法建立线性自抗干扰控制器,实现全局导航。在此基础上,结合Lidar算法对场景中的小块障碍物进行了提取,从而达到了对障碍物的自动定位。上述这2种方法过分依赖于机器人准确的运动学模型,且实时控制效果不佳。为了解决这个问题,提出舰船导航机器人的自动控制研究。
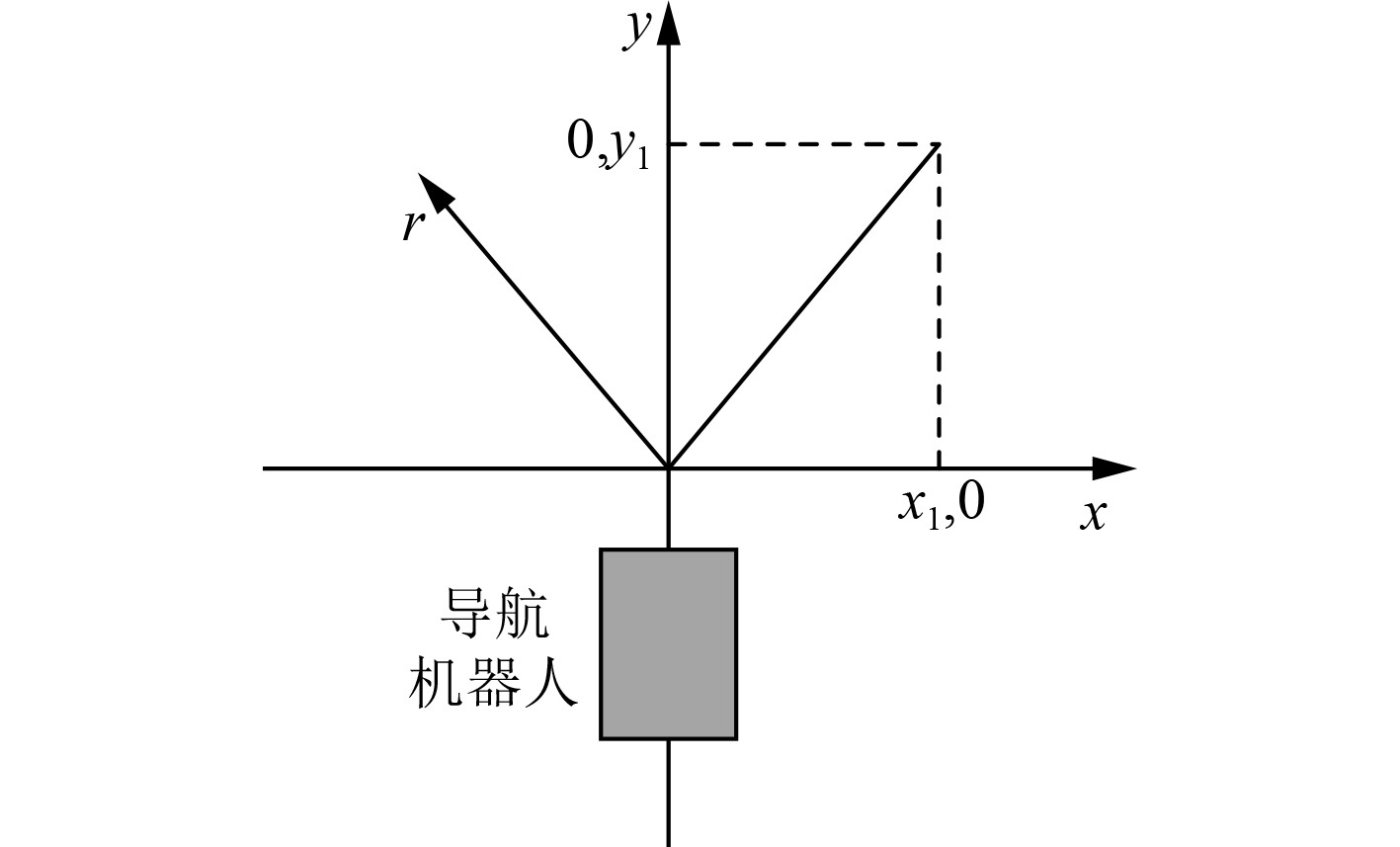
1 目的地位置信息确定要使机器人自主运动,必须准确地确定目标位置,设置若干参考点,以确定目标相对位置[3]。经激光扫描后,该凹陷处为靶位。利用该特性将目标位置信息映射到一个直角坐标中,以求出目标位置信息,目标的位置由凹点特性决定。将扫描器位置作为原点,并在图1中创建一个直角坐标系统。在一次扫描循环中,激光接收机可以进行1800次扫描,每次扫描间隔0.50次。通过一次采集到361条定位信息,可以对管理机位置信息进行精确定位[4-5]。在存储之后,就可以确定目标地具体信息。
|
图 1 激光扫描直角坐标系 Fig. 1 Laser scanning rectangular coordinate system |
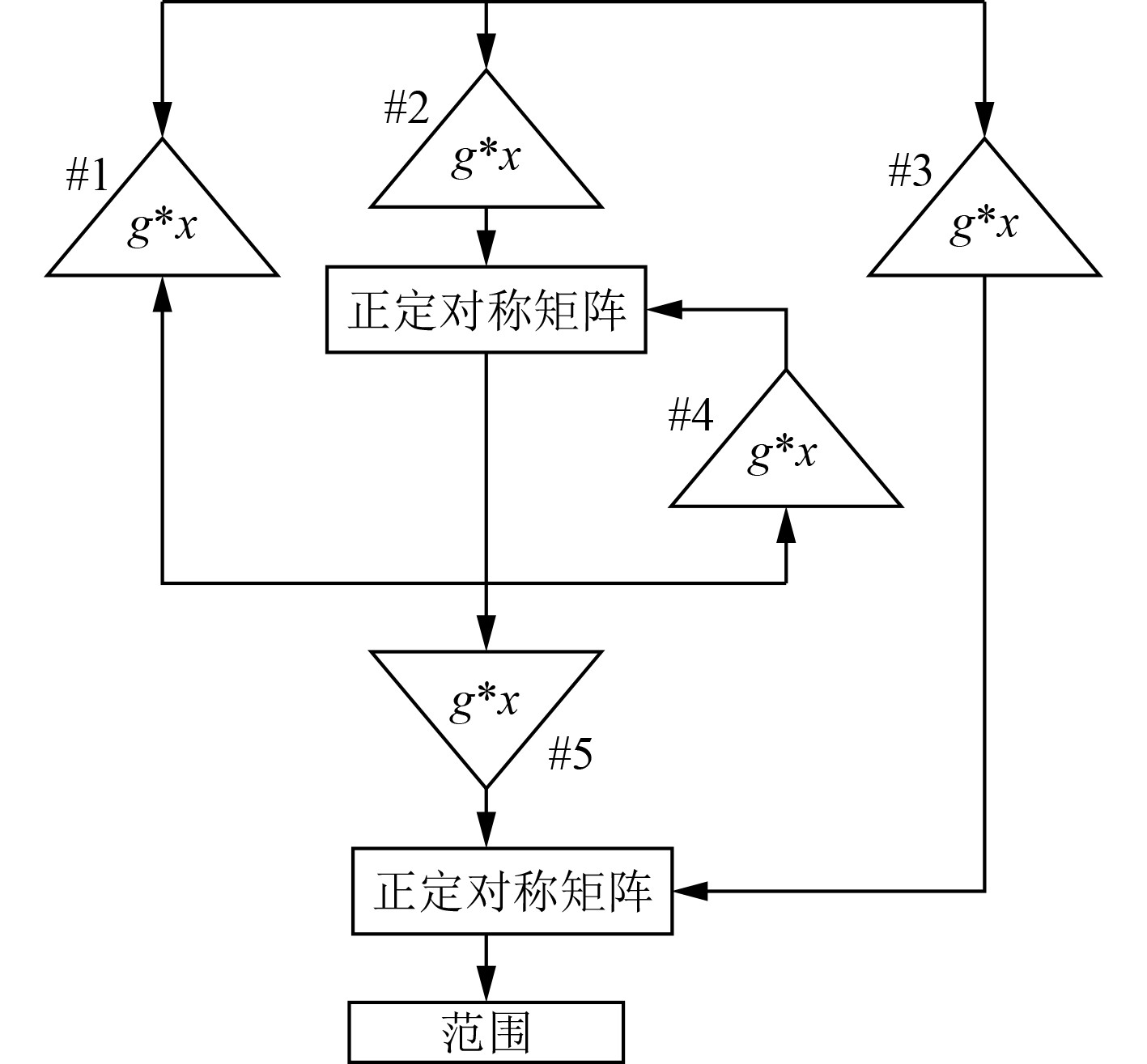
基于视觉导航的机器人最优控制目标是通过对输入进行控制,也就是左、右2个方向上的电压差来减小误差,从而避免机器人偏航[6-8]。最优反馈控制器结构,如图2所示。
|
图 2 最优反馈控制器结构 Fig. 2 Structure of optimal feedback controller |
可知,该控制过程数学模型是一个线性常数,它适合于具有二次性能指数最优反馈控制器,也就是要找到一个最优控制函数,使得二次性能指数函数达到最小:
| $ g(l,x)={{{\displaystyle \int }}^{\text{}}}_{0}^{\infty }\left[{l}^{\text{T}}(t){\boldsymbol Z}^-(t)l(t)+{x}^{\text{T}}(t){\boldsymbol Z}^+(t)x(t)\right]\text{d}t 。$ | (1) |
式中:
结合线性二次最优控制理论,使反馈最优控制函数值取得最小值,可表示为:
| $ x(t) = - {\boldsymbol{g}} \cdot l(t)。$ | (2) |
式中,
结合上述参数,可将舰船导航机器人的自动控制规律用如下公式描述:
| $ \left\{ \begin{gathered} {U_R} = {U_0} - \frac{{\Delta U}}{2} ,\\ {U_L} = {U_0} + \frac{{\Delta U}}{2} 。\\ \end{gathered} \right. $ | (3) |
式中:
| $ \Delta U = - \left( {{g_1}\Delta {V_1} + {g_2}\Delta {V_2} + {g_3}\Delta {V_3}} \right)。$ | (4) |
式中:
导航机器人在跟踪路径时,使系统控制能耗达到最小,具有良好动态响应性能。
2.2 导航机器人避障控制动态窗口法是一种自动障碍算法,它可以通过对控制指令空间的搜索使得目标函数取得最大值的最佳控制指令。该方法的关键在于对机器人的运动速度进行多组采样,并在此过程中对机器人运动轨迹进行仿真。在获得多个轨迹之后,利用评估功能确定包括角速度和线速度在内的最优速度集,从而实现机器人自动控制。为了对其进行仿真,首先需要进行运动建模。基于两轮微分机构运动模式,求出其在世界坐标系中的位置:
| $ \left\{ \begin{gathered} x = {v_x}{{\Delta }}t\cos {\theta _t} - {v_y}{{\Delta }}t\sin {\theta _t},\\ y = {v_x}{{\Delta }}t\sin {\theta _t} + {v_y}{{\Delta }}t\cos {\theta _t}。\\ \end{gathered} \right. $ | (5) |
式中:
在二维空间中,导航机器人运动速度数据较多,为了解决这个问题,提出一种基于安全系统距离限制的新方法。为了确保机器人在遇到障碍前能及时停车,应将其运动速度限制在一个特定区间内。假设机器人在速度
| $ \begin{gathered} v \leqslant \sqrt {2d(v) \times {v_b}},\\ {v_b} \in \left[ {v - {v_c}\Delta t,v + {v_c}\Delta t} \right]。\\ \end{gathered} $ | (6) |
式中:
通过控制机器人运行速度范围,使机器人朝着目的地避免障碍物。
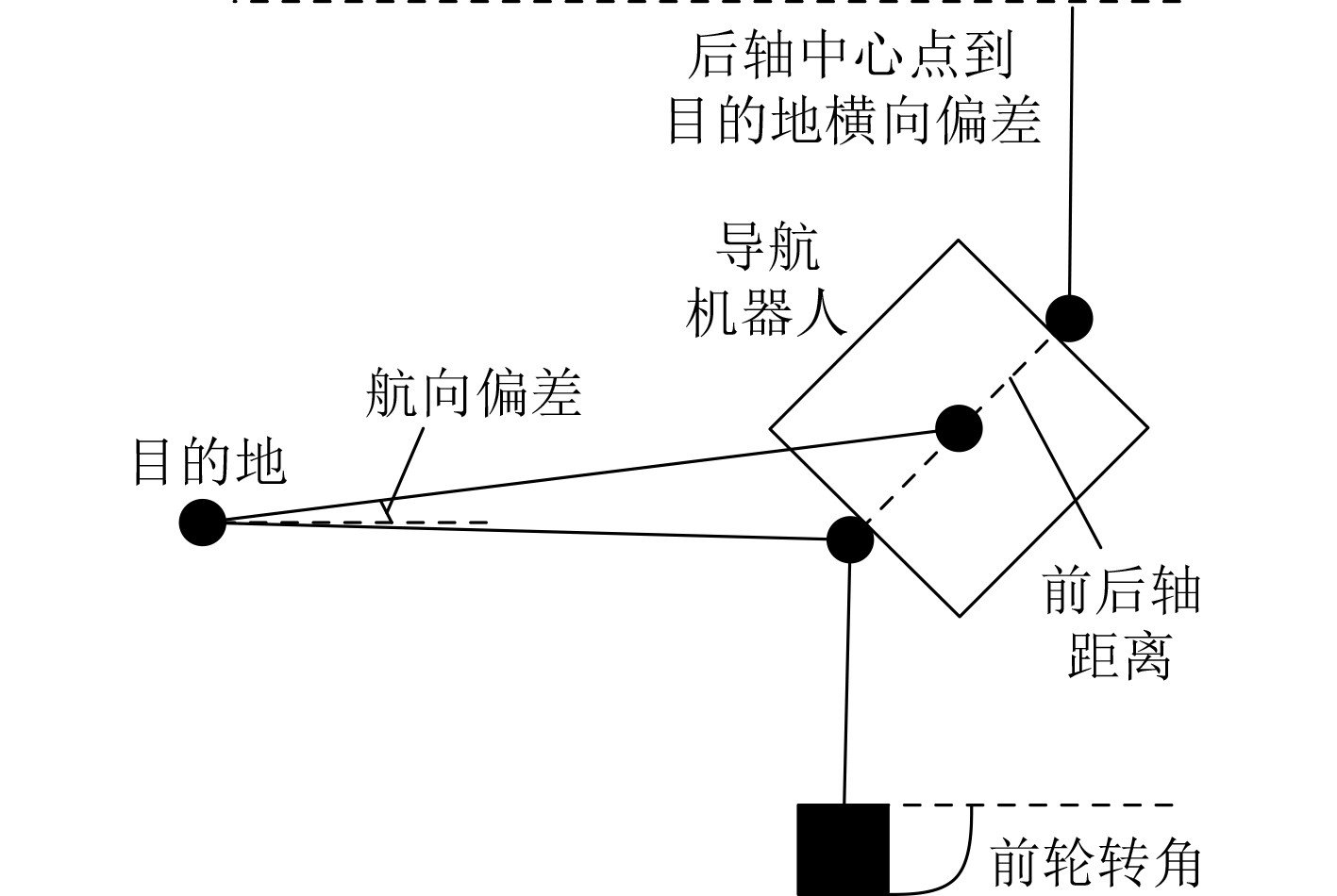
2.3 偏航控制在研究自动控制方案的基础上,假设导航机器人在导航时出现了偏移量,这种偏移量的产生会造成导航出现偏航问题。为了解决这个问题,构建运动学模型,如图3所示。
|
图 3 运动学模型 Fig. 3 Kinematic model |
对于最优反馈控制器结构,需将输入偏差信号转换为论域上的点,可表示为:
| $ {m_i} = IT\left( {{\varepsilon _i} \cdot {\lambda _i}} \right)。$ | (7) |
式中:
由式(7)可以看出,若在论域范围内无转化点,则将其视为输入偏移信号的物理范围至论域转换系数,则可以获得:
| $ {\varepsilon _i} = \frac{{{m_i}}}{{{\lambda _i}}} 。$ | (8) |
在计算结果不超过0.08的情况下,就认为转换因子为0,在这种情况下,模糊控制已不能充分发挥其控制功能,因此必须寻找一种能消除稳定误差的控制器,这种最优控制器能有效地控制偏移。通过设定适当门限,使2个控制器能够顺利地进行转换,从而达到控制系统的目的。在机器人与导航路径偏离较大时,利用模糊控制器进行控制,在误差小于开关门限的情况下,使用最优控制器可以有效地改善机器人动作响应和导航准确性。基于此,推导出导航机器人的运动轨迹方程为:
| $ d = v'\sin \alpha 。$ | (9) |
式中:
| $ \alpha = \frac{{v'}}{s}\tan \beta。$ | (10) |
式中:
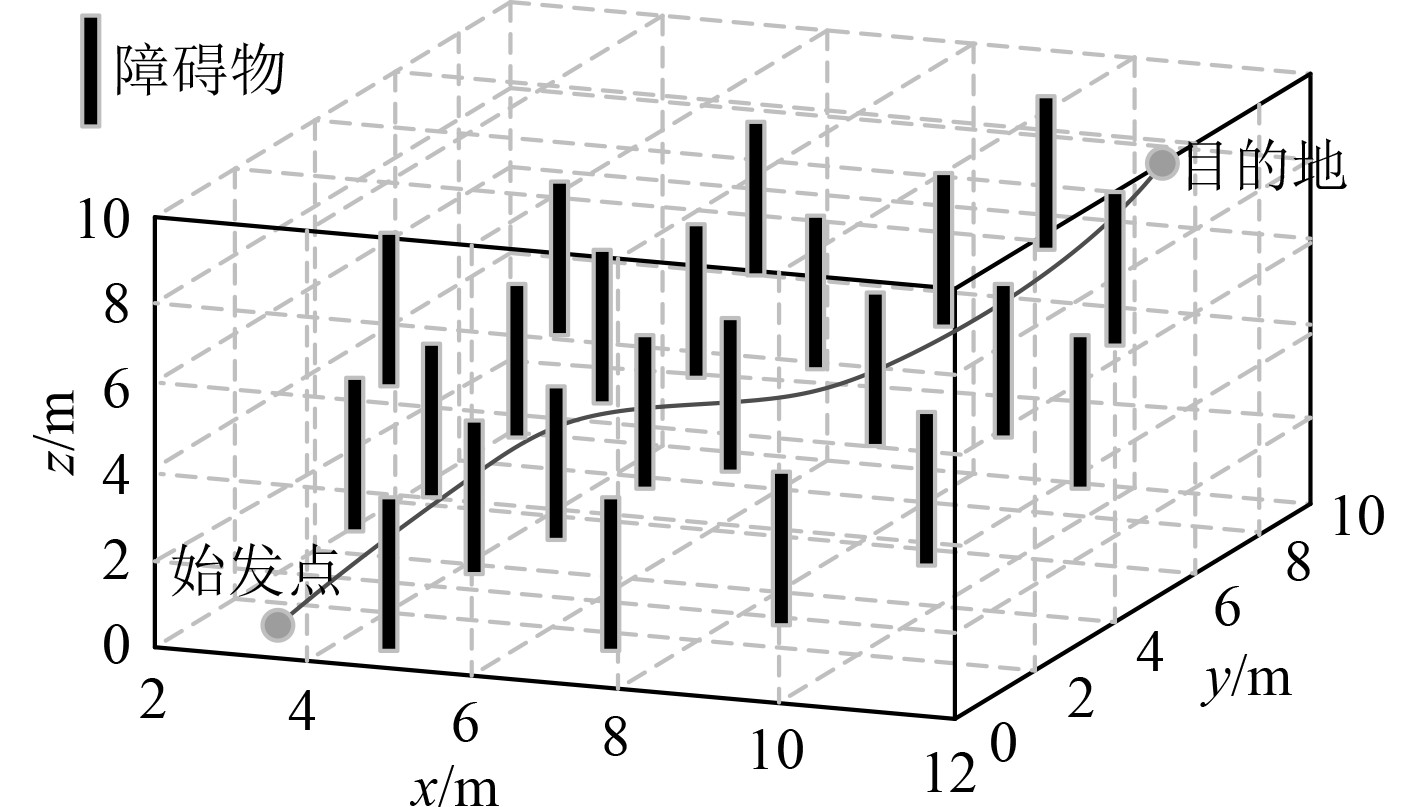
|
图 4 仿真运行结果 Fig. 4 Simulation operation results |
根据机器人航行特点,当其导航路径与拟合路径存在偏差时,依据上述公式可计算出偏差值,从而实现对导航方向的精准控制。
3 性能验证性实验 3.1 避障控制测试使用Matlab软件仿真运行舰船导航机器人行走路径,如图5所示。
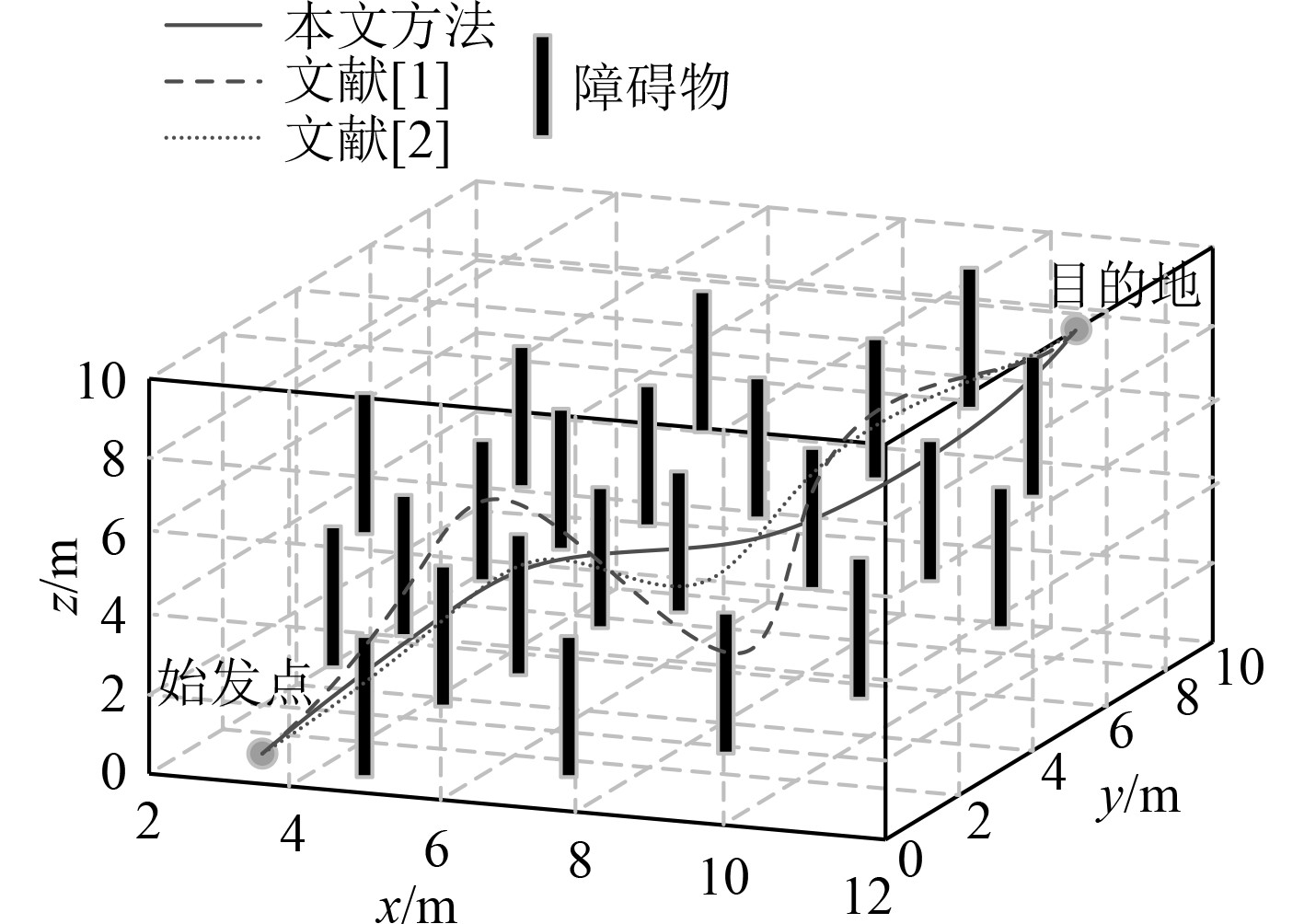
|
图 5 不同方法导航机器人行走路径对比分析 Fig. 5 Comparison and analysis of robot walking paths guided by different methods |
通过仿真运行结果可知,导航机器人顺利避开障碍物到达目的地的同时,生成的导航路径是平滑的。基于此,分别使用文献[1-2]和本文方法对比分析导航机器人行走路径是否与实际路径一致,对比结果如图5所示。可知,使用文献[1-2]的导航机器人行走路径并没有按照原计划导航,且行走路径曲折并不平滑,使用本文方法的导航机器人行走路径与实际路径一致,且导航路径是平滑的。
3.2 角度与位移偏差验证结果分析将角度与位移偏差作为实验指标,分别使用文献[1-2]和本文方法进行对比分析,其中角度偏差控制效果对比结果如图6所示。可知,受到水流影响,舰船导航机器人肯定会存在一定偏航,但只要偏航范围在−5°~−5°范围内,就可保证舰船能够精准到达目的地。其中,使用本文方法能够将角度偏差控制在−5°~−5°范围内,使用文献[1-2]方法无法将角度偏差控制在−5°~−5°范围内,角度偏差范围分别为−15°~−10°、−20°~−15°,由此可知,使用本文方法角度偏差控制效果较好。
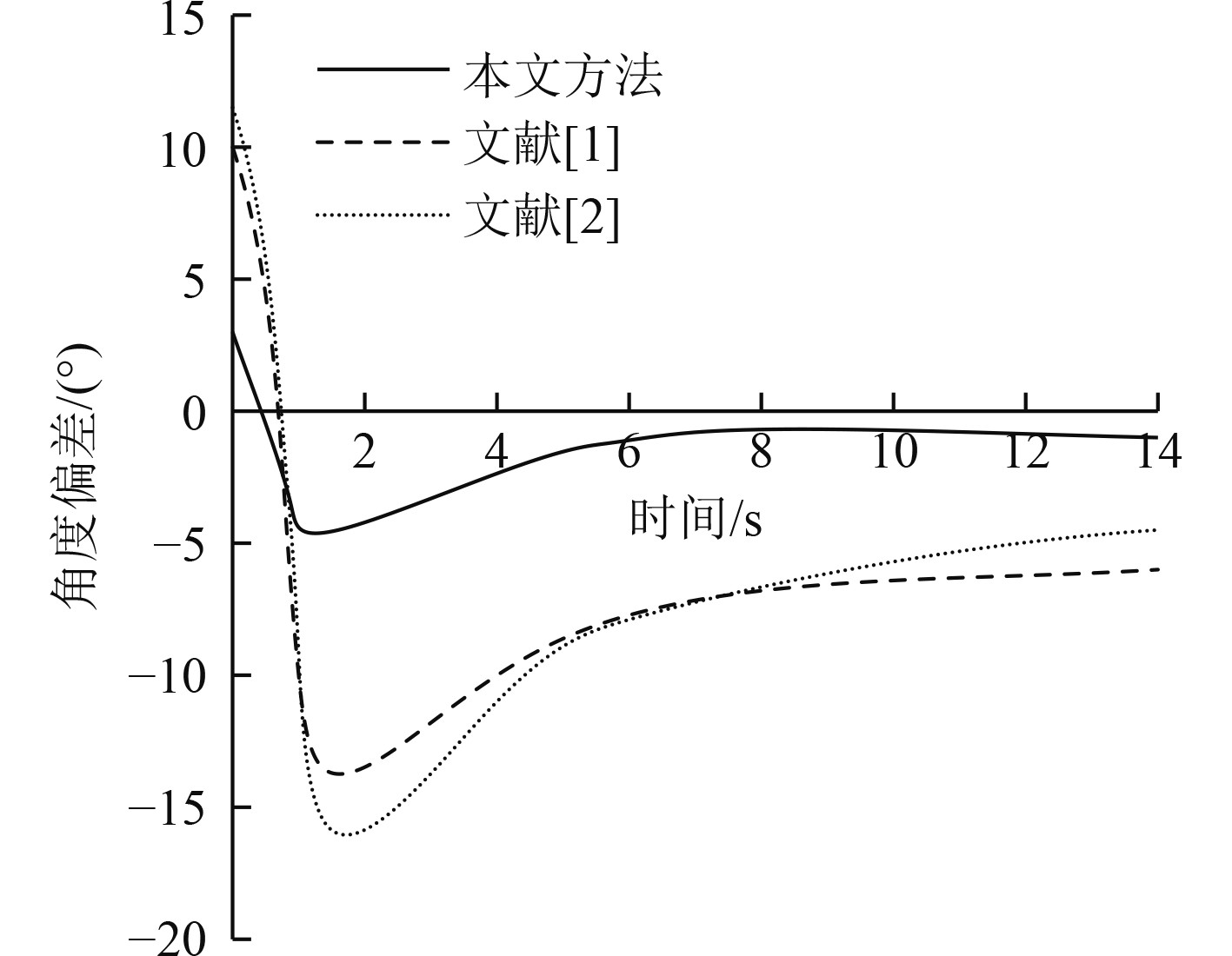
|
图 6 不同方法位移偏差对比分析 Fig. 6 Comparison and analysis of displacement deviation by different methods |
位移偏差控制效果对比结果如图7所示。可知,使用文献[1]的x,y,z三个方向位移偏差大于本文方法,其中x方向相差最大;使用文献[2]的x,y两个方向位移偏差大于本文方法,z方向位移偏差小于本文方法;使用本文方法x方向位移偏差范围为0−0.25 m,y方向位移偏差范围为−1.0−0 m,z方向位移偏差范围为−0.25−0 m,由此可知,使用本文方法位移偏差控制效果较好。
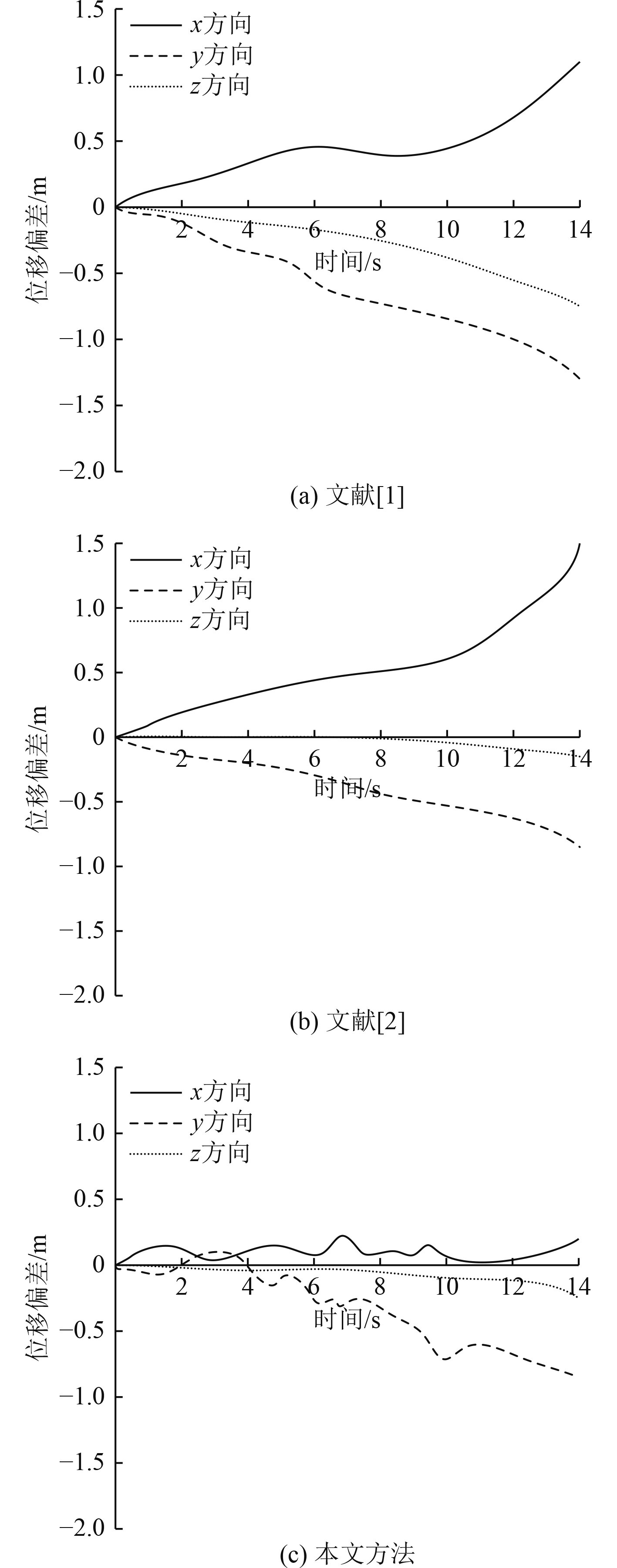
|
图 7 不同方法位移偏差对比分析 Fig. 7 Comparison and analysis of displacement deviation by different methods |
以导航机器人为控制对象,提出一种基于最优反馈的方法实现自动导航。本文所研究的舰船航行机器人的自动控制技术,可以控制角度偏差和位移偏差,从而使其在稳态后的振动减小,提高控制精度。通过实验证明,与传统控制方式相比,该方法在导航品质上有很大的改善,能够实现对系统的自动控制和优化。
| [1] |
丁坤, 王立, 张经炜, 等. 基于改进导航圆算法的光伏阵列清扫机器人路径跟踪控制[J]. 河海大学学报(自然科学版), 2021, 49(2): 190-196. |
| [2] |
李宁. RTK与Lidar组合优化机器人导航控制[J]. 机械设计与制造, 2021(11): 275-278. DOI:10.3969/j.issn.1001-3997.2021.11.062 |
| [3] |
包加桐, 姚小梅, 缪露, 等. 基于云平台地图的侦察机器人室外自主导航[J]. 控制工程, 2020, 27(6): 941-946. |
| [4] |
王钰奉, 陈伟堤, 施祥玲, 等. Delta机器人增广非线性PD控制研究[J]. 组合机床与自动化加工技术, 2021(12): 62-66. |
| [5] |
刘冬, 陈飞, 邹强, 等. 基于情景经验与稀疏点云的移动机器人导航[J]. 华中科技大学学报(自然科学版), 2020, 48(9): 25-30. |
| [6] |
张玉超, 蒋沅, 代冀阳. 三阶多机器人协同编队动态避障控制[J]. 系统仿真学报, 2022, 34(8): 1762-1774. DOI:10.16182/j.issn1004731x.joss.21-0322 |
| [7] |
李航, 王朝耀. 仓库搬运机器人导航运动控制与NURBS轨迹规划[J]. 机械设计与制造, 2020(7): 290-295. DOI:10.3969/j.issn.1001-3997.2020.07.066 |
| [8] |
李峰, 岳云, 张跃进, 等. 基于北斗导航的机器人弹道曲线航道导航系统[J]. 弹道学报, 2021, 33(2): 47-54. |
 2022, Vol. 44
2022, Vol. 44
