0 引　言

从目前船舶智能化、自动化、集成化、大型化的发展趋势上来看，船舶上特别是大型船舶上搭载的电力电子器件会越来越多^[1]。这为船舶带来了更好的性能，也使船舶电力系统面临着更多的问题。

为使船舶电网保持高质量电能，电网在相位、频率、电压幅值等遇到较大变化时需要迅速恢复稳定。而搭载更多电力电子器件后，船舶电网由于谐波问题在相位、频率、电压幅值等方面发生突变时很难迅速恢复稳定。同时船舶电网谐波还会带来其他负面影响包括使船舶运行成本增加，降低电网的电能质量，降低系统运行效率等^[2]。可以说其危害广泛而深远，是一个不能忽略的问题。

目前在电力系统谐波检测问题的研究中，已经取得了很丰富的研究成果。陈倩、等^[3]提出一种应用改进全相位算法与混合卷积窗四谱线插值算法的检测算法。实验结果表明，该算法有着很强的检测能力，整体检测精度较高。李金、等^[4]以瞬时无功功率为理论基础完成了谐波检测，实验验证该算法具备有效性。以上方法在船舶电力系统的应用中存在检测误差大的问题，因此提出一种基于小波包和神经网络的船舶电力系统谐波检测方法。

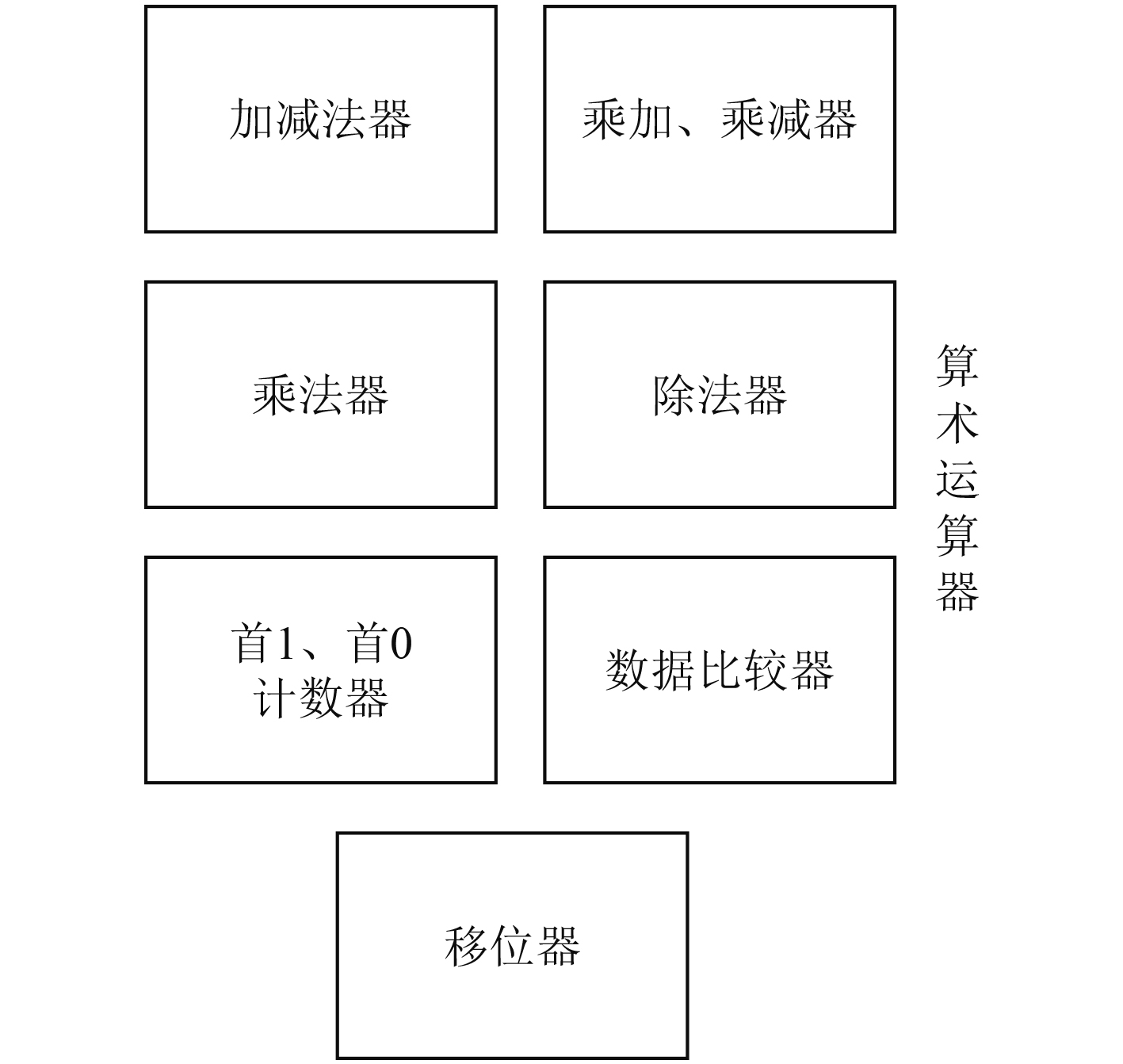
1 船舶电力系统谐波检测方法 1.1 电力系统信号采样

设计船舶电力系统信号采样装置，实施电力系统电流信号与电压信号的采样^[5]。信号采样装置由微处理器、信号采集板、上位机构成。其中微处理器主要用于实现以下功能：与上位机进行通信，信号采样装置的控制以及数据处理。微处理器的设计具体如下：由辅助逻辑模块、逻辑运算器、算术运算器、算术逻辑单元ALU、寄存器堆构成。辅助逻辑模块由译码器和数据选择器构成，其中译码器的作用是写入寄存器堆，选用5位译码器，数据选择器的作用是在多个输入数据中对输出进行选择，选用lpm_mux32x32数据选择器^[6]。逻辑运算器由逻辑异或电路、逻辑或非电路、逻辑或电路、逻辑与电路构成，能够实现各种逻辑运算操作。算术运算器的配置情况如图1所示。在算术逻辑单元ALU的设计中，需要对ALU功能进行编码，在信号采集板上集成电流互感器与电压互感器。电流互感器的设计如下：选择光纤作为电流互感器的传输通道，在高压侧布设有源电子线路。首先设置一个传感器，在其后方设置一个集成电路模数转换器，对检测后的信号实施数字化处理，并设置发光元件对信号实施光电化处理。通过光纤将检测信号直接传输至低电位，并重复数字化与光电化操作。最后通过设置测量装置与继电保护对还原的测得数据进行接收^[7]。电压互感器的设计具体如下：选取的铁芯为矽钢片，根据铁芯的截面积对一次绕组的匝数与二次绕组的匝数进行计算，选择圆形聚脂漆包线进行一次、二次绕组^[8]。并为信号采集板配置寄存器堆，共设置3个专用寄存器与32个三十二位通用寄存器。

1.2 信号高频部分提取

通过小波包算法提取采集的电流信号与电压信号高频部分的有效值。高频部分提取步骤为：

1) 将采样的电流信号为 $ a\left( r \right) $ ，将采样时间 $ R $ 内的电流信号序列用下式表示：

$ a\left( u \right) = \left\{ {a\left( 0 \right),a\left( 1 \right), \ldots ,a\left( {{2^M}-1} \right)} \right\} 。$

(1)

式中， $ M $ 某正整数。

2) 用线性加权的正交小波基函数和表示电流信号，具体如下式：

$ \begin{split} a\left( u \right) = &\sum\limits_{M = 0}^{{2^M}-1} {\sum\limits_{g = 0}^{{2^{H - M}}-1} {f_M^{2p}} } \left( g \right)\vartheta _{M,g}^{2p}\left( u \right) + \\ & \sum\limits_{M = 0}^{{2^M}-1} {\sum\limits_{g = 0}^{{2^{H - M}}-1} {f_M^{2p + 1}} } \left( g \right)\vartheta _{M,g}^{2p + 1}\left( u \right)= \\ & \sum\limits_{g = 0}^{{2^{H - M}}-1} {f_M^0\left( g \right)} {\nu _{M,g}}\left( u \right) +\\ & \sum\limits_{M = 0}^{{2^M}-1} {\sum\limits_{g = 0}^{{2^{H - M}}-1} {f_M^p} } \left( g \right)\vartheta _{M,g}^p\left( u \right)。\end{split} $

(2)

式中： $ f_M^0\left( g \right) $ 为小波尺度函数系数； $ H $ 为某正整数； $ g $ 指某采样时间； $ f_M^{2p + 1}\left( g \right) $ ， $ f_M^{2p}\left( g \right) $ ， $ f_M^p\left( g \right) $ 为小波包变换系数； $ \vartheta _{M,g}^{2p + 1}\left( u \right) $ ， $ \vartheta _{M,g}^{2p}\left( u \right) $ ， $ \vartheta _{M,g}^p\left( u \right) $ 为小波函数系数； $ {\nu _{M,g}}\left( u \right) $ 为小波线性函数。

3) 电压信号的高频部分可以在某一尺度 $ M $ 上用下式表示：

$ \begin{split} \int {{{\left( {a\left( u \right)} \right)}^2}} &{\rm{d}}u = {\int {\left[ \begin{gathered} \sum\limits_{g = 0}^{{2^{H - M}}-1} {f_M^0\left( g \right)} {\nu _{M,g}}\left( u \right) + \\ \sum\limits_{M = 0}^{{2^M}-1} {\sum\limits_{g = 0}^{{2^{H - M}}-1} {f_M^p} } \left( g \right)\vartheta _{M,g}^p\left( u \right) \\ \end{gathered} \right]} ^2}{\rm{d}}u=\\ & \sum\limits_{g = 0}^{{2^{H - M}}-1} {{{\left[ {f_M^0\left( g \right)} \right]}^2}\int {\left[ {{\nu _{M,g}}\left( u \right)} \right]} } {\rm{d}}u +\\ &\sum\limits_{M = 0}^{{2^M}-1} {\sum\limits_{g = 0}^{{2^{H - M}}-1} {{{\left[ {f_M^p\left( g \right)} \right]}^2}\int {{{\left[ {\vartheta _{M,g}^p\left( u \right)} \right]}^2}{\rm{d}}u} } } +\\ &2\sum\limits_{M = 0}^{{2^M}-1} {\sum\limits_{g = 0}^{{2^{H - M}}-1} {f_M^0\left( g \right)f_M^p\left( g \right)\int {{\nu _{M,g}}\left( u \right)\vartheta _{M,g}^p\left( u \right){\rm{d}}u}。} } \end{split} $

(3)

4)用下式表示上式：

$ \int {{{\left( {a\left( u \right)} \right)}^2}} {\rm{d}}u = {\sum\limits_{M = 0}^{{2^M}-1} {\sum\limits_{g = 0}^{{2^{H - M}}-1} {\left[ {f_M^p\left( g \right)} \right]} } ^2} ，$

(4)

则高频部分有效值可以用下式来表示：

$ \begin{split} E =& \sqrt {\frac{1}{R}\int {{{\left( {a\left( u \right)} \right)}^2}} {\rm{d}}u} = \sqrt {\frac{1}{{{2^M}}}{{\sum\limits_{M = 0}^{{2^M}-1} {\left( {\sum\limits_{g = 0}^{{2^{H - M}}-1} {\left[ {a\left( u \right)} \right]} } \right)} }^2}} = \\ & \sqrt {\frac{1}{{{2^M}}}{{\sum\limits_{M = 0}^{{2^M}-1} {\sum\limits_{g = 0}^{{2^{H - M}}-1} {\left[ {f_M^p\left( g \right)} \right]} } }^2}} = \sqrt {\sum\limits_{M = 0}^{{2^M}-1} {{{\left( {Y_M^p} \right)}^2}} } 。\end{split} $

(5)

式中， $ Y_M^p $ 指尺度 $ M $ 上的高频部分有效值。

通过同样的步骤对电压信号高频部分有效值进行提取。在电流信号、电压信号高频部分有效值中对谐波进行检测。

1.3 谐波检测

基于神经网络思想设计Elman神经网络谐波检测器，实现船舶电力系统谐波检测。在检测器中通过主成分分析方法实施Elman神经网络的输出优化，并改进激励函数，降低谐波频率、相位、幅值的测量误差。Elman神经网络谐波检测器由4层结构构成，分别为关联层、输出层、隐含层、输入层。其中输入层负责传输电流信号、电压信号高频部分有效值；隐含层负责对数据进行处理；输出层负责实施处理数据的线性加权，获取谐波信号的频率、相位、幅值；关联层负责对输出层获取结果与理论谐波信号的频率、相位、幅值的误差进行计算。当误差不满足要求，将输出层获取结果作为权重对神经网络的调节进行重新参与。其中隐含层的输出可以用下式表示：

$ {F_Q}\left( u \right) = Z\left[ {\sum\limits_{b = 1}^S {{O_{1cb}}\left( u \right){Q_c}\left( u \right) + \sum\limits_{l = 1}^K {{O_{2cb}}\left( u \right){F_{en}}\left( u \right)} } } \right]。$

(6)

式中： $ {F_{en}}\left( u \right) $ 为 $ u $ 时刻关联层到隐含层实施的谐波信号反馈输出； $ Z\left( \cdot \right) $ 为隐含层的输出函数； $ S $ 为电流信号高频部分有效值信号个数； $ b $ 为某电流信号高频部分有效值信号； $ {O_{1cb}}\left( u \right) $ 为输入层面向隐含层的权值矩阵； $ {Q_c}\left( u \right) $ 为信号高频部分的权值函数； $ K $ 为电压信号高频部分有效值信号个数； $ l $ 为电流信号高频部分有效值信号个数； $ {O_{2cb}}\left( u \right) $ 为关联层面向隐含层的权值矩阵。

其中 $ {F_{en}}\left( u \right) $ 的计算公式具体如下：

$ {F_{en}}\left( u \right){\text{ = }}{F_e}\left( {u - 1} \right) 。$

(7)

式中： $ {F_e}\left( {u - 1} \right) $ 为 $ u-1 $ 时刻关联层到隐含层的非线性状态差值。

在输出层中，通过主成分分析方法实施谐波的频率、相位、幅值的特征提取，用于对Elman神经网络的输出进行优化。在激励函数的改进中，对Sigmoid激励函数进行修正，修正结果如下：

$ \gamma \left(\eta \text{，}\iota \text{，}\kappa \text{，}\lambda \text{，}\mu \right)\text=\iota \text+\frac{\lambda }{1\text+{e}^{-\mu \left(\eta +\kappa \right)}} 。$

(8)

式中： $ \eta $ 为Sigmoid激励函数的自变量； $ \iota $ 为常数项； $ \kappa $ 为可调偏置参数； $ \lambda $ 为扩大函数增益； $ \mu $ 为自变量因子； $ \gamma $ 为Sigmoid激励函数。

2 仿真测试 2.1 测试数据

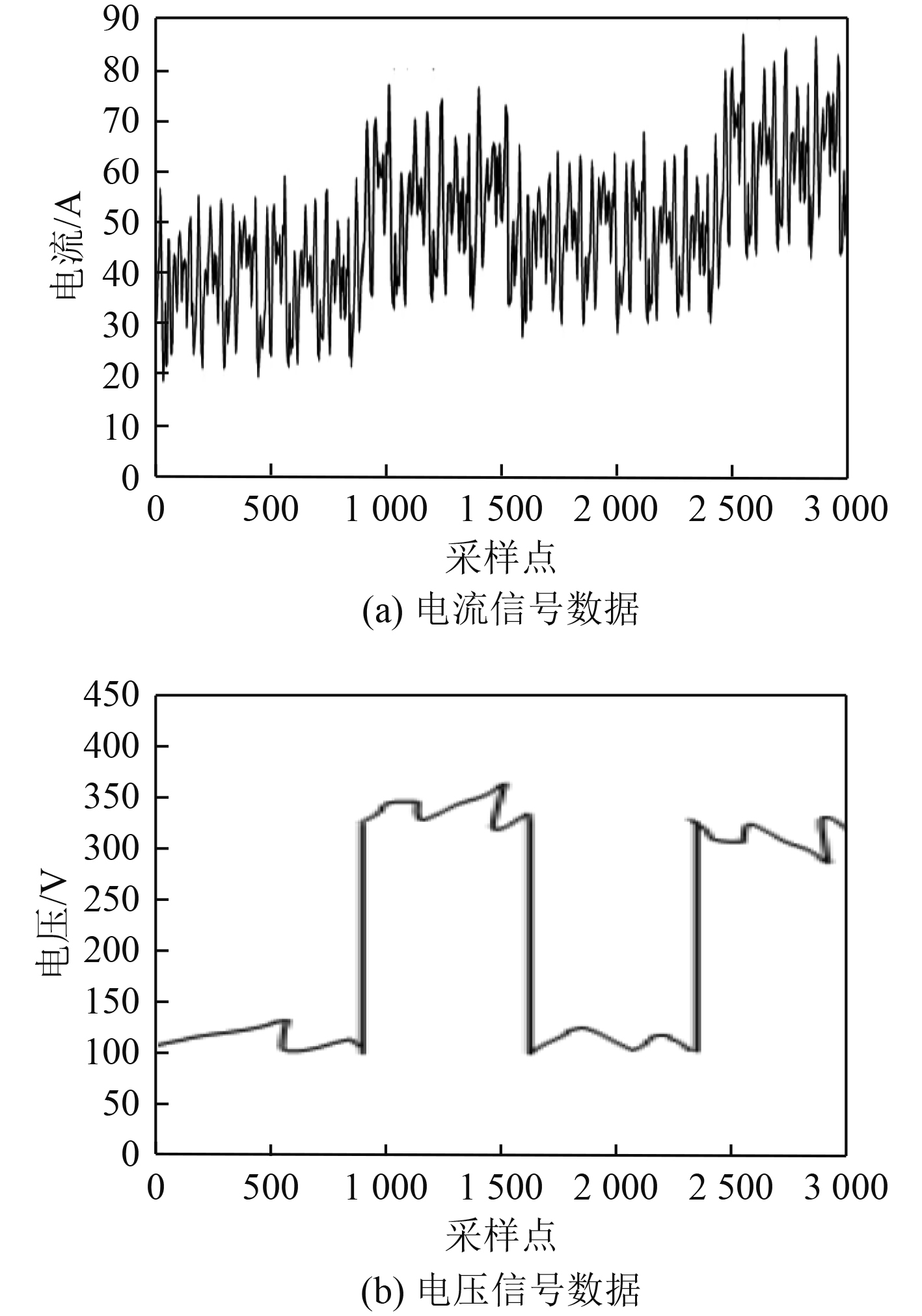
通过实验测试小波包和神经网络的船舶电力系统谐波检测方法的表现性能，验证该方法的有效性。在实验中，首先通过设计的船舶电力系统信号采样装置对某船舶的电力系统信号实施采样。将采样频率设置为3500 Hz，共对3000个点的数据进行采样。采样的船舶电力系统电流信号与电压信号数据具体如图2所示。通过小波包算法提取采样信号的高频部分。在提取中，将基波频率设为50 Hz。基于提取的高频部分，通过设计的Elman神经网络谐波检测器实施实验船舶电力系统的谐波检测。在检测中，首先需要通过一部分实验数据对检测器进行训练，接着利用检测器进行检测。基于检测结果对设计方法的性能进行测试。在测试中，将文献[3-4]中提出的算法作为对比方法，分别将其命名为方法1和方法2，共同进行测试，并对测试结果进行对比分析，观察设计方法的性能表现是否有优势。

2.2 结果分析 2.2.1 检测误差测试

首先对设计方法与方法1和方法2的谐波频率、相位、幅值的检测误差进行测试，测试结果如表1所示。根据表1的误差测试结果，设计方法的平均谐波频率检测误差的区间均值为0.16Hz，平均谐波相位检测误差的区间均值为0.20°，平均谐波幅值检测误差的区间均值为0.12V；方法1的3种区间均值分别为0.24Hz，0.27°，0.19V；方法2的3种区间均值分别为0.25Hz，0.28°，0.19V。整体来说，设计方法的3种区间均值都更低，说明设计方法的检测误差较低。

2.2.2 基波突变点延时测试

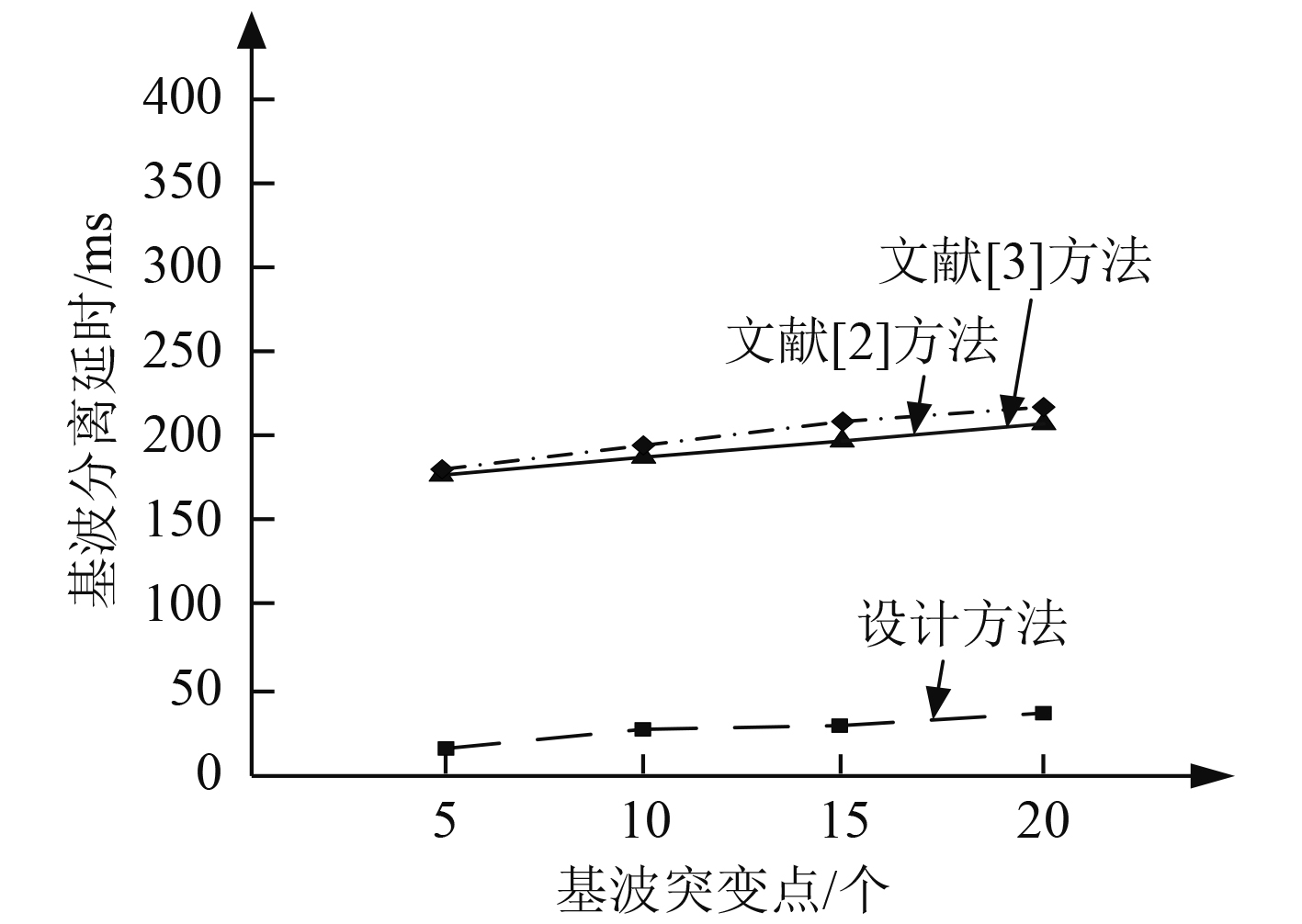
接着测试3种方法在基波突变点发生延时的情况，测试结果如图3所示。结果表明，设计方法几乎实现了基波分离延时问题的克服，整体延时很低，而方法1和方法2的基波分离延时比较相近，均大于150 ms，说明设计方法的检测效率较高。

3 结　语

船舶电力系统谐波问题与电网谐波问题一样，一直是电力系统中需要解决的难题。通过对其进行检测，能够针对性地解决此问题，设计小波包和神经网络的船舶电力系统谐波检测方法，实现了低误差的谐波检测，对于船舶电力系统的稳定运行有重要意义。