2. 上海交通大学 船舶海洋与建筑工程学院,上海 200240
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China
近年来,无人船(autonomous surface vessel, ASV)研究成为海洋工程领域的一个重要课题,许多学者开展了相关研究以提高无人船的自主化程度[1-2]。与单船系统相比,多船系统的协同控制可以实现更优的任务性能和时空特性[3-4]。基于船舶之间的通信,海上作业的可实现性、安全性、效率和稳健性得以显著提升。信息传输可以帮助船舶之间进行协商合作,以采取有效行动并避免碰撞[5]。此外,基于协同控制可以探索更多潜在的应用场景,如大型物体捕获和运输[6]、临时浮式结构物组建[7]、特定军事用途[8]等。
多船协同控制系统对于控制策略提出了更高的要求,控制架构的选择对于海上作业能否实现以及控制效果具有显著影响。传统的集中式控制架构基于全局控制器获取系统的所有可用信息并进行相关计算,目标函数在全局范围内进行优化,具有更高的稳定性,但是对于拓展为大规模问题具有一定劣势,计算成本会随之显著增加。而分布式架构通过独立的控制器对解耦的、局部的最优化子问题进行求解,控制器之间建立通信并进行信息传输迭代,虽然在设计层面更为复杂,但是其计算性能优越,同时具有更高的容错性能。
另一方面,为了提高协同控制系统的性能,学者们也一直致力于研究先进的控制算法并进行数值模拟或试验验证,如非线性反步法[9]、动态面控制方法[10]、神经网络与鲁棒控制相结合的方法[11]、基于深度强化学习的方法[12]等,都展现出了较高的控制性能。其中,模型预测控制(model predictive control, MPC)算法因其优越的约束处理能力和控制性能脱颖而出[13]。MPC算法通过预测模型对未来时刻的输出进行预测,进而通过最小化目标函数来计算控制时域内的最优控制序列,将求得的控制序列的第一个元素作为控制量作用于系统并向前推进一个时刻,重复上述过程以进行滚动优化。Liu等[14-15]分别设计了用于轨迹跟踪和路径跟踪的非线性自适应MPC控制器,引入了系统输入约束、输入增量约束和输出约束,提高了跟踪精度。此外,分布式模型预测控制(distributed MPC, DMPC)在现有的研究中也被广泛应用,因为它可以提高海洋结构物的自主化程度,更能满足协调控制系统的实际需求[16]。Droge等[17]在DMPC框架下开发了一种虚拟领导者(Virtual-Leader)编队控制算法,允许智能体协同地适应领导者的运动和编队参数来通过障碍物区域。Wei等[18]提出了一种非线性DMPC方法,应用于约束条件下的异构无人船编队航行,并将最优化问题的耦合约束解耦为局部约束,通过仿真研究验证了该方法的有效性。
本文基于MPC算法对多无人船系统的协同控制策略进行研究,设计分布式控制架构以实现多无人船系统的协同路径跟踪和编队控制,并通过数值模拟进行综合控制性能的验证和对比分析。
1 多无人船系统模型 1.1 无人船动力学模型对于配备有多个全回转推力器的动力定位无人船,其三自由度(纵荡、横荡和首摇)动力学模型可以描述为:
| $ \left\{ {\begin{aligned} &{{{\dot \eta }_i}(t) = R({\psi _i}(t)){\nu _i}(t)},\\ &{{M_i}{{\dot \nu }_i}(t) + {C_i}({\nu _i}(t)){\nu _i}(t) + {D_i}{\nu _i}(t) = {\tau _{i\_ctrl}}(t) + {\tau _{i\_env}}(t)} 。\end{aligned}} \right. $ | (1) |
式中:下标i表示第i艘船舶。
| $ R({\psi _i}(t)) = \left[ {\begin{array}{*{20}{c}} {\cos ({\psi _i}(t))}&{ - \sin ({\psi _i}(t))}&0 \\ {\sin ({\psi _i}(t))}&{\cos ({\psi _i}(t))}&0 \\ 0&0&1 \end{array}} \right] 。$ | (2) |
式中:
在传统的控制策略中,运动控制与推力分配通常是分离的,即上层运动控制算法首先计算出船舶定位或路径跟踪所需要的广义力(矩),进而通过推力分配算法确定各推力器的推力大小和方向。这种模式使得软件架构更易维护,但是此时上层运动控制算法通常只考虑控制精度,并未考虑底层推力器限制,如推力饱和、推力方向的重置时间、能量消耗等,因此求得的广义力(矩)必然不是最优解。为了解决这一问题,本文基于MPC算法,将运动控制与推力分配进行一体化集成,实现对推力器的直接控制,以及约束处理一致化、规划提前化、调参简易化。
首先需要将运动控制算法的输入从广义力(矩)转换
| $\begin{split} {U_i}(t) =& {[f_i^{\rm{T}}(t),\alpha _i^{\rm{T}}(t)]^{\rm{T}}} = [{f_{1i}}(t),{f_{2i}}(t), \cdots ,\\ &{f_{ni}}(t),{\alpha _{1i}}(t),{\alpha _{{2_i}}}(t), \cdots ,{\alpha _{ni}}(t)]^{\rm{T}} ,\end{split}$ | (3) |
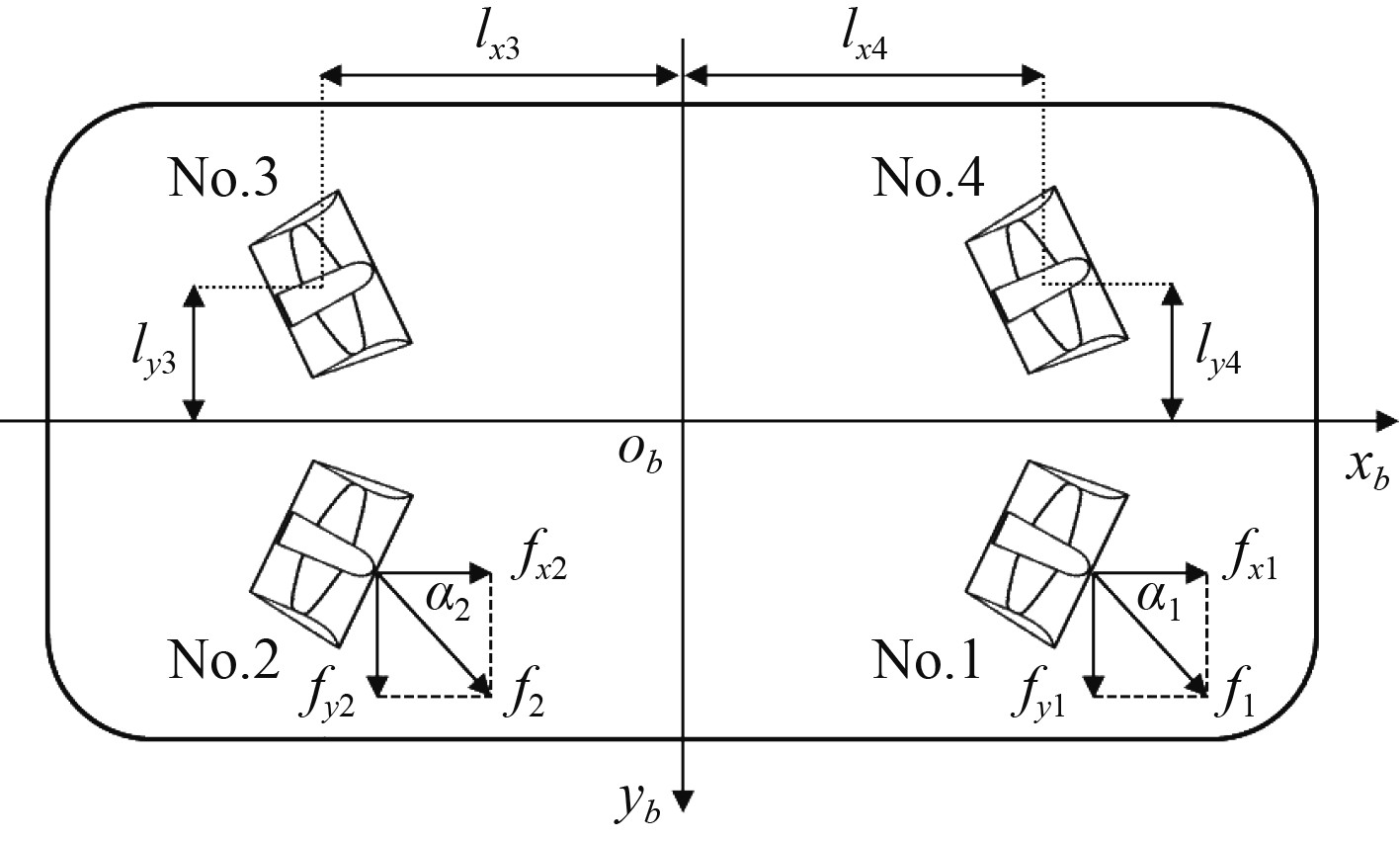
式中,n表示装备在各船舶上的推力器数量。本文所模拟的无人船配备有4个全回转推力器,推力器布置如图1所示。
|
图 1 无人船推力器布置 Fig. 1 Thruster configuration of the ASV |
进一步地,MPC集成式控制分配策略下的推力分配仅需实现广义力(矩)到推力器推力的转变,可以通过简单的伪逆算法实现:
| $ {\tau _{i\_ctrl}}(t) = {T_{i\_conf}}({\alpha _i}(t)){U_i}(t),$ | (4) |
式中:
| $ T_{_{i\_conf}}^n({\alpha _{ni}}(t)) = \left[ {\begin{array}{*{20}{c}} {\cos ({\alpha _{ni}}(t))} \\ {\sin ({\alpha _{ni}}(t))} \\ {{l_{xni}}\sin ({\alpha _{ni}}(t)) - {l_{yni}}\cos ({\alpha _{ni}}(t))} \end{array}} \right] ,$ | (5) |
其中,
综上,可以将船舶的动力学模型表示成连续的状态空间方程的形式:
| $ \left\{ {\begin{array}{*{20}{l}} {X_i}(t) = {f_i}(Xi(t),{U_i}(t),{\tau _{i\_env}}(t)) = \\ \qquad\quad {A_i}(t){X_i}(t) + {B_i}(t){U_i}(t) + {G_i}{\tau _{i\_env}}(t),\\ {{Y_i}(t) = {g_i}({X_i}(t),{V_i}(t)) = {C_i}{X_i}(t) + {V_i}(t)} 。\end{array}} \right. $ | (6) |
式中,
| $ {A_i}(t) = \left[ {\begin{array}{*{20}{c}} {{0^{3 \times 3}}}&{R({\psi _i}(t))} \\ {{0^{3 \times 3}}}&{{M_i}^{ - 1}( - {C_i}({v_i}(t)) + {D_i})} \end{array}} \right],$ | (7) |
| $ {B_i}(t) = \left[ {\begin{array}{*{20}{c}} {{0^{3 \times 3}}} \\ {{M_i}^{ - 1}} \end{array}} \right]{T_{i\_conf}}(t){T_{i\_efficiency}}(t),$ | (8) |
| $ {G_i} = \left[ {\begin{array}{*{20}{c}} {{0^{3 \times 3}}} \\ {{M_i}^{ - 1}} \end{array}} \right],$ | (9) |
| $ {C_i} = [{\begin{array}{*{20}{c}} {{I^{3 \times 3}}}&0 \end{array}^{3 \times 3}}]。$ | (10) |
在建立多无人船系统的分布式控制分配模型之前,首先需要建立船舶之间的通信图以及编队控制方法。
对于所模拟的多无人船系统,建立如图2所示的通信图,包含1艘领航者(Leader)和2艘跟随者(Follower),领航者只向其相邻的跟随者发送信息,跟随者接收并发送信息给其相邻船舶。

|
图 2 无人船通信图 Fig. 2 Communication graph of ASVs |
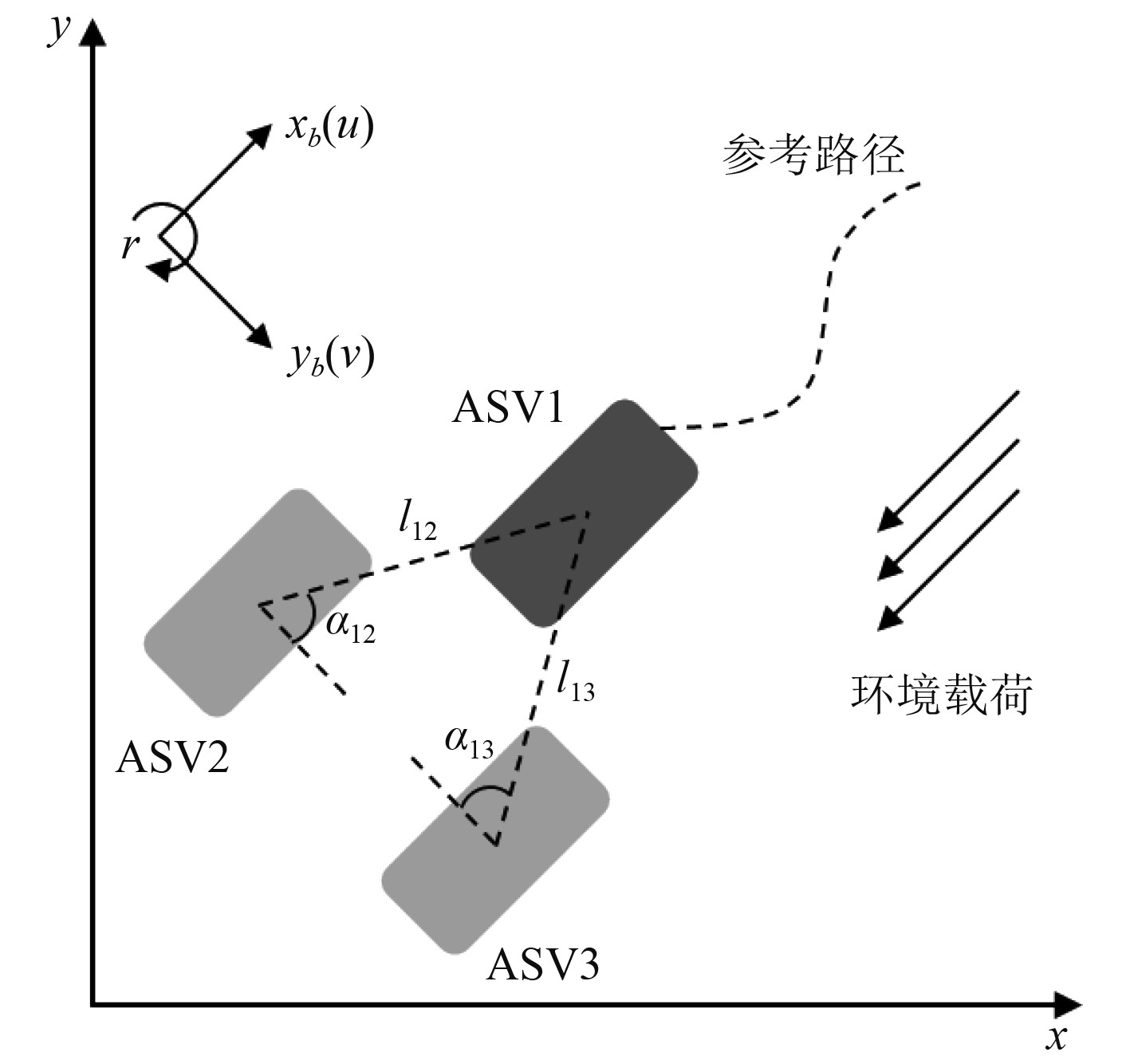
采用领航者-跟随者(leader-follower)的方法来实现船舶的编队控制,具体的协同控制任务场景如图3所示。lij和αij分别表示无人船i与无人船j之间的编队距离和编队角度。通过设置不同的l和α可以改变编队形式或者拓展为包含更多船舶的大规模问题。
|
图 3 无人船协同控制任务场景 Fig. 3 Cooperative operation scenario of ASVs |
建立如图4所示的基于MPC理论的分布式集成式控制分配架构(distributed-integrated MPC, DI-MPC)。控制变量Ui|j表示无人船i的控制器计算得到无人船j的控制序列。每个DI-MPC控制器都是基于预测模型、限制条件以及各自的目标函数分别设计的。根据路径跟踪和编队控制要求,各控制器计算得到相应的控制序列Ui|j并传送到实时迭代框架(iterative negotiation framework)来实现船舶之间的一致性。基于设定的阈值条件(见式(11)),经过有限次的迭代后,各控制器将计算得到的最优控制序列Ui|j*作用于船舶来执行相应指令,并输出船舶的位置和首向角Yi。进一步地,基于卡尔曼滤波的状态观测器依据此进行最优状态估计,将

|
图 4 DI-MPC协同控制分配架构 Fig. 4 DI-MPC structure for cooperative operation |
| $ \left\{ {\begin{array}{*{20}{c}} {{{\left\| {{U_{i|i}}(k|k) - {U_{i|nb}}(k|k)} \right\|}_2} \leqslant {U_{tol}}} ,\\ {{U_{i|i}} \ne {U_{i|j}},i \ne j} 。\end{array}} \right. $ | (11) |
式中,下标nb和tol分别为neighbor和tolerance的缩写。
2.2 线性预测模型MPC通过预测模型来预测系统行为并进行优化,从而获取每一时间步最优的控制序列。因此,预测模型的构建对于整个控制分配过程非常重要,其准确性和适用性很大程度上决定了系统综合性能。如果直接采用非线性模型,即式(6),那么MPC的预测和优化过程将会非常耗时。Zheng等[19]对采用非线性MPC和线性MPC的ASV控制器进行了轨迹跟踪性能和计算时间的比较。结果表明,非线性MPC的计算复杂度远高于线性MPC,尤其是在较长的预测时域下。此外,采用实时迭代框架应用于分布式协同控制器的设计,以实现船舶之间的一致性,每一时间步计算耗时的增加将会使得整个系统运行时间大大增加。因此,有必要建立MPC线性预测模型:
| $ \left\{ {\begin{array}{*{20}{l}} {X_i}(k + 1|k) = {A_i}^J(k|k){X_i}(k|k) + {B_i}^J(k|k){U_i}(k|k) +\\ \qquad\qquad\quad {G_i}^J(k|k){\tau _{i\_env}}(k|k),\\ {{Y_i}(k|k) = {C_i}^J(k|k){C_i}^J(k|k) + {V_i}(k|k)} 。\end{array}} \right. $ | (12) |
式中,
| $ {A_i}^J(k|k) = {\left. {\frac{{\partial {f_i}}}{{\partial {X_i}}}} \right|_{{X_i}^e(k|k)\,,{U_i}^e(k|k),{\tau _{i\_env}}^e(k|k)}},$ | (13) |
| $ {B_i}^J(k|k) = {\left. {\frac{{\partial {f_i}}}{{\partial {U_i}}}} \right|_{{X_i}^e(k|k)\,,{U_i}^e(k|k),{\tau _{i\_env}}^e(k|k)}},$ | (14) |
| $ {G_i}^J(k|k) = {\left. {\frac{{\partial {f_i}}}{{\partial {\tau _{i\_env}}}}} \right|_{{X_i}^e(k|k)\,,{U_i}^e(k|k),{\tau _{i\_env}}^e(k|k)}} = {G_i},$ | (15) |
| $ {C_i}^J(k|k) = {\left. {\frac{{\partial {g_i}}}{{\partial {X_i}}}} \right|_{{X_i}^e(k|k)\,,{U_i}^e(k|k),{\tau _{i\_env}}^e(k|k)}} = {C_i}。$ | (16) |
在分布式控制架构下,由于目标函数、限制条件等的不同,领航者和跟随者的控制器需分别设计。在所模拟的协同控制任务中,领航者需跟踪一条参考路径,其目标函数可以设计为:
| $ \begin{split} & \min {J_1}({U_1}(k)) = \sum\limits_{j = 1}^{{N_p} - 1} {({Q_{err}}\left\| {{{\hat Y}_1}(k + j|k) - r(k + j)} \right\|_2^2)} + \\ &\qquad {q_{ter}}{Q_{err}}\left\| {{{\hat Y}_1}(k + {N_p}|k) - r(k + {N_p})} \right\|_2^2 + \\ & \qquad \sum\limits_{j = 0}^{{N_c} - 1} {({Q_{in}}\left\| {{U_1}(k + j|k)} \right\|_2^2 + {Q_{din}}\left\| {\Delta {U_1}(k + j|k)} \right\|_2^2)}。\end{split} $ | (17) |
式中,Np和Nc分别为预测时域和控制时域。r(k+j)表示第k+j步的参考路径点信息,包括位置和首向角。
跟随者需要与相邻船舶保持编队,其目标函数可以设计为:
| $ \begin{split} \min {J_i}&({U_i}(k)) = \sum\limits_{j = 1}^{{N_p} - 1} ({Q_{fm}}\left\| ({{\hat Y}_i}(k + j|k) - {Y_{nb}}(k + j|k)) -\right.\\ &\left.(Y_i^d(k + j|k) - Y_{nb}^d(k + j|k)) \right\|_2^2) + \\ & {q_{ter}}{Q_{fm}}\left\| ({{\hat Y}_i}(k + {N_p}|k) - {Y_{nb}}(k + {N_p}|k)) -\right.\\ & \left.(Y_i^d(k + {N_p}|k) - Y_{nb}^d(k + {N_p}|k)) \right\|_2^2 + \\ & \sum\limits_{j = 0}^{{N_c} - 1} {({Q_{in}}\left\| {{U_i}(k + j|k)} \right\|_2^2 + {Q_{din}}\left\| {\Delta {U_i}(k + j|k)} \right\|_2^2)}。\\[-22pt] \end{split} $ | (18) |
式中:
综上,考虑推力器的物理限制和协同控制任务场景的安全距离限制,各无人船控制器的最优化模型可建立如下:
| $ \begin{split}&\mathrm{min}{J}_{i}({U}_{i}(k)),\\ &{\rm{s.b.}}\forall i\in [1,2,3],\forall j\in Np,\\ &{X}_{i}(k|k)={X}_{i}(k),\\ &{Y}_{i}(k|k)={Y}_{i}(k),\\ &{U}_{i\_\mathrm{min}}\leqslant {U}_{i}(k+j|k)\leqslant {U}_{i\_\mathrm{max}},\\ &\Delta {U}_{i\_\mathrm{min}}\leqslant \Delta {U}_{i}(k+j|k)\leqslant \Delta {U}_{i\_\mathrm{max}},\\ &{d}_{i|nb}(k+j|k)\geqslant {d}_{i\_safe}。\end{split} $ | (19) |
基于所提出的DI-MPC控制分配策略,对多无人船系统进行路径跟踪和编队控制的时域模拟,并与相对应的集中式控制分配策略(centralized-integrated MPC, CI-MPC)进行综合控制性能的对比分析。无人船模型参数以及数值模拟参数列于表1。
|
|
表 1 数值模拟参数设置 Tab.1 Parameter setting |
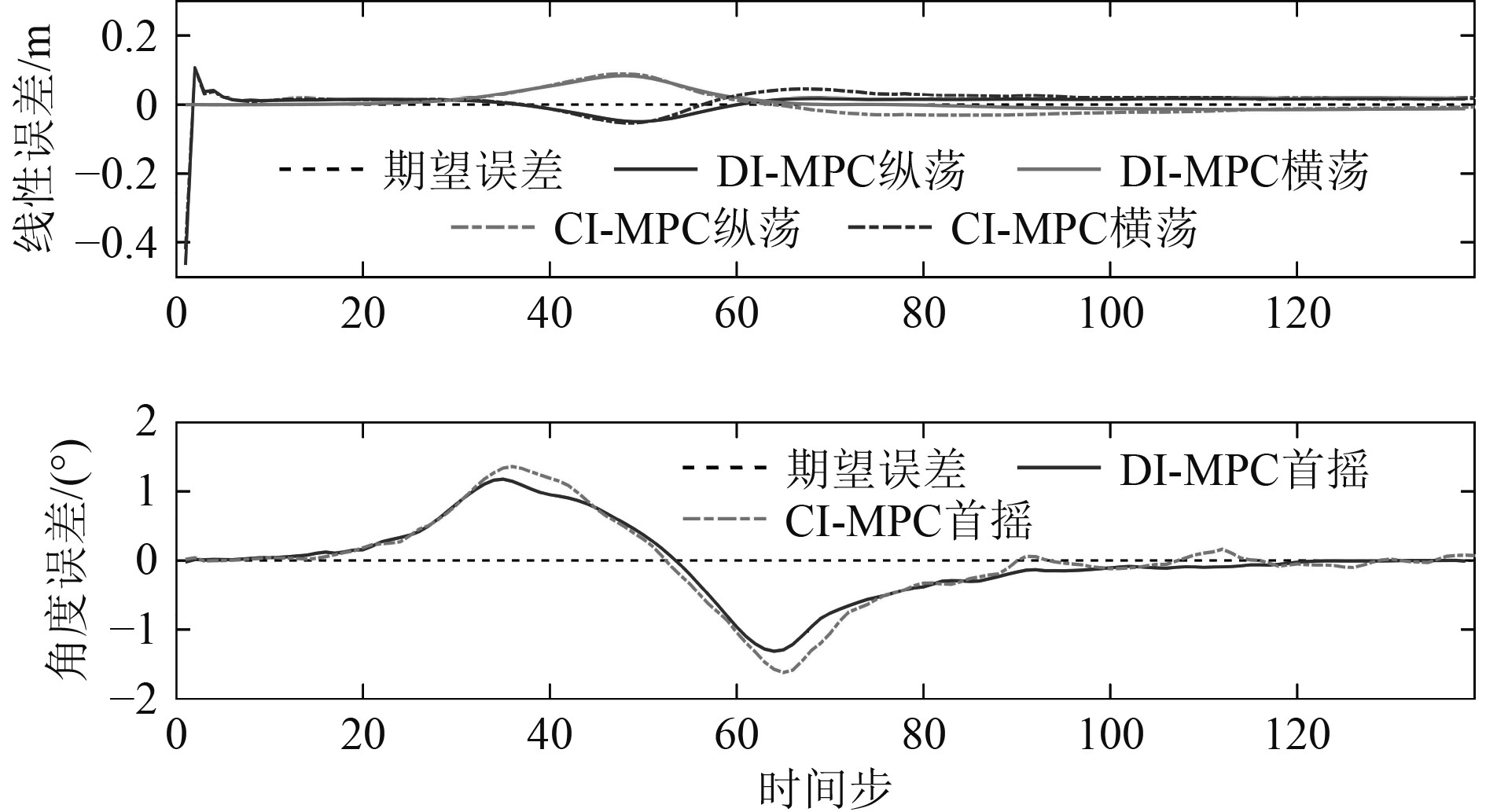
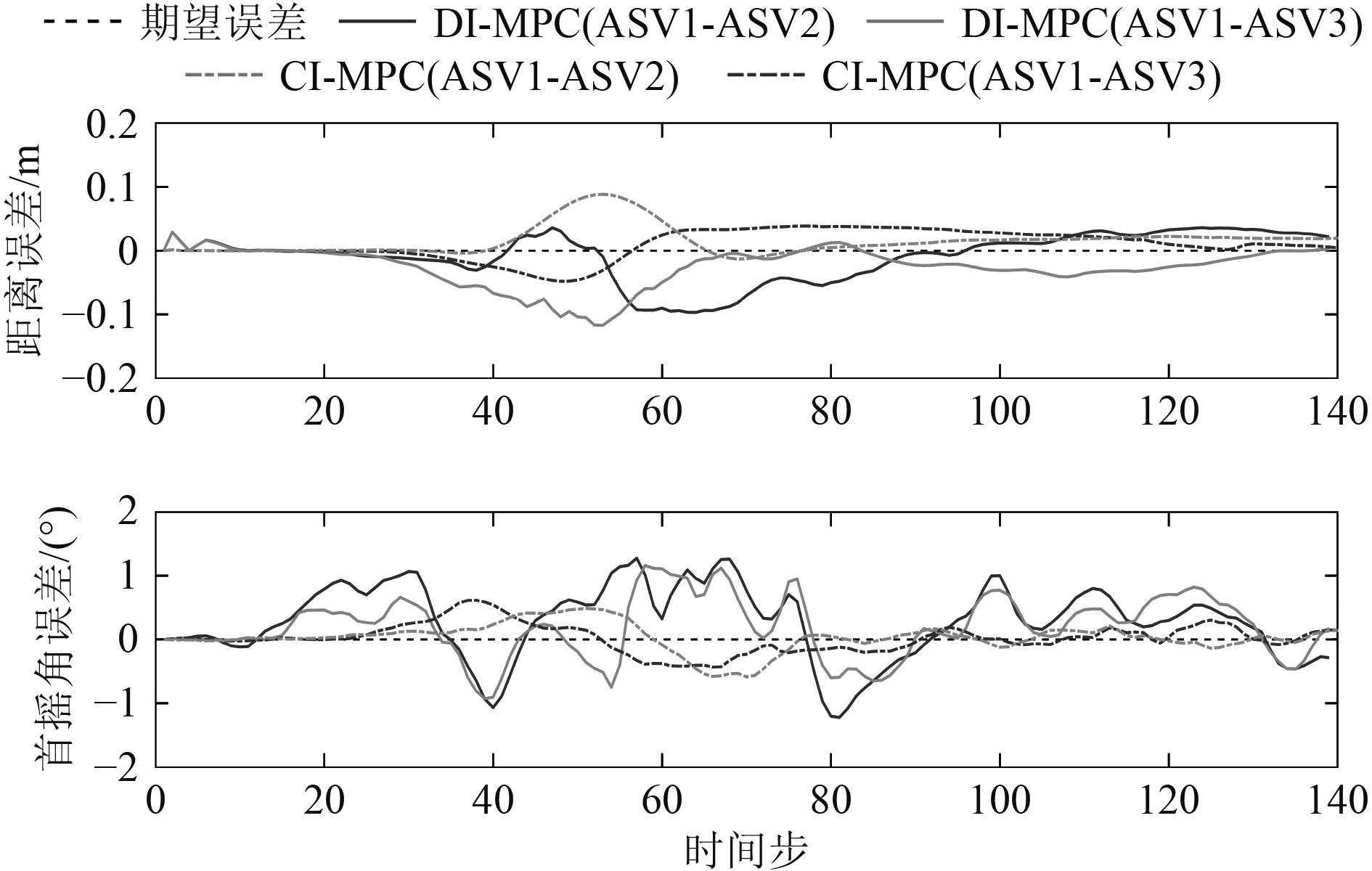
基于DI-MPC与CI-MPC的无人船路径跟踪与编队控制结果如图5所示。2种控制分配策略都能实现领航者的路径跟踪和跟随者的协同编队任务,且控制精度较高。从领航者的路径跟踪误差来看(见图6),2种算法下的误差结果较为接近。在系统稳定后,纵荡、横荡以及首摇的最大误差分别为[0.11 m, 0.08 m, 1.31°]和[0.10 m, 0.09 m, 1.62°],标准差分别为[0.04 m, 0.03 m, 0.52°]和[0.04 m, 0.03 m, 0.60°]。在曲线段,DI-MPC的控制效果更优,且使得无人船在后续的直线段能保持更平稳的运动状态。其原因可能在于分布式控制架构下,领航者的控制器求解的最优化问题相比集中式控制器的维度更小,更易求解。从跟随者的编队误差来看(见图7),CI-MPC的控制效果明显优于DI-MPC,有限的信息传输导致了分布式控制的抖振。2种算法下编队距离和编队角度的最大误差分别为[0.11 m, 1.27°]和[0.09 m, 0.61°],标准差分别为[0.04 m, 0.56°]和[0.02 m, 0.2°]。

|
图 5 基于DI-MPC与CI-MPC的无人船路径跟踪与编队控制结果 Fig. 5 Path following and formation control results of ASVs under DI-MPC and CI-MPC |
|
图 6 基于DI-MPC 与CI-MPC 的无人船路径跟踪误差 Fig. 6 Path following errors of ASV under DI-MPC and CI-MPC |
|
图 7 基于DI-MPC 与CI-MPC 的无人船编队误差 Fig. 7 Formation errors of ASVs under DI-MPC and CI-MPC |
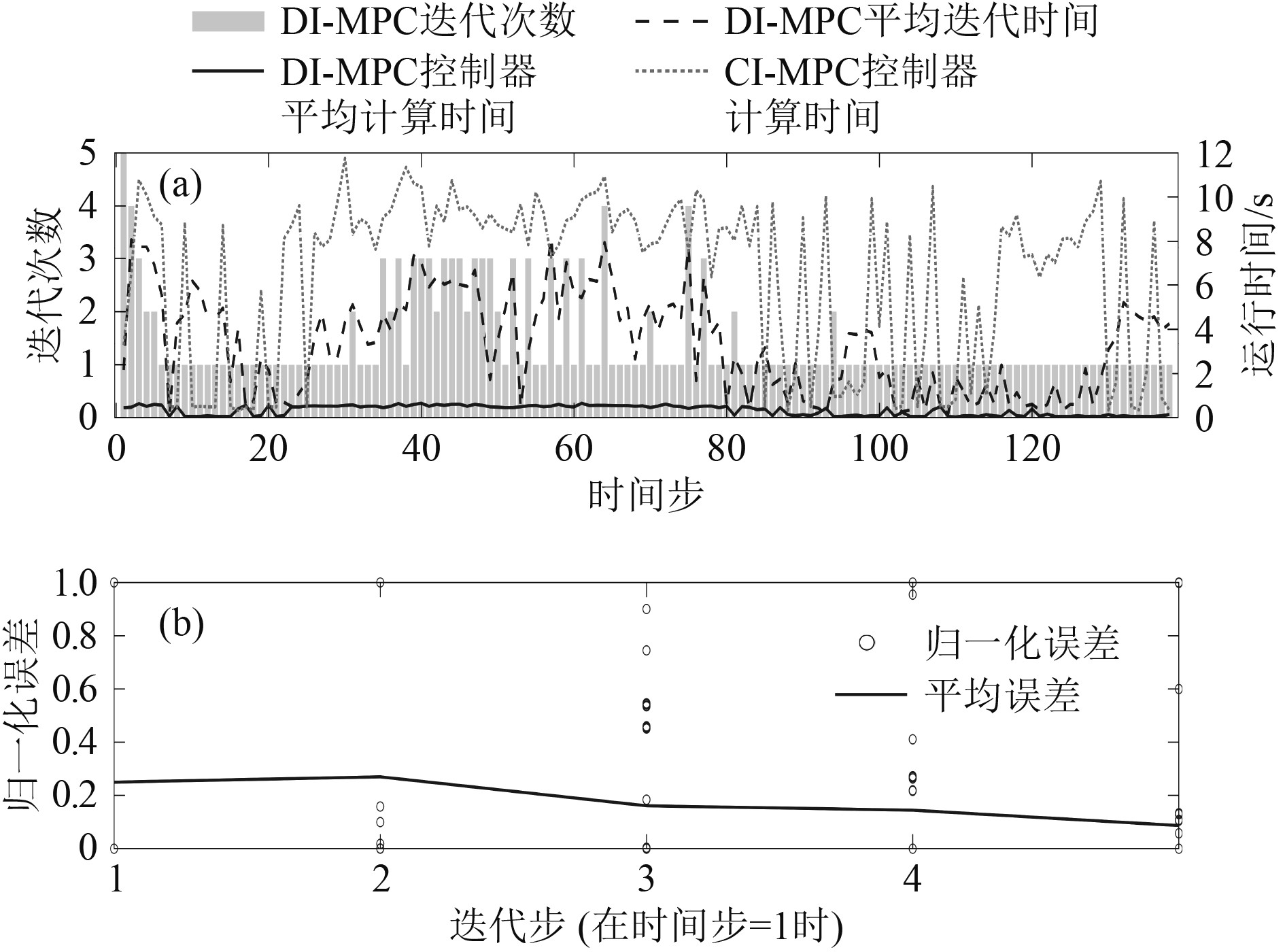
图8(a)对比了DI-MPC与CI-MPC策略在路径跟踪与编队控制任务下的计算性能。由于分布式控制器在实际工作中可以并行运算,因此分析单个DI-MPC控制器在每一时间步的平均计算耗时,其最大值为0.66s。而不同DI-MPC控制器之间达到一致所需的迭代次数小于5次,大部分情况下仅需迭代1次,可见系统较为稳定,收敛速度较快。从图8(b)也可以看出,在实时迭代框架下,控制变量之间的误差逐步减小,最终能够满足设定的阈值。迭代时间与迭代步数基本呈现出一致的变化趋势,最大迭代时间为8.15s。因此,可以粗略认为单个DI-MPC控制器的总计算耗时为8.81s。对于CI-MPC控制器,其在曲线段路径有明显的计算耗时增加,单步最大计算耗时为11.75s。换言之,分布式控制器节约了约25.02%的计算成本,有利于协同控制问题拓展为更大规模的任务场景,其计算时间成本的增加主要在于相邻船舶的控制器之间的迭代,而不在于单个控制器的求解。这种耗时增加取决于通信图的复杂程度,通常比较少。反观集中式控制架构,由于船舶数量(变量维数)增加导致的计算耗时增加相对明显。
|
图 8 DI-MPC与CI-MPC的计算性能 Fig. 8 Computational performance of DI-MPC and CI-MPC |
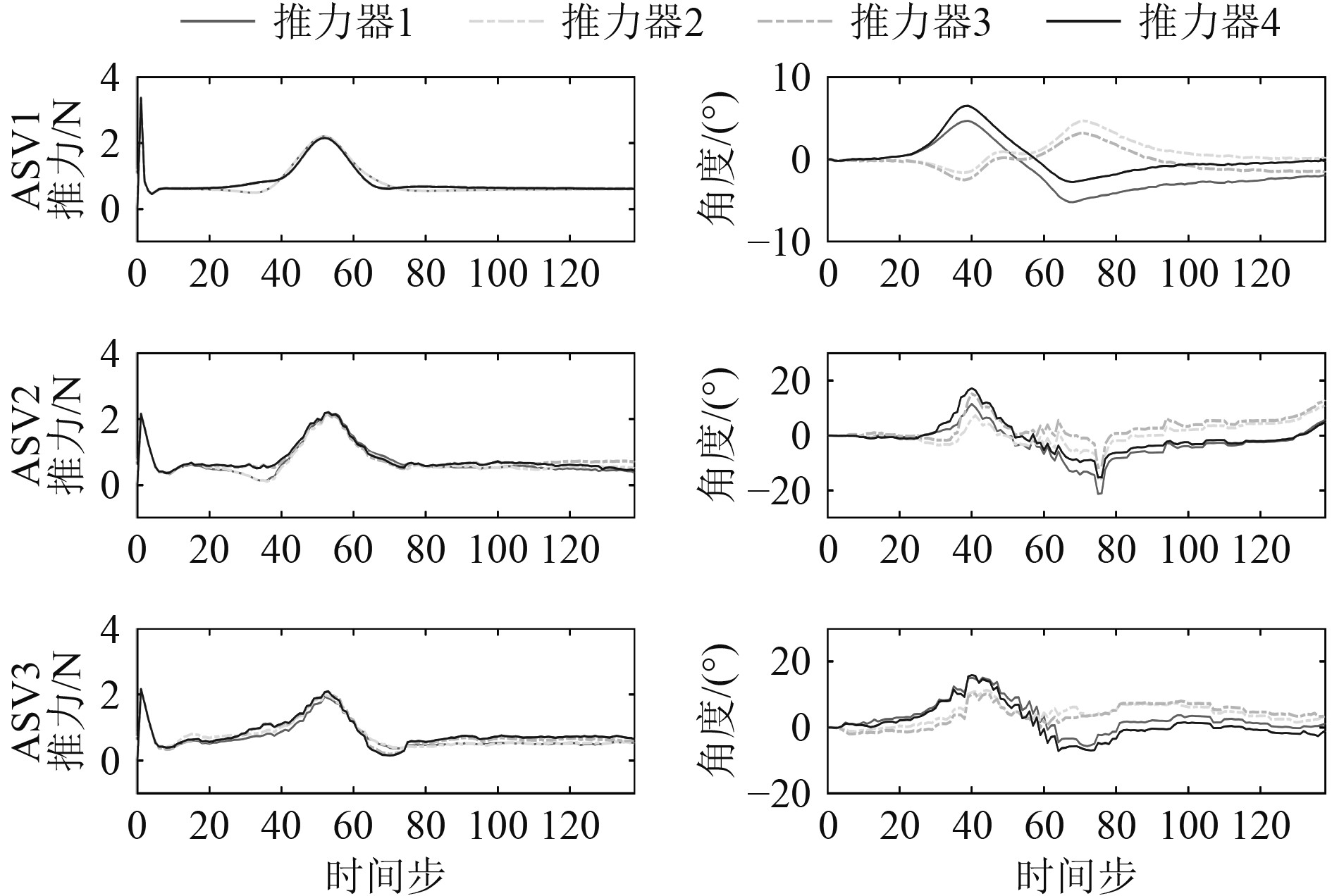
2种策略下各无人船的推力器推力、角度及其变化情况如图9-图12所示。从图9和图10可以看出,2种策略下领航者的推力器运行情况较为接近,前方推力器(1号和4号)与后方推力器(2号和3号)从曲线段开始呈现出相反的角度变化趋势,推力变化趋势则基本相同。对于跟随者而言,2种策略下各推力器的推力变化趋势基本一致。在DI-MPC策略下,其前方推力器与后方推力器的变化趋势仍基本相同,而在CIMPC策略下则出现相反的变化趋势。这也体现了2种控制策略的不同特性,集中式控制策略下由于仅使用一个全局控制器,不同无人船之间的控制结果呈现出更高的一致性,而分布式控制策略下由于各控制器的控制目标、限制条件等的不同使得各无人船的控制结果不尽相同。另一方面,CI-MPC策略下推力器角度的变化范围相对更小,特别是对于跟随者而言,这体现了集中式策略的全局稳定性。
|
图 9 基于DI-MPC的无人船推力器推力与角度 Fig. 9 Thrust and azimuth angle of ASVs under DI-MPC |
|
图 10 基于DI-MPC的无人船推力器推力与角度变化 Fig. 10 Thrust and azimuth angle variation of ASVs under DI-MPC |

|
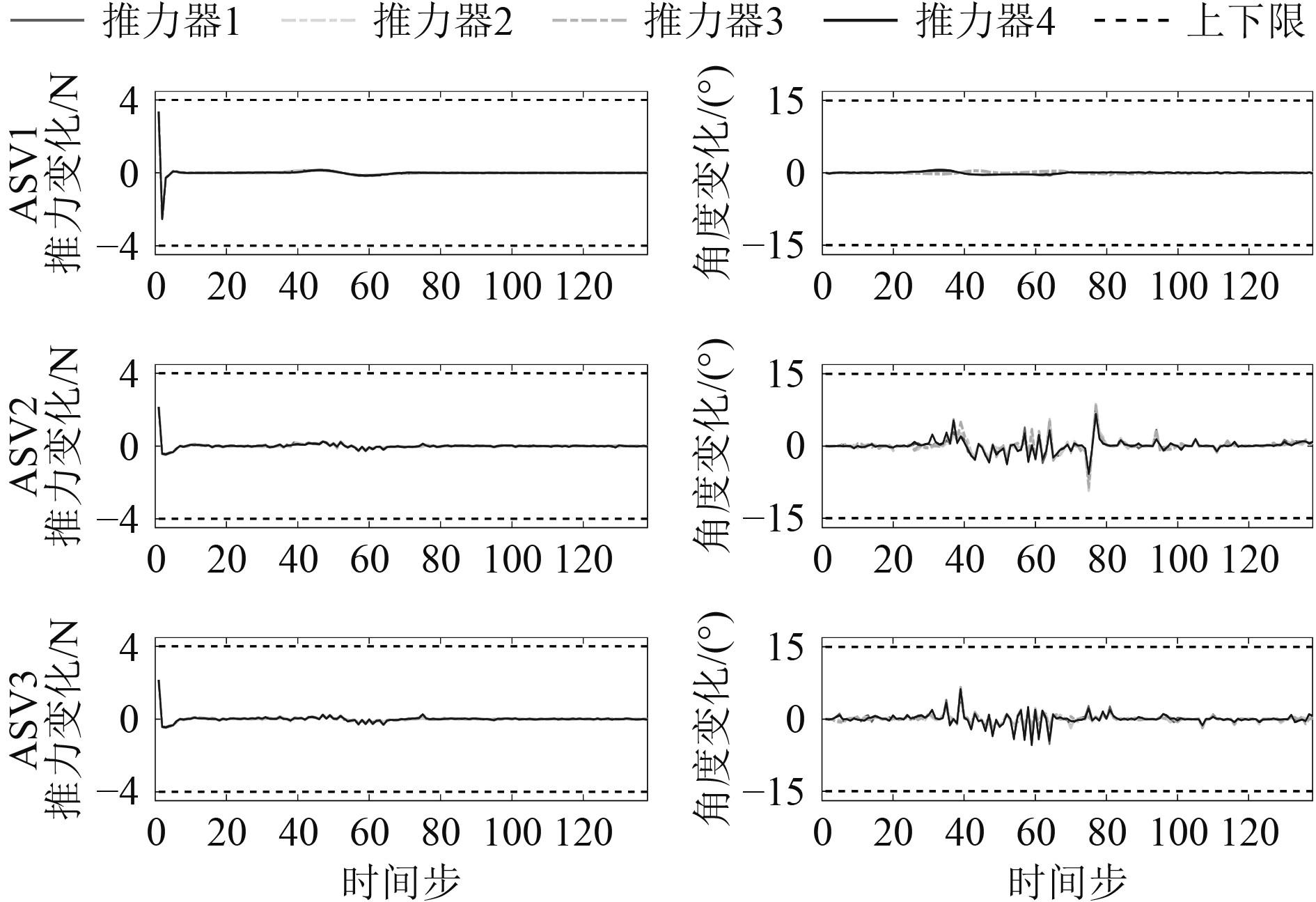
图 12 基于CI-MPC的无人船推力器推力与角度变化 Fig. 12 Thrust and azimuth angle variation of ASVs under CI-MPC |
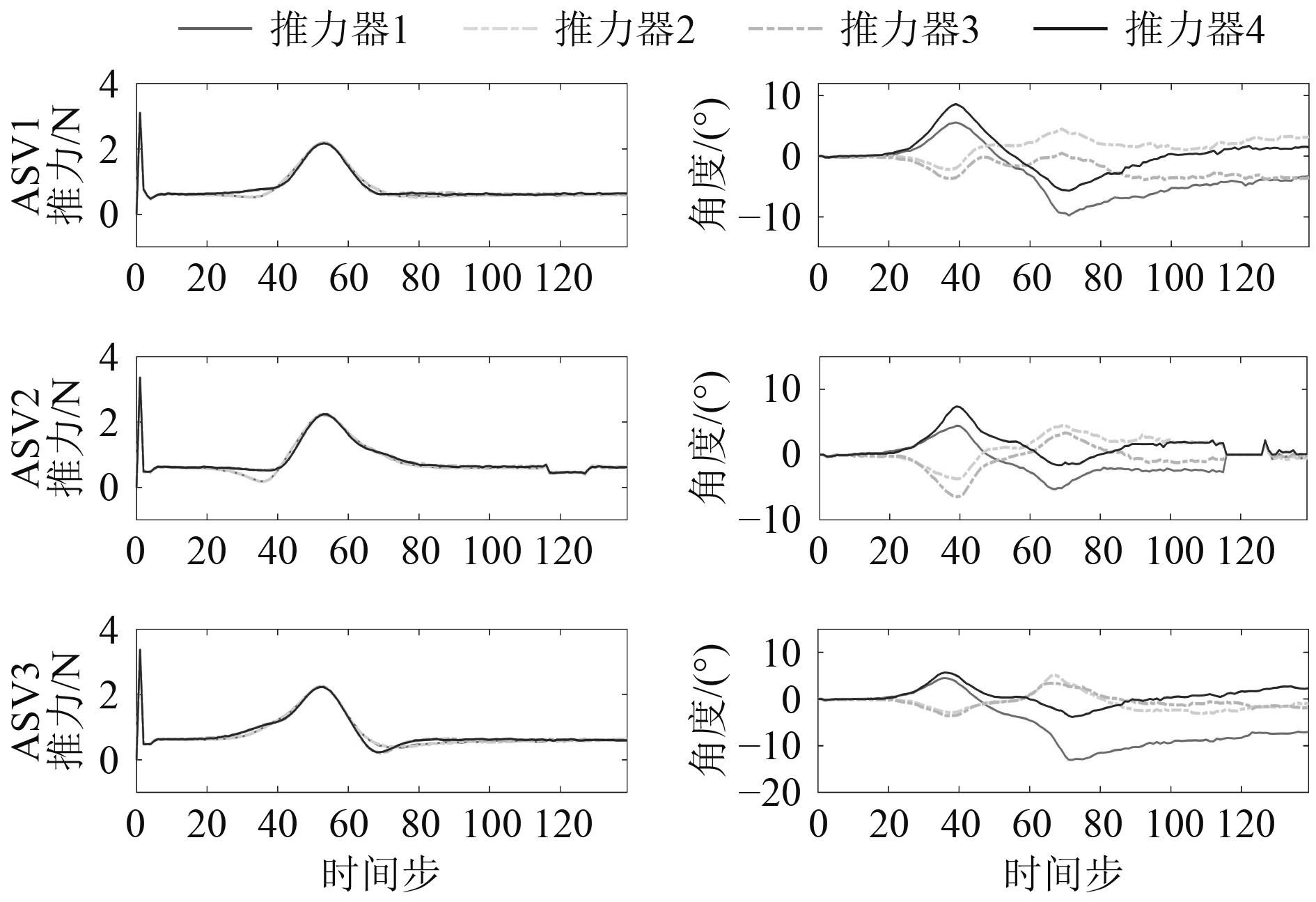
从推力器推力和角度的变化量来看(见图11和图12),2种策略下领航者的推力和角度变化量情况基本相同,而DI-MPC策略下的跟随者推力器抖振情况较为严重。根据通信图,在分布式架构下,领航者仅需传输信息给跟随者而不需要接收来自其他船舶的信息,且它所需要跟踪的轨迹是已知的,因此对于领航者而言其控制器也是一个全局控制器,本质上等同于集中式控制。对于跟随者的控制器而言,它们需要基于接收到的信息做出决策,不同控制器之间的计算偏差和有限的信息传输造成了控制误差和系统抖振。从这点来看,集中式策略表现出了更优良的控制性能,控制结果更为平稳。
|
图 11 基于CI-MPC的无人船推力器推力与角度 Fig. 11 Thrust and azimuth angle of ASVs under CI-MPC |
图13列出了各推力器推力和角度变化量的归一化标准差。可以很明显地看到,2种控制策略下领航者的推力器变化情况较为接近,而跟随者则区别较大。DI-MPC更注重于减缓推力器的推力变化,尤其是在数值模拟的初始阶段,同时,实时迭代框架也能够加速系统收敛,而CI-MPC则更注重于减缓推力器的角度变化。

|
图 13 无人船推力器推力与角度变化标准差 Fig. 13 Normalized standard deviation of thrust and azimuth angle variation of ASVs |
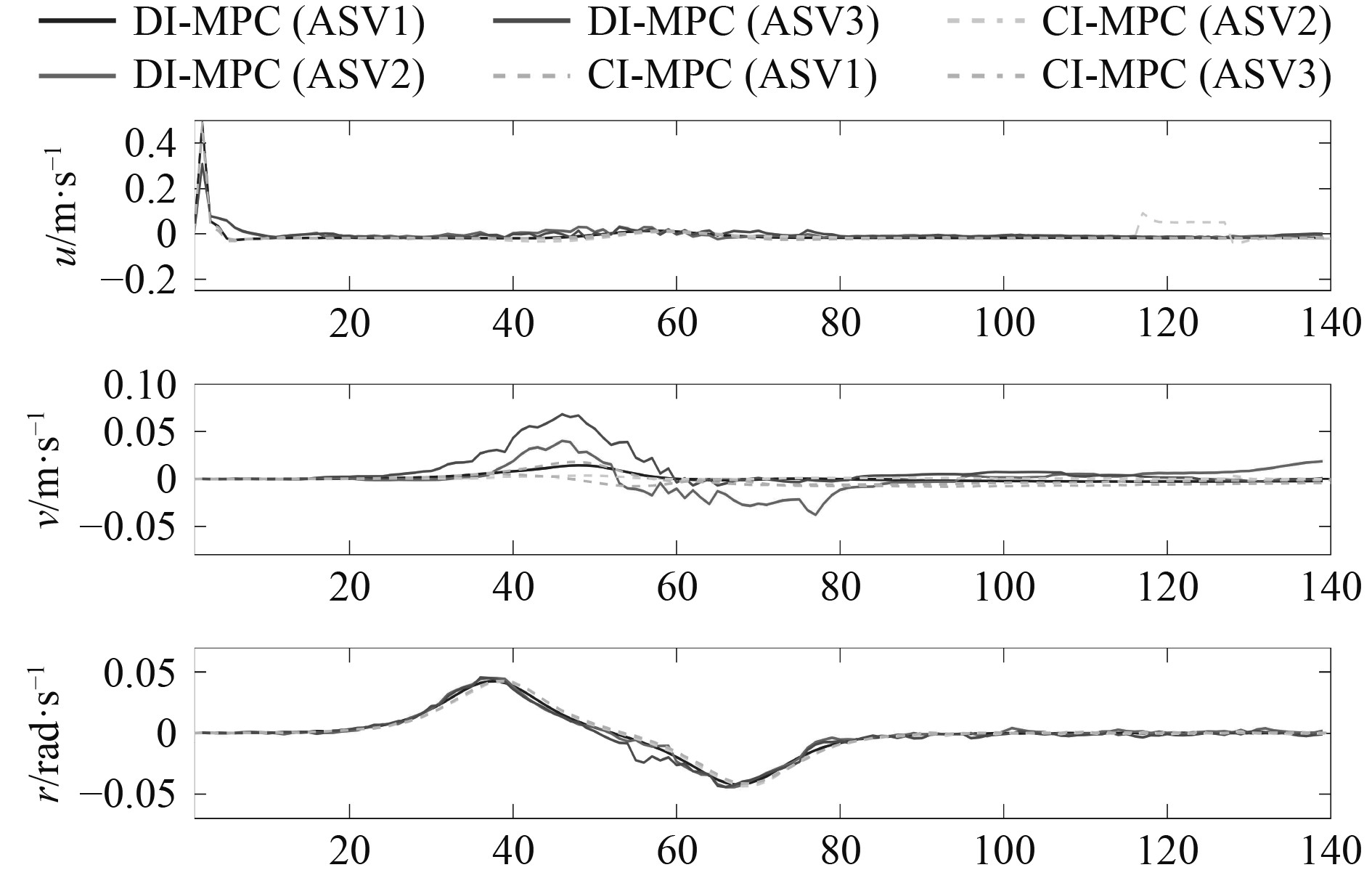
无人船的线速度和角速度变化如图14所示。可以看到,纵向速度基本保持定值,这是由于在数值模拟过程中MPC的预测步长恒定不变。而横向速度和角速度变化程度较大,特别是在参考路径点变化较大的曲线段。总体来看,分布式的控制架构和有限的信息传输迭代使得DI-MPC策略下无人船的速度变化较CI-MPC更为剧烈。
|
图 14 无人船线速度和角速度 Fig. 14 Linear and angular velocities of ASVs |
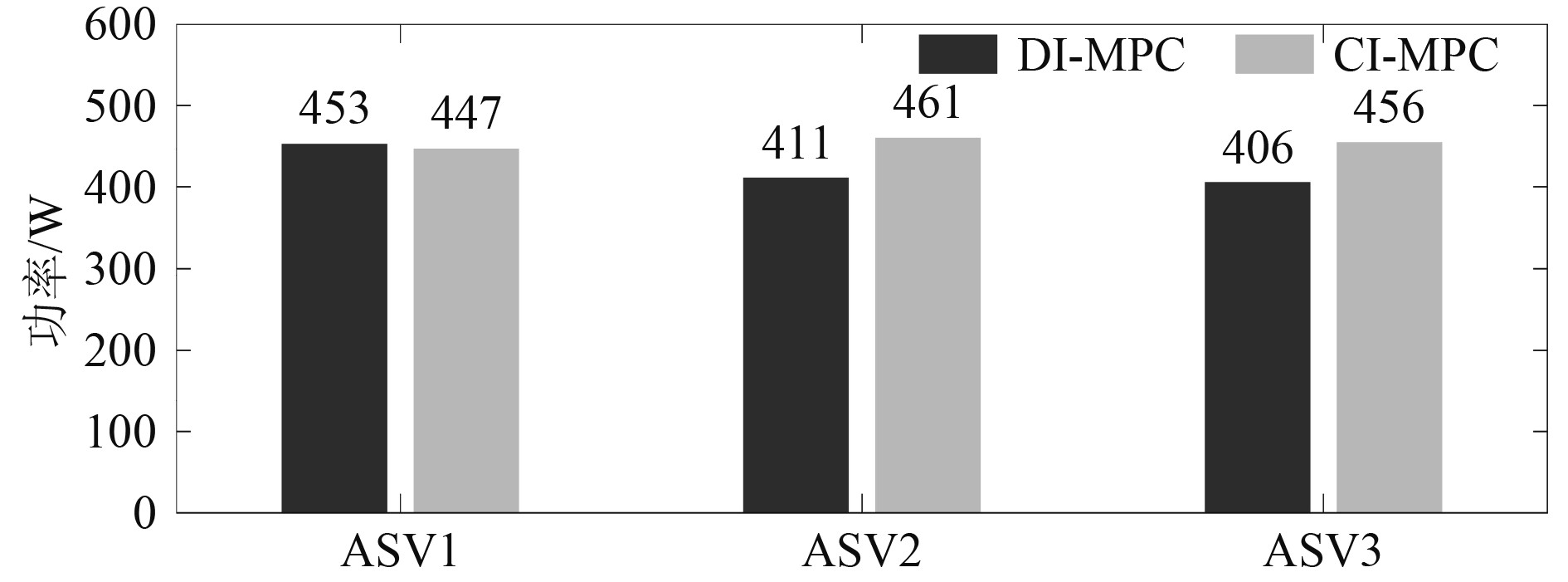
图15对比了2种策略下各无人船的功率消耗,分别为[453 W, 411 W, 406 W]和[447 W, 461 W, 456 W]。在此场景下,DI-MPC的总功率消耗相比CI-MPC降低了约6.89%。此外,2种控制策略也展现出了不同的功率消耗特性。DI-MPC策略下,跟随者的功率消耗小于领航者,而CI-MPC则相反。这说明当无人船的协同控制拓展为更大规模的任务场景时,分布式控制架构更有利于节约能源,具有较强的经济性。
|
图 15 无人船功率消耗 Fig. 15 Power consumption of ASVs |
本文提出了一种分布式集成式协同控制策略(DI-MPC)以处理多无人船系统的协同路径跟踪与编队控制问题。每艘无人船的控制器都是基于MPC理论、通信图以及编队控制方法独立设计的,并且对运动控制与推力分配进行一体化集成以实现对推力器的直接控制。控制器之间通过实时迭代来达到船舶之间的一致性。基于数值模拟将所提策略与集中式策略(CI-MPC)进行对比分析,以验证其有效性。数值模拟结果显示,分布式策略与集中式策略在无人船的协同路径跟踪以及编队控制任务中都能展现出较好的控制性能,但两者的控制特性有明显差别。集中式控制下系统的稳定性更优,而分布式控制能够提高系统对外部环境变化的适应性,并减少计算成本25.02%,降低能耗6.89%。分布式控制对于包含多个子系统的大规模协同控制问题具有一定的实际应用价值。未来的工作将进一步考虑不同应用场景(如避障、编队变换)下的数值模拟或者模型试验研究,以验证并提高所提策略的适用性。
| [1] |
CAMPBELL S, NAEEM W, IRWIN G. , Irwin G. A review on improving the autonomy of unmanned surface vehicles through intelligent collision avoidance manoeuvres[J]. Annual Reviews in Control, 2012, 36: 267-283. DOI:10.1016/j.arcontrol.2012.09.008 |
| [2] |
LIU Z, ZHANG Y, YU X,et al. Unmanned surface vehicles: An overview of developments and challenges[J]. Annual Reviews in Control, 2016, 41: 71-93. DOI:10.1016/j.arcontrol.2016.04.018 |
| [3] |
ADAMEK T, KITTS C A, MAS I. Gradient-based cluster space navigation for autonomous surface vessels[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20: 506-518. DOI:10.1109/TMECH.2013.2297152 |
| [4] |
LI S, LIU J, NEGENBORN R R. Distributed coordination for collision avoidance of multiple ships considering ship maneuverability[J]. Ocean Engineering, 2019, 181: 212-226. DOI:10.1016/j.oceaneng.2019.03.054 |
| [5] |
CHEN L, HOPMAN H, NEGENBORN R R. Distributed model predictive control for vessel train formations of cooperative multi-vessel systems[J]. Transportation Research Part C:Emerging Technologies, 2018, 92: 101-118. DOI:10.1016/j.trc.2018.04.013 |
| [6] |
CHEN L, HOPMAN H, NEGENBORN R R. Distributed model predictive control for cooperative floating object transport with multi-vessel systems[J]. Ocean Engineering, 2019, 191: 106515. DOI:10.1016/j.oceaneng.2019.106515 |
| [7] |
KAYACAN E, PARK S, RATTI C, et al. Learning-based nonlinear model predictive control of reconfigurable autonomous robotic boats: Roboats[J]. IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2019, 8230-8237. |
| [8] |
ROWLEY J. Autonomous unmanned surface vehicles (usv): A paradigm shift for harbor security and underwater bathymetric imaging[J]. OCEANS 2018 MTS/IEEE Charleston, 2018, 1-6. |
| [9] |
ALMEIDA J, SILVESTRE C, PASCOAL A. Cooperative control of multiple surface vessels in the presence of ocean currents and parametric model uncertainty[J]. International Journal of Robust and Nonlinear Control, 2010, 20(14): 1549-1565. DOI:10.1002/rnc.1526 |
| [10] |
LU Y, ZhANG G, SUN Z, et al. Adaptive cooperative formation control of autonomous surface vessels with uncertain dynamics and external disturbances[J]. Ocean Engineering, 2018, 167: 36-44. DOI:10.1016/j.oceaneng.2018.08.020 |
| [11] |
SHOJAEI K. Neural network formation control of underactuated autonomous underwater vehicles with saturating actuators[J]. Neurocomputing, 2016, 194: 372-384. DOI:10.1016/j.neucom.2016.02.041 |
| [12] |
ZHOU X, WU P, ZhANG H, et al. Learn to navigate: cooperative path planning for unmanned surface vehicles using deep reinforcement learning[J]. IEEE Access, 2019, 7: 165262-165278. DOI:10.1109/ACCESS.2019.2953326 |
| [13] |
DAI L, CAO Q, XIA Y, et al. Distributed MPC for formation of multi-agent systems with collision avoidance and obstacle avoidance[J]. Journal of the Franklin Institute, 2017, 354(4): 2068-2085. DOI:10.1016/j.jfranklin.2016.12.021 |
| [14] |
LIU C, ZHENG H, NEGENBORN R R, et al. Trajectory tracking control for underactuated surface vessels based on nonlinear model predictive control[C]// International Conference on Computational Logistics. 2015: 166-180.
|
| [15] |
LIU C, ZHENG H, NEGENBORN R, et al. Adaptive predictive path following control based on least squares support vector machines for underactuated autonomous vessels[J]. Asian Journal of Control, 2021, 23(1): 432-448. DOI:10.1002/asjc.2208 |
| [16] |
FAN Z, LI H. Two-layer model predictive formation control of unmanned surface vehicle[C]// 2017 Chinese Automation Congress (CAC). 2017: 6002-6007.
|
| [17] |
DROGE G. Distributed virtual leader moving formation control using behavior-based MPC[C]// 2015 American Control Conference (ACC). 2015: 2323-2328.
|
| [18] |
WEI H, SUN Q, CHEN J, et al. Robust distributed model predictive platooning control for heterogeneous autonomous surface vehicles[J]. Control Engineering Practice, 2021, 107: 104655. DOI:10.1016/j.conengprac.2020.104655 |
| [19] |
ZHENG H, NEGENBORN R R, LODEWIJKS G. Trajectory tracking of autonomous vessels using model predictive control[J]. IFAC Proceedings Volumes, 2014, 47(3): 8812-8818. DOI:10.3182/20140824-6-ZA-1003.00767 |
 2022, Vol. 44
2022, Vol. 44

