2. 上海海事大学 商船学院,上海 200135
2. Merchant Marine College, Shanghai Maritime University, Shanghai 200135, China
船舶设备的振动与噪声一直是一个难以解决的问题。随着科技水平的提高,对船舶设备的隔振性能和隔声性能提出了更高的要求。船舶设备的振动与噪声控制技术已经成为了船舶工程领域的研究热点[1]。在现代声学研究中,运用计算机技术和数值计算相结合的方法来优化隔声技术是实现辐射噪声控制的重要研究方向。通常运用有限元软件来描述运动结构的动力学振动响应,然后提取设备表面振动响应作为边界条件建立边界元辐射声场模型,从而求解动力设备低中频域的一些声学参数[2]。时胜国等[3] 比较了水下噪声声辐射方面的各种研究方法。曹贻鹏[4]利用有限元法和边界元法相结合建立声振耦合方程同时计算结构表面振动和声辐射,这种方法的优点在于能够同时解决表面振动和声辐射问题,能够适应于复杂结构。崔淑梅[5]也利用Ansys和Sysnoise相结合的方法模拟计算永磁直流电机的声压频响特性,并通过实验进行对比研究,最大相对误差为85%,满足工程设计精度要求。有限元和边界元相结合的方法既利用了有限元较容易建立模型,得到振动特性的优点,又发挥了边界元可以快速得到声响特性的优势,加快了计算速度,更好进行系统隔声特性的优化。
浮筏隔振系统起源于20世纪50年代,是由多个动力设备通过上层隔振器安装在中间浮筏上再通过下层隔振器整体安装在基础上而构成的一个多机组、多激励的复杂隔振系统。张树桢等[6-8]详细介绍了浮筏隔振系统各部分的组成与建模处理,并运用有限元法和功率流法对整个系统进行隔振性能分析。方媛媛等[9]对船舶辅机浮筏隔振装置简化进行理论分析,结果与软件仿真对比后为浮筏隔振系统设计提供理论依据。带隔声罩空压机组浮筏隔振系统是将空压机组和管系整体放置于隔声罩中,浮筏隔振装置降低振动和固体传声,隔声罩降低空气传声,能够同时实现振动与噪声控制。毕风荣等[10]采用实验手段研究了小型柴油发电机组的噪声源和噪声特性,对不同频率范围的噪声提出了具体可行的隔声罩结构优化措施,降低发电机组噪声。孙洪军等[11]设计了空压机组隔声罩并满足使用要求。本文采用有限元边界元相结合的方法,分析带隔声罩空压机组浮筏隔振系统的声辐射和隔声量,辅以实验测量,以验证仿真方法的准确性,达到噪声控制的目的。
1 带隔声罩空压机组浮筏隔振系统声场模型的建立 1.1 边界元模型的建立通过Ansys对系统的有限元模型进行振动谐响应分析,然后提取带隔声罩空压机组浮筏隔振系统有限元模型的表面网格作为声学边界元模型。
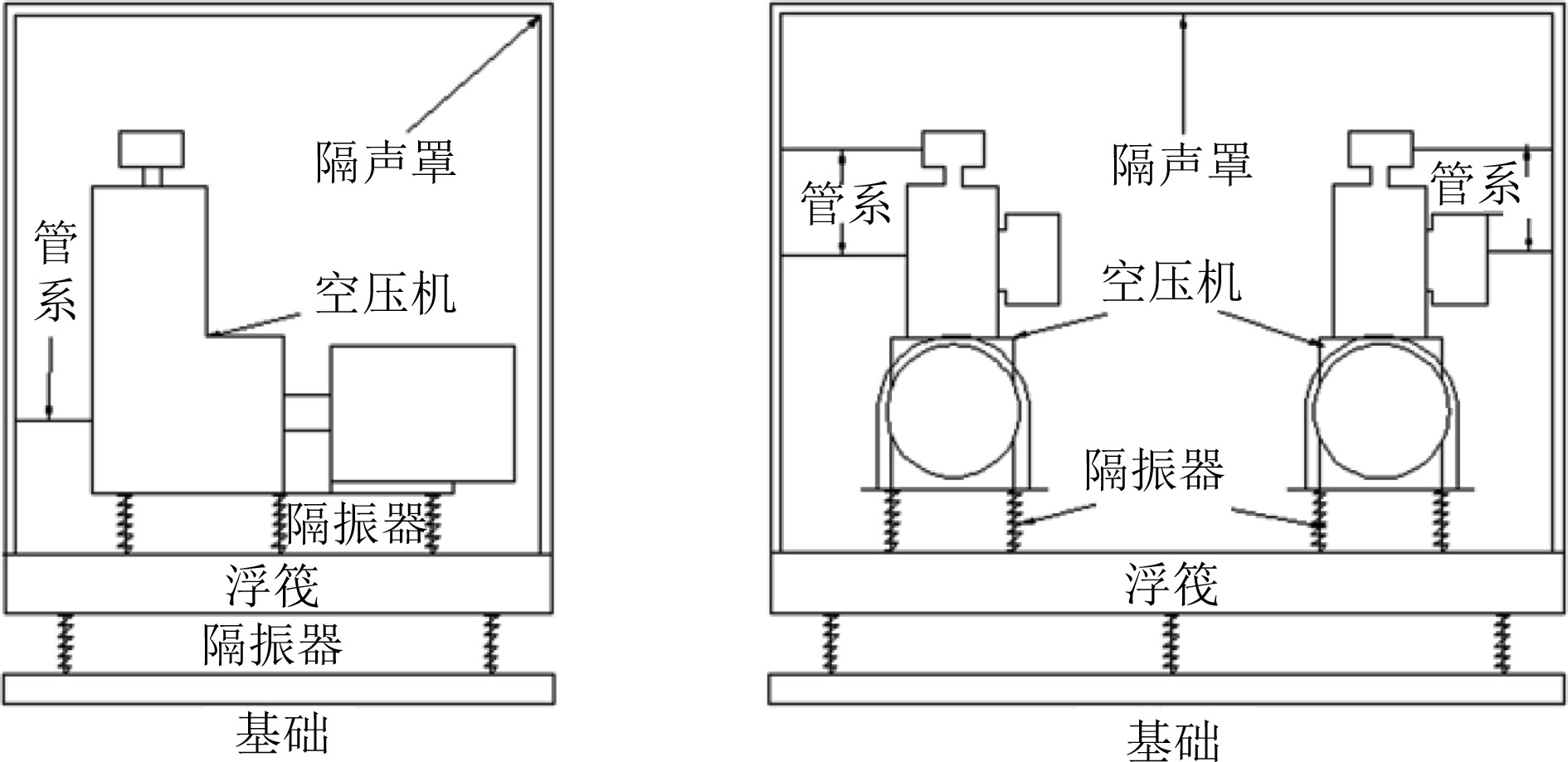
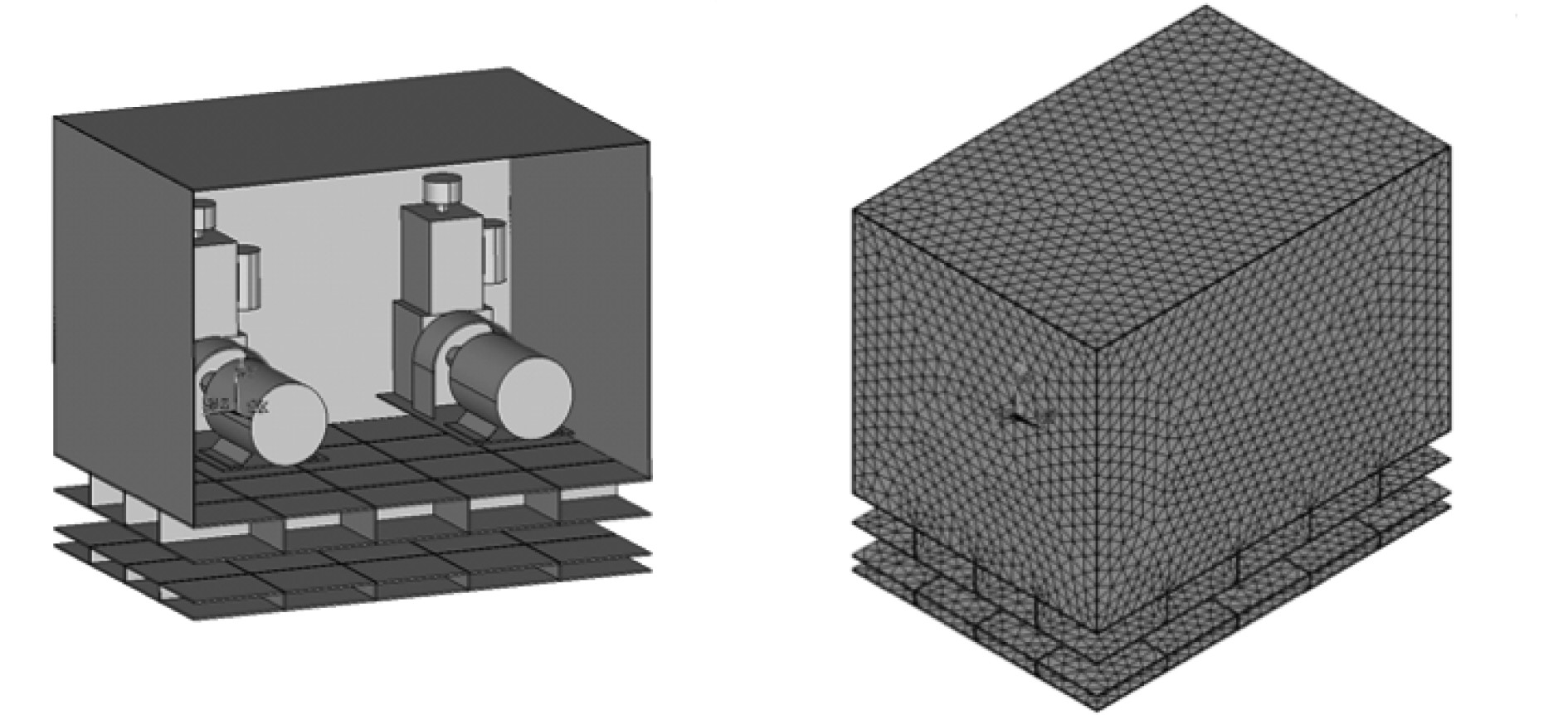
1.1.1 有限元模型建立空压机型号WP135,功率26 kW,转速970 r/min;压缩机净重400 kg,外形尺寸640 mm×763 mm×1187 mm(长×宽×高);电机为Y200L-6-H型,净重300kg,整体机组外形尺寸为1465 mm×840 mm×1370 mm(长×宽×高);整体机组净重1000 kg。空气压缩机整体体积0.265 m3。中间筏体是由1 cm钢板焊接而成对称的平板架式,尺寸为2.6 m×1.8 m×0.2 m,质量964 kg。弹性基础也是由1 cm钢板焊接而成对称的平板架式,尺寸为2.6 m×1.8 m×0.1 m。隔声罩是3 mm钢板和47 mm阻尼材料组成的尺寸为2.6 m×1.8 m×1.6 m的双层结构,整体质量为440 kg[12]。整个系统采用Solid45单元进行,隔声罩上的内部加筋、维修门和孔洞忽略,内部管系选用X,Y,Z等3个方向Combin14单元进行建模,刚度为338000 N/m。空压机组通过6个ZTG-400型橡胶隔振器与中间筏体相连,浮筏通过6个JSD-1250型橡胶隔振器与弹性基础相连,选择Combin14单元进行隔振器建模[13],隔振器仿真参数如表1所示。图1和图2为带隔声罩空压机组浮筏隔振系统基本结构图和模型图。
|
|
表 1 隔振器仿真参数 Tab.1 Parameters of vibration isolator simulation |
|
图 1 系统基本结构图 Fig. 1 System basic structure |
|
图 2 系统有限元模型图 Fig. 2 System finite element model |
1)电机扰动力
空压机电机额定转速为970 r/min,《动力机器基础设计规范》[14]规定,750 r/min <动力机械运转速度<1000 r/min时的扰动力计算公式为:
| $ {P_x} = 0.2{W_g},$ | (1) |
| $ {P_z} = {P_x},$ | (2) |
| $ {P_y} = 0.5{P_x}。$ | (3) |
式中:
2)空压机扰动力计算
一阶不平衡离心力通常是1%的不平衡回转质量,即
| $ {F_{acf}} = \frac{1}{{100}}{m_j}R{w^2}。$ | (4) |
式中:
一阶气缸爆发压力可引起空压机做垂向振动[15],即
| $ {F_{ap}} = {P_a}A\sin (2\pi f + \theta ) 。$ | (5) |
式中:
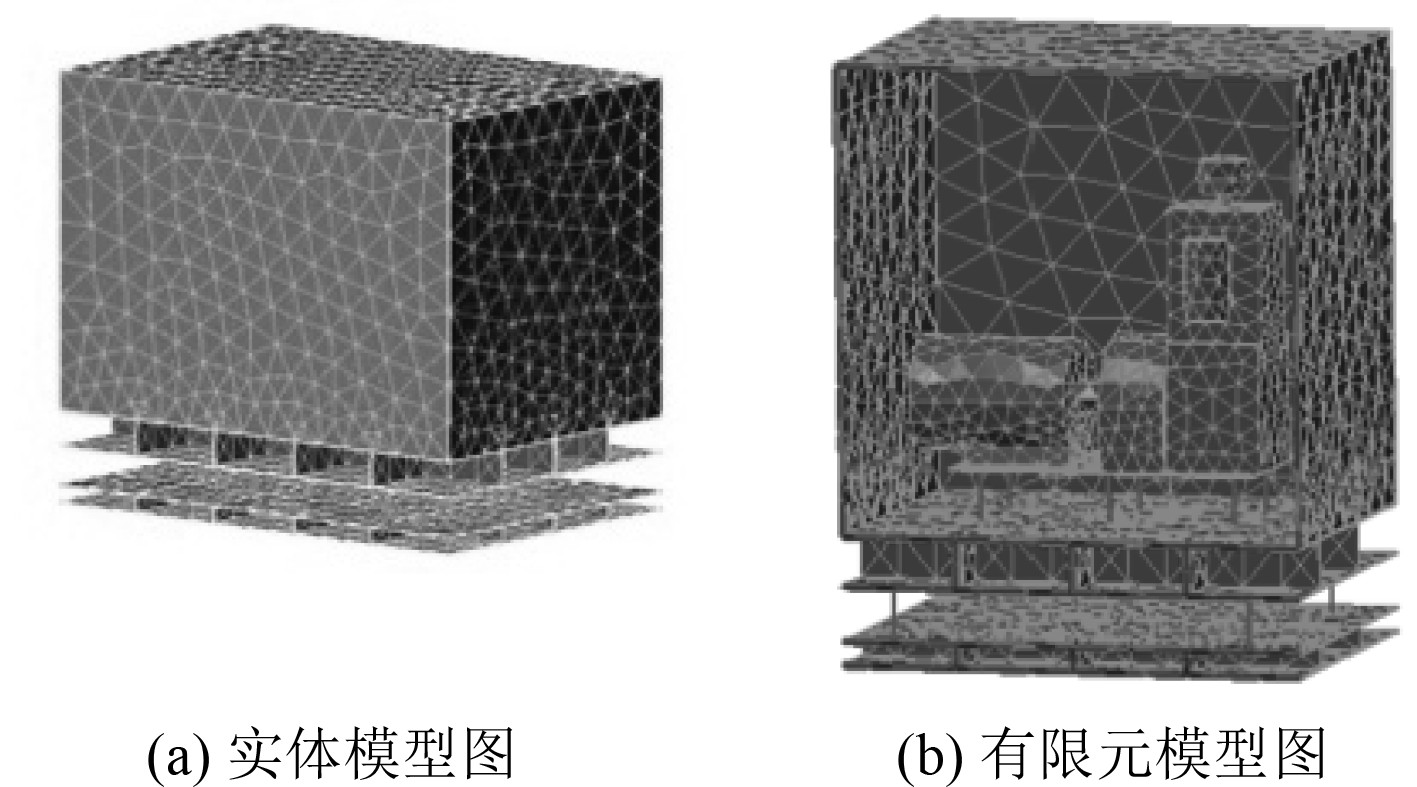
通过Ansys对系统的有限元模型进行振动谐响应分析,计算出系统结构各节点振动响应,这些数据以能够导入LMS Virtual.Lab Acoustics的*.rst的结果文件保存,导入的时候要注意单位的统一[16]。图3为边界元模型。
|
图 3 带隔声罩空压机组浮筏隔振系统声学边界元模型 Fig. 3 System acoustic boundary element model |
该方法的优点是能够直接利用已有有限元模型单元和节点的数据信息,只需要提取结构网格中的面网格就行,不需要重新划分网格,并且有限元谐响应计算得到的节点位移、速度、加速度等可直接映射到声学边界元模型网格上。缺点就是网格比较细,对计算机性能要求比较高。
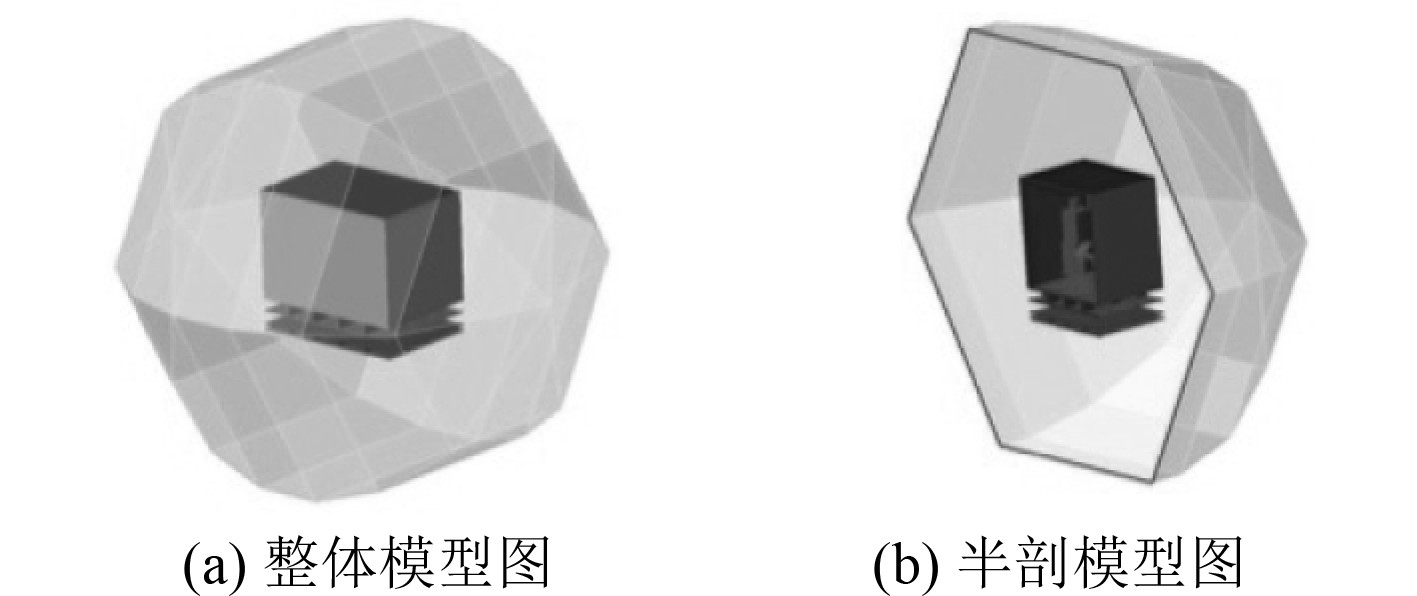
1.2 声场模型的建立在流体材料和流体属性设置中,设定系统结构外部流场为空气,相应的声速为340 m/s,密度1 kg/m3。在声学边界元网格表面施加有限元分析得到的位移载荷,分析频率为0~1000 Hz,步长为20 Hz,形成一个符合ISO声功率测试标准的声场模型,这个模型能在LMS Virtual.Lab Acoustics中自动生成,近似球面半径为4 m,如图4所示。
|
图 4 带隔声罩空压机组浮筏隔振系统声场模型 Fig. 4 System sound field model |
根据有限元软件Ansys求出的带隔声罩空压机组浮筏隔振系统谐响应分析结果,将节点的振动位移量与声场边界元对应节点进行映射。使用的映射算法为Maximum Distance算法,它以目标网格节点为圆心的一个圆半径值,半径为20 mm,圆内的原始网格节点能够影响目标节点。运用边界元的方法计算出带隔声罩空压机组浮筏隔振系统的外场声辐射,进而能够获得各项声学参数[17-19]。
2.1 声场声功率级声功率级采用对数来度量声功率,公式如下:
| $ {L_w} = 10\lg \frac{W}{{W{}_0}} 。$ | (6) |
式中,
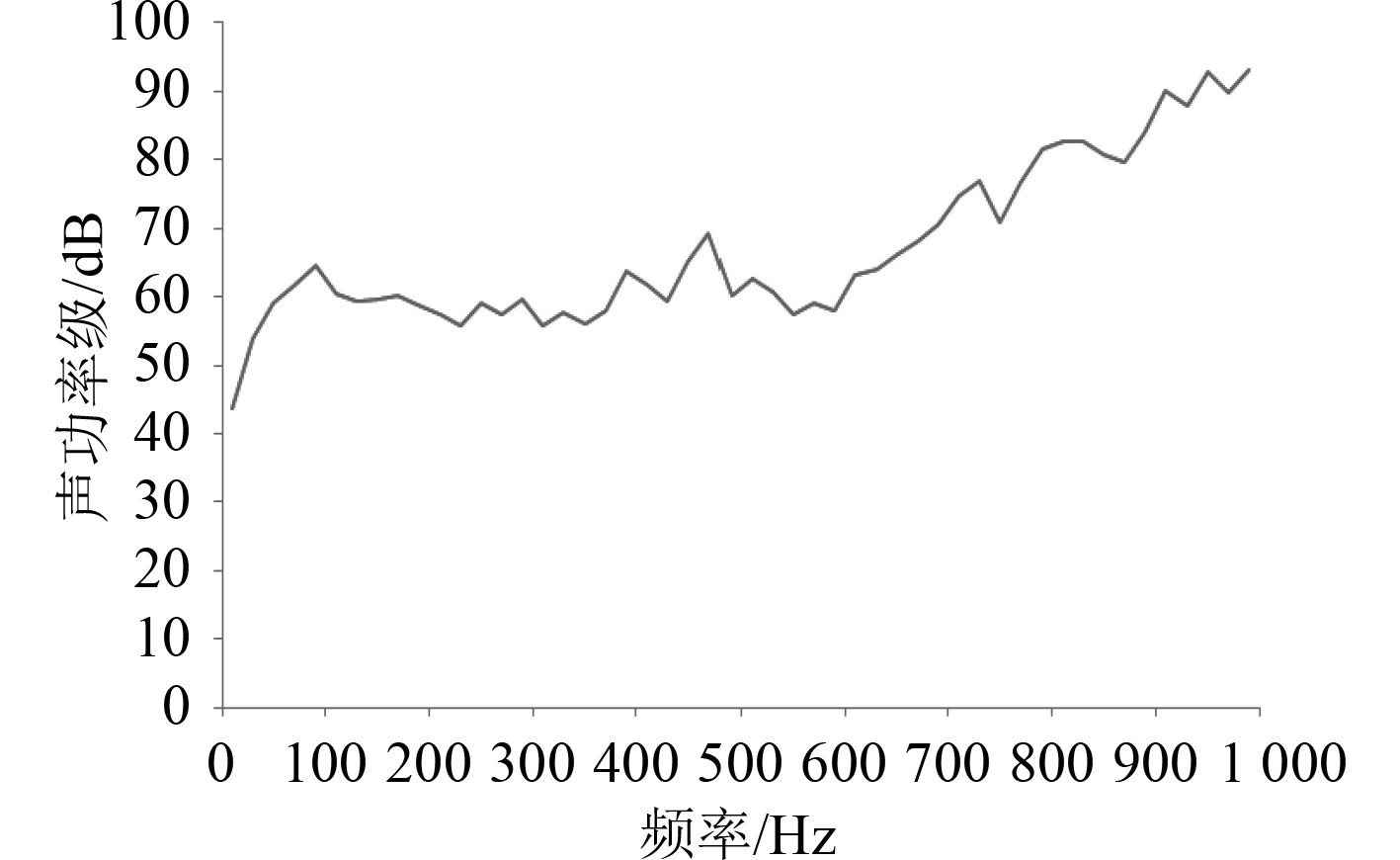
图5为带隔声罩压机组浮筏隔振系统辐射声场声功率级频谱图。整个带隔声罩压机组浮筏隔振系统辐射声场声功率级平均为66.2 dB,声功率级随着频率的增加而增加。在0~100 Hz时,声功率级比较低,在65 dB以下;在100~600 Hz时,整体声功率级基本呈均匀分布,变化不大;在600~1000 Hz时,声功率级显著变大,最高可以达到92.75 dB。
|
图 5 声功率级频谱图 Fig. 5 Sound power level spectrum |
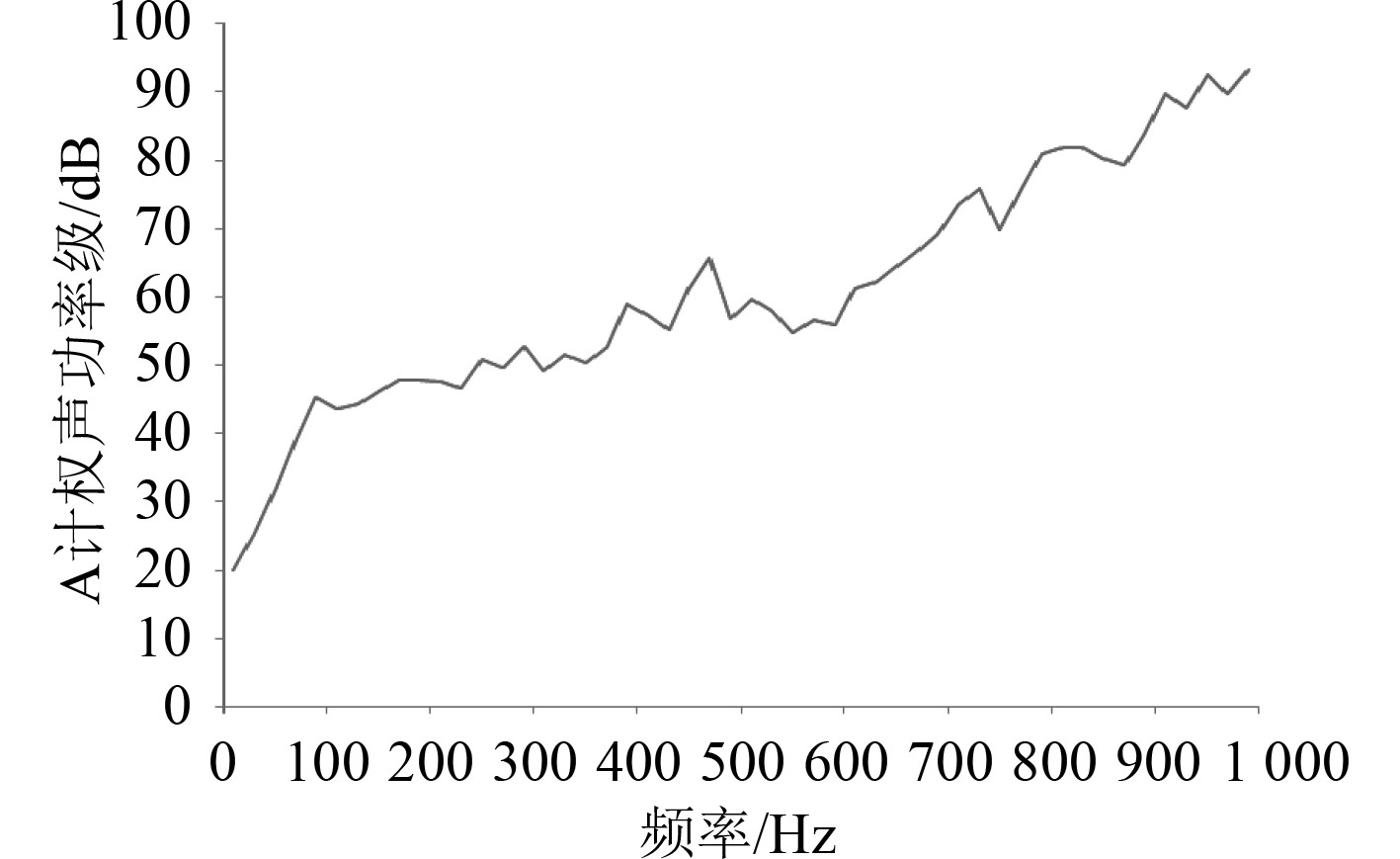
带隔声罩压机组浮筏隔振系统辐射声场A计权声功率级频谱如图6所示。对比图5和图6可以发现,不计权声功率级和A计权声功率级的变化趋势基本一致,这说明带隔声罩压机组浮筏隔振系统产生的噪声是一种对人耳比较敏感的噪声。
|
图 6 A计权声功率级频谱图 Fig. 6 A weighted sound power level spectrum |
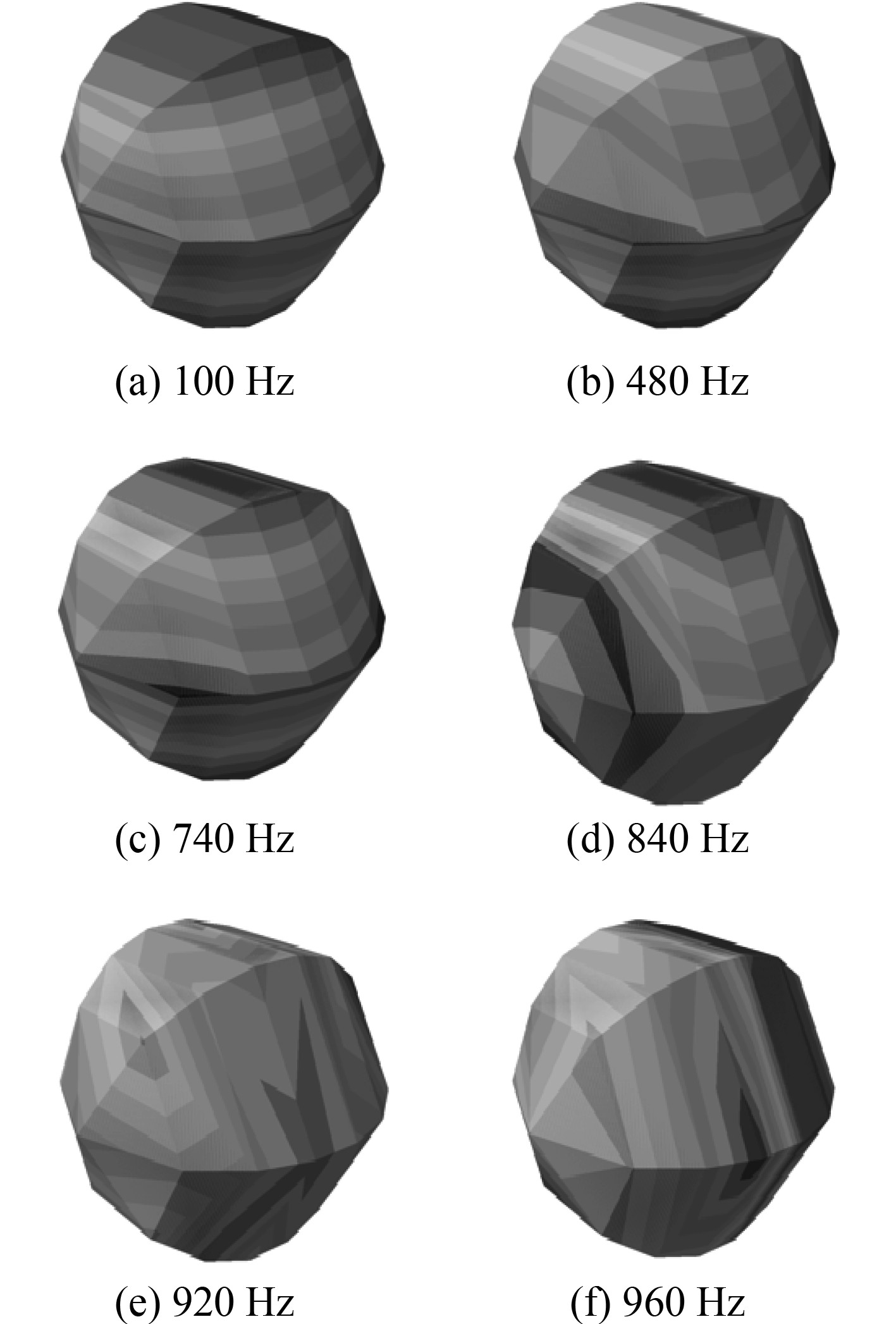
可以根据辐射声场中的声压级云图找出不同频率下的声压分布情况。0~1000 Hz频率范围内有6个声功率级较大的典型频率,分别为100 Hz,480 Hz,740 Hz,840 Hz,920 Hz,960 Hz,可以得到相应的的声压级分布。
图7为带隔声罩压机组浮筏隔振系统典型辐射声场声压级分布云图。可以看出,在一定区域内声压级相差很大,能够比较明显看出系统结构噪声源,并且随着频率的增加,在小范围内的声压也变得相差很大。在低频区域时,系统结构的噪声主要是局部噪声,并且声压级对称分布。随着频率的增加,系统结构的噪声呈现叠加混合趋势,小范围内声压差别较大。
|
图 7 辐射声场声压级分布云图 Fig. 7 Cloud diagram of sound pressure level distribution |
为了准确描述带隔声罩空压机组浮筏隔振系统辐射声场声压级情况,在整个辐射声场中设定典型位置观测点,对这些典型位置观测点的声压级进行分析,可以得到整个频率范围内带隔声罩空压机组浮筏隔振系统辐射声场的变化规律。总共选取6个观测点,分别为位于辐射声场的前(靠近空压机电机一侧)、后(靠近空压机压缩机一侧)、左、右、上、下。
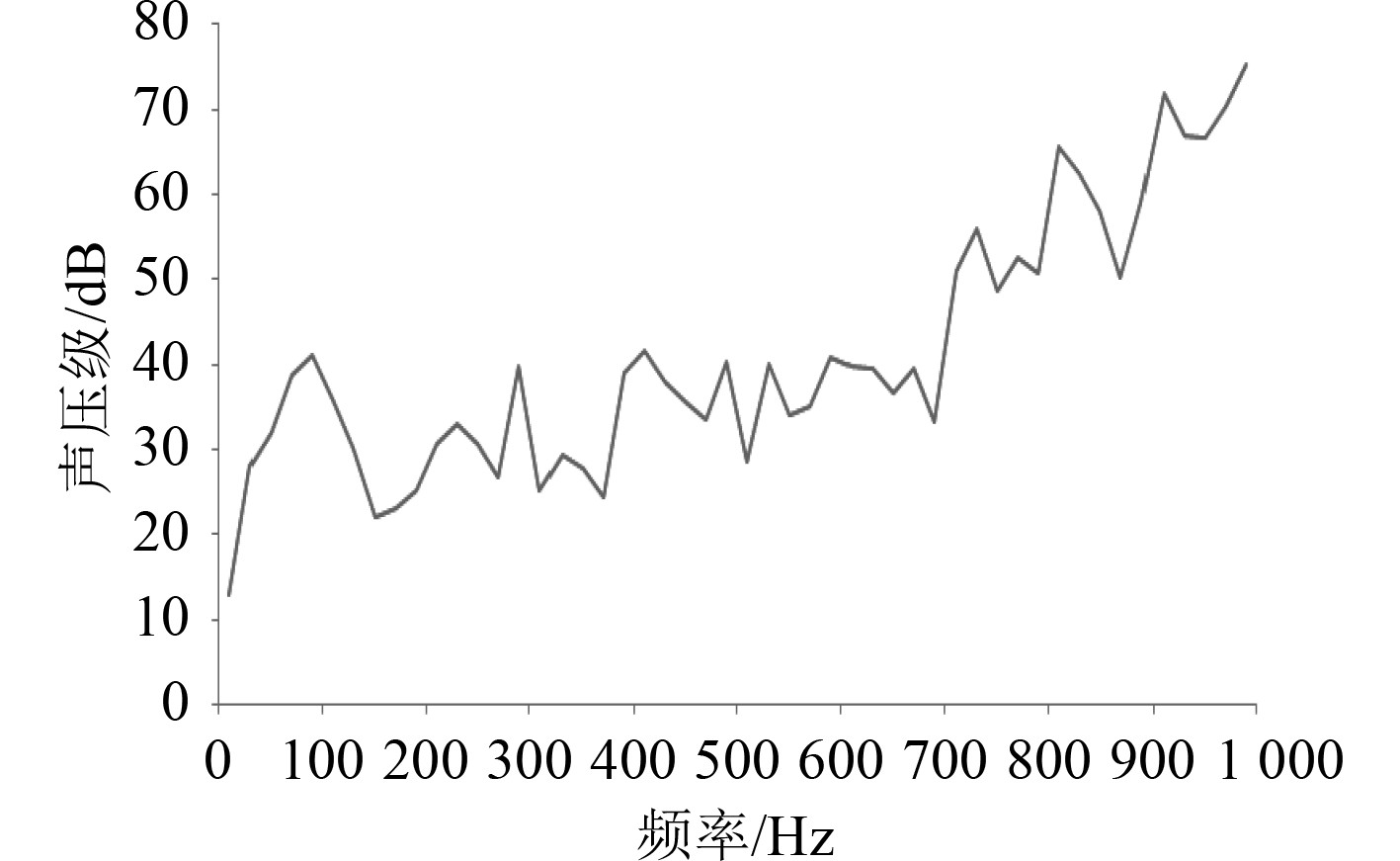
2.3.1 辐射声场前观测点的声压级频率响应图8为辐射声场前观测点的声压级频谱。随着频率的升高,前观测点的声压级响应成升高趋势,700~1000 Hz的频率范围内观测点的声压级显著增高,前观测点声压级响应最大值为75.31 dB,平均声压级为41.1 dB。
|
图 8 辐射声场前观测点的声压级频谱图 Fig. 8 Sound pressure level of front point |
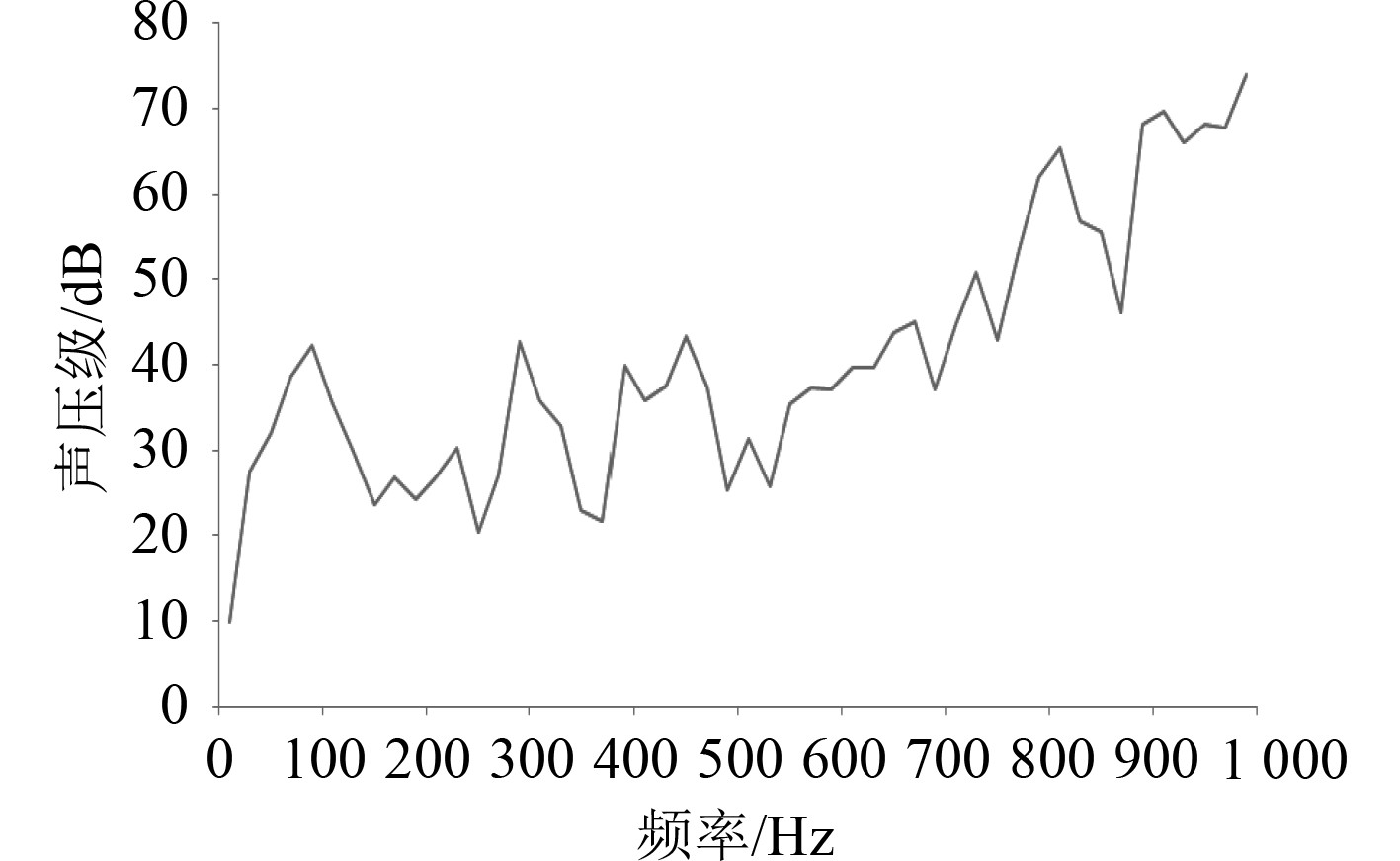
图9为辐射声场后观测点的声压级频谱图。随着频率的升高,后观测点的声压级响应也成升高趋势,后观测点声压级响应最大值为73.93 dB,平均声压级为40.7 dB,并且带隔声罩空压机组浮筏隔振系统前面的噪声要大于后面的噪声。
|
图 9 辐射声场后观测点的声压级频率响应 Fig. 9 Sound pressure level of back point |
图10为辐射声场左观测点的声压级频谱图。随着频率的升高,左观测点的声压级响应成升高趋势,左观测点声压级响应最大值为71. 37 dB,平均声压级为42.3 dB。

|
图 10 辐射声场左观测点的声压级频谱图 Fig. 10 Sound pressure level of left point |
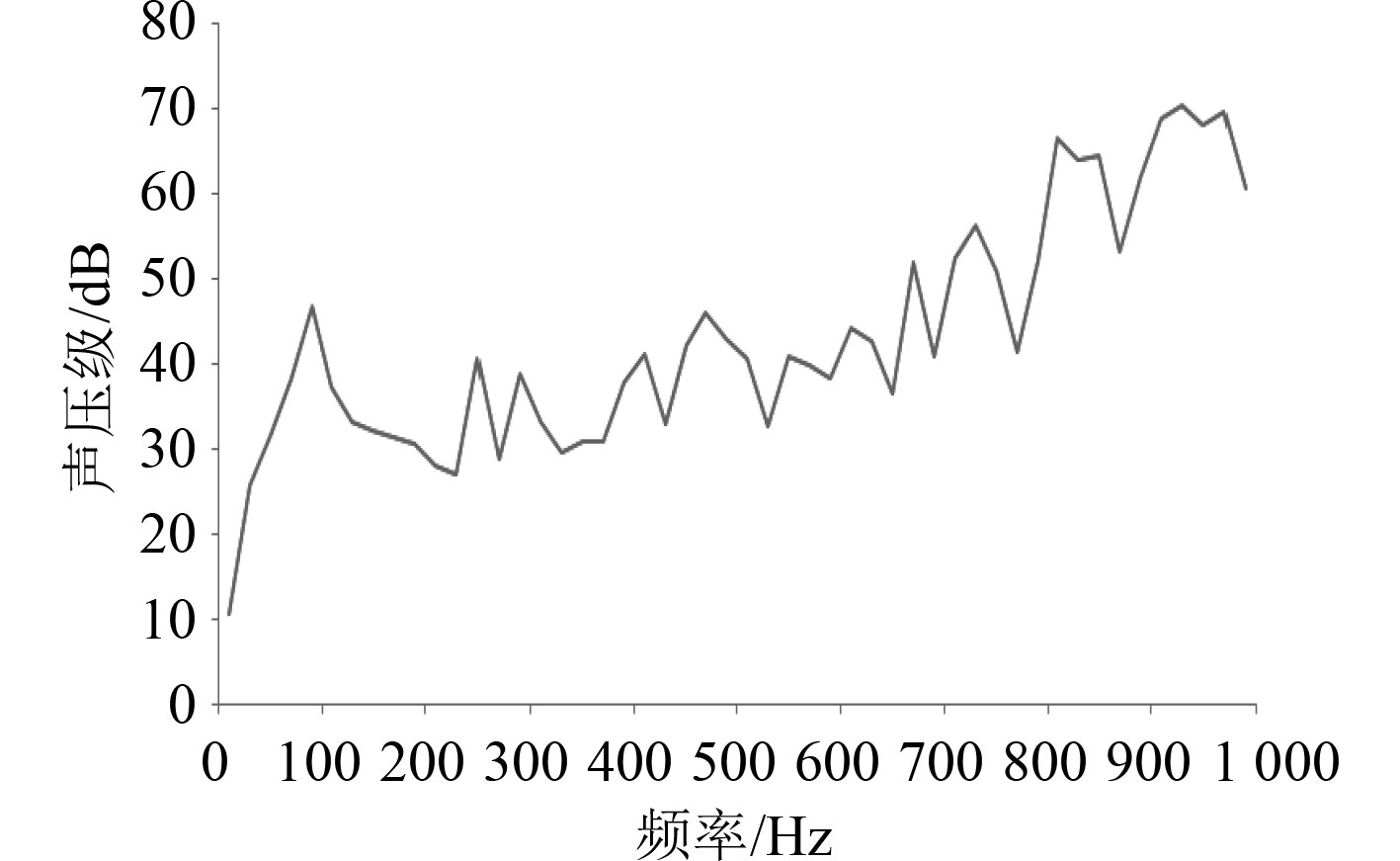
图11为辐射声场右观测点的声压级频谱图。随着频率的升高,右观测点的声压级响应成升高趋势,左观测点声压级响应最大值为70.34 dB,平均声压级为43.2 dB,并且带隔声罩空压机组浮筏隔振系统右面的噪声要大于左面的噪声。
|
图 11 辐射声场右观测点的声压级频谱图 Fig. 11 Sound pressure level of right point |
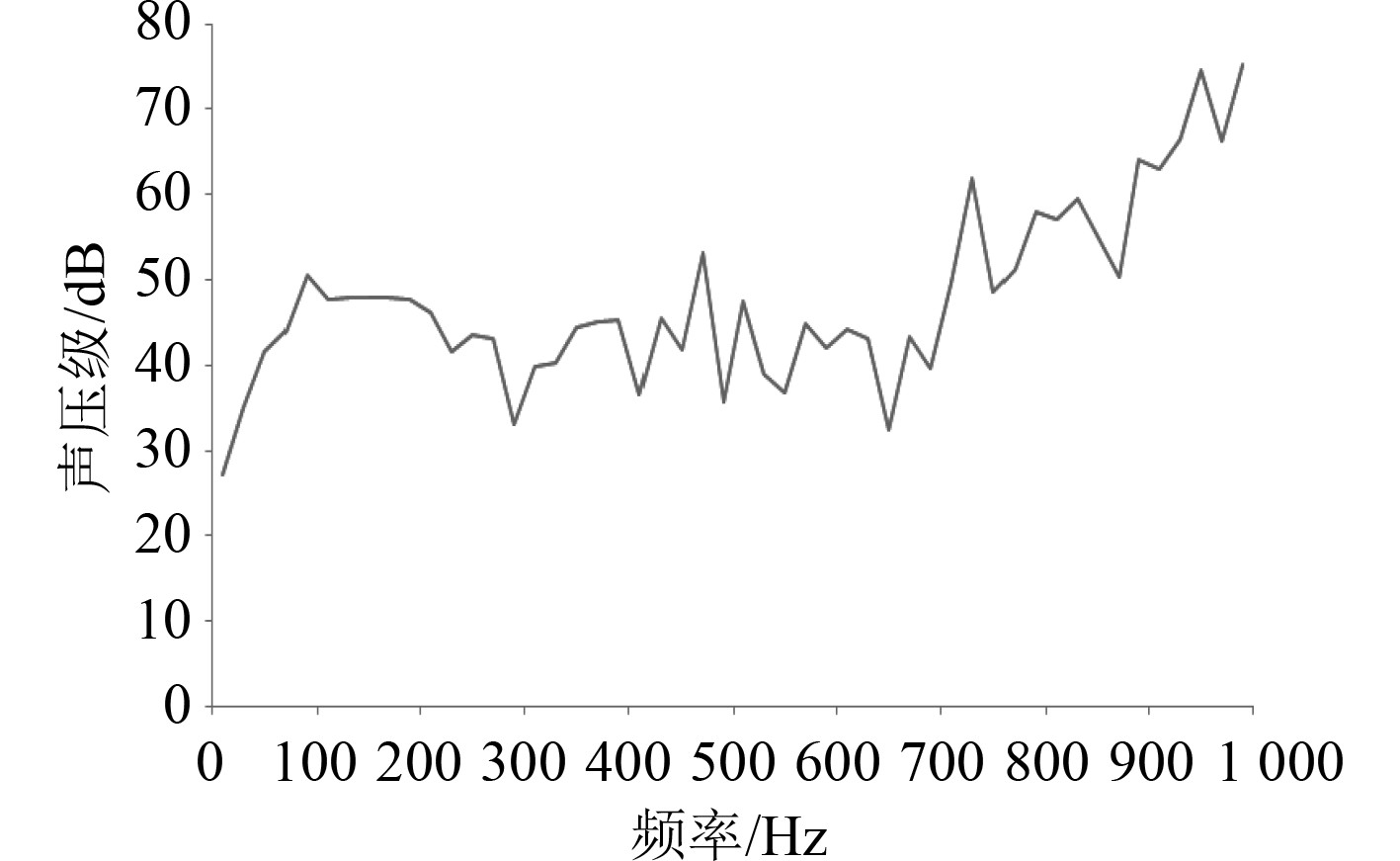
图12为辐射声场上观测点的声压级频谱图。随着频率的升高,上观测点的声压级响应成升高趋势,左观测点声压级响应最大值为75.13 dB,平均声压级为47.73 dB。
|
图 12 辐射声场上观测点的声压级频谱图 Fig. 12 Sound pressure level of up point |
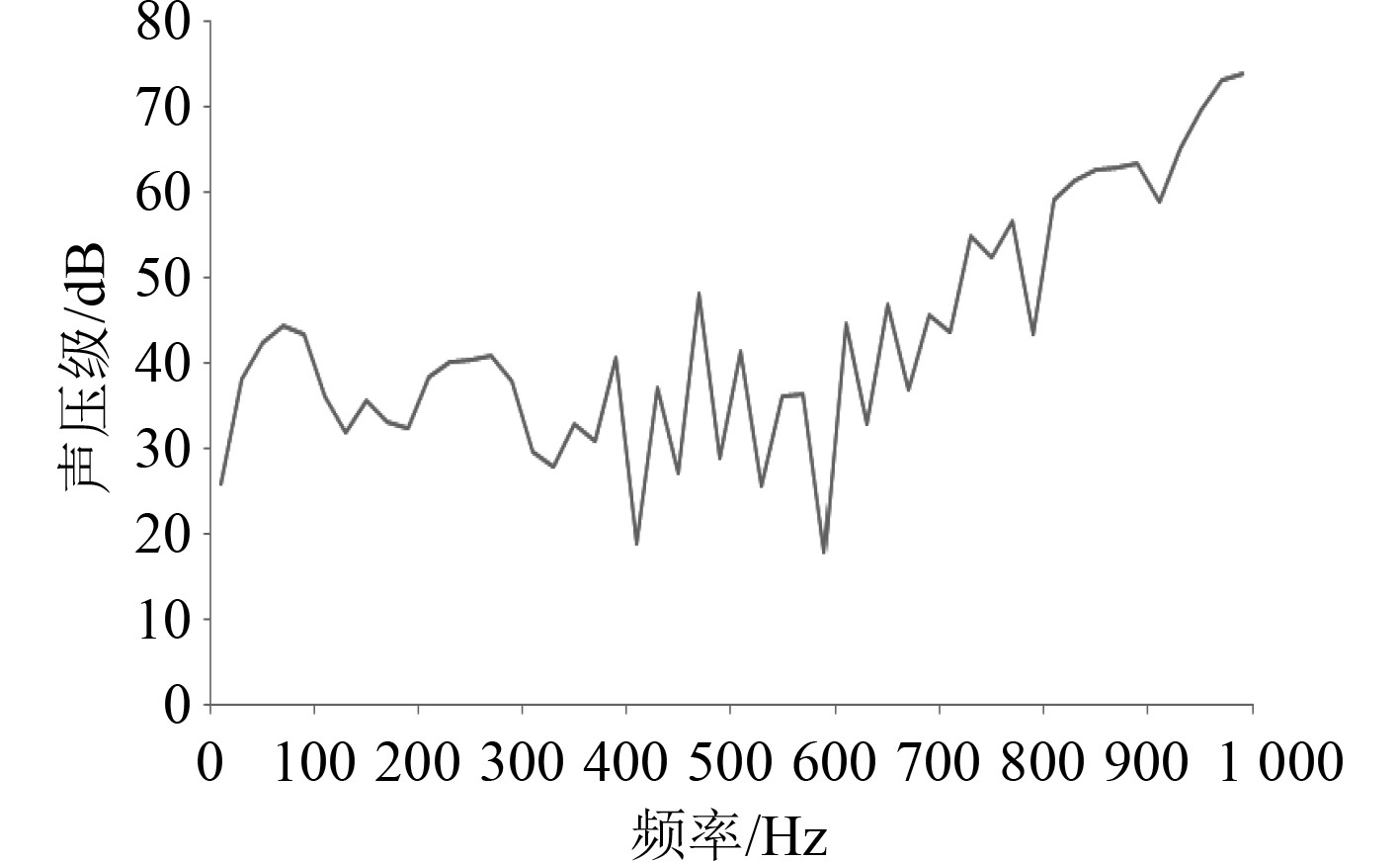
图13为辐射声场下观测点的声压级频谱。右观测点的声压级响应随着频率的增加而升高,左观测点声压级响应最大值为74.03 dB,平均声压级为42.99 dB,并且带隔声罩空压机组浮筏隔振系统上面的噪声要大于下面的噪声。
|
图 13 辐射声场下观测点的声压级频谱 Fig. 13 Sound pressure level of down point |
通过计算空压机组浮筏隔振系统辐射声场,对比带隔声罩空压机组浮筏隔振系统的辐射声场。计算空压机组浮筏隔振系统辐射声场时采用的方法与前面计算带隔声罩空压机组浮筏隔振系统辐射声场的方法一样。运用有限元软件Ansys计算空压机组浮筏隔振系统的谐响应,以*.rst的格式保存结果文件,再将结果文件导入LMS Virtual.Lab Acoustics得到边界元模型,如图14所示。

|
图 14 空压机组浮筏隔振系统声学边界元模型图 Fig. 14 Acoustic boundary element model |
定义系统结构外部流体是空气。将有限元谐响应结果与边界元模型进行映射,在声学边界元网格表面施加位移载荷,分析频率为0~1000 Hz,步长为20 Hz,形成一个符合ISO声功率测试标准的声场模型,这个模型能在LMS Virtual.Lab Acoustics中自动生成,近似球面半径为4 m,如图15所示。

|
图 15 空压机组浮筏隔振系统声场模型图 Fig. 15 System sound field model |
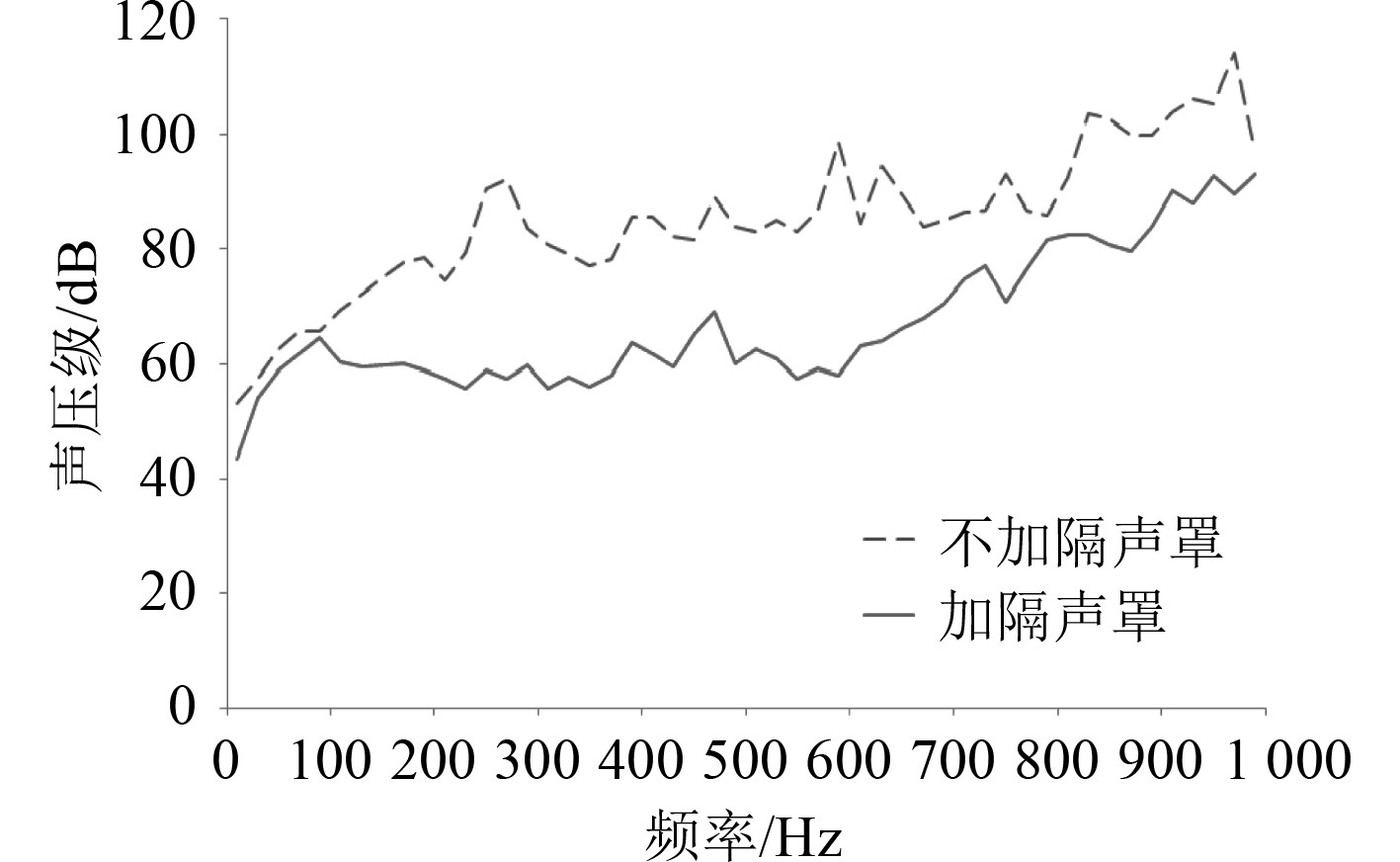
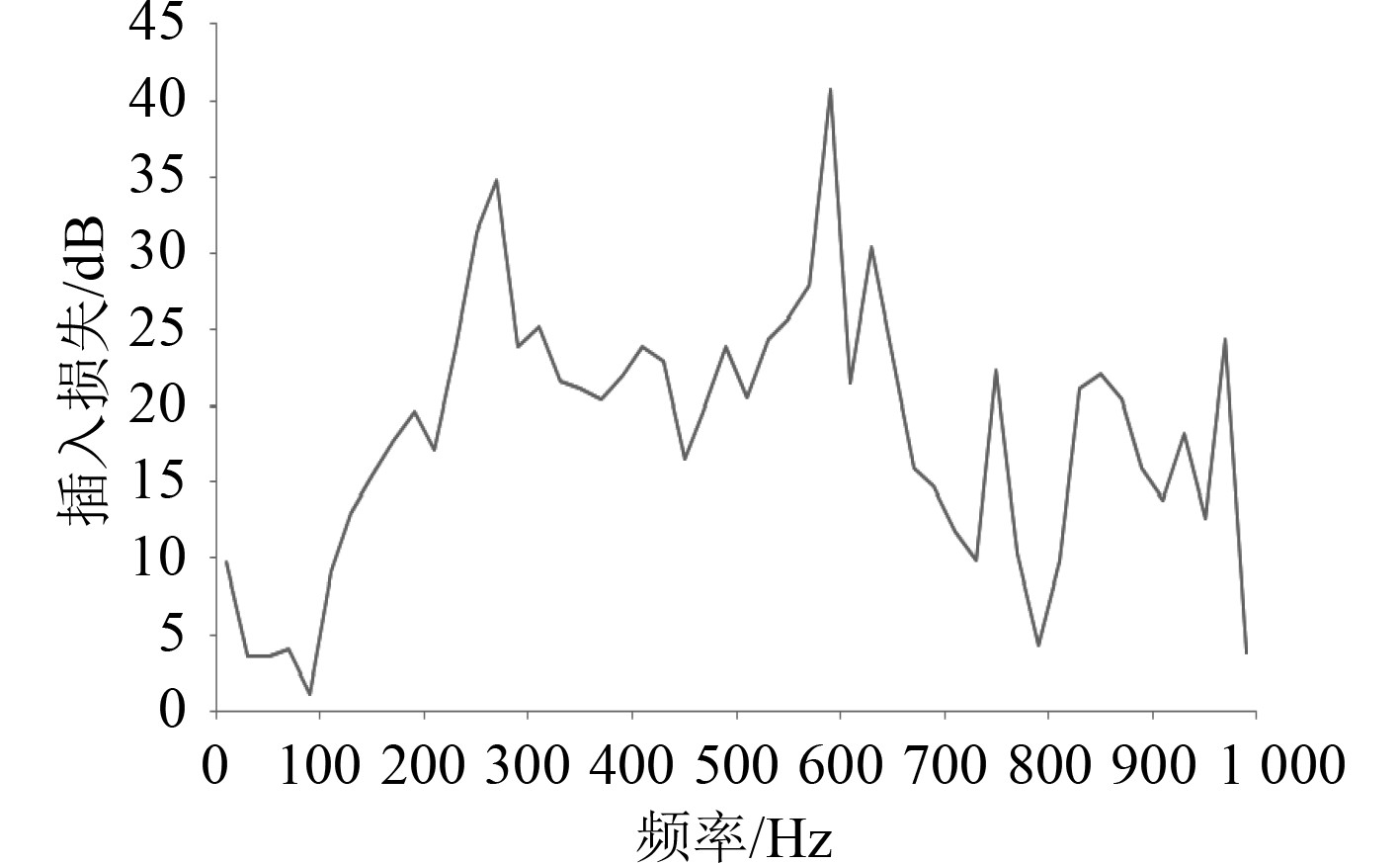
运用边界元的方法计算出空压机组浮筏隔振系统的外场声辐射,进而能够获得各项声学参数。图16为隔声罩影响下空压机组浮筏隔振系统声压级频谱图。图17为隔声罩结构的插入损失曲线图。从图中可以看出:安装隔声罩结构后,声压级在整个频率范围内都有不同程度的下降,0~100 Hz范围内隔声罩隔声效果较差,最低为1.19 dB,这可能是引起了结构的共振,振动噪声变大;100~800 Hz范围内隔声罩隔声效果较好,最高可达40.77 dB。总体来讲,隔声罩结构能够使空压机组浮筏隔振系统隔声效果变好,平均能有18.22 dB的隔声效果。所以在中间浮筏上面加装隔声罩能够有效地隔离空压机组的噪声,极大降低机舱内的空气噪声。
|
图 16 空压机组浮筏隔振系统声压级频谱图 Fig. 16 Sound pressure level spectrum |
|
图 17 隔声罩结构的插入损失曲线图 Fig. 17 Insert loss curve |
噪声测量中,以GB/T 3767-1996 《声压法测定噪声源反射面上方近似自由场的工程法》为测试标准[20],以距带隔声罩空压机组浮筏隔振系统中心上前后左右4 m处布置5个测点。机组在970 r/min转速下运行。测试仪器是4189型传声计、3050-A-060型信号采集分析系统等。测量设备外围声压级,测试频率范围为1/3倍频程0 Hz~1 kHz[21]。
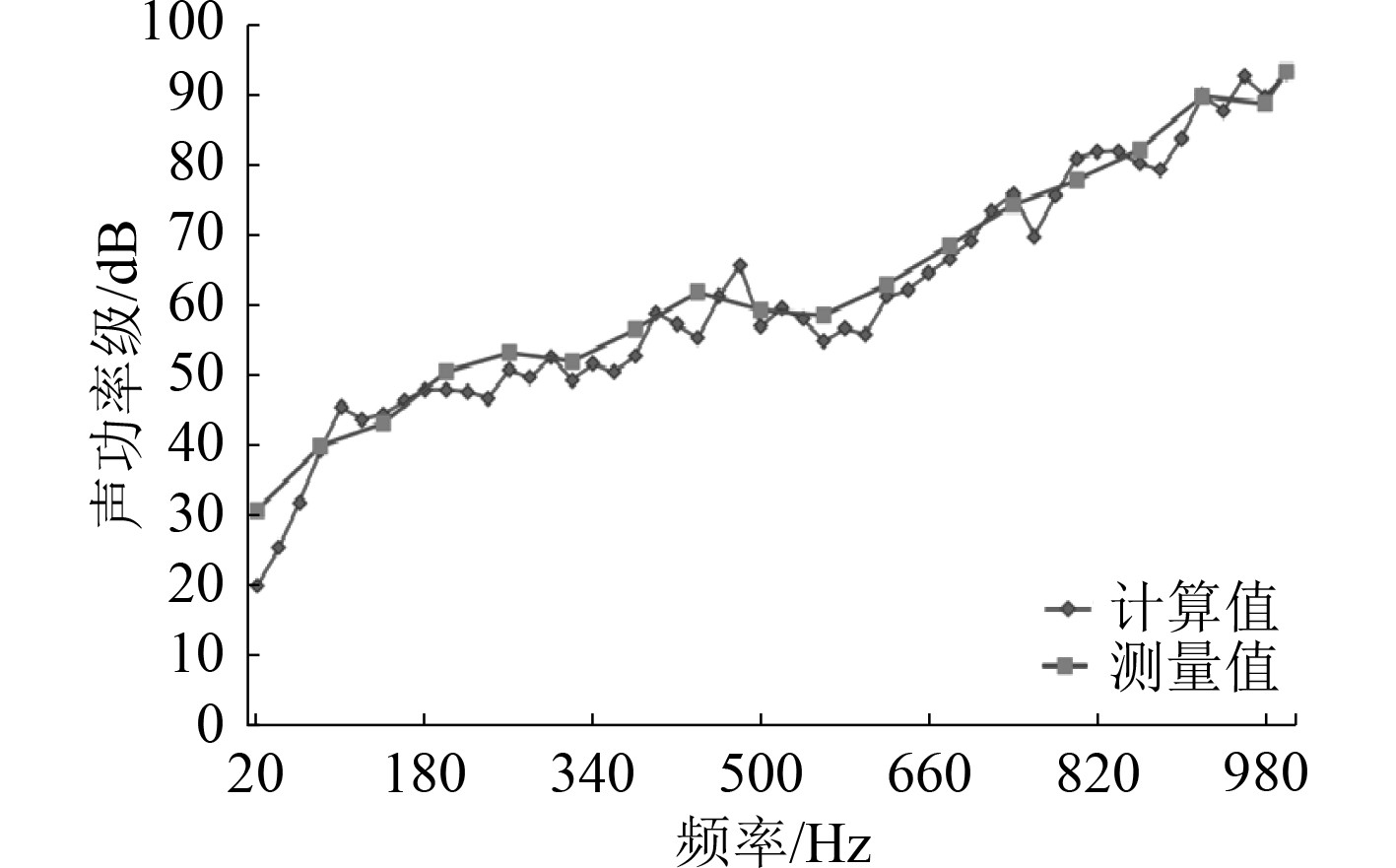
图18为带隔声罩空压机组浮筏隔振系统辐射噪声测量声功率图。整个系统辐射噪声实测指标与仿真计算值基本相符,误差约3.25 dB,与实测相比误差约为4.62%,满足技术指标要求,验证了此方法计算动力装置辐射噪声的准确性。部分构件漏声会产生上述误差,还有仿真计算时,没有充分考虑空压机组进排气管的气动噪声问题。
|
图 18 系统辐射噪声测量声功率图 Fig. 18 Sound power diagram of system radiated noise measurement |
为了提高带隔声罩空压机组浮筏隔振系统的隔声性能,提出3种隔声罩设计方案。现将隔声罩钢板厚度分别改为2 mm,3 mm和5 mm,内壁吸声材料厚度不变,对带隔声罩空压机组浮筏隔振系统隔声性能进行优化,运用的方法是前面使用的有限元和边界元相结合的方法。
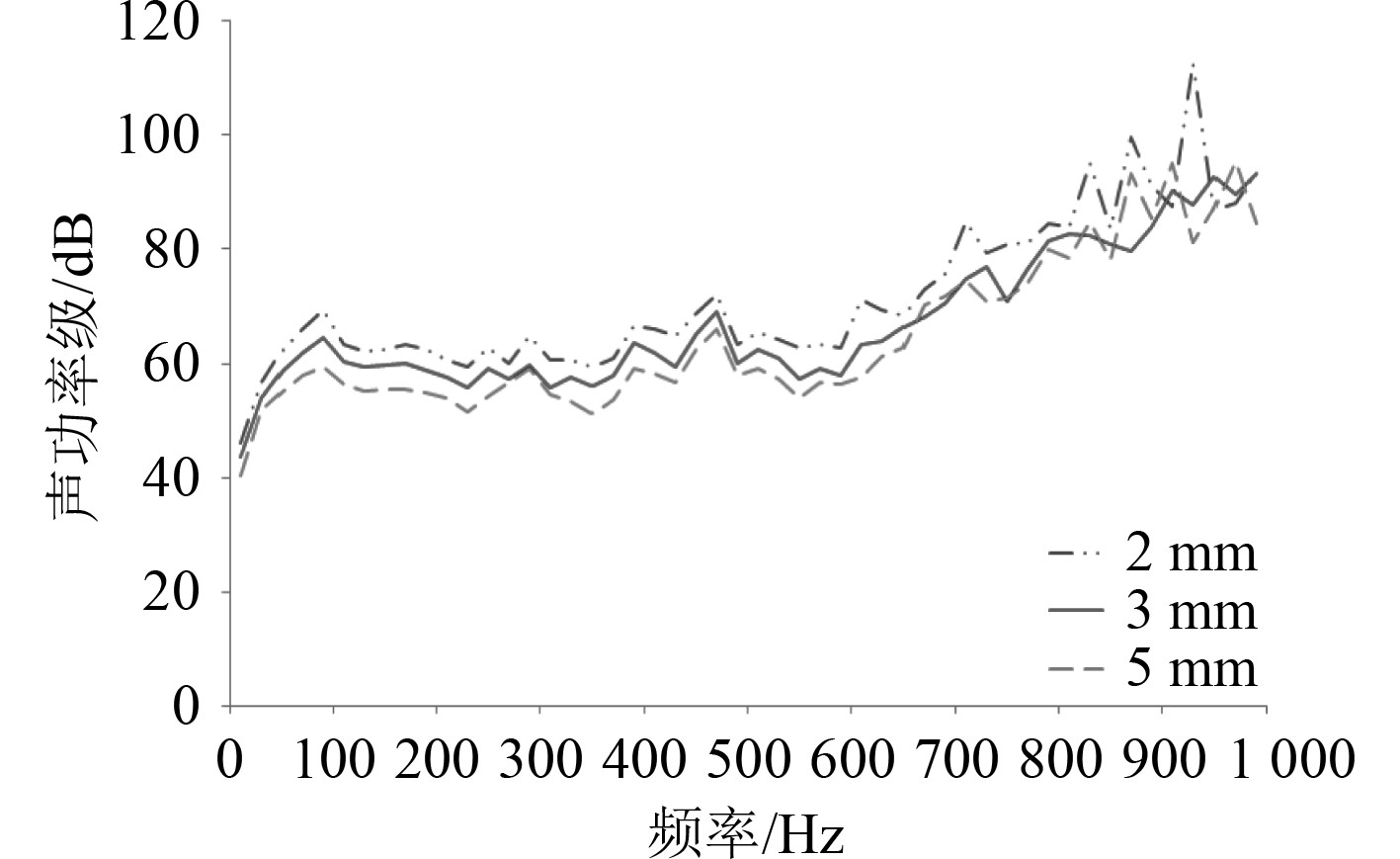
图19为隔声罩钢板厚度对带隔声罩空压机组浮筏隔振系统隔声性能影响图。从图中可以看出增加隔声罩钢板厚度能够减小带隔声罩空压机组浮筏隔振系统声场声功率级,提高系统的隔声性能。采用2 mm厚隔声罩钢板的系统外声场声功率级平均为71.5 dB,采用3 mm厚隔声罩钢板的系统声场声功率级平均为66.2 dB,采用5 mm厚隔声罩钢板的系统声场声功率级平均为64.7 dB。
|
图 19 隔声罩钢板厚度对系统隔声性能影响图 Fig. 19 Steel plate thickness influence |
为了进一步提高带隔声罩空压机组浮筏隔振系统的隔声性能,提出3种不同材料的隔声罩设计方案。将隔声罩材料分别换为钢板、铝板和胶合板,隔声罩的尺寸和厚度均为3 mm,内壁吸声材料材质、厚度也相同,对带隔声罩空压机组浮筏隔振系统隔声性能进行优化,运用的方法也是前面使用的有限元和边界元相结合的方法。表2为不同隔声罩材料的特性表。
|
|
表 2 不同隔声罩材料的特性 Tab.2 Characteristics of different sound insulation cover materials |
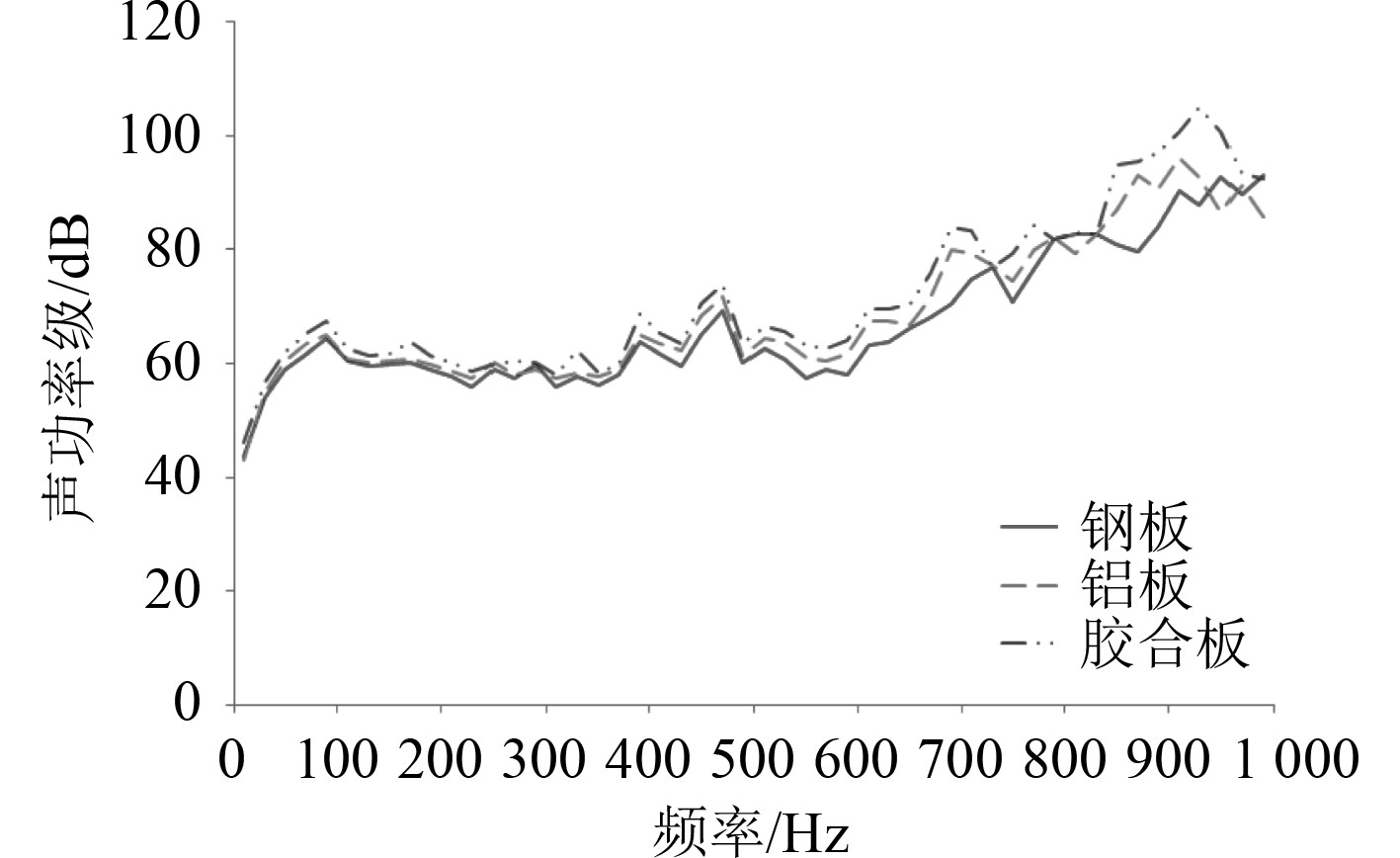
图20为采用同样方法计算的不同隔声罩材料对系统隔声效果的影响。钢板材质的隔声罩隔声效果要优于铝板和胶合板材质,采用钢板材质的隔声罩的系统外声场声功率级平均为66.2 dB,采用铝板材质的隔声罩的系统声场声功率级平均为69.0 dB,采用胶合板材质的隔声罩的系统声场声功率级平均为71.9 dB。这是因为隔声罩的隔声特性一般总是质量控制型,无论是改变钢板厚度还是选用密度较大的金属材料都能增加隔声罩重量,进而能够提高隔声效果。
|
图 20 隔声罩材料对系统隔声性能影响图 Fig. 20 Material science influence |
本文采用有限元和边界元相结合的方法,建立船用带隔声罩空压机组浮筏隔振系统声场模型。以结构振动、声辐射理论为基础,从声辐射声压级、声功率的角度出发,通过典型频率和典型测点研究带隔声罩空压机组浮筏隔振系统的声辐射。主要结论如下:
1)设计的系统平均声功率级为66.2 dB,隔声效果较好;系统上面区域辐射噪声最大,最大为75.13 dB,可以通过增加隔声罩上表面吸声材料厚度来控制上面区域噪声。
2)隔声罩结构能够使空压机组浮筏隔振系统隔声效果变好,相对于不加隔声罩的空压机组浮筏隔振系统能提高18.22 dB的隔声效果,所以在中间浮筏上面加装隔声罩能够有效地隔离空压机组的噪声,极大地降低机舱内的空气噪声。
3)通过改变隔声罩钢板厚度和隔声罩材料对带隔声罩空压机组浮筏隔振系统隔声性能进行优化,随着隔声罩钢板厚度的增加,带隔声罩空压机组浮筏隔振系统隔声性能变好,并且钢板材料的隔声罩隔声效果要优于铝板和胶合板材质的隔声罩隔声效果。
| [1] |
姚熊亮, 张阿漫. 船体振动与噪声[M]. 北京: 国防工业出版社, 2010
|
| [2] |
李清, 杨德庆, 郁扬. 舰船低频水下辐射噪声的声固耦合数值计算方法[J]. 振动与冲击, 2018, 37(3): 174-179. DOI:10.13465/j.cnki.jvs.2018.03.028 |
| [3] |
时胜国, 杨德森, 何元安. 水下结构辐射噪声工程估算方法研究[J]. 哈尔滨工程大学学报, 2002, 23(1): 43-47. DOI:10.3969/j.issn.1006-7043.2002.01.019 |
| [4] |
曹贻鹏. 船舶柴油发电机组隔振与隔声设计[D]. 哈尔滨: 哈尔滨工程大学, 2005
|
| [5] |
崔淑梅, 于天达, 宋立伟. 基于ANSYS和SYSNOIS的电机噪声仿真分析方法[J]. 电机与控制学报, 2011, 15(9): 63-67. DOI:10.3969/j.issn.1007-449X.2011.09.011 |
| [6] |
张树桢, 陈前. 柔性浮筏隔振系统的理论建模与仿真研究[J]. 船舶力学, 2012, 16(10): 1187-1198. DOI:10.3969/j.issn.1007-7294.2012.10.013 |
| [7] |
WU G, SHEN R, HUA H. Mode mechanical impedance synthesis method and its application in flexible isolation system[J]. Journal of Ship Mechanics, 2004, 8(6): 135-142. |
| [8] |
王真, 赵志高, 刘芳. 全柔性浮筏隔振系统建模与隔振性能分析[J]. 振动、测试与诊断, 2017, 37(1): 70-75. DOI:10.16450/j.cnki.issn.1004-6801.2017.01.011 |
| [9] |
方媛媛, 夏兆旺, Water T, 等. 船舶辅机浮筏半主动非线性隔振系统振动特性分析[J]. 船舶力学, 2019, 23(5): 583-590. DOI:10.3969/j.issn.1007-7294.2019.05.010 |
| [10] |
毕风荣, 杨晓, 马腾. 小型柴油发电机组隔声罩结构优化设计研究[J]. 机械科学与技术, 2018, 37(1): 1-7. DOI:10.13433/j.cnki.1003-8728.2018.0101 |
| [11] |
孙洪军, 钱网生, 何金龙. 压缩机机组隔声罩设计与应用[J]. 噪声与振动控制, 2007, 37(5): 125-127. DOI:10.3969/j.issn.1006-1355.2007.05.034 |
| [12] |
邹祥依, 江国和, 甄松刚, 等. 船用带隔声罩空压机组浮筏隔振系统设计[J]. 上海海事大学学报, 2015, 36(4): 68-73. DOI:10.13340/j.jsmu.2015.04.014 |
| [13] |
荣先成. 有限元法[M]. 成都: 西南交通大学出版社, 2006
|
| [14] |
GB50040-96. 动力机械基础设计规范[S]. 北京: 世界知识出版社, 1997
|
| [15] |
李增光. 机械振动噪声设计入门[M]. 北京: 化学工业出版社, 2013
|
| [16] |
祝家麟, 袁政强. 边界元分析[M]. 北京: 科学出版社, 2009
|
| [17] |
IBRAHIM R. Recent advances in nonlinear passive vibration isolators[J]. Journal of Sound and Vibration, 2008, 314(3-5): 371-452. DOI:10.1016/j.jsv.2008.01.014 |
| [18] |
蒋坤, 向阳, 张波, 等. 不同耦合模式水下结构声辐射计算方法研究[J]. 噪声与振动控制, 2019, 6(3): 11-17,34. DOI:10.3969/j.issn.1006-1355.2019.03.003 |
| [19] |
CHOI W, XIONG Y, SHENOI R. Power flow analysis for a floating sandwich raft isolation system using a higher-order theory[J]. Journal of Sound and Vibration, 2009, 319(1): 228-246. |
| [20] |
张关根, 郭乃林, 李江翔. 浮筏减振降噪技术在某型海洋测量船上的应用[J]. 船舶, 2000(3): 29-34. DOI:10.3969/j.issn.1001-9855.2000.03.005 |
| [21] |
ISO 3744-2010. 声压法测定噪声源反射面上方近似自由场的工程法[S] . 国际标准化组织, 1996
|
 2022, Vol. 44
2022, Vol. 44
