2. 上海交通大学 船海计算水动力学研究中心,船舶海洋与建筑工程学院,上海 200240
2. Computational Marine Hydrodynamics Lab(CMHL), School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China)
船舶在航行过程中遇到与船首向呈一定夹角的斜流情况很常见,如船舶航线与水流方向不一致,或者船舶操舵以改变航向或者回转时。处于斜向流场中的船舶,不仅船舶的航行阻力会出现变化,螺旋桨与舵之间的流场特性也将发生变化,而且舵是活动部件,转舵过程对螺旋桨的影响也不能忽略,因此研究斜向流场中桨-舵系统的性能变化规律,对于提升船舶性能、促进节能都有重要意义。
螺旋桨与舵之间相互作用规律直接影响着船舶操纵与推进性能、能耗效率等,因此始终是船舶水动力研究的重要课题。当前研究主要集中在固定舵角或较小舵角对桨-舵系统的水动力特性。Molland与Turnock[1-3]利用风洞试验先后研究了螺旋桨载荷对舵性能、船舶性能的影响、不同漂角下螺旋桨对平板舵性能的影响以及水流矫直效应、桨舵之间相互作用对船舶推进能量效率的影响。何磊等[4]基于势流理论对桨-舵系统进行非定常计算,指出Lamb-Oseen涡模型对于消除舵面周围强涡及高诱导速度影响有显著优势,非定常计算所得舵系数小于时间平均格式计算所得。何苗[5]基于势流理论,提出了一种流场中含有2个升力面的桨-舵系统水动力研究方法,计算结果精度较高。Charles等[6]采用CFD方法研究了斜流中不同轴向长度整流板对桨-舵系统影响的变化规律,结果表明较短尺寸的整流板对于桨-舵系统所产生的水流矫直效应更加明显。Krasilnikov等[7]以低速运行的桨-舵系统为研究对象,对比分析了不同网格划分方法对计算精度的影响。孙帅等[8]利用分离涡模型研究了敞水螺旋桨尺度效应对于尾部涡结构、流场等的影响,结果表明在轻载荷工况下,全尺度螺旋桨的平均展向环流较大,表现出的脱落涡较强。王超等[9]利用滑移网格技术研究了桨舵之间轴向距离对于桨-舵干扰的影响,指出桨舵之间轴向距离增大,则桨舵之间的相互干扰减弱,且舵的存在对桨后剖表面的各向诱导速度影响有所不同。张祎[10]以特种舵及常规螺旋桨构成的节能桨-舵系统为研究对象,研究了桨舵轴向间距大小、−4°~4°舵角对螺旋桨水动力特性的影响。A Lungu[11]运用不可压缩分离涡模型对斜流中的敞水螺旋桨进行研究,结果表明相较于直流中,斜流中螺旋桨所受到的推力有所减小。Guilmineau等[12]则运用不同的湍流模型分别研究斜流、直流中桨后涡结构演变,研究表明RANS-LES湍流模型对于涡的演变模拟较好。胡健等[13]利用LES(大涡)湍流模型,借助Q-Criterion方法对斜流中螺旋桨的尾流及涡的演变进行研究,指出斜流角改变引起桨后涡偏移,但偏移角度与斜流角存在差异。
本文以肥大型油船KVLCC2的桨-舵系统为研究对象,选用SS
为真实还原船舶航行中所处的流场,假定螺旋桨在不可压缩流体中进行定轴转动,且流场特性为:均匀来流、斜向、粘性流场。故本文在求解过程中采用不可压缩流动RANS方程,其中作为控制方程的连续方程和动量方程如下:
| $ \frac{{\partial {U_i}}}{{\partial {x_i}}} = 0,$ | (1) |
| $ \frac{{\partial {U_i}}}{{\partial t}} + {U_j}\frac{{\partial {U_i}}}{{\partial {X_i}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + \frac{\mu }{\rho }\frac{{{\partial ^2}{U_i}}}{{\partial {x_j}\partial {x_j}}} - \frac{1}{\rho }\frac{{\partial \left( {\rho \overline {{u_i}{u_j}} } \right)}}{{\partial {x_{ij}}}}。$ | (2) |
式中:
对计算的精度和效率两方面进行综合考虑,本文所选用的湍流模型为经过Menter改进所得的SS
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {k_{{u_i}}}} \right)}}{{{\partial _{{x_i}}}}} = \frac{\partial }{{{\partial _{{x_j}}}}}\left[ {{\varGamma_k}\frac{{{\partial _k}}}{{{\partial _{{x_j}}}}}} \right] + {G_k} - {Y_k} $ | (3) |
| $ \frac{{\partial \left( {\rho \omega } \right)}}{{{\partial _t}}} + \frac{{\partial \left( {\rho {\omega _{{u_i}}}} \right)}}{{{\partial _{{x_i}}}}} = \frac{\partial }{{{\partial _{{x_j}}}}}\left[ {{\varGamma_\omega }\frac{{{\partial _k}}}{{{\partial _{{x_j}}}}}} \right] + {G_\omega } - {Y_\omega } + {D_\omega } $ | (4) |
式中:
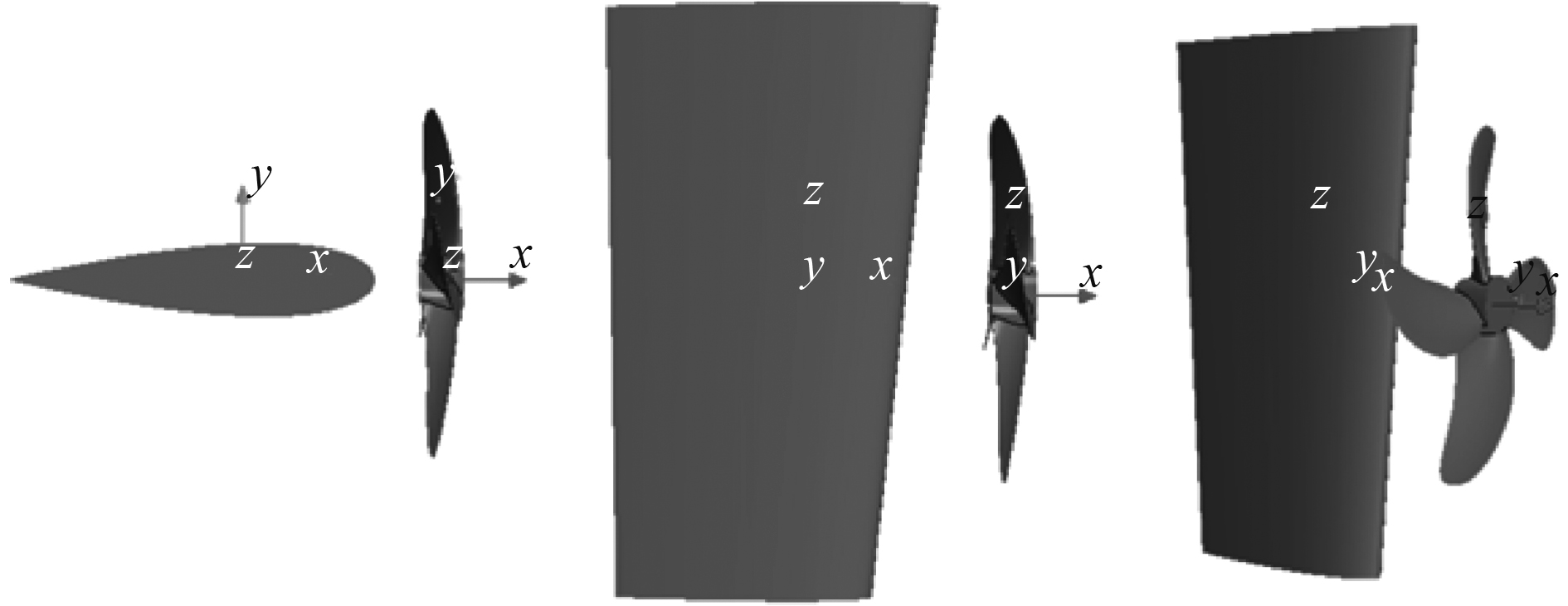
本文所选取的研究对象为肥大型船舶KVLCC2的附体:KP458螺旋桨与NACA0018舵,模型缩尺比为1∶46.426。螺旋桨与舵的模型如图1所示,几何参数的详细数据如表1所示。
|
图 1 桨-舵系统模型 Fig. 1 Propeller-rudder system model |
|
|
表 1 桨-舵系统几何参数 Tab.1 Geometric parameters of propeller-rudder system |
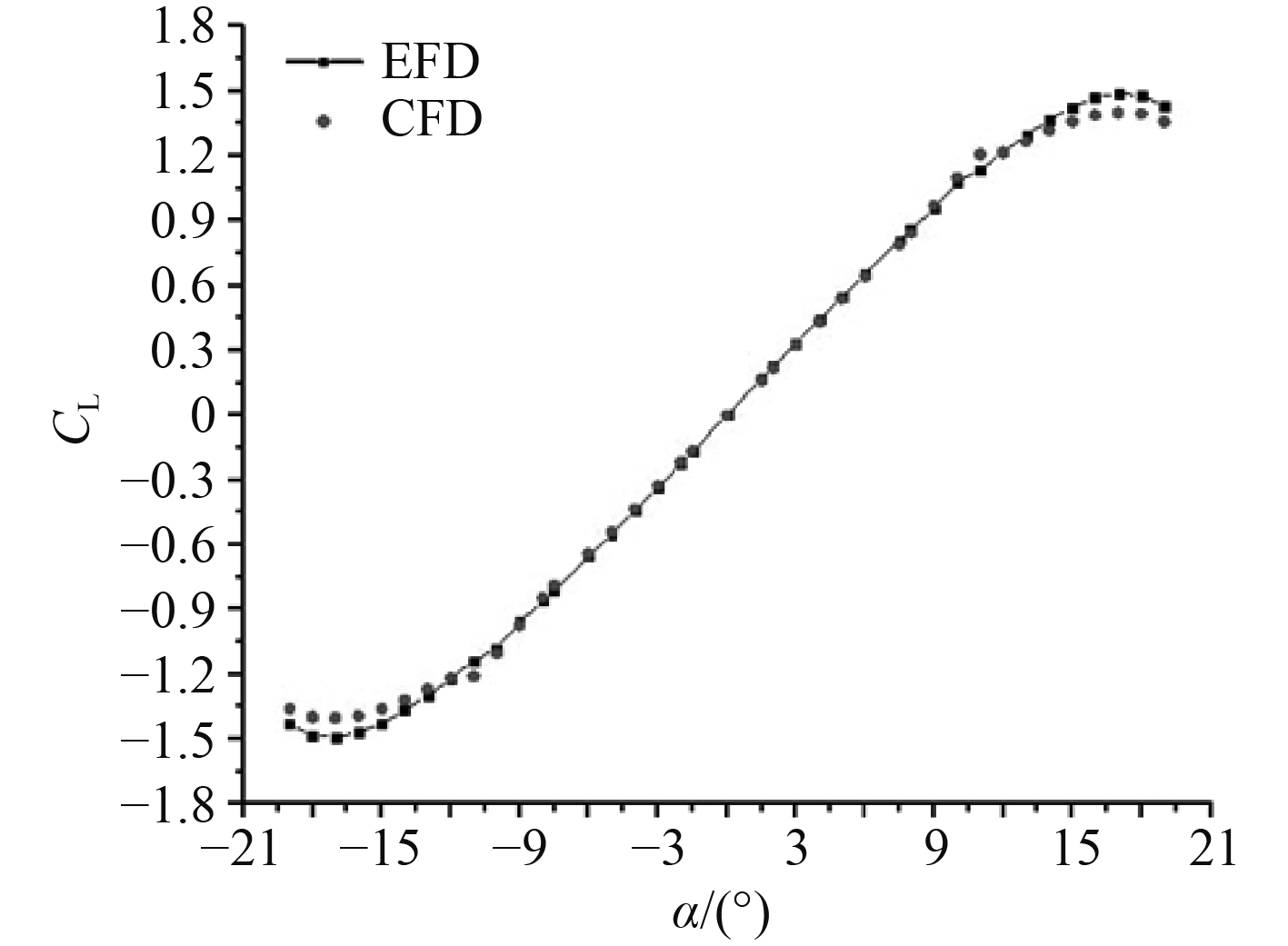
NACA0018舵的翼型数据取自Airfoil Tools[14]。翼型验证的计算域形状及边界条件如图2所示,其中翼型弦长b为0.21 m。整个计算域采用多面体网格,翼型周围布置10层棱柱层网格,总厚度为0.02 m,Y+值控制在1左右。计算域入口水流方向与舵的夹角,即舵角的范围为

|
图 2 翼型计算域 Fig. 2 Computational domain of airfoil |
|
图 3 翼型升力曲线 Fig. 3 Airfoil lift curve |
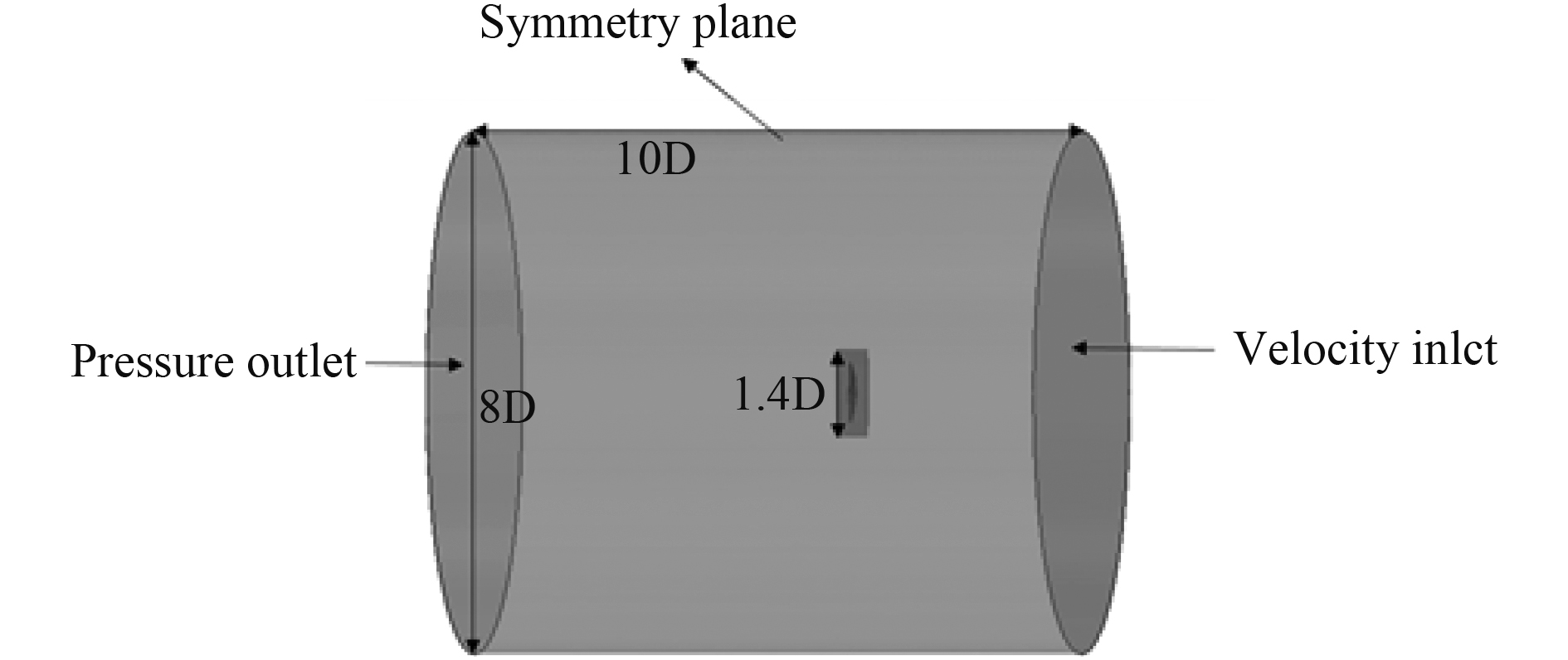
对KP458螺旋桨在进速系数J=0.1~0.7范围内的敞水特性进行数值验证。在计算中,螺旋桨转速固定为9.9 r/s,通过改变入口流速来实现进速系数的变化。计算域分为采用切割体网格的静域和采用多面体网格的旋转域,两区域之间通过Interface交界面实现数值交换。整个计算域的具体尺寸和边界条件设定如图4所示,其中流场入口、出口距螺旋桨盘面处距离分别为4 D与6 D。整体网格基础尺寸设置为0.02 m,对螺旋桨设置10层棱柱层,总厚度为0.1 mm。
|
图 4 KP458桨敞水计算域 Fig. 4 Open water calculation domain of KP458 propeller |
计算所得结果与试验数据对比曲线,如图5所示。可知,转矩系数

|
图 5 KP458桨敞水性能曲线 Fig. 5 Open water performance curve of KP458 propeller |
选取进速系数J=0.1与0.5进行网格无关性验证,将网格细化率设置为
|
|
表 2 网格收敛性分析 Tab.2 Grid convergence analysis |
对比表中数据可知:模拟计算所得水动力系数与试验结果之间的误差会随网格数量的增加而减小,即随网格数量的增加,螺旋桨的水动力系数呈现严格的单调收敛,且2种工况下的误差均在5%以内。在对计算精度与计算效率进行综合考虑后,采用中等网格中的相关网格划分设置进行下一步研究。
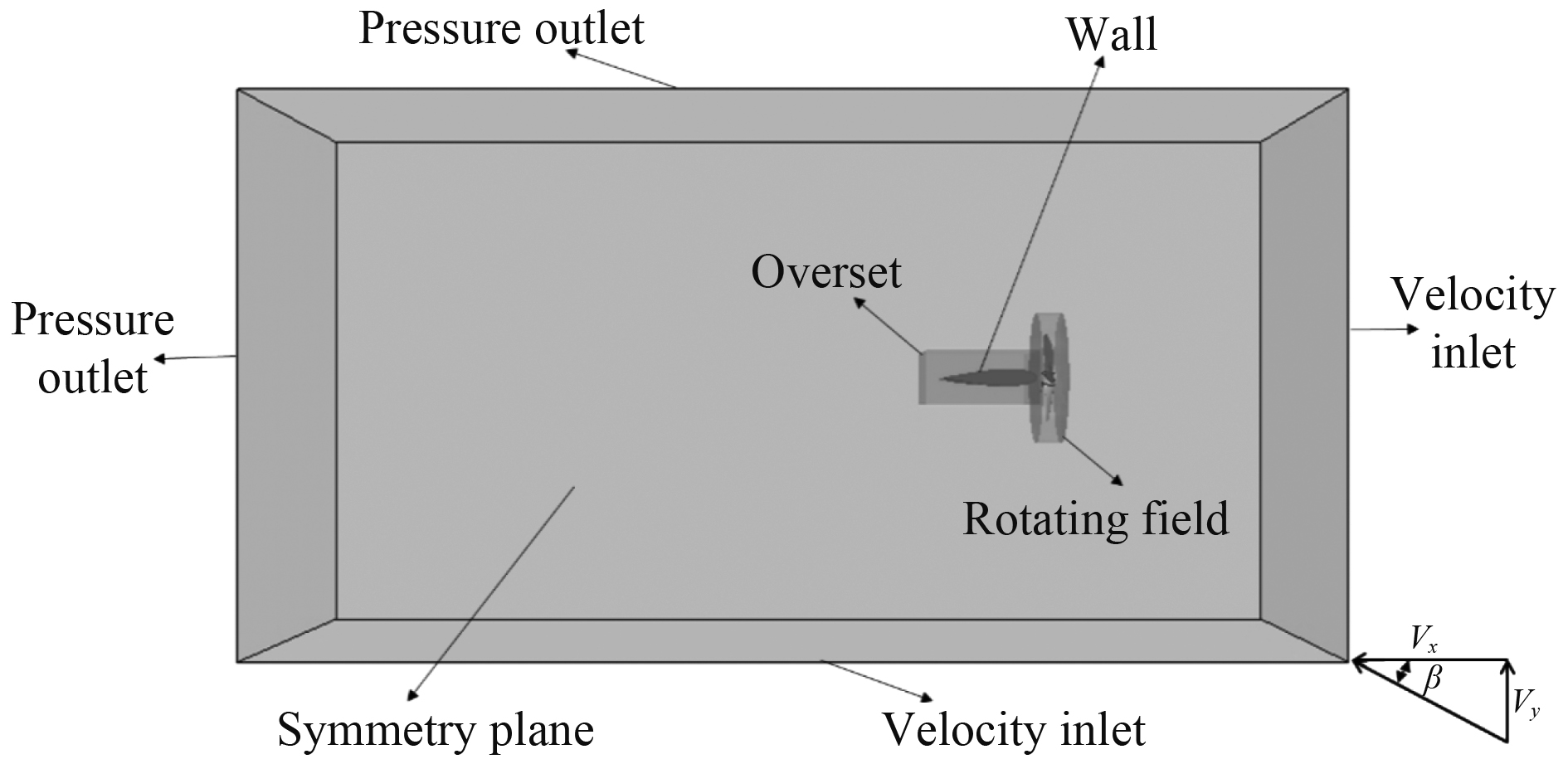
2.2 桨-舵系统的数值设置图6为计算域边界条件设置示意图,计算域分为螺旋桨运动的旋转域、舵运动的重叠网格域以及背景域,具体尺寸及边界类型设置如表3所示。为保证桨后涡充分发展,流场出口设置在距离螺旋桨盘面8 D位置处。将上、下边界设定为对称平面是为避免水深对计算影响。其中,入口的速度设置为:
|
图 6 流场边界条件示意图 Fig. 6 Schematic diagram of smooth boundary conditions |
|
|
表 3 计算域尺寸及边界类型设置 Tab.3 Calculation field size and boundary type setting |
| ${V_x} = - V \times cos\beta ,$ |
| $ {V_y} = V \times cos\beta。$ |
式中:
计算模型分为背景域、旋转域及重叠区域,其中旋转域为直径大小1.5 D的圆柱,重叠区域为契合舵尺寸的长方体。背景域及舵运动的重叠区域运用切割体网格及棱柱层网格,旋转区域采用多面体网格,边界层参数设置延续应用上文验证中的参数。为满足捕捉桨后涡精度要求,对桨后区域进行加密,网格布置如图7所示。
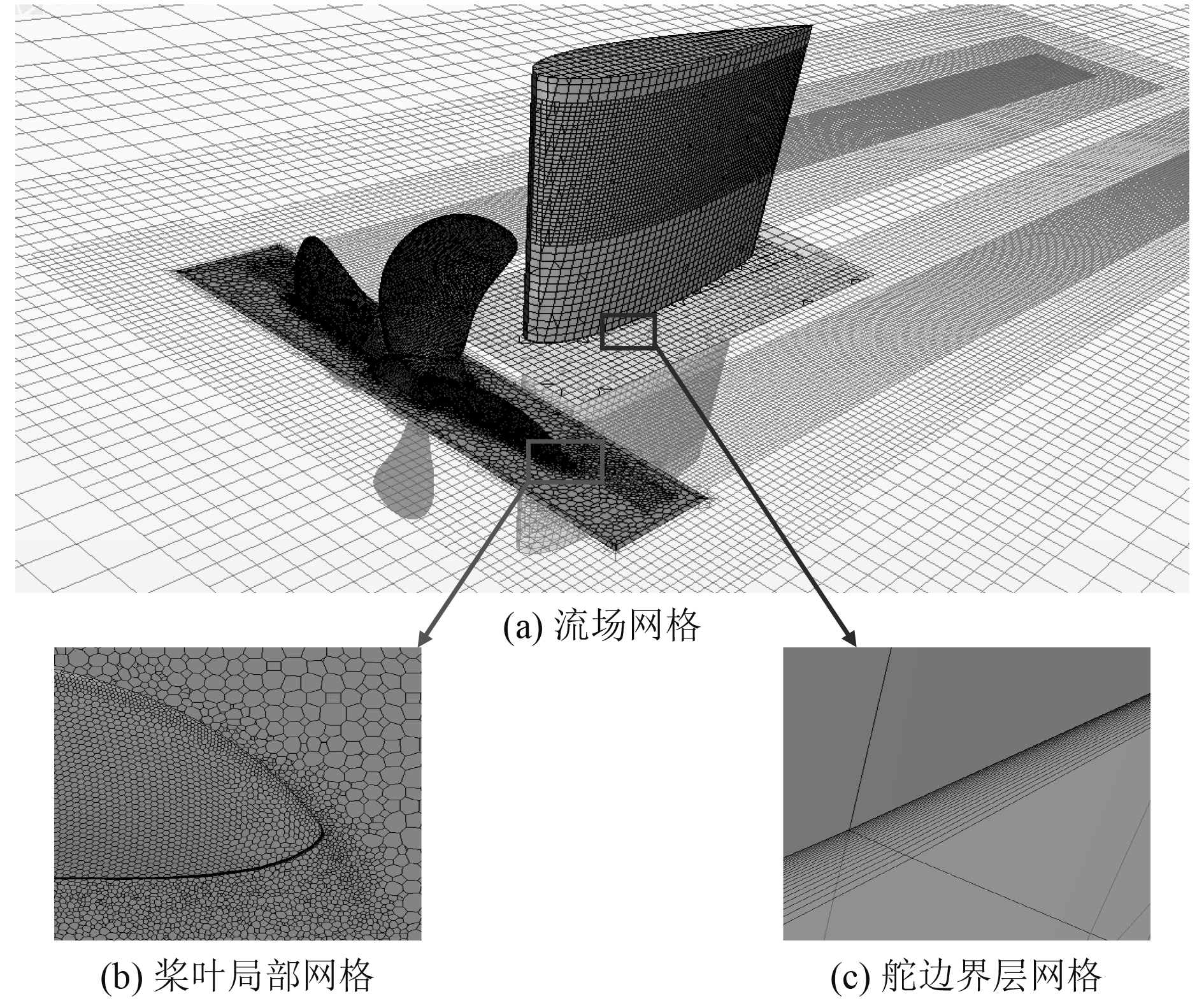
|
图 7 流场及桨-舵系统局部网格示意图 Fig. 7 Flow field and partial grid diagram of propeller-rudder system |
以KVLCC2的Fr=0.142为中间基准,选择3个傅汝德数工况来设置计算域的入口水流速度,并考虑了斜流角、舵角以及操舵速率对于螺旋桨性能的影响。计算工况的具体参数如表4所示。
|
|
表 4 计算工况参数 Tab.4 Calculation of working condition parameters |
图8为舵角
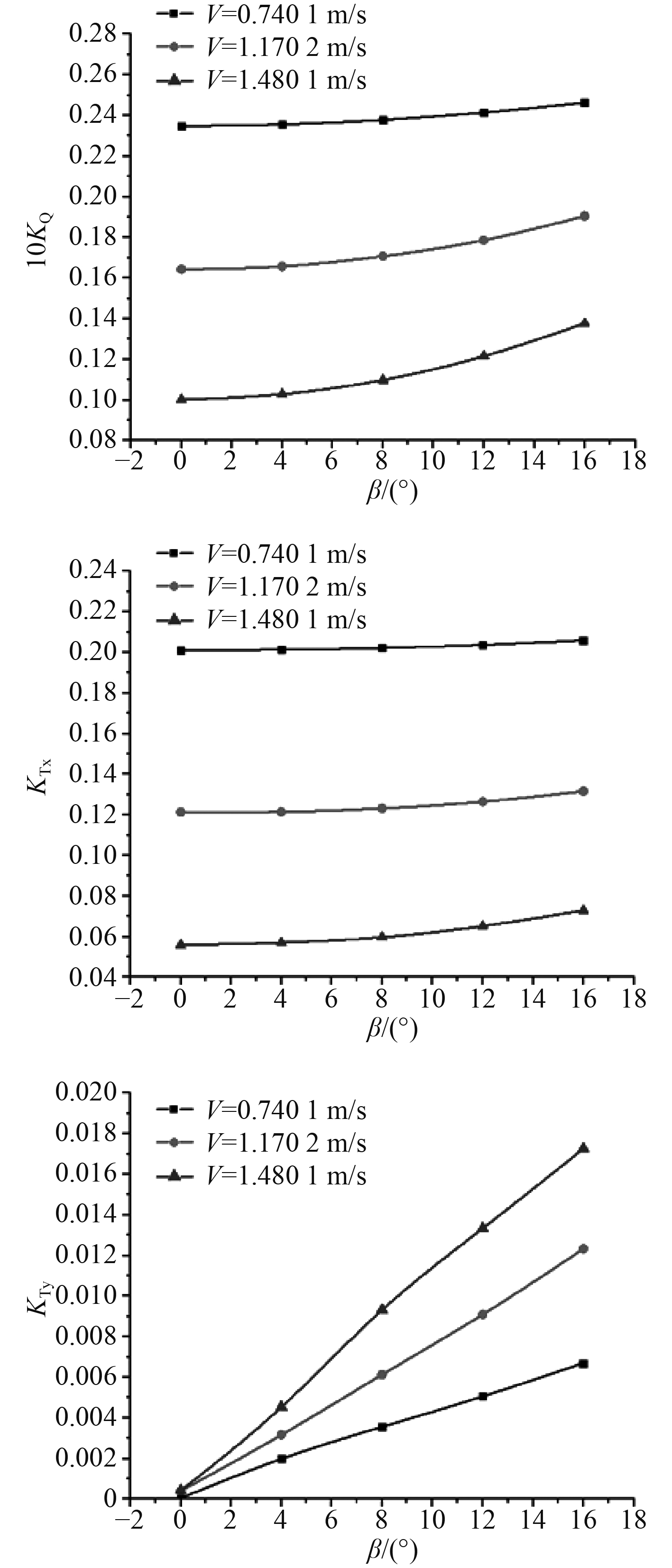
|
图 8 斜流角、流速对螺旋桨水动力特性影响 Fig. 8 Influence of flow angle and velocity on hydrodynamic |
图9为不同流速和斜流角下,螺旋桨所产生推力与横向力之间比值关系的曲线图。可知:随着斜流角的增大,螺旋桨所产生的推力、横向力均逐渐增大,但是相较于推力的变化,横向力变化幅值较大。这主要是由于斜流促使螺旋桨产生横向力,横向力随斜流角的增大而增大,且横向力的增长率在重载情况下较大;推力系数及横向力系数之间的比值会随斜流角的增大而增大,且在较高来流速度工况下两者之间占比关系更加突出。通过对比推力系数及横向力系数的数值可知:随着斜流角的增加,螺旋桨所产生的横向力逐渐增加且增幅最大,将影响螺旋桨和桨轴的强度,其脉动压力产生的振动和噪声也将逐渐显著。

|
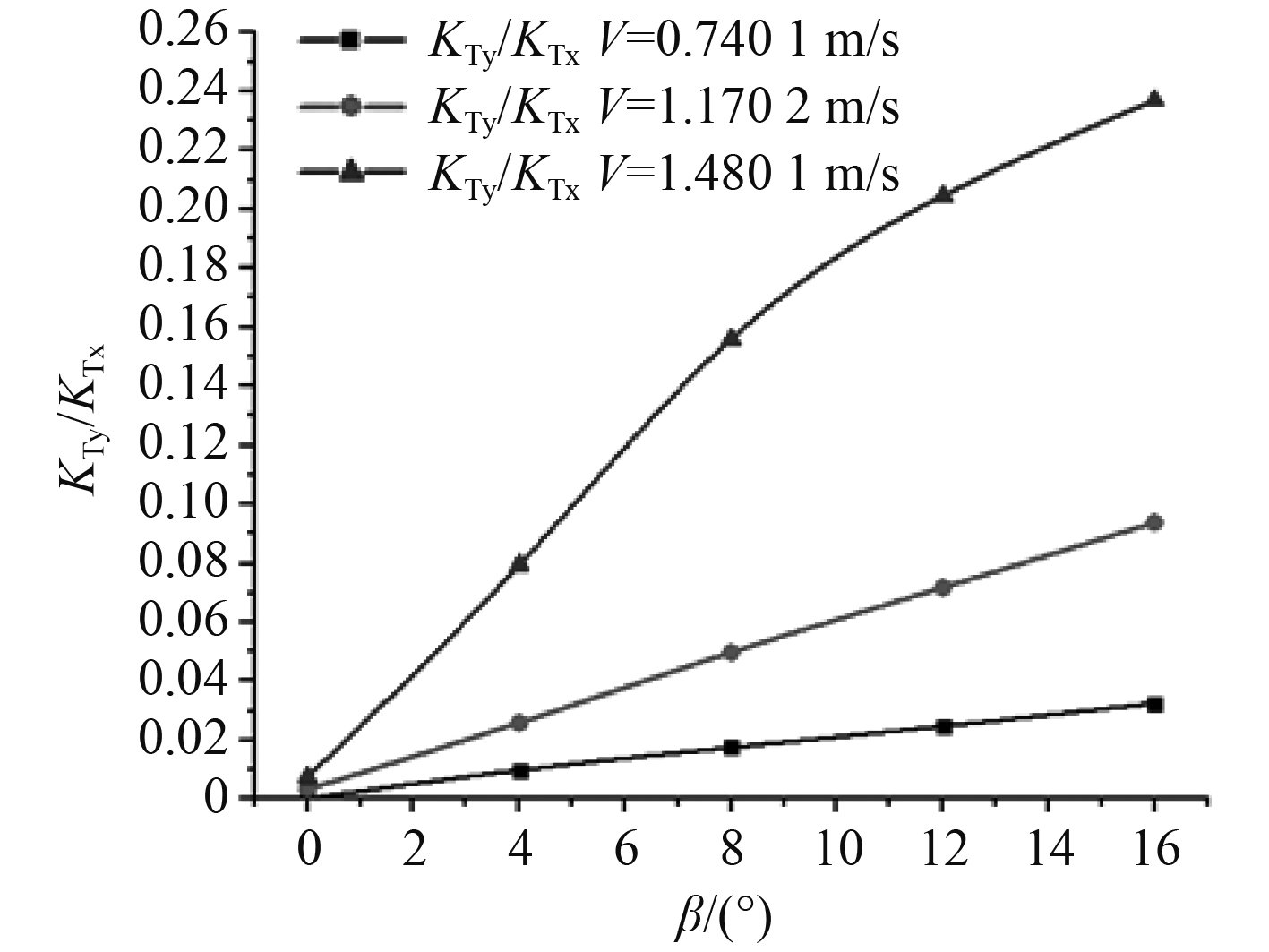
图 9 不同流速和斜流角下,推力和横向力比值的变化曲线 Fig. 9 Variation curves of the ratio of thrust to lateral force under different flow velocities and oblique flow angles |
如图10所示,固定舵角下随斜流角度增大,螺旋桨的推力、横向力及扭矩均有所增大。图11为流速V=1.1702m/s,斜流角
|
图 10 固定舵角,不同斜流角下螺旋桨水动力特性变化曲线 Fig. 10 Fixed rudder angle, propeller hydrodynamic characteristics change curve under different oblique flow angle |

|
图 11 斜流角β=12°,不同舵角下螺旋桨水动力变化曲线 Fig. 11 Variation curve of propeller hydrodynamic characteristics under different rudder angle with oblique flow angle β=12° |
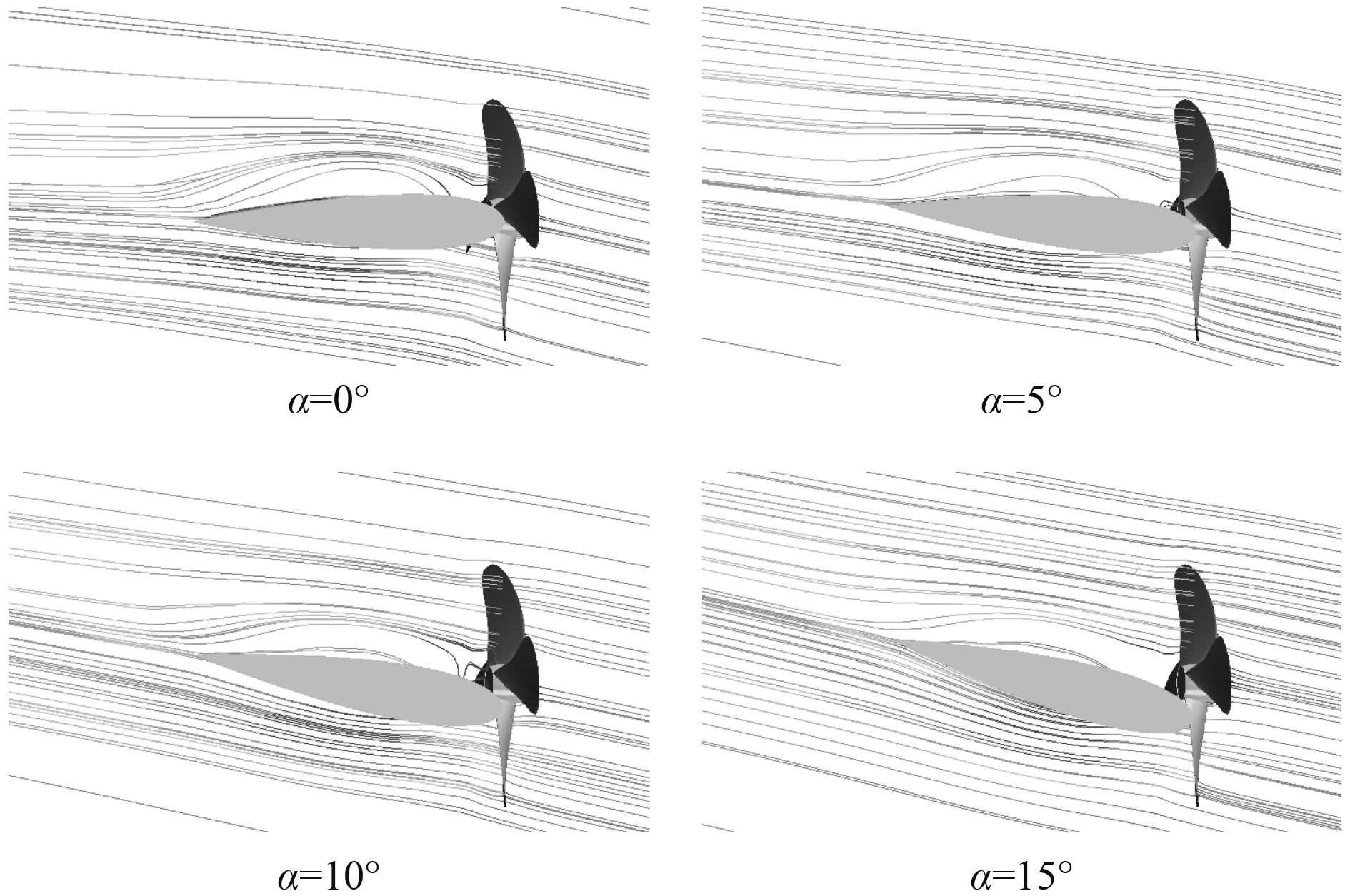
|
图 12 斜流角β=12°,不同舵角工况下流场分布流线图 Fig. 12 Streamline diagram of flow field distribution under different rudder angles with oblique flow angle β = 12 |
在斜流角、桨后舵角的影响下,螺旋桨尾涡方向及涡量强度会发生变化。图13为不同斜流角下的平面涡量图,其中颜色矢量代表涡量强度。可知,桨后涡随斜流角的变化而发生偏移,但偏移角度略小于斜流角。在舵角、斜流角均保持在

|
图 13 斜流角对桨后涡影响的平面涡量图Z=0(上侧为左舷,下侧为右舷) Fig. 13 Plane vorticity diagram Z=0 of the influence of oblique flow angle on the vortex behind propeller (upper is port side and lower is starboard side) |
图14和图15分别为不同斜流工况下桨后涡的三维结构图。借助于Q-Criterion函数对桨后涡结构进行捕捉,其中Q=20,并以轴向速度函数进行着色,颜色深浅代表轴向速度大小。由图14已知,随斜流角增大,螺旋桨毂涡及舵根涡偏移程度增大,并对右舷梢涡、随边涡产生影响,主要体现在右舷梢涡、随边涡与毂涡发生融合。而由图15已知,螺旋桨所产生的右舷梢涡发展较为完整,但部分梢涡在脱离后随斜流角增大逐渐向右舷扩散。

|
图 14 不同斜流工况下桨后涡结构图(左舷视图) Fig. 14 Structure diagram of vortex behind propeller under different oblique flow conditions (port side view) |

|
图 15 不同斜流工况下桨后涡结构图(右舷视图) Fig. 15 Structure diagram of vortex behind propeller under different oblique flow conditions (starboard view) |
图16为斜流角

|
图 16 舵角对桨后涡演变影响的平面涡量图Z=0(上侧为左舷,下侧为右舷) Fig. 16 Plane vorticity diagram Z=0 of the influence of rudder angle on the evolution of vortex behind propeller (upper is port side and lower is starboard side) |
本文以KVLCC2船的桨-舵系统为研究对象,主要分析了斜流中斜流角、来流速度、舵角对螺旋桨水动力特性及桨后涡演化的影响规律,得出以下结论:
1)舵角
2)在固定流速斜向流场中,操舵能够减小横向力,且横向力与舵角之间呈负相关。
3)流速及舵角一定时,桨后涡偏移角度随斜流角增大而增大,右舷梢涡强度逐渐增大,毂涡强度增大且吸附于舵左表面;在毂涡偏移的影响下,螺旋桨左舷梢涡、随边涡与毂涡出现融合,部分右舷梢涡在脱离后向左舷扩散。
4)流速及斜流角一定时,桨后毂涡随舵角增大逐渐淤积于舵面首部,部分脱离的毂涡强度逐渐增大,有与左舷梢涡融合的发展趋势。
本文分析结果为了解斜流中操舵对螺旋桨水动力性能的影响提供了参考意义,可为船舶斜航时的水动力性能研究提供技术参考,但工程中需以实际工程情况为准。
| [1] |
MOLLAND A F, TURNOCK S R. The design and construction of model ship propeller blades in hybrid composite materials[J]. Composites Manufacturing, 1991, 2(1): 39-47. DOI:10.1016/0956-7143(91)90157-C |
| [2] |
MOLLAND A F , TURNOCK S R , SMITHWICK J . Design studies of the manoeuvring performance of rudder-propeller systems[M]. Elsevier, 1998.
|
| [3] |
MOLLAND A F, TURNOCK S R. A propeller thrust and torque dynamometer for wind tunnel models[J]. Strain, 2010, 38(1): 3-10. |
| [4] |
HE L, KINNAS S A. Numerical simulation of unsteady propeller/rudder interaction[J]. International Journal of Naval Architecture and Ocean Engineering, 2017, 9(6): 677-692. DOI:10.1016/j.ijnaoe.2017.02.004 |
| [5] |
何苗, 黄胜, 王超, 常欣. 桨舵系统非定常水动力性能预报方法研究[J]. 华中科技大学学报(自然科学版), 2011, 39(10): 41-45. HE Miao, HUANG Sheng, WANG Chao, et al. Research on the prediction method of non-constant hydrodynamic performance of paddle and rudder system[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2011, 39(10): 41-45. |
| [6] |
BADOE C E, PHILLIPS A B, TURNOCK S R. Influence of drift angle on the computation of hull–propeller–rudder interaction[J]. Ocean Engineering, 2015, 103(15): 64-77. |
| [7] |
KRASILNIKOV V, PONKRATOV D, CREPIER P. A numerical study on the characteristics of the system propeller and rudder at low speed operation[C]//Second International Symposium on Marine Propulsors. 2011, (2): 12.
|
| [8] |
SUN S, WANG C, GUO C, et al. Numerical study of scale effect on the wake dynamics of a propeller[J]. Ocean Engineering, 2020, 196(15): 1-14. |
| [9] |
王超, 黄胜, 常欣, 郭春雨. 基于滑移网格与RNG k-ε湍流模型的桨舵干扰性能研究[J]. 船舶力学, 2011, 15(7): 715-721. WANG Chao, HUANG Sheng, CHANG Xin, et al. Study of propeller–rudder interference performance based on slip grid and RNG k-ε turbulence model[J]. Ship Mechanics, 2011, 15(7): 715-721. DOI:10.3969/j.issn.1007-7294.2011.07.002 |
| [10] |
张祎. 基于CFD桨舵组合节能装置的水动力性能研究[D]. 大连理工大学, 2020.
|
| [11] |
LUNGU A. Hydrodynamic loads and wake dynamics of a propeller working in oblique flow[J]. IOP Conference Series: Materials Science and Engineering, 2020, 916(1).
|
| [12] |
GUILMINEAU E, DENG G B , LEROYER A, et al. Numerical simulations for the wake prediction of a marine propeller in straight-ahead flow and oblique flow[J]. Journal of Fluids Engineering, 2018, 140(2).
|
| [13] |
HU Jian, ZHANG Wei-peng, GUO Hang, et al. Numerical simulation of propeller wake vortex–rudder interaction in oblique flows[J]. Ships and Offshore Structures, 2020, 1-12. |
| [14] |
http://airfoiltools.com [EB/OL]./polar/details?polar=xf-naca0018-il-1000000-n5.
|
| [15] |
http://www.simman2019 [EB/OL].kr/contents/KVLCC2.php.
|
| [16] |
冀楠, 杨春, 万德成, 等. 限制水域内船后螺旋桨梢涡特性研究[J]. 水动力学研究与进展(A辑), 2021, 36(2): 153-162. JI Nan, YANG Chun, WAN De-cheng, et al. Study of propeller tip vortex characteristics behind a ship in restricted waters[J]. Hydrodynamics Research and Progress (Series A), 2021, 36(2): 153-162. |
 2022, Vol. 44
2022, Vol. 44


