0 引　言

螺旋桨设计及优化一直是研究船舶快速化、经济性的紧迫任务之一。但由于螺旋桨参数众多、建模繁琐、水动力计算周期长等问题^[1]，长期限制船舶设计初期对螺旋桨的高效优化设计。建立一套包括螺旋桨几何变形和重构、水动力性能预测近似模型以及多目标优化的螺旋桨构型优化设计方法^[2]，对促进螺旋桨高效优化设计具有重要意义。

螺旋桨的快速建模、高效优化始终是国内外学者关注的热点研究。Ramin等^[3]采用Non-Gradinet-based Algorithm和梯度法分别对弦长、厚度以及螺距沿半径的分布进行数值优化；Florian等^[4]基于B-spline对螺距、拱度、厚度、弦长、曲率和倾角沿半径分布进行拟合，并以最大效率和最小脉动压力为目标进行了螺旋桨优化。叶礼裕^[5]结合定常面元法和克里格近似理论建立螺旋桨参数与性能特征的预测模型，并利用粒子群算法对螺旋桨参数进行了多目标优化设计。王超^[6]用试验设计方法为神经网络近似模型的建立提供足量且高质量的训练样本，利用遗传算法可以获得更广解集范围更广，而且耗时间大幅度缩减。马丹萍^[2]借助于ISIGHT优化平台，集成螺旋桨的FFD方法和CFD水动力数值评估，提出了一套从构型-数值求解-优化的螺旋桨设计优化方法。

针对目前螺旋桨研究中存在的螺旋桨模型构造周期长、水动力性能评估耗时多的问题，本文结合基于NURBS基函数的自由变形算法（NURBS-based free-from deformation，NFFD）、多输出高斯近似模型以及NSGA-Ⅱ多目标优化算法，构建一套包括螺旋桨变形重构—水动力性能快速预测—多目标优化的螺旋桨高效自动优化方法，即以NFFD技术实现螺旋桨三维模型的变形与重构，采用有限元数值仿真得出样本螺旋桨的水动力性能，基于多输出高斯近似理论建立螺旋桨水动力性能预测近似模型，结合近似模型和NSGA-Ⅱ算法对KP505桨进行多目标优化设计，验证该方法的可行性。

1 NFFD方法及螺旋桨变形控制

基于Sederberg等^[7]提出的自由曲面变形（free form deformation，FFD）方法，研究人员将FFD技术扩展为很多不同形式^[8-9]，基本包括：构建参数控制体；将变形物嵌入参数控制体；参数控制体变形；计算变形物形变后的几何坐标^[10]。基于FFD方法，Lamousin等^[8]提出NFFD算法，将顶点加权与非均匀框架结合，引入权因子和节点作为变量，增加了变形操作的自由度，从而达到更好的变形。马丹萍^[2]、张人会^[10]、李冬琴^[11]、WU^[12]、马明生^[13]、唐静^[14]已将NFFD技术应用于船型与螺旋桨变形控制与重构，并在船型与螺旋桨优化设计方面取得了丰硕成果。

螺旋桨上任意一点绝对坐标可以用局部坐标系 $ (T,U,V) $ 表示为：

$ Q = {Q_0} + tT + uU + vV。$

(1)

式中： $ {Q_0} $ 为局部部坐标原点； $ (t,u,v) $ 为点 $ Q $ 的局部坐标； $ (T,U,V) $ 为局部坐标系标准方向向量；即控制体基本坐标系。螺旋桨曲面参数化控制节点 $ {P_{i,j,k}} $ 可表示为：

$ {P_{i,j,k}} = {Q_0} + {i / {l \cdot }}T + {j / {m \cdot }}U + {k / {n \cdot }}V 。$

(2)

式中：l，m，n分别表示局部坐标在 $ (T,U,V) $ 3个方向的等分份额， $ i = 0,1, \cdots l $ ； $ j = 0,1, \cdots m $ ； $ k = 0,1, \cdots n $ 。

更进一步，螺旋桨上任一点绝对坐标可以用局部坐标表示为：

$ Q\left( {t,u,v} \right) = \sum\limits_{i = 0}^l {\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^n {{P_{i,j,k}}{B_{il}}} } } (t){B_{jm}}(u){B_{kn}}(v) 。$

(3)

式中：（v，u，t）为局部坐标；P_i,j,k为参数化控制节点； $ {B_{il}}(t) $ ， $ {B_{jm}}(u) $ ， $ {B_{kn}}(v) $ 为Bernstein基函数，表示为：

$ {B_{il}}(t) = \frac{{l!}}{{i!(l - i)!}}{t^i}{(l - t)^{(l - i)}}。$

(4)

NFFD方法利用NURBS基函数替换Bernstein函数，螺旋桨任意一点Q坐标可表示为：

$ Q\left( {t,u,v} \right) = \frac{{\displaystyle\sum\limits_{i = 0}^l {\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^n {{P_{i,j,k}}{W_{i,j,k}}{B_{il}}(t){B_{jm}}(u){B_{il}}(v)} } } }}{{\displaystyle\sum\limits_{i = 0}^l {\sum\limits_{j = 0}^m {\sum\limits_{k = 0}^n {{W_{i,j,k}}{B_{il}}(t){B_{jm}}(u){B_{il}}(v)} } } }}。$

(5)

式中，W_i,j,k为参数化控制节点P_i,j,k的权重因子。

在式（5）基础上采用deBoor-Cox递推定义^[15]和Deboor算法^[16]推导得出NURBS体三次矩阵表示方法：

$ Q(t,u,v) = \frac{{\hat {\boldsymbol{V}}{{\boldsymbol{M}}_k}(\hat {\boldsymbol{T}}{{\boldsymbol{M}}_i}{P_{i,j,k}}{W_{i,j,k}}{\boldsymbol{M}}_j^{\rm{T}}{{\hat {\boldsymbol{U}}}^{\rm{T}}})}}{{\hat {\boldsymbol{V}}{{\boldsymbol{M}}_k}(\hat {\boldsymbol{T}}{{\boldsymbol{M}}_i}{W_{i,j,k}}{\boldsymbol{M}}_j^{\rm{T}}{{\hat {\boldsymbol{U}}}^{\rm{T}}})}} 。$

(6)

式中： $\hat {\boldsymbol{T}}$ ， $\hat {\boldsymbol{U}}$ ， $\hat {\boldsymbol{V}}$ 分别为3个轴向节点矢量(T,U,V)进行参数化矩阵；M_i，M_j，M_k分别为(T,U,V)3个轴向系数矩阵。

最后将螺旋桨嵌入以上参数控制体，并对采样点进行归一化处理，利用牛顿法逆向搜索非线性方程组的最优解，即可得到螺旋桨采样点局部坐标。

在建立螺旋桨与参数体的相互关系后，保持每个采样点在参数体中相应的局部坐标(t,u,v)不变，通过改变参数化控制节点P_i,j,k或其权重因子W_i,j,k即可得到新的带权控制点矩阵，代入式（6）中即可求解得出螺旋桨变形后的局部坐标。

以KP505桨为例，利用Matlab实现了螺旋桨几何形变与重构，初始输入螺旋桨表面离散点集的坐标值，并选取0.2R，0.4R，0.6R，0.7R和0.9R处的叶宽、厚度、螺距比、曲率、倾角、最大厚度位置共30个参数作为螺旋桨形状控制设计变量，输出螺旋桨变形后的表面离散点集的坐标值。KP505桨形状控制效果和网格模型如图1所示。

2 性能预测高斯近似模型 2.1 多输出高斯近似模型

近似模型是基于不同模型函数对设计变量和设计目标组成的样本数据进行近似拟合，具有计算成本低、函数关系明确等特点^[17]。常用的近似模型方法包括：响应面法（RSM）、克里格法（Kringing）和人工神经网络技术^[18]。高斯近似是基于Kringing和贝叶斯定理的一种机器学习方法，对少量样本的高阶非线性问题具有良好的适应性^[19-22]。

给定训练样本：

$ {S_{learn}} = \left\{ {({x_i},{y_i}),i = 1, \cdots ,{N_{learn}}} \right\} ，$

其中，任意一组样本 $ ({x_i},{y_i}) $ 是随机且相互独立的，通过近似逼近，输出向量 $ {y_i} \in Y \subset R $ 与输入向量 $ {x_i} \in X \subset {R^P} $ 之间存在一些未知函数关系：

$ {\hat y_i} \approx f({x_i}) ，$

高斯近似模型为了保证预测值 $ {\hat y_i} $ 与输出向量 $ {y_i} $ 更接近真实值，将预测值 $ {\hat y_i} $ 表示为包含高斯噪声的形式：

$ {\hat y_i} = f\left( {{x_i}} \right) + \varepsilon ，$

其中， $ \varepsilon $ 表示为独立同分布的高斯噪声， $ \varepsilon \sim N\left( {0,\sigma _n^2} \right) $ 。

含有高斯噪声的预测值 $ {\hat y_i} $ 先验表示为：

$ {cov} \left( {\hat y} \right) = {K_n}\left( {X,X} \right) + \sigma _n^2I 。$

式中： $ {K_n}\left( {X,X} \right) $ 为n×n阶对称半正定协方差矩阵，该矩阵的元素 $ {K_{ij}} = k({x_p},{X_q}) $ 表示 $ {x_p} $ 与 $ {X_q} $ 之间的相关性；I为n×n阶单位矩阵。

多输出高斯近似模型协方差矩阵K表示为：

$ {K_n} = {K_f} \otimes {K_x} ，$

式中， $ {K_f} $ 和 $ {K_x} $ 分别表示输出和输入向量的相关性。

训练样本的输出向量 $ {y_i} $ 和测试点 $ {x_{test}} $ 对应的目标输出 $ f\left( {{x_{test}}} \right) $ 服从如下联合先验分布：

$ \left[ \begin{gathered} y \\ f\left( {{x_{test}}} \right) \\ \end{gathered} \right] \sim N\left( {\left[ \begin{gathered} 0 \\ 0 \\ \end{gathered} \right],\left[ \begin{gathered} K\left( {X,X} \right) + \sigma _n^2I{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k(X,{x_{_{test}}}){\kern 1pt} \\ k({x_{test}},X){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k({x_{_{test}}},{x_{_{test}}}) \\ \end{gathered} \right]} \right)。$

式中， $ k({x_{test}},X) $ 和 $ k(X,x) $ 分别为n×1和1×n阶向量。在得到y和 $ f({x_{test}}) $ 之间的联合先验概率分布之后，可以分析得到 $ f({x_{test}}) $ 的后验概率分布如下式：

$ \left. {f\left( {{x_{test}}} \right)} \right|X,y,{x_{test}} \sim N\left( {\bar f({x_{test}}),{\sigma ^2}({x_{test}})} \right) ，$

其中预测均值 $ \bar f({x_{test}}) $ 和方差 $ {\sigma ^2}({x_{test}}) $ 分别如下式：

$ \bar f({x_{test}}) = k{(X,{x_{test}})^{\rm{T}}}{\left[ {K\left( {X,X} \right) + \sigma _n^2I} \right]^{ - 1}}y ，$

$ \begin{split}{\sigma ^2}({x_{test}}) =& k({x_{test}},{x_{test}}) - k{(X,{x_{test}})^{\rm{T}}}\times \\ &{\left[ {K\left( {X,X} \right) + \sigma _n^2I} \right]^{ - 1}}k(X,{x_{test}}) 。\end{split} $

本研究中的输入向量 $ X $ 和输出向量 $ Y $ 分别表示为：

$ \left\{ \begin{gathered} X = \left\{ {x_i^a,x_i^b,x_i^c,x_i^d,x_i^e,x_i^f\cdots\cdots} \right\} ，\\ Y = \left\{ {{K_T},10{K_Q},{\eta _0},{P_{\min }}} \right\} 。\\ \end{gathered} \right. $

式中：a~f分别表示某一剖面处的叶宽、厚度、螺距比、曲率、倾角、最大厚度位置；i=0.2R，0.4R，0.6R，0.7R和0.9R，K_T，10K_Q，η₀以及P_min分别表示螺旋桨推力系数、扭矩系数、效率以及最小空化压力。

2.2 敞水性能数值仿真

以STAR-CCM+13.0流体动力学软件对KP505桨的敞水性能进行仿真计算。利用NFFD建立的原始螺旋桨曲面生成实体模型，构建非结构化六面体网格，采用k-ωSST模型，并基于MRF方法求解雷诺平均Navier-Stokes方程计算不同进速下的螺旋桨性能。

以进速系数J=0.893为例，在计算单元达到26000000时，螺旋桨的端涡和根涡现象如图2所示，即在此时实现了网格收敛。

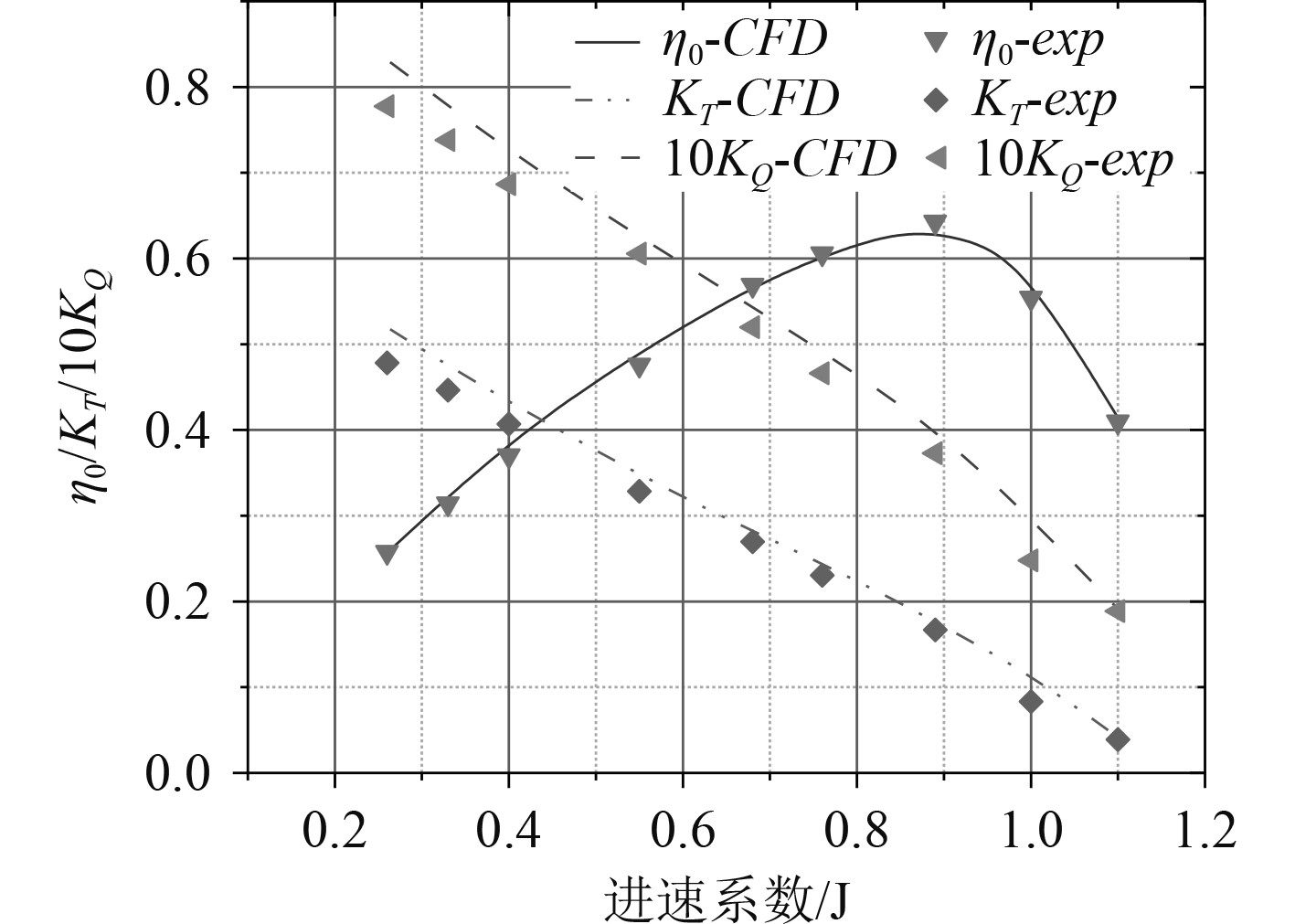
图3为进速系数J=0.2~1.1时，螺旋桨推力系统、仿真计算结果与试验结果对比，仿真与试验所得推力系数K_T、扭矩系数10K_Q、效率η₀的均方差分别为1.63%，2.41%，0.63%，说明以该软件和网格数量计算的螺旋桨敞水性能精度可信。

为给高斯近似模型提供初始样本，以0.2R，0.4R，0.6R，0.7R和0.9R处的叶宽、厚度、螺距、曲率、倾角、最大厚度位置共30个参数作为螺旋桨形状控制设计变量，采用NFFD技术生成100个螺旋桨计算样本，并计算进速系数J=0.893时K_T，10K_Q，η₀以及P_min。

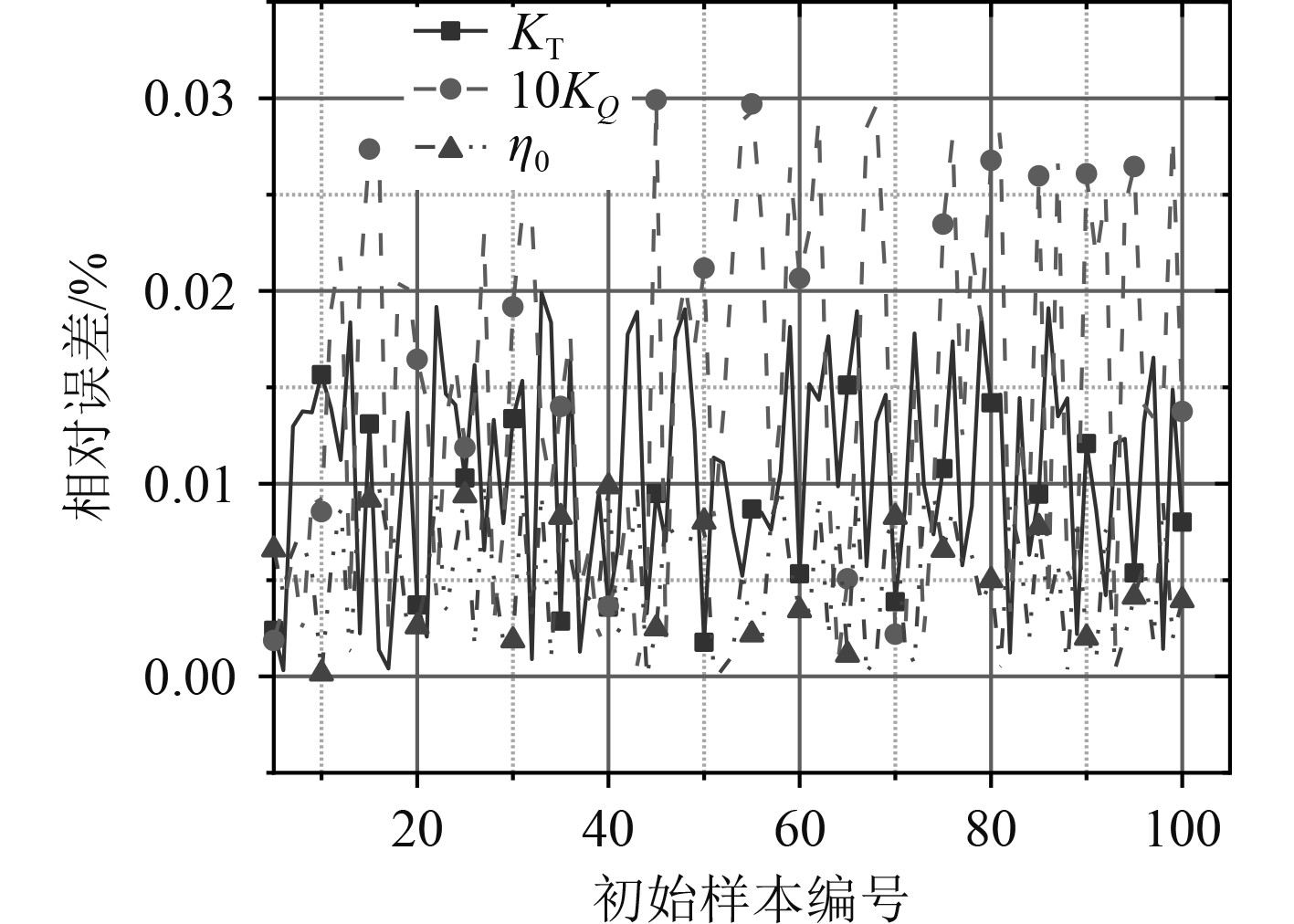
2.3 近似模型的验证

对100个初始样本采用交叉验证方法对训练后的多输出高斯代理模型进行评估。通过交叉验证得到的100个测试样本预测误差如图4所示。

结果表明，各测试样本K_T，10K_Q，η₀以及P_min预测值与数值模拟结果的相对误差在3%以内，精度满足要求。训练后的多输出高斯代理模型可用于多目标优化中目标函数值的评估。

3 螺旋桨多目标优化 3.1 NSGA-Ⅱ多目标优化

NSGA-Ⅱ是由Kalyanmoy等^[23]针对NSGA提出的一种改进进化算法，该算法具有多目标适度简化、最优解拓展、求解精度高、高鲁棒性等优点，尤其针对少量样本、多变量多目标优化问题就较快的求解速度。

螺旋桨敞水性能多目标优化问题可以描述为：

$ \left\{\begin{array}{l}目标：\left\{\begin{array}{l}\mathrm{max}{\eta }_{0}，\\ \mathrm{min}{K}_{Q}，\end{array}\right.\\ 约束：\left\{\begin{array}{l}{K}_{T}\geqslant {K}_{T}{}_{\text{initial}}，\\ {K}_{Q}\leqslant {K}_{Q}{}_{\text{initial}}，\\ {P}_{\mathrm{min}}\geqslant {P}_{\text{min-initial}}，\\ {x}_{\mathrm{min}}\leqslant {x}^{a/b/c/d/e/f}\leqslant {x}_{\mathrm{max}}，\\ 0.4\leqslant {A}_{e}/{A}_{d}\leqslant 1.4。\end{array}\right.\end{array}\right. $

式中：叶宽 $ 0 \leqslant {x^a} \leqslant 0.27 $ ，叶片厚度 $ 0.08 \leqslant {x^b} \leqslant 0.095 $ ，螺距比 $ 1.2 \leqslant {x^c} \leqslant 2.9 $ ，曲率 $ - 0.01 \leqslant {x^d} \leqslant 0.02 $ ，倾角 $ - 0.5 \leqslant {x^e} \leqslant 0.3 $ ，最大厚度位置 $ 0.45{x^b} \leqslant {x^f} \leqslant 0.75{x^b} $ ， $ {A_e} $ 螺旋桨展开面积， $ {A_d} $ 面螺旋桨盘面积。

利用以100个样本建立的多输出高斯近似模型计算螺旋桨敞水性能，并以NSGA-Ⅱ算法进行螺旋桨的优化设计，将种群交叉遗传概率设置为0.92，变异概率设置为0.08。经过1000代的演化，可得到Pareto非支配最优解集。

初始种群和Pareto解集的扭矩系数和效率如图5所示。可以看出最优解是在原始设计空间之外的，其中Pareto前沿上A点为综合最优设计，表示Pareto前沿中的最优综合性能点，同时兼顾了扭矩系数和效率。

3.2 优化设计结果及分析

选取优化结果中A点进行根据优化结果分析，原模型的效率提高了2.6%、扭矩降低了3.3%。此外，盘比降低了2.5%，但螺旋桨模型的空化特性并未恶化，因为推进器旋转区域的最小压力增加了7%。优化方案4桨叶r/R=0.7处剖面轮廓如图6所示。可以看出，经过优化，叶片的厚度和宽度发生了明显的变化，在相对半径0.7处变小，但倾角有所增加。

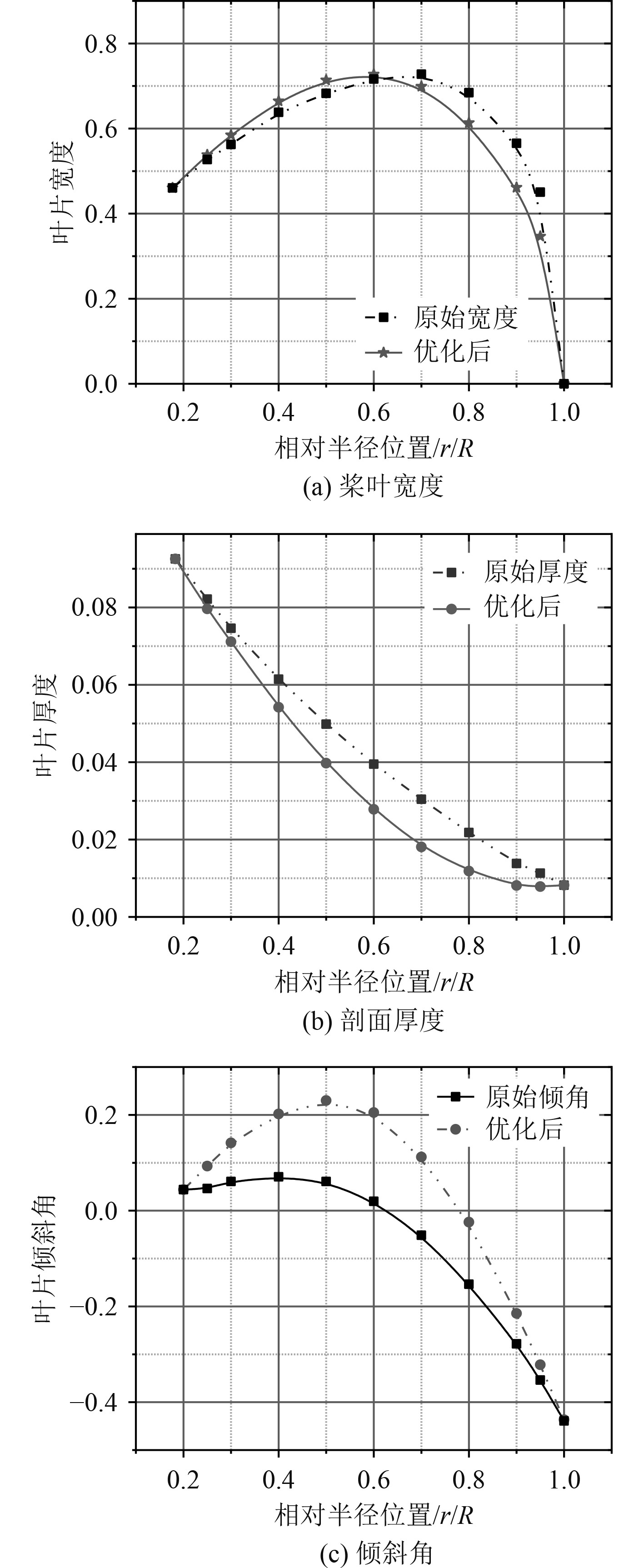
桨叶宽度、剖面厚度、倾斜角沿径向的分布如图7所示。可以看出，经过优化，桨叶厚度、宽度、倾斜角在相对半径r/R=0.7处明显变小，而曲率在此处所有增加。

优化前后螺距比和曲率沿径向的分布如图8所示。优化前后螺旋桨的螺距比趋势相似，而且各半径处螺距比较对相近。此外，优化结果表明，螺旋桨螺距比在靠近桨叶根部较大。从推进设计的角度来看，螺旋桨螺距比在靠近桨叶根部的逐渐增大可以增加推力，从而提高效率。但是，通过增加螺距比，需要提高螺旋桨轴功率以及螺旋桨流动区域的最小压力。优化前后螺旋桨曲率沿半径分布特征相似，优化后的螺旋桨桨叶根部曲率变为负值，而且优化后的曲率变小，有利于降低螺旋桨噪声。

4 结　语

1）以有限元仿真结果为样本，以螺旋桨参数沿半径的分布为输入，基于多输出高斯近似模型建立螺旋桨水动力性能预测模型。该模型与数值仿真结果得出的螺旋桨推力系数和效率误差在3%以内，可以较为准确预测螺旋桨水动力性能。

2）应用本文提出的螺旋桨高效自动优化方法，开展KP505桨的优化设计，实现了对KP505桨降低扭矩系数、提高效率的多目标优化，形成了Pareto解集，获得了理论上的最佳设计方案。

3）根据对优化结果的分析，0.65R～0.95R处螺距比和0.4R～0.6R处倾斜角对KP505桨的效率有较大影响。

综上所述，本文方法可以有效提高螺旋桨优化的效率和自动化程度，并能得到最佳设计方案。在后续工作中，将进一步探讨应用该方法对考虑船后流场响应的螺旋桨优化设计的有效性。