0 引　言

海上交通流数据既包括船舶流量、尺寸等宏观数据，又包括航行速度、航迹等微观数据，交通流数据的采集对于海事监管、港口调度、航运公司船舶管理有重要意义，采集海上交通流特征信息的意义在于以下几点：

1)改善水上航运交通

通过分析海上交通流的数据特征，可以从统计学等角度揭示水上航道的交通规律，得到某一时间段、某一港口或航道的交通密度，引导海上监管和交通调度，从而改善水上航线的交通状态。

2)助力海上交通学科理论发展

近年来海上航运交通等相关工程学科得到了广泛重视，交通流特征是海上交通学科理论的一个重要研究领域。

3)提高海上航运交通的安全性^[1]

海上交通流行为特征能够指导水上交通安全管理部门进行安全措施制定，根据交通流密度、事故发生频次等信息选取合适的海上安全救援点位，一旦海上交通船舶出现事故，可以快速的响应和提供海上救援服务。

4)指导港口和航道规划建设

港口、航道的布局建设需要参考海上船舶交通流的密度、航迹等行为特征，不仅要满足当前货物吞吐量的要求，也要保证航道、通航效率、泊位等功能要求。

本文研究方向是建立一种海上船舶交通流行为特征的概念模型，基于高斯拟合等数学算法，建立海上船舶交通流行为特征提取系统。

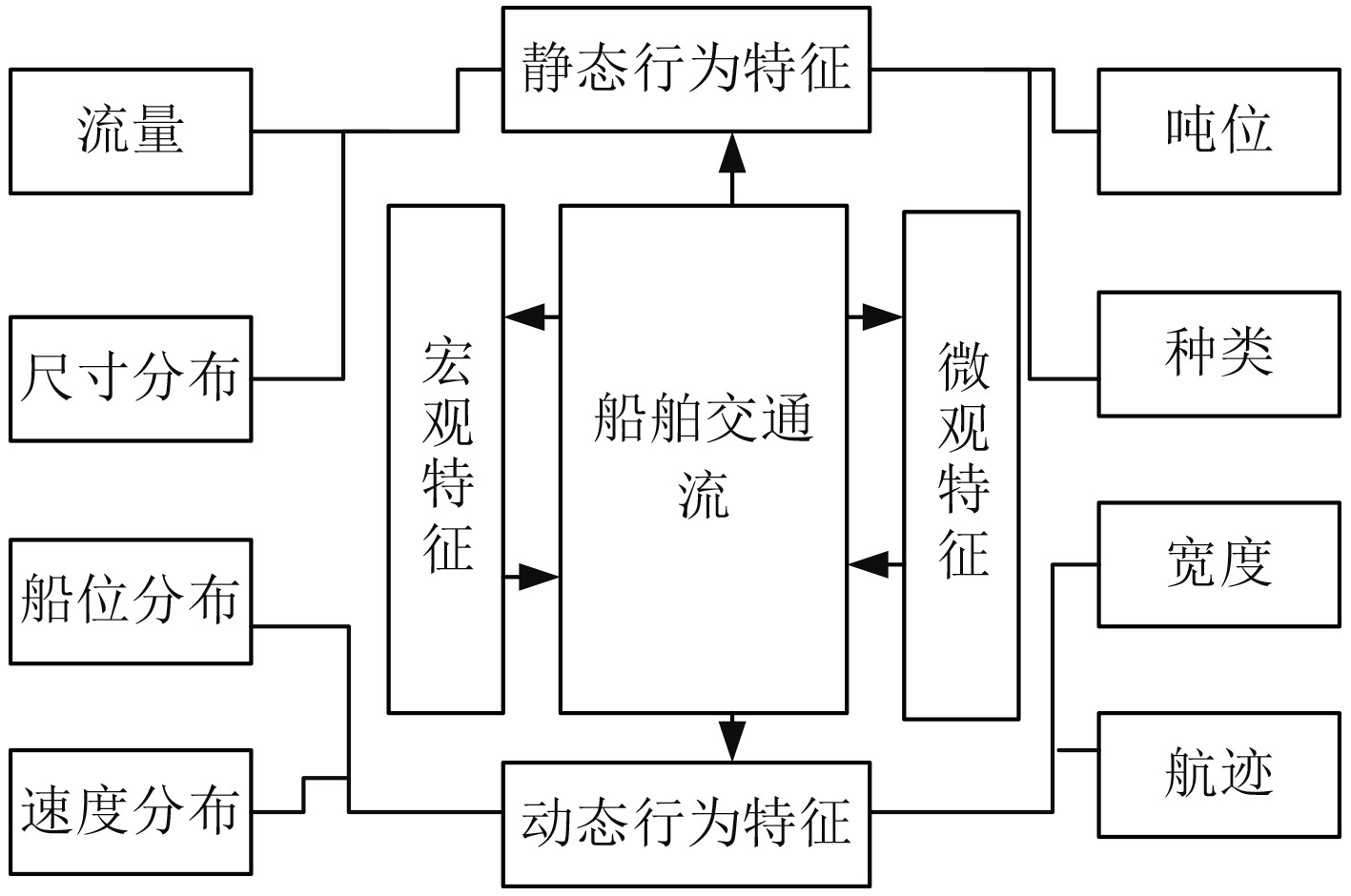
1 海上船舶交通流行为特征的概念模型及拟合算法 1.1 海上船舶交通流行为特征的概念模型

海上船舶交通流特征包括宏观和微观特征等，具体如图1所示。

船舶交通流包括动态和静态行为特征，要对交通流速度、流量、宽度等要素进行详细研究。

1)交通流速度

海上船舶交通流的速度可用航迹长度与经过该航迹下船舶的航行时间表示，如下式：

$ {V_0} = \dfrac{l}{{\displaystyle\sum\limits_{i = 1}^n {\dfrac{{{t_i}}}{n}} }} \text{。} $

式中： $ n $ 为航迹分段个数； $ l $ 为航迹总长度； $ {t_i} $ 为船舶航行所需的时间。

2)流量

流量表示某航道单位时间内通过的船舶总数，用下式计算：

$ {Q_0} = \frac{1}{n}\sum\limits_{i = 1}^n {{q_i}} \text{。} $

式中， $ {q_i} $ 为某时间间隔内通过的船舶数量。

3)宽度

海上船舶交通流的宽度并不限定为航道的宽度，而是大量船舶在同一区域或同一航线下形成的交通流宽度，且宽度随着船舶数量等信息不断发生变化，想要详细描述船舶交通流的宽度就需要在一定时间内进行大量宽度数据的拟合。

1.2 海上船舶交通流行为特征的拟合

本文使用的交通流行为特征拟合算法包括灰色理论拟合和高斯拟合2种，分别如下：

1)灰色理论拟合法^[2]

灰色理论拟合法是将离散数据进行整理，利用灰色微分方程建立动态模型，一阶灰色微分方程如下式：

$ {x^{\left( 0 \right)}}\left( i \right) + \rho {H^{\left( 1 \right)}}\left( i \right) = k \text{。} $

其中： $ {x^{\left( 0 \right)}} $ 为交通流原始数据阵列； ${x^{\left( 0 \right)}}\left( i \right) = \displaystyle\sum\limits_{m = 1}^n {{x^{\left( m \right)}}} \left( i \right)$ 。

动态拟合模型如下式：

$ \frac{{{\rm{d}}{x^{\left( 0 \right)}}}}{{{\rm{d}}x}} + \rho {{\boldsymbol{Y}}}{x^{\left( m \right)}} = {\boldsymbol{B}}{k_1} \text{。} $

式中： ${\boldsymbol{ Y}}$ 为拟合后的交通流数据向量， ${\boldsymbol{Y }}= \Big[ {x^{\left( 0 \right)}}\left( 1 \right), {x^{\left( 0 \right)}}\left( 2 \right),{x^{\left( 0 \right)}}\left( 3 \right)...,{x^{\left( 0 \right)}}\left( n \right) \Big]^{\rm{T}}$ ； $ B $ 为拟合后的矩阵， ${\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} { - 1}&1 \\ 1&M \\ {{x^{\left( 0 \right)}}\left( 2 \right)}&1 \\ {{x^{\left( 0 \right)}}\left( n \right)}&0 \end{array}} \right]$ 。

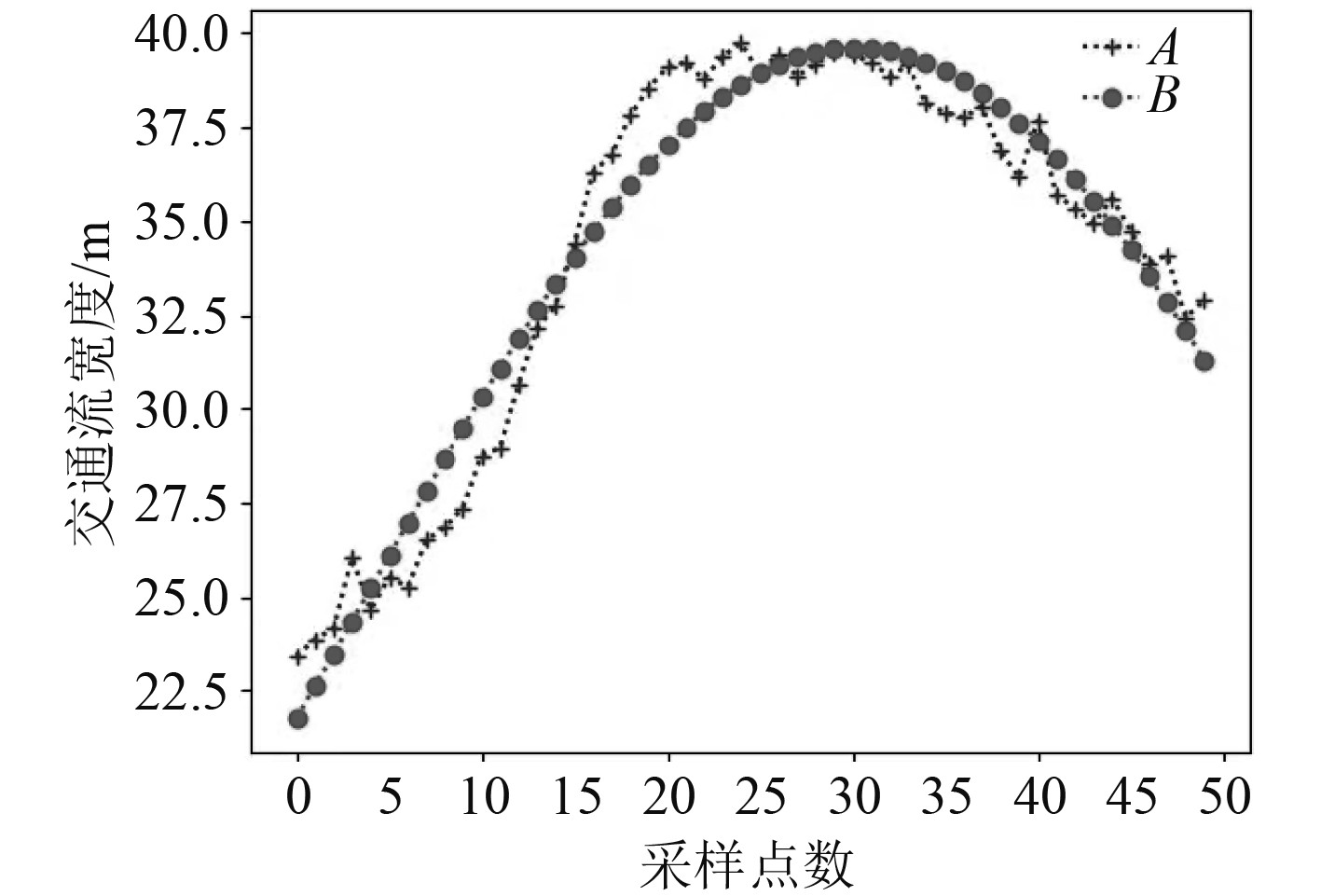
图2为船舶交通流宽度特征的灰色理论拟合效果图，其中A为实际曲线，B为拟合曲线。

2)高斯拟合法

高斯拟合法在数学、统计学等领域有非常广泛的应用，高斯拟合函数用下式表示：

$ f(x) = A \cdot \exp \left( { - \frac{{{{\left( {x - {\mu _{}}} \right)}^2}}}{{2\sigma _{}^2}}} \right) \text{。} $

其中： $A = \dfrac{1}{{{\sigma _{}}\sqrt {2\text{π} } }}$ ； $ \mu $ 为均值； $ \sigma $ 为均方差。

定义船舶交通流密度特征矩阵为 ${\boldsymbol{W }}= ( {r_1}, {r_2},..., {r_n} )$ ，密度区间的宽度为m，可得交通流密度分布的高斯均值为：

$ {\mu _c} = \dfrac{{\displaystyle\sum\limits_W r \cdot {M_{r,c}}}}{{\displaystyle\sum\limits_W {{M_{r,c}}} }} 。$

方差为：

$ {\sigma _c} = \sqrt {\dfrac{{\displaystyle\sum\limits_{r \in W} {{r^2}} \cdot {M_{r,c}}}}{{\displaystyle\sum\limits_{r \in W} {{M_{r,c}}} }} - \mu _c^2} 。$

交通流密度函数为：

$ f(x) = \dfrac{1}{{{\sigma _c}\sqrt {2\text{π} } }} \cdot \exp \left( { - \dfrac{{{{\left( {x - {\mu _c}} \right)}^2}}}{{2\sigma _c^2}}} \right) 。$

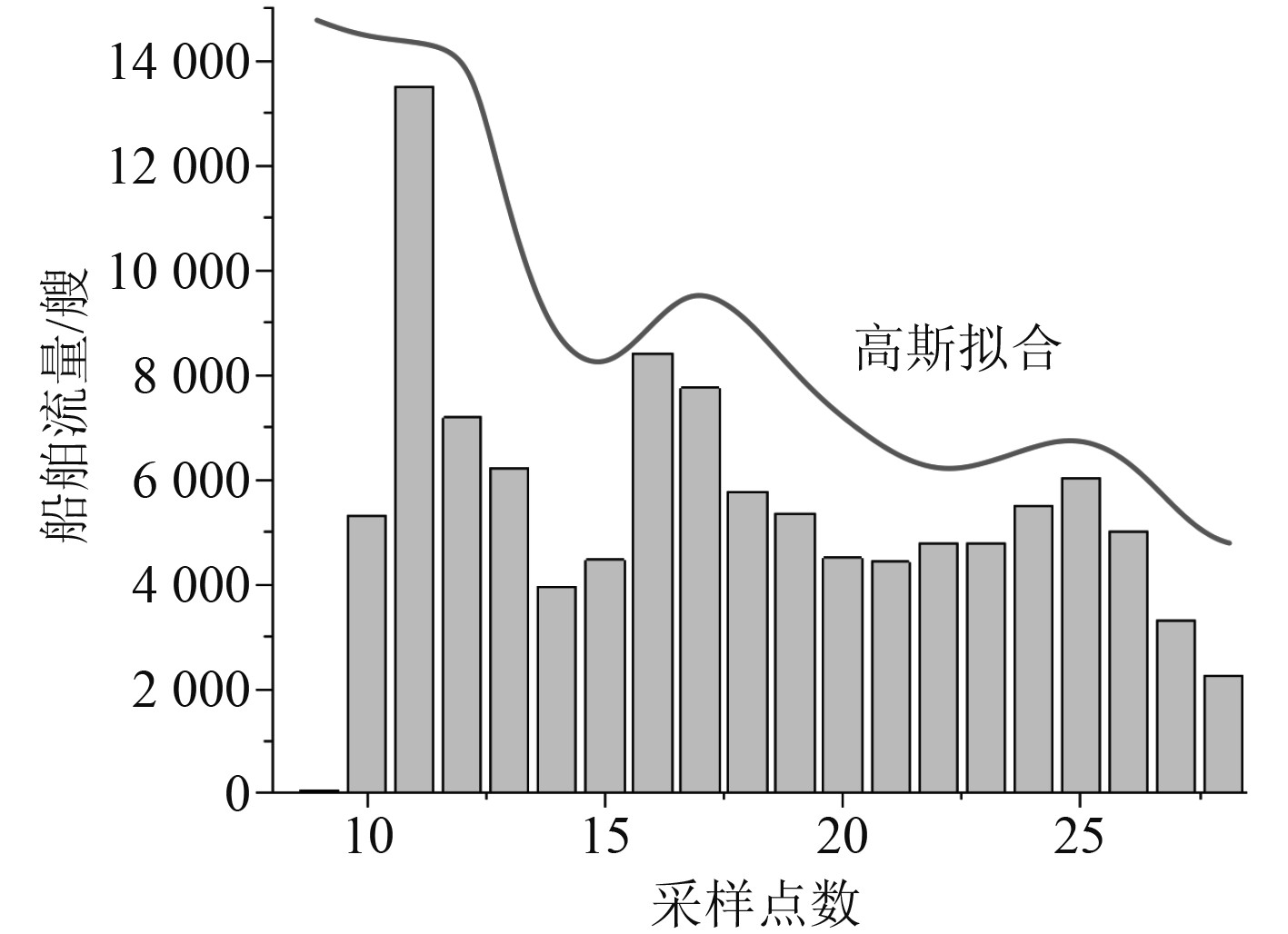
图3为船舶交通流量的高斯拟合过程示意图。

2 基于深度学习算法的船舶交通流行为特征提取系统的开发 2.1 海上船舶交通流行为特征提取系统构成

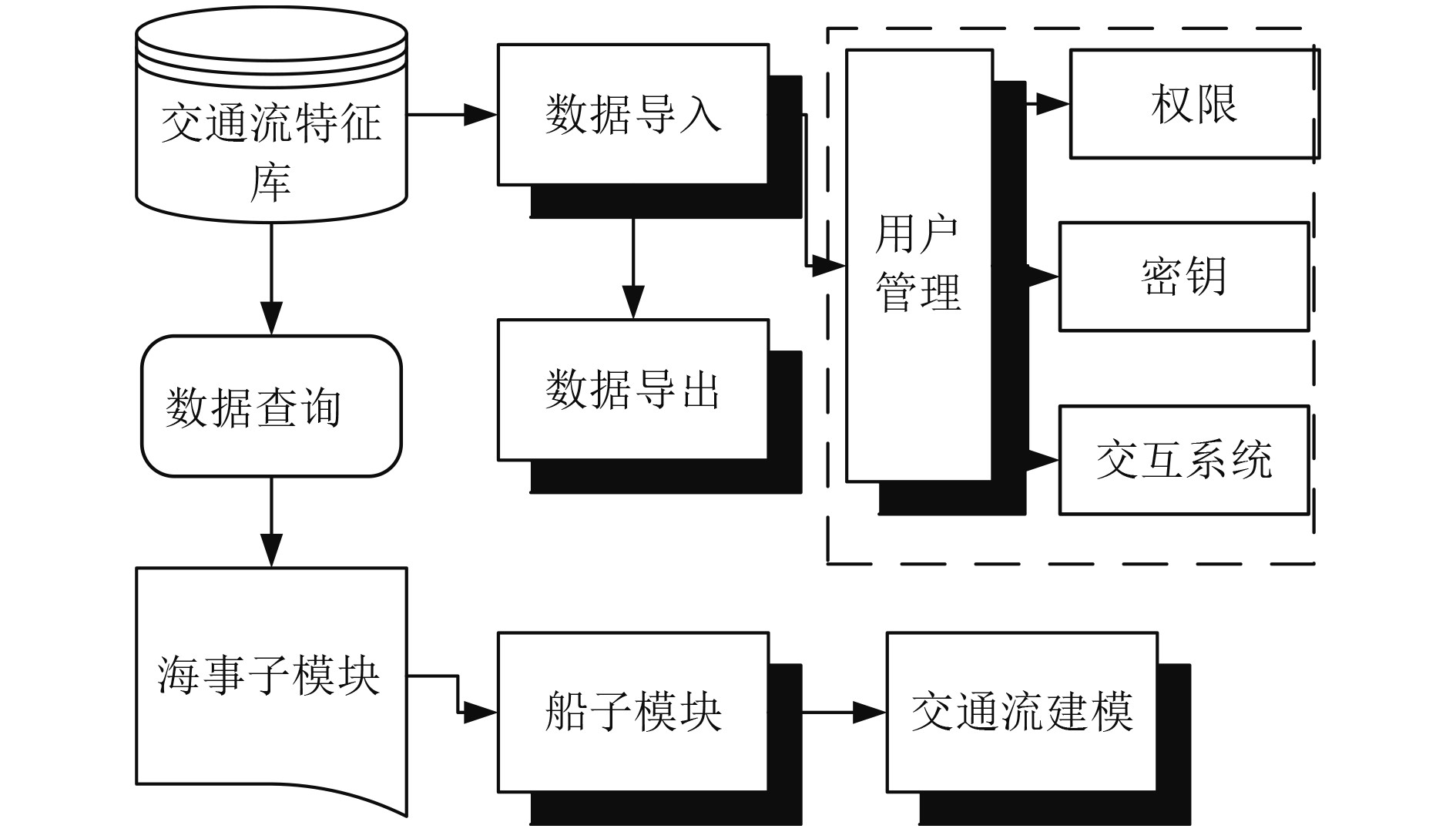
本文针对海上船舶交通流行为建立了一种特征提取系统，基本构成如图4所示。

该系统的关键组成包括：

1)交通流特征库

系统集成了包括船舶流量、速度、宽度、尺寸等交通流宏观和微观特征，并利用灰色理论和高斯拟合算法建立船舶交通流的拟合特征。

2)数据查询

系统为用户提供多种关键字查询功能，用户可以根据需求对船舶交通流某一特征或多个特征进行在线查询。

3)用户管理

针对船舶交通流行为特征提取系统用户开发了包括登录权限、密钥管理^[3]、交互系统等功能模块，提高系统的安全性。

4)交通流建模

系统将导入的交通流数据进行统计和拟合，获取不同尺度、不同吨位船舶的交通流特性，并通过图形化建模将提取结果展示给用户。

2.2 基于深度学习算法的船舶交通流行为特征提取

使用深度学习算法实现交通流行为特征的提取，选用BP神经网络算法进行数据的学习，采用的激励函数为s型函数，如下式：

$ f(x) = \frac{1}{{1 + {e^{ - bx}}}}\;\;,b > 0 \text{。} $

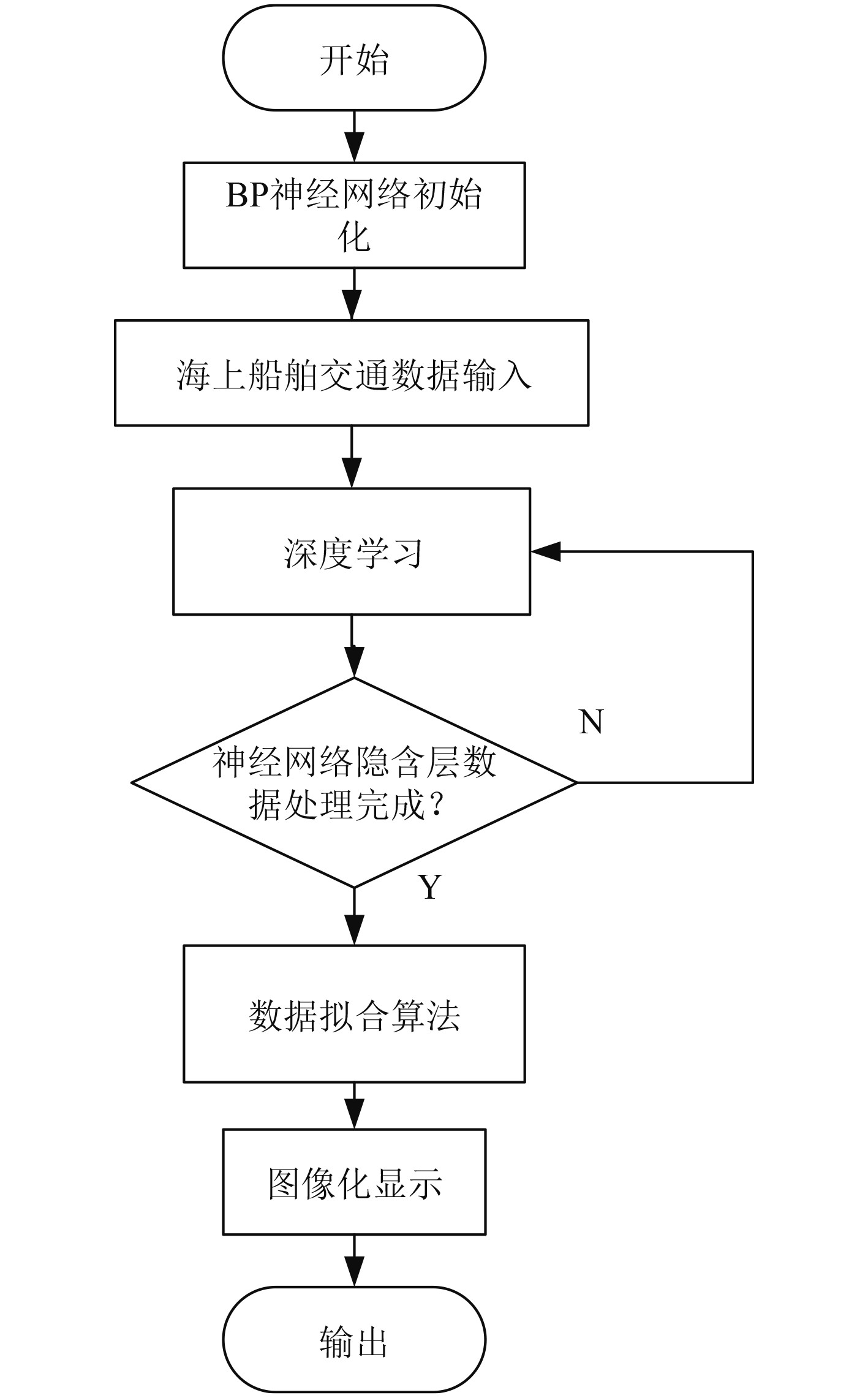
基于深度学习算法的海上船舶交通流行为特征提取流程如图5所示。

通过大量船舶数据特征提取可知，船舶交通流量特征服从泊松分布^[4]，如下式：

$ P\left( X \right) = k\frac{{\left( {\lambda t} \right)k{e^{ - \lambda t}}}}{{k!}}\;\;,\left( {k = 0,1,...} \right) \text{。} $

式中：k为船舶数量； $ \lambda $ 为航线上船舶的通过率。

在一定时间内，船舶数量低于x的航线通过率如下式：

$ P\left( {X < x} \right) = \sum\limits_{k = 0}^x {} \frac{{\left( {\lambda t} \right)k{e^{ - \lambda t}}}}{{k!}}\; \text{，} $

在一定时间，船舶数量高于x低于y的航线通过率如下式：

$ P\left( {x < X < y} \right) = \sum\limits_{k = x}^y k \frac{{\left( {\lambda t} \right)k{e^{ - \lambda t}}}}{{k!}}\; \text{。} $

其他情况， $ P\left( {X = 0} \right) = {e^{ - \lambda t}} $ 。

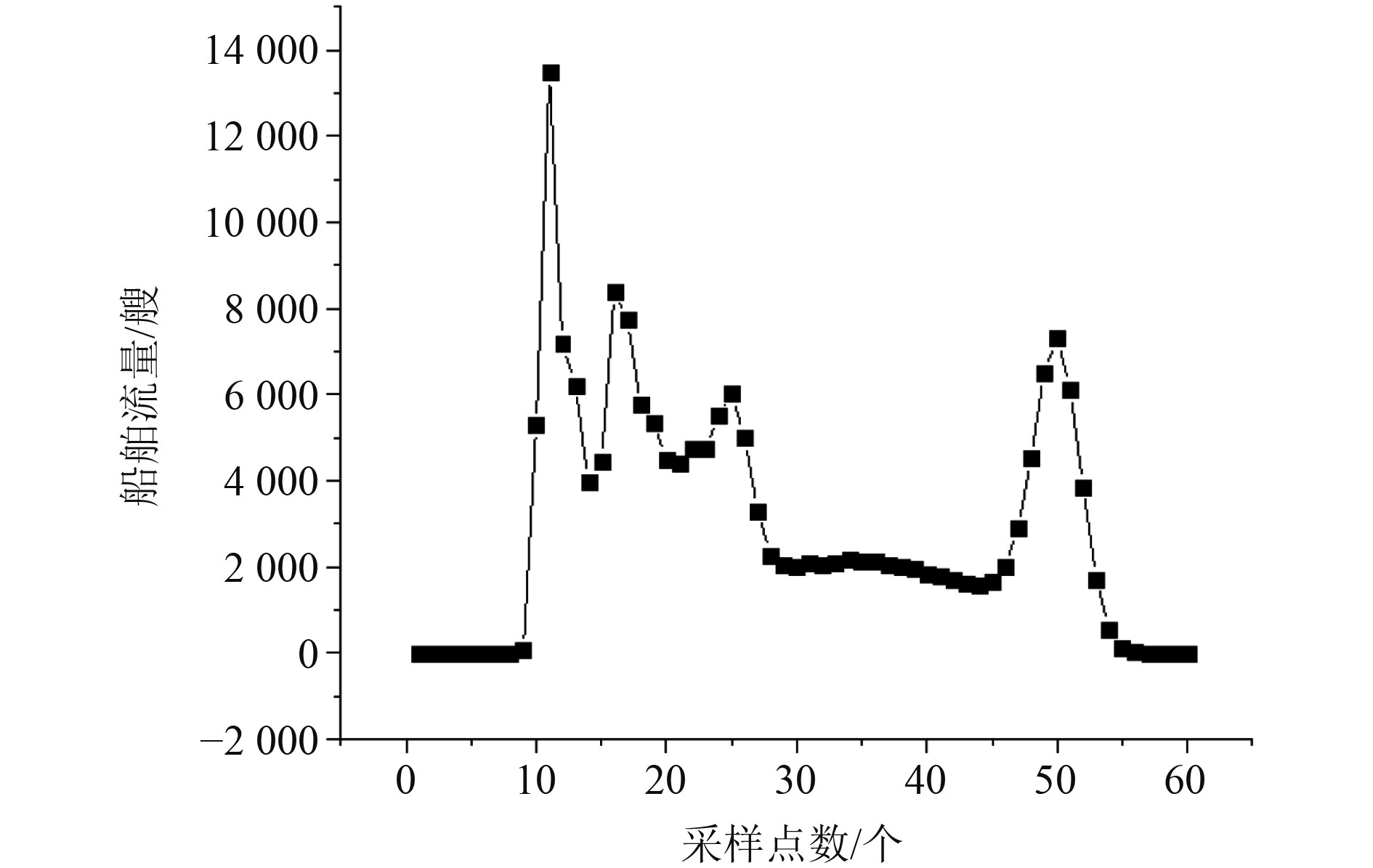
基于特征提取系统对某航线船舶的流量特征进行了模拟，得到船舶流量仿真曲线如图6所示。

3 结　语

海上船舶交通流行为特征对于海上监管、船舶调度等有重要意义，本文介绍了船舶交通流行为特征的基本概念，采用深度学习算法、灰度理论拟合和高斯拟合等算法建立交通流行为特征提取系统，阐述系统原理并进行了交通流量的模拟。