2. 中国船舶及海洋工程设计研究院,上海 200011
2. Marine Design and Research Institute of China, Shanghai 200011, China
勘探船是矿产、油气资源调查以及海洋科学研究的重要装备,相比于调查船和科考船,勘探船具有进行海底深部钻探取样的能力,可以对海底矿产的组成以及储量进行深入评估。从国内外深海矿区勘探需求来看,大洋勘探船具有明显的市场应用前景。
月池是贯穿船底和甲板的开口,以便船上的设备进入水下进行操作。为满足钻探需要,勘探船通常在船中位置布置较大的月池,另外为方便ROV以及其他探测设备的收放还会设置较小的月池。月池的存在对船舶的稳性和强度不利,使水动力性能与普通船舶有较大的差异,月池内流体的复杂运动会导致勘探船航行阻力、耐波性能复杂的多。
Gaillarde和Cotteleer[1]通过实验研究了抑制月池内运动不同装置的试验,以减少月池内的自由表面高度变化。还对沿船体深度方向的截面形状的月池进行研究,减少月池内水的运动。Larsson等[2]将船舶的整体阻力分为2个部分:波浪阻力和粘性阻力。在这2个阻力部分中,带有月池的钻井船对波浪阻力影响不大,但会影响粘性压阻力,这主要是由于月池压力不平衡产生的。Molin[3]采用线性化势流理论,得出了二维和三维月池的活塞模式和晃动模式的固有频率的理论公式以及活塞和晃荡模式的自由表面形状公式。月池的共振振荡是由船舶航行时在月池的上游底端形成的漩涡引发的。Veer等[4]对具有不同长宽比月池的钻井船进行了模型试验,并研究了月池形状与月池增阻之间的关系,分析了月池吃水宽度比与月池内自由表面高度的变化的关系。Tholen[5]试验研究了长宽比Lm/Bm=2的月池,其研究的焦点在于减阻装置减少附加的船舶瞬态阻力。在早期的设计阶段,主要通过模型试验与已有的船型数据相结合得出带月池船舶的阻力曲线。但是这种方法要准确估计月池的增阻大小仍然很困难,船体以及月池通常变化很大,而可用的数据比较有限,无法实现阻力曲线的准确预测。Sivabalan.P[6]通过CFD方法对一艘带月池的钻井船在低航速下阻力特性进行了研究,傅汝德数范围为0.0196~0.157,月池为矩形月池,发现航速最高时月池增阻约为25%。
本文针对带有月池的勘探船进行航行阻力研究,通过CFD方法开展勘探船静水阻力预报研究,考虑直立型首和球鼻型首2种船型以及无月池、首月池和双月池3种方案组合,分析各船型方案的总阻力以及月池增阻情况,将船体阻力按照傅汝德分类法分为摩擦阻力和剩余阻力分量,分别探究不同船型及月池方案的摩擦阻力和剩余阻力分量的规律。
1 计算模型 1.1 模型主尺度研究对象为两大类船型,分别为球鼻型首船型和直立型首船型,两船型的主尺度相同。两船型的主尺度见表1。
|
|
表 1 船舶主尺度 Tab.1 Main dimensions of the two type ships |
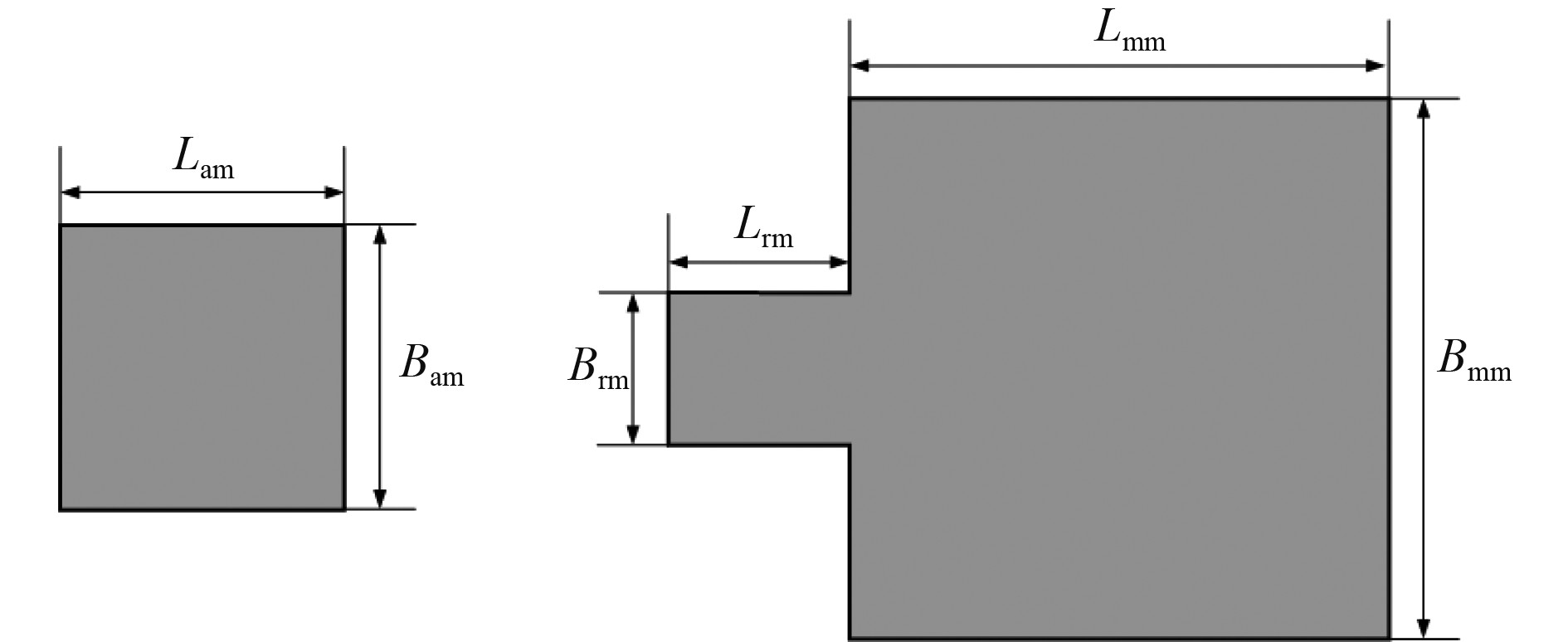
含2种类型的月池,后月池截面为正方形,后月池为截面为正方形,首月池为“凸”字形,凸起方向指向船体尾部。后月池尺度相对较小,设计吃水和压载航行状态时的长度吃水比分别为0.54和0.67。首月池主体部分截面为正方形,后端设置矩形截面凹槽。设计吃水和压载航行状态时,首月池主体部分的长度吃水比分别为1.08和1.34。水深吃水比是月池水动力特性的重要影响因素,对月池的增阻作用有较大的影响。月池布置及尺寸见图1、图2及表2、表3。

|
图 1 船型三维图 Fig. 1 3D view of ship shape |
|
图 2 月池尺寸示意图 Fig. 2 Sizes of moonpools |
|
|
表 2 后月池尺寸 Tab.2 Size of after moonpool |
|
|
表 3 首月池尺寸 Tab.3 Size of bow moonpool |
考虑到勘探船的作业吃水有一定变化,月池的长度吃水比(Lm/T)也相应发生变化,可能导致月池内主导的振荡模式发生转变,所以计算时选择2种吃水状态,即设计吃水状态(钻井作业)和压载航行状态,LC1代表设计吃水,LC2代表压载吃水。为覆盖勘探船可能的服务航速,计算时取航速范围为7~15 kn,间隔为1 kn。计算工况如表4所示。
|
|
表 4 计算工况 Tab.4 Calculation conditions |
数值模拟使用FINE/Marine软件,其采用了粘性ISIS-CFD求解器。
1)计算域及边界条件
采用半模计算,计算域宽度为2LPP,计算域长度为5.5LPP,船后长度为3.5 LPP,船前长度为1 LPP,计算域高度为2LPP,空气域高度为0.5LPP,水域高度为1.5 LPP。计算域与船体中纵剖面重合面为对称平面,上部和下部为压力出口,计算域其余边界为远场边界。
2)计算时间步长设置
ITTC (75-03-02-04, 2014) 推荐的计算船舶阻力的时间步长与船舶的航速以及船长有关,计算时间步长取为:
| $ \Delta t = 0.005\sim 0.01{{{L_{{\text{PP}}}}} \mathord{\left/ {\vphantom {{{L_{{\text{PP}}}}} V}} \right. } V} 。$ | (1) |
式中:LPP为船舶的垂线间长,V为对应的航速。
计算时间步长根据航速调整,各计算工况的计算时间步长具体如表5所示。
|
|
表 5 各工况的计算时间步长 Tab.5 Computation time steps of different conditions |
3)平均阻力提取方法
由于阻力随时间波动,尤其在月池长度较大的时候,提取阻力时以计算结果的平稳段时间平均值作为平均阻力。在阻力出现明显周期性波动时,截取时间段要足够长,截取时间尽量等于整数个周期,以减小数据处理带来的误差。
4)网格收敛性验证
为进一步验证计算结果与网格数的独立性,针对球鼻型首双月池模型,设计吃水,实船航速Vs=7 kn(LC1-BB-2MP-V7)工况采用3套网格划分方案进行验证,网格数分别为193万、237万和369万,方案2和方案3的结果接近,网格数为237万时计算结果在误差允许范围内可以接受。因此带月池工况网格划分方案采用与方案2类似的网格加密方法。
|
|
表 6 三种网格方案计算结果对比 Tab.6 Comparison of calculation results of three grid schemes |
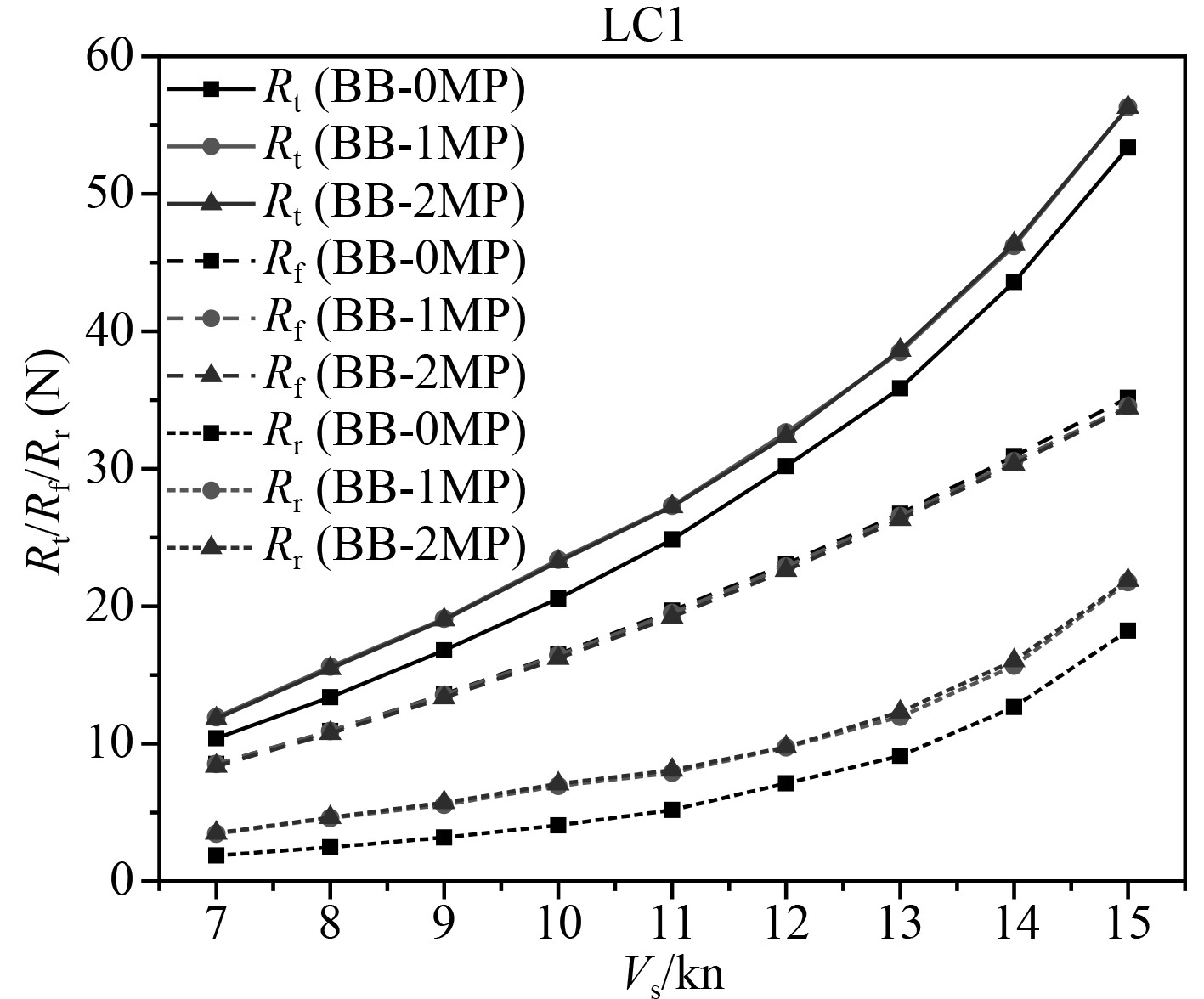
图7为球鼻首船型设计吃水阻力曲线,按照傅汝德分类法的思想,将总阻力Rt分为摩擦阻力Rf和剩余阻力Rr。可以看出单月池和双月池布置的总阻力差别不大,无月池、单月池和双月池布置的摩擦阻力接近,而单月池和双月池布置的剩余阻力要比单月池船型的大,这也是导致单月池和双月池布置的总阻力比无月池船型总阻力大的主要原因。
|
图 7 球鼻首船型设计吃水阻力曲线 Fig. 7 Resistance curve of bulb bow at designed draft |
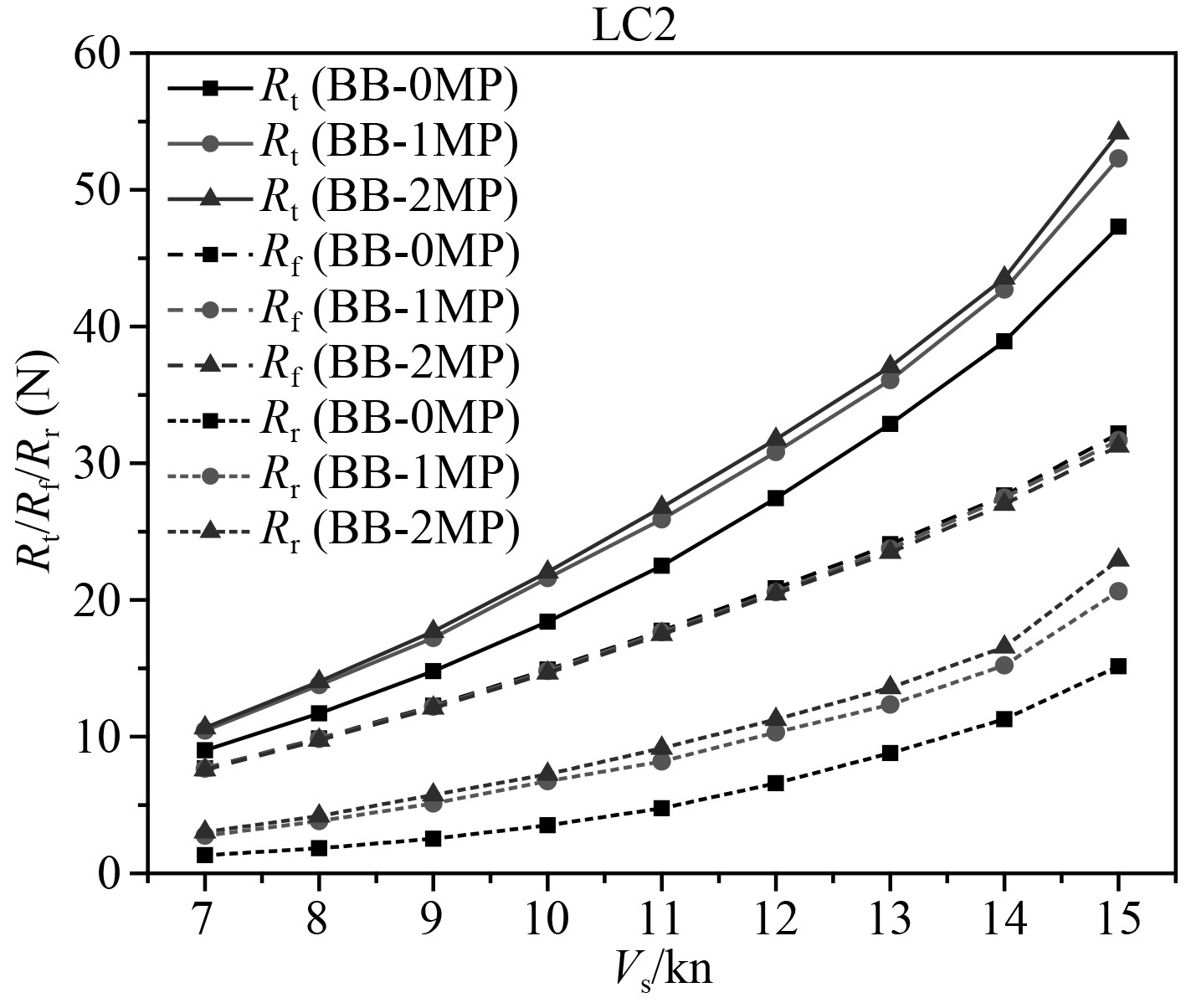
图8为球鼻首船型压载吃水阻力曲线。结合设计吃水结果来看,发现吃水减小后,单月池和双月池布置的总阻力差别增大,主要是由剩余阻力分量引起的。由于总的湿面积减小,在相同的船底剪切湿面积损失情况下,3种布置的摩擦阻力的差别也稍有增大。
|
图 8 球鼻首船型压载吃水阻力曲线 Fig. 8 Resistance curve of bulb bow at ballast draft |
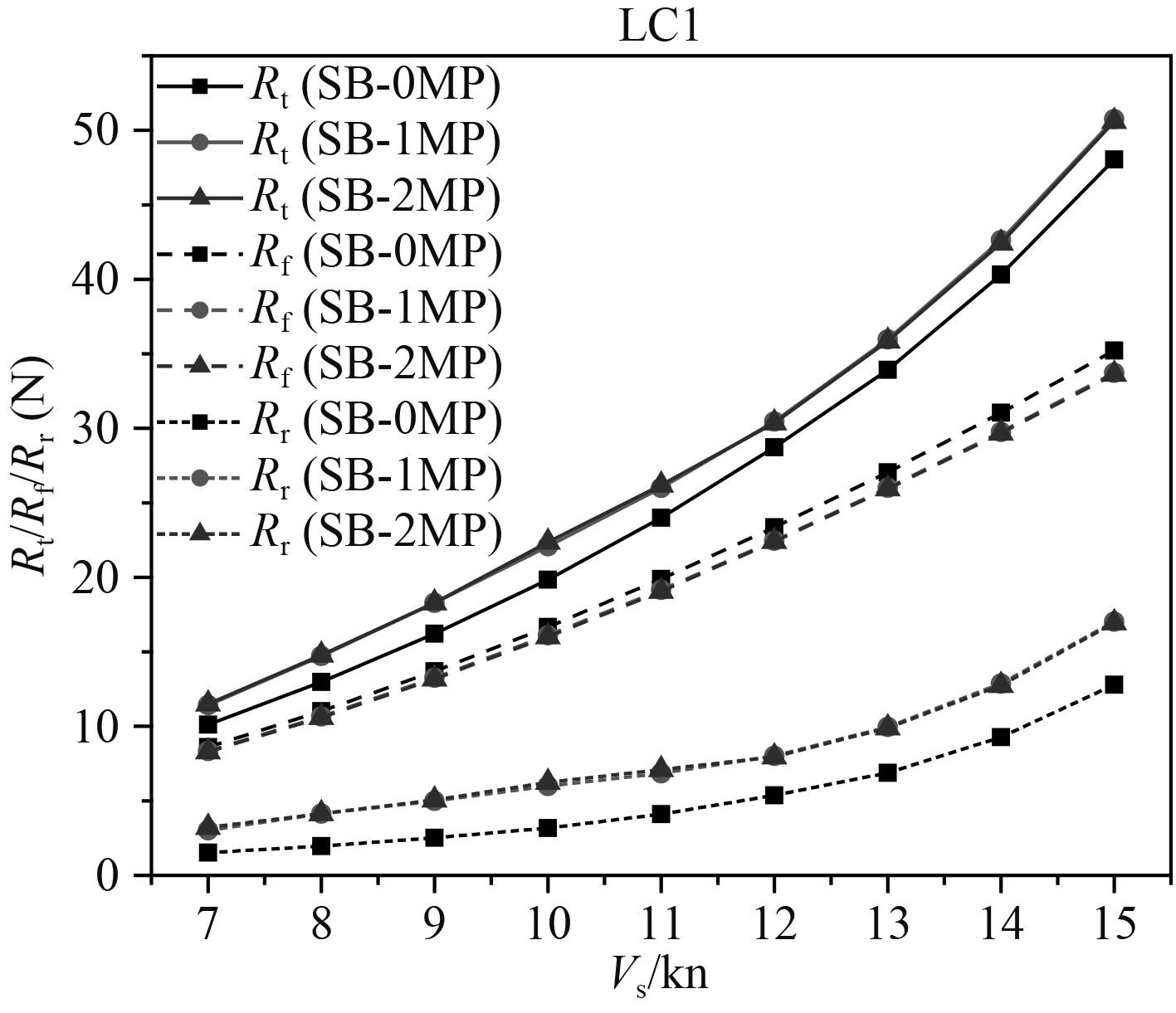
图9为直立首船型设计吃水阻力曲线。单月池和双月池布置的总阻力以及摩擦阻力和剩余阻力分量差别均不大。相比于无月池,带月池布置(单月池和双月池型)的摩擦阻力有一定降低,而剩余阻力增加较大,导致总阻力有一定增加。
|
图 9 直立首船型设计吃水阻力曲线 Fig. 9 Resistance curve of straight bow at designed draft |
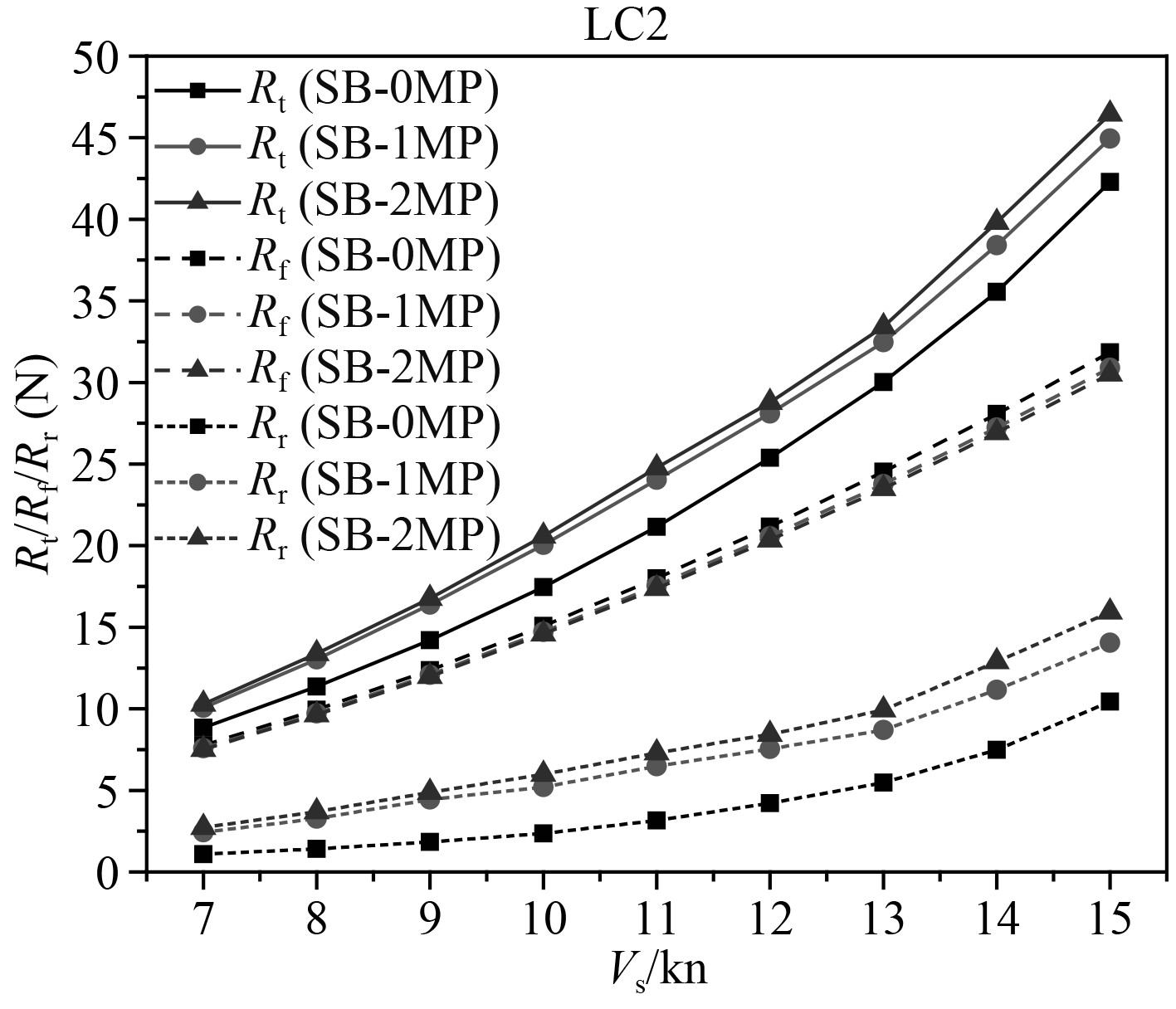
图10为直立首船型压载吃水阻力曲线。压载吃水状态3种布置的各阻力成分均有明显差别。双月池布置的总阻力和剩余阻力最大,单月池次之,无月池最小。而摩擦阻力成分与此相反,但单月池和双月池的摩擦阻力差别并不明显。
|
图 10 直立首船型压载吃水阻力曲线 Fig. 10 Resistance curve of straight bow at ballast draft |
通过对不同船型以及月池布置方案阻力计算结果对比可以发现:
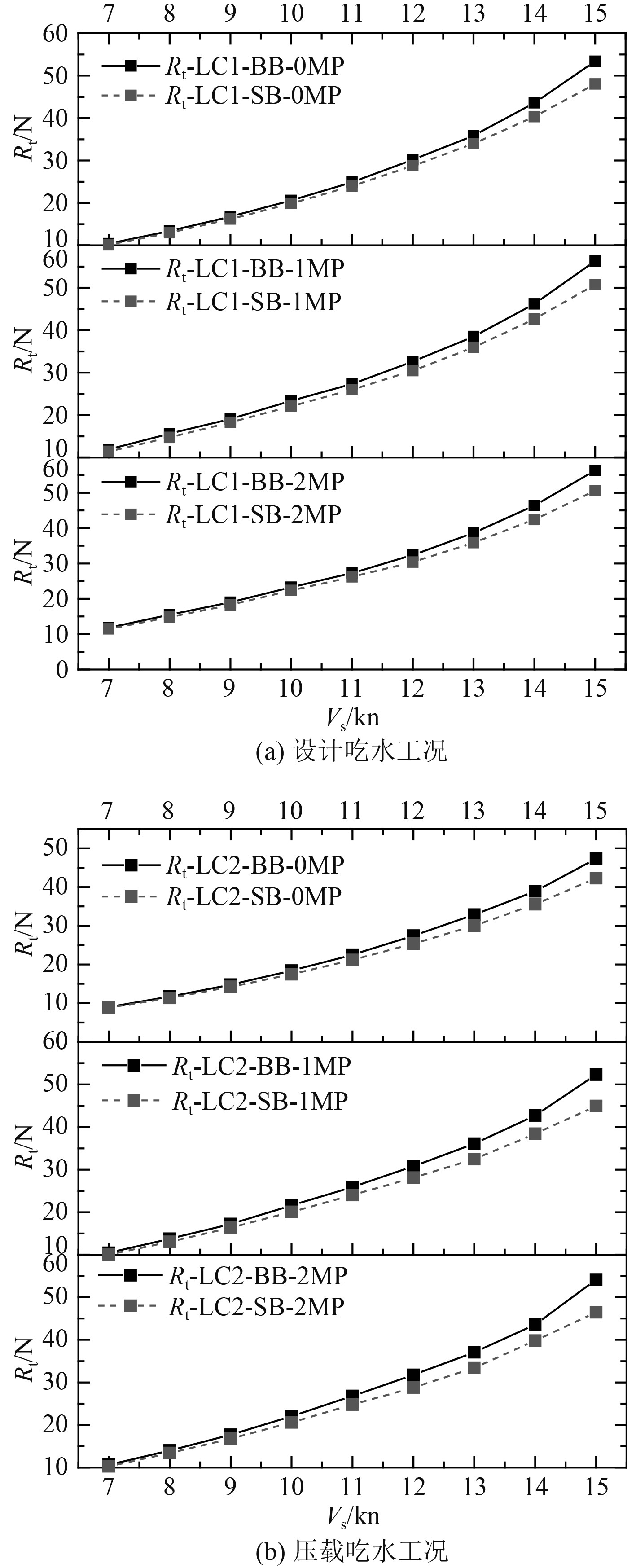
1)对于相同的月池布置方案的船型,无论是在设计吃水还是在压载吃水状态,球鼻首船型的总阻力均大于直立型船型。设计航速设计吃水状态,球鼻首船型的无月池、单月池和双月池方案的阻力比直立型船型分别大5.4%,6.6%和7.1%;在设计航速压载吃水状态,球鼻首船型的无月池、单月池和双月池方案的阻力比直立型船型分别大8.7%,10.0%和9.8%。两船型的总阻力对比如图11所示。
|
图 11 两船型阻力对比 Fig. 11 Comparison of resistance of two different ship types |
2)通过对单月池和双月池方案对比发现:在设计吃水状态下单月池和双月池方案的总阻力差别不大,而在压载吃水状态双月池方案总阻力比单月池方案稍大一些。具体来看,设计航速设计吃水状态和压载吃水状态,球鼻型双月池阻力比单月池阻力分别增大3.1%和2.7%,直立型双月池阻力比单月池阻力分别增大3.1%和2.9%。
3)月池形式的变化对阻力的影响主要体现在剩余阻力增加上,另外月池的存在会减小摩擦阻力。
4)吃水状态对月池产生的剩余阻力影响较大,进而影响不同船型的总阻力大小。
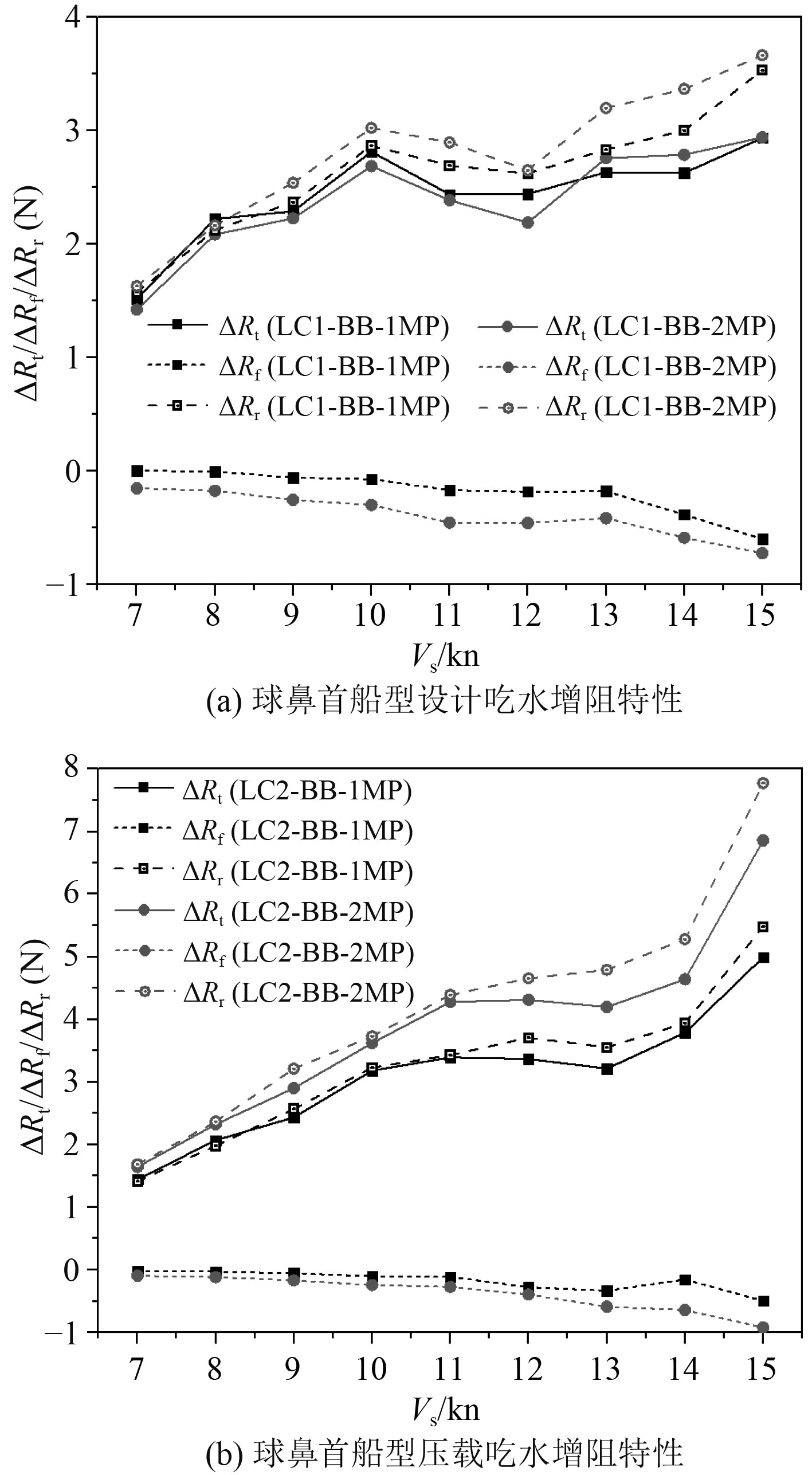
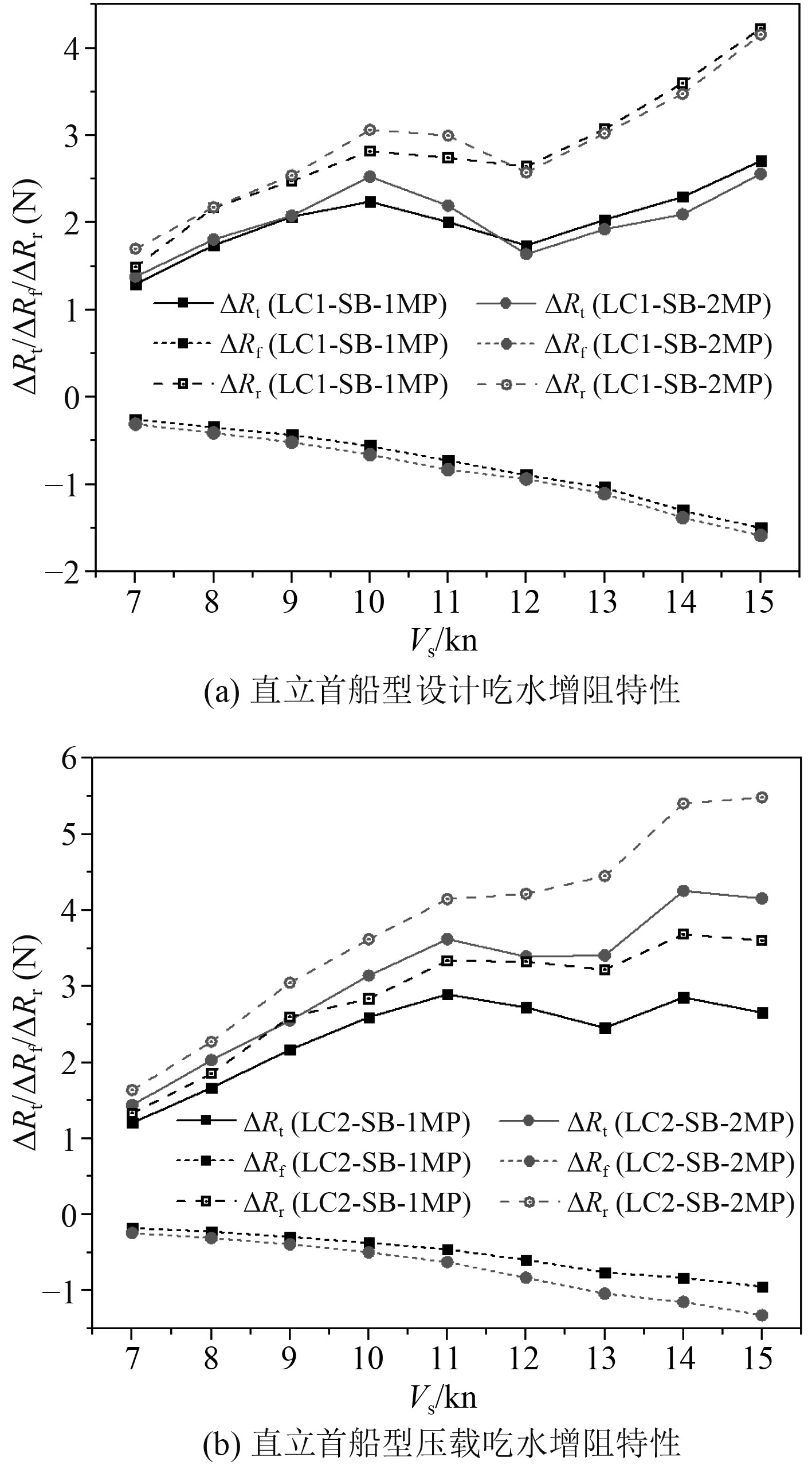
通过提取带月池勘探船与不带月池勘探船的阻力差,可以得到月池增阻。本文将总阻力、剩余阻力、摩擦阻力分别提取得到相应的月池增阻。2种船首以及2种吃水状态下单月池和双月池方案的月池增阻如图12和图13所示。
|
图 12 球鼻首船型月池增阻曲线 Fig. 12 Curve of added resistance of moonpool of bulb bow |
|
图 13 直立首船型月池增阻曲线 Fig. 13 Curve of added resistance of moonpool of straight bow |
可以看出,低航速时,月池增阻随航速增加,而航速在11~13 kn附近出现拐点,月池增阻呈下降或平稳趋势,航速大于13 kn后,增阻趋势随吃水及船型的不同而呈现不同的趋势。
无论何种船型或吃水状态,月池的存在导致摩擦增阻为负值,即月池会降低船体的摩擦阻力。双月池方案摩擦阻力减小程度更大一些。
月池的剩余阻力增量为正值,摩擦阻力增量为负值,摩擦阻力的增量的绝对值要比剩余阻力的增量绝对值小,两者叠加后的总阻力增量为正值。高航速下摩擦阻力的增量的绝对值约为剩余阻力的增量绝对值的1/4左右。
3 结 语对不同船型以及月池布置方案阻力数值计算结果对比可以发现:
1)对于相同的月池布置方案的船型,无论是在设计吃水还是在压载吃水状态,球鼻首船型的总阻力均大于直立型船型。
2)通过对单月池和双月池方案对比发现:在设计吃水状态下单月池和双月池方案的总阻力差别不大,而在压载吃水状态双月池方案总阻力比单月池方案稍大一些。
3)低航速时,月池增阻随航速增加,而航速在上升到一定值附近会出现拐点,月池增阻呈下降或平稳趋势,航速继续增大后,增阻趋势会随吃水及船型的不同而呈现不同的趋势,但无论何种船型或吃水状态,月池的存在导致摩擦增阻为负值,即月池会降低船体的摩擦阻力。双月池方案摩擦阻力减小程度更大一些。
| [1] |
GAILLARDE G, COTTELEER A. Water motion in moonpools Empirical and theoretical approach[C]//. AssociationTechnique Maritime etAeronautique, France: ATMA, 2004.
|
| [2] |
LARSSON L, RAVEN H C. The principles of naval architecture series; ship resistance and flow[M] The Society of Naval Architects and Marine Engineers, 2010.
|
| [3] |
MOLIN B. On the piston and sloshing modes in moonpools[J]. Journal of Fluid Mechanics, 2011, 430(430): 27-50. |
| [4] |
VEER RVt, THOLEN H J. Added resistance of moonpools in calm water[C]// Proceedings of the ASME27th Internactional Conference on Offshore Mechanics and Arctic Engineering. 2008.
|
| [5] |
THOLEN H J. added resistance of moonpools atforward speed in calm water[D]. MSc Thesis TU Delft, 2008
|
| [6] |
SIVABALAN P, SURENDRAN S. CFD simulation of the moonpool on the total resistance of a drillship at low forward speed[C]//10th International Conference on Marine Technology, MARTEC 2016.
|
 2022, Vol. 44
2022, Vol. 44
