0 引　言

在舰船领域，雷达、瞄准设备、声呐设备等一系列现代电子设备的装机量越来越高，这些高精度现代电子设备的广泛应用一方面提升了舰船的性能，提升了目标探测、导弹打击的精度。另一方面，大量现代化电子设备的装机对于船舶的运动特性有了更高的要求，比如船体在波浪作用下的摇摆运动等，不仅会导致现代电子设备的精度下降使用，运动过程中的附加载荷还可能导致电子设备的机械结构出现疲劳损伤甚至失效。因此，高精度船舶设备在设计和安装过程中需要重点考虑舰船在波浪作用下的振动的影响^[1]。

舰船在海上受海浪作用会产生横向的振动，振动的幅频特性与海浪作用力的大小有关，一旦船舶横向运动的幅值超过船舶自身平衡的控制边界后，船舶可能出现失稳、倾覆等严重的事故。因此，为了提升船舶的安全性、可靠性，有必要对波浪作用下的船舶横向振动进行控制。

本文建立波浪载荷的动力学模型，搭建基于减摇鳍技术的船舶横向振动控制系统，采用主动减摇的方式进行横向运动控制，取得了良好的横向振动控制效果。

1 波浪作用下的船舶横向振动边界条件与船舶运动建模

海浪作为船舶横向振动的主要载荷来源，有必要对其频谱特性进行系统研究。首先建立海浪幅频模型为：

$\xi (t) = \sum\limits_{i = 1}^n {{\xi _0}(t)\cos ({k_1}\delta + {w_0}t + \varphi )} \text{。}$

式中： ${\xi _0}(t)$ 为波浪幅值； ${w_0}$ 为波浪传输的角速度； $\varphi$ 为初始相位^[2]。

定义波浪能谱密度公式^[2]如下：

$\eta ({\omega _0}) = \frac{{{k_1}}}{{{\omega _0}^3}}\exp \left(\frac{{ - {k_2}}}{{{\omega _0}^4}}\right) \text{。}$

其中： ${k_1} = 7.9 \times {10^{ - 3}}{g^2}$ ； ${k_2} = \dfrac{{3.09}}{{{h_0}^2}}$ ； ${h_0}$ 为波浪的义波高。

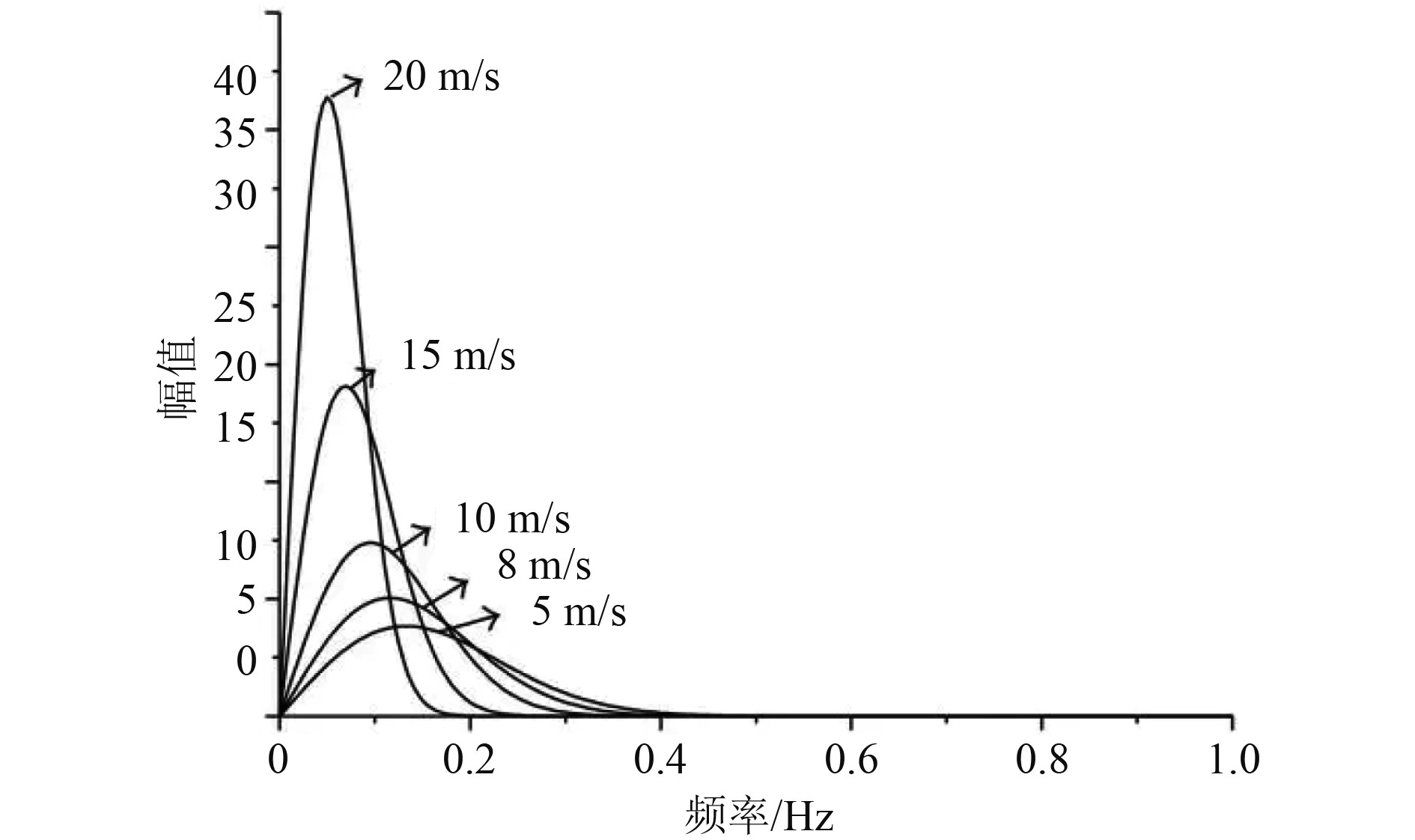
波浪在不同传输速度下的幅频特性曲线如图1所示。

在建立船舶波浪条件下的横向振动模型时，需要建立流体动力边界和运动学边界条件，分别如下：

1）流体动力学边界^[3]

根据海水的不可压缩性，建立船舶运动模型的动力学边界为：

$\frac{{\partial \phi }}{{\partial t}} + \frac{1}{2}\nabla {\phi ^{^2}} + g\delta = 0 。$

式中： $g$ 为重力加速度； $\phi$ 为海水的速度势； $\delta$ 为粘度系数。

2）运动学边界

$\frac{F}{M} = \frac{{\rm{d}}}{{{\rm{d}}t}}f\left[ {x,y,z} \right] \text{。}$

其中， $\left\{ \begin{gathered} x = x(t) \\ y = y(t) \\ z = z(t) \\ \end{gathered} \right.$ 为沿x，y，z三个方向的速度分量，进一步展开可得：

$\frac{{{\rm{d}}F}}{{{\rm{d}}t}} = \frac{{\partial F}}{{\partial t}}\frac{{{\rm{d}}z}}{{{\rm{d}}t}} + \frac{{\partial F}}{{\partial t}}\frac{{{\rm{d}}y}}{{{\rm{d}}t}} + \frac{{\partial F}}{{\partial t}}\frac{{{\rm{d}}x}}{{{\rm{d}}t}} = 0 。$

3）根据船舶在波浪条件下的力学特性，建立船舶横向振动运动模型如下式：

$\left\{ {\begin{array}{*{20}{c}} {\left( {{J_{}} + \Delta {J_{}}} \right)w + 2\kappa w + \dfrac{1}{2}Dh\theta = {T_0}}，\\ {M\dfrac{{{\rm{d}}{u_i}}}{{{\rm{d}}t}}\sin \theta + M\dfrac{{{\rm{d}}{u_j}}}{{{\rm{d}}t}}\cos \theta = {F_0}}。\end{array}} \right.$

式中：M为船舶重量； $J$ 为船舶的转动惯量； $\Delta J$ 为附加转动惯量； $\kappa$ 为阻尼系数； $D$ 为船舶宽度； $\theta$ 为船舶的横向振动角度； $h$ 为船舶吃水深度； ${T_0}$ 为波浪对船舶产生的倾覆力矩； ${F_0}$ 为波浪对船舶产生的作用力。

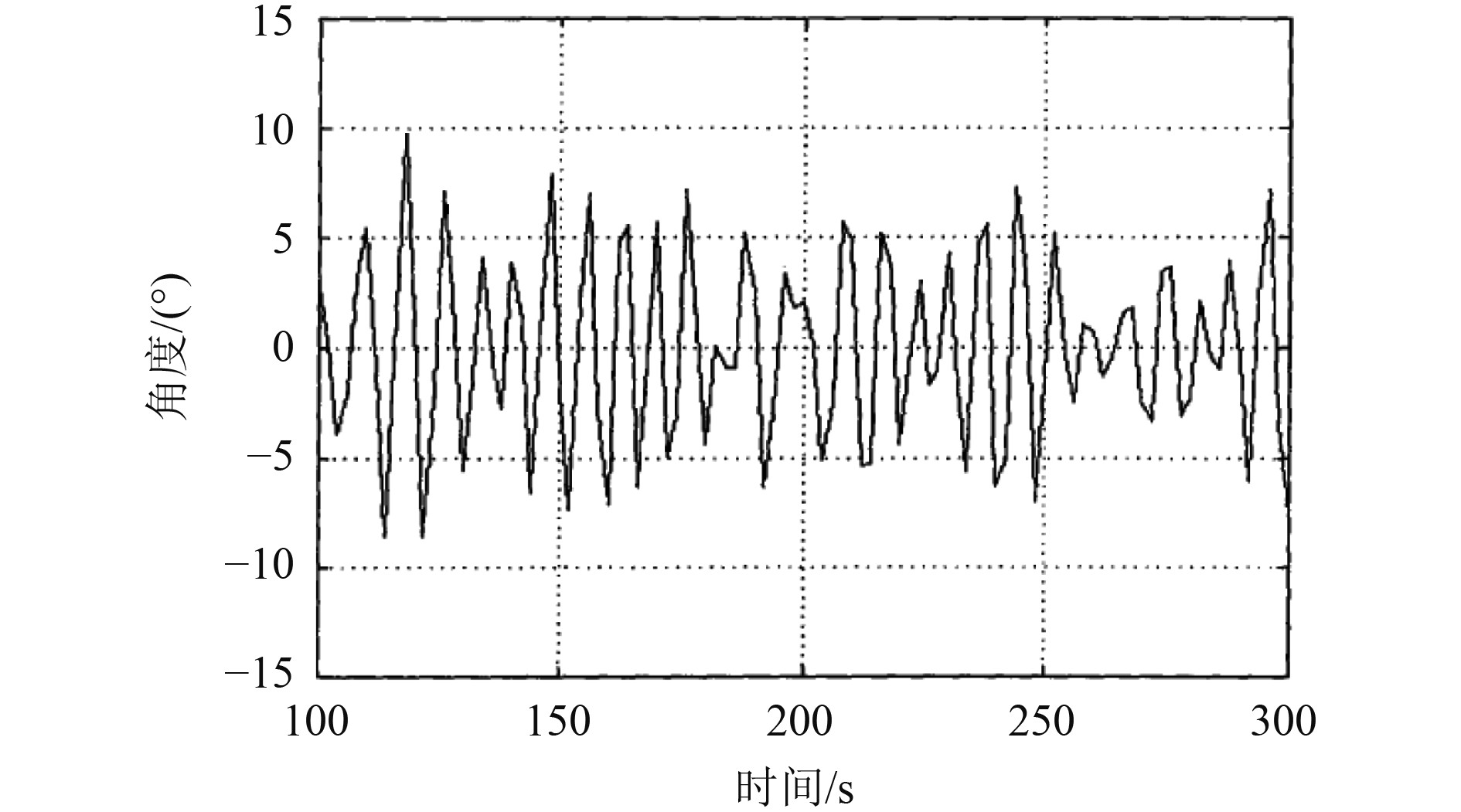
采集100～200 s船舶横向振动角度，得到角度曲线数据如图2所示。

2 基于减摇鳍的船舶横向振动控制系统设计及仿真 2.1 减摇鳍流体力学的基本原理

船舶的横向振动控制一直以来都是船舶领域的重点研究方向，横向振动控制技术从原理上可以分为主动式振动控制和被动式振动控制2种。其中，被动式振动控制是利用船体自身的动平衡、减摇水舱等结构，在横向振动发生后降低振动幅度和频率，缩短船体平衡的时间。主动式控制技术中，减摇鳍是目前使用最广泛的振动控制装置，它利用减摇鳍与流体表面产生的水动力，产生横向振动控制力矩，抵消波浪扰动力矩。

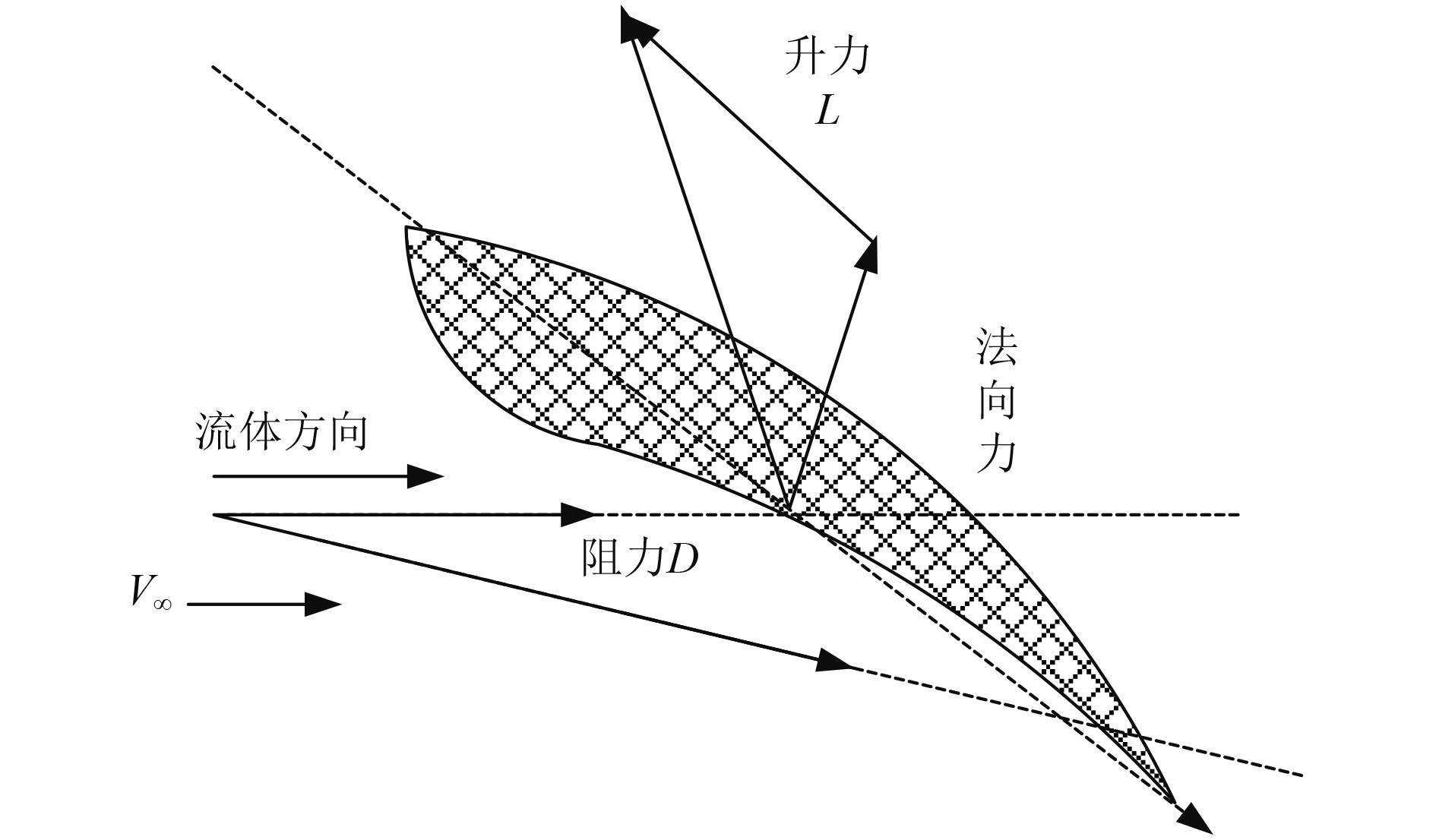
经过数十年的发展，减摇鳍的设计水平不断提高，减摇鳍的翼型直接决定了其水动力参数，也决定了横摇运动发生时产生的恢复力矩大小，减摇鳍翼型设计特征示意图如图3所示。

减摇鳍翼的关键特征参数包括升力系数、阻力系数和压强系数，根据图3可知：

1）升力系数

${C_L} = \dfrac{L}{{\dfrac{1}{2}\rho V_\infty ^2c}} \text{。}$

式中： $V_\infty ^{}$ 为流体与减摇鳍的相对运动速度； $L$ 为翼型长度， $c$ 为海水粘度系数。

2）阻力系数

${C_D} = \dfrac{D}{{\dfrac{1}{2}\rho V_\infty ^2c}} \text{。}$

式中： $D$ 为翼剖面的厚度比。

3）压强系数

${C_p} = \dfrac{{P - {P_\infty }}}{{\dfrac{1}{2}\rho V_\infty ^2}} \text{。}$

式中： $P$ 为静水压力； ${P_\infty }$ 为无穷远处近似压力。

船舶减摇鳍为了抵抗船体产生的横向振动，过程中的抵抗力模型为：

$- {F_0} = {F_k} = \dfrac{1}{2}{\rho _{}}S \cdot {C_L}{V_\infty }^2 \text{。}$

式中： $S$ 为减摇鳍与波浪的相互作用面积。

抵抗力矩模型为：

$- {T_0} = {T_s} = \dfrac{1}{2}h\sin \theta {F_k}\cos \beta \text{。}$

式中： $\beta$ 为鳍角；h为减摇鳍所处的水深。

针对船舶横向振动的减摇鳍设计参数如表1所示。

2.2 减摇鳍鳍型变换液压系统设计

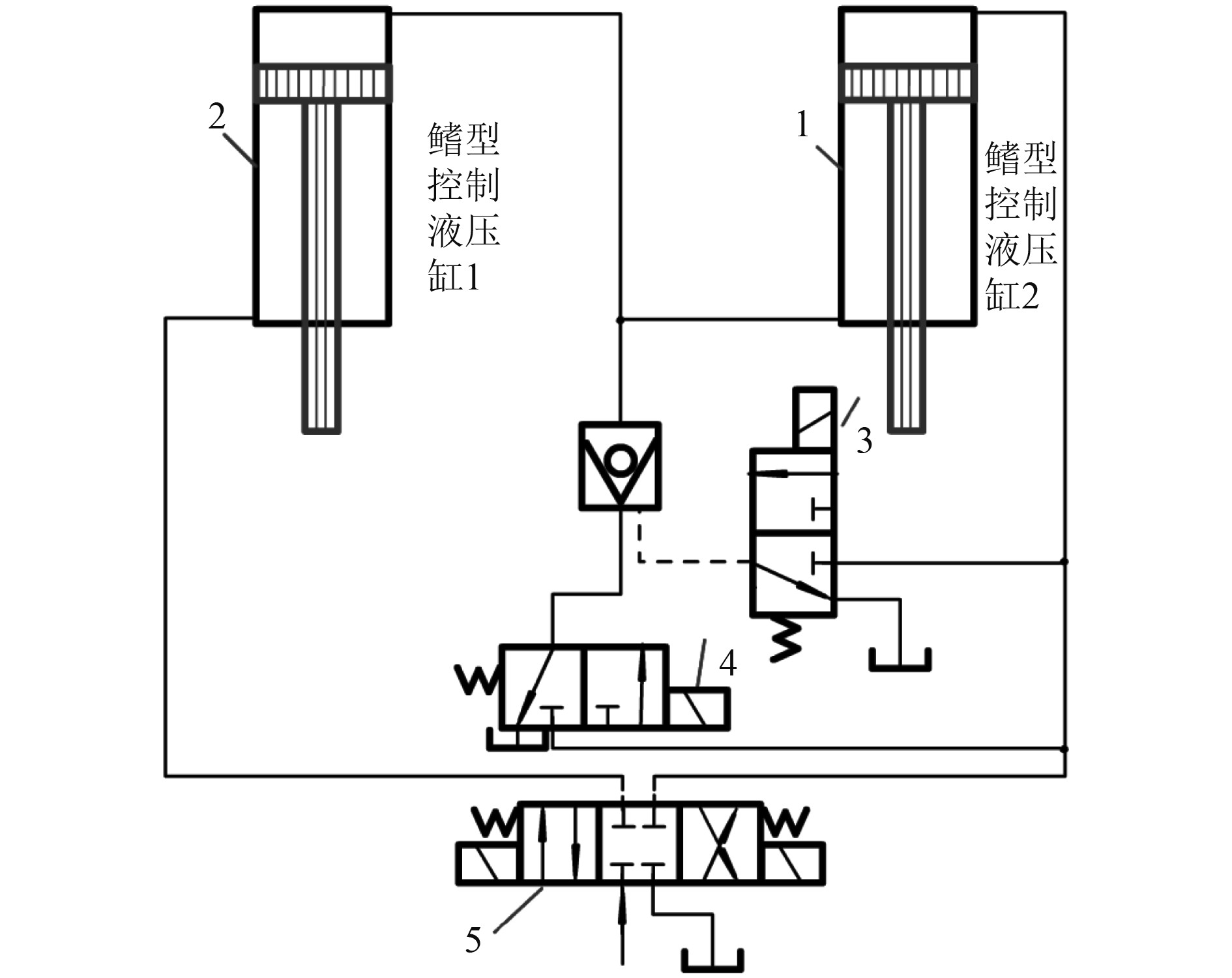
针对波浪作用下的船舶振动控制技术，采用可调式减摇鳍，具体液压回路原理如图4所示。

2个液压缸分别驱动船舶两侧减摇鳍，实现鳍型的变化，根据波浪作用力的大小调节恢复力矩的大小，横向运动控制力矩与液压回路的控制模型如下式：

${M_{\text{Z}}} = \dfrac{{\text{π} D_d^2p{R_0}{\eta _m}}}{{4{{\cos }^2}\alpha }} \text{。}$

其中： $D_d^{}$ 为油缸的直径； $p$ 为油缸压力； ${R_0}$ 为油缸作用位置到减摇鳍重心的距离； ${\eta _m}$ 为液压系统效率； $\alpha$ 为减摇鳍的旋转角度。

2.3 波浪作用下船舶横向振动控制系统设计

使用非线性控制技术，结合减摇鳍液压控制系统，设计一种船舶横向振动控制系统，具体过程如下：

首先定义横向振动非线性系统模型为

$f(t) = Ax\left( t \right) + By\left( t \right) \text{，}$

式中： $t \in {R^ + }$ ， $x\left( t \right)$ 为船舶的横向振动状态向量； $y\left( t \right)$ 为输入向量， $y\left( t \right) \in {R^n}$ 。

将横向振动控制系统进行分解，如下式：

$\left\{ {\begin{array}{*{20}{c}} {{{\dot f}_1}(t) = {A_1}{x_1}\left( t \right) + {B_1}{y_1}\left( t \right)}，\\ {{{\dot f}_2}(t) = {A_2}{x_2}\left( t \right) + {B_2}{y_2}\left( t \right)}，\\ {...} \\ {{{\dot f}_n}(t) = {A_n}{x_n}\left( t \right) + {B_n}{y_n}\left( t \right)} 。\end{array}} \right.$

式中： ${A_i}$ ， $B$ 均为 $n \times n$ 阶矩阵。

建立控制模态函数为：

$S(x,t) = Cx(t) = 0 \text{，}$

式中， $C$ 为n*1矩阵。

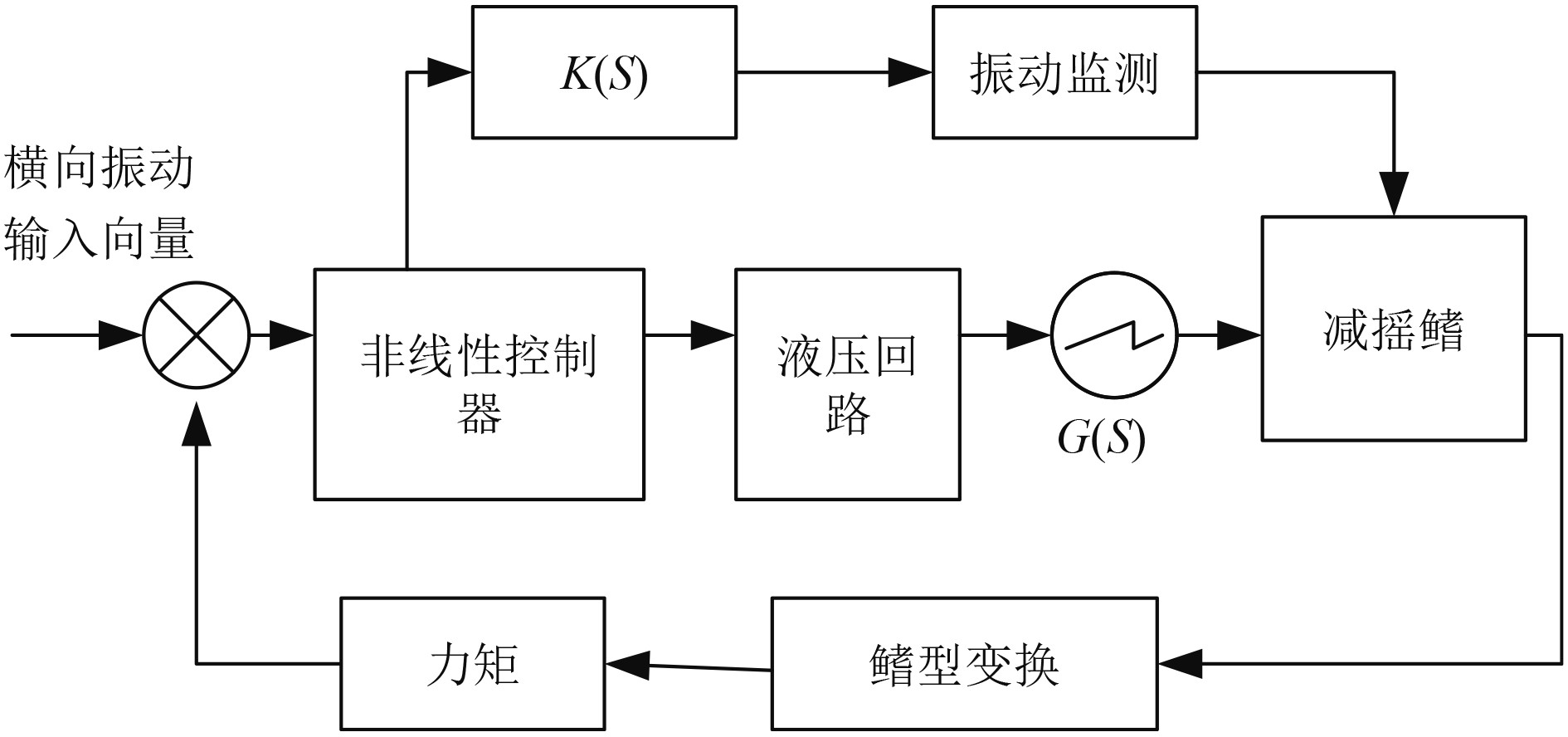
船舶横向振动控制系统原理图如图5所示。

系统的传递函数 $G(s)$ 为：

$G(s) = {k_1} + \frac{{{k_2}}}{\omega } + \frac{{{k_3}}}{{{\omega ^2}}}{s^2} \text{。}$

其中： $\omega = 5.7\,\,{\rm{rad}}/s$ ； ${k_1}$ ， ${k_2}$ ， ${k_3}$ 分别为非线性控制的积分、微分、比例参数。

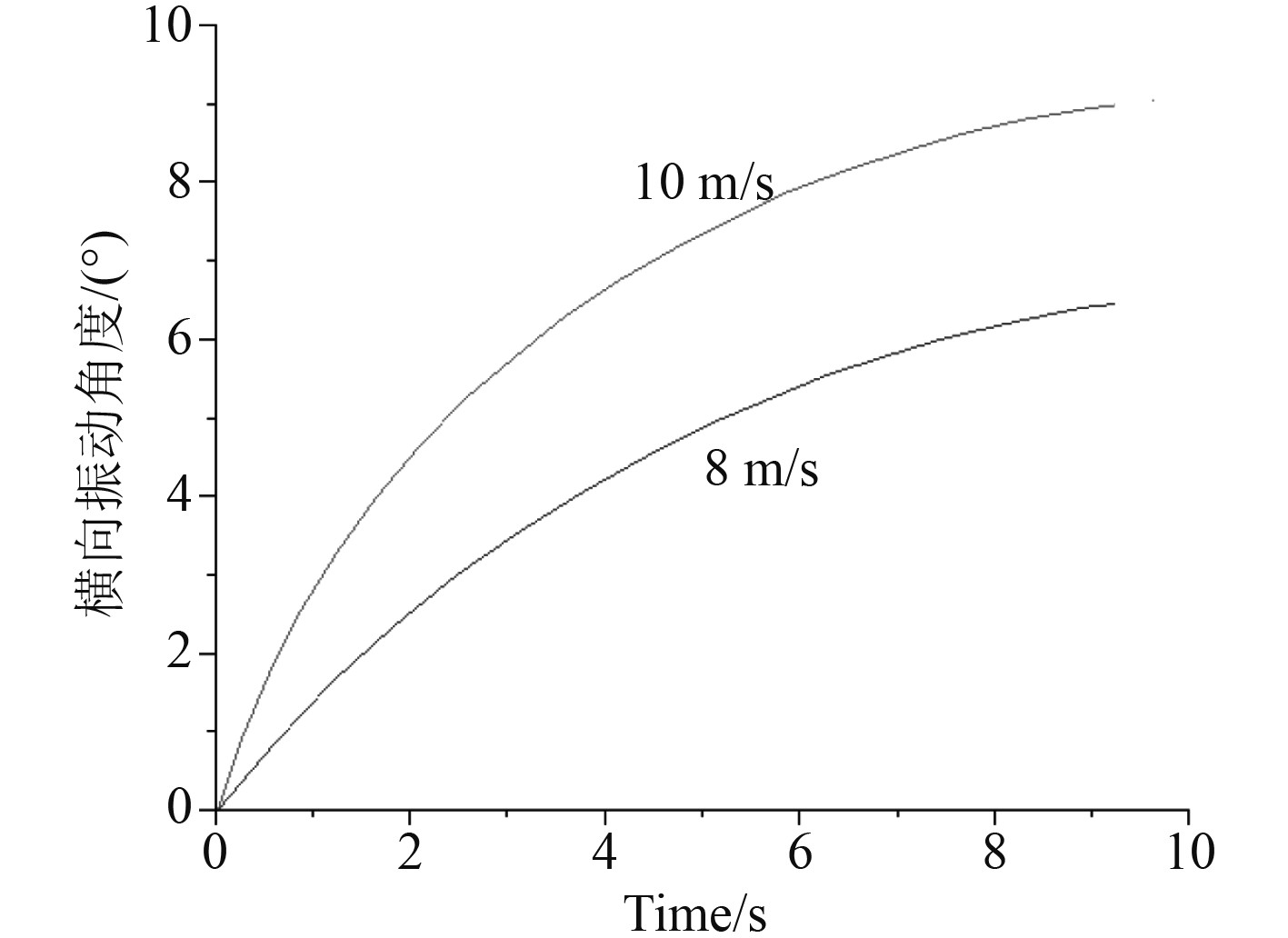
采集2组波浪条件下的横向振动角度控制曲线，如图6所示。可见该振动控制系统具有较好的效果。

3 结　语

本文针对波浪作用下的船舶横向振动控制技术进行研究，结合减摇鳍、液压控制、非线性控制技术，设计一种横向振动控制系统。仿真结果表明，该控制系统的响应速度快，控制效果好。