2. 江苏省海洋资源开发研究院,江苏 连云港 222005
2. Jiangsu Institute of Marine Resources Development, Lianyungang 222005, China
随着能源需求的不断增加,海上油气资源开采和运输日益增加,国际市场对大型液货船的需求日益增长。液货船具有宽度较大、装载率高的特性。在遇到一定范围的波浪时,船体运动会导致剧烈的液舱晃荡,并且晃荡载荷会对船体结构和运动响应造成重大安全隐患。
针对液货船的液舱晃荡问题,蔡忠华[1]基于VOF法建立数值计算模型,结果与模型晃荡试验对比,验证了数值方法解决晃荡问题的可行性,对含有内部构件的VLGC液舱数值模型研究,发现内部构件减小共振频率下晃荡冲击载荷的同时,改变了舱内液体的固有频率,当外激励频率在此频率附近时,冲击载荷反而更大。张秋艳[2]使用ADIDA软件模拟纵荡激励下二维矩形液舱晃荡的数值模型,其液面波动情况与Faltinsen的解析解对比,验证了该模型的有效性。对二维弹性液舱进行数值模拟,分析了不同壁厚、不同频率对液体晃荡的影响。金鑫[3]基于有限差分法对NS方程进行数值离散,建立纵荡与升沉耦合激励下流体晃荡三维数值模型,基于势流理论推导出纵荡与升沉耦合激励下理想流体晃荡解析解,验证了数值模型。结果表明当激励频率的和值或者差值接近流体系统自然频率时,耦合激励也可以激发共振晃荡波。Zhang [4]采用有限差分法对垂直激励槽内的非线性液体晃荡问题进行数值模拟,通过σ变换将不规则液体域映射到一个矩形区域,在迭代过程中对自由液面进行预测,该方法可以精确计算出垂直晃荡过程中的自由液面高度与晃荡压力。Ida M. Strand[5]对带有柔性侧壁的二维矩形液舱进行数值分析,研究晃荡与柔性舱壁之间的耦合问题,通过分析和数值计算,得到了2种不同膜长度下由摇摆激励引起的耦合本征频率和传递函数,分析结果与数值结果一致。宁德志[6]采用高阶边界元法,模拟了二维刚性矩形液舱在水平与垂直激励下的晃荡运动,结果表明在耦合晃荡问题中,水平激励对波浪的形状起主导作用。Mashy D. Green[7]基于SPH法,提出改进公式,能够捕获液舱的晃荡频率,并且准确模拟液舱长时间晃荡的液面形状。Constantin[8-9]对矩形液舱在垂直简谐激励下的晃荡运动进行实验研究,定性和定量解释了阻力饱和点和耗散效应,以及区分不同晃荡状态的指标。建立基于SPH法的数值模型和基于弹跳球模型的等效力学模型,结果与实验对比发现2种模型在晃荡的初始阶段均具有较好的预测能力,但仅有SPH模型能预测后续的流态。
本文针对多自由度下液舱晃荡问题,采用基于VOF法的多相流模型,建立多组复合激励工况,探究复合激励下液舱晃荡的压力变化特点以及频率对压力影响,研究结果对舱体结构设计具有指导意义。
1 无关性分析本文计算采用二维矩形液舱[10],液舱的尺寸,横摇中心与横摇角大小如图1所示,其中P点是25% H时自由液面高度,也是压力监测点所在位置。

|
图 1 液舱模型尺寸与横摇参数(m) Fig. 1 Tank size and rolling parameters (m) |
在25%装载高度下,时间步大小设置为0.002 s,横摇角度为12°,设置网格数量分别为1万、2.4万、3万、4万、5万和6.25万,分别计算在P点的晃荡载荷变化,见图2。结果显示,随着网格数量的增大,计算精度逐渐提高。当网格数量达到2.4万后,网格数量的提高对计算结果影响大幅降低,计算结果逐渐收敛。

|
图 2 不同网格数量下晃荡压力计算结果 Fig. 2 Calculation results of sloshing pressure under different grid numbers |
液体固有频率计算公式:
| $ f_n=\frac{1}{2{\text{π}}} \sqrt{g\frac{n {\text{π}}}{L}tanh \left(\frac{n {\text{π}}}{L}H\right)}。$ | (1) |
式中:fn为n阶固有频率,Hz;ɡ为当地重力加速度;L表示液舱运动方向自由液面长度;H表示液舱内液体装载高度。液舱纵摇时,L等于液舱长度。本文研究包括液舱横摇状态,故L等于液舱宽度。当n等于1时,即液体的最低固有频率,此时的频率最容易被激发,且在此频率附近晃荡最剧烈,对舱壁产生的冲击力也最大。
计算可得25% H下,矩形液舱的固有频率为0.81 Hz,理论计算结果与实际频率有一定的误差,所以在数值模拟时,选择在固有频率0.81 Hz上下增减0.05 Hz,选择5个频率,工况如表1所示。为进一步确保数值计算的精确度,在3万网格的基础上选择时间步为0.001 15 s。
|
|
表 1 25%装载率横摇工况 Tab.1 Rolling condition of 25% loading rate |
使用Fluent中UDF驱动液舱模型横摇转动,角速度为:
| $ \omega =A_I \cos 2{\text{π}} f_rt。$ | (2) |
其中:fr为横摇激励频率,由于转动角度为12°,经计算可得:
| $ A_I=\frac{2{\text{π}}^2 f_r}{15} 。$ | (3) |
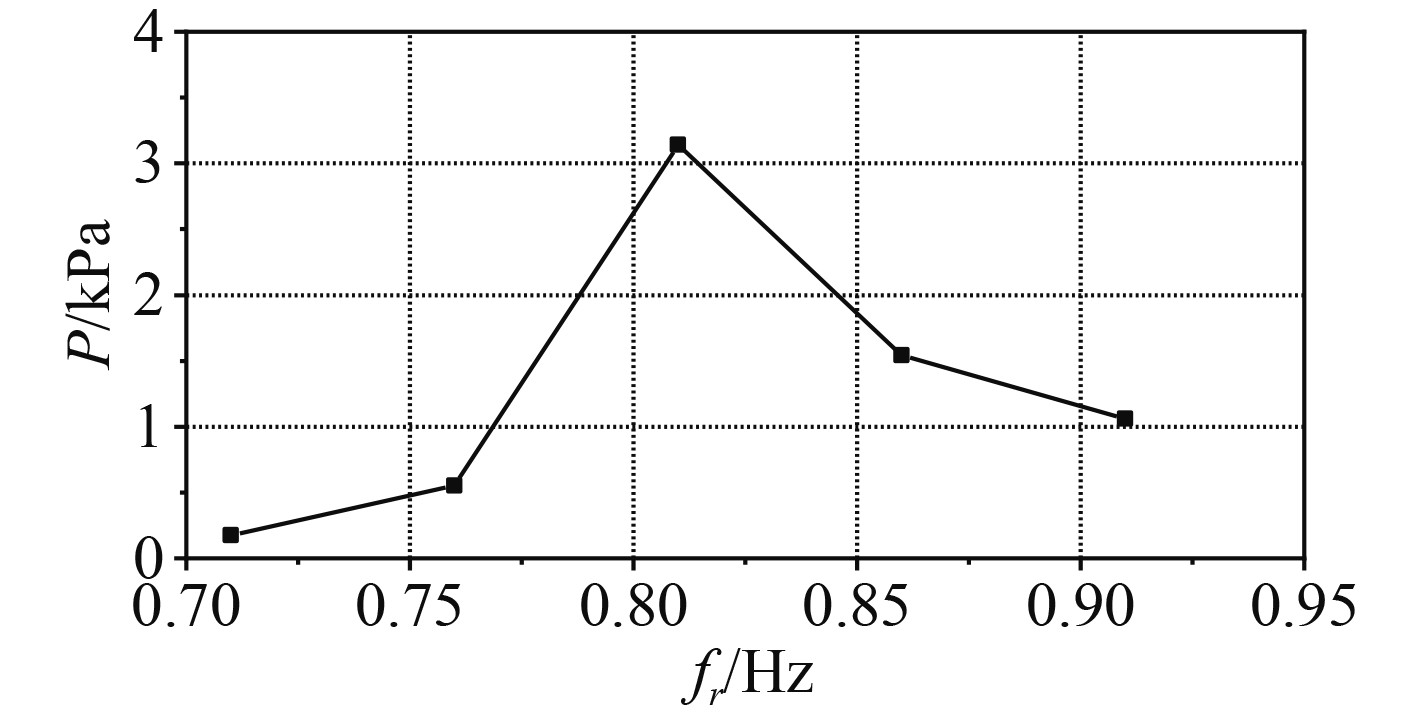
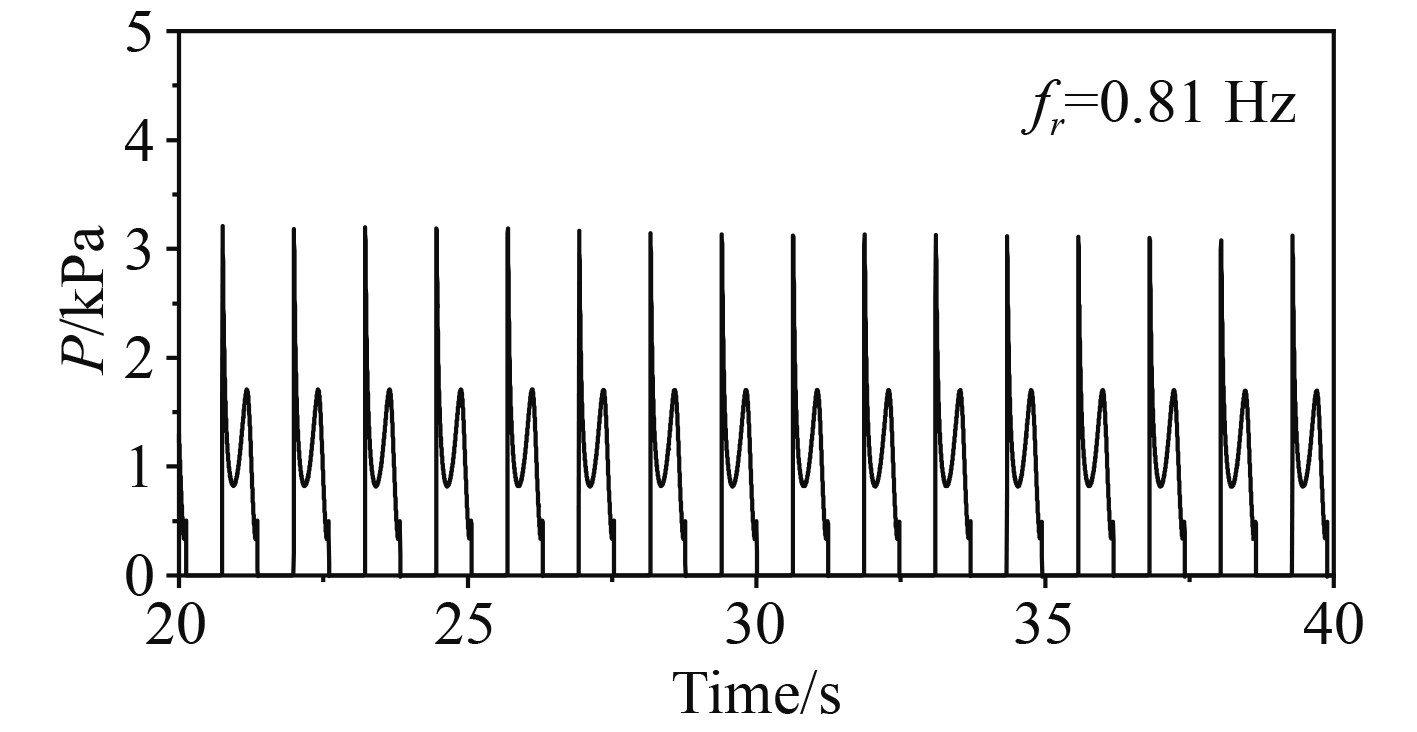
由图3可知,矩形液舱25% H,横摇激励频率在0.81 Hz附近时,舱壁受到的砰击载荷最大,所以此时的共振频率在0.81 Hz附近。当激励频率小于共振频率时,晃荡载荷随频率增加的速率较快,在大于共振频率时,晃荡载荷随频率减小的速率较慢。图4为单纯横摇激励fr=0.81 Hz时,晃荡压力曲线呈现明显的双峰特征,由于液体猛烈砰击在竖直壁面,所以首峰数值较大,持续时间较短,次峰值较小,持续时间较长。
|
图 3 25%H横摇激励晃荡压力随频率分布特点 Fig. 3 Distribution characteristics of sloshing pressure with rolling excitation under 25%H |
|
图 4 fr=0.81 Hz点P处压力时程曲线 Fig. 4 Pressure time history curve at point P with fr = 0.81 Hz |
基于上述液舱的单纯横摇运动,对液舱运动增加垂荡激励,激励幅值为0.1 m。通过UDF驱动液舱模型的垂荡运动,垂向运动线速度为:
| $ V=A_2\sin 2 {\text{π}} f_ht ,$ | (4) |
由于垂荡幅值为0.1 m,经过计算得:
| $ A_2=0.1{\text{π}} f_h。$ | (5) |
其中,fh为垂荡激励频率。选择fh时,综合考虑横摇激励频率与共振频率,制定复合激励工况如表2所示。
|
|
表 2 复合激励工况 Tab.2 Compound excitation working condition |
针对这一数值模型对解决垂荡激励下液舱晃荡问题的有效性,选择Constantin L[9]中的液舱模型,在30%装载高度,8.3 Hz垂荡简谐激励频率,采用本文数值模型模拟的自由液面变化如图5所示。图6为Constantin L实验中的自由液面变化。可以清晰看出,数值模拟的自由液面变化与实验结果基本吻合,说明此数值模型可以很好的模拟垂荡激励下的晃荡问题。

|
图 5 数值模拟垂荡激励下自由液面变化 Fig. 5 Numerical simulation of free surface change under heaving excitation |

|
图 6 Constantin L垂荡激励实验自由液面变化 Fig. 6 Free surface change in Constantin L heaving excitation experiment |
单纯横摇激励下,每个运动周期内晃荡压力变化规律基本相同。横摇激励在共振频率附近时压力曲线呈现双峰特征,首峰峰值大且持续时间短,次峰相对较小但持续时间较长。复合激励时,影响晃荡载荷的频率因素增多,舱体运动变得复杂,此时压力曲线会出现多个运动周期组合的大周期。
由图7(a)可知,当fr=0.71 Hz,fh=0.6 Hz,两者都远离一阶共振频率时,晃荡压力数值较小,结合气液分布图可知此时晃荡剧烈程度较低,在单个运动周期内液面沿着舱壁上下轻微起伏,再由于两自由度复合激励运动,其中影响频率较多,压力曲线表现出更大的周期性。当fr=fh=0.71 Hz时,每个运动周期内舱体运动变化相同,所以其压力变化基本一致,由于远离一阶固有频率,压力数值仍然较小,但由于激励频率相同,压力曲线的周期性降低。当fr=0.71 Hz,fh=0.81 Hz,即fr远离共振频率,但fh在一阶共振频率时,压力数值有较明显的上升。当fr=0.71 Hz,fh=1.13 Hz,即垂荡激励频率大于一阶共振频率时,压力数值继续增大,晃荡形式变得复杂,压力双峰大小交替周期性变化。与图3相比,压力时程曲线呈现的周期增多,在fr远离共振频率时,压力未出现瞬时快速增大的现象,fr=0.71 Hz系列工况的自由液面变化特征如图7(b)所示,此系列复合激励自由液面变化很小,整个运动周期内自由液面沿舱壁爬升幅度很低,所以此时舱壁受到压力载荷较小。

|
图 7 工况1~工况9晃荡特征 Fig. 7 Sloshing characteristics under conditions 1~9 |
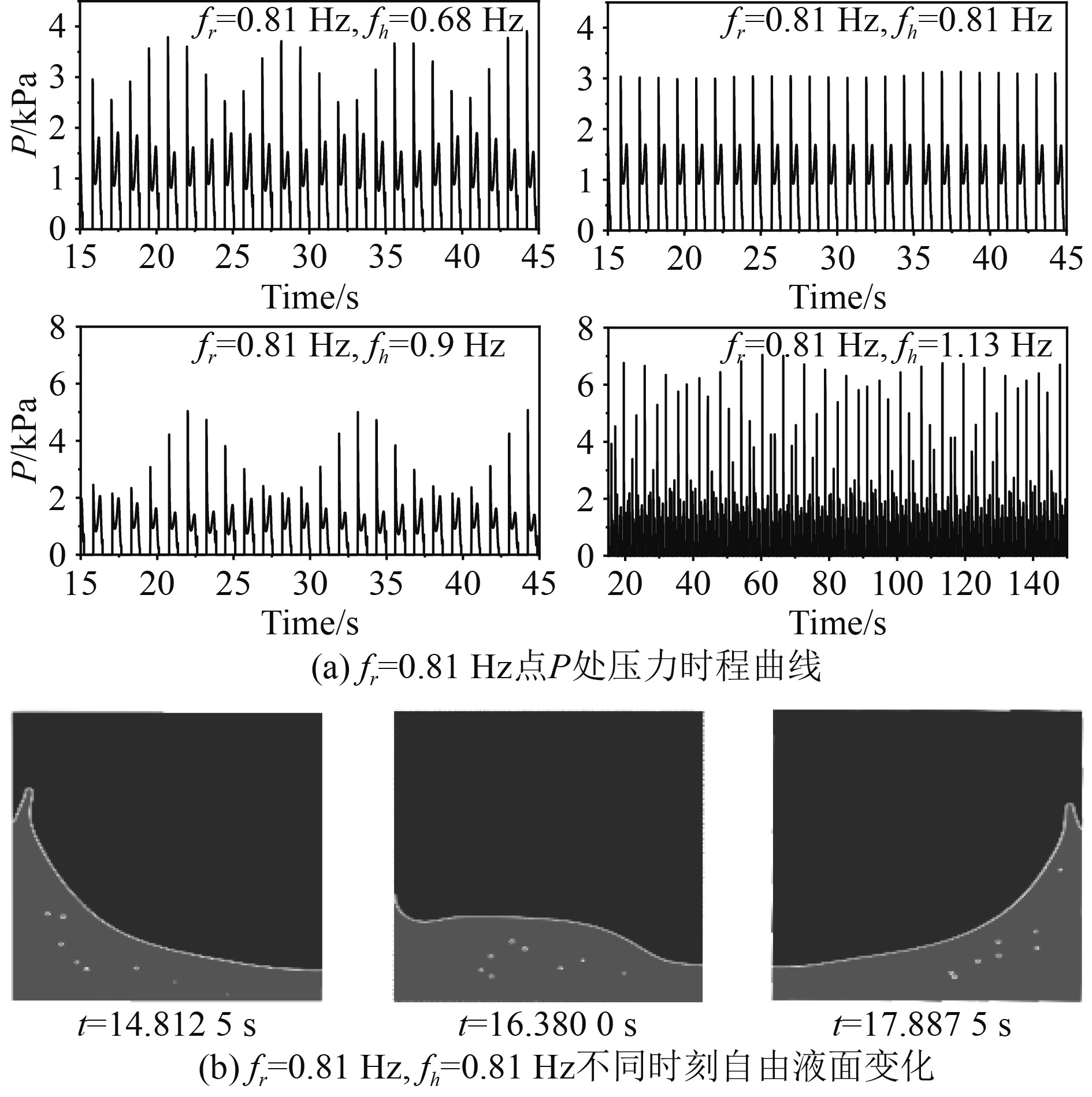
图8(a)表明,fr处于一阶共振频率时,压力曲线与单纯横摇激励时类似,压力载荷曲线呈明显的双峰特征,首峰峰值大且持续时间短,次峰相对较小,持续时间较长。区别在于当fh=0.68 Hz远离共振频率时,压力曲线呈周期性变化,一开始首峰峰值大且持续时间短,次峰峰值较小但时间相对较长,两者差距很大,随着运动周期增加,首峰逐渐降低,两者差距逐渐缩小再增大,差距在0.61~2.19 kPa之间。当fh=fr=0.81 Hz,两者都处于一阶共振频率时,舱内液体晃荡较为剧烈,在每个运动周期内的压力变化规律相同,首峰压力峰值基本稳定在3.04 kPa左右,但相较于fr=0.81 Hz的其他复合激励工况,此时的晃荡压力峰值略小。fh=0.9 Hz时,压力的变化规律与fh=0.6 Hz时相似,但峰值变化更加明显,首峰与次峰的差距变化在0.18~3.6 kPa。此系列压力时程曲线与图4 fr=0.81 Hz单纯横摇激励相比,两者都有明显的双峰特征,但由于复合激励下液舱运动形式会周期性变化,所以复合激励下的压力时程曲线周期性更多。fr=0.81 Hz复合激励系列工况的自由液面变化特征如图8 (b)所示,此系列工况下液体晃荡剧烈,自由液面沿舱壁爬升较高且出现射流,液体内部裹挟了大量气泡。
|
图 8 工况19~工况27晃荡特征 Fig. 8 Sloshing characteristics under conditions 19~27 |
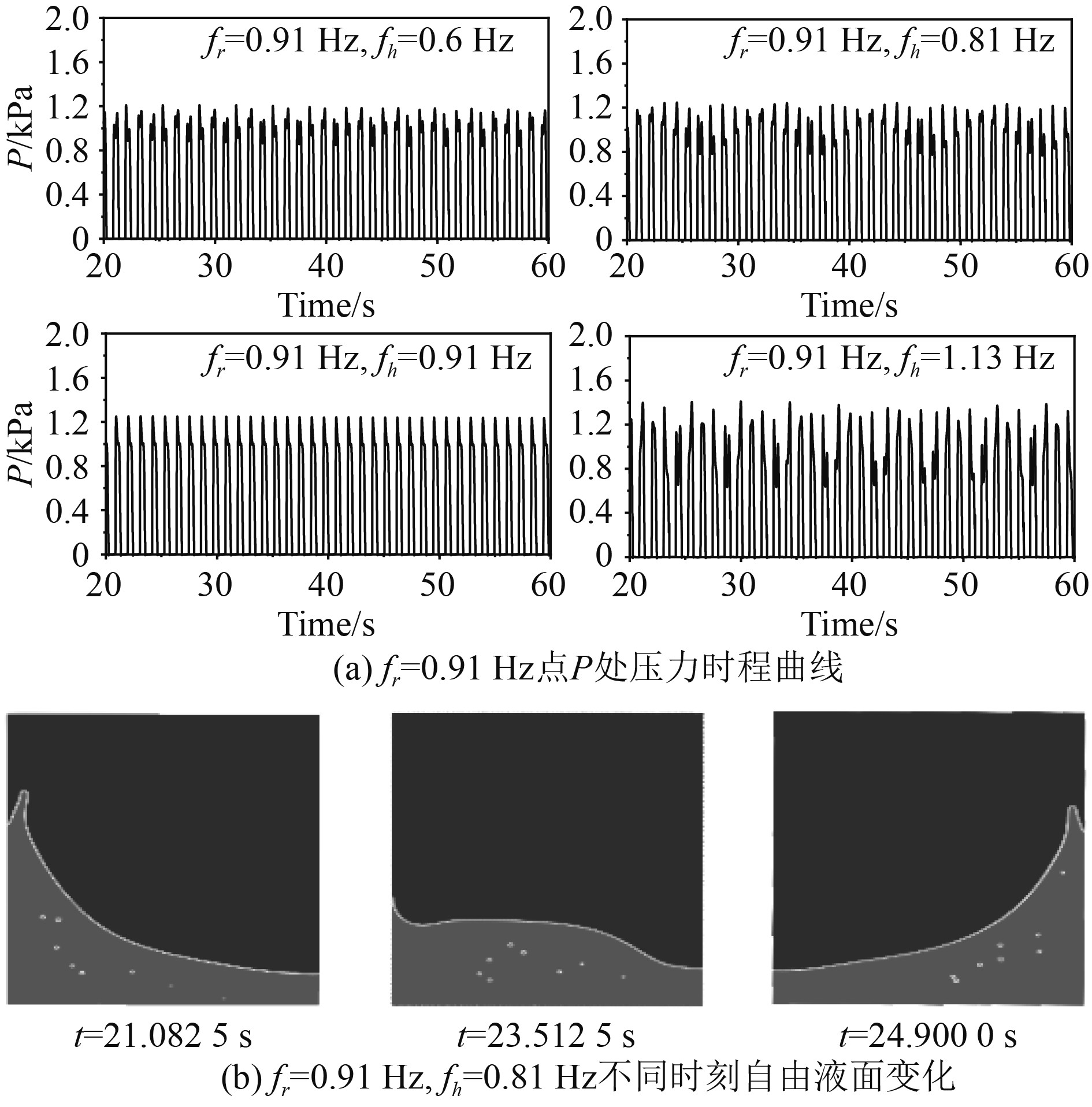
图9表明,当fr=0.91 Hz,fh=0.6 Hz时,激励频率都远离一阶共振频率,压力载荷相对图8有明显的降低,其压力峰值基本在1~1.5 kPa左右,压力曲线的首峰与次峰呈周期性交替变化,双峰数值差距不大,持续时间均较短。当fh=0.81 Hz时,双峰大小周期性变化特征更加显著,且此时转换周期比fh=0.6 Hz时更长。当fh=fr=0.91 Hz时,压力曲线与单纯横摇激励类似,单个运动周期内压力载荷较大且持续时间较短,此时由于远离一阶共振频率,液体晃荡相对较为缓和。当fh=1.13 Hz时,激励频率均远离一阶共振频率,相比于fh=0.6 Hz,压力载荷首峰与次峰大小依旧呈现周期性变化,此时压力大小有一定增大。与图4相比,压力曲线的双峰特征不明显且数值较小。此系列晃荡的液面变化特征如图9(b)所示,相比图8(b)此系列工况液体晃荡有明显缓和,但液体沿舱壁爬升仍较高,内部裹挟有少量气泡。
|
图 9 工况37~工况45晃荡特征 Fig. 9 Sloshing characteristics under conditions 37~45 |
综合各工况下压力时程曲线与气液两相分布图,可以发现当矩形液舱激励频率fr≠fh时,其每个运动周期内的压力载荷变化会出现多种类型的压力载荷变化,多个运动周期组合形成的更大周期,这表明复合激励内存在更多影响其压力载荷的频率。
当激励频率fr=fh时,压力载荷曲线特征与单纯横摇相同,每个运动周期内的压力载荷变化稳定,两者在一阶共振频率0.81 Hz时压力曲线有明显的双峰特征,此时晃荡最为剧烈,在液体爬升舱壁的极限位置出现射流且液体内部裹挟有大量的气泡。
3.3 复合激励下晃荡压力频域特征统计表2中各工况下的压力载荷大小,分析其随频率变化特点。再以fr=0.81 Hz为例,对其各个工况的压力时程曲线进行傅里叶分析,研究影响压力载荷的主要频率。
图10中浅色点代表矩形液舱在25%装载率时,单纯横摇激励下晃荡压力载荷大小,黑色表示表2各工况下晃荡压力载荷大小。可以看出,垂荡频率对晃荡载荷的影响基本呈V字变化,拐点出现在fr=fh时,此时复合激励下的晃荡载荷与单纯横摇激励相差不大。当fr≠fh时,fh的加入对晃荡载荷有增大作用,尤其是当fh>fr时,晃荡载荷的增加更为显著,且随着的增加,晃荡载荷继续呈增加的趋势。可以看出,图10(a)和图10(d),fr远离0.81 Hz的工况,晃荡载荷在垂荡激励的放大作用下始终没有超过图10(b)和图10(e)的最小值。同样的图10(b)和图10(e),在接近一阶共振频率的工况,晃荡载荷也始终未达到图10(c)中的最小值。说明在本文工况中,垂荡激励对于晃荡载荷的放大效果有限,起主导作用的始终是横摇激励。

|
图 10 横摇与垂荡复合激励工况下晃荡压力变化 Fig. 10 Variation of sloshing pressure under compound excitation of roll and heave |
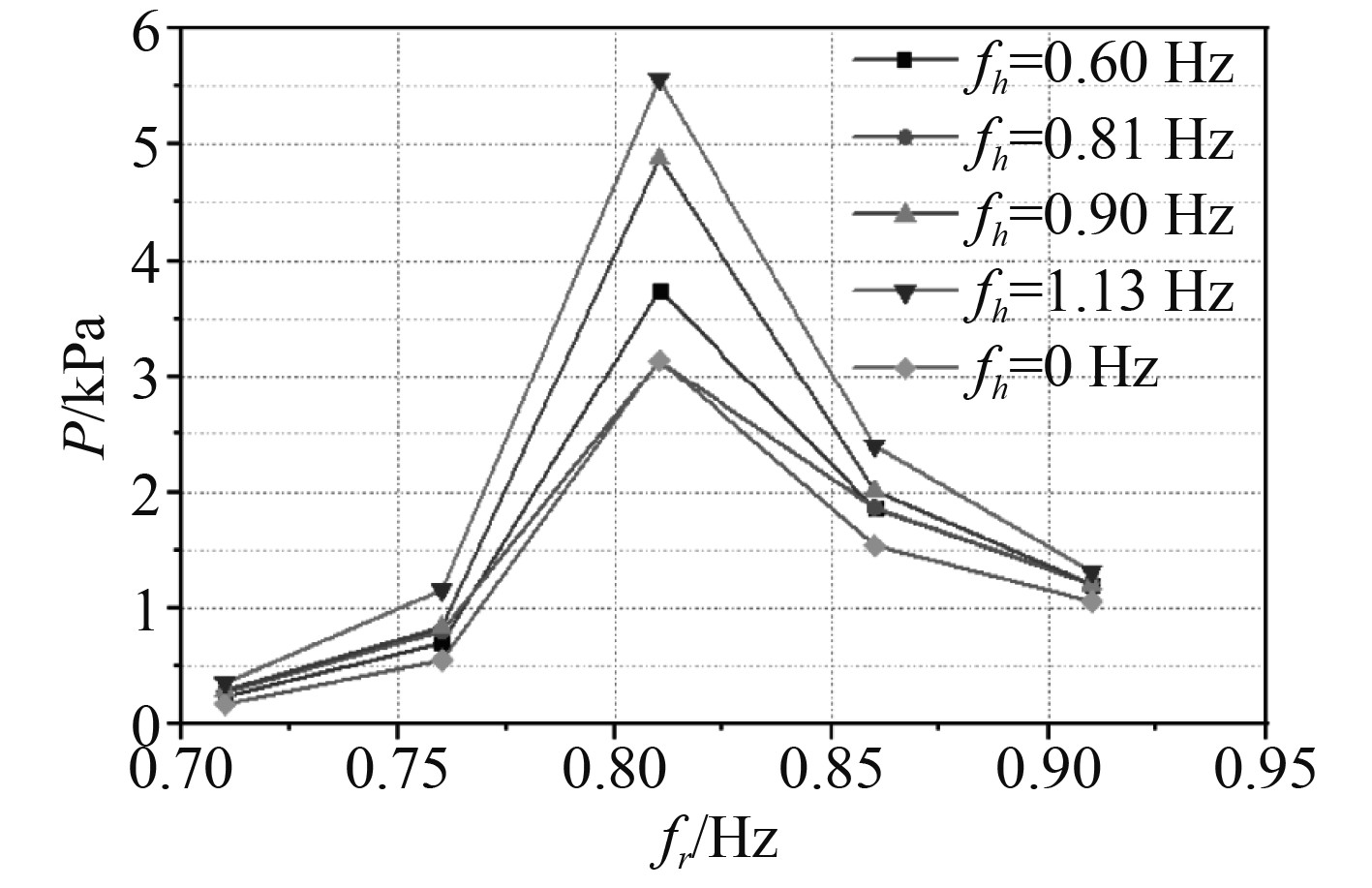
从图11可以看出,各组复合激励下晃荡载荷随横摇激励频率的变化规律与单纯横摇激励时相同。晃荡压力在fr=0.81 Hz时最大,随着横摇频率逐渐远离共振频率,复合激励的晃荡压力也在逐渐减小。垂荡激励对晃荡压力的放大作用在fr=0.81 Hz,即一阶共振频率时最为明显,其效果随着fr逐渐远离一阶共振频率而逐渐降低,放大作用效果也随着垂荡频率的增加而增大。
|
图 11 fh不同,晃荡载荷随fr变化情况 Fig. 11 Variation of sloshing load with fr for different fh |
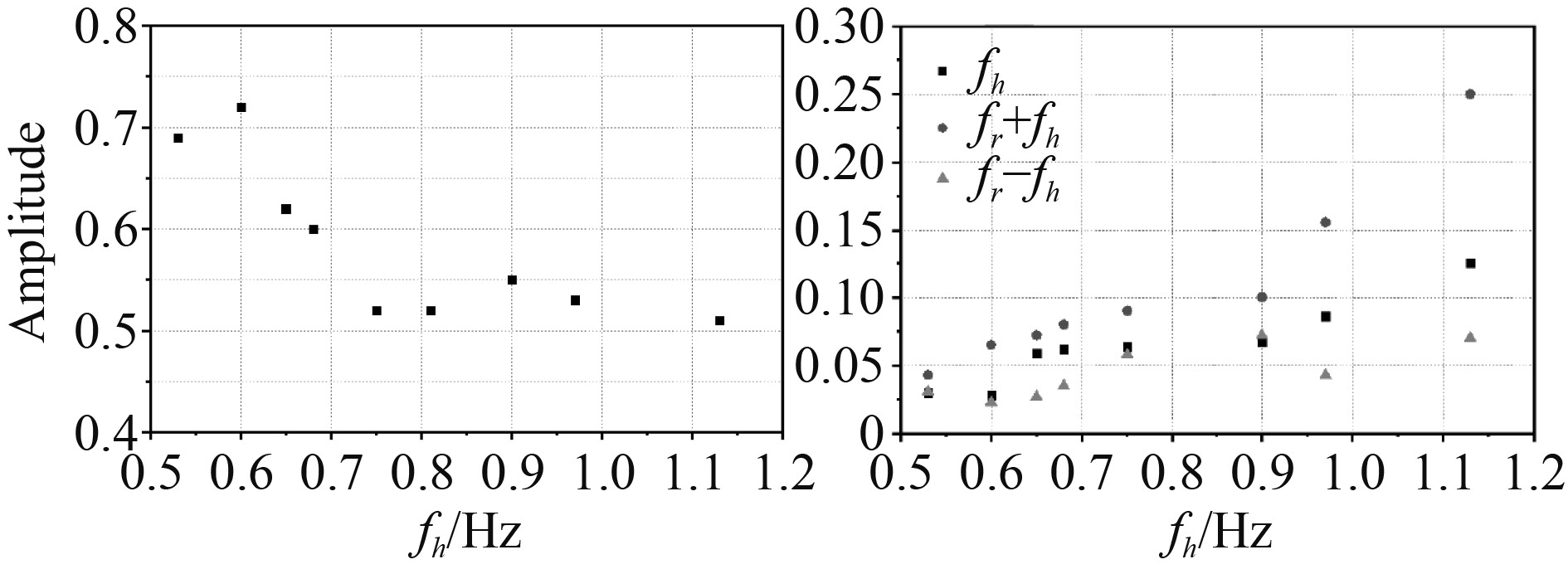
为了进一步探究复合激励下频率对晃荡压力的影响,对fr=0.81 Hz系列工况的晃荡压力时程曲线进行傅里叶分析,对其中影响因素较大的频率极其幅值进行统计,如图12所示。
|
图 12 各主要频率的幅值变化 Fig. 12 Amplitude variation of main frequencies |
本文研究的复合激励包含横摇激励与垂荡激励,对压力时程曲线进行傅里叶变换后可以发现,对晃荡载荷影响最大的为n倍的fr(n为非零正整数)。如图12(a)所示,随着垂荡激励的不断增大,fr的幅值整体呈下降趋势,但仍大于图11(b)中各频率的幅值,说明此时横摇频率依然是影响晃荡载荷的主要因素。除了nfr以外,nfh,n(fr+fh),n(fr−fh)都是影响晃荡载荷的重要频率因素。如图12(b),3种频率的幅值随着垂荡激励的增大而不断增大,在欠共振阶段幅值增速较慢,在超共振阶段,频率的幅值增速较快,其中增速最快的是fr+fh。
4 结 语本文基于VOF法多相流模型模拟横摇与垂荡复合激励下二维矩形液舱的晃荡问题,研究分析了在25% H低装载下自由液面处压力载荷的时域与频域特征,得到以下结论:
1)当fr≠fh时,每个运动周期内的压力载荷变化会出现多种类型的压力载荷变化,多个运动周期组合形成的更大周期;当fr=fh时,压力载荷曲线与单纯横摇相同,每个运动周期内的压力载荷变化稳定。
2)横摇与垂荡复合激励中,横摇激励频率起主导作用,当fr=fh时,垂荡激励会减小晃荡压力,fh>fr时垂荡激励放大晃荡压力的作用会更加明显,但效果没有改变横摇激励频率显著。
3)随着fh的不断增大,fr对晃荡压力的影响会逐渐降低但仍为主要影响因素,fh,fr+fh,fr−fh对压力载荷的影响不断增加,多种频率的影响使压力时程曲线呈现多种周期形式,在这些周期内压力双峰大小交替性变化。
本文仅研究25%装载率矩形液舱在横摇-垂荡复合激励下晃荡压力变化,对于中高装载率与其他多种复合激励还需要做进一步研究,从而全面探索液舱晃荡多种运动下的晃荡压力变化规律,为工程设计提供参考与建议。
| [1] |
蔡忠华. 液货船液舱晃荡问题研究[D]. 上海: 上海交通大学, 2012.
|
| [2] |
张秋艳. 二维矩形液舱内液体晃荡的数值模拟[D]. 大连: 大连理工大学, 2011.
|
| [3] |
金鑫, 刘飞飞, 邹寅劼, 等. 纵荡与升沉耦合激励下晃荡波特性及响应规律研究[J]. 水道港口, 2021, 42(3): 309-317. DOI:10.3969/j.issn.1005-8443.2021.03.004 |
| [4] |
ZHANG Hai-tao , SUN Bei-bei. Numerical simulation of nonlinear sloshing in a 2D vertically moving container[J]. Advanced Materials Research, 2013, 2717(819-819).
|
| [5] |
IDA M S, ODD M. Faltinsen.. Linear sloshing in a 2D rectangular tank with a flexible sidewall[J]. Journal of Fluids and Structures, 2017, 73. |
| [6] |
NING De-Zhi, SONG Wei-Hua, LIU Yu-Long, et al. A boundary element investigation of liquid sloshing in coupled horizontal and vertical excitation[J]. Journal of Applied Mathematics, 2012, 2012. |
| [7] |
GREEN M D, ZHOU Yipeng, DOMINGUEZ J M, et al.. Smooth particle hydrodynamics simulations of long-duration violent three-dimensional sloshing in tanks[J]. Ocean Engineering, 2021, 229. |
| [8] |
CONSTANTIN L, D COURCY J J, TITURUS B, et al.. Sloshing induced damping across Froude numbers in a harmonically vertically excited system[J]. Journal of Sound and Vibration, 2021, 510. |
| [9] |
CONSTANTIN L, DE COURCY J, TITURUS B, et al. Analysis of damping from vertical sloshing in a SDOF system[J]. Mechanical Systems and Signal Processing, 2020(prepublish).
|
| [10] |
邹昶方. 液舱晃荡非线性动力学行为研究[D]. 上海: 上海交通大学, 2016.
|
 2022, Vol. 44
2022, Vol. 44
