桥墩的阻碍、船舶规模的增大、船舶速度的增加等各种因素共同作用下,船桥相撞事故发生的概率大增[1]。一旦发生相撞事故,不仅会造成严重的经济损失、人员伤亡,甚至还会造成漏油现象,污染了自然水环境,造成了严重的环境污染[2]。面对这种情况,如何减轻船桥相撞造成的灾难性损失已经成为一个重要研究课题。在设计船舶时,船舶的结构强度以及动力响应要重点考虑,这关系到船舶在船桥碰撞时的抗撞击能力和承载力[3]。在此背景下,了解船桥碰撞下船体结构强度及动力响应情况具有重要的现实意义。
潘晋等[4]以武汉长江二桥和5 000 吨级船舶作为相互碰撞的对象,利用AIS获取了船舶信息以及航行信息,设计碰撞模型,采用显式有限元法模拟了碰撞过程,对碰撞以及冲击响应进行了分析。张爱锋等[5]通过碰撞过程数值模拟结构损伤情况,研究了5种工况下的船舶结构动力响应随时间变化规律。邱吉廷等[6]以84000 m3VLGC为例,利用有限元分析法建立该船舶的模型,设计荷载,计算船舶的结构的强度,为船舶设计提供参考。结合前人研究经验,进行船桥碰撞下船体结构强度及动力响应分析,为船舶设计和运行提供可利用数据。
1 船桥有限元模型构建有限元模型的构建是进行碰撞下结构强度和动力响应分析的前提和基础[7]。有限元模型构建过程如下:
1) 几何模型
几何模型,即结合尺度及主要参数,是有限元模型建立的基础数据[8]。船舶和桥梁的几何模型如表1所示。选择桥墩作为对象,建立有限元模型。
|
|
表 1 几何模型 Tab.1 Geometric model |
2) 单元类型选择
船舶和桥梁的单元类型选择结果如表2所示。
|
|
表 2 单元类型表 Tab.2 Unit type table |
3) 材料本构模型
针对上述选出的单元,对其特性进行定义,建立材料本构模型,具体如表3所示。
|
|
表 3 材料本构模型 Tab.3 Material constitutive model |
4) 网格划分
网格划分是有限元模型建立的关键,即将船舶和桥梁通过划分大小不一的单元格形式描绘出来,构成有限元模型,以便于进行复杂的强度分析和动力响应分析[9]。图1和图2为船舶和桥梁的有限元模型。图1模型网格大小设置为500 mm,共计65821个;图2模型网格大小设置为400 mm,共计42220个。最后对建立的有限元模型设置边界条件,然后进行检查,检查通过后即可用于后续分析,否则需要进行模型调整[10]。

|
图 1 船舶有限元模型 Fig. 1 Ship finite element model |

|
图 2 桥梁有限元模型 Fig. 2 Bridge finite element model |
利用构建的船舶和桥梁有限元模型数值模拟二者之间碰撞发生时的动态过程,分析该过程中船体结构强度变化情况以及动力响应情况。
2.1 荷载设置荷载是指船体结构产生内力和变形的作用力。船舶所承受的荷载主要来自水动载荷、货物压力以及船体自身重量。水动载荷计算公式为:
| $ {G_t} = {E_t}F\sin \left( {\alpha {t_j} + {\beta _t}} \right) 。$ | (1) |
式中:Gt为
货物压力为货物载荷以面压力的形式施加,计算公式为:
| $ {A_t} = a\left( {10 \cdot B + \frac{{0.35BD}}{C}} \right) 。$ | (2) |
式中:At为
在获得上述荷载之后,利用线性外插法将载荷施加到构建的模型上。
2.2 船舶碰撞描述方程针对船舶和桥梁碰撞问题,建立如下方程组:
| $ \left\{ \begin{gathered} P = {b_1}{c_1} + {d_1}{{\hat c}_1} + {f_1}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{c} }_1},\\ 0 = {M_2}{g_2} + h{{\hat g}_2} + q\left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} }_2} - {{\hat k}_1}} \right) 。\\ \end{gathered} \right. $ | (3) |
其中:
| $ P = \left[ {q\left( {{x_1} - {x_2} - {x_3}} \right) + 2u\sqrt {q\frac{{{b_1}{M_2}}}{{{b_1} + {M_2}}}} } \right] \cdot J\left( {{x_1} - {x_2} - {x_3}} \right) 。$ | (4) |
式中:
不同速度、撞击位置、撞击角度都会给分析造成不同的影响。基于此,为全面了解船桥碰撞下船体结构强度及动力响应情况,设计以下6种工况,如表4所示。
|
|
表 4 工况设计方案 Tab.4 Working condition design scheme |
根据表4设计的工况,借助Ansys软件动态模拟船舶模型撞击桥梁桥墩过程,如图3所示。

|
图 3 船桥撞击动态模拟示意图 Fig. 3 Schematic diagram of dynamic simulation of bridge impact |
基于船桥撞击动态模拟过程,结合船舶碰撞描述方程计算船体结构在6个工况下的变形和极限强度,实现船体结构强度分析,结果如图4所示。可以看出:工况3的最大相对变形量要比其他5种工况的最大相对变形量要更大,此时相对最大相对变形量达到了4.52m,极限强度(出现破坏时所能承受的最大应力)达到最小值,为73.25MPa,说明船舶最大速度行驶下正面撞击产生的破坏力最大。船体强度从低到高排序分别为工况2<工况1<工况6<工况5<工况4。由此可以得出,船舶行驶速度越快、撞击越正面,角度越大,产生的破坏力越强。

|
图 4 最大相对变形量和极限强度对比图 Fig. 4 Comparison diagram of maximum relative deformation and ultimate strength |
动力响应是指船体结构发生撞击问题后随着时间的推移而产生的动力特性。响应指标包括碰撞力、能量以及撞深,分别如图5~图7所示。从图5可以看出,无论是何种工况下,碰撞力曲线变化趋势大致相同,只有碰撞力大小的区别。大致分为4个阶段。首先船体结构与桥梁初步接触,碰撞力从0 N开始迅速上升;然后船体结构与桥梁深入接触,船体结构发生破损,这里会出现一个卸力过程,使得碰撞力出现小幅度的减小。再后船体结构与桥梁继续深入接触,船体结构发生严重破损,碰撞力再次上升并且达到顶峰。最后船体结构与桥梁停止碰撞,碰撞力迅速下降,直至达到0 N。
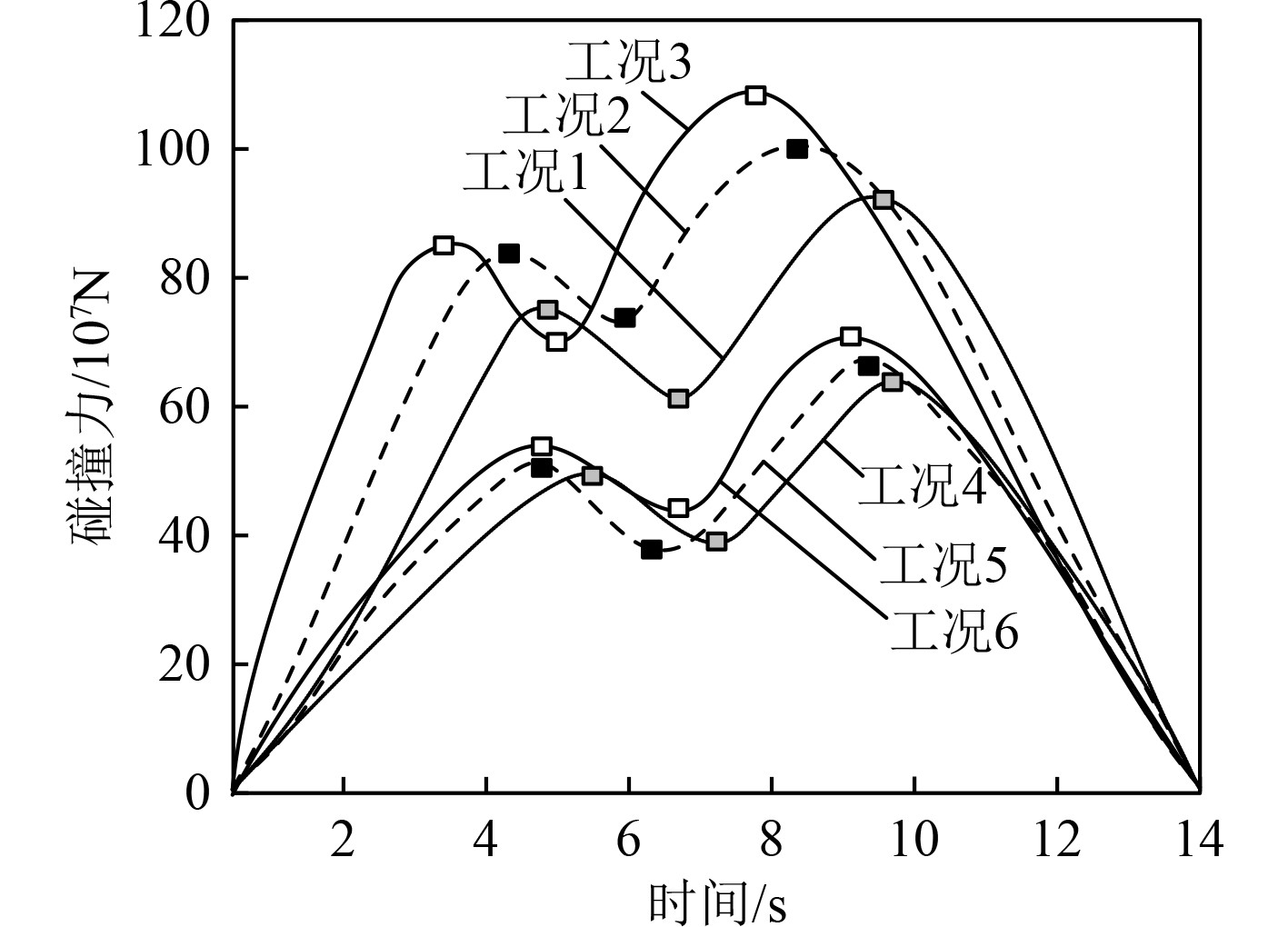
|
图 5 碰撞力曲线图 Fig. 5 Impact force curve |

|
图 7 撞深对比图 Fig. 7 Comparison diagram of impact depth |
从图6可以看出,船舶的动能逐渐减少,内能逐渐升高,这是因为碰撞发生后船舶的一部分动能转化成内能,二者发生了交换。船舶行驶速度越快、撞击越正面,角度越大,动能越小,内能越大,说明船体结构发生的不可逆变形越大。
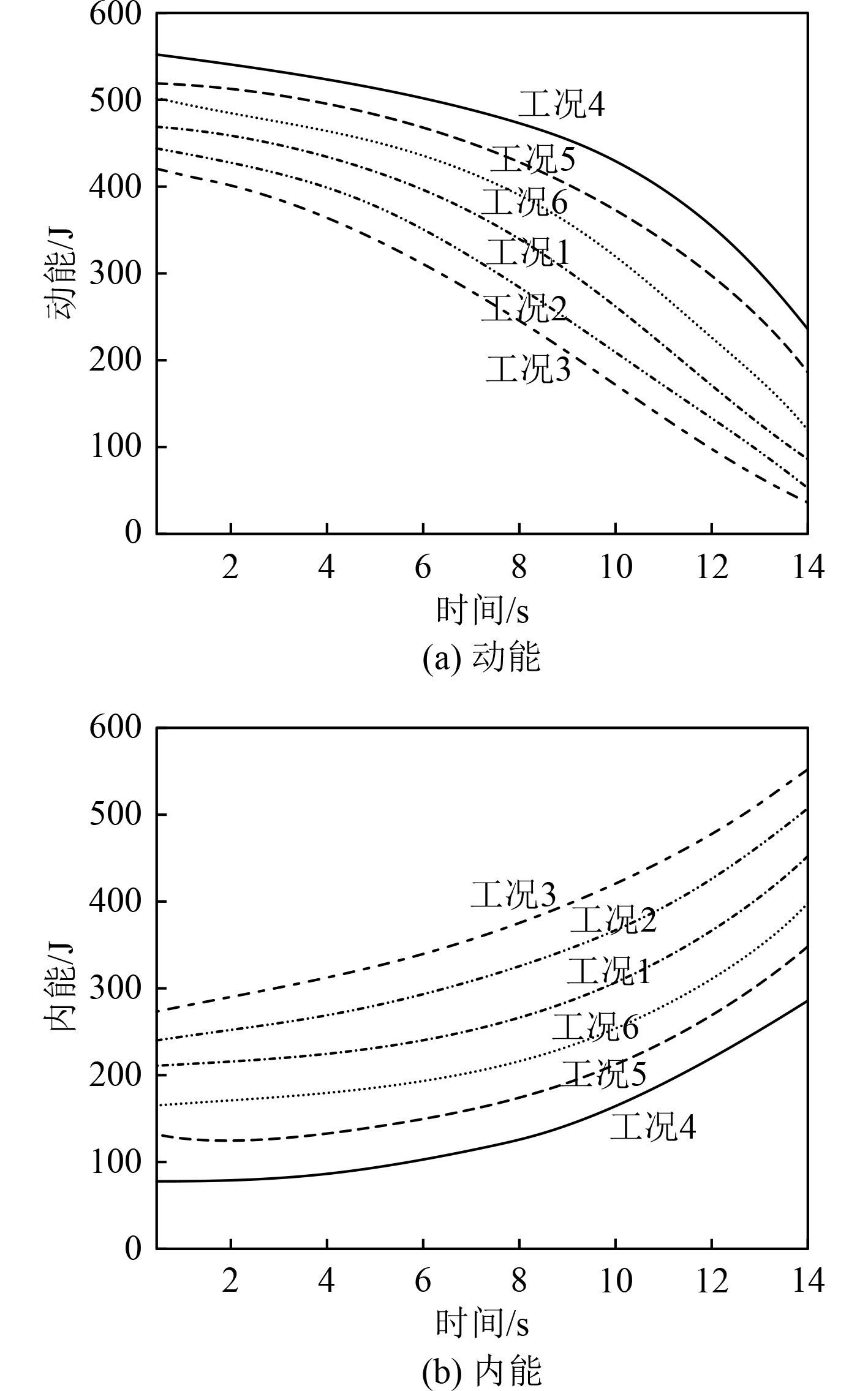
|
图 6 能量对比图 Fig. 6 Energy comparison chart |
从图7可以看出:撞深整体呈现先升高再降低最后维持平稳的变化特征。船体结构与桥梁发生冲击开始,船体结构开始逐渐受到挤压变形,一直到停止撞击,达到最大撞深,然后受到船舶结构的影响,略有一些回弹,撞深出现些许下降,最终维持在平稳状态。船舶行驶速度越快、撞击越正面,角度越大,撞深越大。
5 结 语综船桥撞击时有发生,为了能够减轻撞击时造成的损失,在设计船体结构时,需要进行反复测试来验证船桥碰撞下船体结构强度及动力响应。本文首先建立有限元模型,针对该模型进行碰撞模拟,模拟不同工况下的船体结构强度及动力响应情况,通过测试得出了变形量、极限强度、碰撞力、能量以及撞深等指标,为船舶结构设计提供参考。
| [1] |
王贵春, 吉喆, 李武生, 等. 考虑桩土作用的船桥碰撞动力性能及影响因素分析[J]. 桥梁建设, 2021, 51(4): 17-24. DOI:10.3969/j.issn.1003-4722.2021.04.003 |
| [2] |
曹明, 张南, 沈强, 等. 船桥撞击力影响因素有限元仿真模拟分析[J]. 防灾减灾工程学报, 2021, 41(3): 603-611. |
| [3] |
戴志伟, 方海, 刘伟庆, 等. 考虑墩顶约束作用的桥墩船撞力学模型及其响应[J]. 南京工业大学学报(自然科学版), 2020, 42(3): 366-372. |
| [4] |
潘晋, 黄义飞, 夏天, 等. 基于AIS数据的桥梁防船撞结构冲击响应分析[J]. 桥梁建设, 2020, 50(1): 32-37. DOI:10.3969/j.issn.1003-4722.2020.01.006 |
| [5] |
张爱锋, 刘少康, 姚苗苗, 等. 船桥碰撞结构损伤及船撞力影响因素分析[J]. 重庆交通大学学报(自然科学版), 2021, 40(3): 121-127. |
| [6] |
邱吉廷, 李文华, 郑文青. VLGC舱段结构强度有限元分析方法[J]. 船海工程, 2020, 49(1): 61-66+71. DOI:10.3963/j.issn.1671-7953.2020.01.015 |
| [7] |
王靖, 张春涛, 崔铭超. 80000 m~3大型养殖工船船体结构屈服强度分析[J]. 船舶工程, 2021, 43(12): 63-68. |
| [8] |
甄春博, 周清婉, 王晓鹏, 等. 玻璃钢双体船结构强度直接计算研究[J]. 复合材料科学与工程, 2022(4): 50-55. DOI:10.19936/j.cnki.2096-8000.20220428.008 |
| [9] |
刘俊杰, 丁震, 马琳, 等. 总纵弯曲下舰船上层建筑结构强度钢模试验[J]. 中国舰船研究, 2022, 17(2): 135-141. DOI:10.19693/j.issn.1673-3185.02240 |
| [10] |
陈志雄, 臧志鹏, 王琮, 等. 有限水深多载荷作用下细长圆管水动力响应试验研究[J]. 船舶力学, 2022, 26(8): 1160-1170. DOI:10.3969/j.issn.1007-7294.2022.08.006 |
 2022, Vol. 44
2022, Vol. 44
