穿浪双体船最早于20世纪80年代初提出,其航行时船首频繁出水入水,由于船体与波浪之间剧烈的相对运动,船首处容易发生砰击现象。在入水瞬间,结构的运动引起周围流体介质运动,流体介质同时对结构物施加反作用力,此时结构物将遭受巨大的流体砰击载荷,这会对结构体的结构强度造成严重威胁。本文将穿浪双体船船首剖面简化为2个完全相同的二维楔形体。
Zhao和Ma等[1-2]研究了无重力影响时二维楔形体压力分布的峰值位置,表明底升角大约大于40°时峰值位置由射流根部转移到楔形体尖端。Chen[3]建立的二维直升机V形浮标的数值模拟结果也验证了Zhao和Ma等[2]的结论。陈震[4]表明二维楔形体入水压力峰值的传播速度随着入水角度的增大而减小。张健[5]、王玲等[6]、Chen[7]和陈光茂等[8]分别对二维楔形体的入水砰击问题进行仿真分析,研究压力峰值与底升角、入水角度和入水速度的关系。Ma[9]模拟了二维楔体垂直和斜入的入水和水动力冲击过程。Wu等[10]表明有限高度非对称二维楔形体斜入水速度增大时,一段较长时间内的重力效应可以忽略。Sun等[11]首次分析了二维楔形体在波浪中的入水过程,并研究了重力对楔形体入水过程和物面压力分布的影响。陈翔等[12]表明了楔形体入水底升角越小流体沿物面爬升速度越快,射流越明显。Zhang等[13]表明对称楔形体入水过程中两侧受到的压力也是对称的。
本文采用OpenFOAM开源软件,建立具有不同底升角单楔形体和双楔形体在静水中入水的CFD数值模拟模型,采用有限体积法(FVM)离散平均雷诺数方程和连续性方程组成的控制方程组,采用流体体积法(VOF)追踪自由表面。将基于粘流理论的CFD数值结果与前人基于势流理论的数值结果进行对比分析,研究粘流方法与势流方法在处理入水问题过程中的差别,并重点分析重力和粘性在此过程中所起的作用。
1 数值过程对于不可压缩粘性流体,可采用连续性方程和雷诺平均方程来建立流场的控制方程组。连续性方程形式为:
| $ \nabla \cdot u = 0 \text{,} $ | (1) |
式中,u为速度矢量。
雷诺平均方程可以表达为:
| $ \dfrac{{\partial {\boldsymbol{u}}}}{{\partial t}} + \left( {{\boldsymbol{u}} \cdot \nabla } \right){\boldsymbol{u}} = - \frac{{\nabla p}}{\rho } + \nu {\nabla ^2}{\boldsymbol{u}} + {\boldsymbol{F}} \text{。}$ | (2) |
式中:ν为流体运动粘性系数;F为质量力;ρ是流体密度;p为压力。
采用VOF方法逼近空气与水的交界面,在模型中不同的流体状态共用着一套控制方程组,通过引进相体积分数这一变量,实现对每一个计算单元相界面的追踪。对于波物相互作用流场,存在空气和水2种流体流动,用
| $ \rho = \alpha {\rho _{{\text{water}}}} + \left( {1 - \alpha } \right){\rho _{{\text{air}}}} \text{,}$ | (3) |
| $ \left\{\begin{array}{l}\alpha =\text{0}\text{,}空气 \text{,} \\ \text{0} \lt \alpha \lt 1\text{,}自由表面 \text{,} \\ \alpha =\text{1}\text{,}水 \text{。} \end{array} \right.$ | (4) |
使用SST k-ω两方程湍流模型来闭合RANS方程,SST k-ω湍流扩散方程为:
| $ \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k\overline {{u_i}} } \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\Gamma _k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k} \text{,} $ | (5) |
| $ \frac{\partial }{{\partial t}}\left( {\rho \omega } \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho \omega \overline {{u_j}} } \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\Gamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + {G_\omega } - {Y_\omega } + {D_\omega } + {S_\omega } \text{。}$ | (6) |
式中:
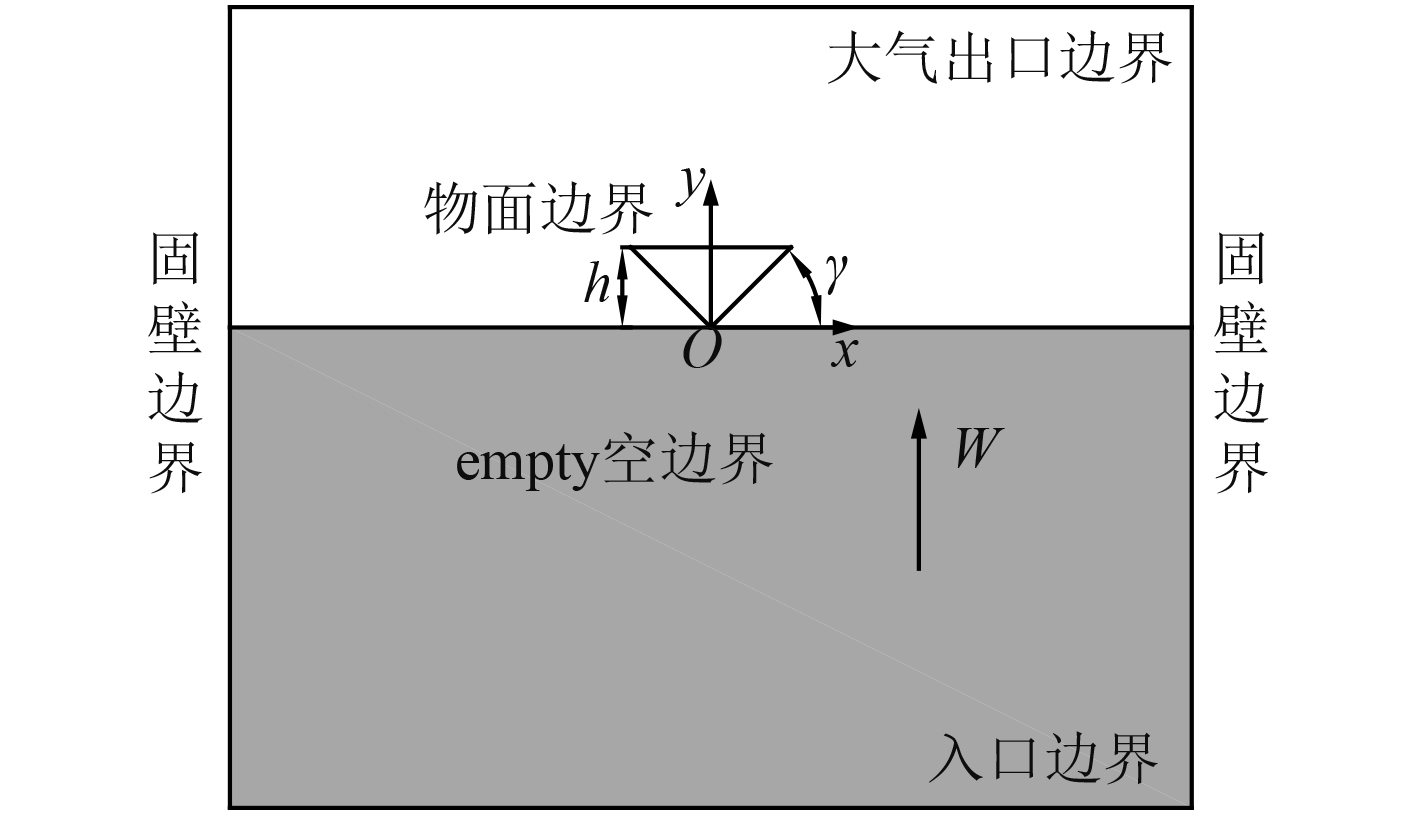
如图1所示,笛卡尔坐标系
|
图 1 坐标原点和边界条件示意图 Fig. 1 Sketch of the origin of coordinates and boundary conditions |
使用blockMesh工具绘制背景网格,计算域尺度为宽度6 m,厚度0.5 m,高度5 m,其中空气域为2 m,水深为3 m,如图2所示。为了较为准确地模拟楔形体的压力分布,使用snappyHexMesh网格生成器分裂加密楔形体周边网格,最小网格尺度为2.6 mm×2 mm,如图3所示。

|
图 2 计算域示意图图 Fig. 2 Sketch of the computational domain |

|
图 3 楔形体周边网格示意图 Fig. 3 Sketch of the grid surrounding the wedge |
为了便于分析问题,在下面数值结果中,如无特殊说明,本文将采用垂直速度
|
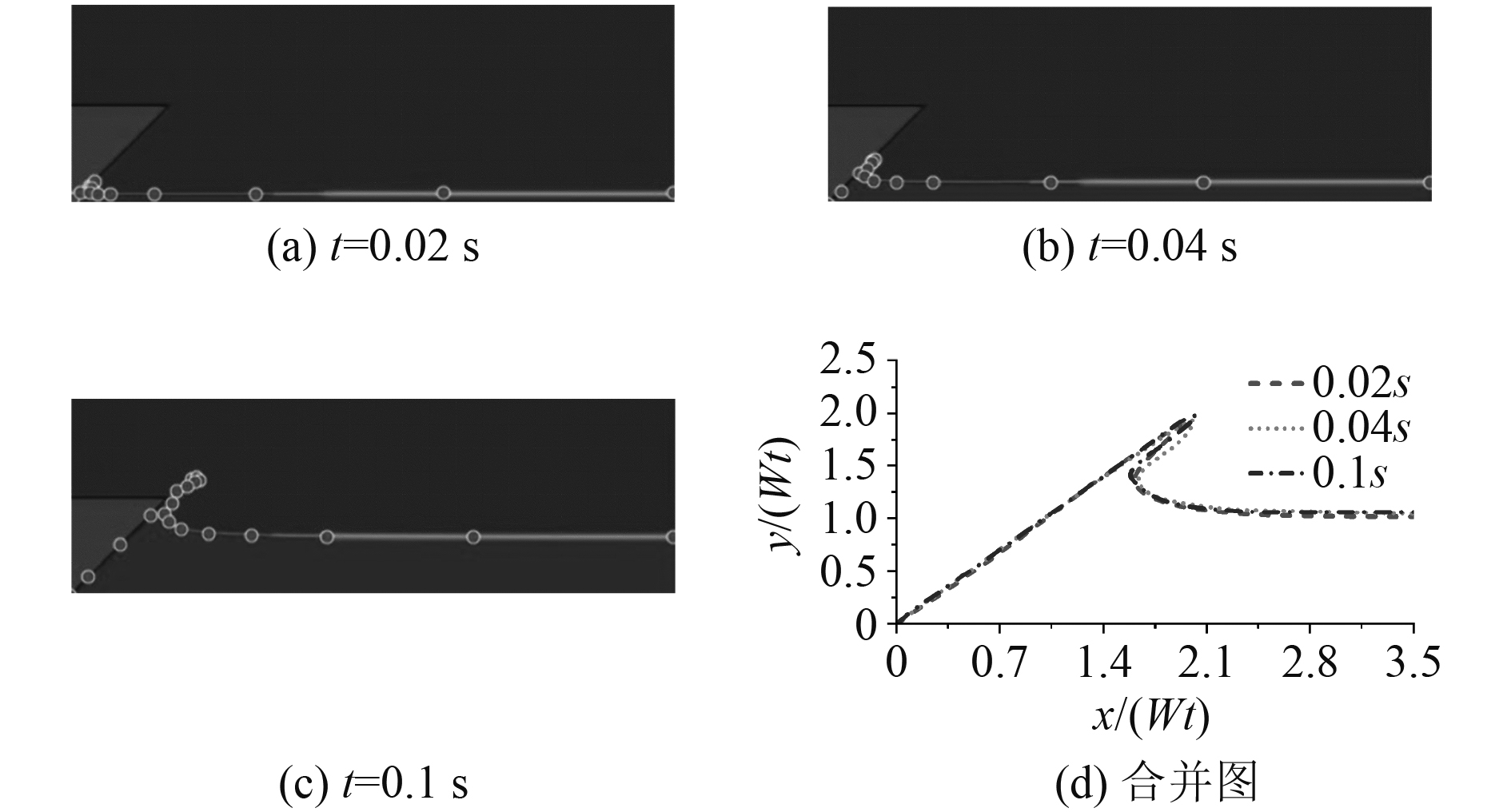
图 4 45°楔形体3 m/s入水自由液面形状 Fig. 4 The free surface profile of 45° wedge with 3 m/s |
|
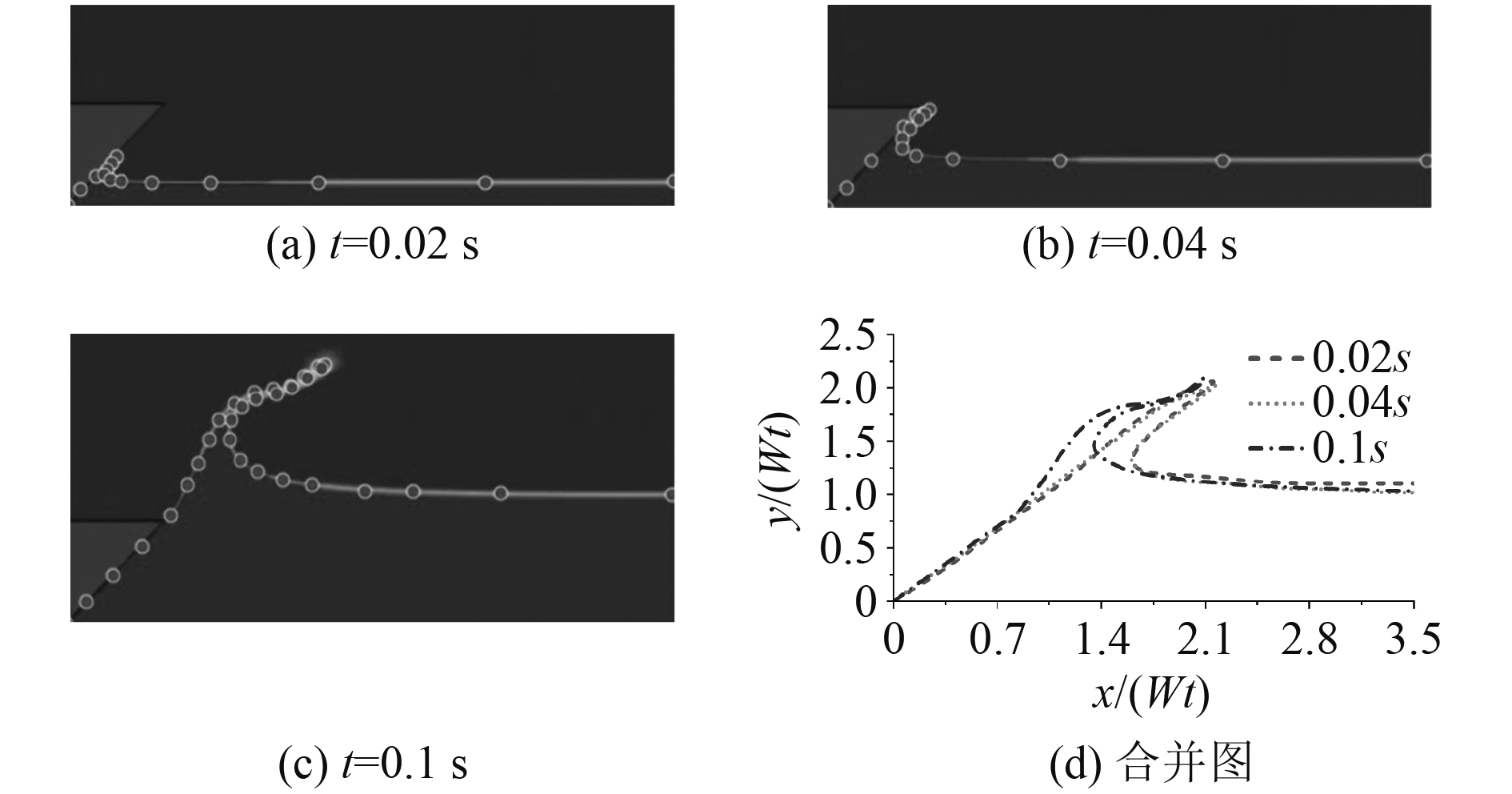
图 5 45°楔形体6 m/s入水自由液面形状 Fig. 5 The free surface profile of 45° wedge with 6 m/s |

|
图 6 重力影响下45°楔形体表面压力分布 Fig. 6 The pressure on the 45° wedge surface with the gravity effect |
由图4和图5可知,当入水时间较短时,自由液面沿物面快速爬升。随着入水时间的增加,射流尖端到达楔形体顶部,射流沿楔形体顶部飞出,形成了射流分离现象。入水时间相同,重力的作用效果也基本相同,而图5比图4射流更高的直接原因是其对应的楔形体入水速度更高,被楔形体扰动的射流获得了更高的分离速度。不考虑重力和射流分离影响时,楔形体的入水问题是自相似的,而图5中
图6(a)中 t= 0.01 s 的数值结果与其余3条曲线有明显差别。这是由于采用VOF方法确定的气液交界面是一条密度逐步过渡的细带状区域,这将导致采用CFD方法计算的压力在入水瞬间计算的不够精准。速度提升了1倍后,相同时刻楔形体入水距离已经达到一定距离,楔形体表面压力不再受自由液面影响,见图6(b)。但同时在0.1 s,物面压力又急剧降低,这是由于相似解没有考虑重力,而基于粘流理论的CFD结果考虑了重力,随时间增加重力的作用越来越明显,导致物面压力急剧下降,并且远离相似解。此外,所有CFD压力数值结果都是小于相似解的,前面描述的重力只是其中的一个次要原因,另外一个重要原因是砰击发生时物面压力梯度较大,CFD方法由于网格尺度限制在处理大压力梯度问题时存在一定困难。
2.2.2 30°底升角单楔形体入水
|
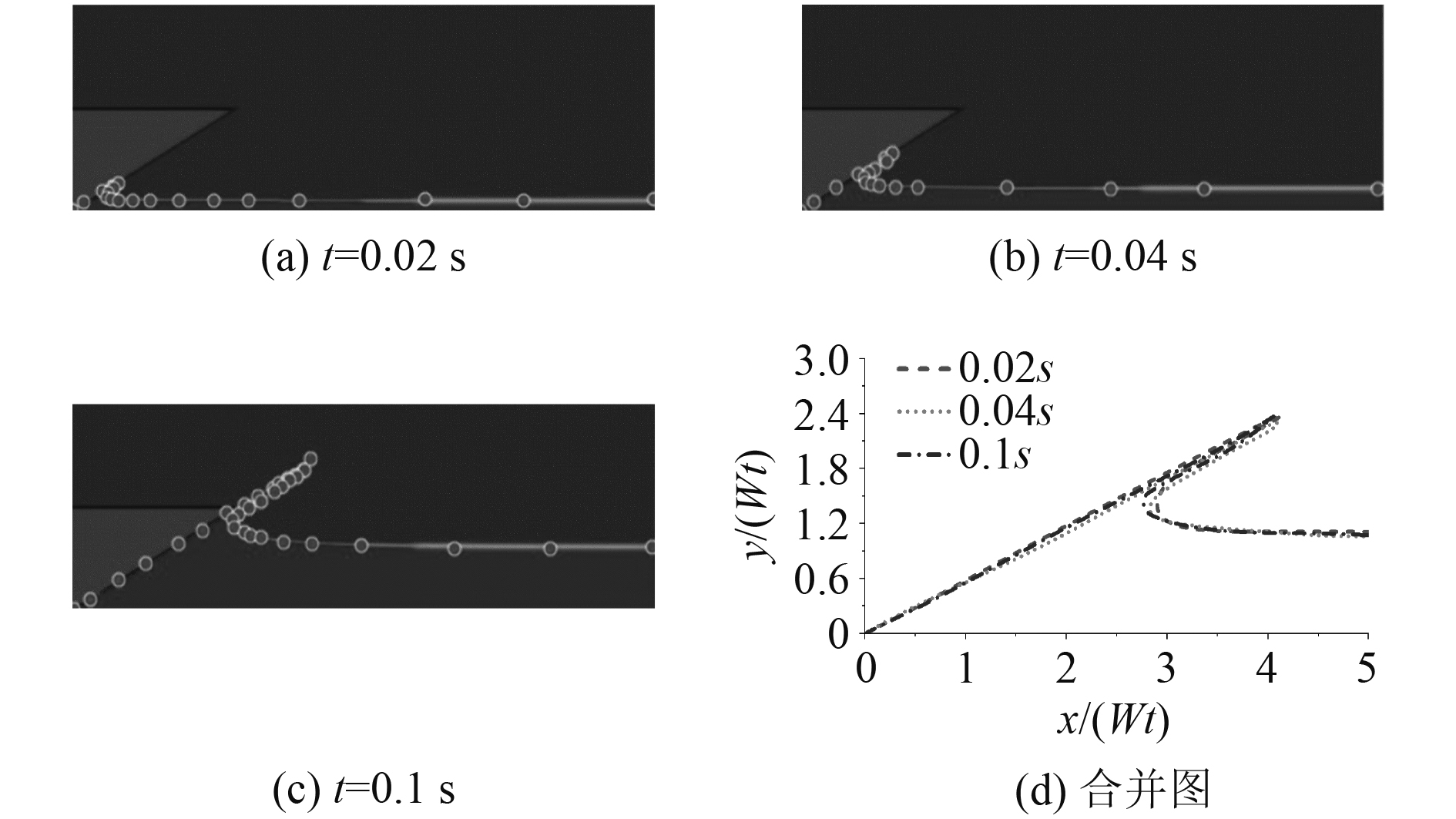
图 7 30°楔形体3 m/s入水自由液面形状 Fig. 7 The free surface profile of 30° wedge with 3 m/s |
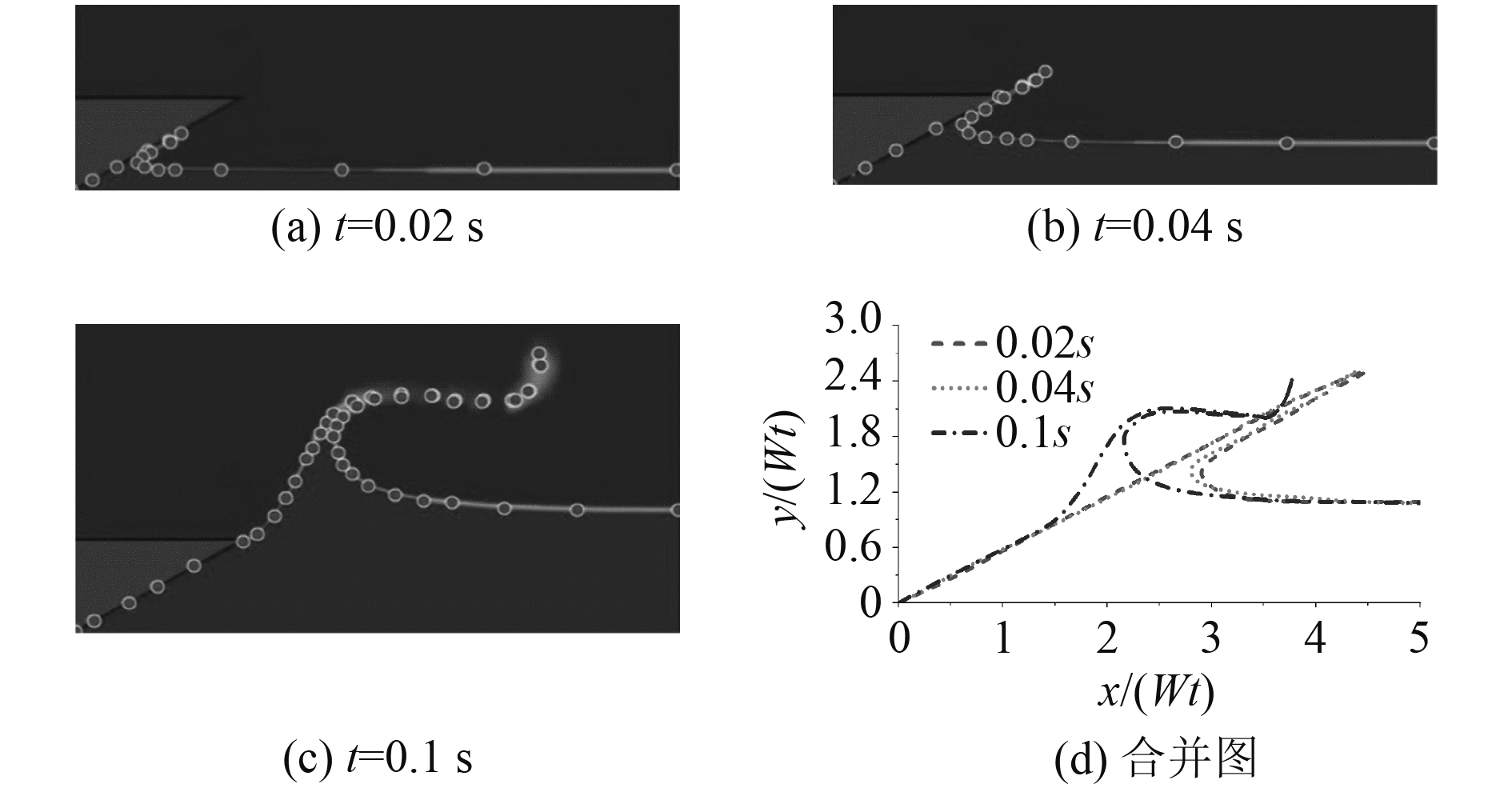
|
图 8 30°楔形体6 m/s入水自由液面形状 Fig. 8 The free surface profile of 30° wedge with 6 m/s |
|
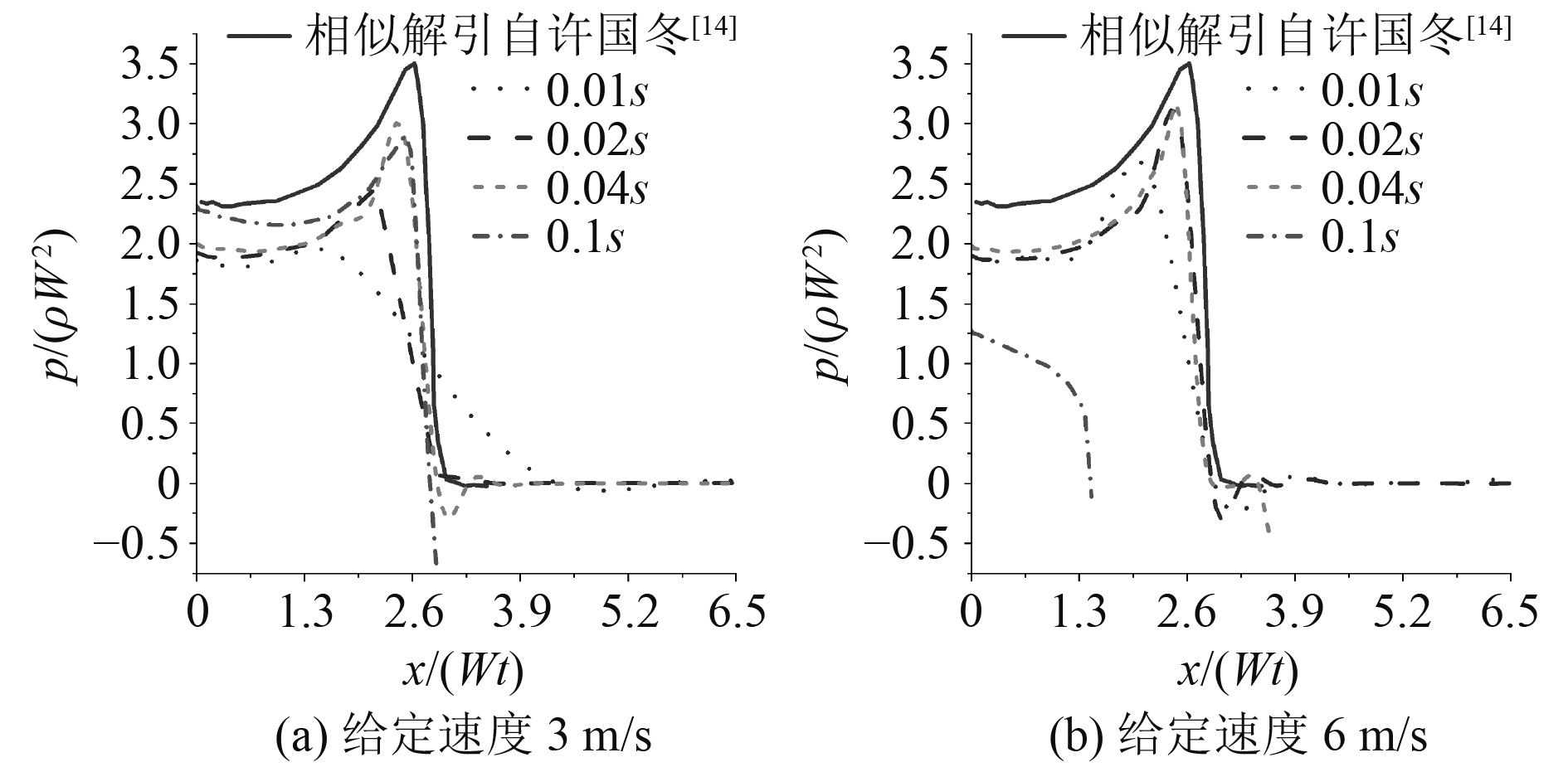
图 9 重力影响下30°楔形体表面压力分布 Fig. 9 The pressure on the 30° wedge surface with the gravity effect |
相同入水速度相同时刻,
除上一个算例对压力曲线的分析原因,影响压力另外一个重要原因是射流分离和重力,见图9(b)的0.1 s压力结果,附体射流层的0压力线在曲线中消失,且压力值降低。
2.2.3 双楔形体以给定速度入水的数值结果分析如图10所示,双楔形体A和B两个顶点的距离设置为0.5 m,其余设置与图1一致。
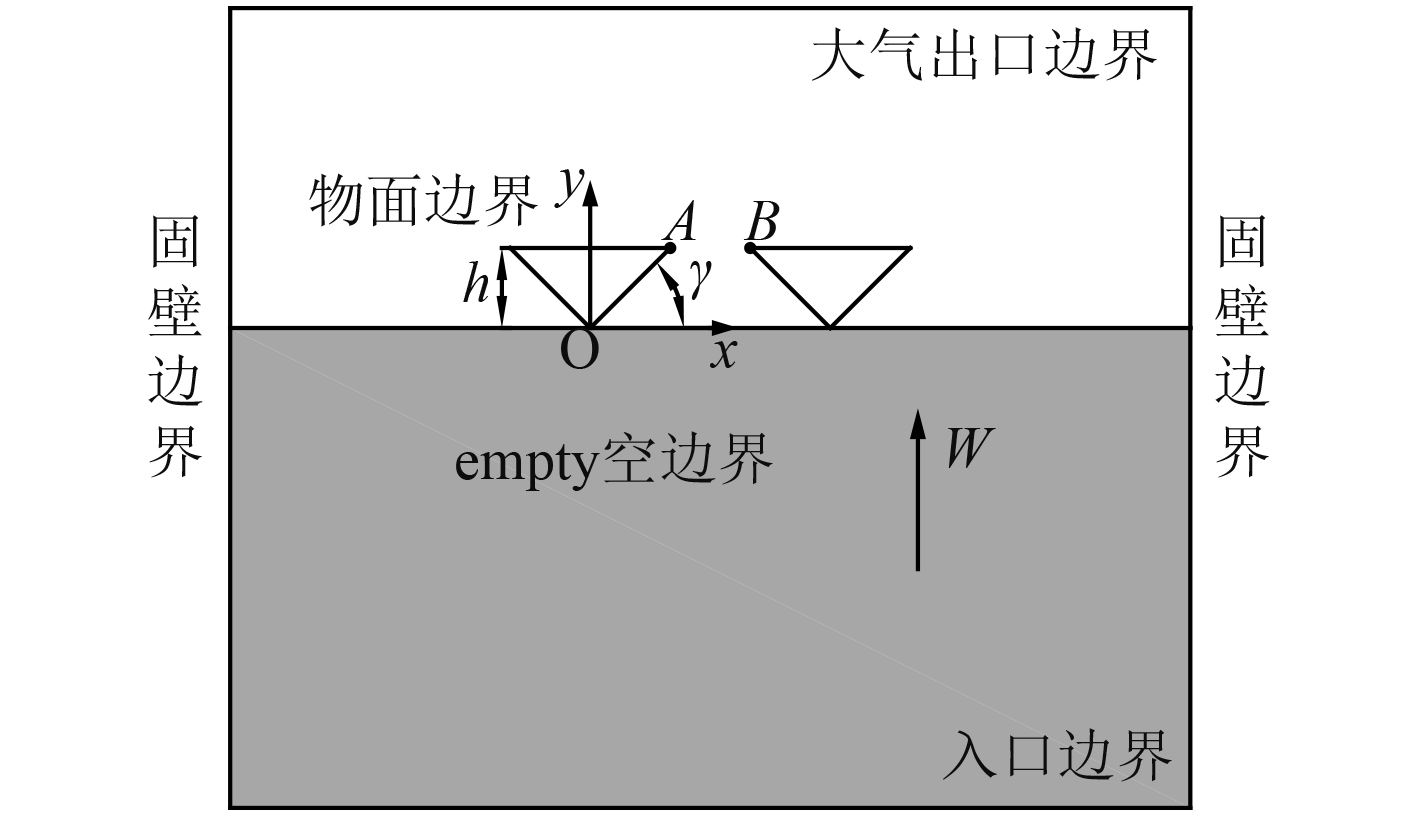
|
图 10 双楔形体模型坐标原点和边界条件示意图 Fig. 10 Sketch of the origin of coordinates and boundary conditions of the double wedges |
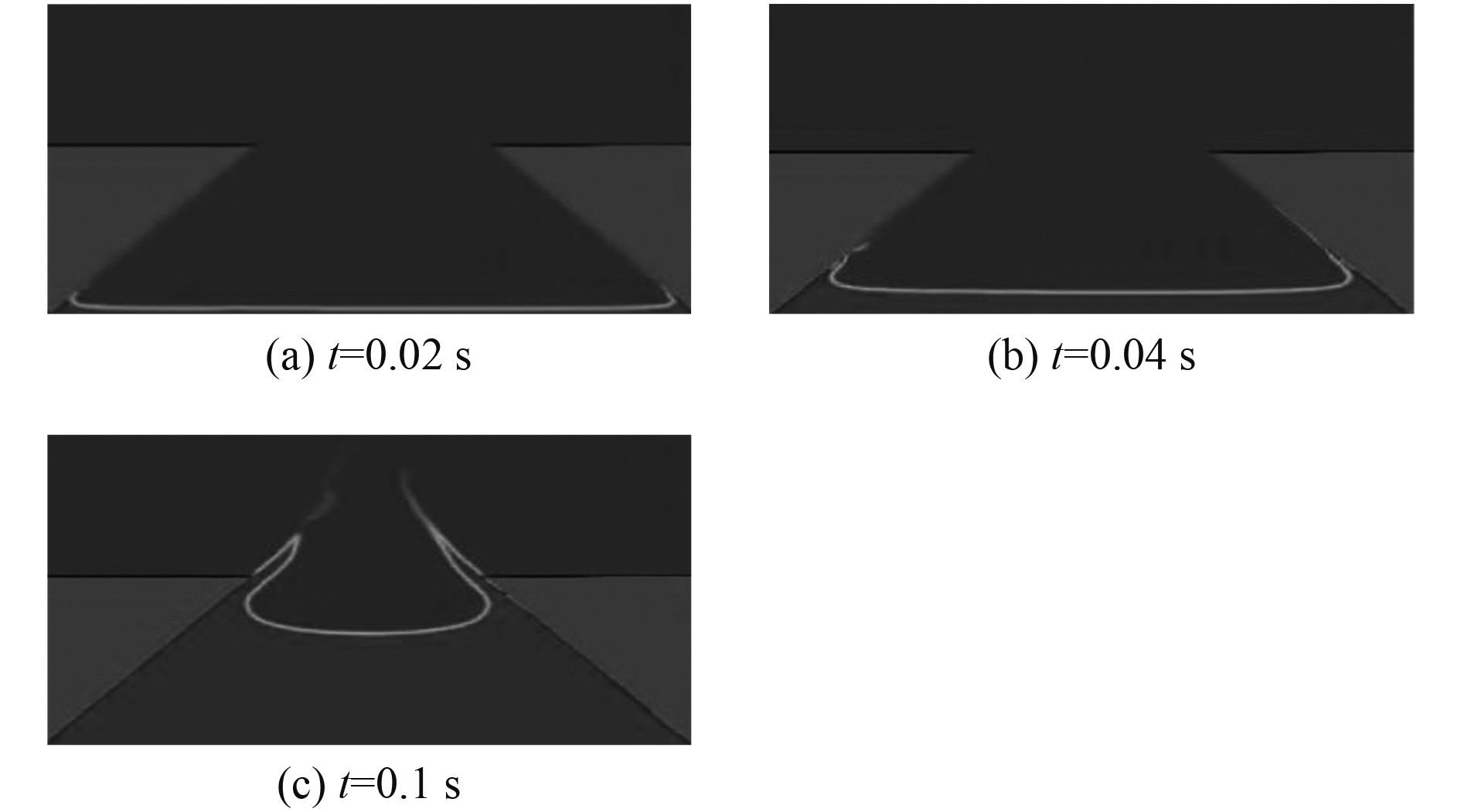
|
图 11 45°双楔形体3 m/s入水自由液面形状 Fig. 11 The free surface profile of 45° double wedges with 3 m/s |

|
图 13 3 m/s匀速入水45°双楔形体表面压力分布 Fig. 13 The pressure on the 45° double wedges surface of entry with constant velocity 3 m/s |

|
图 14 6 m/s匀速入水45°双楔形体表面压力分布 Fig. 14 The pressure on the 45° double wedges surface of entry with constant velocity 6 m/s |
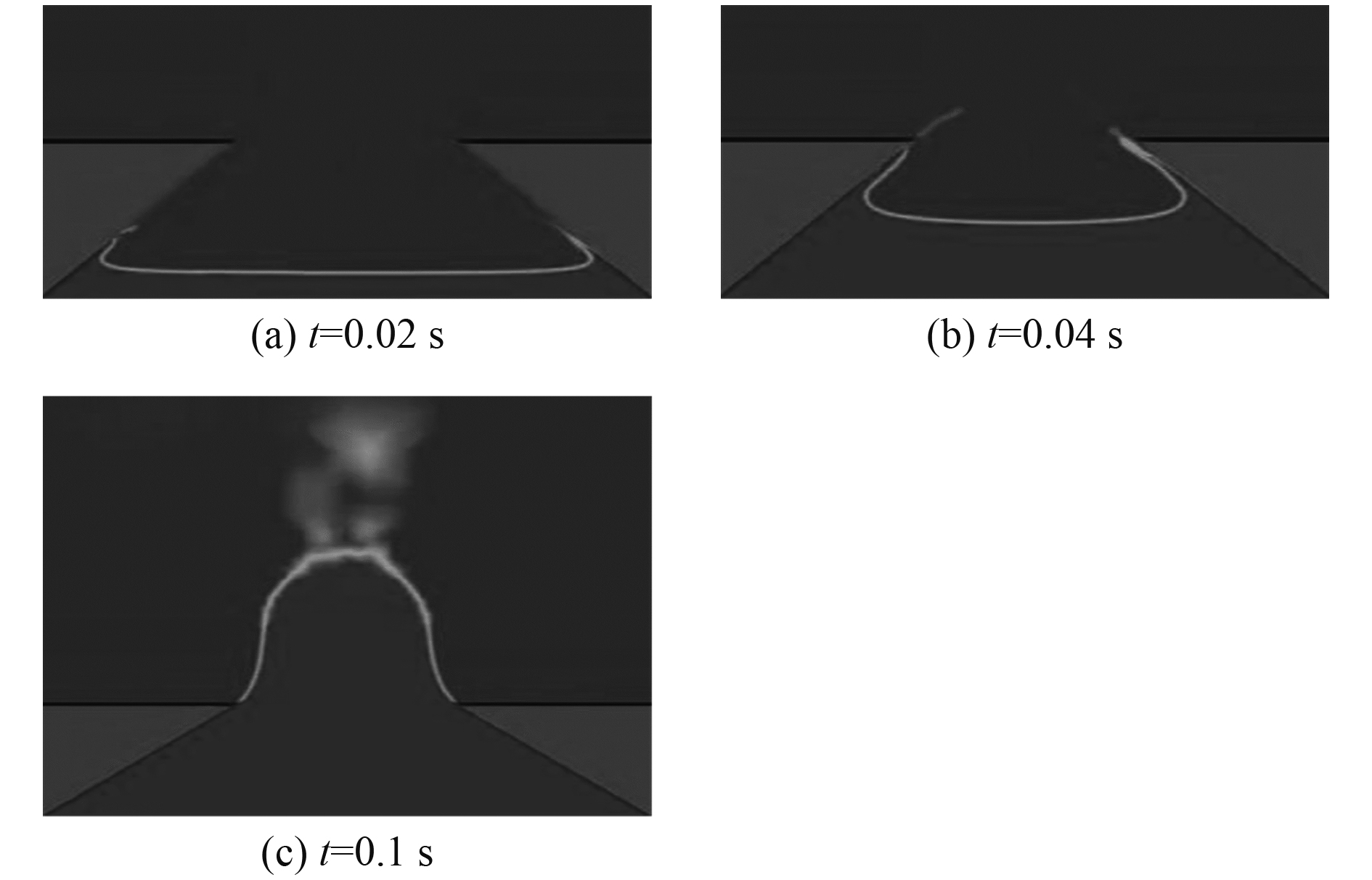
由图11可知,自由面沿物面快速爬升,形成粘附于物面的附体射流,最终脱离物体顶部,形成一小段自由射流,在双楔形体中间,自由液面连同自由射流形成一个开口气腔。图12中双楔形体入水速度提高一倍,附体射流较快地演变为自由射流,
|
图 12 45°双楔形体6 m/s入水自由液面形状 Fig. 12 The free surface profile of 45° double wedges with 6 m/s |
由图13和图14可知,压力曲线整体趋势和峰值出现的相对位置几乎不变,双楔形体压力峰值都大于单楔形体压力峰值。图13(d) t = 0.1 s 的数值结果与其余不同,双楔形体压力显著高于单楔形体压力。这是因为对于单楔形体入水,一部分流体受到扰动以后以射流形式沿着物面向上运动,一部分流体沿着自由面向远方流动,而对于双楔形体,向远方流动的流体被前方楔形体阻挡,被阻断的流体只能以更高的速度向上运动来满足动量守恒定律,因此物面压力显著上升。可以预见,在砰击发生的短暂时间内,入水速度越大,入水时间越长,双楔形体之间的相互压力影响便越显著。当时间足够大时,重力的影响变得明显,这一结论不一定适用,但是长时间的流体与结构相互作用问题并不是本课题的研究内容。14(d)的差别更大是由于速度越高,流体扰动速度越大,流体更快达到相邻楔形体,相邻楔形体压力也升高的更快。
|
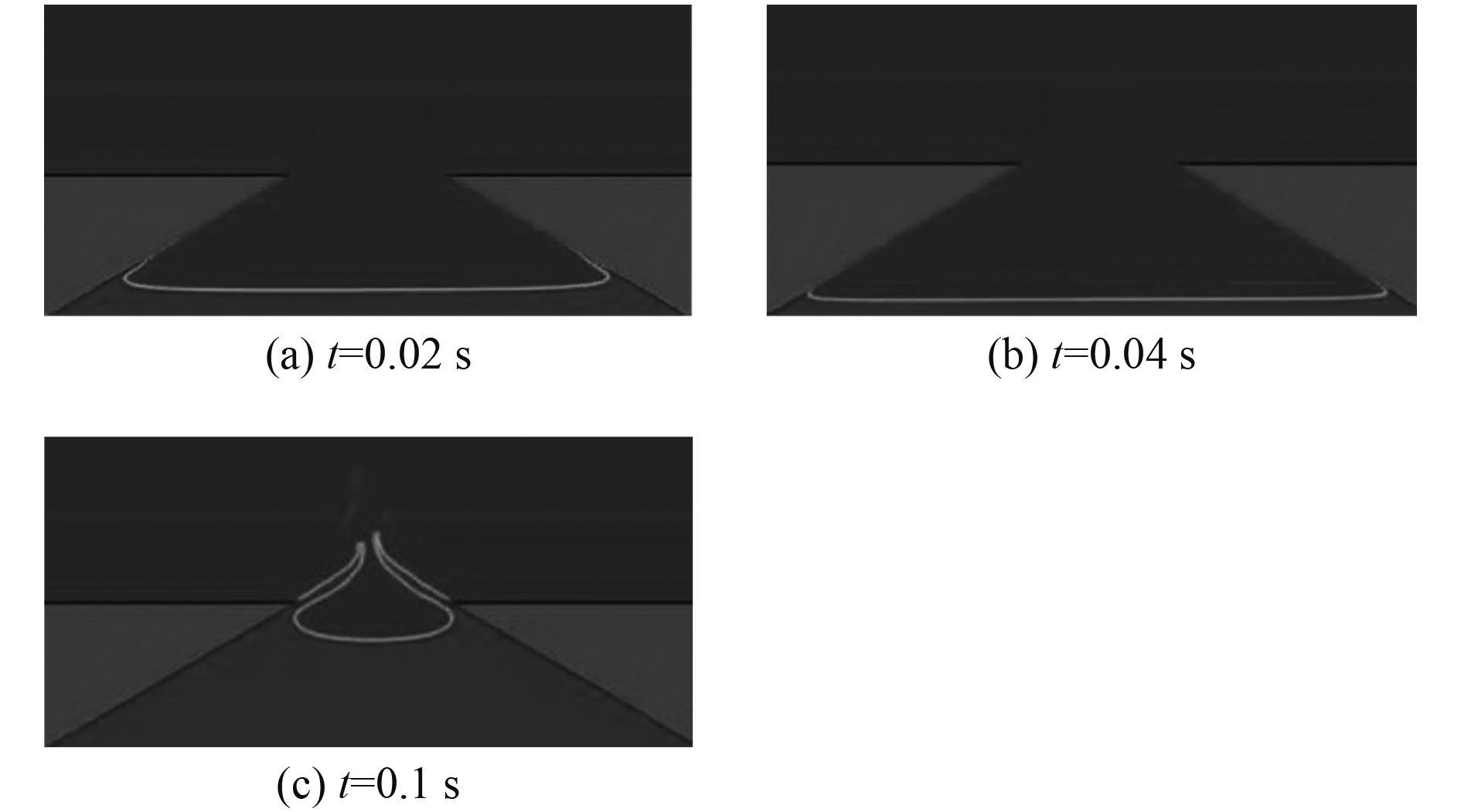
图 15 30°双楔形体3 m/s入水自由液面形状 Fig. 15 The free surface profile of 30° double wedges with 3 m/s |
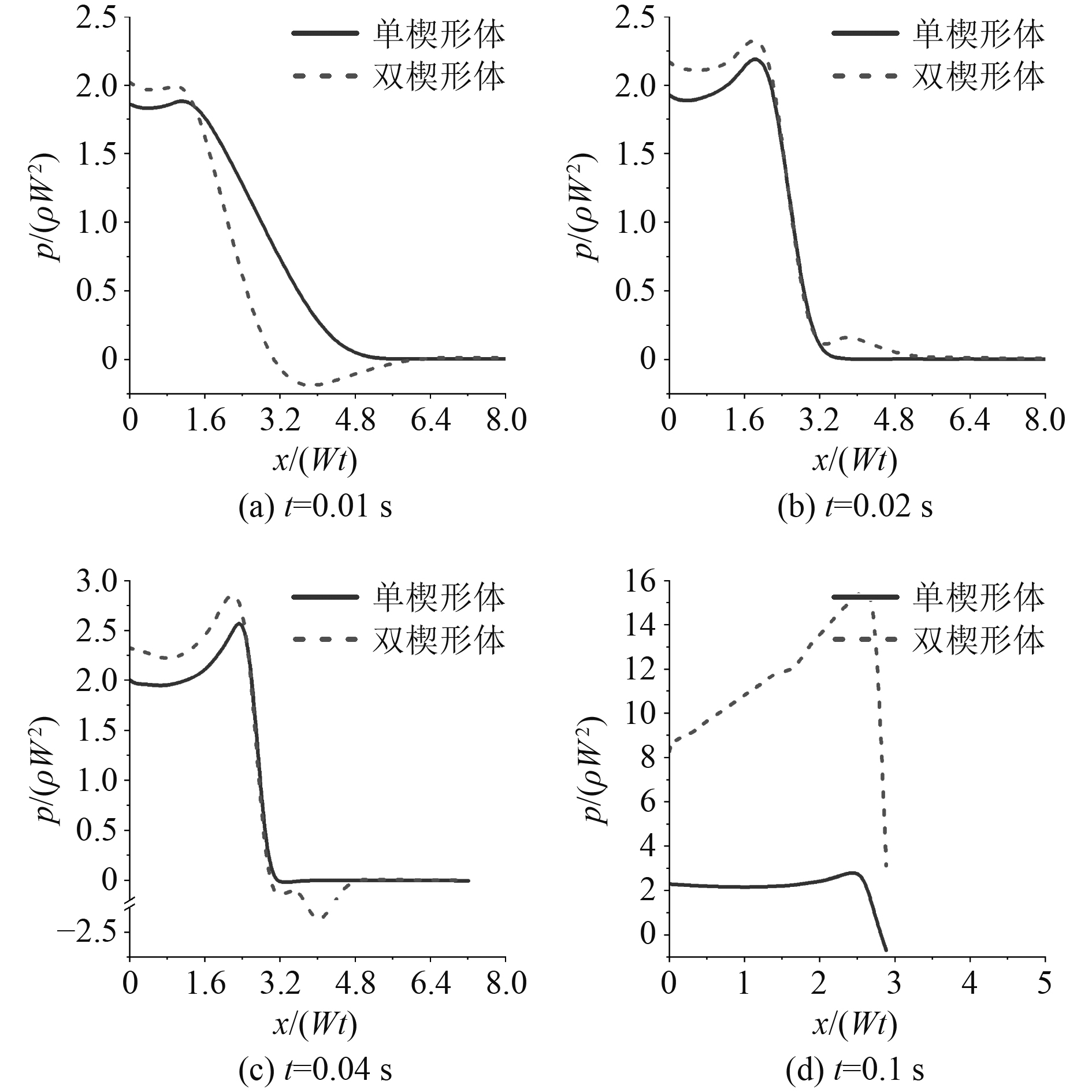
|
图 17 3 m/s匀速入水30°双楔形体表面压力分布 Fig. 17 The pressure on the 30° double wedges surface of entry with constant velocity 3 m/s |

|
图 18 6 m/s匀速入水30°双楔形体表面压力分布 Fig. 18 The pressure on the 30° double wedges surface of entry with constant velocity 6 m/s |
不同于图11的气腔开口,图15的气腔基本封闭了,原因是小底升角导致射流速度更高,射流长度变得更长,使得气腔更容易封闭,所以图16(c)中的双楔形体中间的拱形射流也具有更高的高度。与上一个算例类似,在图17和图18中,由于双楔形体之间的相互影响需要时间,时间越长,单楔形体和双楔形体压力差别越大。与上一个算例不同的是,本算例楔形体底升角更小,受到扰动的流体运动得更快,因此本算例单楔形体和双楔形体压力之间的距离较前一个算例要大。由此可以得出另外一个结论,在楔形体间距不变的条件下,小底升角会使楔形体之间的影响时间提前,影响幅度扩大。

|
图 16 30°双楔形体6 m/s入水自由液面形状 Fig. 16 The free surface profile of 30° double wedges with 6 m/s |
本文采用基于粘流理论的CFD方法,模拟重力作用下不同底升角单楔形体和双楔形体以给定速度在静水中的入水过程,得到如下结论:
1)当入水时间较短时,不同时刻的无量纲自由液面曲线基本重合,随着时间的增加,射流从物体顶部分离,自由射流在重力作用下发生弯曲向下的现象。
2)当入水时间较短时,排除初始阶段的不准确压力,不同时刻的物面无量纲压力曲线是基本重合的,并且与基于势流理论的自相似解非常接近,随着时间的增加,重力的作用变得显著,压力在重力作用下降低。
3)在相同入水速度和相同底升角条件下,双楔形体物面压力大于单楔形体物面压力,并且在砰击发生的短暂时间范围内,刚开始影响不大,从某一时刻开始,受一个楔形体扰动的流体到达相邻楔形体以后,相邻楔形体压力差值瞬间变得显著。此外,若提升速度,被楔形体扰动的流体速度加快,相邻楔形体受到的压力影响更大。
4)当降低楔形体底升角时,相当于增加楔形体周围被扰动的流体速度,因此相邻楔形体受到的压力也提升的更快。
| [1] |
ZHAO R, FALTINSEN O. Water entry of two-dimensional bodies[J]. Journal of Fluid Mechanics, 1993, 246(4): 593-612. |
| [2] |
MA L, ZHAO X, LIU H. Two-phase SPH simulation of vertical water entry of a two-dimensional structure[J]. Journal of Hydrodynamics, 2018, 30(5): 841-850. DOI:10.1007/s42241-018-0102-x |
| [3] |
CHEN Q T, YANG G G. Study on the effect of two-dimensional helicopter v-buoy's way of water entry on water impact[J]. Journal of Harbin Institute of Technology, 2019, 26(3): 91-96. |
| [4] |
陈震, 肖熙. 二维楔形体入水砰击仿真研究[J]. 上海交通大学学报, 2007, 41(9): 1425-1428. DOI:10.3321/j.issn:1006-2467.2007.09.008 |
| [5] |
张健, 尤恽, 王珂, 等. 基于气垫效应的二维楔形体入水砰击载荷预报方法研究[J]. 舰船科学技术, 2016, 38(2): 7-12. DOI:10.3404/j.issn.1672-7649.2016.2.002 |
| [6] |
王玲, 朱仁庆, 李红艳. 三维对称楔形体入水的水弹性力学分析[J]. 舰船科学技术, 2018, 40(3): 19-25. DOI:10.3404/j.issn.1672-7649.2018.03.004 |
| [7] |
CHEN G, LI Y. Numerical simulation of fluid structure interaction in water entry problems by smoothed particle hydrodynamics method[C]//The Second Conference of Global Chinese Scholars on Hydrodynamics. 2016: 386-394.
|
| [8] |
陈光茂, 郑小波, 毋晓妮, 等. 二维楔形体入水问题的数值和实验研究[J]. 舰船科学技术, 2021, 43(1): 53-60. |
| [9] |
MA Z H, QIAN L. Numerical simulation of wave slamming on wedges and ship sections during water entry[J]. Ocean Systems Engineering, 2018, 8(2): 183-199. |
| [10] |
WU G X, XU G D, BAO C M. Simulation of water entry of a two-dimension finite wedge with flow detachment[J]. Journal of Fluids and Structures, 2016, 65: 44-59. DOI:10.1016/j.jfluidstructs.2016.05.010 |
| [11] |
SUN S Y, SUN S L, WU G X. Oblique water entry of a wedge into waves with gravity effect[J]. Journal of Fluids and Structures, 2015, 52: 49-64. DOI:10.1016/j.jfluidstructs.2014.09.011 |
| [12] |
陈翔, 饶成平, 万德成. MPS方法数值模拟楔形体入水问题[J]. 计算力学学报, 2017, 34(3): 356-362. DOI:10.7511/jslx201703013 |
| [13] |
ZHANG J, YOU Y, YAO Z, et al. Sensitivity analysis of the effect of speed and inclination angle on water-entry slamming pressure of the bow[J]. China Ocean Engineering, 2020, 34(3): 432-440. DOI:10.1007/s13344-020-0039-z |
| [14] |
许国冬. 流体/刚体砰击问题及相似解研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
|
 2022, Vol. 44
2022, Vol. 44

