2. 西北工业大学 航海学院,陕西 西安 710072
2. School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China
火箭助飞鱼雷由于兼具空中高速远程打击和水下高隐蔽打击的优势,在现代海战中扮演着越来越重要的角色。鱼雷在航行过程中,会遭遇入水带来的恶劣力学环境。鱼雷入水一般指从鱼雷头部开始触水到完全沾湿的一段过程,包括撞水、侵水、带空泡航行、全沾湿转入受控运动4个阶段,气-水-固三相之间发生强烈的相互作用:在鱼雷作用下形成包含空泡的生成、发展、闭合、溃灭等复杂多相流场;流体也会对鱼雷施加强烈的反作用力,特别在入水初期的毫秒级内鱼雷会遭受巨大的冲击载荷,引起结构发生弹性塑性变形,甚至断裂、破损和屈曲,导致内部仪器的失灵以及运行轨迹的变化,如忽扑、跳水和弹道失稳等问题[1]。早在1929年,Von Karman[2]基于势流理论,采用附加质量代替入水冲击过程的流体作用计算物体的入水冲击载荷,并根据刚性结构体入水时的动量守恒定律计算得到了入水冲击过程中流体对结构体的冲击压力。之后,Wagner[3]提出了近似平板理论,考虑楔形体入水过程中液面隆起和喷溅厚度,建立了小斜升角模型,同时引入水波影响修正因子,并运用伯努利方程,得到了楔形体沾湿面压力分布,更加符合实验测试的结果,为以后的入水理论研究奠定了基础。Wang等[4]基于RANS控制方程和VOF多相流模型研究了流体可压缩性对楔形体自由落体入水运动和载荷的影响,发现流体可压缩性对低速入水载荷的影响可以忽略,但对空泡演化的影响不可忽略。
近年来,随着高性能火箭助飞鱼雷的发展,更高的入水速度成为一个重要的指标要求,高速入水会导致一系列新的入水力学特征,涉及入水冲击、过载、弹道等。尤其,高速入水带来的冲击载荷急剧增加,给鱼雷的结构强度提出了严峻的挑战。由于高速入水形成强烈的相互作用力,导致流体的可压缩性显著,从而影响入水空泡演化、弹道稳定性以及载荷特性等。施红辉等[5]实验研究了子弹350 m/s高速垂直入水过程中空泡形态特征,发现随着入水深度增加弹道偏移逐渐显著。Truscott[6]采用步枪发射研究了不同外形子弹小角度高速入水试验,发现钝头长细比的外形有助于弹道的稳定。黄闯等[7-8]基于VOF多相流模型对水下超空泡射弹的载荷及空泡形态进行了数值研究,发现当射弹速度达到超声速范围,水的可压缩性作用形成的超空泡尺寸随着速度的增加急剧减小。洪尧等[9]采用均质流模型和SG状态方程,研究了可压缩性对二维圆柱高速入水冲击载荷的影响。张凌新等[10]通过建立气-水-汽三相可压缩性模型,并引入空化模型,分析了钝体高速入水空泡形态及水中压力波的传播特性。李达钦等[11-12]研究了考虑气液可压缩性的水下超空泡航行器高速航行情况,发现随着运动速度的增加,压力波逐渐转化为激波。陈晨等[13]通过数值模拟的手段,分析了液相可压缩性对入水空泡、自由液面、压力场等的影响,发现跨声速入水会在头部产生弓形激波,并随着入水深度增加,激波斜角逐渐减小。曹雪洁等[14]通过数值模拟的手段,分析了液相可压缩性对空泡的影响,发现马赫数Ma>0.5时流体可压缩性不能忽略。李国良等[15]通过数值模拟的手段,分析了湍流模型、入水速度等对回转体高速入水可压缩性的影响,发现入水速度小于100 m/s时,液体可压缩性对入水冲击载荷影响可以忽略;入水速度大于200 m/s时,液体可压缩性的影响逐渐显著。
上述研究大多聚焦于高速入水或水下高速航行时流体可压缩性对空泡形态、压力场等的分析,但缺少针对气液两相可压缩性对高速入水载荷的全面分析,导致流体可压缩性对入水载荷的影响机理不清晰,从而无法实现准确的数值模型建立以及缩比试验设计。此外,由于实际应用中,冲击响应对结构体的模态紧密相关,为排除结构体振动模态的影响,本文选取理想刚性结构体入水过程的流体阻力特性进行分析。基于均质平衡流理论和VOF(流体体积法)多相流模型建立气-液-汽三相耦合流动数学模型,并通过嵌套网格技术,实现多相流与6DOF刚性结构体高速入水过程分析,揭示气/液相可压缩对高速入水载荷的影响机理,并进一步讨论不同入水速度和不同头型下流体可压缩性的影响,从而对流体可压缩性的影响进行较全面的分析,研究结果有助于清晰认识高速入水载荷的形成机理及影响规律。
1 模型描述 1.1 几何模型图1为流体域和结构体几何模型及网格划分情况。流体域的长宽高分别为1500×1500×1500 mm,水面高度为1000 mm(上为空气,下为水);结构体长度和直径分别为140×49 mm,锥形头横升角为10°。网格采用六面体网格,结构体通过嵌套网格技术实现与流体域耦合的六自由度运动。

|
图 1 几何模型及网格划分 Fig. 1 Geometrical model and meshing |
基于均质平衡流理论建立结构体高速入水数学模型,考虑水的自然空化,并假设气、汽、液三相共享一个密度场、速度场和压力场,相应的控制方程如下:
1)控制方程
由于高速入水过程中温度变化为小量,因此此处不考虑能量方程[8],数学模型主要基于连续方程和动量方程建立,依次如下:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \left( {\rho \overrightarrow U } \right) = 0 ,$ | (1) |
| $ \rho \frac{{\partial \overrightarrow U }}{{\partial t}} + \rho \overrightarrow U \cdot \nabla \overrightarrow U = \nabla \left\{ {\mu \left[ {\nabla \overrightarrow U + {{\left( {\nabla \overrightarrow U } \right)}^{\text{T}}}} \right]} \right\} - \nabla p。$ | (2) |
其中,动量方程采用基于RANS的Realizable k-ε模型进行求解。假设各相之间可相互贯穿,基于此引入相体积分数,此处选取VOF均质多相流模型,认为多相流为单一的混合流体介质,此时混合相的密度表示为:
| $ {\rho _{{m}}} = {\rho _{{g}}}{\alpha _{{g}}} + {\rho _{{v}}}{\alpha _{{v}}} + {\rho _l}\left( {1 - {\alpha _{\text{g}}} - {\alpha _{\text{v}}}} \right)。$ | (3) |
其中:α为体积分数;ρ为密度;m,v,g和l下标分别为混合相、水蒸气、空气和水。
2)状态方程
水蒸气和空气服从理想气体状态方程,水服从Tait方程[8],如下:
| $ \rho = {\rho _0}{\left( {1 + \dfrac{{n\left( {p - {p_0}} \right)}}{{{E_0}}}} \right)^{\frac{1}{n}}}。$ | (4) |
其中:p0为参考压力;ρ0为参考压力对应的密度;E0参考压力对应的体积模量;n为密度指数;p为当前压力;ρ为当前压力对应的密度。
3)空化模型
采用Schnerr-Sauer空化模型描述水蒸气和水之间的质量转化,如下:
| $ \begin{split} & \frac{{\partial {\alpha _{\text{v}}}{\rho _{\text{v}}}}}{{\partial t}} + \nabla \left( {{\alpha _{\text{v}}}{\rho _{\text{v}}}{{\overrightarrow U }_{\text{v}}}} \right) = \\ &\frac{{3\left( {{\alpha _{\text{v}}} + {\alpha _{{\text{nuc}}}}} \right)\left( {1 - {\alpha _{\text{v}}}} \right)}}{{{R_{{B}}}}}\frac{{{\rho _{\text{l}}}{\rho _{\text{v}}}}}{{{\rho _{{m}}}}}\sqrt {\frac{2}{3}\frac{{{p_{{\text{sat}}}} - p}}{{{\rho _{\text{l}}}}}} \left( {p < {p_{{\text{sat}}}}} \right) - \\ & \frac{{3{\alpha _{\text{v}}}\left( {1 - {\alpha _{\text{v}}}} \right)}}{{{R_{{B}}}}}\frac{{{\rho _{\text{l}}}{\rho _{{v}}}}}{{{\rho _{{m}}}}}\sqrt {\frac{2}{3}\frac{{p - {p_{{\text{sat}}}}}}{{{\rho _{\text{l}}}}}} \left( {p \geqslant {p_{{\text{sat}}}}} \right) 。\\[-10pt] \end{split} $ | (5) |
其中:RB为气核半径;αnuc为非凝结气体的体积分数;psat为饱和蒸汽压力。
边界条件:如图1所示,流体域底部为速度进口边界,入口速度为0 m/s,水的体积分数为100%;流体域侧边和顶端为出口压力边界,侧边压力随水的深度变化,流体体积分数根据设计的水面坐标,坐标上侧边界空气体积分数为100%,坐标下侧边界水的体积分数为100%。流体域与结构体通过重叠区域网格的插值实现物理量的传递。结构体表面为无滑移壁面。
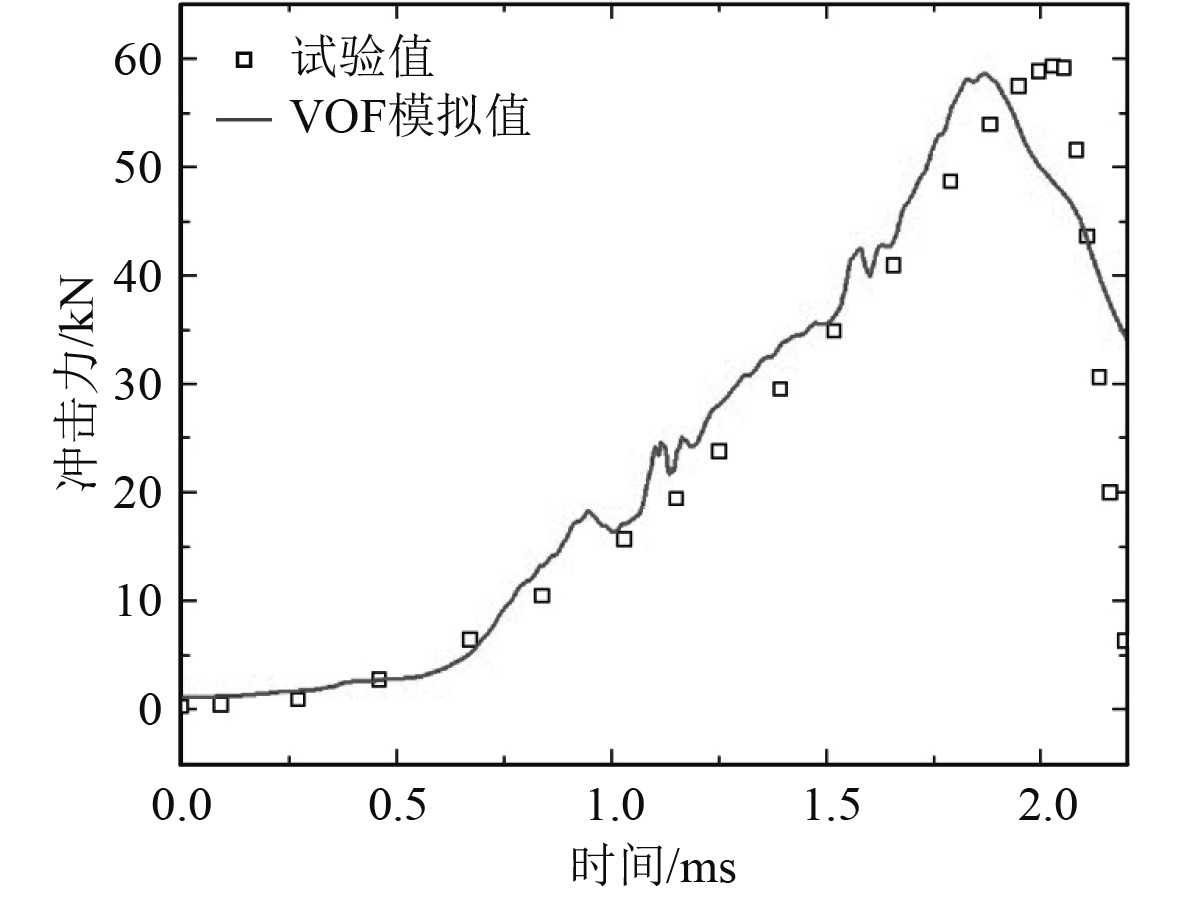
1.3 模型验证该数学模型通过STAR-CCM+12.02进行瞬态求解,时间步长取1×10−6 s。采用El Malki Alaouil等[16]针对锥形头入水冲击载荷试验数据进行数值模型的对比验证,试验模型直径为330 mm,圆柱段长度为30 mm,横升角为7°。图2为相应的数值结果与试验结果的对比情况。由图可知,数值结果与试验结果吻合较好,表明所建立的数学模型合理且有效。
|
图 2 数值结果与试验结果的对比 Fig. 2 Comparison between the simulated and experimental results |
为了方便表述,定义入水阻力系数如下:
| $ {C_{{d}}} = \dfrac{{{F_{{d}}}}}{{\dfrac{1}{2}\rho {u^2}S}}。$ | (6) |
式中:Fd为入水过程形成的流体阻力;ρ为水的密度;u为入水速度;S为结构体横截面积。
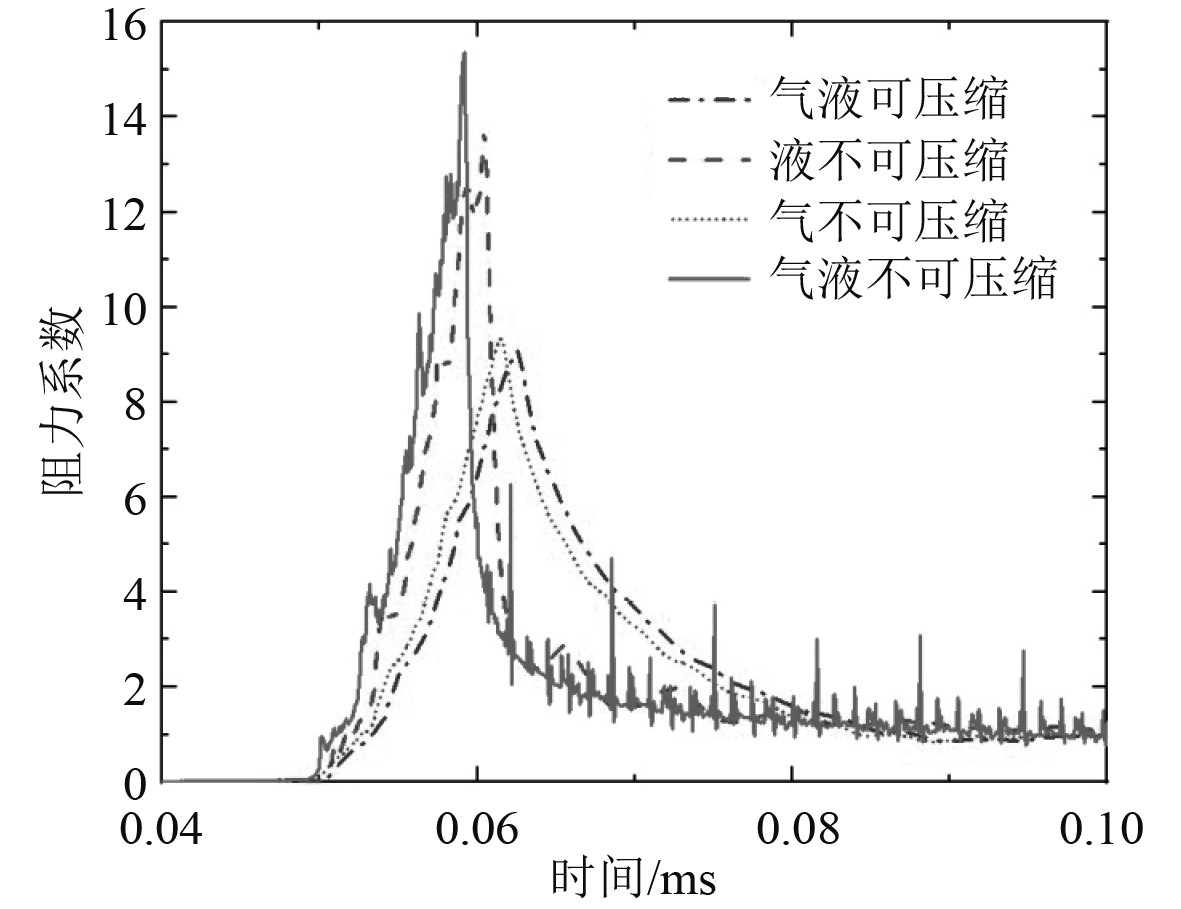
2.1 流体可压缩性对入水载荷的影响以300 m/s垂直入水为例,分析气、液相不可压缩分别对入水阻力系数的影响,如图3所示。可知,不同相可压缩性的影响主要体现在冲击峰值不同,峰值过后的阻力系数比较接近。进一步,由“气液可压缩”和“气不可压缩”对比可知,不考虑气相可压缩性时,冲击峰值会略微增加2.5%,这是因为在高速入水过程中,头部来不及逃逸的空气会形成局部的空气垫,受压后起到一定的缓冲作用;由“气液可压缩”和“液不可压缩”对比可知,不考虑液相可压缩性时,冲击峰值会增加51%。对比发现,高速入水过程中,水的可压缩性作用远比空气显著的多。考虑液相可压缩性时,流体和结构体相互作用的时间更长(这一点可从冲击力的脉宽比较得到验证),根据动量定律,相互作用时间越短,对应的力越大。当气液两相均不可压缩时,冲击峰值会增加69.1%。而且,当不考虑水可压以及气液均不可压缩时,载荷表现出越来越明显的震荡。综上,水的可压缩性对高入水冲击载荷起主导作用。
|
图 3 流体可压缩性对入水载荷的影响 Fig. 3 Effects of fluid compressibility on water-entry loads |
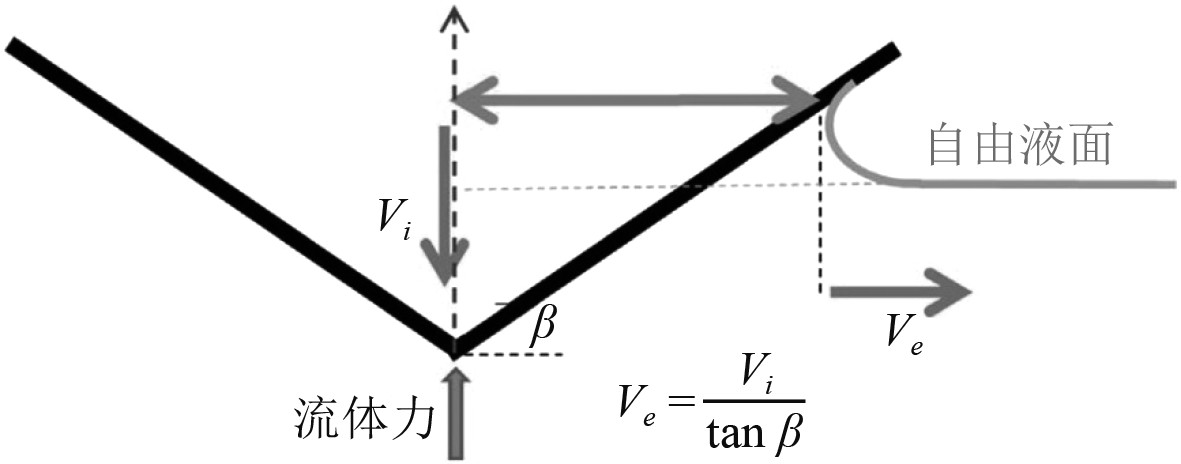
为了进一步分析水的可压缩性对冲击载荷的影响机理,选取头部入水过程进行详细分析。图4为楔形头入水过程示意图。Vi为结构体入水速度;β为锥形头的横升角;Ve为头部附近液体的横向扩展速度,三者关系如图中公式所示。锥形头入水过程中,由于自由液面与结构体接触区域为沾湿和未沾湿区域的交界,结构体以Vi速度入水时,会使与之接触的流体获得Ve的横向扩展速度,交界区域流体瞬间获得较大的动量,从而产生脉冲力和压强,导致自由液面与头部接触区域形成高压区。
|
图 4 楔形头入水过程示意图[17] Fig. 4 Schematic diagram of fluid-solid interaction during conical nose water entry |
图5为头部全沾湿时刻液相不可压缩和液相可压缩对应的压力场分布。可知,不论液相是否可压缩,锥形头的两肩处均形成了上述分析的高压区,但液相不可压缩和液相可压缩对应的高压区聚集程度有区别,后者比前者更加聚集。这是因为横升角10°的锥形头300 m/s垂直入水时,考虑横向扩展速度后其局部流体获得的合速度高达1728 m/s(实际考虑液相可压缩时,水的音速为1500 m/s),这会导致相应的压力扰动传递速度小于流体运动速度,两肩处的高压区向轴中心传递受阻(实际上并不是完全无法传递,因为朝远离壁面方向,流体速度快速衰减,压力扰动受阻的现象会逐渐衰减),导致液相可压缩情况的头部高压区比较聚集。相比之下,当液相不可压缩时,其压力扰动传递更快,头部压力相对分布的更均匀。因此,液相可压缩时,虽然压力场局部最高压力高达683 MPa,但由于液相可压缩导致扰动传递受阻,局部高压区未完全在头部沾湿面展开;液相不可压缩时,压力场局部最高压力相对较低,为491 MPa,但液相不可压缩导致扰动波传递很快,但整个沾湿面区域压力分布较均匀,这导致液相不可压缩的头部整体受力更大,对应的冲击峰值更高。

|
图 5 300 m/s入水时液相可压缩性对压力场的影响 Fig. 5 Effect of liquid compressibility on the pressure distribution at the speed of 300 m/s |
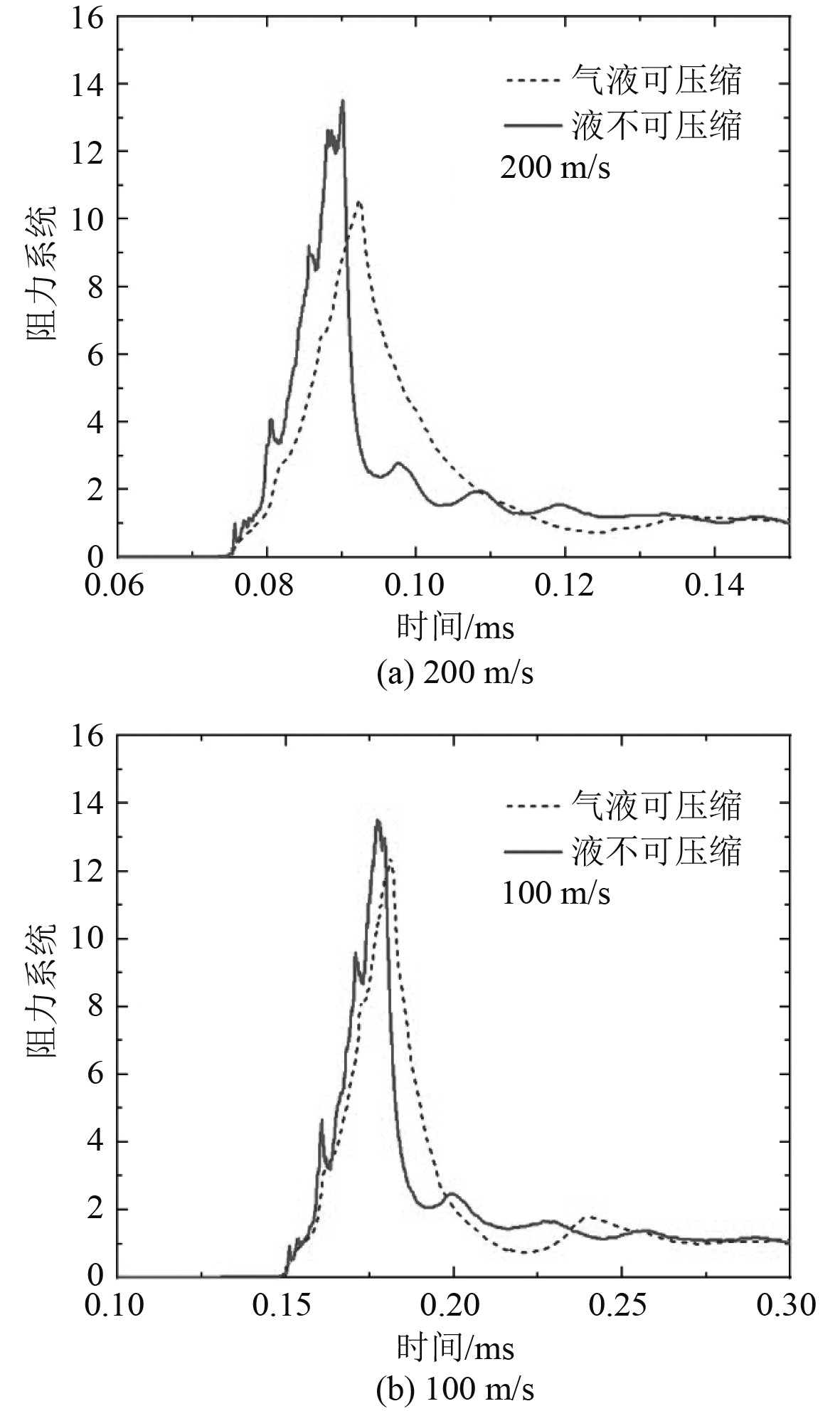
图6为200 m/s和100 m/s入水时液相可压缩性对阻力系数的影响。结合图1入水速度300 m/s时的载荷曲线可以发现,随着入水速度降低,液相可压缩性的影响逐渐降低。具体地,入水速度300 m/s,200 m/s和100 m/s时,液相不可压缩会导致冲击峰值分别增大51%,25.9%和9.2%。这主要是因为随着入水速度减小,水和结构体交界面局部速度减小至水的音速以下,压力扰动可以更快向轴中心传递,分布更均匀从而更接近液相不可压缩情况,这导致液相不可压缩和液相可压缩的冲击峰值差别逐渐减小。
|
图 6 入水时液相可压缩性对载荷的影响 Fig. 6 Effect of liquid compressibility on the water entry loads |
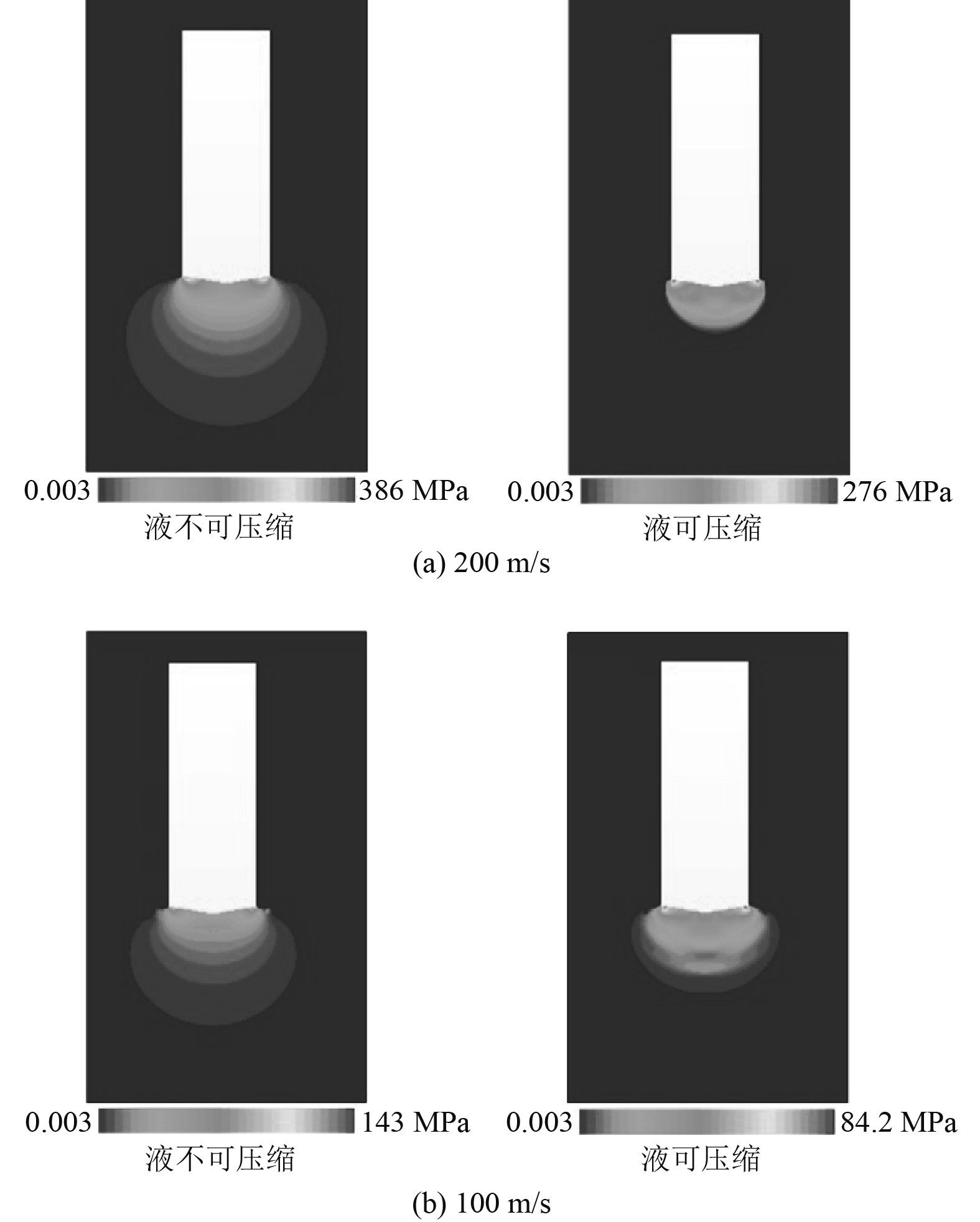
图7为200 m/s和100 m/s入水时液相可压缩性对压力场分布的影响。当入水速度降至200 m/s和100 m/s时,相应的局部合速度分别为1152 m/s和576 m/s,对应流体的马赫数分别为0.77和0.38。由图可以看出,液相可压缩时锥形头两肩位置有明显聚集的高压区;相比之下,液相不可压缩时,压力沿空间扩散更快,壁面处分布也相对均匀。仔细观察可以发现,对于200 m/s和100 m/s入水,液相不可压缩的最高压力大于液相可压缩的。这是因为液相不可压缩时,由于相互时间短,形成的局部脉冲力和压强更高。而300 m/s入水时,液相不可压缩的最高压力小于液相可压缩的。这是因为其对应的局部合速度超过当地音速,局部形成的脉冲压力扰动有叠加效果。
|
图 7 入水时液相可压缩性对压力场的影响 Fig. 7 Effect of liquid compressibility on the pressure distribution |
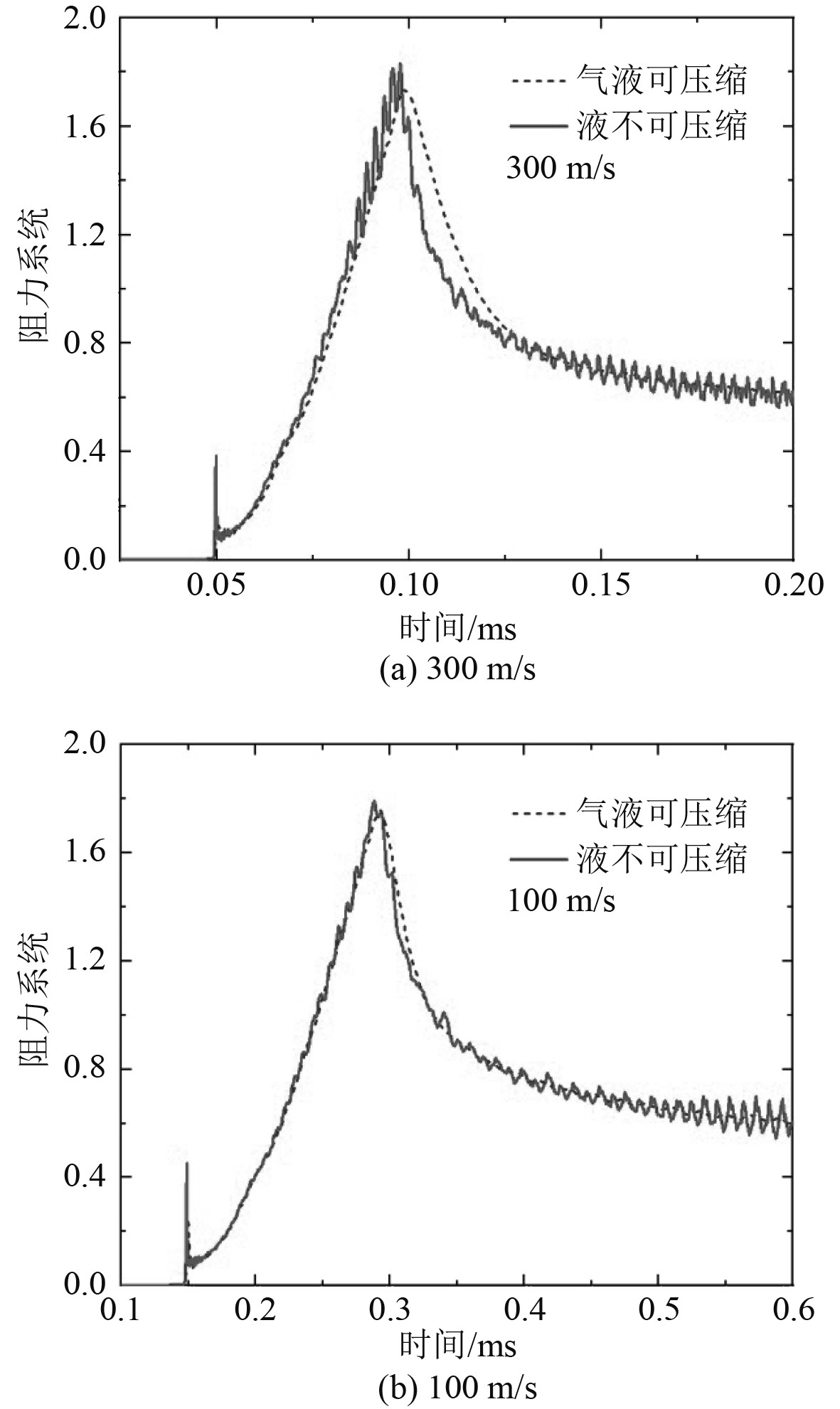
基于上述分析,液相可压缩性的影响与流体局部合速度有关,因此有必要研究不同横升角头型对入水冲击载荷的影响。以横升角10°和40°的2种锥形头进行对比分析,2种模型的圆柱段尺寸相同。图8为横升角40°的锥形头300 m/s和100 m/s入水时液相可压缩性对阻力系数的影响,局部合速度分别为467 m/s和155 m/s,对应流体的马赫数分别为0.31和0.1。可以看出,2种速度下可压缩性的影响均很小,尤其100 m/s入水时,液相可压缩性对载荷的影响几乎可以忽略。因此,高速入水冲击载荷分析与气动分析类似,即马赫数越低可压缩性的影响越小。
|
图 8 横升角40°的锥形头入水时液相可压缩性对载荷的影响 Fig. 8 Effect of liquid compressibility on the water entry loads of conical nose with the deadrise angle of 40° |
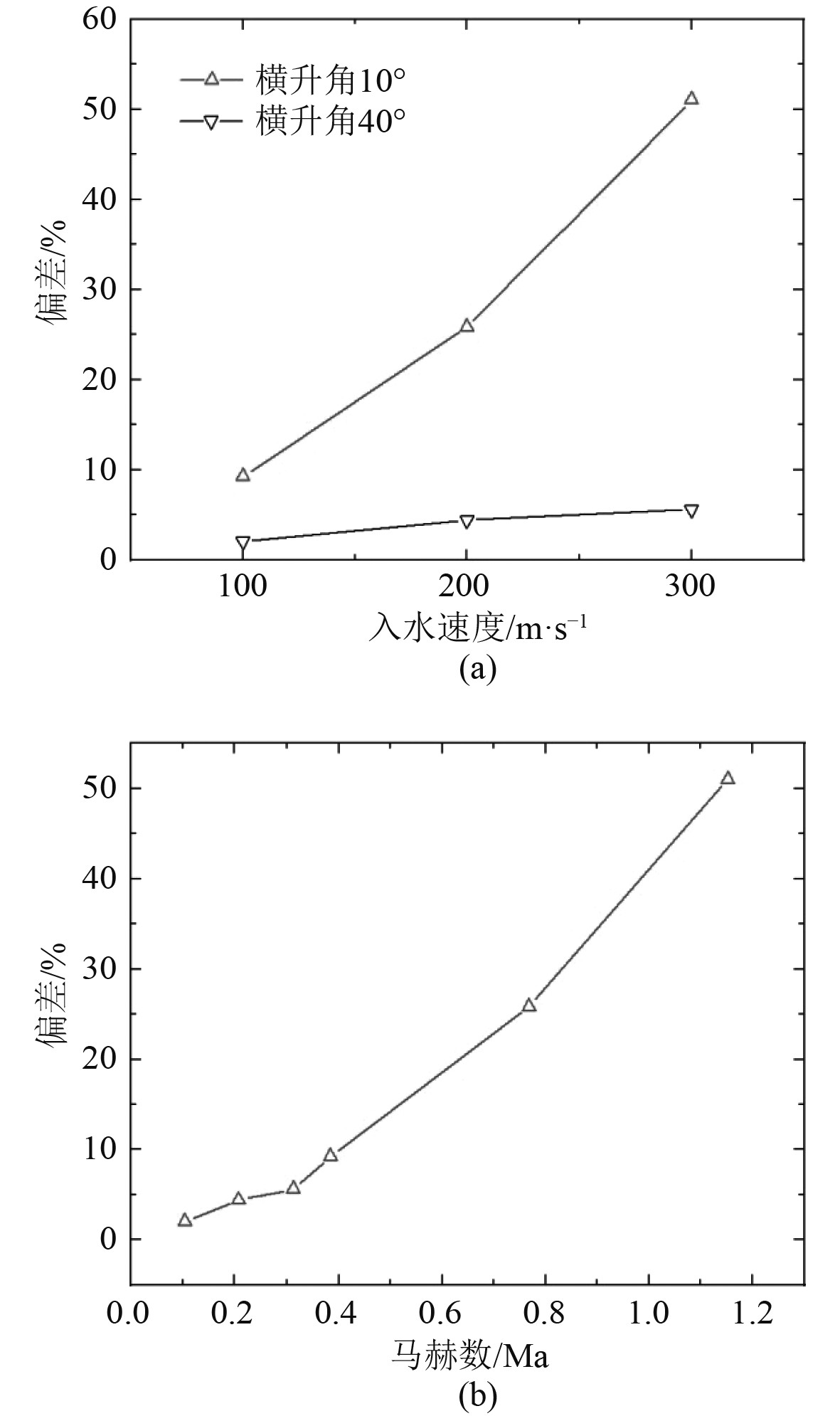
图9归纳了不同头型和入水速度分别对液相可压缩性作用的影响。由图9(a)可知,随着入水速度的增加,液相不可压缩造成的冲击载荷偏差逐渐增大,尤其对于小横升角的头型,偏差随速度的增加非常明显。进一步,结合局部合速度对应的液相马赫数,可归纳出不同液相马赫数对液相可压缩性作用的影响规律,如图9(b)所示。可以看出,随着液相马赫数的增加,液相不可压缩造成的冲击载荷偏差呈现出较好的递增性规律。其中,在液相马赫数为0.38时,忽略液相可压缩性会导致冲击载荷被高估9.2%。以此为参考,可初步认为高速入水冲击载荷与传统气动力学分析类似,在液相马赫数大于0.4时,液相可压缩性的影响将逐渐明显,忽略其会引起误差高达10%以上。
|
图 9 不同头型、入水速度和马赫数对液相可压缩性作用的影响 Fig. 9 Effects of different noses and speeds on the liquid compressibility role and the water entry impact |
本文采用VOF多相流模型和嵌套网格技术,开展流体可压缩性对100~300 m/s结构体垂直入水的载荷影响研究,揭示了流体可压缩性对入水冲击载荷的作用规律和机理,主要结论如下:
1)气-液两相流体可压缩性主要对冲击载荷有影响,其中液相可压缩性影响占主导作用;
2)液相可压缩性的作用机理主要是,可压缩性会使沾湿面附近压力扰动传递受阻,局部高压区表现出更强的聚集性,导致作用在沾湿面全局的流体阻力减小。
3)基于结构体挤压流体局部形成合速度对应的液相马赫数,可以作为液相可压缩性对冲击载荷的影响判别特征数。液相马赫数越大,液相可压缩性的影响将逐渐明显,液相马赫数大于0.4时,液相不可压缩会使冲击载荷被高估10%以上。
| [1] |
徐宣志, 欧阳吕伟, 严忠汉. 鱼雷力学[M]. 北京: 国防工业出版社, 1992.
|
| [2] |
KARMAN T Von. The impact on seaplane floats during landing[R/OL]. National Advisory Committee for Aeronautics, 1929.
|
| [3] |
WAGNER H. Phenomena associated with impacts and sliding on liquid surfaces[J]. Z Angew Math Mech, 1932, 12(4): 193-215. DOI:10.1002/zamm.19320120402 |
| [4] |
WANG S, SOARES C. Effects of compressibility, three-dimensionality and air cavity on a free-falling wedge cylinder[J]. Ocean Engineering, 2020, 217: 107589. DOI:10.1016/j.oceaneng.2020.107589 |
| [5] |
SHI H, ITOH M, TAKAMI T. Optical observation of the supercavitation induced by high-speed water entry[J]. Journal of Fluids Engineering, 2000, 122(4): 806-810. DOI:10.1115/1.1310575 |
| [6] |
TRUSCOTT TT. Cavity dynamics of water entry for spheres and ballistic projectiles[D]. Massachusetts: Massachusetts Institute of Technology, 2009.
|
| [7] |
黄闯, 党建军, 李代金, 等. 跨声速运动对射弹阻力及空化特性的影响[J]. 兵工学报, 2016, 37(8): 1482-1488. HUANG Chuang, DANG Jianjun, LI Daijin, et al. Effect of transonic flight on drag and cavitation characteristics of projectile[J]. Acta Armamentarii, 2016, 37(8): 1482-1488. DOI:10.3969/j.issn.1000-1093.2016.08.021 |
| [8] |
黄闯, 罗凯, 白杰, 等. 液体可压缩性对超空化流动的影响[J]. 上海交通大学学报, 2016, 50(8): 1241-1245. HUANG Chuang, LUO Kai, BAI Jie, et al. Effect of liquid compressibility on supercavitation flow[J]. Journal of Shanghai Jiao Tong University, 2016, 50(8): 1241-1245. DOI:10.16183/j.cnki.jsjtu.2016.08.016 |
| [9] |
洪尧, 王本龙, 刘桦. 二维高速入水物体砰击载荷数值研究[C]//第九届全国流体力学学术会议, 南京, 2016. Hong Yao, Wang Benlong, Liu Hua. Numerical study of slamming load during the high-speed water entry of two-dimension body[C]//The 9th National Conference on Fluid Mechanics, Nanjing, China, 2016. |
| [10] |
张凌新, 褚学森, 邵雪明. 高速物体入水过程的可压缩数值计算方法研究[C]//第十四届全国水动力学学术会议暨第二十八届全国水动力学研讨会, 长春, 2017. ZHANG Lingxin, CHU Xuesen, SHAO Xueming. Investigation of compressible numerical computation method for high-speed water entry process[C]//The 14th National Hydrodynamics Conference and the 28th National Hydrodynamics Workshop, Changchun, China, 2017. |
| [11] |
李达钦. 高速航行体可压缩超空泡流动数值计算[D]. 北京: 北京理工大学, 2016.
|
| [12] |
Li D, Zhang J, Zhang M, et al. Experimental study on water entry of spheres with different surface wettability[J]. Ocean Engineering, 2019, 187: 106123. DOI:10.1016/j.oceaneng.2019.106123 |
| [13] |
陈晨, 魏英杰, 王聪, 等. 射弹跨声速入水初期阶段多相流场特性数值研究[J]. 振动与冲击, 2019, 38(6): 46-61. CHEN Chen, WEI Yingjie, WANG Cong, et al. Numerical study on the multiphase flow characteristics durging the initial stage of transonic water entry of projectile[J]. Journal of Vibration and Shock, 2019, 38(6): 46-61. DOI:10.13465/j.cnki.jvs.2019.06.007 |
| [14] |
曹雪洁, 胡俊, 于勇. 液体可压缩性对高速射弹超空泡流的影响[J]. 兵工学报, 2020, 41(S1): 72-78. CAO Xuejie, HU Jun, YU Yong. Effect of liquid compressibility on supercavitation flow of high-speed projectile[J]. Acta Armamentarii, 2020, 41(S1): 72-78. |
| [15] |
李国良, 尤天庆, 孔德才, 等. 旋成体高速入水可压缩性影响研究[J]. 兵工学报, 2020, 41(4): 720-729. LI Guoliang, YOU Tianqing, KONG Decai, et al. Effect of compressibility on high-speed water entry of revolution body[J]. Acta Armamentarii, 2020, 41(4): 720-729. DOI:10.3969/j.issn.1000-1093.2020.04.011 |
| [16] |
ALAOUIL AEM, NÊME A, TASSIN A, et al. Experimental study of coefficients during vertical water entry of axisymmetric rigid shapes at constant speeds[J]. Applied Ocean Research, 2012, 37: 183-197. DOI:10.1016/j.apor.2012.05.007 |
| [17] |
ELHIMER M, JACQUES N, El MALKI ALAOUI A, et al. The influence of aeration and compressibility on slamming loads during cone water entry[J]. Journal of Fluids and Structures, 2017, 70: 24-46. DOI:10.1016/j.jfluidstructs.2016.12.012 |
 2022, Vol. 44
2022, Vol. 44

