随着自主船舶技术的发展,船舶自主航行的安全尤为重要。当船舶执行避障或狭窄水域航行等高机动任务时,需要建立准确的动力学模型来预见船舶未来的运动状态或轨迹,判断控制策略是否有效或规划路径是否满足船舶运动特性,并提前采取行动避免碰撞。高精度船舶数学模型可以提供准确的运动预测,对于船舶智能导航和控制器的设计至关重要。
船舶动力学模型辨识的目标是建立数学模型,在给定船舶运动状态、推力和舵角作为输入的情况下,生成船舶测量的运动状态与模型预测运动状态之间的最佳拟合。输入和输出之间的映射越准确,现实世界与模型之间的差距就越小。
目前,船舶动力学建模主要分为基于先验模型的参数化建模和基于数据的非参数化建模。由于船舶表面不规则,水动力分析极其复杂,用第一原理建模非常困难,有许多先验模型结构用于近似表达船舶动力学。其中一些模型广泛用于水面船舶的动力学建模,如基于泰勒展开的三次Abkowitz模型[1]和二次Norrbin模型[2]。围绕这些模型,参数化建模开展了大量的研究工作。诸如最小二乘法[3]、扩展卡尔曼滤波器 (EKF)[4] 和最小二乘支持向量回归(LSSVR)[5-6]等方法已用于船舶运动辨识。然而,这些方法都存在一些固有的缺点,如涉及参数过多,导致的多重共线性会使参数识别不准确,2组不同的系数可以同样好地预测某一特定工况,而它们在另一个工况中表现不佳,泛化性不足。许多方法被提出来克服参数漂移的影响[7],最优截断奇异值分解 (T-SVD)[8]和最优截断最小二乘支持向量回归(T-LSSVR)[9-11]被证明可以减少估计参数的不确定性。然而,这些方法是一种有偏估计,降低了水动力系数的准确性,从而降低了参数的方差,参数不确定性问题仍未完全解决。也有各种消除变量和简化参数的模型[12-13]。然而,船舶的“真实”模型结构是未知的,确定船舶的模型结构一直是参数化建模实际应用中的一个难题。建立模型的目标是获得准确的预测,不一定是获得正确的水动力系数。
与参数化建模相比,非参数化建模几乎不需要船舶模型结构的先验信息,无需分析复杂的流体动力学,也可以获得正确的输入输出映射。近年来,支持向量回归(SVR)和局部加权学习(LWL)等机器学习方法被用于船舶动力学建模。广义椭球基函数模糊神经网络[14]用于模拟大型油轮的运动,但是,神经网络的结构难以确定。
高斯过程回归(GPR)可以通过最大化边际似然函数来自动优化超参数,还可以克服过拟合问题,它广泛应用于机械臂[20]和赛车[21]的动力学建模。最近,它也被引入到船舶的动力学建模中,多输出高斯过程被用来模拟集装箱船运动[22]。薛[23]通过使用带有人工噪声的模拟数据,提出了一种考虑噪声输入高斯过程来进行船舶动力学建模,但目前仅限于模拟数据,没有对实验数据进行建模。
在本文研究中,基于高斯过程的非参数回归被用于船舶动力学模型辨识,通过建立模型预测难以测量的船舶加速度。同时提出多步预测模型以提供船舶未来一段时间加速度、速度和位置信息。KVLCC2的实验数据用于验证所提出方法的有效性。
1 船舶动力学参数模型和非参数模型船舶动力学参数模型极其复杂,该模型包含辐射引起的附加质量、阻尼和恢复力。描述船舶动力学的参数化数学模型有很多,常用的运动方程[24]可以表示为:
| $ M\dot{s}+C\left(s\right)s+D\left(s\right)s+g\left(\eta \right)+{g}_{0}=\tau +{\tau }_{wind}+{\tau }_{wave}。$ | (1) |
其中,船速
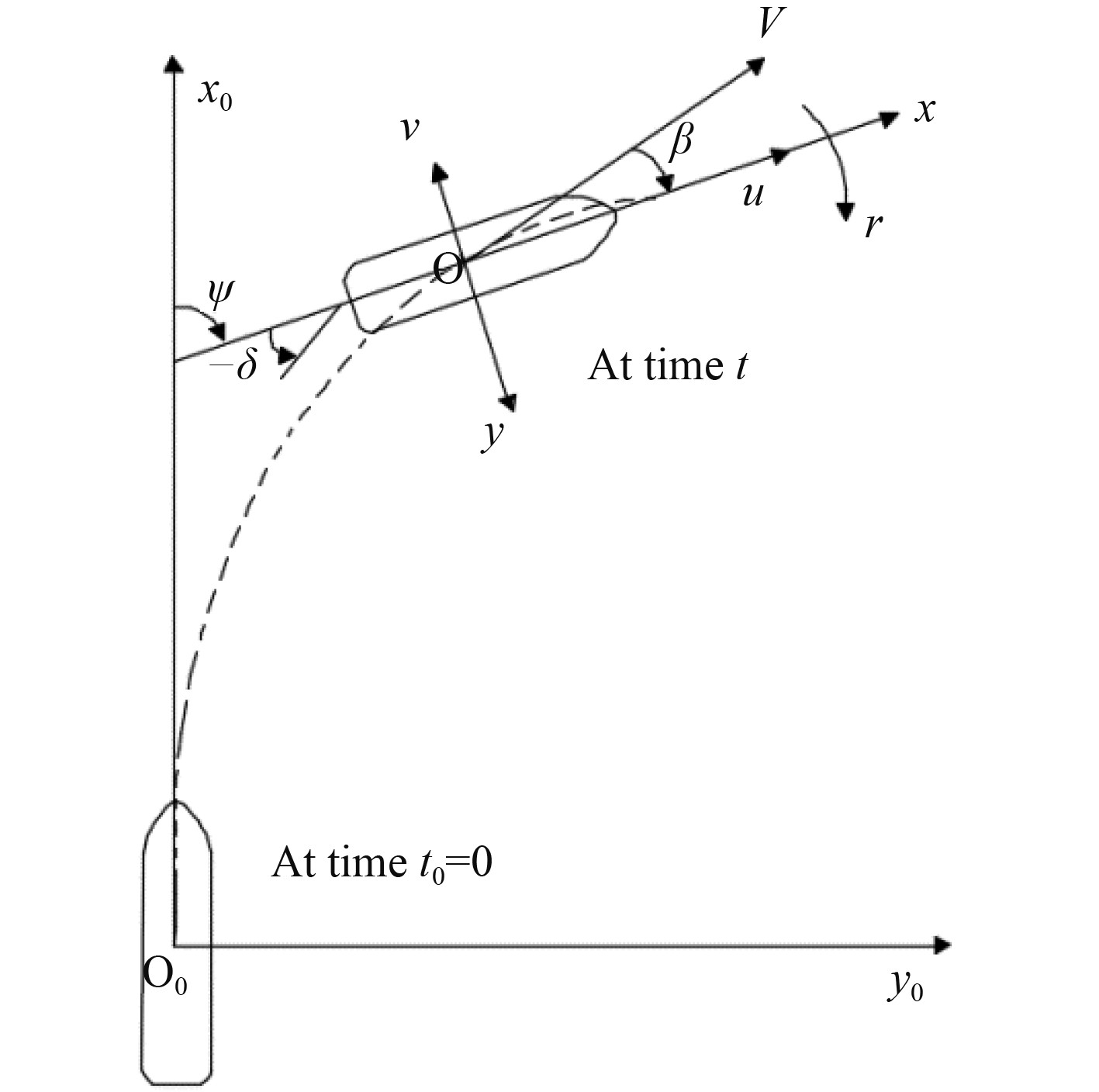
|
图 1 地球和船舶固定坐标系 Fig. 1 Earth and ship-fixed coordinate systems |
当只考虑3个自由度模型(纵向、摇摆和偏航)时,静水恢复力和流体记忆效应可以忽略不计,不考虑外界风和流的影响,方程(1)可以简化为:
| $ M\dot{s}+C\left(s\right)s+D\left(s\right)s=\tau。$ | (2) |
由于阻尼力D(s)的非常复杂,参数模型中通常使用二次或三次模型进行估计。根据参数化模型的表达形式,提出船舶动力学的非参数化表达如下:
| $ \dot{s}=f(s,\tau )。$ | (3) |
其中:
| $ {\dot{u}}_{k}={f}_{u}\left({u}_{k},{v}_{k},{r}_{k},{T}_{k},{\delta }_{k}\right) ,$ | (4) |
| $ {\dot{v}}_{k}={f}_{v}\left({u}_{k},{v}_{k},{r}_{k},{T}_{k},{\delta }_{k}\right),$ | (5) |
| $ {\dot{r}}_{k}={f}_{r}\left({u}_{k},{v}_{k},{r}_{k},{T}_{k},{\delta }_{k}\right) 。$ | (6) |
| $ {y}_{i}=f\left({x}_{i}\right)+\varepsilon ,\varepsilon \sim N(0,{\mathrm{\sigma }}_{n}^{2}),$ | (7) |
在高斯过程回归[25]中,
| $ \left[\begin{array}{c}y\\ {f(x}^{*})\end{array}\right] \sim N\left(0,\left[\begin{array}{cc}K\left(\mathrm{X},\mathrm{X}\right)+{{\mathrm{\sigma }}_{n}}^{2}I& K\left({x}^{*},\mathrm{X}\right)\\ K\left(\mathrm{X},{x}^{*}\right)& K\left({x}^{*},{x}^{*}\right)\end{array}\right]\right),$ | (8) |
| $ {f(x}^{*})=k\left({x}^{*},X\right){\left(\mathrm{K}\right(\mathrm{X},\mathrm{X})+{{\mathrm{\sigma }}_{n}}^{2}{I}_{n})}^{-1}y ,$ | (9) |
| $\begin{split} Var\left[{f(x}^{*})\right]=&k\left({x}^{*},{x}^{*}\right)-\\ &k\left({x}^{*},X\right){\left(\mathrm{K}\right(\mathrm{X},\mathrm{X})+{{\mathrm{\sigma }}_{n}}^{2}{I}_{n})}^{-1}k\left(X,{x}^{*}\right) \end{split},$ | (10) |
通常采用平方指数协方差函数作为核函数:
| $ k\left({x}_{i},{x}_{j}\right)={f\left({x}_{i}\right)}^{{\rm{T}}}f\left({x}_{j}\right)={{\mathrm{\sigma }}_{f}}^{2}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{1}{2}({x}_{i}-{x}_{j})^{{\rm{T}}}\mathrm{\Lambda }({x}_{i}-{x}_{j})\right)。$ | (11) |
其中,
在控制船舶时,通常希望在执行控制命令后预测未来k步船舶的运动响应。一个简单的方法是按顺序应用单步预测模型k次。在传感器信号丢失的情况下,多步预测模型用于提供未来一段时间的轨迹估计。
对于船舶动力学模型,多步预测模型的主要输入为:初始速度状态
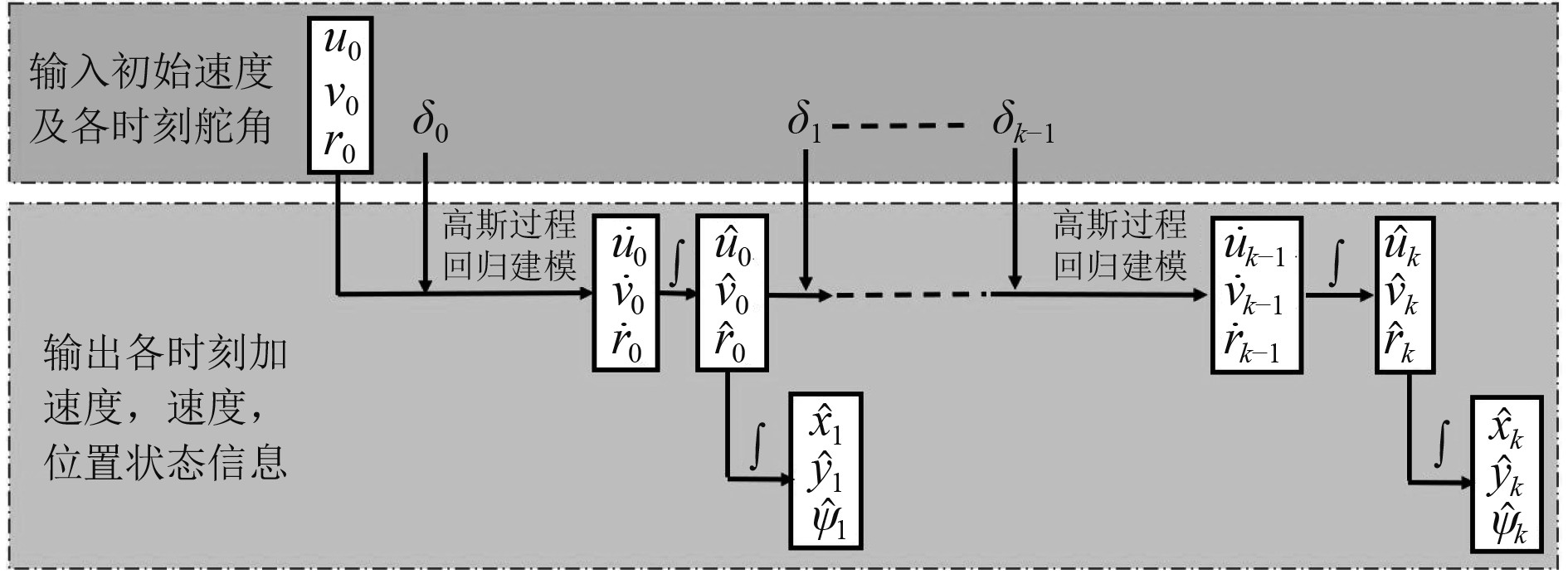
|
图 2 多步预测模型的输入和输出 Fig. 2 The inputs and outputs of multi-step prediction model |
多步预测模型容易受到误差累积问题的影响,过去的误差会传播到未来的预测中。因此,有必要尽可能提高单步预测的准确性。
3 KVCLL2船舶动力学辨识 3.1 实验船模型和数据集自由航行试验是船舶动力学识别的常用方法。这种方法只需要测量船舶的位置和速度等状态信息,不需要测量力。此外,它还可以应用于全尺寸船舶以避免规模效应。KVLCC2是一艘大型油轮,在国际上已被用作验证船舶模型辨识方法的基准船型。本文使用的试验数据来自在德国汉堡水箱(HSVA)进行的KVLCC2模型自由航行试验。KVLCC2模型的主要参数详见表1。试验开展了一系列Z形测试,所有的数据用在20 Hz的采样率采集。此研究中所用的试验数据见表2。
|
|
表 1 KVLCC2型号参数及尺寸 Tab.1 Parameters and dimensions of the KVLCC2 model |
|
|
表 2 KVLCC2试验数据 Tab.2 Test data of the KVLCC2 model |
传统的机动运动预测需要预测超调角和战术直径。然而,在规划路线或控制船舶避开障碍物时,操作员更需要知道在执行完一段控制命令后预测的船舶状态响应或轨迹是否与实际情况一致。因此,必须确保辨识中的控制指令和试验中的控制命令始终相同。基于高斯过程回归的非参数回归被用于船舶动力学建模。历史的控制命令和运动响应数据用于训练模型。训练后的模型可以准确预测未来任何控制命令的运动响应。
非参数建模主要适用于插值预测,为了学习一个“好”的模型,训练数据必须覆盖船舶状态空间较大范围。因此,使用5°/1°,10°/5°,20°/5°,30°/5°,35°/5°之字形测试来训练模型,数据几乎覆盖了舵角的输入空间。数据太多会使计算变慢,每间隔12个点选1个进入训练集,训练集中共有1512个训练点。25°/5°之字形测试作为验证集,预测间隔为0.05 s。
通常,加速度无法测量或者测量不准确,可以直接用速度差分代替加速度。虽然会放大噪声,使加速度不可靠,但不影响模型预测结果,因为高斯过程回归可以应用于噪声数据回归,辨识得到准确的加速度值。25°/5°Z形试验加速度的3700步预测值和试验值如图3所示。可以发现,试验中速度差分得到的加速度具有较强的振荡性,通过高斯过程回归可以很好地得到准确的加速度预测值。
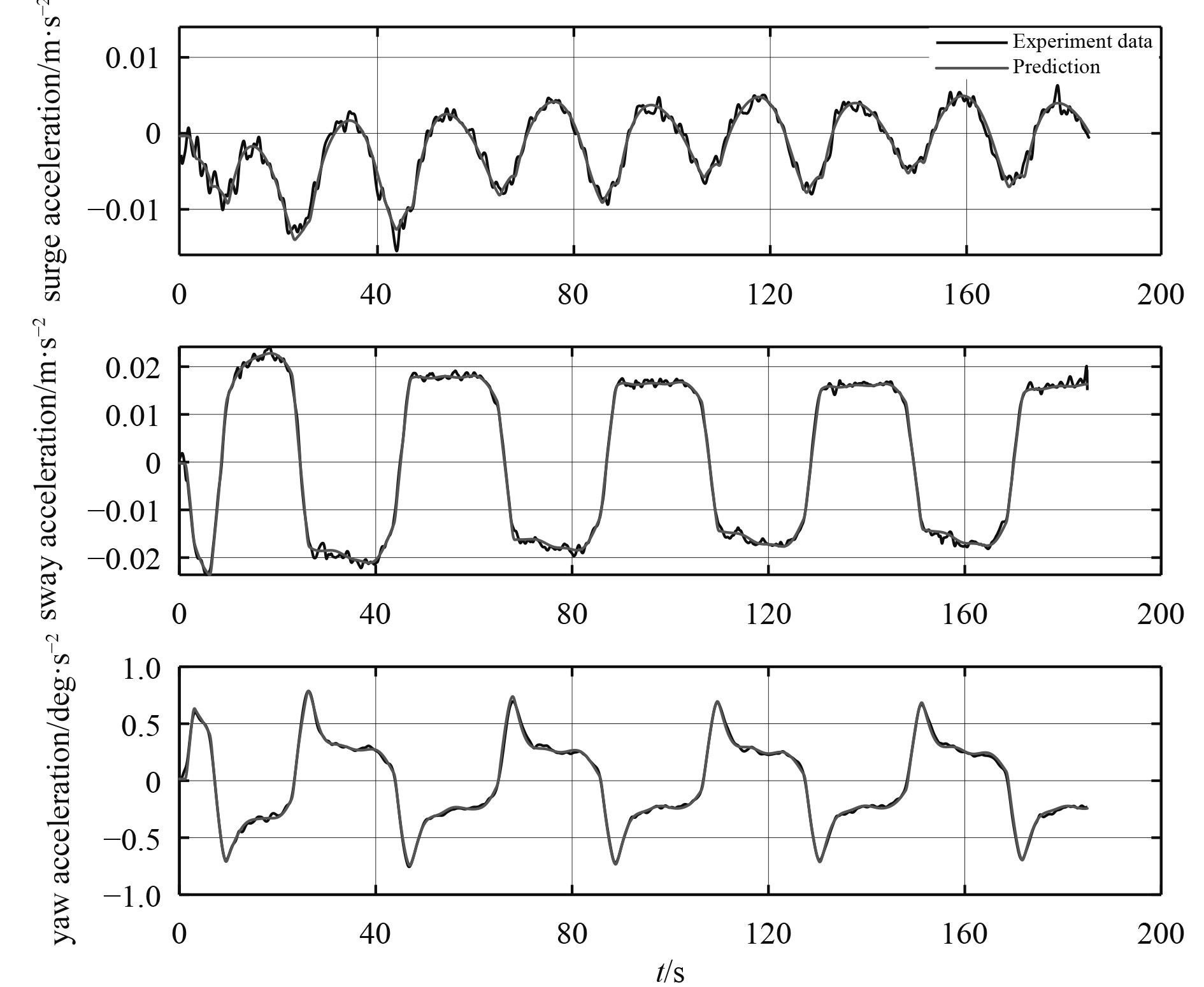
|
图 3 25°/5°Z形运动中的加速度3700步预测 Fig. 3 3700 steps prediction of acceleration in 25°/5° zigzag maneuver |
通过欧拉积分可以得到船的速度
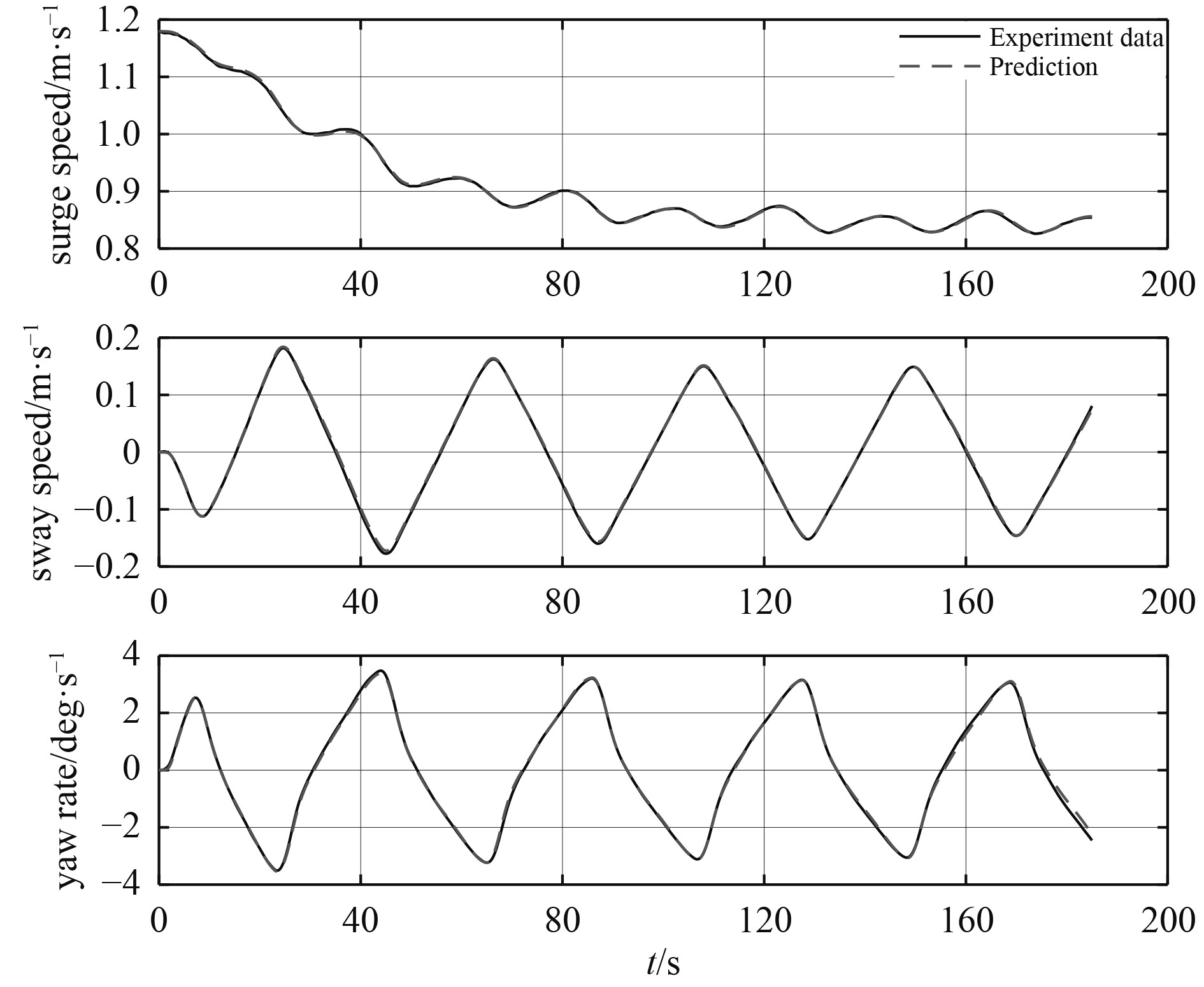
|
图 4 25°/5°Z形运动中的速度3700步预测 Fig. 4 3700 steps prediction of speed in 25°/5° zigzag maneuver |
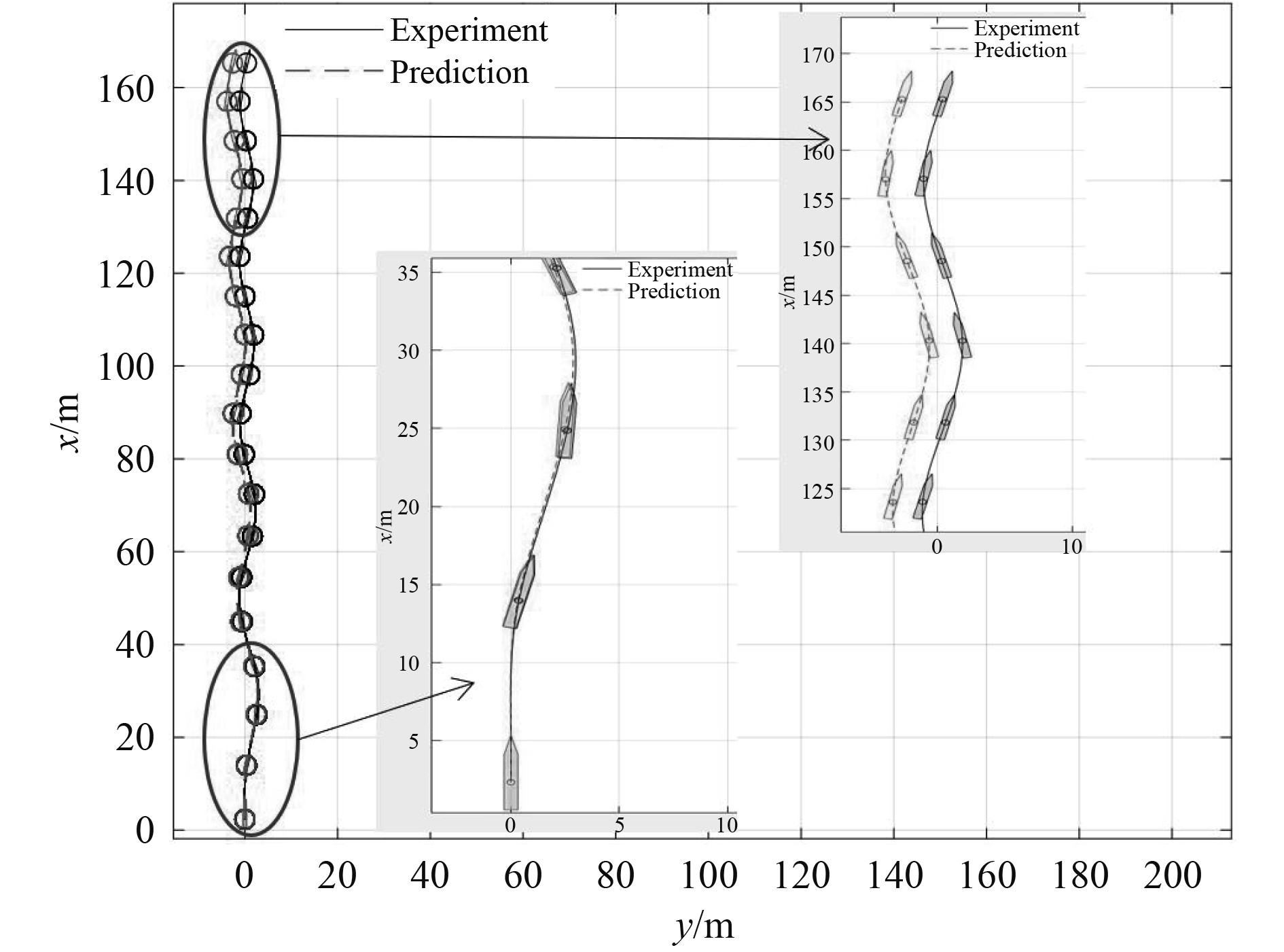
|
图 5 25°/5°Z形运动中的轨迹3700步预测 Fig. 5 3700 steps prediction of position in 25°/5° zigzag maneuver |
该模型训练时间为87 s,然而,训练时间并不重要,因为模型只需要离线训练一次,相比之下,预测时间更为重要,预测时间越短,可实现控制频率越高。选择不同的起始点来进行多步预测,比较预测时间和预测精度。如表3所示,一步预测准确率高,预测所需时间短。随着预测步数的增加,预测时间会在一定程度上增加,累积误差也会增加,欧拉积分方法会导致误差随着时间的推移而增加。但模型仍能保持较高的预测精度,100步的位置跟踪误差为0.013 m,1000步的位置跟踪误差为0.599 m。
|
|
表 3 25°/5°Z形试验多步预测RMSE的精度 Tab.3 Multi-step prediction accuracy assessed by the RMSE of the 25°/5° zigzag test |
在预测船舶运动响应时,通常假设控制输入舵角在预测区间内恒定或缓慢变化,因此时间间隔应尽可能小。在大区间预测中,舵角变化较大时,预测精度会降低。因此,为了实现多步高精度预测,应尽量选取较小的区间。
4 结 语基于高斯过程的非参数回归被用于船舶的动力学辨识,KVLCC2的试验数据用于验证所提方法的有效性。结果表明,通过高斯过程回归辨识得到的模型可以准确预测船舶未来一段时间的运动响应。在传感器信号丢失的情况下,模型未来仍能提供准确的船舶加速度、速度和位置信息,1000步的位置预测误差为0.599 m。
基于高斯过程回归的船舶动力学建模模型的优点可以概括为:1)与参数辨识不同,基于高斯过程回归的模型不需要知道船舶动力学的先验模型结构,可以得到准确的从输入到输出的映射;2)与LSSVR等其他黑盒识别相比,该模型可以通过最大化边际似然来自动调整超参数,减少因超参数不准确而导致的预测精度损失;3)该模型可以应用于噪声数据而不会过拟合,它可以准确估计难以测量的加速度。
但是,所提出方法的许多问题还需要进一步研究:对于非参数识别,训练数据必须覆盖转向角的输入空间,回转的预测和随机舵运动预测是否需要改变训练集有待进一步的实验数据验证。同时数据量越大,预测精度越高,但训练时间会更长甚至无法计算。未来的研究可以尝试将局部高斯过程回归应用于大数据船舶动力学建模。
| [1] |
ABKOWITZ M A. Measurements of hydrodynamic characteristics from ship maneuvering trials by system identification[C]// Transactions SNAME 88, 1980: 283−318.
|
| [2] |
NORRBIN N H. Ship Manoeuvring with Application to Shipborne Predictors and Real-Time Simulators[J]. Journal of Mechanical Engineering Science, 1972, 14(1): 91−107.
|
| [3] |
HOLZHUTER T. Robust identification scheme in an adaptive track-controller for ships[C]// IFAC Proceedings Volumes, 1990, 23: 461−466.
|
| [4] |
YOON H K, RHEE K P. Identification of hydrodynamic coefficients in ship maneuvering equations of motion by Estimation-Before-Modeling technique[J]. Ocean Engineering, 2003, 30(18): 2379−2404.
|
| [5] |
LUO W L, MOREIRA L, SOARES C G. Manoeuvring simulation of catamaran by using implicit models based on support vector machines[J]. Ocean Engineering, 2014, 82(15): 150−159.
|
| [6] |
ZHU M, HAHN A, WEN Y Q. Identification-based simplified model of large container ships using support vector machines and artificial bee colony algorithm[J]. Applied Ocean Research, 2017, 68(1): 249-261. |
| [7] |
LUO W L, LI X. Measures to diminish the parameter drift in the modeling of ship manoeuvring using system identification[J]. Applied Ocean Research, 2017, 67(1): 9-20. |
| [8] |
XU Haitong, HASSANI V, SOARES C G. Parameters Estimation of Nonlinear Manoeuvring Model for Marine Surface Ship Based on PMM Tests[C]. ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, 2018, 11: 19−23.
|
| [9] |
XU Haitong, SOARES C G. Experimental investigation of shallow water effect on vessel steering model using system identification method[J]. Ocean Engineering, 2017, 199: 106940.
|
| [10] |
XU Haitong, HASSANI V, SOARES C G. Uncertainty analysis of the hydrodynamic coefficients estimation of a nonlinear manoeuvring model based on planar motion mechanism tests[J]. Ocean Engineering, 2019, 173: 450−459.
|
| [11] |
XU H, HINOSTROZA M, HASSANI V, et al. Real-time parameter estimation of nonlinear vessel steering model using support vector machine[J]. Journal of Offshore Mechanics and Arctic Engineering, 2019, 141(6): 1−9.
|
| [12] |
MU D, WANG G, FAN Y, et al. Modeling and Identification for Vector Propulsion of an Unmanned Surface Vehicle: Three Degrees of Freedom Model and Response Model[J]. Sensors, 2018, 18(6): 1889.
|
| [13] |
SUTULO S, SOARES C G. An algorithm for offline identification of ship manoeuvring mathematical models from free-running tests[J]. Ocean Engineering, 2014, 15(79): 10−25.
|
| [14] |
WANG N, ER M J, HAN M. Large tanker motion model identification using generalized ellipsoidal basis function-based fuzzy neural networks[J]. IEEE Transactions on Cybernetics, 2015, 45(12): 2732−2743.
|
| [15] |
WANG Z, XU H, XIA L, et al. Kernel-based support vector regression for nonparametric modeling of ship maneuvering motion[J]. Ocean Engineering, 2014, 216: 10−25.
|
| [16] |
W, REN J, LI T. Modified genetic optimization-based locally weighted learning identification modeling of ship maneuvering with full scale trial [J]. Future Generation Computer Systems, 2019, 93: 1036−1045.
|
| [17] |
MORENO-SALINAS D, MORENO R, PEREIRA A, et al. Modelling of a surface marine vehicle with kernel ridge regression confidence machine[J]. Applied Soft Computing Journal, 2019, 76(1): 237−250.
|
| [18] |
MORENO R, MORENO-SALINAS D, Aranda J. Black-box marine vehicle identification with regression techniques for random manoeuvres[J]. Electronics, 2019, 8(5): 492−492.
|
| [19] |
MORENO R, BESADA-PORTAS E, ARANDA J, Symbolic regression for marine vehicles identification[J]. IFAC-Papers Online, 2015, 48(16): 210−216.
|
| [20] |
CARRON A, ARCARI E, WERMELINGER M, et al. Data-driven model predictive control for trajectory tracking with a robotic arm [J]. IEEE Robotics and Automation Letters, 2019, 4(4): 3578−3765.
|
| [21] |
KABZAN J, HEWING L, LINIGER A. Learning-based model predictive control for autonomous racing [J]. IEEE Robotics and Automation Letters, 2019, 4(4): 3363−3370.
|
| [22] |
RAMIRE W A, LEONG Z Q, HUNG N, et al. Non-parametric dynamic system identification of ships using multi-output Gaussian Processes[J]. Ocean Engineering, 2018, 166: 26−36.
|
| [23] |
XUE Y, LIU Y, JI C, et al. System identification of ship dynamic model based on Gaussian process regression with input noise [J]. Ocean Engineering, 2020, 216: 107862.
|
| [24] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. 2011: 134−135.
|
| [25] |
RASMUSSEN C E, WILLIAMS K I. Gaussian processes for machine learning[M]. 2006: 8−31.
|
 2022, Vol. 44
2022, Vol. 44
