潜艇使用单个小口径自航式声诱饵防御声自导鱼雷时,潜艇指挥员需要在短时间内进行潜艇防御鱼雷指挥决策,迅速抉择较优的防御方案,确定潜艇机动规避的参数(时机、转向角、变深航深)和声诱饵发射参数(发射时机、一次转向角、变深航深、二次转向角)等。这些参数的选择相互关联[1],导致潜射声诱饵防御鱼雷问题比较复杂。
在机动建模基础上采用优化算法求解潜射声诱饵防御鱼雷问题是一个有效途径,文献[1]通过分析潜艇使用自航式声诱饵防御声自导鱼雷的作战过程,在一定防御态势下,建立了自航式声诱饵有效发射时机与有效初始航向的解析模型,以此确定了自航式声诱饵发射时机和初始航向的有效取值范围。文献[2]根据诱饵的航向应使鱼雷对声诱饵的捕获概率最大的原则,通过几何分析求出声诱饵的最佳航向。文献[3]通过数学仿真分析,得到了不同鱼雷报警舷角下声诱饵的可行发射区域以及最不利发射方向角。文献[4]采用线性规划方法,求取了最优的潜艇规避角度和诱饵航向。文献[5]建立了“过程仿真+方案搜索”的防御方案优化模型,采用并行算法进行求解。文献[6]采用并行算法进行求解。文献[7]将其看成一个组合优化问题,然后利用遗传算法进行求解。文献[7-9]采用遗传算法进行求解。对于潜艇机动规避正在进行蛇形搜索的声自导鱼雷并使用单个自航式声诱饵防御的优化问题,为提升仿真真实性,建立三维仿真模型,模拟鱼雷的蛇形机动、环形机动以及尾追机动,以及潜艇目标强度、声诱饵尾部盲区等声学特性,为提升解算效率,采用基于并行计算的粒子群算法进行求解,获得使得潜艇和鱼雷距离较远的潜艇机动规避和声诱饵机动参数可行解。
1 模型建立 1.1 仿真模型潜艇声诱饵防御鱼雷的仿真流程如图1所示。在该仿真流程中,机动参数为潜艇机动规避的参数(时机、转向角、变深航深)和声诱饵发射参数(发射时机、一次转向角、变深航深、二次转向角)。输入机动参数后,可以根据文献[10]机动模型计算出潜艇和声诱饵的机动轨迹。而鱼雷的机动则需要通过逐步判别鱼雷的主被动声自导能否发现目标来确定,即根据主被动声呐方程来判别。这一过程中机动假设和声学假设如下:
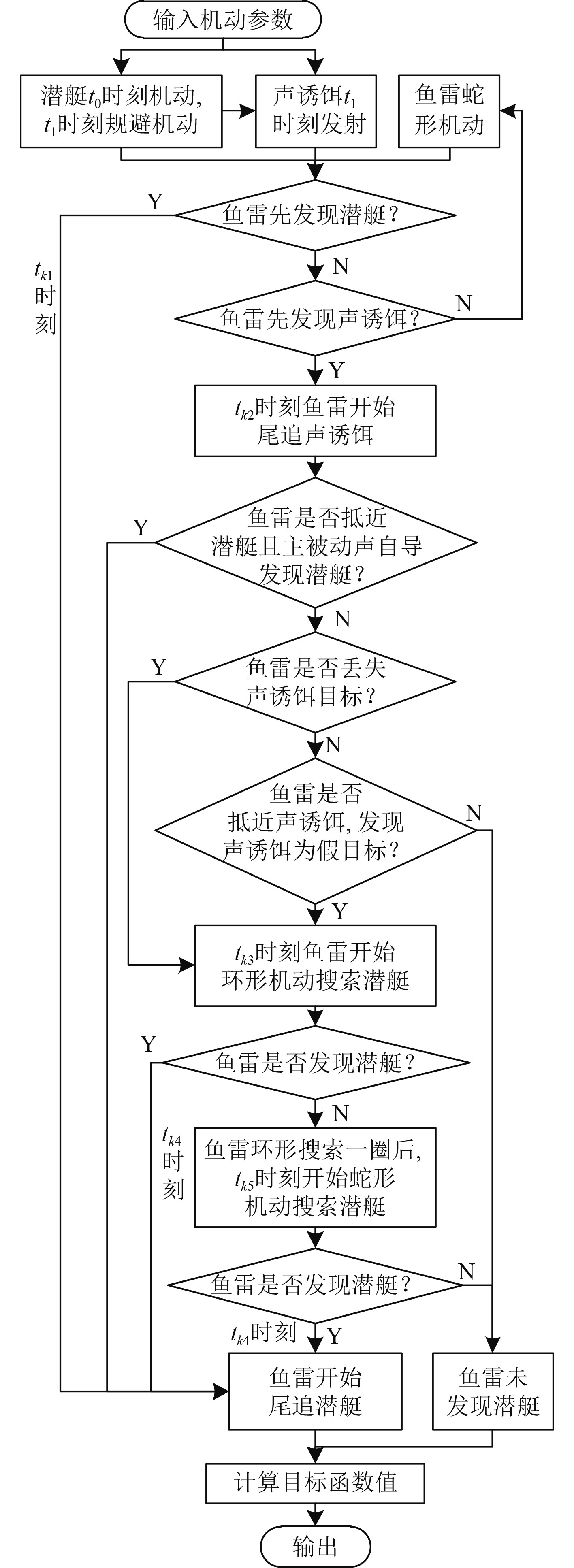
|
图 1 潜艇声诱饵防御鱼雷仿真流程 Fig. 1 Flow diagram of defending torpedo by acoustic decoy of submarine |
1)机动假设
假设仿真空间是三维空间,潜艇加速至最大航速进行规避,转向规避的转向轨迹为圆形。鱼雷搜索时进行蛇形机动、环形机动以及尾追机动[10]。目标或诱饵一旦进入鱼雷的自导作用范围,鱼雷开始尾追目标或诱饵。鱼雷丢失或识别出声诱饵目标后再搜索阶段,环形搜索一圈,鱼雷不变深机动搜索。
2)声学假设
传播损失TL采用Baker给出的表面声道经验公式计算[11]。海洋环境噪声NL服从Kundson谱[11]。潜艇反射强度TS随信号入射方向的变化规律可以近似表示为蝴蝶形[10]。潜艇辐射噪声强度采用文献[10]经验公式计算。声诱饵尾部存在±30°的盲区[7]。如果目标和诱饵同时进入鱼雷的自导作用范围,则鱼雷优先跟踪目标[7]。鱼雷的主被动声自导能否发现目标采用基于声呐方程的鱼雷主动检测模型和被动检测模型[9-10]进行判别。鱼雷接收频段内的鱼雷自噪声随深度变化[10]。
1.2 数学模型采用地理坐标系,以本艇发现鱼雷的位置为原点,x,y,z坐标轴分别对应东北天坐标系。以本艇发现鱼雷的时刻为t=0 s时刻。
| $ \begin{array}{*{20}{l}} {\max }&{d = f({t_1},{\alpha _1},{z_1},{t_2},{\alpha _2},{z_2},{\alpha _3})} \\ {{\rm{s.t.}}}& 0 \leqslant {t_i} \leqslant {t_{end}} \\ {}& - 180 \leqslant {\alpha _1} \leqslant 180 \\ {}& - 90 \leqslant {\alpha _j} \leqslant 90,j = 2,3 \\ {}& 10 \leqslant {z_i} \leqslant 300 \\ {}&{t_i},{z_i},{\alpha _k} \in Z,i = 1,2,k = 1,2,3 \text{。} \end{array} $ | (1) |
式中:d为潜艇声诱饵防御鱼雷仿真结束时潜艇与鱼雷距离。因为涉及到鱼雷的机动过程比较复杂,函数f无法用解析表达式来表达,其实现仿真流程如图1所示。输入参数
并行粒子群算法相对粒子群算法能够好地发挥多处理器计算能力,提升计算效能,为指挥决策赢得时间。并行计算的粒子群算法对潜艇声诱饵防御鱼雷数学模型进行寻优的算法流程如图2所示。
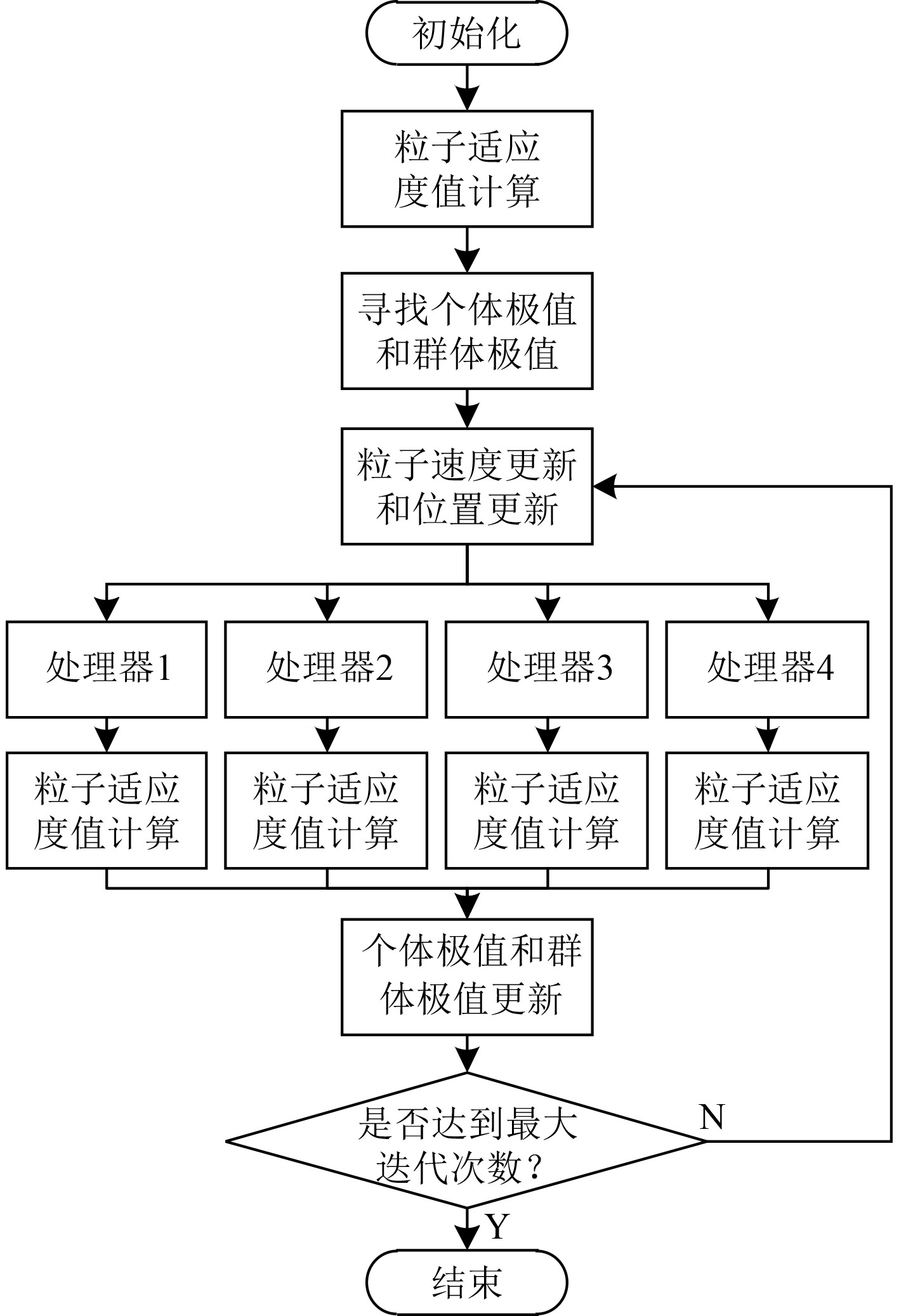
|
图 2 基于并行计算的粒子群算法流程 Fig. 2 Flow diagram of PSO algorithm based on parallel computation |
初始化指粒子速度和粒子位置初始化。设D(D=7)维空间中,由n个粒子组成的种群为
粒子适应度值计算指通过图1的仿真流程进行计算,得到每个粒子对应的式(1)的目标函数值。初始化个体极值
| $ V_i^{k + 1} = V_i^k + {c_1}{r_1}\left( {P_{ig}^k - P_i^k} \right) + {c_2}{r_2}\left( {P_{gbest}^k - P_i^k} \right)\text{,} $ | (2) |
| $ P_i^{k + 1} = P_i^k + V_i^{k + 1} \text{。}$ | (3) |
式中:
采用四线程并行计算对一次迭代过程中的多个粒子适应度值进行计算,每个线程之间相互独立,且每次迭代也独立,可以拓展到多线程并行计算。
3 仿真计算结果潜艇航向为90°,鱼雷报警舷角右舷140°,航向为40°,航深为40 m。仿真时长
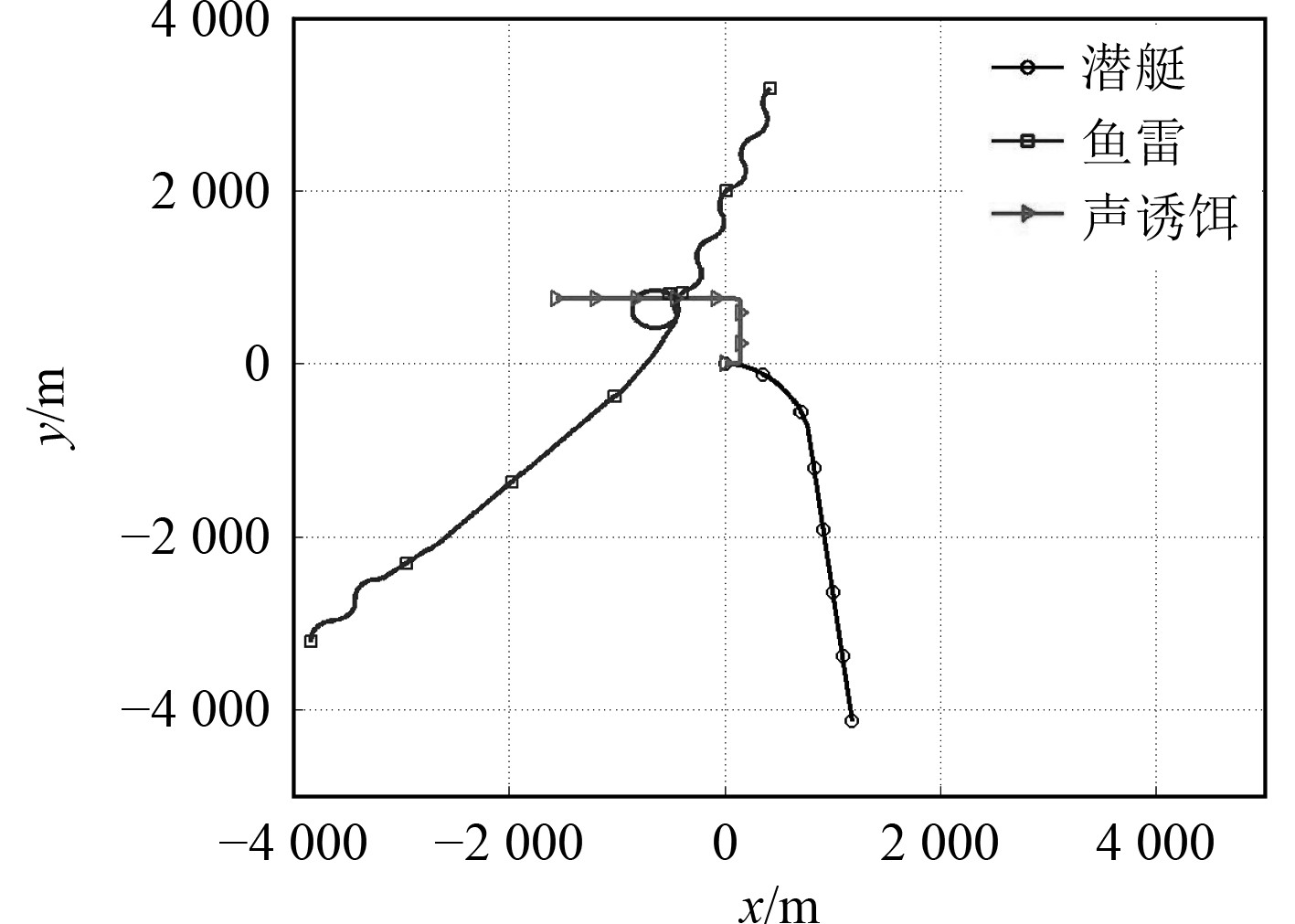
|
图 3 潜艇声诱饵防御鱼雷仿真轨迹 Fig. 3 Simulation track of defending torpedo by acoustic decoy of submarine |
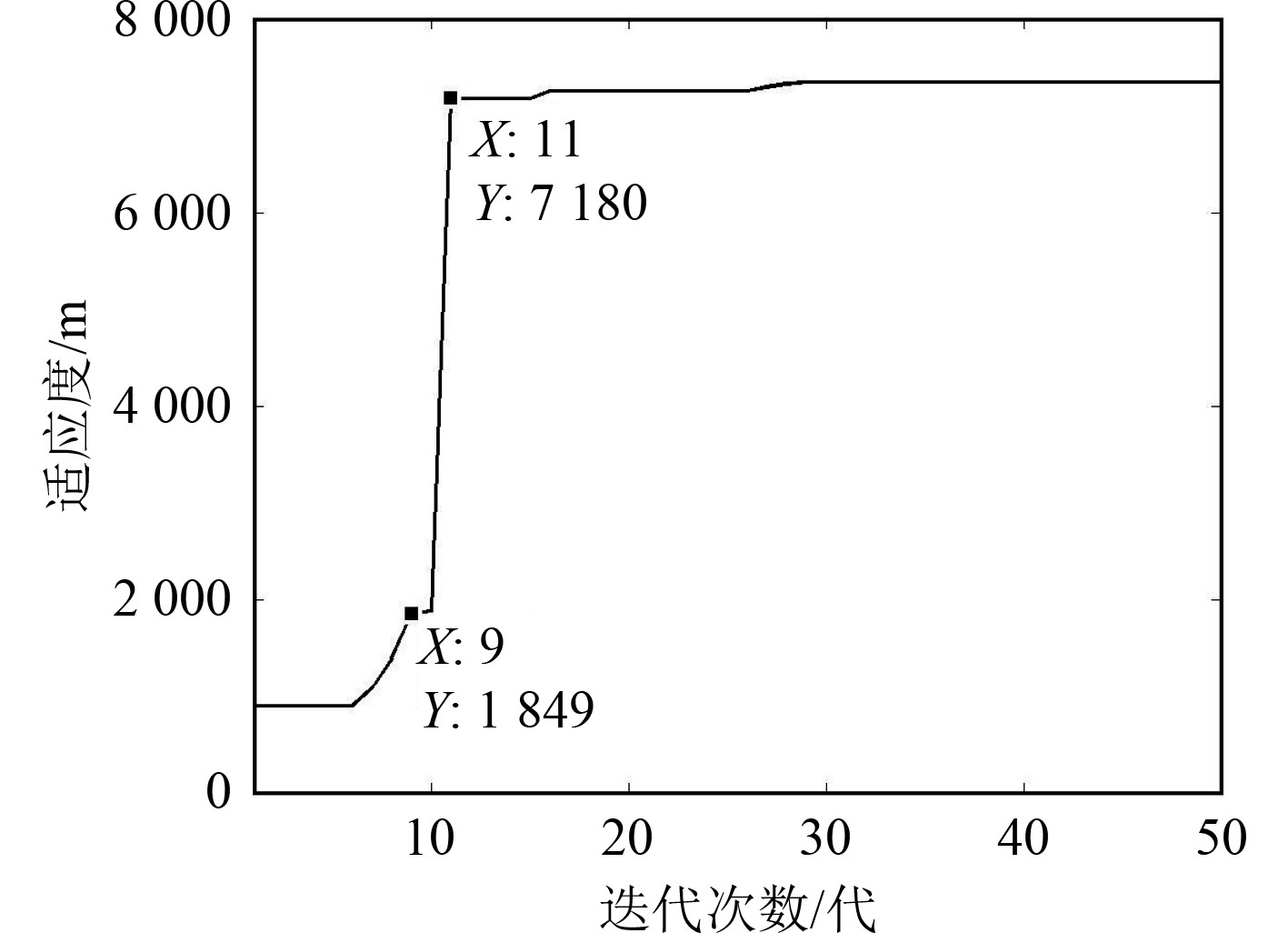
|
图 4 群体极值的适应度值 Fig. 4 Fitness of global best |
|
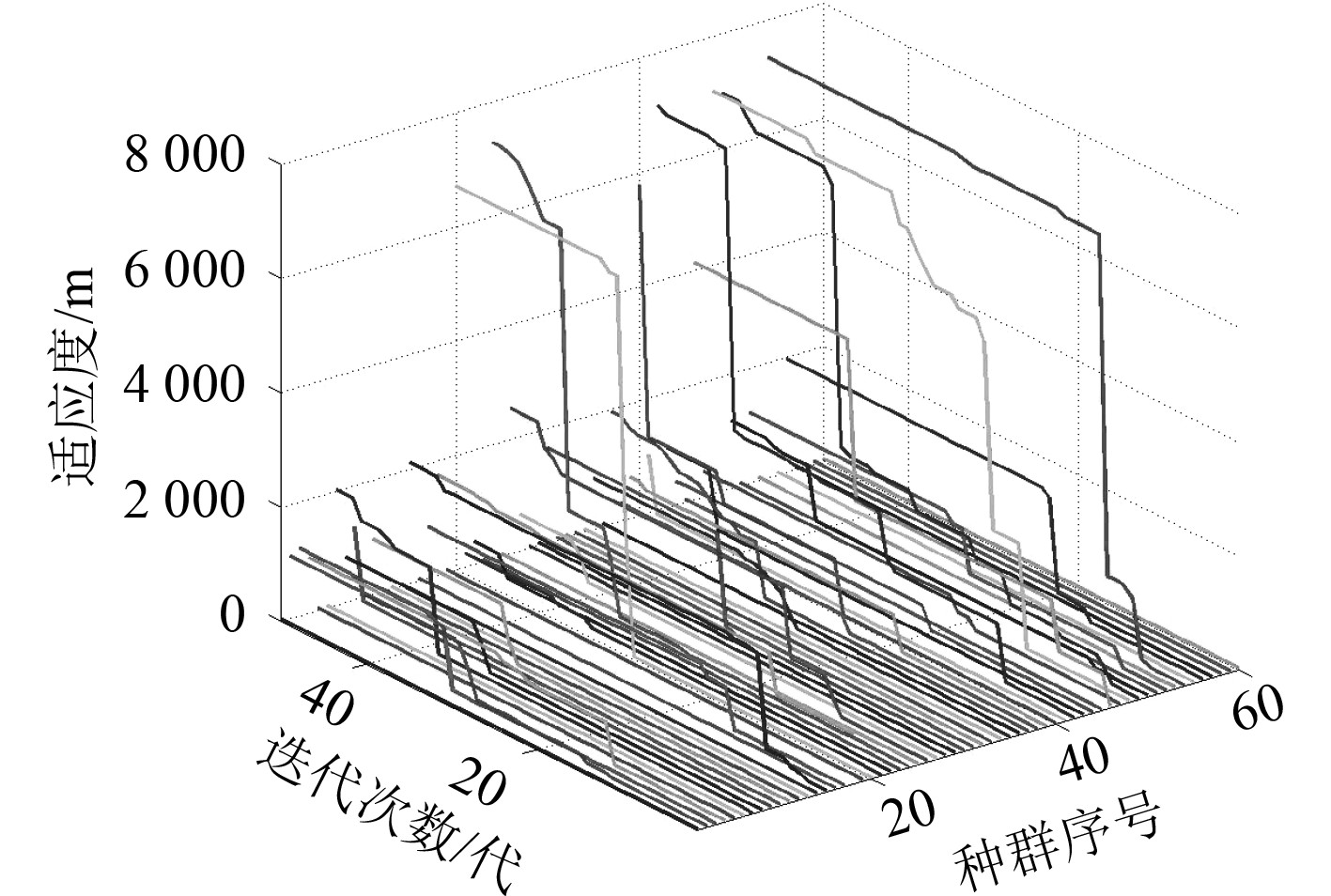
图 5 每个粒子个体极值的适应度值 Fig. 5 Fitness of personal best of each particle |
|
|
表 1 最后一次迭代粒子个体极值适应度值最大的前10个粒子 Tab.1 The first 10 particle which have the maximum fitness of personal best in the last iteration |
从表1可以看出前10个粒子个体之间仍表现出一定的差异,反映了粒子群的多样性,但是潜艇发射时机以及声诱饵发射时机、一次转向角、变深航深这4个参数基本一致。表明潜艇需要在第一时间发射声诱饵并机动规避,潜艇和声诱饵转向规避。一次转向角基本一致表明声诱饵发射后第一次转向左转90°。8个粒子声诱饵变深航深都趋于最浅航深10 m,其中有7个粒子适应度值大于4000 m。
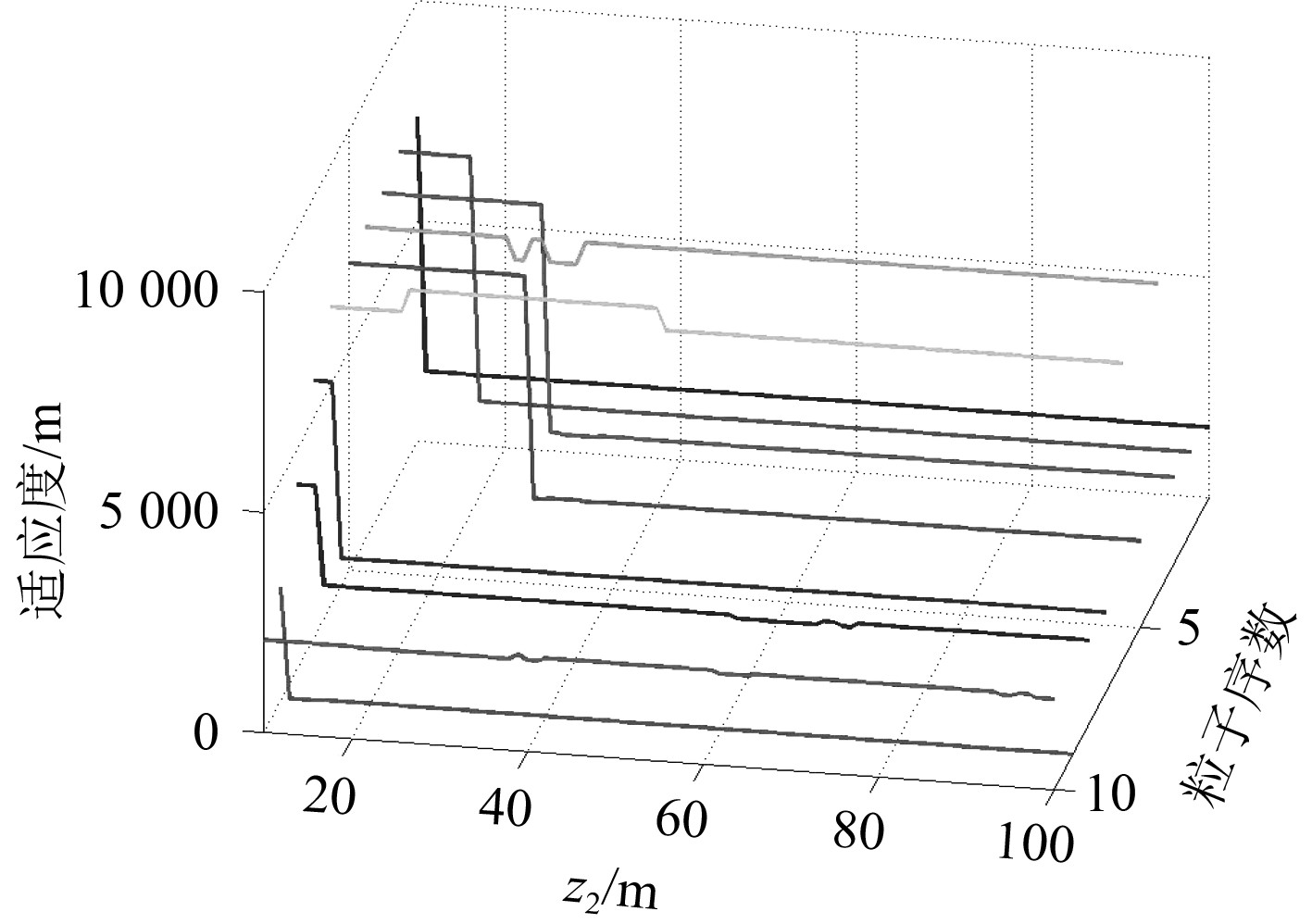
以表1中10个粒子为例进行研究声诱饵变深航深对仿真结果的影响,保持每个粒子其他参数不变,只改变声诱饵变深航深
|
图 6 前10个粒子适应度值随声诱饵变深航深变化情况 Fig. 6 The fitness of the first 10 particle changed with navigable depth of acoustic decoy |
可知,除了排名第4,6,10的粒子适应度值基本不随
|
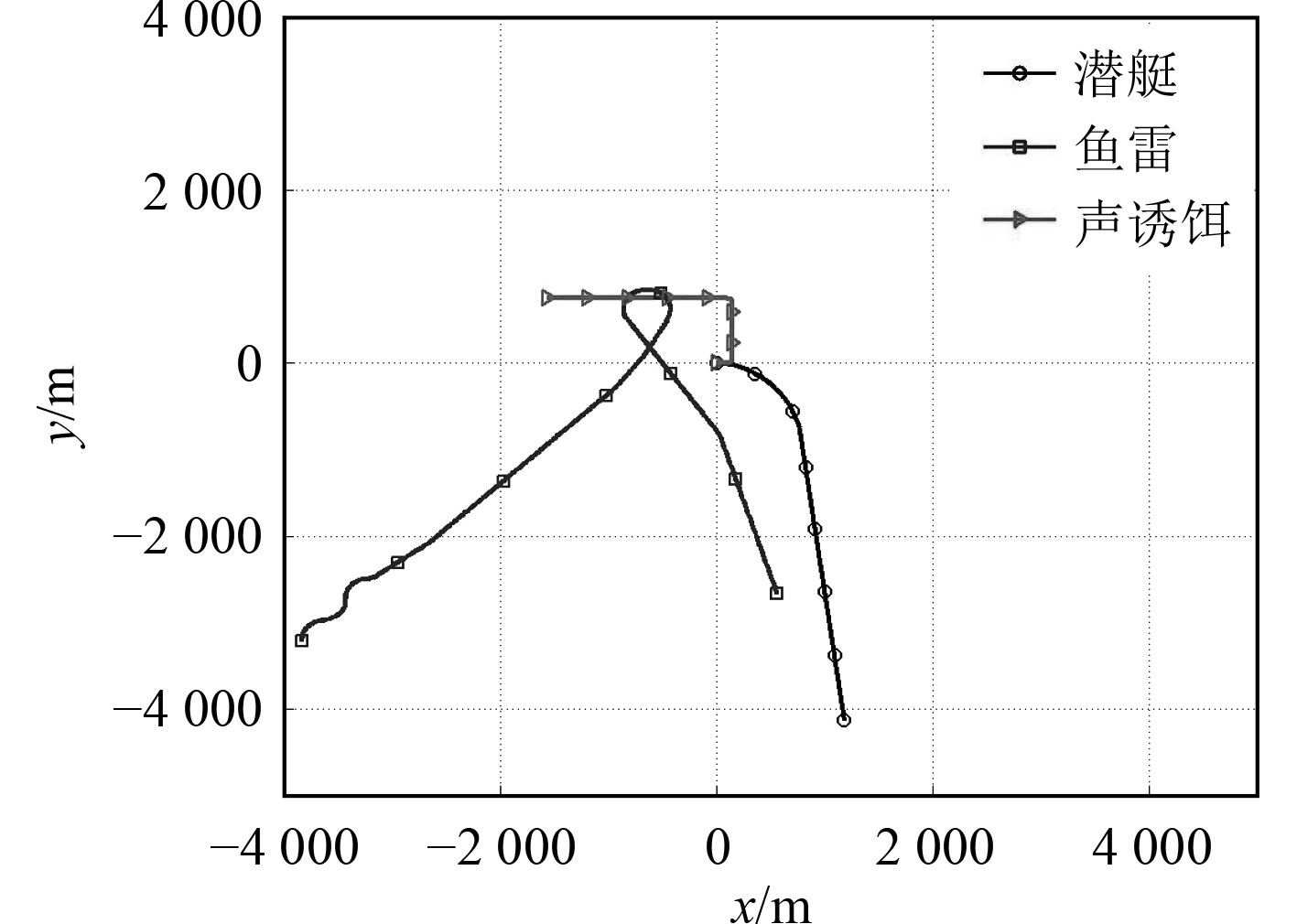
图 7 第1个粒子变深航深为11 m 时仿真轨迹 Fig. 7 Simulation track of the first particle which navigable depth of acoustic decoy was 11 m |
图中,d=1595 m,鱼雷在环形搜索阶段268 s开始尾追潜艇。鱼雷发现声诱饵后尾追声诱饵,其航行深度接近声诱饵深度,鱼雷自噪声受航行深度的影响,根据文献[10]知深度越深自噪声越小,导致鱼雷在环形搜索主动探测越容易探测到潜艇。
4 结 语采用基于并行计算的粒子群算法求解潜艇机动规避和声诱饵机动参数的方法能够避免进行海量计算,在短时间内提供潜艇防御鱼雷指挥决策的可行解。其获得的可行解有助于进一步分析各个参数对仿真模型的影响,从而判别每个参数对仿真结果的影响,进而分析总结潜艇机动规避并使用单个自航式声诱饵防御鱼雷的规律。研究发现,对于适应度值较大的前10个粒子声诱饵变深航深都趋于最浅航深10 m这个问题进行研究,发现适应度随深度增加突降,这是由于鱼雷自噪声随航行深度增加而减小,导致主动探测越容易探测到潜艇。该结论仅适用于再搜索阶段鱼雷不变深机动搜索的情况,再搜索阶段鱼雷变深机动搜索的情况需要进一步研究。此外,研究的方向是通过分别改变种群粒子数、迭代次数、粒子速度被限制的区间取值和加速度因子等方法,研究这些因素对算法的影响并进行算法改进,使得算法收敛得更快。
| [1] |
李长军, 王顺意. 潜射自航式声诱饵发射时机与初始航向模型[J]. 鱼雷技术, 2010, 18(6): 471-475. |
| [2] |
林宗祥, 周明, 门金柱. 一种求解自航式声诱饵航向的方法[J]. 舰船科学技术, 2008, 30(6): 167-168. LIN Z X, ZHOU M, MEN J Z. A method of calculating the course of mobile acoustic decoy[J]. Ship Science and Technology, 2008, 30(6): 167-168. DOI:10.3404/j.issn.1672-7649.2008.06.037 |
| [3] |
于李洋, 袁志勇. 潜艇自航式声诱饵的使用时机研究[J]. 鱼雷技术, 2006, 14(4): 59-61. |
| [4] |
侯琳, 胡波, 章桂永. 潜艇自航式声诱饵发射方向的仿真研究[J]. 计算机仿真, 2009, 26(6): 23-25. HOU L, HU B, ZHANG G Y. Simulation of launching direction of swim-out acoustic decoy for submarine[J]. Computer Simulation, 2009, 26(6): 23-25. DOI:10.3969/j.issn.1006-9348.2009.06.006 |
| [5] |
程健, 张会. 潜艇使用声抗器材防御鱼雷方案优化模型及模型求解策略[J]. 指挥控制与仿真, 2019, 41(6): 48-51. DOI:10.3969/j.issn.1673-3819.2019.06.009 |
| [6] |
李雯, 迟利华, 张会, 等. 潜艇使用自航式声诱饵防御鱼雷模型并行计算方法研究[J]. 计算机工程与科学, 2020, 42(12): 2163-2168. LI W. CHI L H, ZHANG H, et al. Research on the parallel computing method of submarine's torpedo defense model with self-propelled acoustic decoy[J]. Computer Engineering & Science, 2020, 42(12): 2163-2168. DOI:10.3969/j.issn.1007-130X.2020.12.008 |
| [7] |
陈迎春, 吴碧, 蔡旭东. 自航式声诱饵对抗声自导鱼雷的策略[J]. 舰船科学技术, 2012, 34(6): 83-86. CHEN Y C, WU B, CAI X D. Optimal strategy for swim-out acoustic decoy to countermeasure torpedo[J]. Ship Science and Technology, 2012, 34(6): 83-86. DOI:10.3404/j.issn.1672-7649.2012.06.020 |
| [8] |
彭会斌. 基于遗传算法的潜艇组合使用声诱饵防御鱼雷技术研究[J]. 指挥控制与仿真, 2018, 40(1): 52-55. DOI:10.3969/j.issn.1673-3819.2018.01.010 |
| [9] |
高学强, 杨日杰. 运用遗传算法的反鱼雷对抗优化方案研究[J]. 哈尔滨:哈尔滨工程大学学报, 2010, 31(10): 1286-1292. |
| [10] |
孟庆玉, 张静远, 宋保维. 鱼雷作战效能分析[M]. 北京: 国防工业出版社. 2003: 131−162.
|
| [11] |
刘伯胜, 黄益旺, 陈文剑, 等. 水声学原理(第三版)[M]. 北京: 科学出版社. 2019: 121−137.
|
| [12] |
史峰, 王辉, 郁磊, 等. MATLAB智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2011: 131−136.
|
 2022, Vol. 44
2022, Vol. 44
