离心泵作为船舶系统不可或缺的一部分,其在运行时起到了关键作用,进而对驱动电机的控制效果和性能等提出了很高要求[1]。电机能否正常稳定运行,直接影响到离心泵能否稳定工作,进而影响到船舶各系统[2]。因此,运用自动化技术和智能优化算法实现离心泵电机更加精确、稳定并快速的控制,提升离心泵的运行效率,具有非常重要的意义。
PID控制由于应用广泛,原理易懂,因而得到了普遍运用[3]。PID控制器参数整定优化的结果对于离心泵电机的控制效果起决定作用,然而在传统PID参数整定过程中含有复杂棘手、难度大等缺点[4],传统方式很难在复杂系统中整定出理想的最优值,致使其控制效果不佳,不能满足系统的控制要求。
现如今,随着学者们对智能算法的深入研究,众多群智能算法被引入到PID参数整定优化问题中[5]。但随着研究的深入,算法中的问题也逐步显现出来。比如PSO算法存在精度差、易陷入局部最优等问题[6]。为此,本文提出一种将蝙蝠随机移动概念引入粒子群算法中来优化PID参数的方法,在保留算法简单、易实现的基础上,算法的精度、全局搜索能力等得到了显著提高,优化后的PID控制器能更好地达到系统的控制要求,且调节时间少、稳定性强,使得离心泵电机能够更加安全稳定运行。
1 PID控制PID控制器由3部分构成,分别为比例、积分和微分等[5],一般形式下式:
| $ u(t) = {K_p}e(t) + {K_i}\int_0^t {e(\tau )} + {K_d}\frac{{{\rm{d}}e(t)}}{{{\rm{d}}t}}。$ | (1) |
式中:e(t)为系统误差;Kp,Ki,Kd分别对应PID控制器中3个部分的系数,通过调整这3个系数,找到最优值,就能够得到最好的控制成果,达到改善控制性能的目的[6]。PID的性能由这3个参数是否合理决定,所以,优化其参数具有重大意义。将式(1)转换为传递函数形式:
| $ {G_{\left( s \right)}} = \frac{{{N_{\left( s \right)}}}}{{{U_{\left( s \right)}}}} = Kp\left( {1 + \frac{1}{{{T_i}s}} + {T_d}s} \right)。$ | (2) |
式中:Ti和Td为其所对应的时间常数。
在众多的性能指标中,选用ITAE作为误差性能指标,一般形式如下式:
| $ J = \int_0^\infty {{{t}}\left| {{e_{\left( t \right)}}} \right|} {\rm{d}}t。$ | (3) |
在船舶系统中,离心泵作为一种重要设备需向系统中输送水和油等液体,用于消防、抽水、排水等系统中,它是运用离心力的原理运行的,并将电机产出的机械能转换成被甩入液体的动能和势能。离心泵大致由泵体、叶轮、泵轴、轴承、密封环等构成[7],其结构如图1所示。
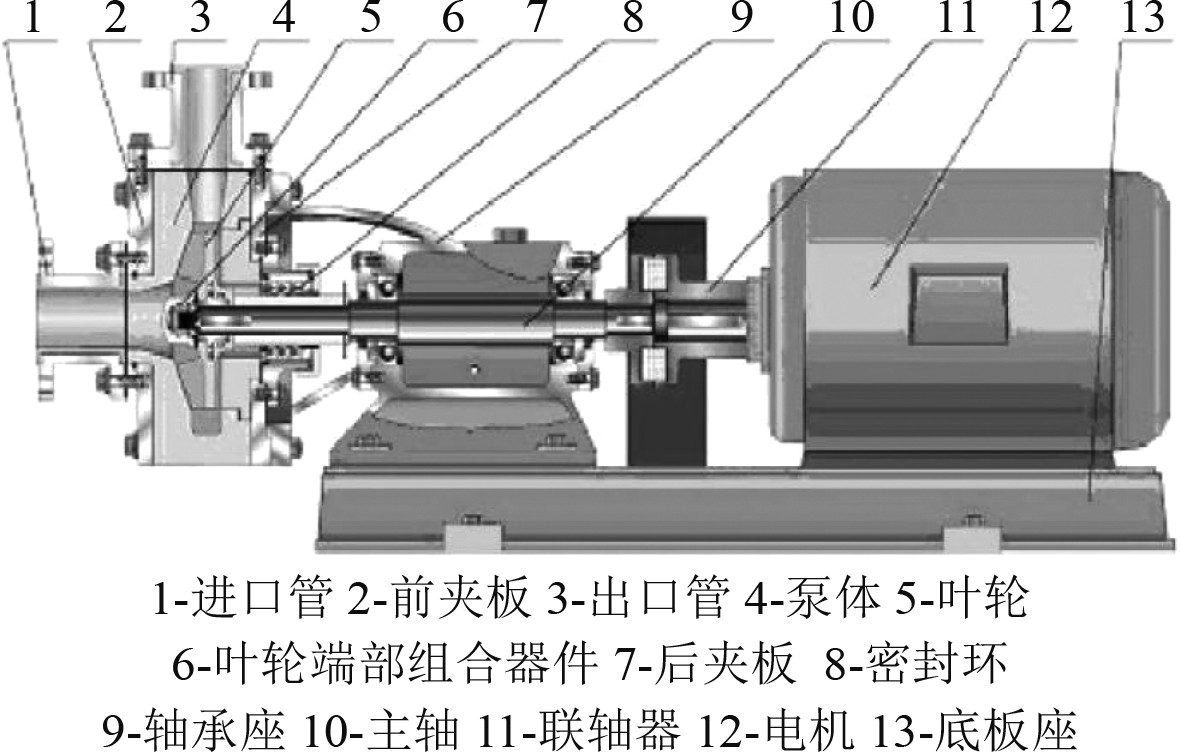
|
图 1 离心泵结构图 Fig. 1 Structure diagram of centrifugal pump |
通电后电机获得电能并驱动离心泵运转,同时又要求电机在一定的环境下稳定工作。所以正确选择驱动电机是使得离心泵效率高并稳定运行的关键,需仔细探讨其性能和可靠性等因素。在实际使用中遭遇意外情况或故障时,对驱动电机的效率、调节时间等有着很高的要求,以达到能快速启停、增减速等效果。在众多的驱动电机中,永磁直流电机特点显著,因其损耗小,运行简便,便于控制,响应速度快,易调速等特性,将其用作船用离心泵的驱动电机。
2.2 电机传递函数运用电机的机械特性和参数等,能简单并快速获取传递函数。与他励直流电机相比,永磁直流电机用永久磁体取代了励磁绕组,其电路图如图2所示。电磁转矩
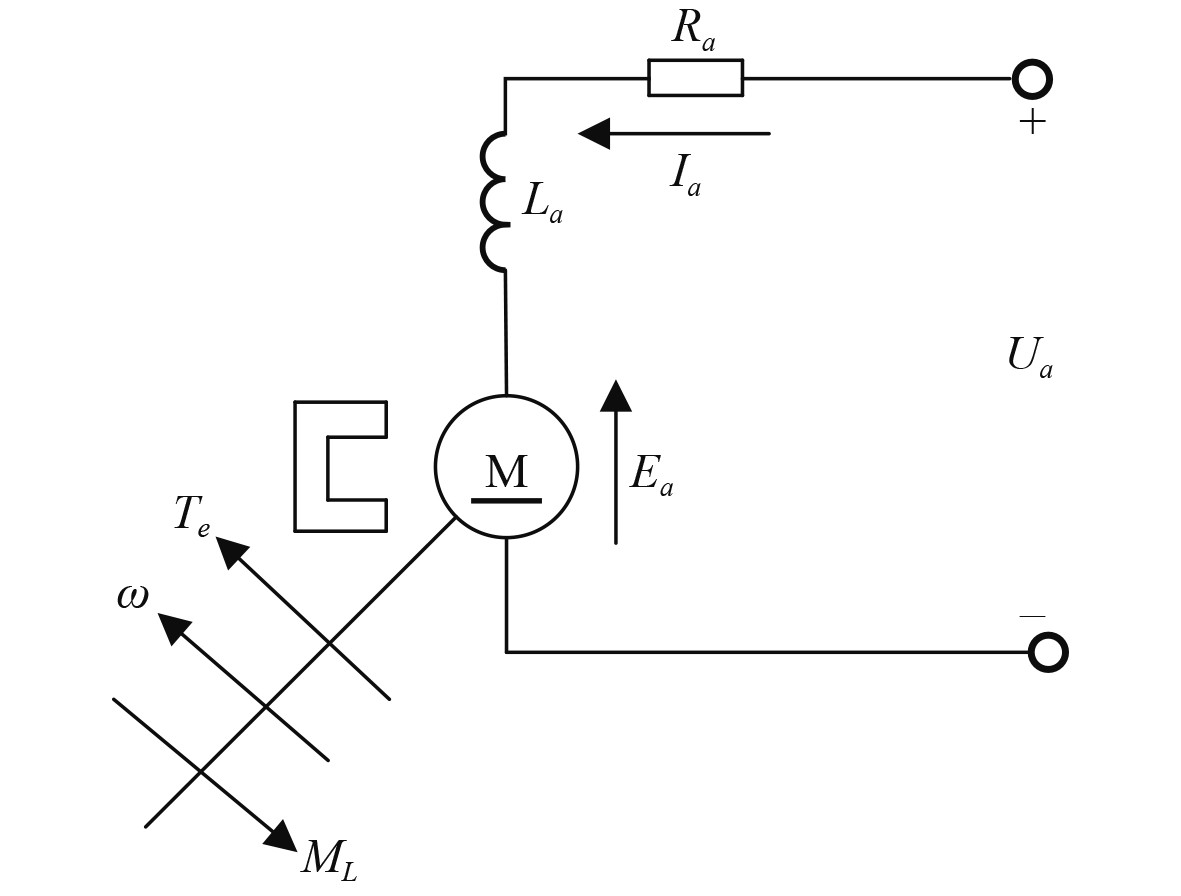
|
图 2 永磁直流电机等效电路图 Fig. 2 Equivalent circuit diagram of permanent magnet DC motor |
永磁直流电机[8]转速n发生变化时,电磁转矩方程为:
| $ {T_e} = {T_2} + J\frac{{{{\rm{d}}\omega }}}{{{{\rm{d}}t}}} + {M_L}\omega 。$ | (4) |
式中:
负载阻转矩方程为:
| $ {M_l} = {C_m} \times {I_a}。$ | (5) |
式中:
电枢电压方程为:
| $ {U_a} = {E_a} + {I_d}{R_a} + {L_a}\frac{{{\rm{d}}{l_a}}}{{{{\rm{d}}t}}} + {{\Delta }}{{{U}}_{{b}}} 。$ | (6) |
式中:
令
| $ {G_{\left( {\text{s}} \right)}} = \frac{{{K_{\text{e}}}}}{{J{L_a}{s^2} + J{R_a}s + {K_{\text{e}}}{C_{\text{m}}}}}。$ | (7) |
采用某型号永磁直流电机,将其参数代入式(7)中,可得传递函数为:
| $ {G_{\left( {\text{s}} \right)}} = \frac{{68}}{{{s^2} + 4.5s + 1}}。$ | (8) |
此系统为典型的2阶系统,对永磁直流电机控制系统的传递函数在Matlab软件中仿真,其在Simulink环境下其仿真图如图3所示。
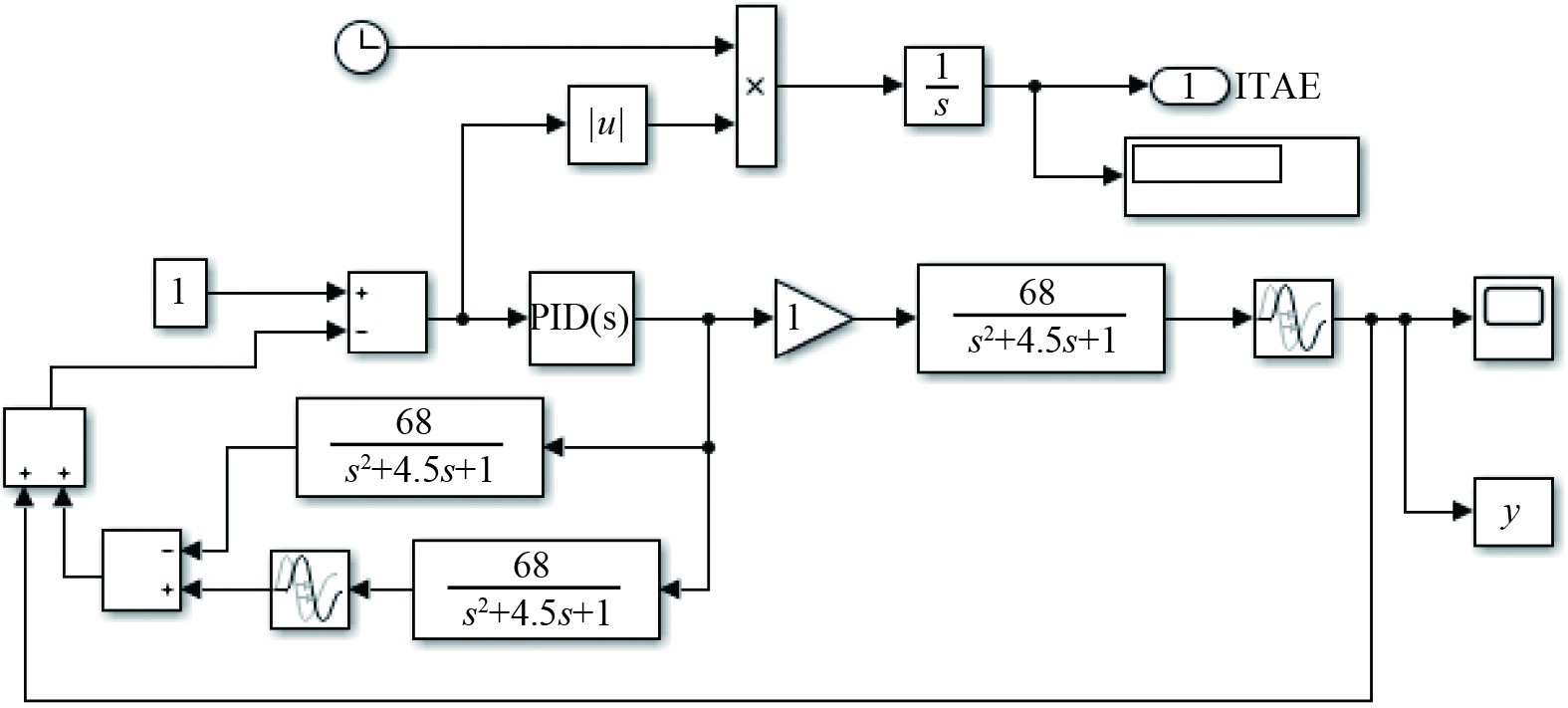
|
图 3 Simulink环境下PID仿真图 Fig. 3 PID simulation diagram under Simulink environment |
粒子群算法(简称PSO)主要是运用粒子间的彼此配合,共享全局最优位置来搜寻待优化问题的最优解。该算法以所有个体的位置作为待优化问题的解,用适应度函数来计算粒子的适应值,通过将所有个体的适应值进行对照,判断粒子位置的好与坏。当所有个体在待优化问题解的空间中移动时,每次迭代中粒子的移动方向和距离由一个速度变量所决定。经过不断更新个体位置和最优位置,粒子在搜索空间中逐渐逼近最优位置[10]。
粒子在搜索空间中的速度和位置由式(9)和式(10)来确定:
| $ {v_{t + 1}} = \omega {v_t} + {c_1}{r_1}\left( {{P_{prime}} - {x_t}} \right) + {c_2}{r_2}\left( {{G_{prime}} - {x_t}} \right),$ | (9) |
| $ {x_{t + 1}} = {x_t} + {v_{t + 1}}。$ | (10) |
式中:x为粒子位置,v为粒子速度,C为学习因子;
运用PSO优化PID参数的大致流程如图4所示。
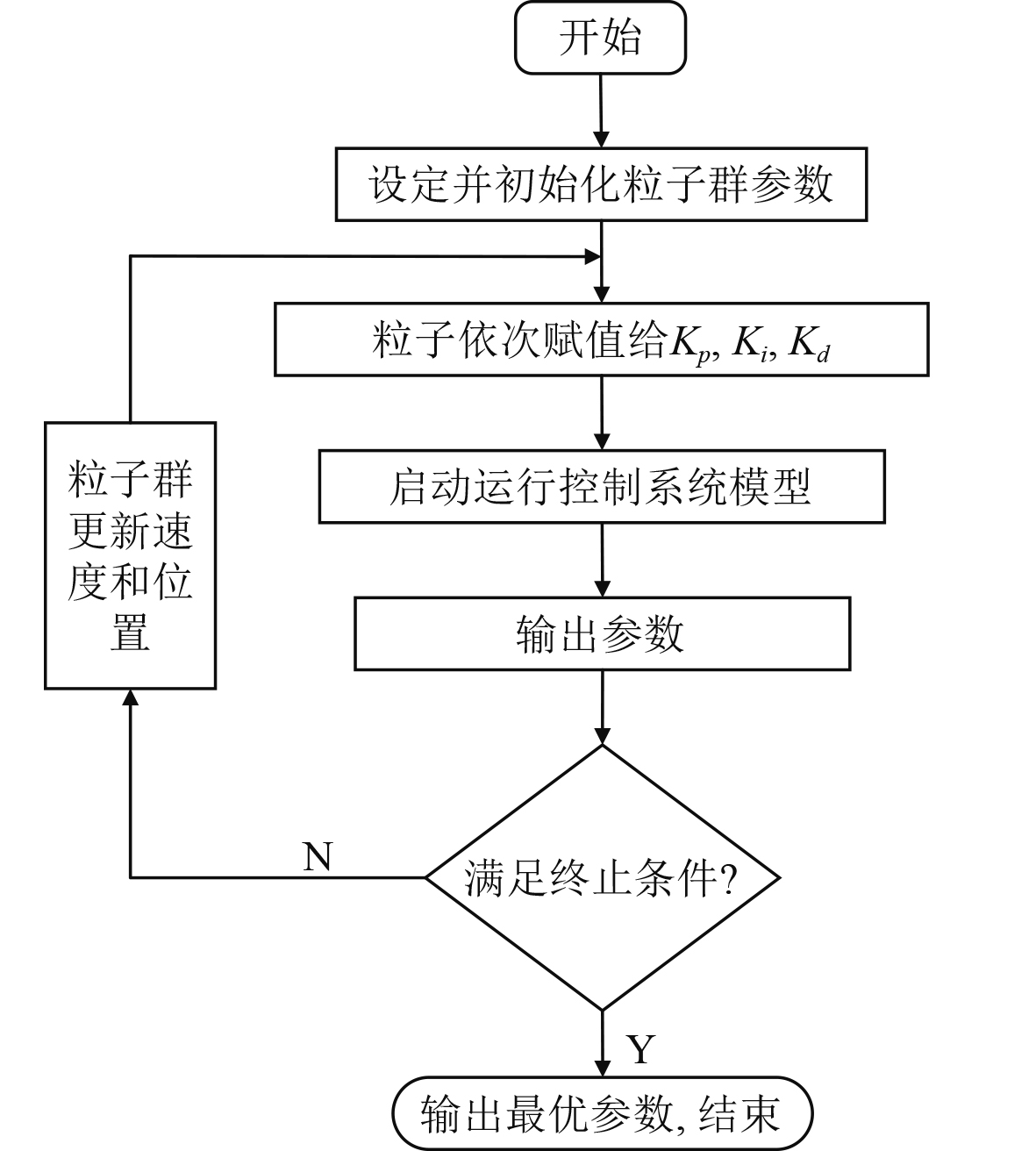
|
图 4 PSO优化PID过程图 Fig. 4 PSO Optimization PID process diagram |
蝙蝠算法[12](简称BA)是利用蝙蝠觅食时回声定位特性的一种群智能算法。其中,蝙蝠靠随机改变其速度、位置和超声波频率等来搜寻猎物。当它靠近猎物时,蝙蝠发出的超声波频率会加强,与此同时响度也会降低,表明距离猎物越来越近。效仿蝙蝠搜索猎物过程,运用式(11)更新其频率,运用式(12)更新其速度,运用式(13)更新其位置。
| $ {f_i} = {f_{\min}} + \left( {{f_{\max}} - {f_{\min}}} \right) \xi,$ | (11) |
| $ {\nu _i}^{t + 1} = {\nu _i}^t + \left( {{x_{{\rm{prime}}}} - {x_i}^t} \right){f_i},$ | (12) |
| $ {x_i}^{t + 1} = {x_i}^t + {\nu _i}^{t + 1}。$ | (13) |
式中:
当确定了当下最优值后,每只蝙蝠按照式(14)做随机移动,进而产生一组新解。
| $ {x_n} = {x_o} + \tau {A^t}。$ | (14) |
式中:
对于PSO存在容易陷入局部最优等问题,提出混合粒子群算法(简称HPSO)。将蝙蝠算法融入到PSO算法中,增强粒子多样性,并加强局部搜索能力。将蝙蝠算法里种群中的每个个体都可以描述成PSO中的粒子进行搜索,将算法里蝙蝠随机移动的概念引入到PSO中,对其位置进行更新,此方法可增强粒子位置的多样性。位置更新公式如下式:
| $ \begin{split} & {\nu _i}^{t + 1} = \omega {v_i}^t + \omega \left( {{P_{prime}} - {x_i}^t} \right){f_i} + {c_1}{r_1}\times \\ & \left( {{P_{prime}} - {x_0}^t} \right) + {c_2}{r_2}\left( {{G_{prime}} - {x_0}^t} \right),\end{split} $ | (15) |
| $ {y_i}^{_{t + 1}} = {x_i}^{_{t + 1}}{x_0} + \tau {A^t} + {v_i}^{_{t + 1}}。$ | (16) |
式中:
运用式(15)和式(16)进行反复迭代,通过反复更新粒子的位置,将其产生的新位置和目前的最优位置进行对比,找出最优解继续迭代,直至找出全局最优解,进而找到最佳参数值[13]。
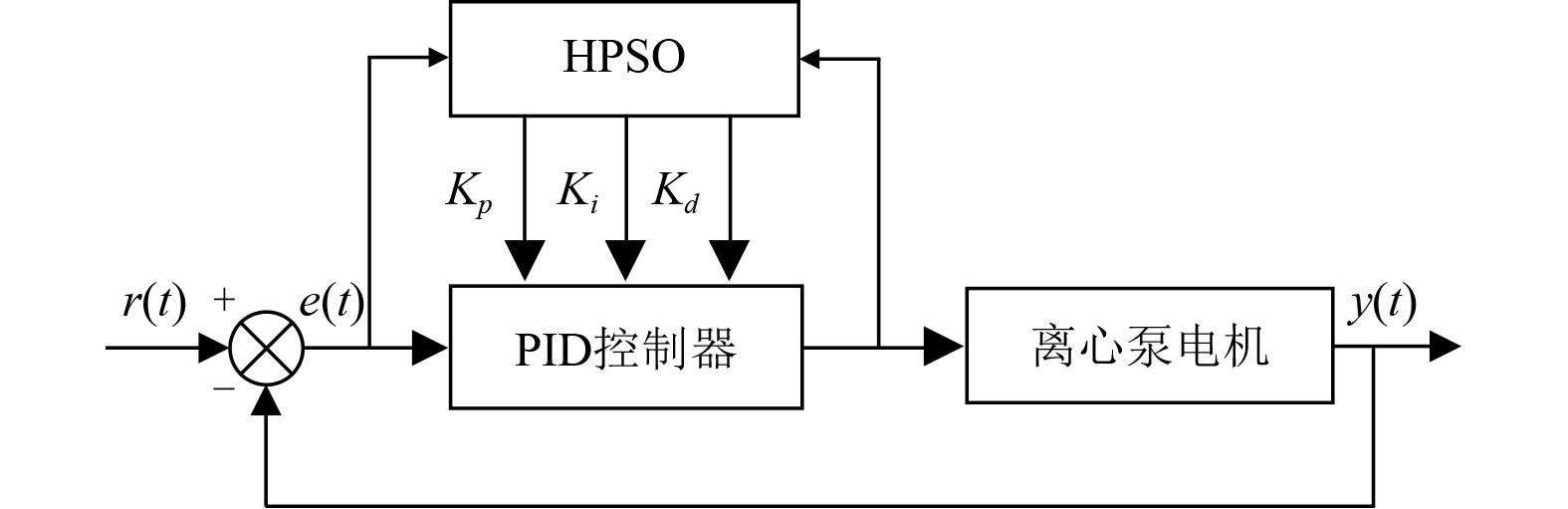
运用HPSO优化其参数的结构图如图5所示,其大致流程如下[14]:
|
图 5 HPSO整定PID参数控制图 Fig. 5 HPSO tuning PID parameter control diagram |
步骤1 初始化参数。拟定粒子数目,Kp,Ki,Kd和惯性权重的范围,学习因子的值,音量参数值,设定最大迭代次数maxIter,然后将种群中所有个体的位置和速度初始化。
步骤2 调用sim函数。把所有粒子的位置分量的值各自赋给Kp,Ki,Kd,启动系统仿真模型,得到性能指标,并输出每个粒子对应的适应值。
步骤3 对粒子群的运动状态进行更新。运用式(8)重新更换其速度,运用式(9)重新更换其位置,判断其速度和位置是否越过了既定区域,若其越过,则用范围限值替换当前的速度或位置。
步骤4 对于每个个体,把它的适应值和所有群体所经过的最佳位置
步骤5 对于每个个体,把它的适应值和此粒子所经过的最佳位置
步骤6 引入BA算法中随机移动理念,运用式(15)和式(16)计算下一代的位置,更新
步骤7 判别其有没有达到结束要求。要是已达到,则输出最佳参数,即PID参数的最佳组合,要是没有达到,返回步骤3重新执行。
4 仿真结果与对比分析分别选用HPSO,PSO和传统方法对系统进行PID控制器的参数优化。假设粒子数nop=30,迭代次数的最高值maxIter为100次,Kp,Ki,Kd位置搜索范围为[-10,10],学习因子取值皆为2,惯性权重从0.9降低至0.2,音量参数A为0.1,
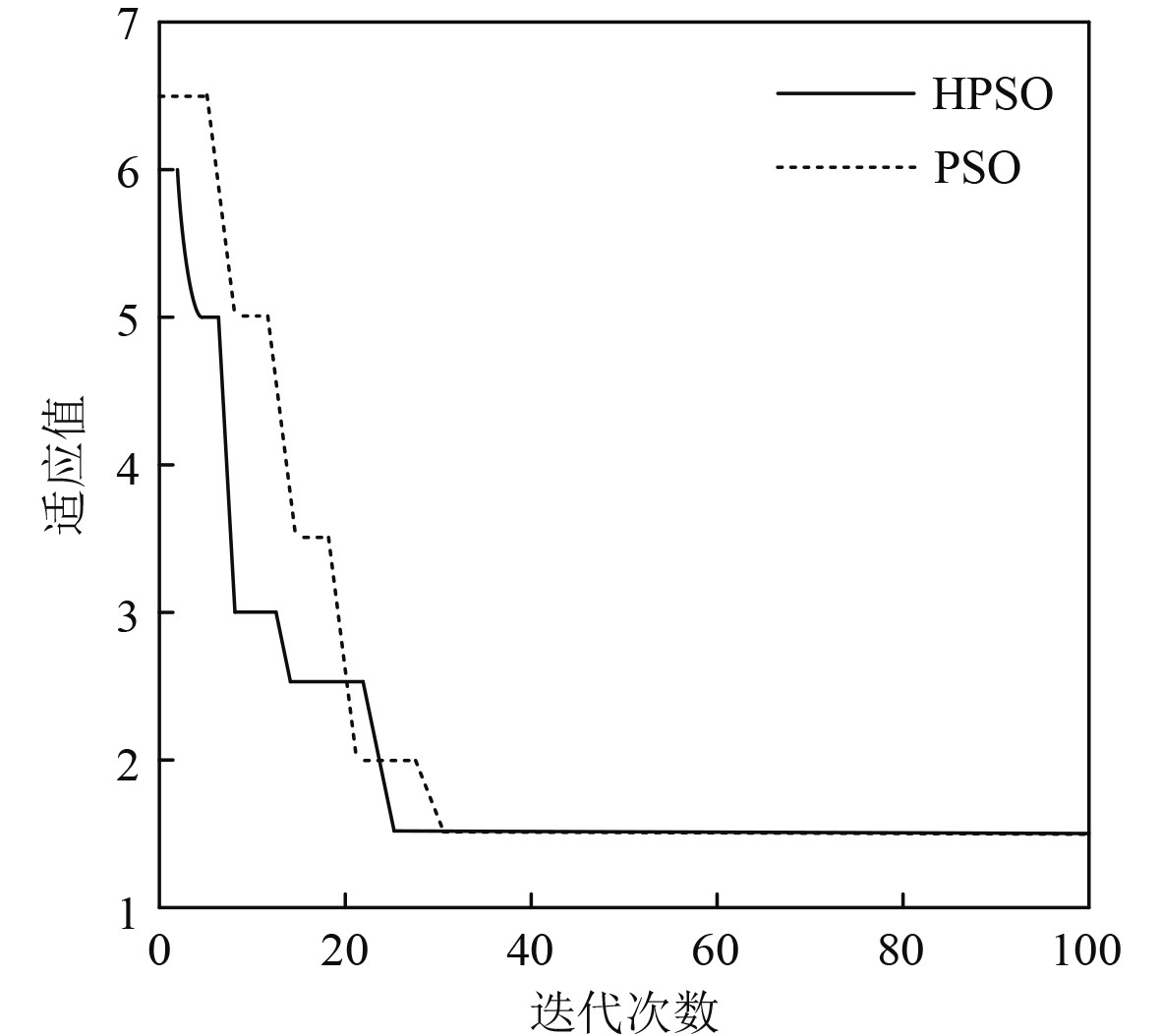
在图3的仿真模型中,其输入为单位阶跃信号,仿真时长设为10 s,采样时长dt=0.001 s。多次迭代后其适应值收敛图如图6所示,输出其各参数如表1所示。
|
图 6 适应值收敛曲线 Fig. 6 fitness convergence curve |
|
|
表 1 PID整定优化结果 Tab.1 PID tuning optimization results |
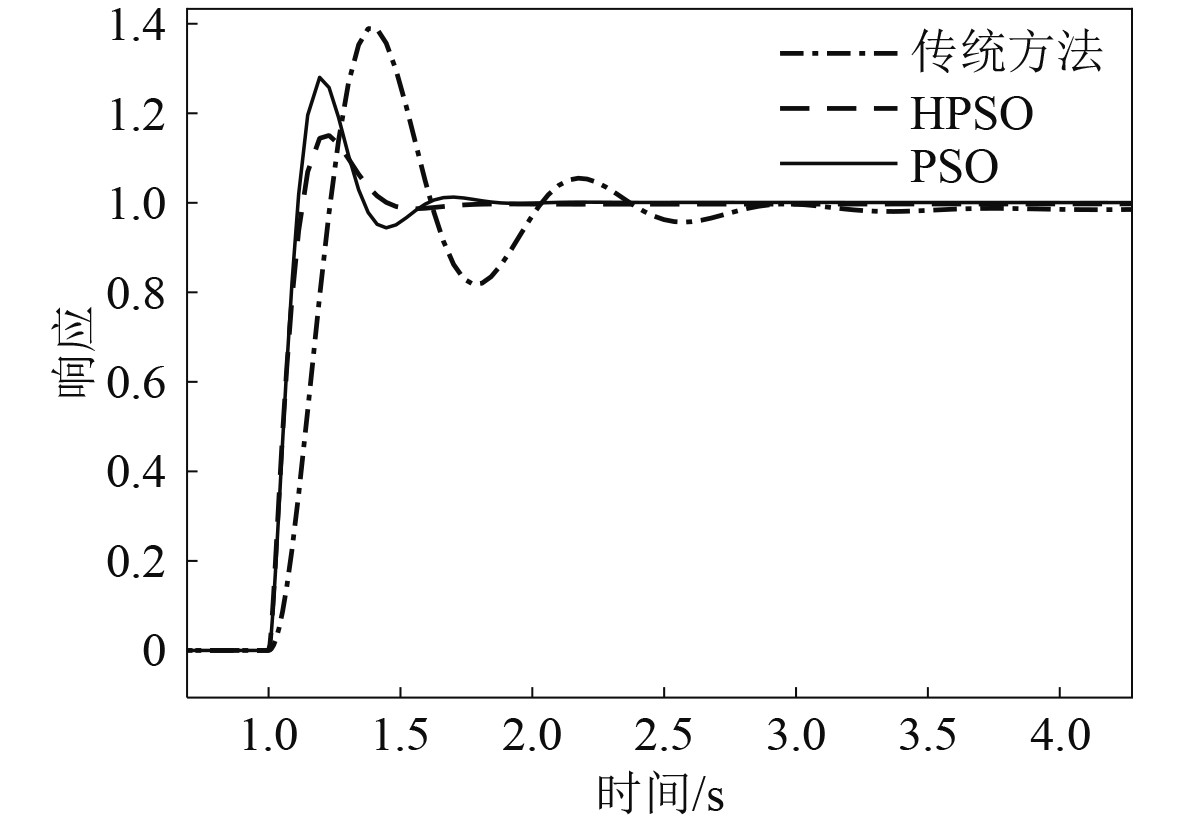
将3种方法优化所得的参数值代入离心泵电机控制系统的PID控制器中,并在Matlab中运行,得出响应曲线如图7所示。
|
图 7 系统阶跃响应输出曲线 Fig. 7 System step response output curve |
由图6可知,随着迭代次数的增加,HPSO在迭代次数为25次时适应值得到了收敛并得到了较高的精度,而PSO迭代到31次时适应值得到了收敛,因此HPSO展现出了收敛速度快、精度高等优势。由图7和表1可知,标准PSO的上升时间短,进而导致PSO的响应速度快于HPSO算法,但在超调量、稳态误差等方面HPSO明显更少。
HPSO到达稳定所用的调节时间为1.81 s,优于PSO稳定的调节时间2.09 s和传统方法的3.54 s,因此系统的调节速度更快,能很快达到稳定状态。经过HPSO优化的PID最佳参数,使其选出的3个K值恰当,能够很好将调节时间和超调量等优化到尽可能少,使得系统能得到良好的控制效果,因而证明此方法的可行性。
5 结 语本文以船舶离心泵电机为研究对象,常规PID控制存在稳定性能差、控制精度低等问题,提出运用HPSO优化PID参数的方法,并验证了引入蝙蝠随机移动概念后的HPSO算法通过增强粒子多样性能改善PSO易陷入局部最优等缺点的可行性。通过对比3种方法参数整定优化的结果,在控制效果、调节时间、性能指标和稳定性等方面,HPSO算法比其他2种方法效果更好,显著提高了系统的稳定状态,有效提升了离心泵电机控制系统性能和运行稳定性。
| [1] |
王凯. 电气设备在船舶中的应用分析[J]. 科技创新与应 用, 2017(7): 131-132. |
| [2] |
宋志鹏, 陈国华. 离心泵电机振动原因分析与处理[J]. 化工管理, 2018(28): 143. DOI:10.3969/j.issn.1008-4800.2018.28.090 |
| [3] |
ZHOU Jian-xin, ZHAO, SONG Ding-li, et al. PID neural network decoupling control based on improved particle swarm optimization[J]. Machine Tool & Hydraulics, 2018, 46(24): 74-79. |
| [4] |
赵广元, 王超. 基于人群搜索算法的直流电机优化设计[J]. 舰船电子工程, 2019, 39(10): 242-246. DOI:10.3969/j.issn.1672-9730.2019.10.054 |
| [5] |
李书霞. 改进群智能算法及其在PID控制器参数整定中的应用[D]. 鞍山: 辽宁科技大学, 2016.
|
| [6] |
张继荣, 张天. 基于改进粒子群算法的PID控制参数优化[J]. 计算机工程与设计, 2020, 41(4): 1035-1040. |
| [7] |
童大鹏, 田野, 任荣社. 船用离心泵典型故障与排除[J]. 中国修船, 2013, 26(5): 48-50. DOI:10.3969/j.issn.1001-8328.2013.05.016 |
| [8] |
陈金涛, 辜承林. 基于遗传算法的永磁直流电机优化设计[J]. 微电机(伺服技术), 2006, 4(8): 17−20+77.
|
| [9] |
施云. 基于模糊PID控制的直流电机控制算法仿真分析[J]. 电子制作, 2020(13): 6-9. DOI:10.3969/j.issn.1006-5059.2020.13.002 |
| [10] |
周斌. 粒子群优化PID的舰船电动机控制系统[J]. 舰船科学技术, 2019, 41(16): 112-114. ZHOU Bin. Ship motor control system based on particle swarm optimization PID[J]. Ship Science and Technology, 2019, 41(16): 112-114. |
| [11] |
姬鹏飞, 侯凡博, 杜毅. 基于混合粒子群算法的注塑机电液伺服系统控制研究[J]. 机床与液压, 2020, 48(16): 132-135. JI Peng-fei, HOU Fan-bo, DU Yi. Research on the control of injection molding machine electro-hydraulic servo system based on hybrid particle Swarm optimization[J]. Machine Tool & Hydraulics, 2020, 48(16): 132-135. DOI:10.3969/j.issn.1001-3881.2020.16.027 |
| [12] |
吕磊, 章国宝, 黄永明. 基于蝙蝠算法的PID参数整定[J]. 控制工程, 2017, 24(3): 548-553. LV Lei, ZHANG Guo-bao, HUANG Yong-ming. PID parameter tuning based on bat algorithm[J]. Control Engineering, 2017, 24(3): 548-553. DOI:10.14107/j.cnki.kzgc.150617 |
| [13] |
丁芳, 周扬, 吴婷娜, 等. 基于PSO-BA算法的飞机地面空调系统仿真[J]. 中国民航大学学报, 2020, 38(2): 28-32. DING Fang, ZHOU Yang, WU Ting-na, et al. Simulation of aircraft ground air conditioning system based on pso-ba algorithm[J]. Journal of China Civil Aviation University, 2020, 38(2): 28-32. DOI:10.3969/j.issn.1674-5590.2020.02.006 |
| [14] |
贺争亮. 基于改进猫群算法的PID参数整定及其在直流 电机控制中应用研究[D]. 南昌: 南昌大学, 2020.
|
 2022, Vol. 44
2022, Vol. 44
