0 引　言

船舶稳性设计一直是船舶行业中的重要研究方向，同时也是较复杂的研究课题。稳性设计是指船舶在装载一定载荷的条件下，能够抵抗外界复杂干扰作用力，产生船体的恢复力矩，从而实现船舶漂浮于水面并保持相对平衡的设计。船舶稳性直接决定了船舶在海浪、海风条件下的航行安全性，是检验船舶设计质量的重要指标。

近年来，随着我国对海上资源开发的不断深入，海上大型船舶的需求猛增，如大型海上风电吊装船、起重船等，这些大型船舶一方面保障了海上工程的施工，产生大量的经济效益；另一方面，大型船舶的作业环境非常复杂，船舶可靠性和安全性面临着一系列的挑战。

本文重点研究大型船舶在波浪条件下的稳定问题，建立外界干扰作用力和大型船舶的运动模型，对船舶在波浪条件下的稳性问题进行详细校核，有助于改善现有船舶的稳性设计。

1 风浪条件下的船舶稳性干扰作用力分析

大型船舶在工作过程中，海浪、海风作用力是主要的外界干扰因素，针对海浪干扰作用力进行数学建模，建立海浪的波面方程为：

$f\left( t \right) = {\theta _m} - B\sin \left( {{w_o}t + {\varphi} _{0}} \right) \text{。}$

式中： $B$ 为海浪的高度（波峰到波谷的距离）； ${w_o}$ 为海浪的频率值； ${\varphi _0}$ 为海浪的初始相位角； ${\theta _m}$ 为最大波面倾角，用下式计算：

${\theta _m} = \frac{{2\pi \zeta }}{\lambda }。$

海浪的波形函数为：

$\varGamma \left( t \right) = \sum\limits_{i = 1}^n {} B\cos \left( {{w_o}t + {\varphi _0} + {\varepsilon _i}} \right) \text{。}$

其中：n为周期内的海浪波数； ${\varepsilon _i}$ 为补偿相位角。

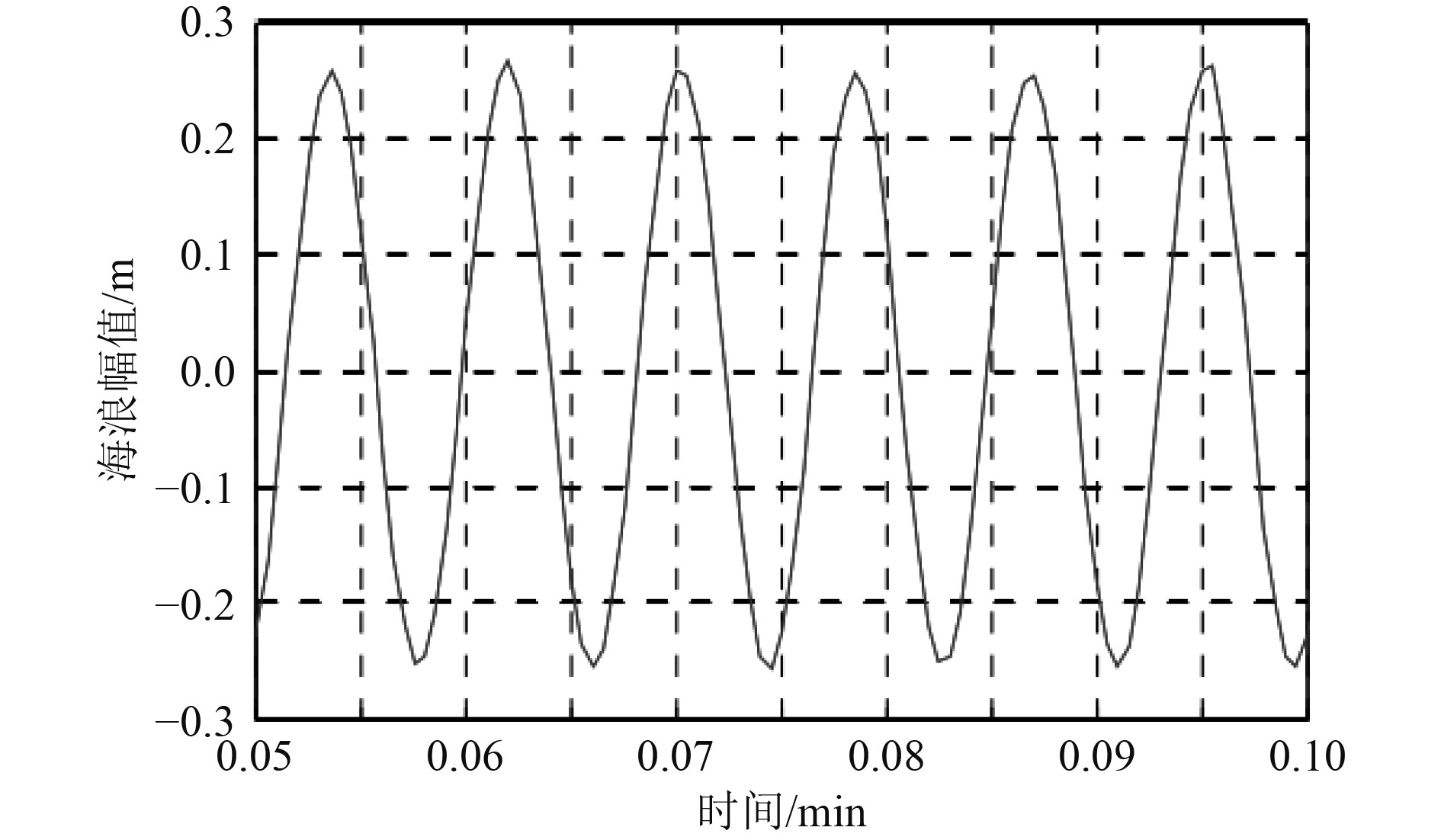
船舶在与海浪的相互作用力下，海浪的波面倾角^[1]呈周期性变化，采集0.1 min内的波面函数曲线如图1所示。

建立大型船舶的海浪干扰力方程为：

$F(t) = \sum\limits_{i = 1}^n {{{\rm{m}}} {a_x}\cos \left( {{w_0}t + {\varepsilon _i}} \right) + } \sum\limits_{i = 1}^n {{{\rm{m}}} {a_y}\cos \left( {{w_0}t + {\varepsilon _i}} \right)} \text{。}$

式中： ${a_x}$ 和 ${a_y}$ 分别为船舶前进方向和船舷侧方向的加速度；m为船舶质量。

建立海风的干扰作用力为；

${F_f}(t) = \sum\limits_{t = 1}^n {\left( {\dfrac{{\sqrt {2s(t)\Delta w} \sin (wt + \theta )}}{2}} \right)} \text{。}$

式中： $w$ 为海风的频率； $s(t)$ 为海风的能谱密度函数； $\theta$ 为来风角度。

2 大型船舶装载和风浪条件下的运动建模

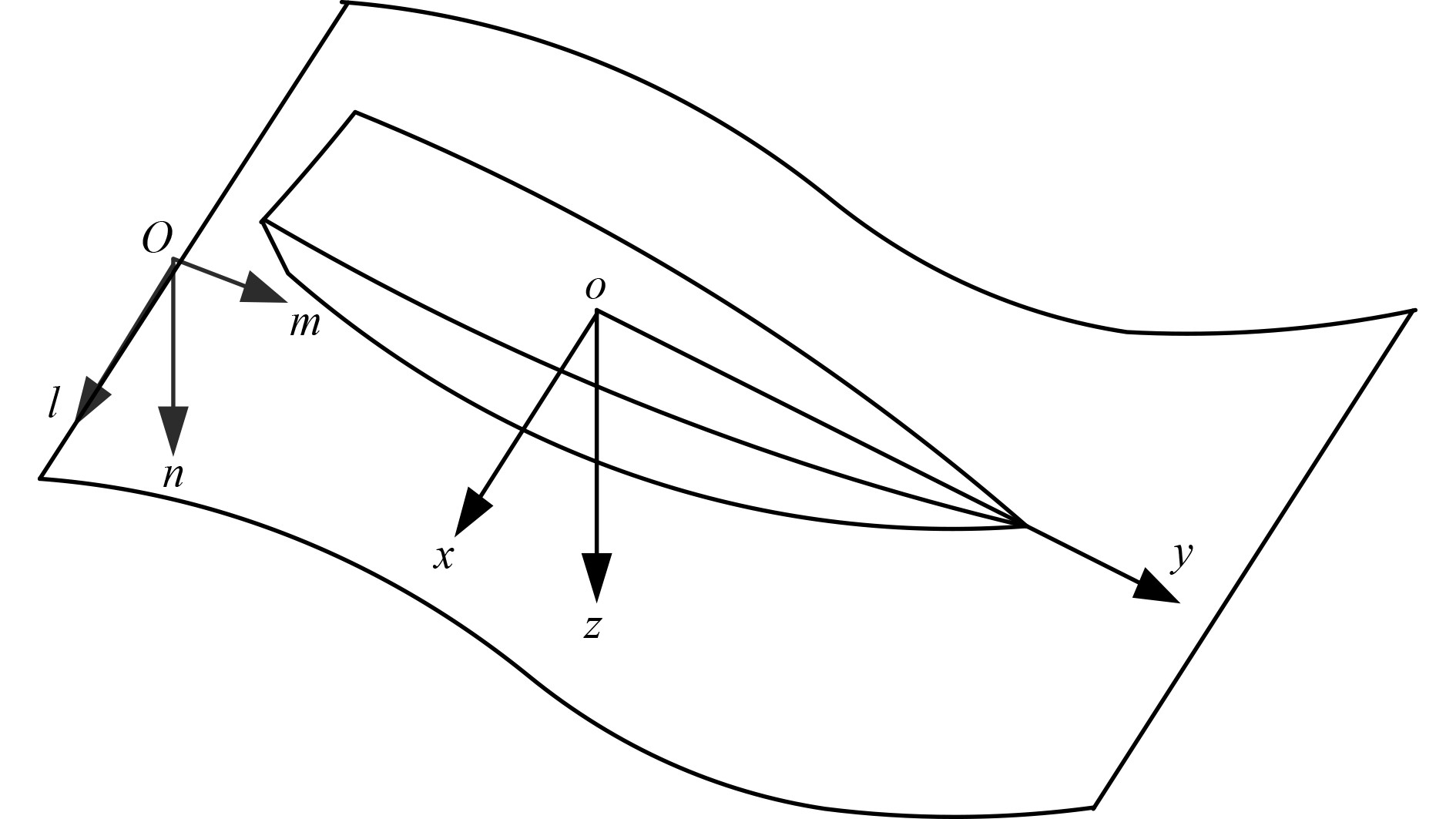
大型船舶的装载和风浪条件下运动建模是进行稳性设计的关键^[2]，建立大型船舶的运动坐标系如图2所示。

可知，运动坐标系O-XYZ的OX方向指向船侧方向，OY指向船舶前进方向，OZ指向地心。静止坐标系为o-lmn，船舶横倾角度为 $\varphi$ ，船舶运动坐标系和静止坐标系的转换关系为：

$\left\{\begin{gathered} l = x ，\\ m = y\cos \varphi - z\sin \varphi, \\ n = y\sin \varphi + z\cos \varphi 。\\ \end{gathered} \right.$

其矩阵形式为：

$\left[ {\begin{array}{*{20}{l}} l \\ m \\ n \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \varphi }&{ - \sin \varphi } \\ 0&{\sin \varphi }&{\cos \varphi } \end{array}} \right]\left[ {\begin{array}{*{20}{l}} x \\ y \\ z \end{array}} \right] \text{。}$

在风浪条件下考虑船舶的纵倾角 $\theta$ 和航向角 $\beta$ ，可得两坐标系的转换关系为：

$\left[ {\begin{array}{*{20}{l}} l \\ m \\ n \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\cos \theta \cos \beta }&{ - \cos \varphi \sin \beta }&{\cos \varphi } \\ {\cos \theta \sin \beta }&{\cos \varphi \cos \beta }&{\cos \beta } \\ { - \sin \theta }&{\sin \varphi \cos \theta }&{\cos \varphi \cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{l}} x \\ y \\ z \end{array}} \right] \text{。}$

在该参考运动坐标系下，建立大型船舶的运动学模型为：

$\left\{ {\begin{array}{*{20}{c}} {{F_X} = m\ddot x = m{a_X}} ，\\ {{F_Y} = m\ddot y = m{a_Y}}，\\ {{F_Z} = m\ddot z = m{a_Z}}。\end{array}} \right.$

式中：m为船舶质量；a_X，a_Y，a_Z分别为沿3个坐标轴的加速度。

船舶在运动坐标系O-XYZ中的位置记（x₀，y₀，z₀），可得船舶运动方程为：

$\left\{ {\begin{aligned} &{{{\dot x}_0} = {V_x}\cos \gamma \cos \beta + {V_y}\cos \gamma \sin \beta } ，\\ &{{{\dot y}_0} = {V_x}\sin \gamma \cos \beta + {V_z}\cos \gamma \cos \alpha }，\\ &{{{\dot z}_0} = - {V_x}\sin \beta + {V_y}\cos \beta \sin \alpha - {V_z}\cos \beta }，\\ &{\dot \alpha = {w_x} + {w_y}\tan \beta \sin \lambda }，\\ &\dot \beta = {w_x}\cos \alpha - {w_z}\sin \alpha ，\\ &\dot \gamma = {w_y}\sin \alpha /\cos \beta 。\\ \end{aligned}} \right.$

式中： $\alpha$ 为船舶的横摇角度； $\ \beta$ 为航向角； $\gamma$ 为横倾角； ${V_x}$ ， ${V_y}$ ， ${V_z}$ 分别为船舶沿ox，oy，oz轴的速度分量； ${w_x}$ ， ${w_y}$ ， ${w_z}$ 分别为船舶绕ox轴、oy轴、oz轴的角速度分量。

3 大型船舶装载和风浪条件下的稳性校核分析 3.1 大型船舶随浪条件下的船舵作用力分析

船舵是船舶的稳性控制关键部件，首先建立风浪条件下船舵的力学模型，如图3所示。

图中， $\alpha$ 为船舵的攻角， $P$ 为海浪作用在船舵表面的合力，可分解为

$P = \sqrt {P_x^2 + P_y^2} \text{。}$

$l$ 为船舵剖面的弦长，定义船舵的压力中心为 ${x_t}$ ，分散系数按下式计算：

$Cp = \frac{{{x_t}}}{l} 。$

在建立船舵作用力前，根据流体动力学理论，首先建立基本控制方程分别如下：

1）连续性方程

$\frac{{{\rm{d}}{\rho _{}}}}{{{\rm{d}}t}} + {\rho _{}}\Delta \cdot {v_c} = 0 \text{。}$

式中： $\Delta$ 为拉普拉斯算式； $\rho$ 为液体密度； ${v_c}$ 为相对运动速度。

2）动量方程

${\rho _{}}\frac{{{\rm{d}}{v_c}}}{{{\rm{d}}t}} = {\rho _{}}f + \Delta \cdot \sigma \text{。}$

式中： $f$ 为海水的体积力； $\sigma$ 为海水的体积域函数。

3）能量方程^[3]

$\rho \frac{{{\rm{d}}E}}{{{\rm{d}}t}} = - \rho \Delta \cdot {v_c} + Q - \Delta q \text{。}$

式中： $Q$ 为海水内能； $E$ 为海水的动能。

建立船舵的作用力模型为：

$\frac{{\partial \left( {\rho {v_c}} \right)}}{{\partial t}} + div\left( {\rho {v_c}} \right) = - \frac{{\partial P}}{{\partial t}} + \frac{{\partial {F_{\tau x}}}}{{\partial x}} + \frac{{\partial {F_{\tau y}}}}{{\partial y}} + \frac{{\partial {F_{\tau z}}}}{{\partial z}} 。$

式中： ${F_{\tau x}}$ ， ${F_{\tau y}}$ ， ${F_{\tau z}}$ 分别为作用力沿3个坐标方向的切应力。

3.2 大型船舶随浪条件下的恢复力矩计算

船舶正常航行状态下处于相对平衡状态，当外界风浪干扰作用力突然施加时，会对船舶的稳定性产生破坏作用，使船舶产生明显的横摇角度，影响船体水线面的变化和船体浮态，进一步影响船体的稳定性。

当船舶发生大倾角稳性问题时，分析船舶倾斜后产生的复原力矩与干扰力的相互作用是关键，当船舶处于静水之中时水线面为一水平面，当在风浪条件时船体的水线面产生倾斜，建立该过程的数学模型如图4所示。

可知，在风浪作用下船舶的水线面产生倾角为 $\theta$ ，海浪作用在船体的作用力如下式：

${F_S} = \frac{1}{2}{\rho _0}{A_O}{C_0}{v^2} \text{。}$

式中： ${\rho _0}$ 为海水的密度； ${A_O}$ 为船舶在海浪方向的投影面积； ${C_0}$ 为升力系数； $v$ 为航行速度。

海浪作用在船体的弯矩如下式：

${M_o} = \frac{1}{2}{k_1}{k_2}{L_b}^2B(\delta + 0.8) \cdot {10^{ - 2}}\;{\rm{kN}} \cdot {\rm{m }} \text{。}$

式中： $L_b^{}$ 为船体纵向长度的投影长度； $B$ 为船体宽度； $\delta$ 为船舶载重系数， $\delta \approx 0.5$ ， ${k_1}$ 和 ${k_2}$ 分别为船舶的弯矩系数，与船舶长度、吃水深度等因素有关，按下式计算：

${k_1} = 4.5{\left( {\frac{{{L_b}}}{{980}} - 0.2} \right)^2} + 0.82 \text{，} {k_2} = 9 - 0.96{\left( {\frac{{300 - {L_b}}}{{100}}} \right)^2} 。$

船舶的恢复力矩由船体重心和船舵作用力共同产生，如下式：

${M_S} = \frac{1}{2}L{\rho _0}{A_O}\cos \theta \text{，}$

式中， $L$ 为船舶中心到剖面中线的距离^[4]。

对比不同吃水深度下的船体稳性倾角变化数据，如图5所示。

4 结　语

船舶的稳性设计和分析是提高船舶航行安全性的关键，也是船舶设计和测试过程中需要重点考虑的因素。本文针对大型船舶在装载和风浪条件下的稳定性问题进行详细建模和研究，建立了干扰作用力模型、船舶运动模型、船舵作用力模型和恢复力矩模型，有助于提高船舶的稳性设计。