2. 中国人民解放军92942部队,北京 100161
2. No. 92942 Unit of PLA, Beijing 100161, China
目前,大多数的布局算法都是启发式与元启发式相结合的方法[1]。其中,启发式算法的求解思路主要是根据问题特点,缩小搜索空间,进而得到最终解。这种算法虽能保证解的质量,但是通用性不强。元启发式方法则是运用遗传算法、粒子群算法等计算机智能优化算法,用随机的方式搜索邻域或者将多个解综合成新解。这种算法通用性强,但是其结果受智能算法收敛性的影响较大,经常性出现结果不稳定的情况[2]。因此,在布局优化中,2种方法经常被混合使用,以提高算法性能。
船舶机舱布局设计作为布局问题的一种,在满足一般性布局问题要求的同时,还需要根据舱室环境的特殊性,结合船舶设计规范以及舱室设备布置要求,进行额外的约束,并在求解过程中,将各类约束转化为罚函数的形式加入到目标函数中,进而利用计算机智能算法进行求解[3-6]。但是求解思路主要集中在对算法的改进与优化上,未能对启发式算法的优势进行充分利用。此外,针对粒子群算法早收敛的特点,Sun J 等提出了量子粒子群算法,并在各个领域作为粒子群算法的改进算法得到了广泛应用[7-10],但是尚未应用于船舶舱室的布局问题。
本文借鉴启发式布局的方式进行初始解的生成,运用量子粒子群算法对某型船舶机舱的设备进行布置,并与遗传算法和粒子群算法进行对比,说明本文给出的基于量子粒子群算法的布局方法具备更佳的算法性能。
1 问题描述与模型建立 1.1 问题描述与模型的简化机舱布局优化问题分为三维布局与二维布局,本文主要在二维层面进行考虑,旨在求得机舱设备摆放位置的集合P,使得船舶的机舱布局最为合理[11]。P可以表示为:P={(x1, y1, α1),···,( xn, yn, αn)},其中(xi, yi)为设备i的形心坐标,αi为设备i摆放的方向,n为设备的数量。
为了合理表述这个复杂的问题,并建立相应的模型求解,本文进行以下简化和假设:
1)在舱室布置时,主要考虑对舱室布局有较大影响的设施,管路、电缆以及壁挂式部件不做考虑。
2)将具有复杂形状的设备简化为规则的长方体。
3)通过垂直投影将三维布局问题简化为以舱室甲板为平面的二维布局问题。
4)舱室内部一些大型设备在设计初期已经固定,如柴油机等。
5)舱室入口和可拆板以及吊装通道的位置已经确定。
6)对不同设备、维修和操作位置可能会有所不同,但是每个设备的维修和操作位置相对为设备本身而言是固定的。
7)设备的摆放朝向问题仅考虑设备的长边与船舶长度方向平行和垂直的2种情况,即αi={0,1}。
1.2 数学模型的建立一般情况下,船舶舱设备布置需考虑船舶舱室的设计规范及设备布置需求,因此该问题是一个带复杂约束的多目标优化问题,可建立方程如下:
| $ \left\{\begin{array}{l}\mathrm{min}F(x)=({f}_{1}(x),{f}_{2}(x),\cdots \text{,}{f}_{m}(x))\;,\\ {\rm{s.t.}}\left\{\begin{array}{l}{g}_{i}(x)\leqslant 0,i=1,2,\cdots ,p\;,\\ {h}_{j}(x)=0,j=1,2,\cdots ,q\;,\\ {L}_{b}\leqslant x\leqslant {U}_{b}\;。\end{array}\right.\end{array}\right. $ | (1) |
式中:X为设计变量,包括设备的位置坐标及方向等参数,gi(x)和hj(x)分别为设备之间的功能性约束与几何约束转化的不等式约束与等式约束,p为不等式约束个数,q为等式约束个数,Lb和Ub则为设备布局的边界。
1.3 目标函数本文主要从满足舱室设备基本布局的基础上,便于设备维修保养的角度出发建立目标函数。主要从不平衡力矩、维修干涉、船员流通距离以及吊装距离等方面进行舱室设备的布置。
1)不平衡力矩最小
相对于纵倾而言,船舶的横倾对船舶的设计以及使用影响更大,因此本文主要考虑横倾,尽量保证设备对船舶中纵剖面力矩的代数和最小。可定义不平衡力矩函数为:
| $ {f_1}(x) = \dfrac{{\left| { \displaystyle \sum\nolimits_{{{i}} = 1}^{{n}} {{m_{{i}}} \times {y_{{i}}}} } \right|}}{{\left| { \displaystyle \sum\nolimits_{{{i}} = 1}^{{n}} {{m_{{i}}} \times {{h}} \times \sin ({\text{π}} /180)} } \right|}}\;。$ | (2) |
式中:n为设备数量,mi为设备i的质量,yi为设备形心到中纵剖面的距离,h为船舶的初稳性高。
2)维修干涉最小
若设备i在维修过程中与设备j发生干涉的概率为Pij,则设备i在维修过程中与周围设备产生干涉的概率Pi=
| $ P_{i j}=\left\{\begin{array}{l} 1, d c_{i j} \leqslant D_{i, \min } \;,\\ \dfrac{D_{i, \min }-d c_{i j}}{D_{i, \max }-D_{i, \min }}, D_{i, \min } \leqslant d c_{i j} \leqslant D_{i, \max } \;,\\ 0, d c_{i j} \geqslant D_{i, \max }\;。\end{array}\right. $ | (3) |
式中:Di,min为设备i的最小维修距离要求,Di,max为设备i的最大距离需求,dcij为设备i与j的距离。在考虑维修干涉的过程中,还应该考虑设备的作业频率fi,因此定义船舶舱室设备维修干涉的目标函数为:
| $ {f_2}(x) = \sum\nolimits_{i = 1}^m {{f_i} \times {P_i}}\;。$ | (4) |
3)人员流通距离最小
良好的设备布局应当满足舱室人员快速出舱的需求,以便在紧急情况下船员能够迅速撤出工作舱室。定义船员的流通距离函数为:
| $ {f_3}(x) = \dfrac{{ \displaystyle \sum\nolimits_{i = 1}^m { \displaystyle \sum\nolimits_{j = 1}^n {{L_{ij}}} } }}{{ \displaystyle \sum\nolimits_{{{i}} = 1}^{{m}} { \displaystyle \sum\nolimits_{{{j}} = 1}^{{n}} {{L_{\max }}} } }}\;。$ | (5) |
式中:Lij为设备i到出口j的距离,m为舱室除舱口外的设备数量,n为舱口数量,Lmax为舱室的对角线长度。
4)吊装距离最小
在对船舶舱室设备进行维修的过程中,需要将部分设备吊装出舱外进行维修,因此需要考虑设备的吊装距离。可定义吊装函数为:
| $ {f_4}(x) = \frac{{ \displaystyle \sum\nolimits_{k = 1}^k {{m_k} \times {T_k}} }}{{ \displaystyle \sum\nolimits_{{{k}} = 1}^{{k}} {{m_{{k}}} \times {T_{{{k}}\max }}} }} \;。$ | (6) |
式中:k为需要吊装设备数量;Tk为设备k到吊装出口d的距离,Tk= |xk−xd|+|yk−yd|;Tkmax为设备在舱室中的顶角布置时,到吊装口的距离。
1.4 约束条件1)设备之间不干涉
在舱室布局的过程中,舱室设备之间不能产生位置的重叠,即设备Ai与Aj应当满足:g1(x)={Ai∩Aj=
| $ \left\{ \begin{gathered} \left| {{x_i} - {x_j}} \right| > {l_i} + {l_j}/2 \;,\\ \left| {{y_i} - {y_j}} \right| > {h_i} + {h_j}/2 \;。\\ \end{gathered} \right. $ | (7) |
式中:li为设备i的长,hi为设备i的宽。
2)设备在舱室内
在设备布置的过程中,设备应当全部在舱室区域M以内,即g2(x)={Ai
| $ \left\{ \begin{gathered} {x_i} - ({l_i}/2) \times {\alpha _i} - ({h_i}/2) \times {\alpha _i} > 0 \;,\\ L - ({x_i} + {l_i}/2 \times {\alpha _i} + {h_i}/2 \times {\alpha _i}) > 0 \;,\\ {y_i} - ({l_i}/2) \times {\alpha _i} - ({h_i}/2) \times {\alpha _i} > 0 \;,\\ H - ({y_i} + {l_i}/2 \times {\alpha _i} + {h_i}/2) > 0 \;。\\ \end{gathered} \right. $ | (8) |
式中:L为舱室长,H为舱室宽,αi为设备i的方向。
3)其他约束
在布置过程中,还需要考虑设备的距离要求以及布置区域等其他类因素,记为:
| $ {g_i}(x) = \{ g({A_i}):{A_i} \in X\} \;。$ | (9) |
式中,X为布局过程中的其他约束要求。
则最后的适应度函数可定义为:
| $ Fit = \sum\nolimits_{i = 1}^n {{\omega _i} \times {f_i}(x)} {\text{ + }punish}\;。$ | (10) |
式中:fi为目标函数;ωi为目标函数的权重,本文取ωi=0.2;punish为违反约束条件的惩罚值。
2 基于量子粒子群算法的布局优化 2.1 遗传算法和粒子群算法遗传算法(GA)是一种基于种群的启发式算法,是当前最流行的进化算法之一。该算法是一种全局收敛性的算法,它通过遗传、变异的方式实现种群内部的信息交换,使拥有较高适应度的染色体得以保留,通过多次迭代进化,进而得到最优解。
粒子群算法(PSO)是一种基于群体智能的进化计算方法[12],具有较强的局部搜索能力。该算法受到鸟类觅食行为的启发,将种群中的每个粒子均视当前的候选解,在迭代过程中,通过种群中的粒子在多维空间搜索过程中的竞争和合作,进而寻找最优解。
2.2 量子粒子群算法粒子群算法虽然有较强的局部搜索能力和一定的全局搜索能力,但是其本身存在一定的局限性,并且已经被学者Van den Bergh证明,该算法不是一个全局收敛的算法。对此Sun等[7]在粒子群算法的基础上,将PSO算法公式进行改进,提出了量子粒子群优化算法(QPSO),并对其全局收敛的性质进行证明[13],其算法公式如下:
| $ \left\{ \begin{array}{l}mbest = (1/M) \times {\displaystyle {\sum }_{i=1}^{M}{P}_{i}} =(1/M) \times \left( {\displaystyle {\sum }_{i=1}^{M}{P}_{i1}, \cdots ,{\displaystyle {\sum }_{i=1}^{M}{P}_{id}}} \right)\;,\\ P{P}_{ij}(t)=ran{d}_{1j}\times {p}_{ij}(t)+(1-randij)\times {p}_{gj}(t)\;,\\ {x}_{i}{}_{j}(t+1) = P{P}_{ij}(t) \pm \omega \times \left|mbes{t}_{j}(t)-{x}_{ij}(t)\right|\times \mathrm{ln}(1/ran{d}_{2j})\;。\end{array} \right.$ | (11) |
式中:rand1j和rand2j是0~1均匀分布的随机数;Pi为第i个粒子所经历的最佳位置pbest,Pi=(pi1,···,pid);Pg为全部粒子所经历的最佳位置gbest,Pg=(g1,···,gn);mbest是粒子群pbest的中间位置向量;PPij为pij和pgj之间的随机点[10];ω为收敛系数,随迭代次数的变化而变化,取ω=0.5+0.5×(gen−t)gen,其中,gen为迭代代数,t为当前迭代代数。
2.3 初始解的生成在布局问题中,为了得到更好的求解结果和效率,设计出了大量的基于不同策略的算法,较为经典的如BL(bottom-left)和BLF(bottom-left-fill)等。这种算法对于二维装箱问题有较强的适用性,但是对于船舶的舱室布局而言,其布置的原则不是以舱室设备的最小占用面积为主要考虑指标,此外在布局过程中还需考虑设备之间的复杂约束以及某些设备必须安装在特殊区域,因此,需要探索适用于船舶舱室布局问题的方法,以提高初始解的生成质量。
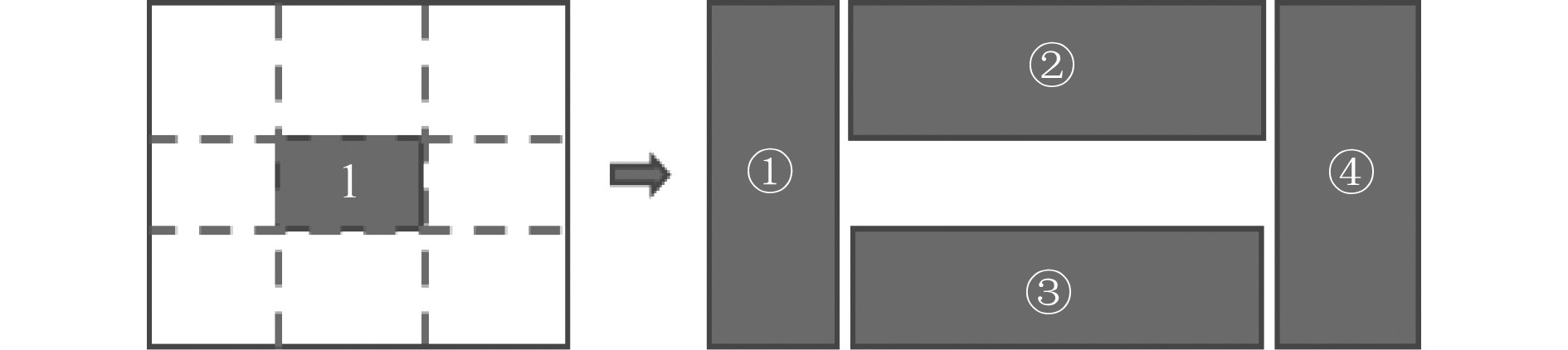
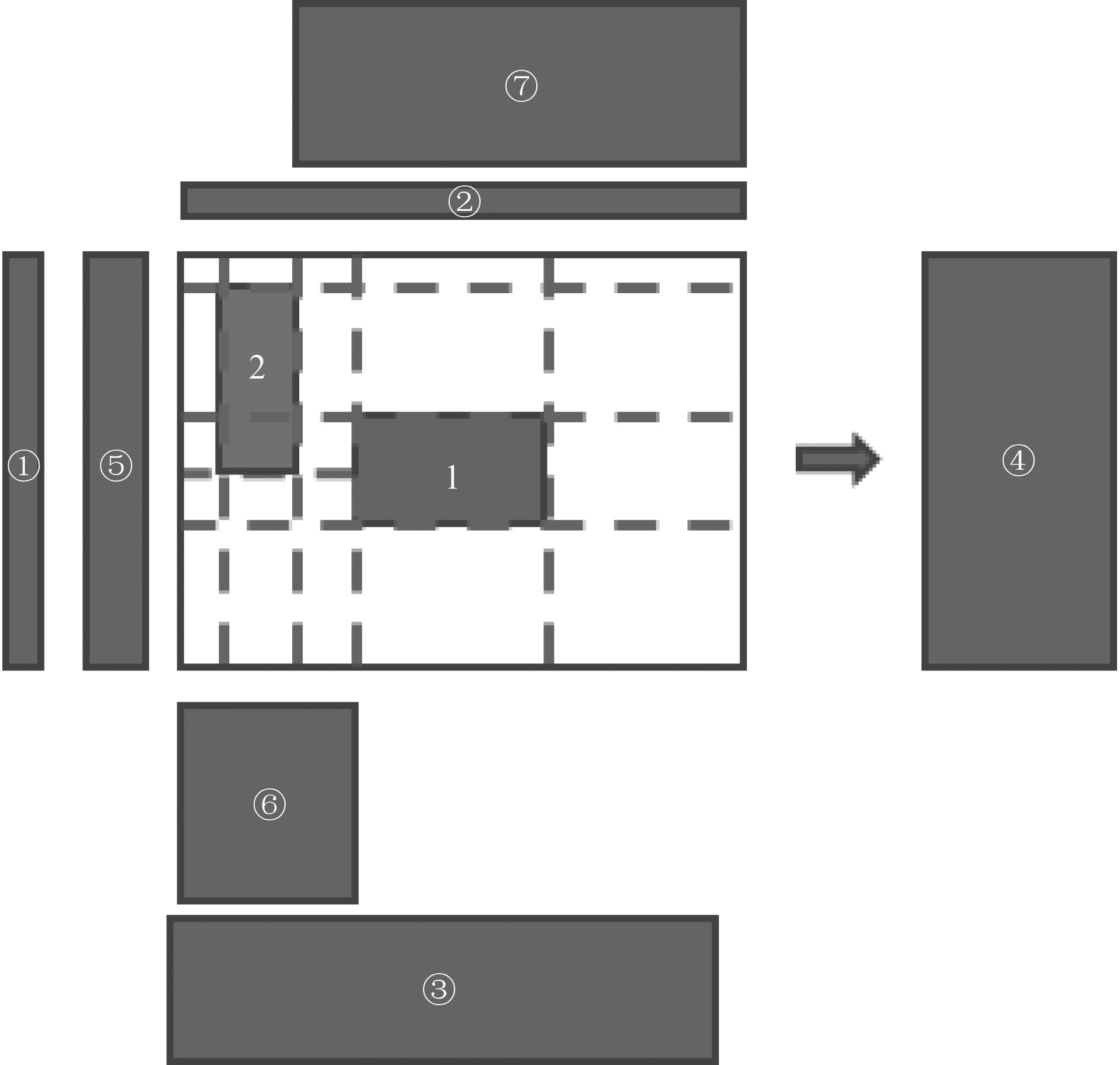
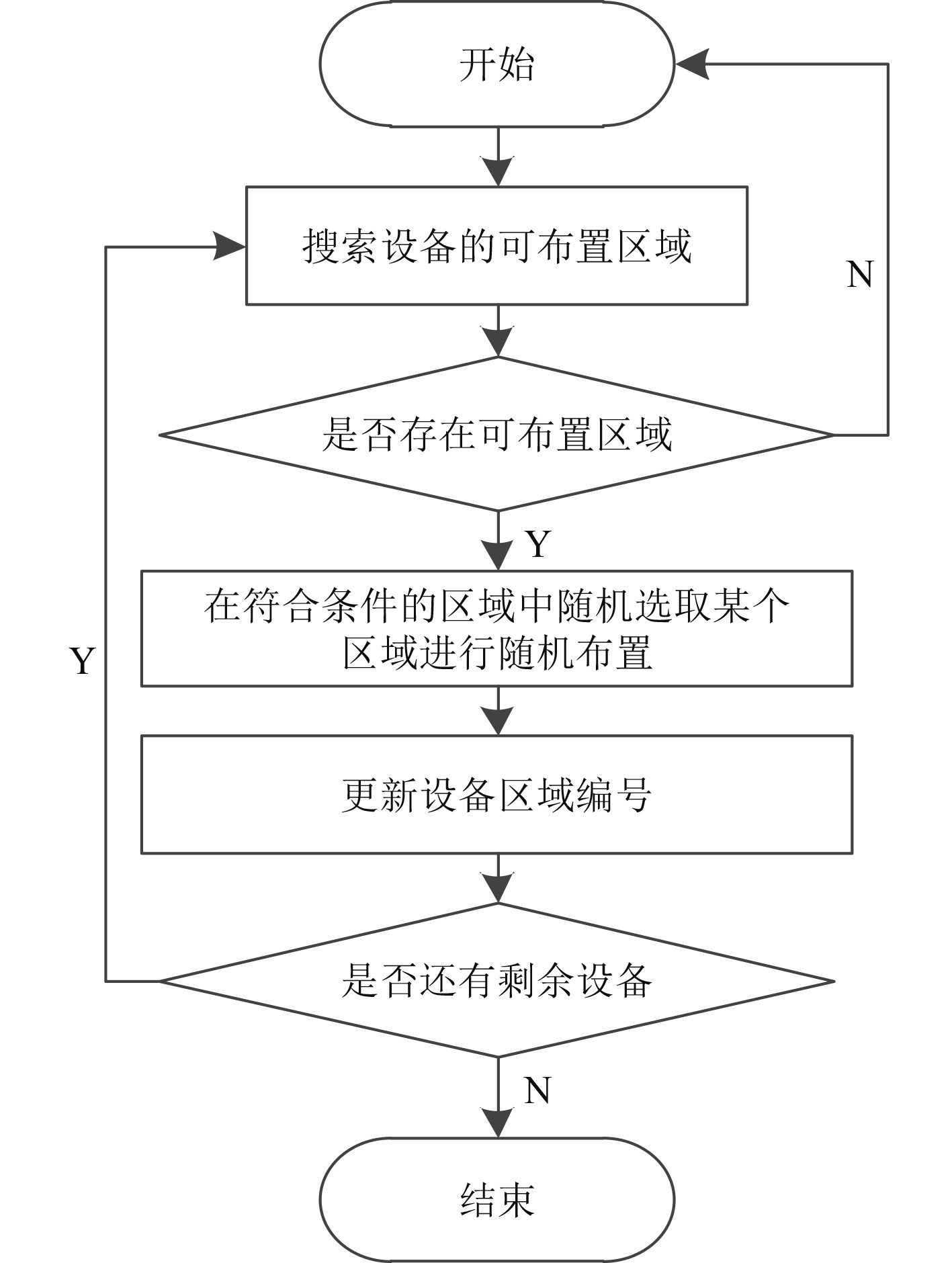
借鉴文献 [14]中对三维空间分割进行初始解生成的思路,本文对二维舱室进行分割[14],根据舱室布置要求,对舱室某个设备放置后,将剩余空间进行分割,如图1所示。对空间进行分割后,依次选择待布置设备,判断分割后的空间能否满足待布置设备的布设;在满足装备能够布置的区域中随机选择某个区域,并在该区域中将待布置设备随机布放,完成设备的布置后,对剩余可布置空间进行更新,如图2所示。依次选取剩余设备,进行设备的布置,直至全部设备布放完毕。舱室设备的布置流程如图3所示。
|
图 1 空间分割示意图 Fig. 1 Schematic diagram of space division |
|
图 2 依次选取设备进行布置并更新剩余空间编号 Fig. 2 Select the equipment in turn for layout and update the number of remaining space |
|
图 3 初始解生成流程图 Fig. 3 Flow chart of initial solution generation |
运用量子粒子群算法求解布局问题,其计算步骤如下:
步骤1 初始化量子粒子群算法的各项参数,种群规模popsize、进化代数gen。
步骤2 随机生成popsize种不同的机舱设备布局方案,根据建立的数学模型,求解种群中粒子的适应度。
步骤3 根据步骤2中所得结果,利用量子粒子群算法对粒子进行更新,并检验所得粒子中的各设备之间是否存在干涉,若存在干涉,则执行步骤4,否则跳到步骤5。
步骤4 若存在干涉,找出干涉设备并寻找区域重新布置,若无法布置,则生成新的粒子并加入种群中进行迭代
步骤5 若不存在干涉,计算新的粒子适应度,并执行粒子的更新操作,直到迭代结束。最终得到优化后的最优解。
3 实例分析与算法比较选用某型船舶机舱为例,进行算法的验证。已知该型船长为6.75 m,宽为3 m,初稳性高为0.8 m,舱室设备原始布置情况及维修需求如表1所示。根据相关规范与标准,设备的布置类约束如表2所示。
|
|
表 1 舱室设备原始布置及维修需求表 Tab.1 Original layout and maintenance requirements of cabin equipment |
|
|
表 2 设备关联性要求 Tab.2 Equipment relevance requirements |
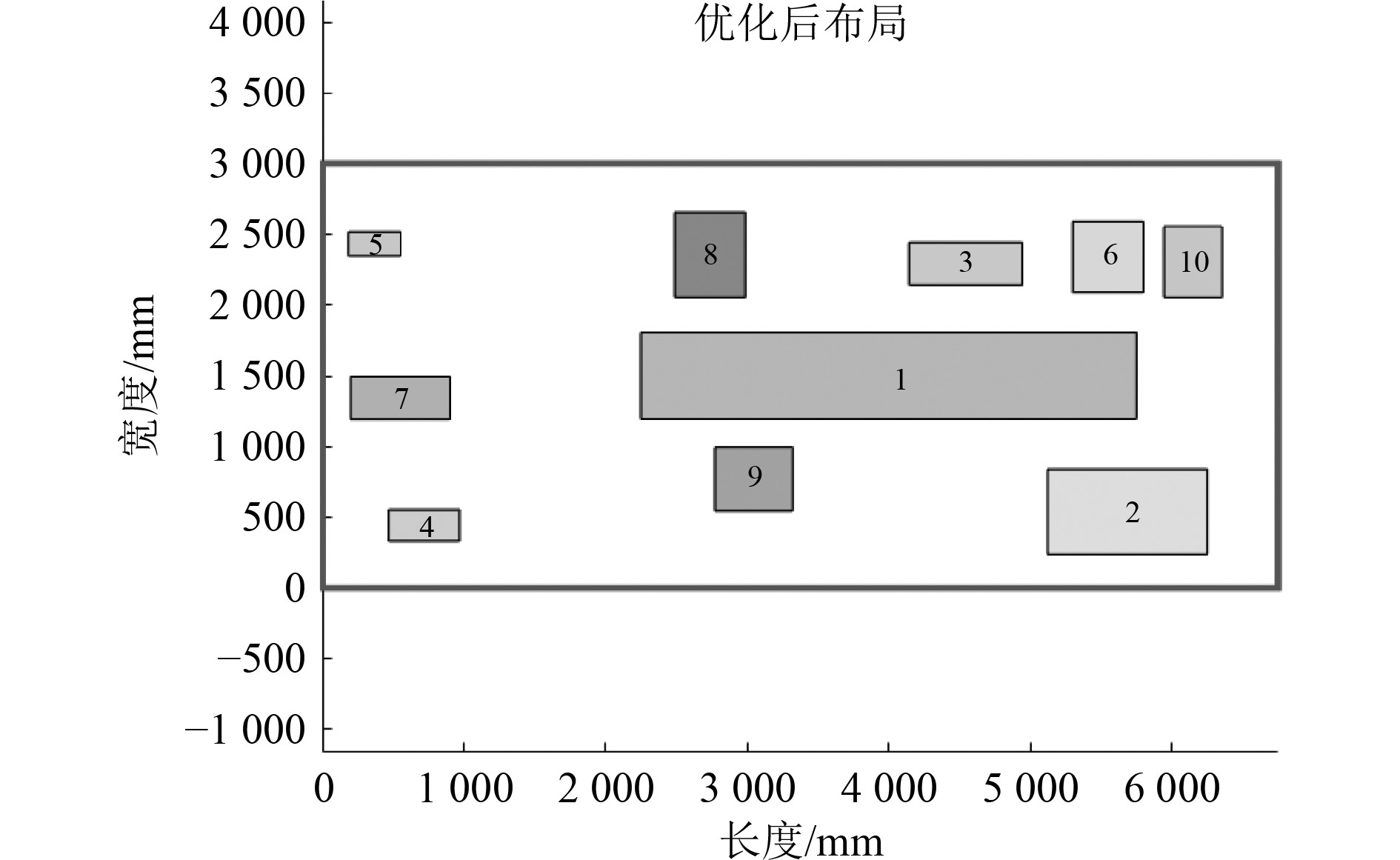
设置种群popsize=800,最大迭代次数gen=2000,运用量子粒子群算法,对舱室的布置进行优化,其优化后的结果与适应度变化曲线分别如图4所示。
|
图 4 基于量子粒子群算法的机舱设备布局结果 Fig. 4 Layout results of cabin equipment based on quantum particle swarm optimization algorithm |
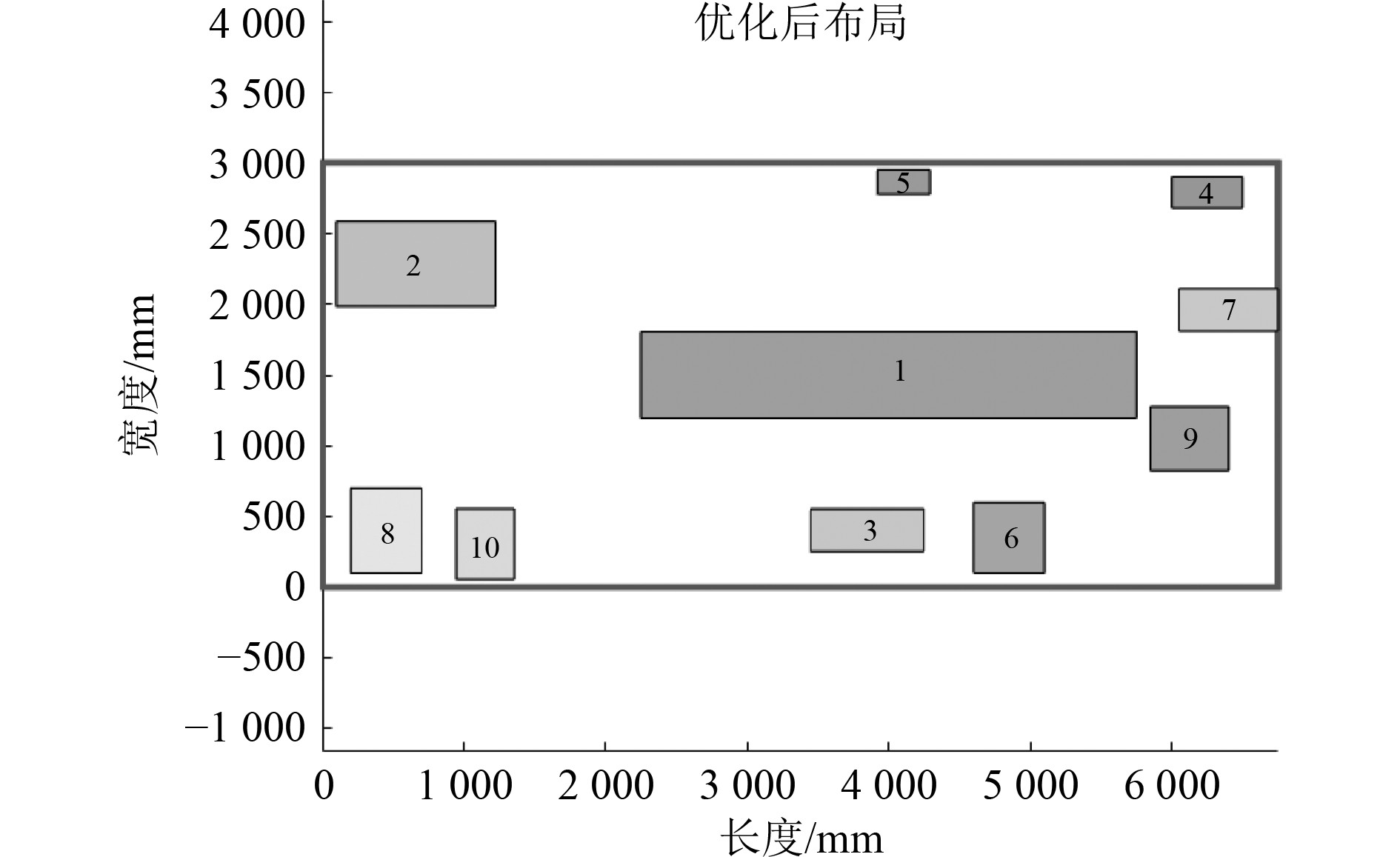
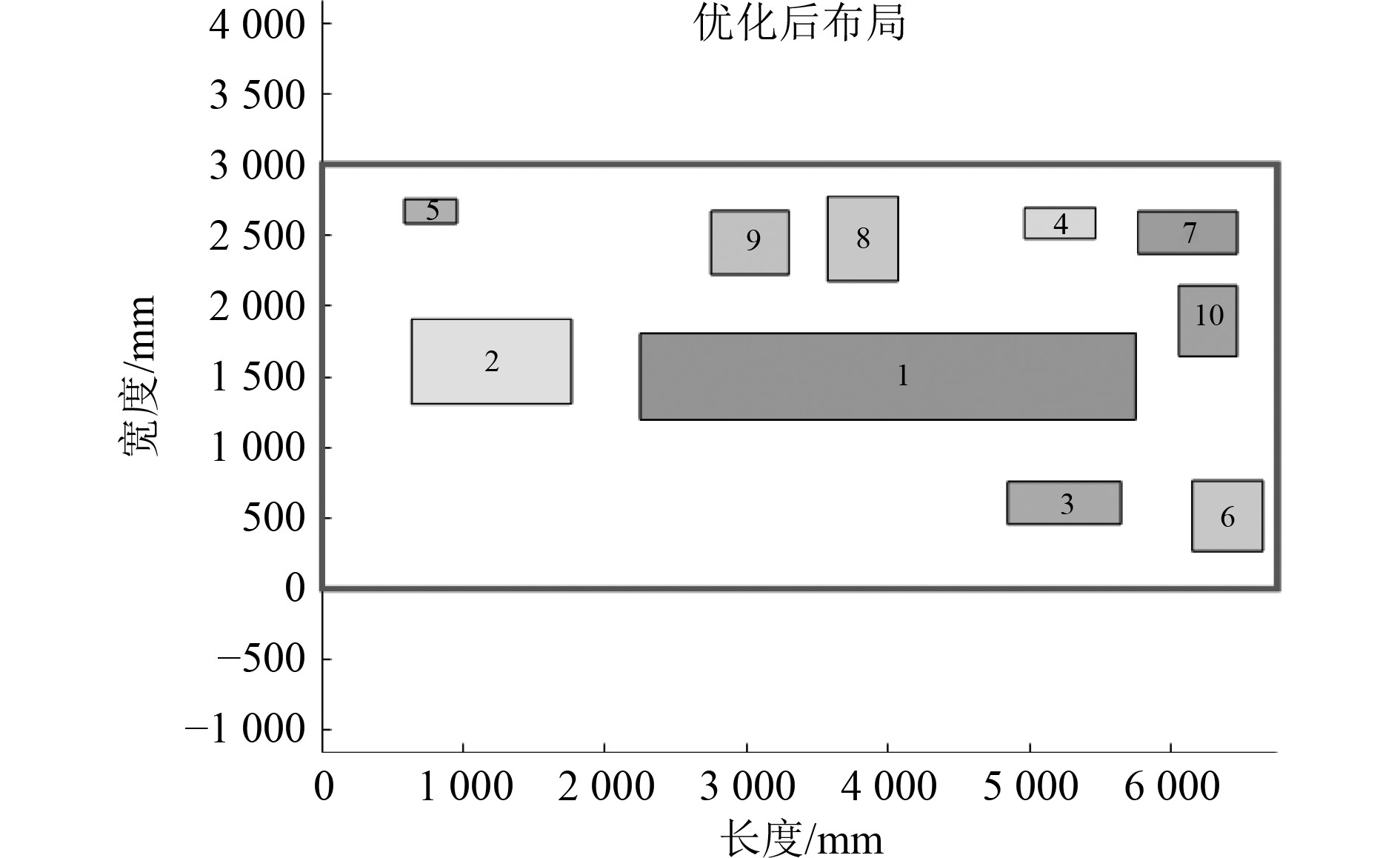
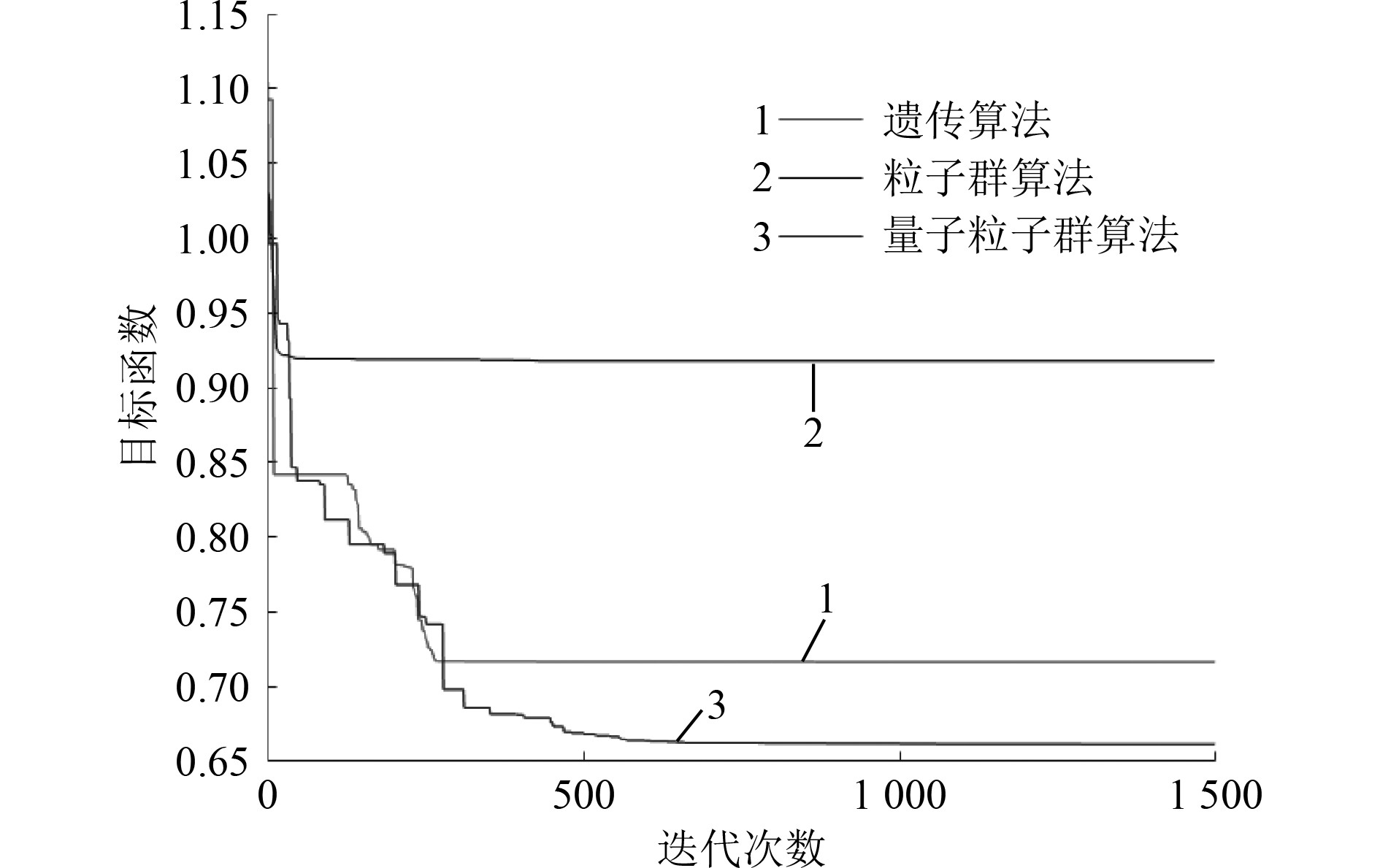
同样条件下,分别运用遗传算法(设置遗传算法的pc=0.8,pm=0.01)和粒子群算法(设置惯性权重ω=0.8,学习因子均设置为0.8)对上述案例进行优化,所得的布局结果如图5和图6所示。将3种算法的适应度变化进行对比,如图7所示。从优化的效果看,量子粒子群算法>遗传算法>粒子群算法。各算法的目标函数值如表3所示。
|
图 5 基于遗传算法的机舱设备布局结果 Fig. 5 Engine room equipment layout results based on genetic algorithm |
|
图 6 基于粒子群算法的机舱设备布局结果 Fig. 6 Layout results of cabin equipment based on particle swarm optimization algorithm |
|
图 7 不同算法的适应度变化 Fig. 7 Fitness changes of different algorithms |
|
|
表 3 不同算法下的优化效果比较 Tab.3 Comparison of optimization effects under different algorithms |
此外,文献 [4]中的粒子群算法的优化效果优于遗传算法效果的结论,在本文中并不成立。因此,对于船舶舱室的布局问题,需要针对具体算法与初始解的生成方式进行具体分析,进而得到相应的结论。
4 结 语1)研究船舶舱室的布局问题时,并不能单纯得出某种智能算法更优的结论,需要将启发式算法与元启发式算法相结合,得到计算结果,进而讨论算法的优劣性。
2)对于机舱布局,在运用本文初始解生成方式的前提下,量子粒子群算法的计算结果优于遗传算法和粒子群算法。
本文研究结果可为船舶机舱的布置与优化提供参考方案。
后续将主要从3个方面进一步研究:一是布局问题初始解生成的生成与规划的问题;二是各类智能算法的改进与优化在布局算法中的应用;三是布局问题的元启发式算法与启发式算法相结合与匹配的问题。
| [1] |
徐义春. 卫星舱布局问题的智能求解方法研究[D]. 武汉: 华中科技大学, 2008.
|
| [2] |
宋婷婷. 二维一刀切装箱问题研究[D]. 哈尔滨: 哈尔滨理工大学, 2020.
|
| [3] |
姜文英, 林焰, 陈明, 等. 基于粒子群和蚁群算法的船舶机舱规划方法[J]. 上海交通大学学报, 2014, 48(4): 502-507. JIANG Wen-ying, LIN Yan, CHEN Ming, et al. Ship cabin planning method based on particle group and ant colony algorithm[J]. Journal of Shanghai Jiaotong University, 2014, 48(4): 502-507. |
| [4] |
周发模. 粒子群算法及其在机舱布置优化的应用研究[D]. 武汉: 武汉理工大学, 2009.
|
| [5] |
LUO X, YANG Y, GE Z, et al. Maintainability-based facility layout optimum design of ship cabin[J]. International Journal of Production Research, 2014, 53(3): 677-694. |
| [6] |
赵士光. 消防船机舱优化布置的可视化研究[D]. 大连: 大连理工大学, 2014.
|
| [7] |
SUN J, XU W, FENG B. Adaptive parameter control for quantum-behaved particle swarm optimization on individual level[C] // IEEE International Conference on Systems, Man and Cybernetics. IEEE, 2006: 3049-3054.
|
| [8] |
赵红超, 周洪庆, 王书湖. 无人机三维航迹规划的量子粒子群优化算法[J]. 航天控制, 2021, 39(1): 40-45. ZHAO Hong-chao, ZHOU Hong-qing, Wang Shu-hu. Quantum particle swarm optimization algorithm for UAV 3D track planning[J]. Aerospace Control, 2021, 39(1): 40-45. DOI:10.3969/j.issn.1006-3242.2021.01.007 |
| [9] |
徐方维, 谭洋洋, 杨洪耕, 等. 兼顾不同角色利益的集中型充电站优化布局[J]. 高电压技术, 2017, 43(4): 1256-1262. XU Fang-wei, TAN Yang-yang, YANG Hong-geng, et al. Optimal layout of centralized charging stations taking into account the interests of different roles[J]. High Voltage Technology, 2017, 43(4): 1256-1262. |
| [10] |
黄建江, 须文波, 孙俊, 等. 量子行为粒子群优化算法的布局问题研究[J]. 计算机应用, 2006(12): 3015-3018. Huang Jian-jiang, XU Wen-bo, Sun Jun, et al. Research on layout problem of quantum behavior particle swarm optimization algorithm[J]. Computer Applications, 2006(12): 3015-3018. |
| [11] |
罗云, 唐丽晴. 粒子群蚁群混合优化算法在船舶机舱布局优化上的应用[J]. 舰船电子工程, 2019, 39(10): 156-161. Luo Yun, Tang Li-qing. Application of particle swarm optimization and ant colony optimization algorithm in ship engine room layout optimization[J]. Ship Electronic Engineering, 2019, 39(10): 156-161. DOI:10.3969/j.issn.1672-9730.2019.10.035 |
| [12] |
窦小敏, 秦宁宁. 电力系统经济调度的量子粒子群改进算法[J]. 重庆邮电大学学报(自然科学版), 2020, 32(4): 528-535. DOU Xiao-min, QIN Ning-ning. Improved quantum particle swarm optimization algorithm for economic dispatching of power system[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2020, 32(4): 528-535. |
| [13] |
方伟, 孙俊, 谢振平, 等. 量子粒子群优化算法的收敛性分析及控制参数研究[J]. 物理学报, 2010, 59(6): 3686-3694. FANG Wei, SUN Jun, XIE Zhen-ping, et al. Convergence analysis and control parameters of quantum particle swarm optimization algorithm[J]. Journal of Physics, 2010, 59(6): 3686-3694. DOI:10.7498/aps.59.3686 |
| [14] |
张钧, 贺可太. 求解三维装箱问题的混合遗传模拟退火算法[J]. 计算机工程与应用, 2019, 55(14): 32-39. ZHANG Jun, HE Ke-tai. Hybrid genetic simulated annealing algorithm for solving three-dimensional packing problem[J]. Computer Engineering and Application, 2019, 55(14): 32-39. DOI:10.3778/j.issn.1002-8331.1902-0127 |
 2022, Vol. 44
2022, Vol. 44
