0 引　言

三体船型是目前船舶领域的一种热门船型，相对于常规船型，三体船型的兴波阻力更小，在恶劣的风浪条件下具有更高的稳定性，这些特点使得三体船的设计、制造成为船舶行业研究的热点，并在护卫舰、巡航舰、军民两用船等船舶类型上展开应用。我国在三体船型的研发和设计上处于世界先进水平，在三体船水动力理论、试验、船型设计等方面投入了大量的时间和物力。

本文的研究方向是基于模块化设计理念的三体船总体设计和优化，首先介绍模块化设计理论的现状，以某高速三体船为研究对象，采用NURBS曲线进行型线的拟合设计，基于型线设计进行三体船的特征曲面设计研究，最后结合流体动力学特性分析对基于模块化设计的三体船特性进行了建模和仿真测试。

1 模块化设计理论基本研究

模块化设计理论最早是20世纪50年代欧美一些国家提出的，在产品大型化和快速化生产、装配过程中，基于模块化设计理论的产品不论是在生产效率、通用性和设计合理性方面，还是在产品的成本方面都具有显著的优势^[1]。

模块化设计理论体系的基本原理如图1所示。

模块化设计理论可以根据产品开发过程大致分为以下4个阶段：

1）模块化总体设计

总体设计是指在模块化设计的过程中对系统进行总体的策划，模块化总体设计的第1步是进行外部分析，整理来自外部的输入条件和需求，确定模块化总体设计的目标；第2步是进行模块化方案设计，在承接内部和外部的需求前提下，对方案进行决策。

2）模块化划分设计

模块化划分设计环节是模块化设计的核心环节，基于系统的总体功能特征，将系统进行不同功能和特性的分类和组合，结合系统的分析形成系统的宏模型，将其划分为若干个功能单元模块。在划分阶段，不能局限于功能本身，要考虑设计、制造不同阶段可能面临的问题，需要权衡利弊得到最优模块的划分解决方案。

3）模块化重组设计

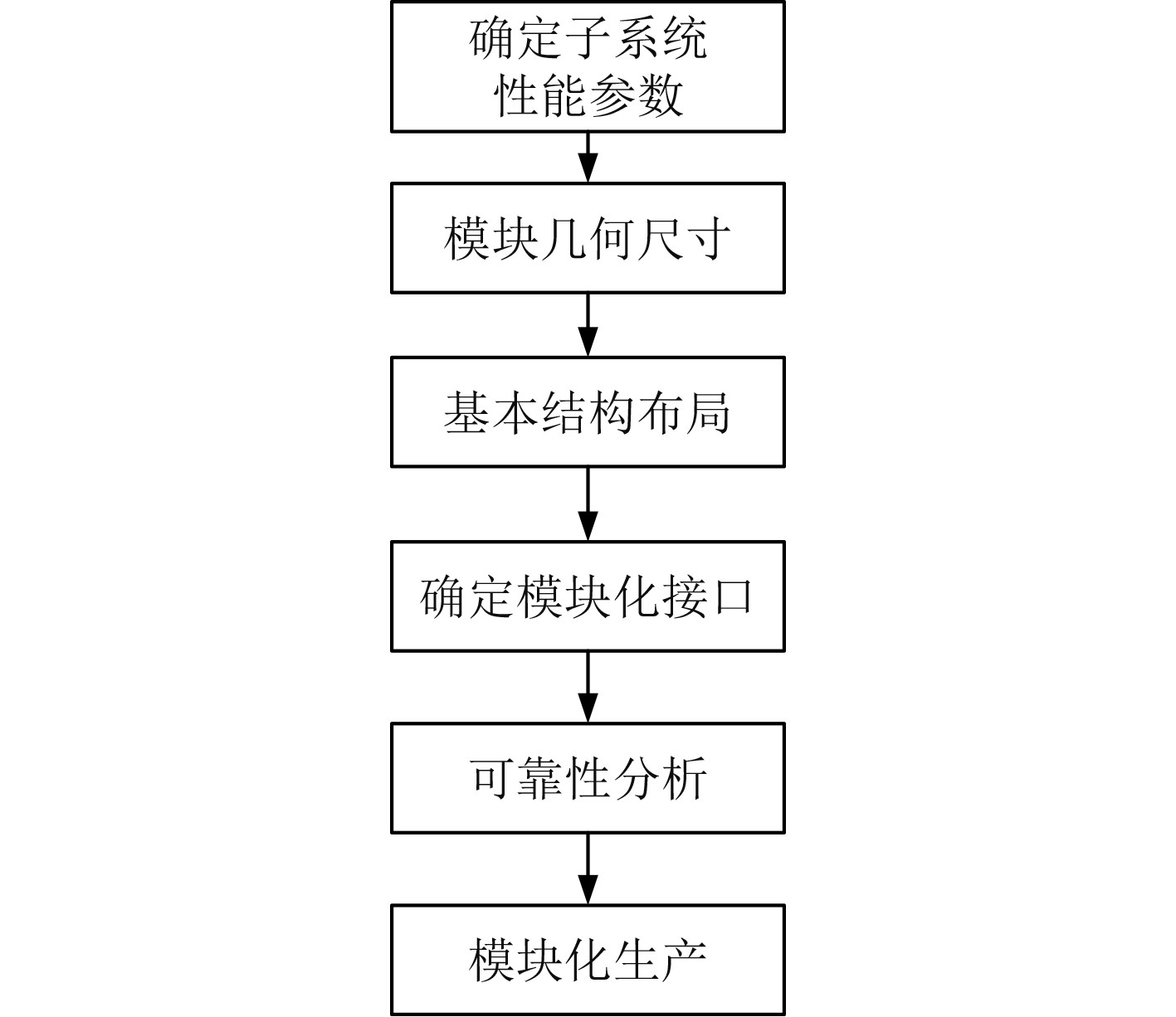
模块化重组设计是指模块化创建与组合设计，模块化重组设计是模块化设计的第3个关键阶段，其目标在于将总体设计过程中产生的方案、子系统等内容进一步细化与重组，形成一个可以实际应用的方案。但产品的重组设计在设计过程中不强调每个具体的产品特性，而是强调大量产品所构成的产品系列特性。重组设计模块化设计的关键环节，主要流程包括确定子系统性能参数、几何尺寸、结构布局、模块接口、可靠性分析等，如图2所示。

4）模块化产品设计

产品设计是模块化设计理论的落脚点和最终目标，也是模块化设计的最后一个环节。

2 基于NURBS的模块化三体船总体设计与优化 2.1 三体船的特征曲面设计

由于三体船的外型结构和流体力学特性相对于传统船舶更加复杂，因此在三体船的特征曲面优化时需要综合考虑大量的特征参数和曲面建模，其中，型线参数如轮廓线、设计水线等，是决定三体船流体动力学特性的关键。

基于模块化设计思路，将三体船划分为不同的区域，每个区域的特征曲面按照由点到线、由线到面的设计思路，在型线设计时采用NURBS曲线进行型线的拟合设计

NURBS曲线模型用下式表示：

$\bar p\left( m \right) = \frac{{\displaystyle\sum\limits_{i = 0}^n {{w_i}{d_i}{N_{i,j}}\left( u \right)} }}{{\displaystyle\sum\limits_{i = 0}^n {{w_i}{N_{i,j}}\left( u \right)} }} \text{。}$

式中： ${w_i}$ 为曲线的特征值， ${d_i}$ 为NURBS曲线的权值因子， ${d_i} \in \left( {0,1} \right)$ ， ${N_{i,j}}\left( u \right)$ 为曲线中的节点矢量， ${N_{i,j}}\left( u \right) = \left[ {{u_{0,}}{u_1},...,{u_i}} \right]$ 。

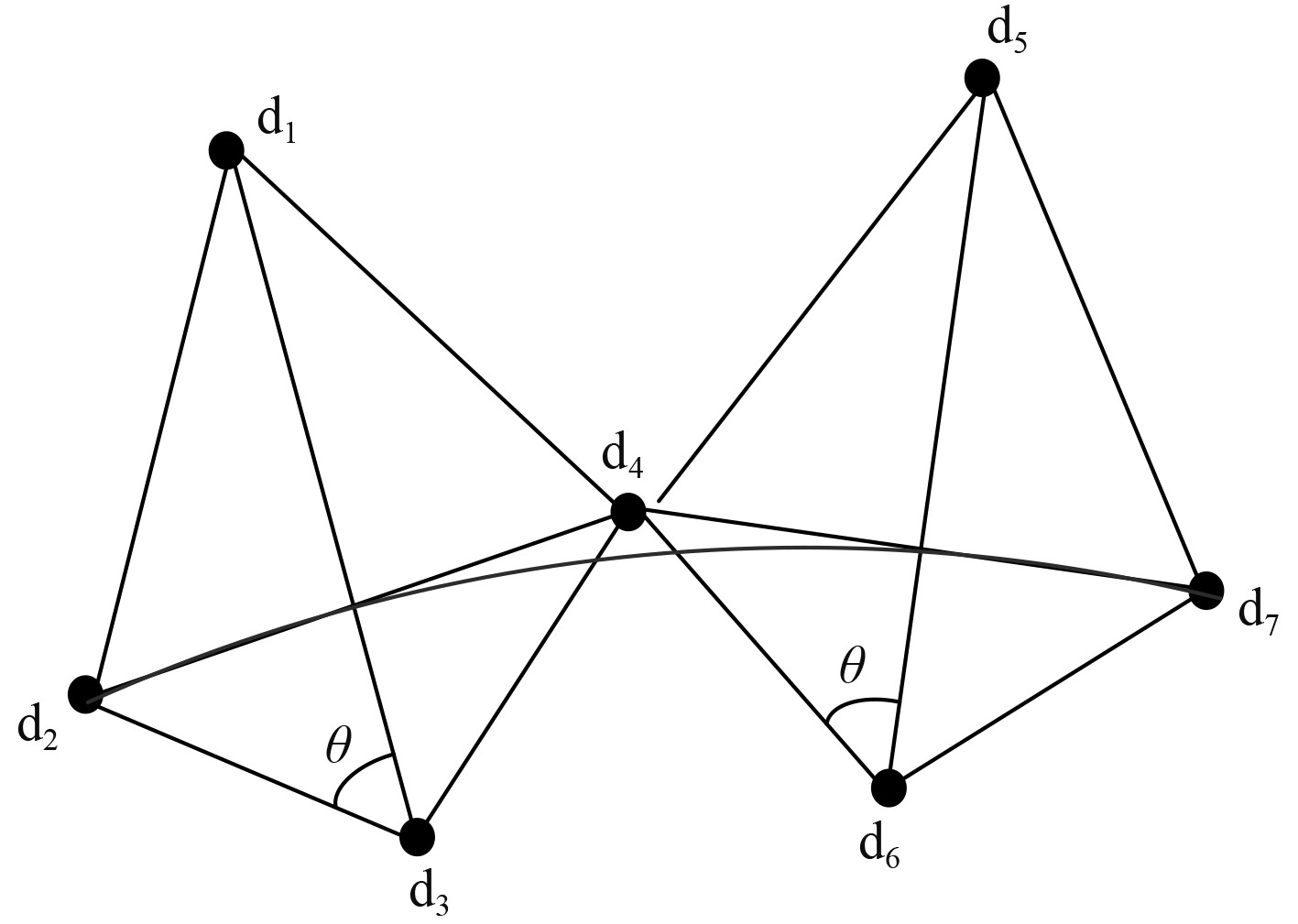
NURBS曲线的拟合过程用图3表示。

基于模块化设计思路的三体船曲面设计分为下述4步：

1）确定特征点元素

根据三体舰船的区域特性，建立特征点控制方程如下式：

$\begin{array}{*{20}{l}} {{f_1} = \min \psi (x,y,z)}，\\ {{f_2} = \max L(t)}，\\ {{f_3} = \min C(t)}，\\ {{f_4} = {F_{x,y,z}}(t)} 。\end{array}$

其中： $\psi (x,y,z)$ 为三体船的剖面曲率参数； $L(t)$ 为三体船的宽度系数； $C(t)$ 为三体船的长度系数； ${F_{x,y,z}}(t)$ 为三体船的高度系数。

2）由特征点建立三体船的特征型线

根据三体船的长度系数 $C(t)$ 与剖面曲率参数 $\psi (x,y,z)$ ，建立纵向特征型线如下式：

${f_s}\left( x \right) = \frac{1}{k}{x_t}gC{\left( t \right)^{{\alpha _0}}}\psi (x,y,z) \text{。}$

其中：k为曲线的曲率参数； ${\alpha _0}$ 为船舶龙骨的纵倾角。结合宽度系数 $L(t)$ 和高度系数 ${F_{x,y,z}}(t)$ ，建立三体船舶的横剖面曲线如下式：

${f_s}\left( x \right) = \frac{1}{{{F_{x,y,z}}(t)*k}}{x_t}gL{\left( t \right)^{{\alpha _0}}} \text{。}$

3）三体船的型线优化

使用NURBS曲线函数对三体船的特征曲线进行优化，首先建立海水流场的物面条件：

$\begin{gathered} \frac{{{\partial ^{}}\psi }}{{\partial \tau }} = 0 ，\\ \frac{{{\partial ^{}}\psi }}{{\partial \tau }} - Vn = 0。\\ \end{gathered}$

式中： $\tau$ 为法向量，即表面不可穿透^[3]。定义海水的波动方程为 $H(x,y,z) = 0$ ，则船体的型线优化模型如下式：

${F_n}(s) = \frac{{{k_1}{v_x} + {k_2}{v_y} + {k_3}{v_z}}}{{\sqrt {{H_x}^2 + {H_y}^2 + {H_z}^2} }} \text{。}$

式中： ${k_1}$ ， ${k_2}$ ， ${k_3}$ 分别为3个坐标轴方向的纵向特征系数； ${v_x}$ ， ${v_y}$ ， ${v_z}$ 分别为3个坐标轴的横剖面特征系数。

4）由三体船型线建立三体船的特征曲面

由线到面的设计过程借助三维软件SolidWorks完成，以特征点为坐标原点，在选定的型线上建立参考基准面，然后通过型线与基准面的平移、旋转、缩放、扫略等变换，生成三体船的特征曲面。

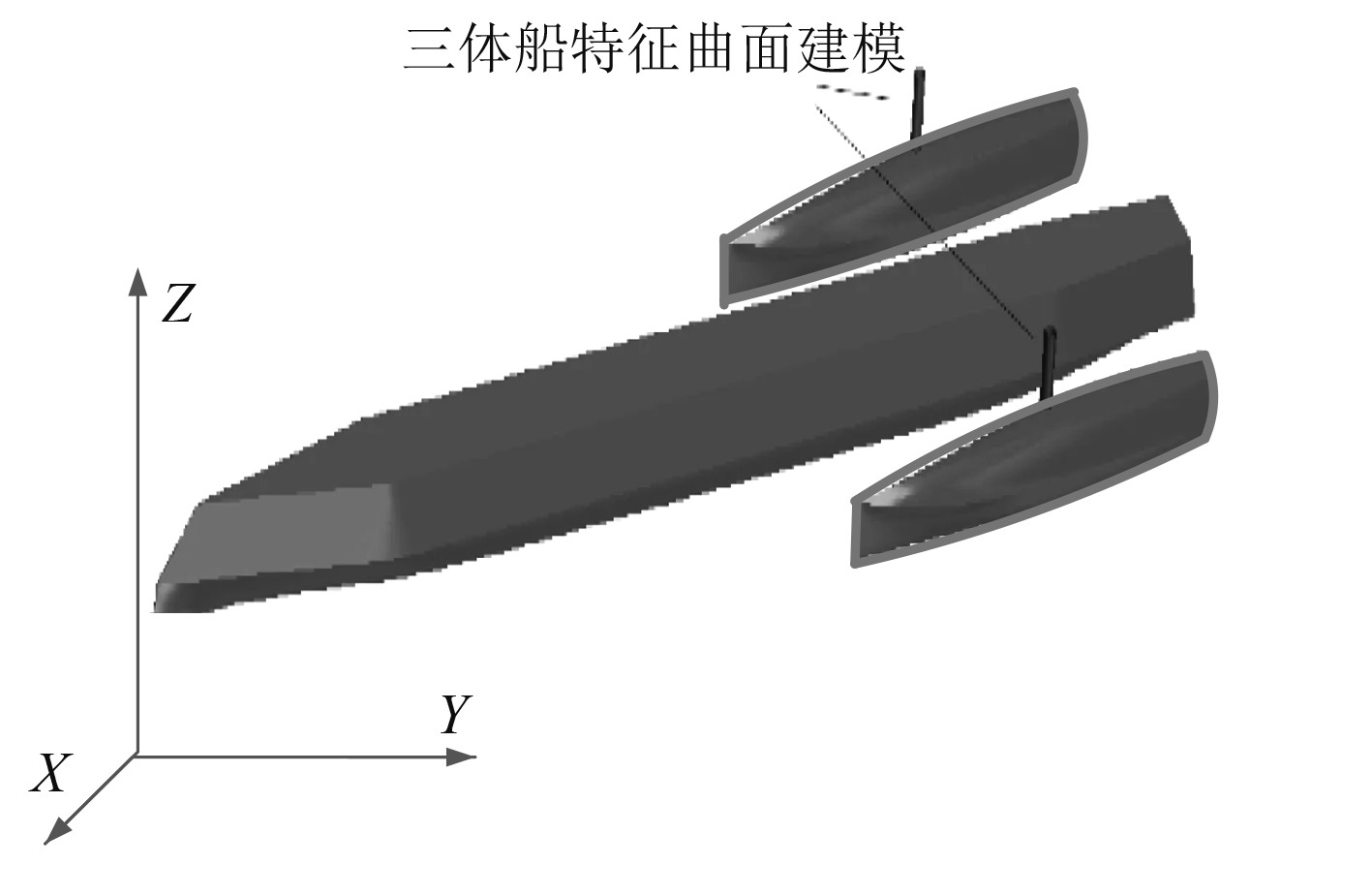
图4为基于SolidWorks产生的三体船特征曲面。

2.2 三体船流体动力学特性分析

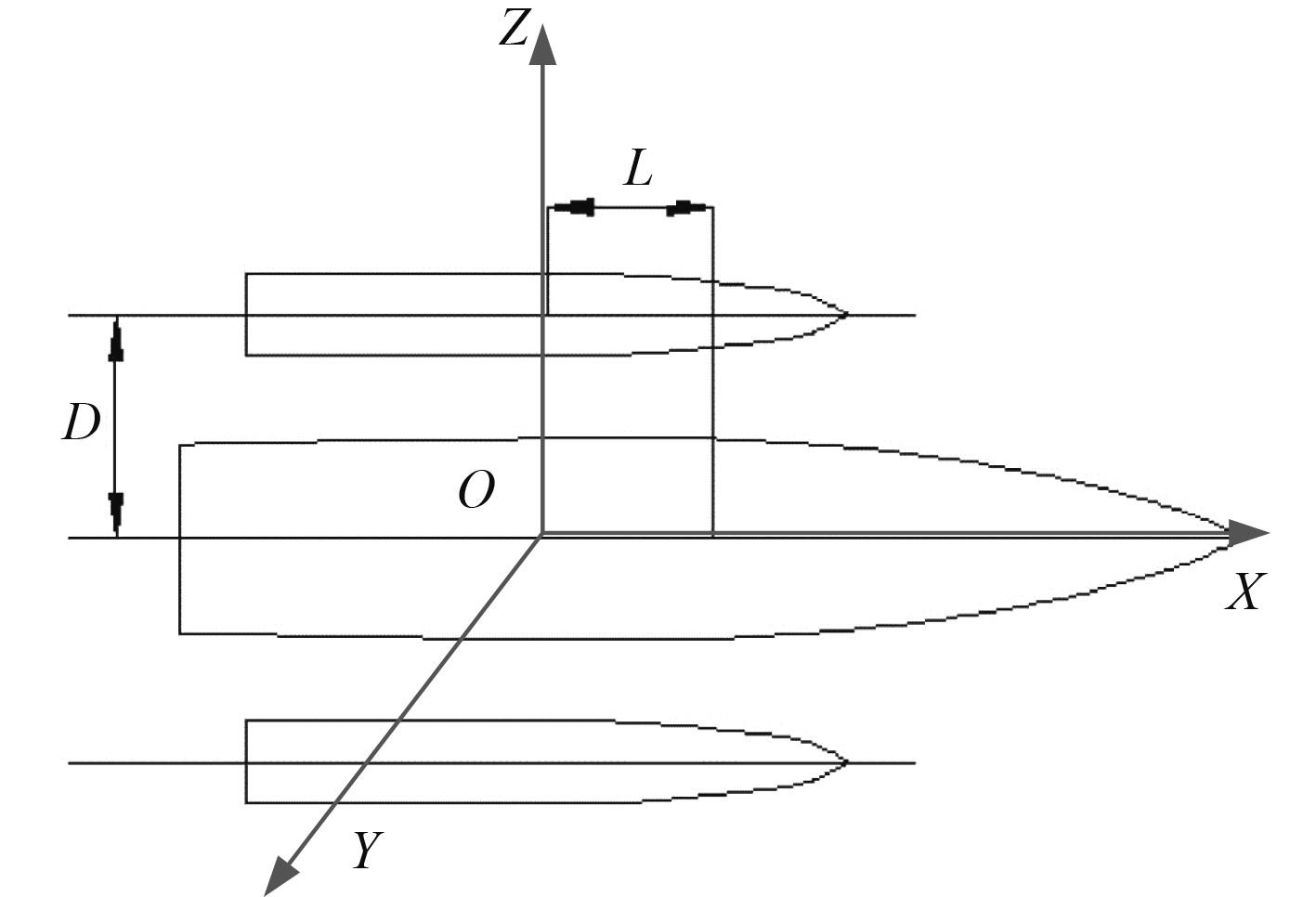
在型线设计的基础上，对三体船的阻力和流体动力学性能进行数学建模和仿真分析，建立三体船的运动坐标系如图5所示。

如图，运动坐标系选取速度方向为OX正向，OY与左舷方向重合，OZ垂向向上，在该坐标系下建立三体船的速度势 $\psi$ 方程为：

${\Delta ^2}\psi {\text{ = }}0 \text{，}$

建立三体船的运动模型为：

$m\frac{{\partial \left( {\rho {u_x}} \right)}}{{\partial t}} + m\frac{{\partial \left( {\rho {u_x}{u_y}} \right)}}{{\partial t}} = m\frac{\partial }{{\partial t}}\left[ {\mu \left( {\frac{{\partial {u_x}}}{{\partial y}} + \frac{{\partial {u_y}}}{{\partial x}}} \right)} \right] + {F_i}\text{。}$

式中： ${u_x}$ ， ${u_y}$ 分别为运动速度分量； ${F_i}$ 为三体船受到的惯性合力。

在流体特性分析时，海水和空气两种流体视为不相容，假设三体船附近的海水和空气流体计算域分别为 ${V_1}$ 和 ${V_2}$ ，定义函数三体船的界面函数 $\alpha \left( {x,t} \right)$ 为：

$\alpha \left( {x,t} \right) = \left\{ \begin{gathered} 0\;\;x \in {V_1} ，\\ 1\;\;\;x \in {V_2} 。\\ \end{gathered} \right.$

式中： $x \in \left( {x,y,z} \right)$ ， $\alpha \left( {x,t} \right)$ 满足

$\frac{{\partial \alpha }}{{\partial t}} + u\frac{{\partial \alpha }}{{\partial x}} + v\frac{{\partial \alpha }}{{\partial y}} + w\frac{{\partial \alpha }}{{\partial z}} = 0 \text{。}$

使用流体的VOF函数 $\varphi$ 积分可得流场 $S\left( V \right)$ 的表达式：

$\int\limits_S {\frac{\partial }{{\partial {t^{}}}}\left( {{\rho _0}\varphi } \right){\rm{d}}V + \int\limits_{}^{} {{\rm{div}}\left( {{\rho _0}\bar \varphi } \right){\rm{d}}V} = } S\left( V \right) \text{。}$

式中： ${\rho _0}$ 为流体的密度。

2.3 三体船流体动力学特性仿真

使用仿真平台Matlab对三体船的流体动力学特性进行仿真，仿真的输入信号包括三体船的型线方程、运动模型和海浪波形函数。其中，输入的海浪波形函数如下：

$\zeta(t)=\sum_{i=1}^{n} \xi \cos \left(k \psi \pm \omega t+\varepsilon_{i}\right) \text{。}$

式中： $\psi$ 为幅值； $w$ 为频率^[4]；k为周期波数； ${\varepsilon _i}$ 为相位角。

三体船仿真模型参数如表1所示。

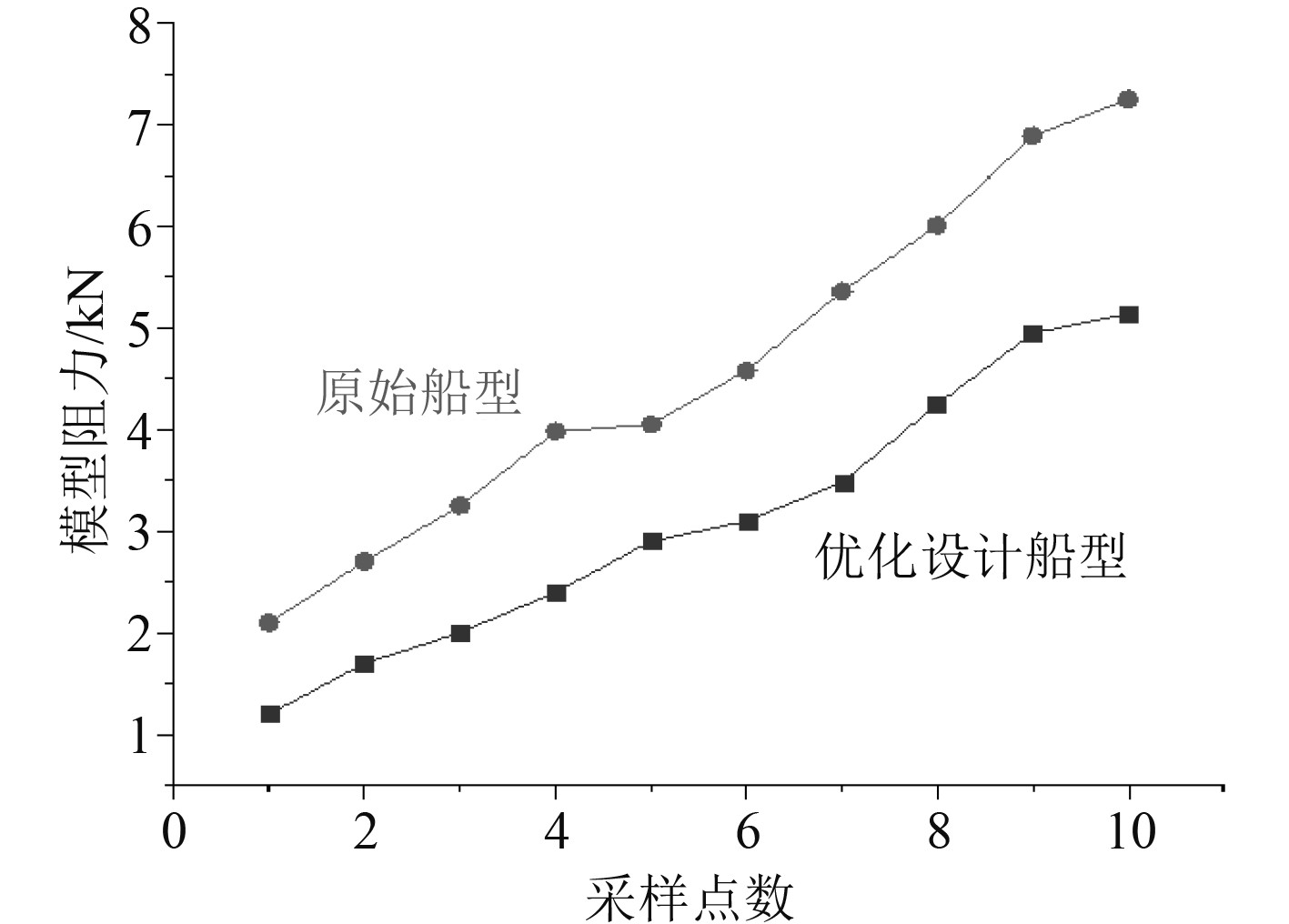
图6为三体船优化时设计前后的模型兴波阻力曲线对比。

3 结　语

三体船作为一种水动力特性更好的新型船舶，目前已经成为研究热点。本文结合模块化设计理念，针对三体船的总体重点利用NURBS曲线完成型线优化设计，基于型线设计完成了三体船的特征曲面设计，并对三体船进行流体动力学特性仿真分析。