0 引　言

船舶零件是用于船舶制造和维修中的零件，当下海洋工程的迅速发展，零件的市场需求和节奏的逐渐增加，并且产品周期较短，传统的生产方式已经不能满足生成需求，因此，对于零件的设计和制造也造成极大挑战^[1]。工程师在进行零件设计时，设计的精度直接影响零件制造后的使用情况。一旦零件的精度存在不足^[2]，将导致相关船舶结构以及相关设备的使用性能，严重则会降低船舶的安全运行^[3]。3D打印是一种快速成型技术，也将其称为增材制造，其主要是依据数字模型文件完成物体的设计，其可通过不同的材料，完成不同物体的打印，在设计过程中实现一次成型，省去多次打磨的步骤。

为保证船舶零件精度，王友利等^[4]对此进行研究后，以功能尺寸最短路径原理为基础，提出相关零件尺寸设计方法；鲁宇明等^[5]针对零件加工布局，提出基于改进MOEAD算法相关方法。上述方法均可提升零件的制造精度，但是，制造后的零件表面仍存在一定粗糙或局部契合精度不足等问题。因此，本文提出基于3D打印的船舶零件高精度设计方法，通过该方法对零件进行设计，以此保证零件制造后精度。

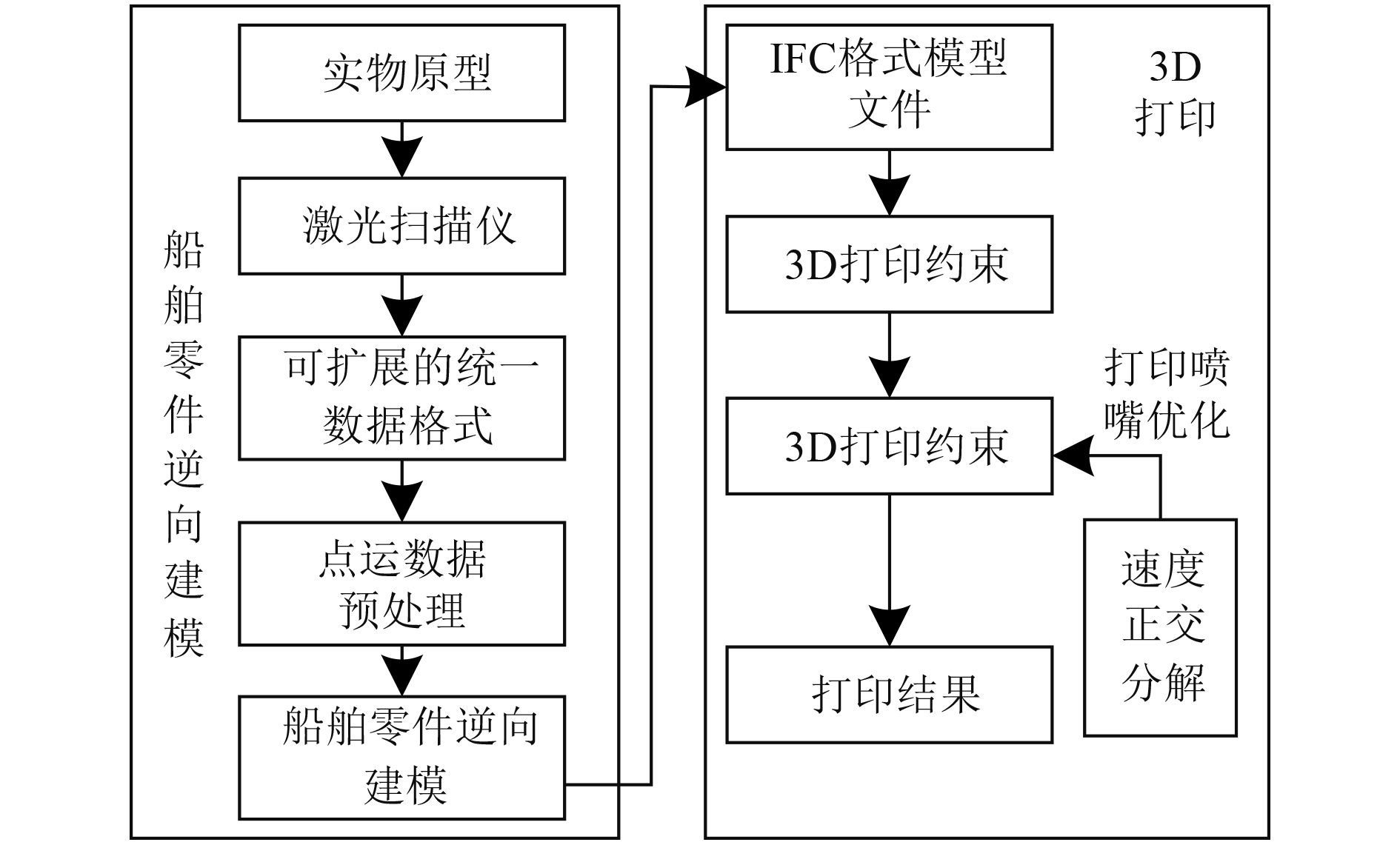
1 船舶零件高精度设计 1.1 船舶零件高精度设计方法架构

船舶零件的类别、复杂程度、应用部位以及尺寸大下等均存在明显差异，由于船舶应用场景的特殊性，所有的船舶零件存在一个共同点，即是该类零件的精度要求较高^[6]，具有极高的契合度，以此可保证船舶在海面的行驶安全。零件制作精度取决于零件的设计精度，因此，本文提出基于3D打印的船舶零件高精度设计方法，该方法的框架如图1所示。

1.2 船舶零件逆向建模 1.2.1 船舶点云数据获取和处理

通过激光扫描仪对设计的船舶零件实体进行扫描，获取船舶零件的实体点云数据，并通过可扩展的统一数据格式(IFC)对数据进行拟合，在拟合过程中，实现船舶零件点云数据的格式转换和存储，为后续船舶零件设计提供可靠数据依据。完成船舶零件点运数据获取后，为保证零件设计精度，需对获取的数据实行精简处理，去除数据中的无效和冗余数据，保留精简数据，以此提升船舶零件的设计精度。采用模型特征策略完成船舶零件点云数据的精简处理，该策略是对模型特征复杂区域中的点云数据进行大部分保留，对其他相对简单区域中的点云数据则进行小部分保留，其以法矢夹角为准则完成。点云数据中任意一点用p_i表示，将p_i和其 $ k $ 邻近点的法矢量点乘积结果的均值定义为法矢夹角，用C(i,j)表示，其计算公式为：

$ C\left( {i,j} \right) = \frac{1}{k}\sum\limits_{j = 1}^k {\left| {{n_{{x_i}}} \cdot {N_{{X_j}}} + {n_{{y_i}}} \cdot {N_{{Y_j}}} + {n_{{z_i}}} \cdot {N_{{Z_j}}}} \right|}。$

(1)

式中： $ \left( {{n_{{x_i}}},{n_{{y_i}}},{n_{{z_i}}}} \right) $ 和 $ \left( {{N_{{X_j}}},{N_{{Y_j}}},{N_{{Z_j}}}} \right) $ 均表示法矢量，前者对应p_i，后者对应 $ k $ 邻近点。

依据该公式可完成船舶零件点云数据的分级处理，并依据采样比例对数据进行不同程度的精简处理，以此得出精简后的船舶零件点云数据。

1.2.2 船舶零件几何模型重构

依据上述小节舰船零件点云数据精简处理后，采用扫描实体(SSR)的表达方式进行船舶零件几何模型重构，该重构主要由精简点云数据切片、边界轮廓确定以及拉伸实体3个部分完成。在进行切片扫描几何模型重构过程中，如果零件的结构不存在斜度，则通过多个直线段进行拟合，每个线段均对应一个切片，通过各个切片之间的连接，还原船舶零件的实际情况，在该情况下，直线段越短，则可更好的保证的切片精度，以此提升船舶零件几何模型重构精度。如果船舶零件存在极小的弧度，则采用二阶曲线为水平线，使船舶零件位于水平切线位置。对船舶零件进行切割，形成 $ J $ 个分片，并且切片为平行模式，同时按照切线方向进行拉伸处理。将精简处理后的点云数据簇进行投影，使其位于 $ x,y $ 平面上；在此基础上，对二次多项式进行拟合，投影至(x_i, y_i)平面上，且该平面上的点数量用 $ n $ 表示，该拟合采用最小化平方误差完成。如果 $ x $ 轴为主方向，则得出：

$ E = \sum\limits_{i = 0}^n {{{\left| {{y_i} - p\left( {{x_i}} \right)} \right|}^2}} 。$

(2)

式中：p(x_i)表示内插值，对应第 $ k $ 次多项式，并可采用线性方程组进行描述；该插值的构建可通过矩阵方程逆变换得出的二次多项式完成。

在上述的基础上，可获取零件的曲线f(x)，且 $ f\left( x \right) = A{x^2} + Bx + C $ ；同时对该曲线上各个插值线的切线进行计算，获取其导数；并依据导数结果求解曲线斜率 $ \tan {t_i} $ ，其计算公式为：

$ \tan {t_i} = 2Ax + B 。$

(3)

式中： $ A $ ， $ B $ ， $ C $ 均表示常数。

依据上述步骤即可完成点云数据的切分细化，并将每一个切片以Z轴为核心，进行旋转；旋转角度用 $ {\varphi _j} $ 表示，其为整体直角坐标 $ y $ 轴各个切片 $ j $ 对齐的法线方向之间夹角；各个切片的法线方向结果可通过切片的中间值 $ x $ 完成。船舶零件在建模过程中，如果存在截面部位，则采用弦高差算法对上述获取的切片进行判断，分析各点是否为切片特征点。在该过程中，需确定各个切片的阈值，其依据计算弦高差均值结果完成，弦高距离d_i和阈值 $ \sigma $ 的计算公式分别为：

$ {d_i} = \frac{{\left| {A{x_i} + B{y_i} + C} \right|}}{{\sqrt {A_i^2 + B_i^2 + C_i^2} }}，$

(4)

$ \sigma = \sum\limits_{i = 0}^{{m_j}} {\frac{{{d_i}}}{{{m_j}}}}。$

(5)

式中：m_j表示点云数量。

依据上述步骤对特征点进行判断后，按照法线方向对切片进行拉升处理，将该结果和平行切分拉伸结果相结合，即完成船舶零件几何模型重构。

1.3 船舶零件高精度设计实现 1.3.1 船舶零件3D打印方法

完成船舶零件几何模型重构后，采用熔融沉积成型的3D打印技术进行打印；该技术在设计时，依据原始模型主模型，且该模型中包含轻量化设计输出子模型，通过该结构方式，避免3D打印过程中，浪费打印材料，以此完成船舶零件的3D打印制作。船舶零件在3D打印过程中，打印方向可直接影响船舶零件打印质量，因此需对打印方向进行约束，使其沿应力集中方向；该方向的约束是依据压力源完成。并且，支撑设计也是影响打印质量的重要因素，该设计与悬空部分的完整性和可靠性存在直接关联，因此，需确定合理的支撑位置和支撑大小。除上述影响因素外，3D打印工艺参数设定也是直接影响打印质量的因素，打印参数包含动态层厚、支撑角度、轮廓、填充密度、走丝速度、支撑粘合强度等，设定合理的打印工艺参数，可保证打印出来的船舶零件外表的光滑程度更佳。

3D打印技术在进行打印过程中，影响因素较多，因此，为保证船舶零件高精度需遵守3D打印约束，包含打印精度约束、支撑约束、零件打印方向约束、船舶零件尺寸约束等。船舶零件3D打印过程，可理解为将3维的零件实行拆分，形成数个2维的零件，并对其进行加工的过程；在此基础上，将拆分的全部2维零件进行组合，再形成一个3维船舶零件。在此过程中，容易受到拆分台阶的影响，导致打印误差的发生，影响船舶零件的设计精度。在对船舶零件3D打印设计加工过程中，待打印的船舶零件用 $ L $ 表示， $ n $ 表示其分割的层数，X_i, i=1, 2, …, n表示船舶零件实物模型，且为第 $ i $ 层，采用叠加的方式将所有数量的X_i实行处理，则得出待打印的船舶零件，计算公式为：

$ T \approx \sum\limits_{i = 1}^n {{X_i}}。$

(6)

1.3.2 基于速度正交分解的3D打印优化算法

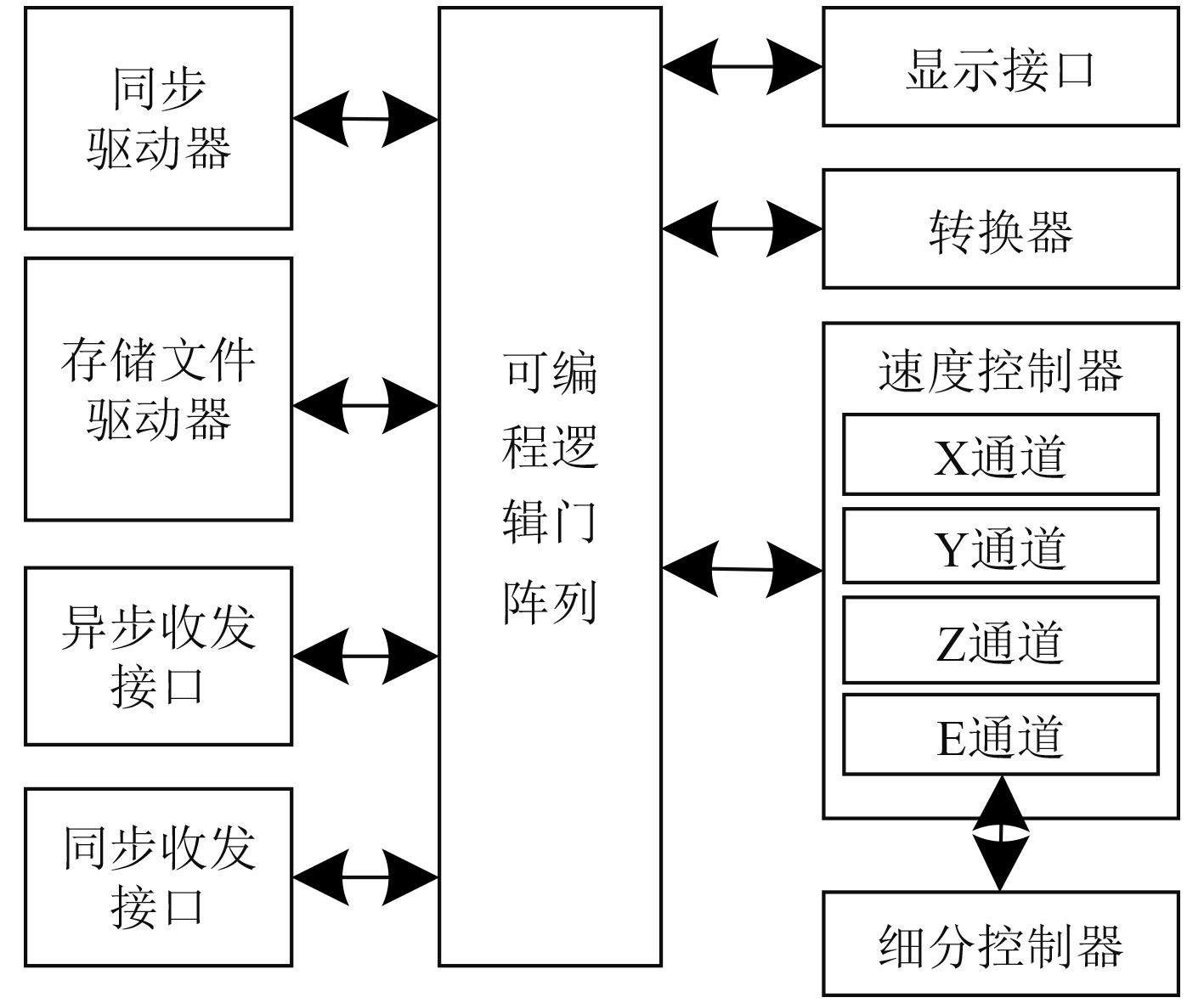
在打印过程中，喷头是通过不断扫描完成零件打印，在扫描过程中，如果扫描路径不合理，会影响打印的稳定性，以此直接导致零件设计的精度受到影响。为保证船舶零件的打印质量，实现高精度、高质量的船舶零件设计，对3D打印过程中喷头的扫描路径实行优化控制，提升零件的精度。该优化采用基于速度正交分解算法完成。该算法在现场可编程逻辑门阵列的基础上，采用嵌入式的方式完成，该打印优化控制方法的结构如图2所示。该打印优化控制算法主要是对3D打印机的扫描路径进行合理规划和控制，保证打印的稳定性，同时避免打印在扫描空行程时发生，发生打印拉丝现象。除此之外，通过速度控制器，控制打印的各个通道，提升打印方向约束效果，并且，在扫描路径规划时，打印方向能够实现任意变化，同时保证匀速运动。以此可极大程度提升船舶零件的3D打印质量，保证零件的设计精度。

2 测试结果与分析

为验证本文方法对船舶零件的设计精度情况，将某船舶零件生产企业生产的船舶零件作为测试对象，采用本文方法对其进行高精度设计，并获取设计结果。由于船舶零件种类较多，测试时间有一定约束，因此，为了降低测试耗时，仅选择齿轮零件作为测试对象，该齿轮实体相关参数见表1。

采用三维激光扫描仪对测试齿轮进行扫描，该扫描仪的扫描精度为0.04 mm，空间点距为0.22 mm，采用该扫描仪获取测试齿轮的点云数据，其数量为150 000个，该数据中包含无效和冗余数据，其占据比例为2.4%。3D打印的默认速度设定为95 mm/s，打印扫描的间距为1 cm。为测试本文方法对点云数据的精简处理效果，采用表面积变化率作为评价指标，该指标的公式为：

$ \rho {\text{ = }}\frac{{\left( {{S_m} - {{S'}_m}} \right)}}{{{S_m}}} \times 100\text{%} $

(7)

式中： $ {S_m} $ 和 $ {S'_m} $ 均表示曲面表面积，前者对应原始模型，后者对应精简处理后验模型。

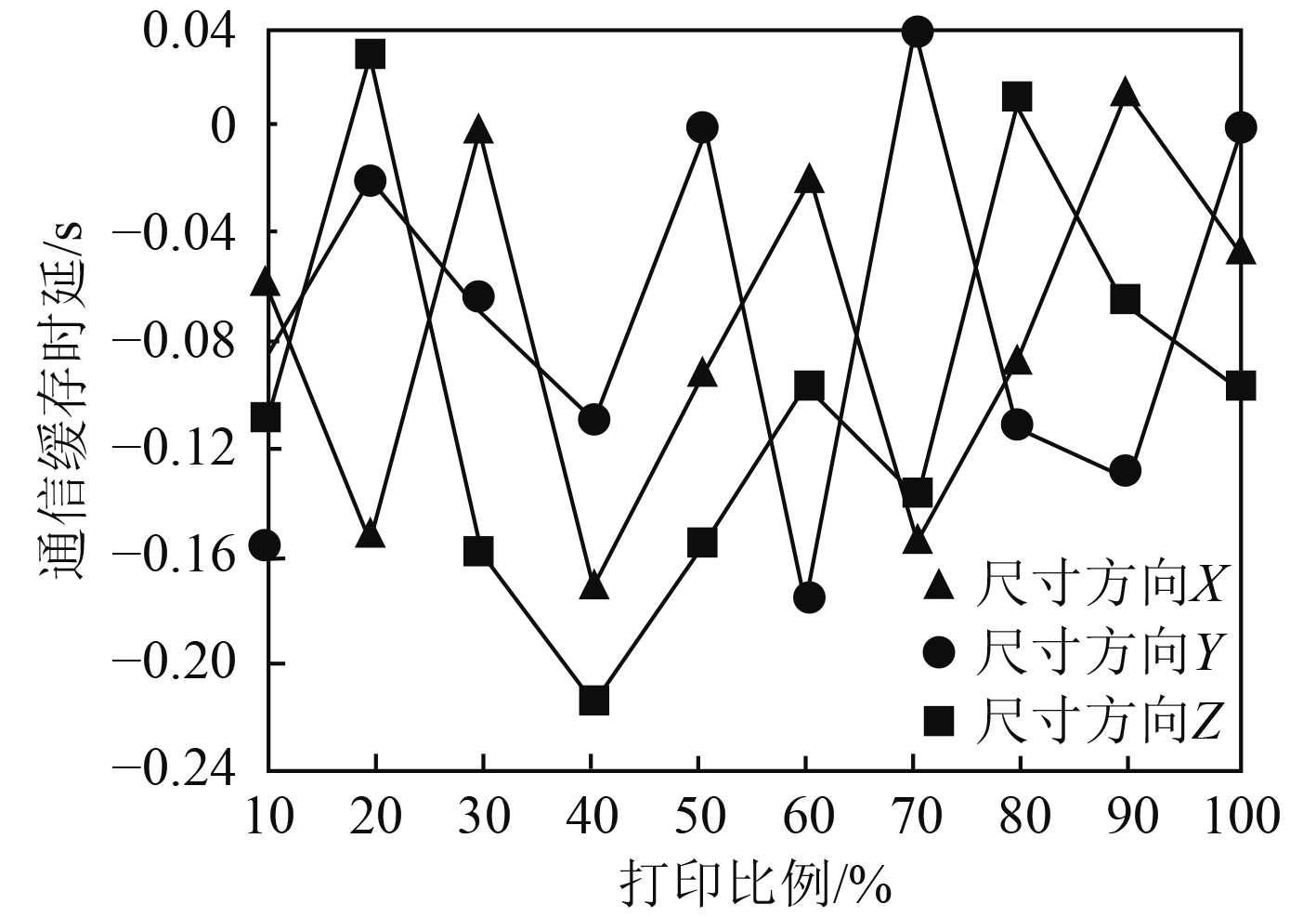
为测试本文方法的对船舶零件的设计性能，测试本文方法在不同的零件打印比例下，打印的误差结果，如图3所示。应用标准为误差范围在−0.040～0.040 mm之间。对图3测试结果进行分析后得出：采用本文方法对齿轮进行打印时，在不同的打印比例下，打印的误差结果均在要求的标准范围内，其中，最大误差值为−0.022 mm，最小误差值为0 mm。因此，本文方法具有良好的打印精度，可保证零件设计的精度。

为验证本文方法优化后，3D打印的效果，获取本文方法前后打印喷嘴在x，y，z三个方向上的误差结果，见表2。对表2测试结果进行分析后得出：随着打印面积的逐渐增加，优化前3D打印喷嘴在x，y，z三个方向上的误差结果均在0.35 mm以上，其中最大误差值为0.52 mm；优化后，3D打印喷嘴在x，y，z三个方向上的误差结果均在0.24 mm以下。因此，本文方法具有良好的优化效果，进一步提升船舶零件的3D打印精度，以保证零件设计精度。

为直观验证本文方法船舶齿轮零件的3D打印设计效果，获取本文方法优化前后，齿轮的设计精度结果，见图4和图5。对图4和图5测试结果进行分析后得出：本文方法在优化前，打印得出的齿轮零件虽然整体没有明显质量缺陷，但是存在一定的粗糙感；经过优化后打印得出的齿轮零件表面光滑，粗糙感显著降低。因此，本文方法能够保证船舶零件的高精度设计。

3 结　语

船舶零件是船舶组成的重要部分，零件的质量和制造精度是保证零件使用效果的前提。并且船舶零件类别和种类较多，其大小也存在显著差异，零件的复杂程度也不同，因此，需对零件进行设计。本文针对零件设计精度进行研究后，提出基于3D打印的船舶零件高精度设计方法，并对该方法的应用效果进行相关测试。结果显示：本文所提方法具有良好的应用性能，打印误差较小，并且打印出来的船舶零件质量极高，满足船舶零件的设计需求。