0 引　言

舰船导航系统为舰船提供航行方向、位置、速度、水平以及方位等基准数据^[1]，实现舰船目的地确定、路径计算和引导等，对舰船的航行进行监控和引导，以此保证舰船的航行安全^[2]。舰船在长时间的航行状态下，受到海面多种环境的影响以及不同磁场的干扰^[3]，会导致导航显示方向和其实际航行方向之间发生明显的偏差角，影响导航精度，偏离目的地。因此，如何提升舰船导航系统的控制精度，成为舰船管理中的重要内容。PLC控制器具有可编辑功能其主要是依据其内部含有的微处理器为核心^[4]，执行逻辑运算、顺序控制等操作，实现设备的自动化控制。

为保证舰船的安全运行，陈志超等^[5]对此分析后，基于改进LOS导航算法提出相关控制方法。祝亢等^[6]则研究舰船的航行特点后，提出基于深度强化学习的相关控制方法。上述方法均可有效控制舰船航迹，但是在应用过程中，仍旧存在一定超调量，因此，本文提出基于PLC的舰船导航系统高精度控制方法。该方法利用PLC的优势和功能，对舰船导航系统进行高精度控制。

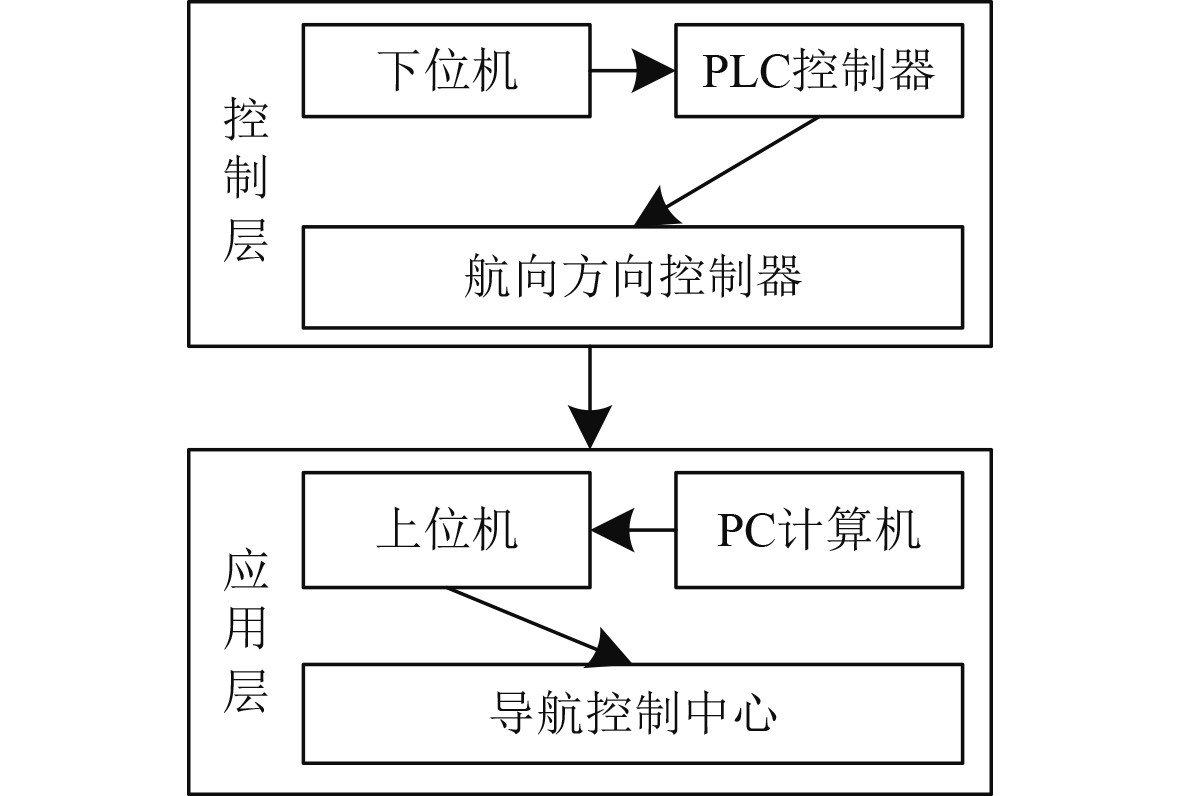
1 舰船导航系统高精度控制 1.1 基于PLC导航系统高精度控制方法框架

舰船在航行过程中，导航系统的导航精准性对于航行安全具有重要意义^[7]，因此，本文提出基于PLC的舰船导航系统高精度控制方法，其整体框架用图1描述。该方法以嵌入式PLC系统结构为主，其整体划分为2个部分，分别是控制层和应用层，控制层是由多种硬件设备组成，包含下位机、航行控制器、PLC控制器；应用层则是对控制层中的硬件进行初始化操作，同时向控制层下达控制指令以及呈现控制结果。

1.2 基于PLC的舰船导航控制实现 1.2.1 基于PLC的舰船导航控制原理

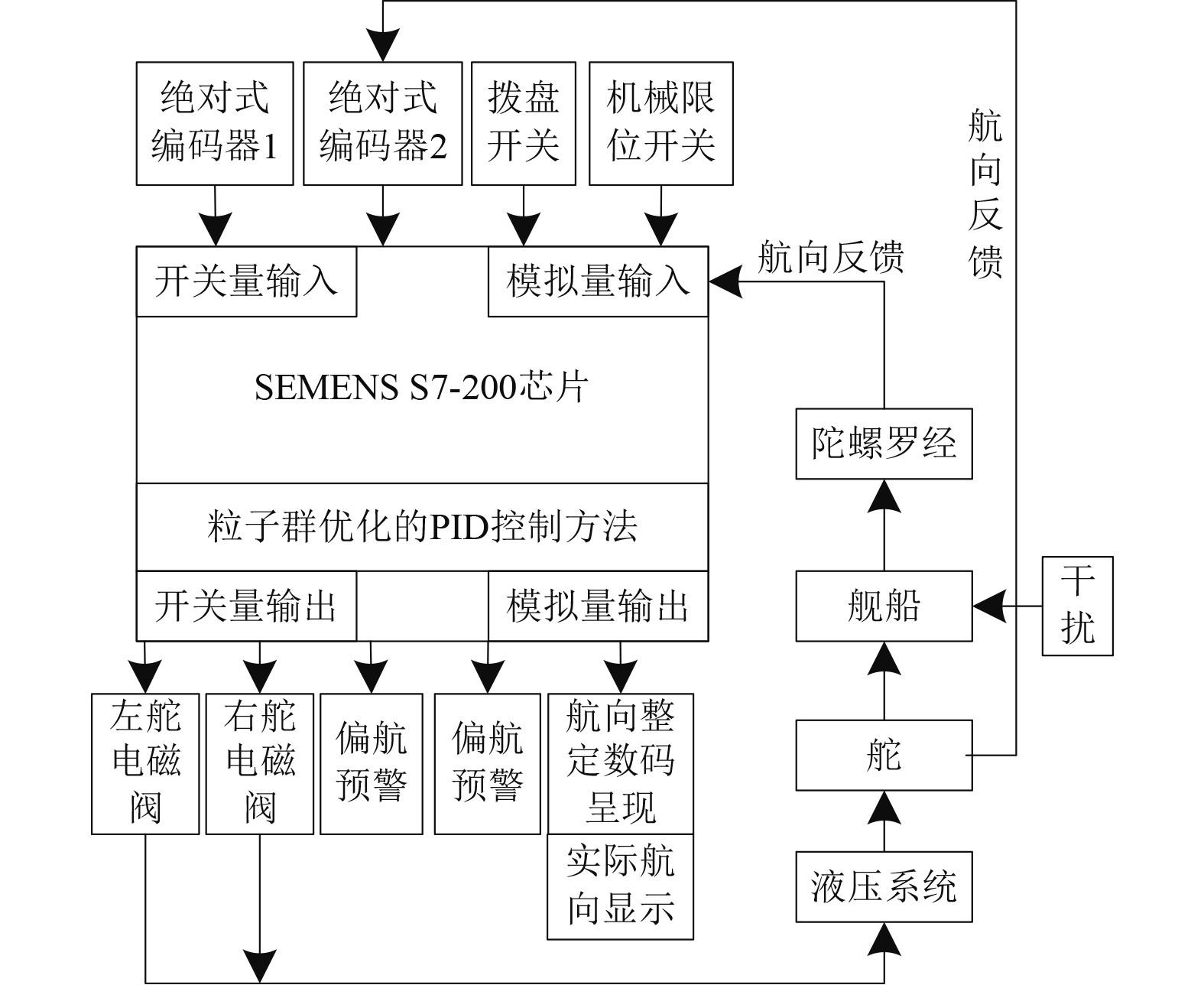
控制层中主要是采用PLC控制器为核心，对舰船导航系统进行控制，主要控制原理用图2描述。该控制器的芯片为SEMENS S7-200，设有3个扩展模块分别是EM223，EM232，EM2345。此外，为提升对舰船导航的控制精度，在其芯片设置粒子群优化的PID控制方法，对导航系统的相关控制参数实行控制，实现舰船导航系统的高精度控制。

依据图2可知：通过PLC控制器对导航系统进行控制后，可对舰船的舵轮、航向、舵角进行全面调整和控制，及时掌握舰船航行的整体情况^[8]。当导航显示方向和舰船实际航行方向之间发生偏差角时，控制器可向应用层发送偏航预警，应用层可通过上位机下达调整指令，进行偏差调整，保证导航精准度。

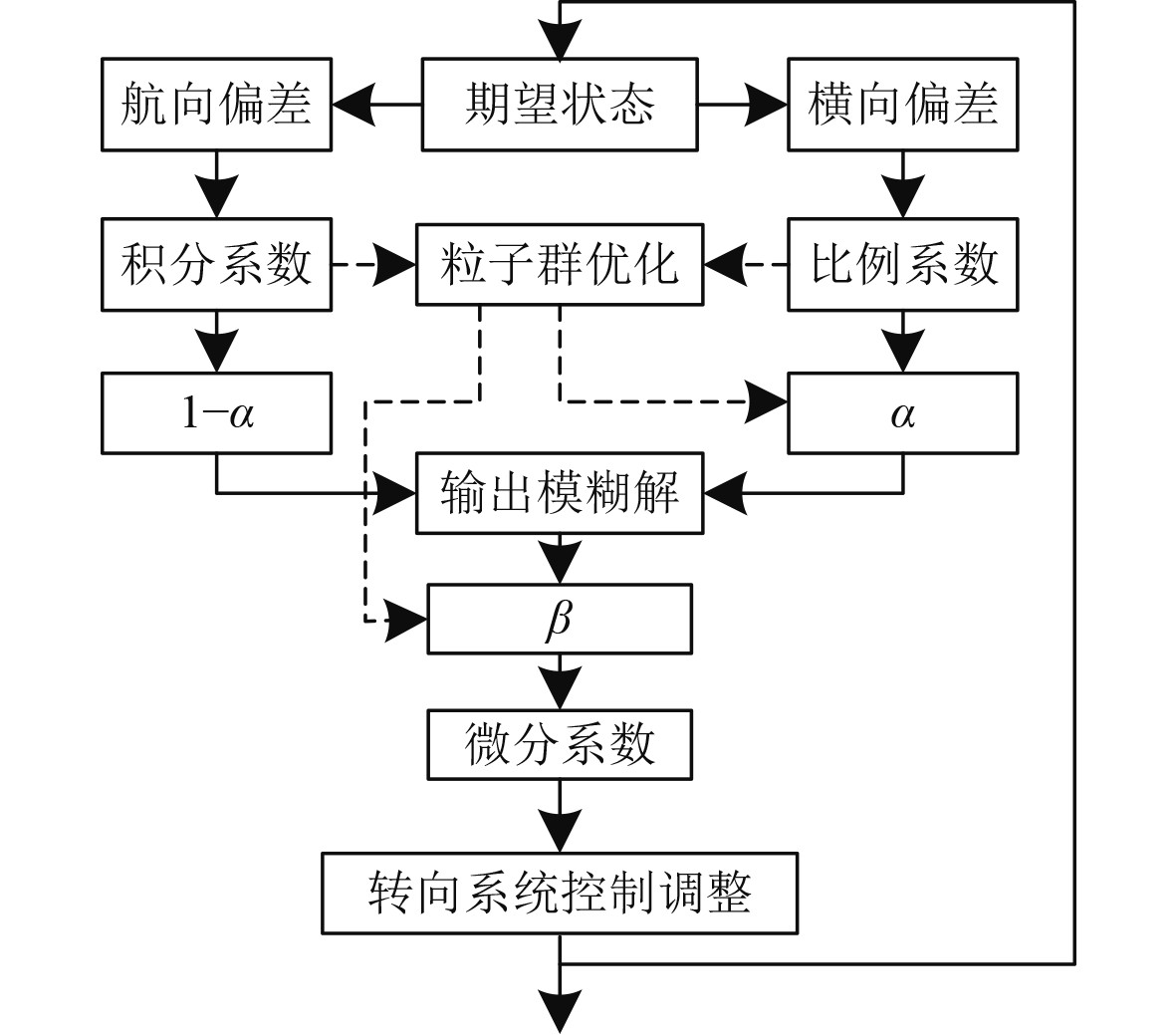
1.2.2 基于粒子群优化的PID导航系统控制方法

PLC控制器在对导航进行控制过程中，为提升控制的稳定性，引入基于粒子群优化的PID控制方法对控制器的参数进行优化控制。该优化方法主要对微分环节实行优化，掌握导航系统偏差信号的变化规律，以此保证控制的稳定性。本文控制方法，是以PID控制器为基础，在此基础上通过粒子群算法对控制器的加权因子 $ \alpha $ 和 $ \beta $ 实行优化，实现PID控制方法的自适应调节，以此保证控制效果。基于粒子群优化的PID控制方法结构用图3描述。

图中， $ \varepsilon ' $ 和 $ \phi ' $ 表示经过量处理后，舰船导航在横向和航向2种偏差结果。该算法主要是对PID控制方法的积分环节进行优化，其计算公式为：

$ u\left( t \right) = {k_p}e\left( t \right) + {k_i}\int _0^t e\left( t \right){\rm{d}}t + {k_d}\frac{{{\rm{d}}e\left( t \right)}}{{{\rm{d}}t}} ，$

(1)

$ {U_{\min }} \leqslant u\left( t \right) \leqslant {U_{\max }} \;。$

(2)

式中： $ {k_p} $ ， $ {k_i} $ 和 $ {k_d} $ 分别为比例、积分和微分系数；在 $ t $ 时刻下，舰船导航系统的偏差用 $ e $ 表示，且该偏差包含横向 $ \varepsilon $ 和航向 $ \phi $ 两部分偏差结果，即 $ e{\text{ = }}\varepsilon + \phi $ ； $ U $ 表示优化控制后的输出精度值。

该方法在控制过程中，其控制指标函数采用横向 $ \varepsilon $ 和航向 $ \phi $ 两部分偏差总和进行描述，计算公式为：

$ f = \alpha \int_0^\infty {t\left| {\varepsilon \left( t \right)} \right|} {\rm{d}}t + \beta \int_0^\infty {t\left| {\phi \left( t \right)} \right|} {\rm{d}}t \;。$

(3)

1.3 基于免疫算法的PID参数优化

PID在对导航系统进行控制过程中，导航系统会对自动舵不断下达调控指令，在此过程中，会发生高频干扰，导致PID控制方法在干扰下，引起自动舵频繁响应，增加导航系统控制随机性，发生超调量。因此，为实现舰船导航系统的高精度控制，采用免疫算法对基于粒子群优化的PID的导航系统控制方法的参数进行优化。免疫算法是依据人体防御机制进行模仿，在数据处理、优化控制等领域中均具有良好的应用效果，本文采用该算法进行基于粒子群优化的PID导航系统控制方法的参数优化，采用粒子描述待优化参数，可在循环迭代过程中获取最优适应度粒子，获取全局最优解，并且在寻优过程中，保证粒子的多样性和种群的完整性，以此保证寻优结果的全面性和可靠性。待优化参数 $ {k_p} $ ， $ {k_i} $ ， $ {k_d} $ ， $ f $ 组成待优化参数集， $ {X_i} $ 表示，则 $ {X_i}{\text{ = }}\left\{ {{k_p},{k_i},{k_d},f} \right\} $ ；对用于描述 $ X $ 的免疫粒子进行迭代处理，获取迭代后的最优适应度，并将该结果对应的粒子存储为记忆微粒。依据免疫机制中，抗体之间基于浓度的相互抑制作用，对种群进行更新；获取亲和力浓度结果，并将其进行降序排列，第 $ i $ 个粒子亲和度A_i的计算公式为：

$ {A_i} = J 。$

(4)

式中： $ J $ 表示绝对误差积分。

粒子概率H_i1的选择是通过A_i完成，其计算公式为：

$ {H_{i1}} = \dfrac{{{A_i}}}{{\displaystyle \sum\limits_{k = 1}^N {{X_i}{A_k}} }}。$

(5)

式中：A_k表示经过 $ k $ 迭代获取的亲和度； $ N $ 表示种群数量。

粒子浓度C_i的计算公式为：

$ {C_i} = \dfrac{1}{{\displaystyle \sum\limits_{k = 1}^N {{X_i}\left| {{J_i} - {J_k}} \right|} }} ，$

(6)

依据C_i选择粒子的概率计算公式为：

$ {H_{i2}} = \dfrac{{C_i^{ - 1}}}{{\displaystyle \sum\limits_{k = 1}^N {{X_i}C_i^{ - 1}} }} ，$

(7)

基于此粒子被选择的总体概率计算公式为：

$ {H_i} = \eta {H_{i1}} + \left( {1 - \eta } \right){H_{i2}} \;。$

(8)

式中： $ i = 1,2, \ldots ,N $ ； $ \eta = \left[ {0,1} \right] $ 表示权重系数。

获取公式(8)的计算结果，并按照降序进行排列，获取计算结果中的缺失粒子以及结果较小粒子，将两者采用上一代记忆微粒进行替代。

通过循环迭代对粒子的适应度值进行重新计算，获取最优粒子对替换进来的记忆微粒进行更新，以此实现 $ {X_i} $ 的优化。

该优化步骤如下：

步骤1　通过初始化对免疫微粒种群实行处理，并设定初始化参数。

步骤2　计算各个粒子的适应度，获取其中最优粒子。

步骤3　通过循环迭代对粒子的位置 $ x_j^i $ 和速度 $ V_j^i $ 进行更新，其计算公式为：

$ x_j^i\left( {k + 1} \right) = x_j^i\left( k \right) + V_j^i\left( {k + 1} \right)，$

(9)

$ \begin{split} V_j^i\left( {k + 1} \right) =&\eta V_j^i\left( k \right) + {c_1}{r_1}\left[ {\overline {P_j^i} \left( k \right) - x_j^i\left( k \right)} \right] + \\ &{c_2}{r_2}\left[ {P_g^i\left( k \right) - x_j^i\left( k \right)} \right]。\end{split} $

(10)

式中： $ {c_1} $ ， $ {c_2} $ 表示学习因子； $ {r_1} $ ， $ {r_2} $ 表示随机数； $ P_j^i $ 和 $ P_g^i $ 均表示最优位置，前者对应个体，后者对应种群。

步骤4　依据最新迭代获取粒子适应度更新记忆粒子信息库。

步骤5　当满足设定的最大迭代次数时，进入步骤6；反之则回转至步骤3进行重新迭代。

步骤6　获取的最优微粒位置的粒子结果即为优化后X_i的结果，以此完成控制优化。

2 测试结果与分析

为验证本文方法在舰船导航系统高精度控制中的应用效果，将本文方法用于某舰船导航系统控制中，该舰船主要用于远程进出口运输，且为满载状态，其详细情况用表1描述。

为验证本文方法对舰船导航系统的控制性能，采用绝对误差积分 $ \gamma $ 作为评价指标，计算公式为：

$ \gamma = \int_0^T {t\left| {\varepsilon \left( t \right)} \right|} {\rm{d}}t 。$

(11)

式中： $ T $ 表示最大迭代次数。

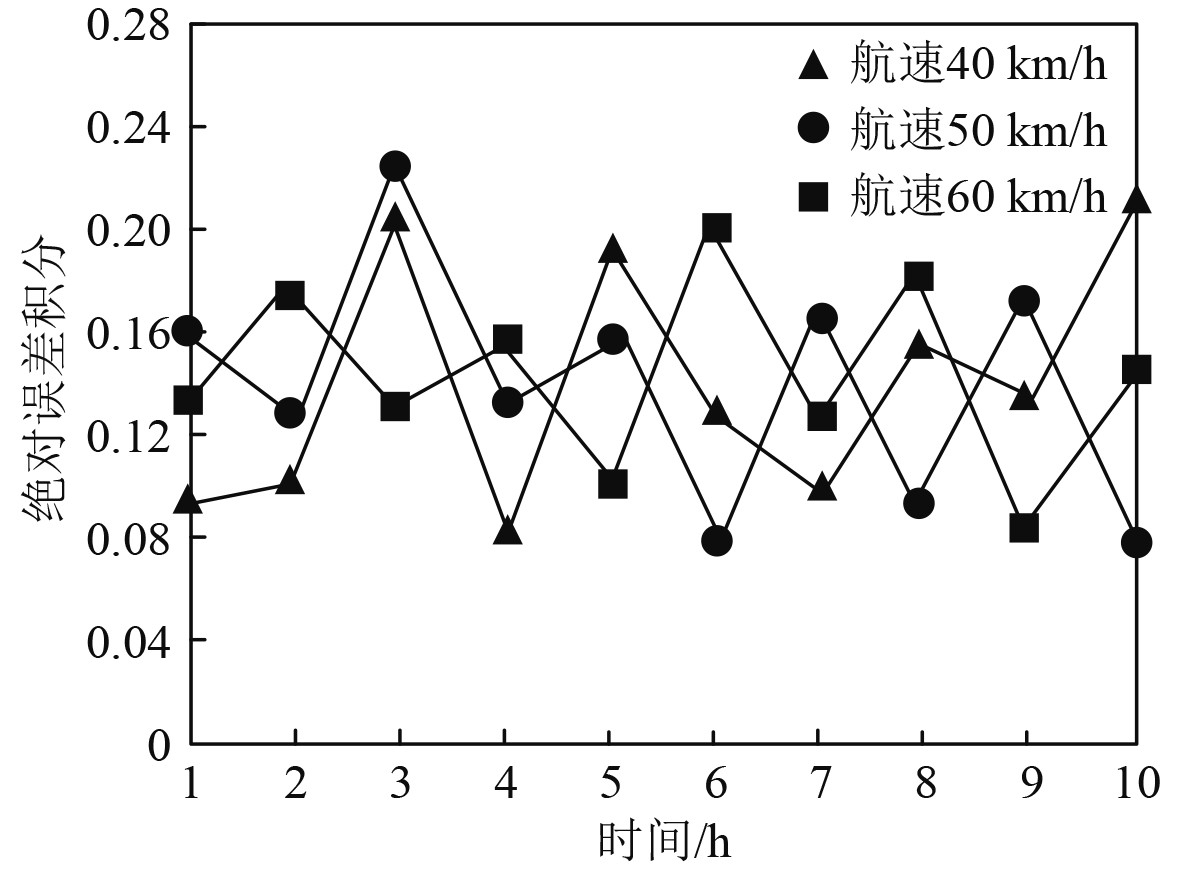
依据该公式计算舰船在不同速度下，指标的计算结果，如图4所示。由图4可知：舰船在不同的航行速度下，随着航行时间的逐渐增加，本文方法对舰船导航系统控制后 $ \gamma $ 的指标结果均在0.25以下，满足应用标准。其中最大结果为0.22左右，最小值为0.07左右。因此，本文方法具有良好的舰船导航控制性能。

为测试本文方法对舰船导航系统的高精度控制效果，采用横向和航向2个偏差作为衡量指标，获取本文方法在不同的航行距离下，2个偏差的结果，如表2所示。2个偏差的应用标准分别在(−2～2) cm和(−3.5°～3°)之间。由表2可知，应用本文方法后，有效完成舰船导航系统的高精度控制，使其横向和航向2个偏差结果均在应用标准范围内，其中横向最大误差为1.55 cm，航向最大误差为−2.2°。本文在进行导航系统控制过程中，将横向和航向2个偏差值作为粒子群优化的PID的导航系统控制方法对导航系统的控制指标函数，实现导航控制，因此可保证高精度的控制效果。

为进一步验证本文方法对舰船导航的高精度控制效果，在不同的舰船期望航向下，采用本文方法在有风干扰和无风干扰情况下，进行导航控制，获取控制过程中的超调量结果(应用要求超调量低于0.1%)，如图5所示。可知，采用本文方法对舰船导航系统进行高精度控制后，舰船期望航向角的不断变化，导航系统控制的超调量均在0.1%以内，其最大超调量为0.05%，最小超调量为0%。因此本文方法具有较好的舰船导航高精度控制能力，可保证舰船的导航精准程度。

3 结　语

舰船在航行过程中会受到海洋环境等干扰，导致航行精准度受到直接影响。本文研究基于PLC的舰船导航系统高精度控制方法，并对该方法的应用情况进行测试。结果显示，本文方法具有良好的控制性能，有效控制横向和航向2个偏差结果，导航高精度控制能力良好，可保证舰船的导航精准程度。