随着科学技术的快速发展,在舰船机电设备上安装非线性冲击缓冲元件成为保护机电设备安全运行的重要手段。隔振器作为缓冲元件之一,成为机电设备保护装置设计与开发的重点[1-3]。在设计隔振器时,要运用理论建模方法计算出冲击响应效果,确保隔振器受到碰撞时能够快速发展位移响应和加速度响应,最大程度减小对机电设备自身的冲击破坏。
1 舰船机电设备非线性冲击 1.1 冲击隔离在研究舰船机电设备非线性冲击前要分析冲击环境,冲击环境是在短时间内突然产生的扰动,包括冲击速度、冲击加速度和冲击位移。舰船受到冲击后,快速传递动能,呈现出非周期性的瞬态运动。冲击产生的瞬态运动具有不规则、波形复杂的特点,在理论研究领域,需将复杂的波形转化为性状规则的脉冲波形,如倒正弦波、锯齿波、矩形波、半正弦波等。强烈冲击波在对船舶机电设备产生瞬态冲击时先将能量存储在隔振器中,导致隔振器瞬间变形,之后再以缓和的形式发生固定振动,释放出隔振器能量,达到缓冲保护机电设备的目的[4-7]。冲击隔离器在处理冲击能量时,需快速响应冲击作用力,在冲击释放时间较长的情况下会放大冲击,冲击隔离传递效率如图1所示。
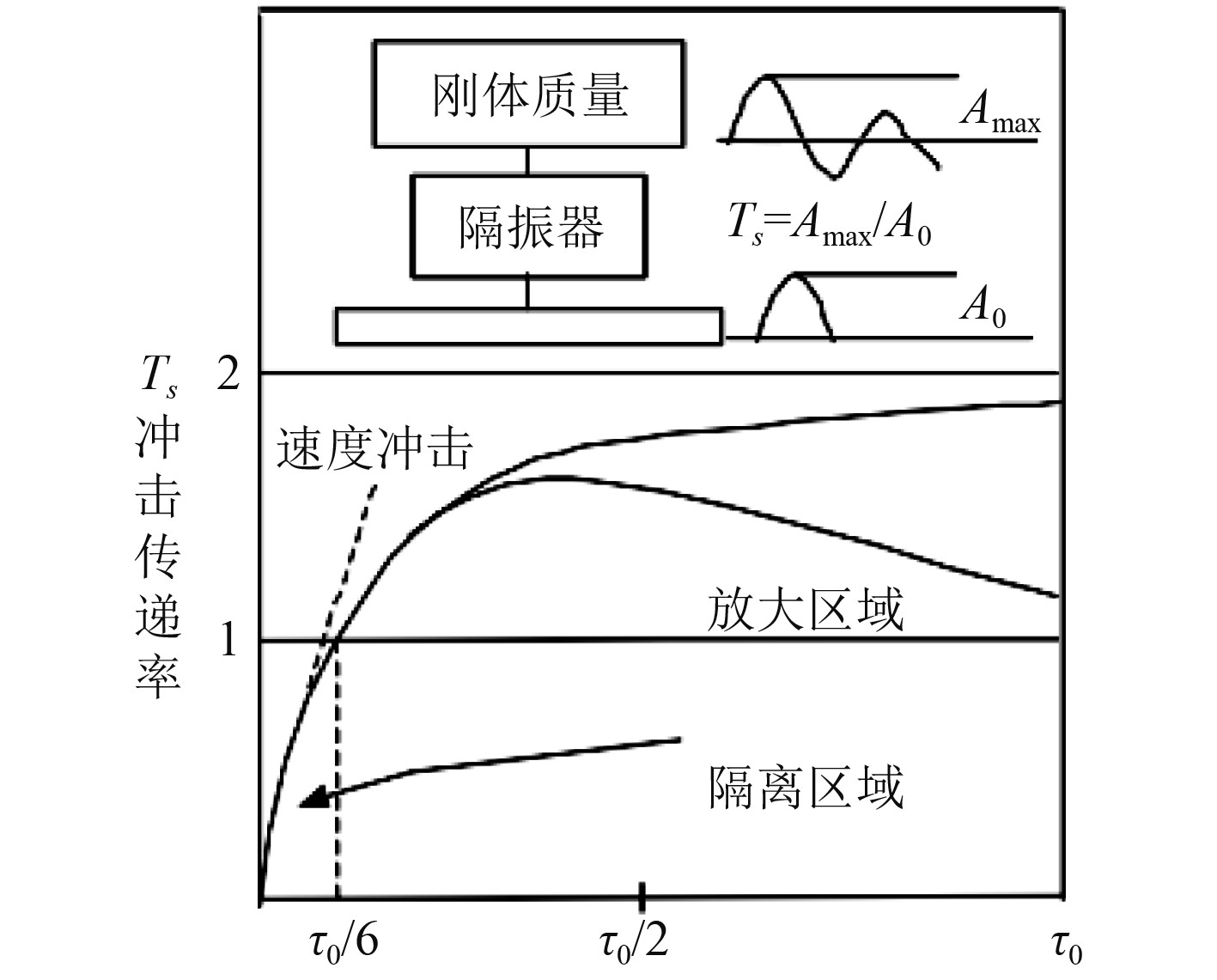
|
图 1 舰船机电设备冲击隔离传递效率示意图 Fig. 1 Schematic diagram of shock isolation transmission efficiency of marine electromechanical equipment |
非线性冲击隔振器主要用于缓冲瞬间冲击力对舰船机电设备带来的影响,要求隔振器具备缓冲和隔振功能,能够平衡处理传递加速度与物理位移之间的关系。非线性隔振器的刚度特性如图2所示。
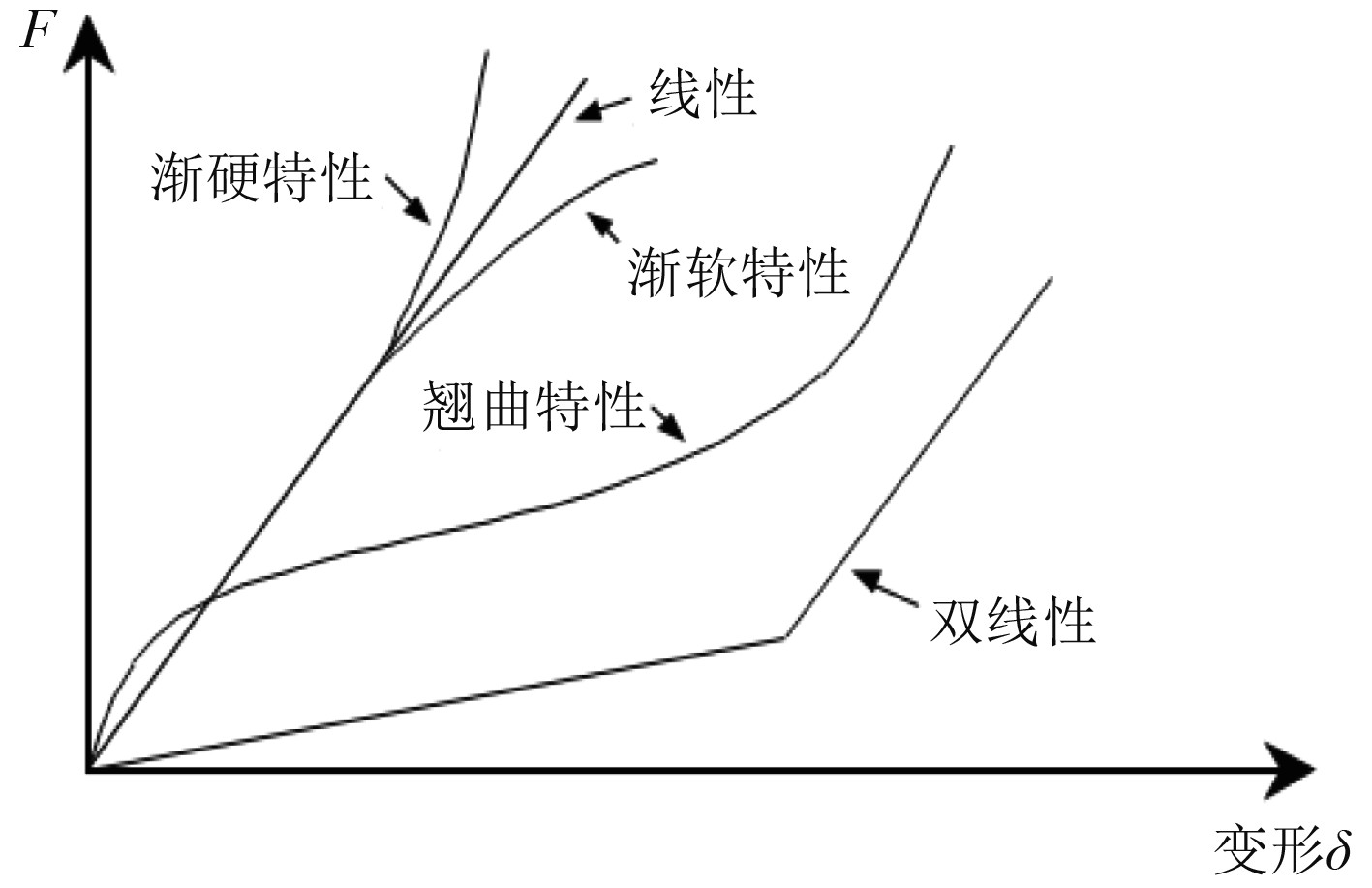
|
图 2 非线性冲击隔振器的刚度特性 Fig. 2 Stiffness characteristics of nonlinear impact isolator |
非线性隔振器分为多种类型,包括正切弹性隔振器、双曲正切弹性隔振器、双线性刚度隔振器、多项式弹性隔振器、翘曲刚度特性隔振器等。不同隔振器适用于不同的非线性冲击响应条件,包括:正切弹性隔振器采用渐硬隔振器刚度特性描述突然触碰底部后产生的最大位移量;双曲正切弹性隔振器用于描述机电设备表层受到起始刚度作用时产生的位移变化;通过减少在塑性范围内的屈服,进而起到降低机电设备受物体冲击力的影响;多项式弹性隔振器运用幂指数计算平方弹性和立方弹性,描述机电设备在渐硬状态下的连续变化;翘曲刚度特性隔振器将刚度曲线描述为S型,采用数值积分法处理数据。不同类型的非线性冲击隔振器采用不同的算法模型,以正切弹性隔振器为例,其函数表达式为:
| $ F(\delta ) = \frac{{2{K_0}}}{\text{π} }\tan \left(\frac{{{\text{π}} \delta }}{{2{\delta _n}}}\right) \text{。} $ |
式中:
| $ {F_{r\max }} = \frac{{2{k_0}{\delta _0}}}{{\text{π}} }\int_0^{{\delta _{\max }}} {\tan \left(\frac{{{\text{π}} \delta }}{{2{\delta _0}}}\right)} {\rm{d}}\delta 。$ |
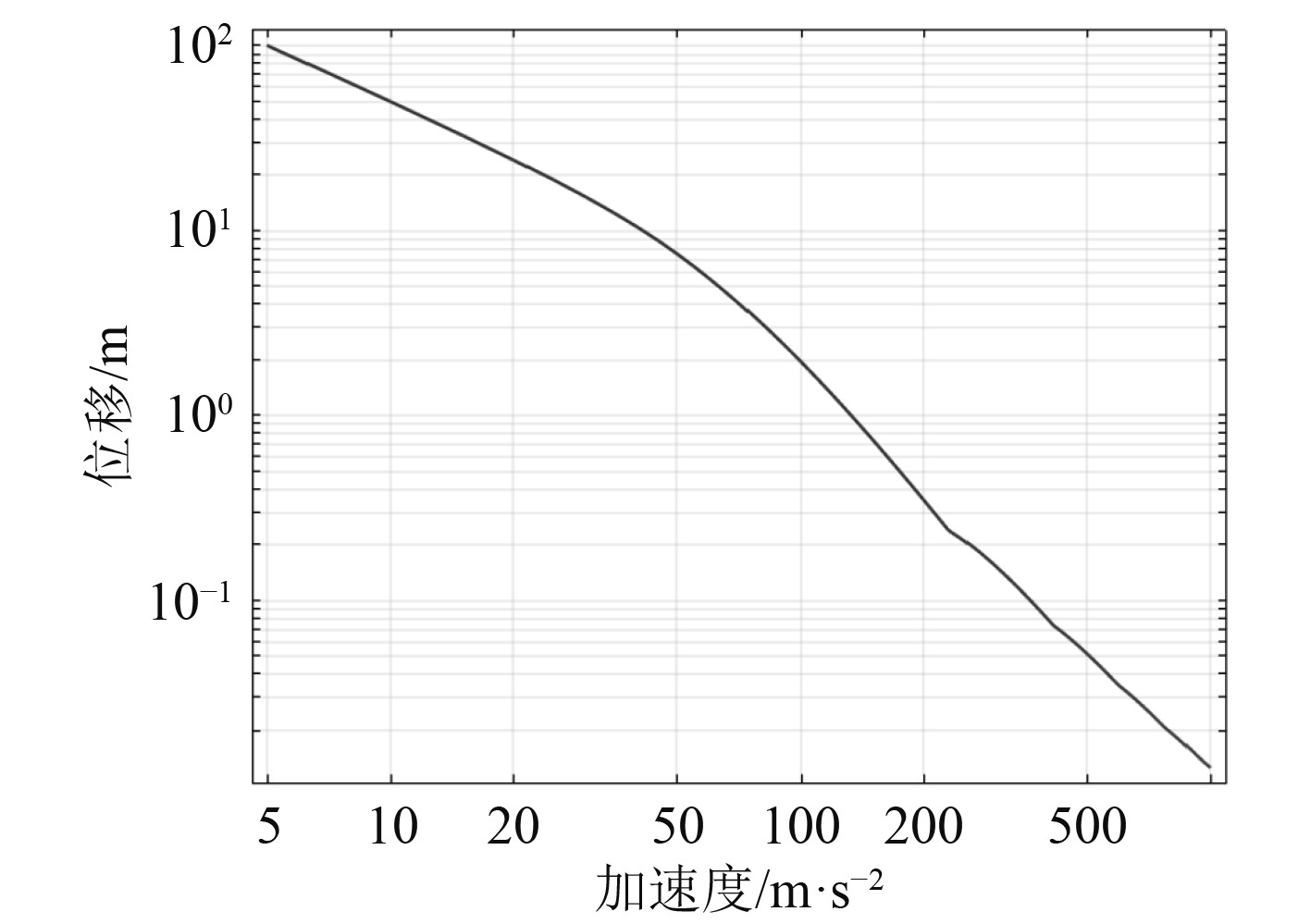
由图3可知,正切弹性隔振器在非线性冲击下的位移响应较小,加速度响应较大,为保证满足舰船机电设备的非线性冲击响应要求,对正切弹性隔振器的隔离系统进行优化设计,计算出加速度响应的最小值。在优化设计隔振器时,要充分考虑设备受到的冲击力最大允许值范围,控制设备与隔振器之间的位移量。
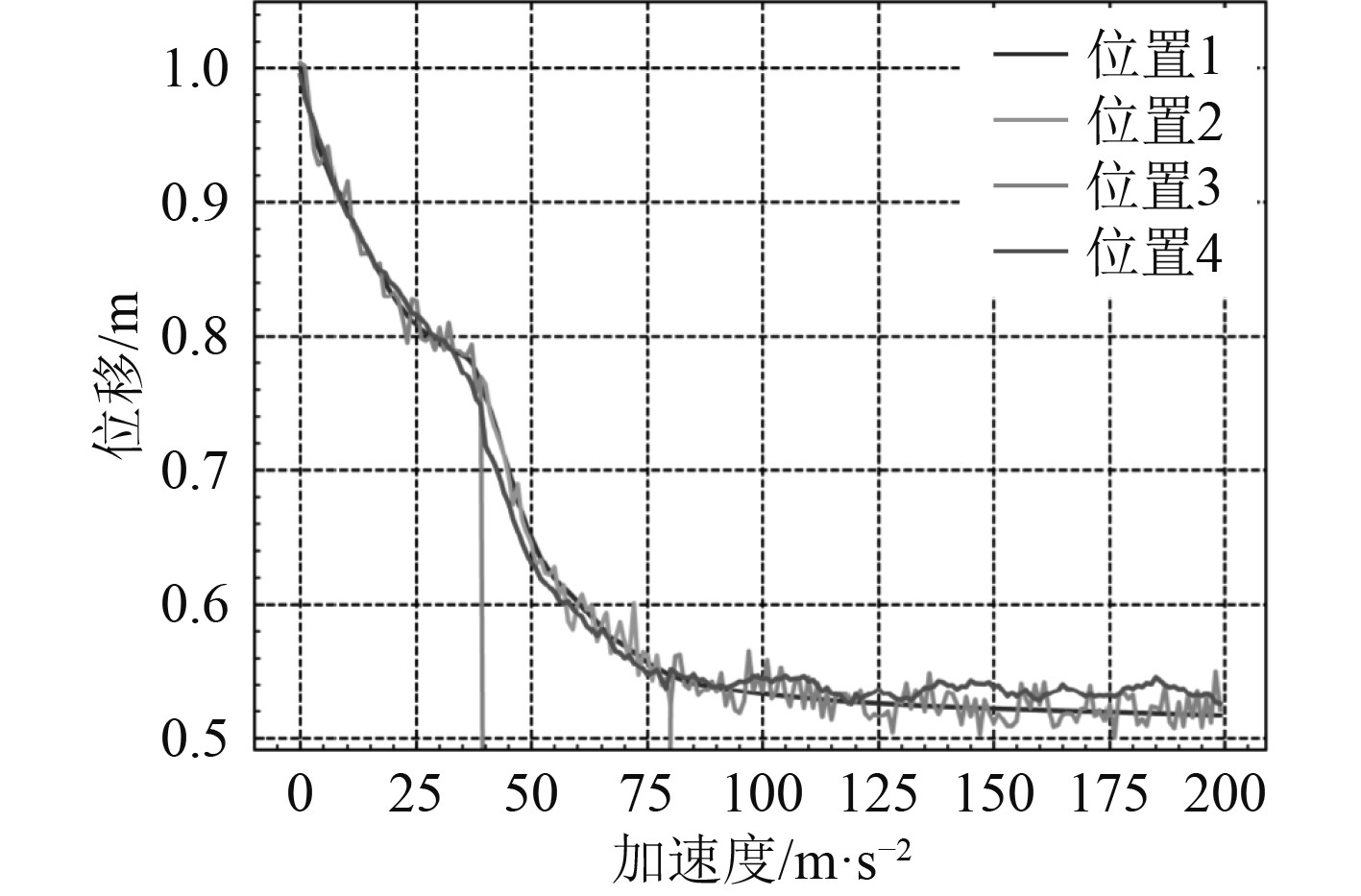
|
图 3 非线性冲击下正切弹性隔振器无阻尼隔离系统对冲击加速度和位移响应曲线图 Fig. 3 Response curve of non damping isolation system of tangent elastic isolator to impact acceleration and displacement under nonlinear impact |
隔振器是舰船机电设备非线性冲击保护中的重要缓冲元件,在设计隔振器时要满足以下要求:隔振器具有摩擦刚度特性,在冲击力较小的情况下,冲击力作用到隔振器上,此时机电设备能够受到安全载荷的保护。当冲击力较大的情况下,隔振器无法完全隔离冲击力作用,此时机电设备出现相对位移;隔振器3项刚度满足水下爆炸对舰船机电设备的三向冲击激励作用,尤其对于横向刚度而言,需满足隔离冲击力的要求;隔振器设计要将阻尼比控制在0.24~4.0之间,阻尼比过大会增加隔振器对冲击力的传递,阻尼比过小会降低隔振器的能量消耗,弱化缓冲效果;隔振器设计要保证3个方向的阻隔冲击强度足够大,当冲击能量消耗较大时,需要承受强雷的冲击,要求隔振器具备刚度软化特性。
本文提出的舰船机电设备非线性冲击隔离器要满足响应速度的要求,为此采用基于神经网络技术设计新型抗冲击的电控隔振器,配合加速度传感器一同使用,能够在发生非线性冲击力一瞬间通过加速度传感器快速采集到相关信息,借助神经网络训练传输到电控隔振器上,实现最短时间内的隔冲性能配置。当非线性冲击力波及到船体时,神经网络算法能够快速计算出爆炸载荷的力度和方向,调整隔振器参数信号,控制隔振器作出瞬时响应。
2 舰船机电设备非线性冲击响应的理论建模 2.1 理论建模坐标在建立舰船机电设备非线性抗冲击响应的理论模型时引入动力学方程,采用隆格-库塔法计算数值,利用仿真实验软件编写非线性冲击响应计算程序,用于分析不同类型隔振器、不同冲击激励等试验条件下的机电设备非线性冲击响应效果。将舰船机电设备视为刚体,受舰船结构的限制,各类型刚体安装呈无规则状态,无法找到刚体的质量分布中心,使得安装以非对称性形式为主。在建立模型坐标系时满足以下要求:在刚体处于静止状态,隔振器未发生变形时取惯性坐标的原点,即刚体重心;以刚体重心为原点,构建正交坐标系,形成连体基座;计算出姿态坐标,将刚体与隔振器的固结点作为轴向拉力点,垂直径向建立连体基,运用有限转动四元素法将坐标变换成矩阵。
2.2 开发非线性冲击响应计算程序在仿真实验软件中输入基本参数,包括机电设备质量、设备惯性矩等参数,使安装设备尽量趋于直角平行六面体,惯性矩趋于0,离心力矩设置为0。惯性主轴重合于设备结构,上述实验条件同样适用于不对称结构的机电设备。在机电设备上安装隔振器,安装方向为静态弹性力方向,轴向拉力呈位移曲线状态,分别向2个方向施加推力。本次实验选用的隔振器3个方向与冲击力频率相关。冲击方向分别设置为90°,90°和0°,即垂直冲击方向。冲击形式利用加速度时间历程方程表示,引入半正弦和衰减正弦函数,利用已知的加速度最大值、固有振动频率和对数衰减率计算出冲击载荷。将单个时间与对应的基础加速度输入到仿真软件中,得出基础冲击激励值,按照指数函数的计算程序计算出冲击起始时间、结束时间,评估非线性冲击响应效率。
本文提出构建NLRC计算程序,程序包含以下内容:主程序MAIN,赋初始变量值,调用其他程序执行主程序;子程序DATAIN是从输入文件中读出设备参数、隔振器参数和冲击载荷参数,构建质量矩阵,转变成坐标矩阵,用于查看输入参数是否存在错误;子程序SUBA,计算隔振器静变形和系统响应需求。计算静变形时调用SUB6,SUB7和SUB8子程序,采用二分法计算出隔振器的变形量,计算出子程序SUB7的力矩和返回加速度;子程序SUB9,SUB10用于计算响应求解,输出结果;子程序DATAOUT控制结果输出,通过调用子程序SUB11转换成文本文件OUT,得出机电设备在时域范围内的变形速度、位移、冲击频率和加速度响应最大值。
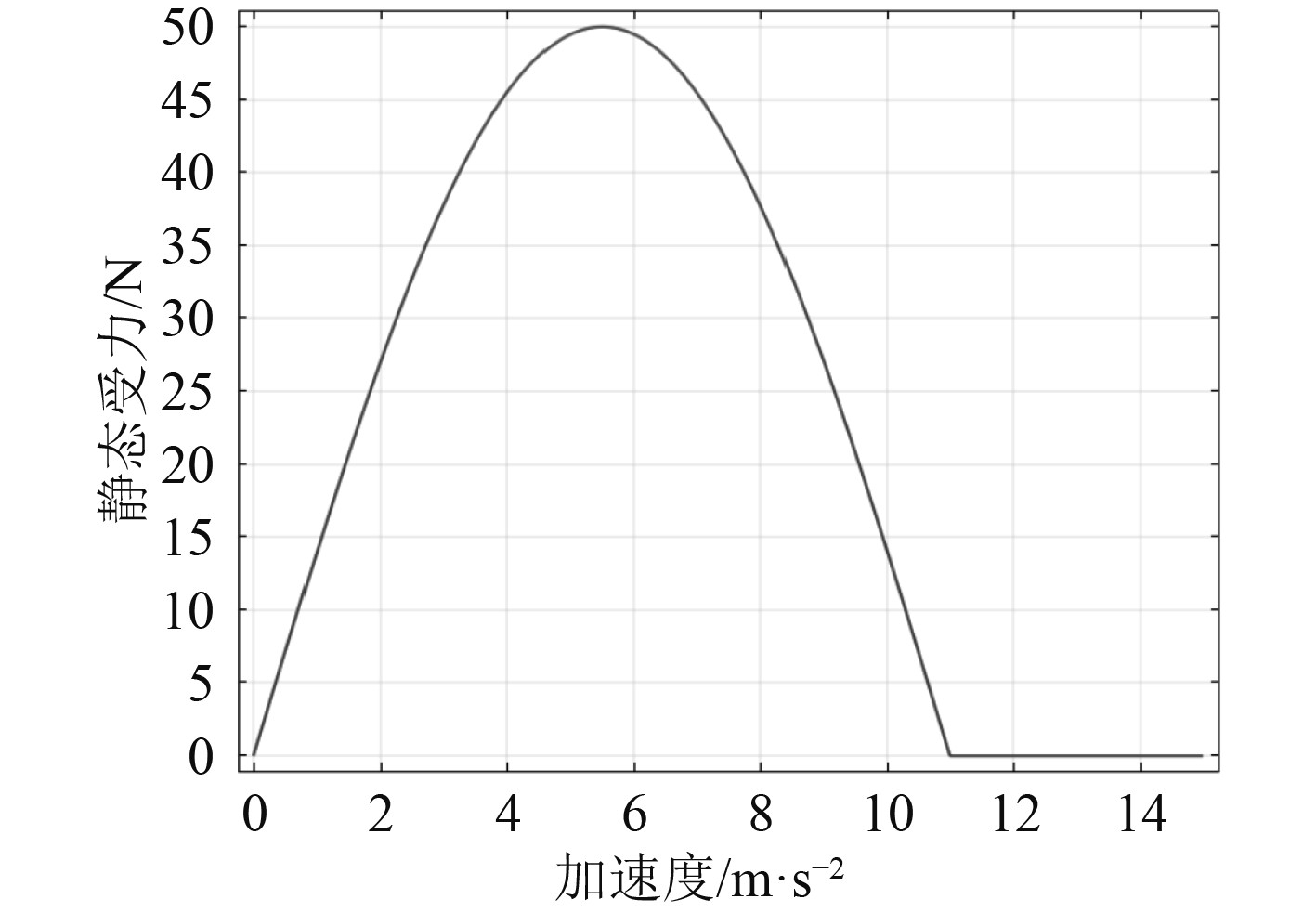
2.3 不同隔振器的响应结果比较按照上述实验条件,对不同特性的隔振器响应结果进行分析,假设机电设备质量为150 kg,3个方向的转动惯量分别为3.2 kg·m2,6.25 kg,0,隔振器的静态弹性力—位移特性实验数据为:当位移为2 mm,6 mm,10 mm,14 mm,18 mm,22 mm,26 mm,30 mm时,弹性力分别为0.24 kN,0.55 kN,0.76 kN,0.95 kN,1.06 kN,1.15 kN,1.22 kN,1.32 kN。隔振器编号1的x,y,z轴向的安装数据为0,–250 mm,–38.5 mm;隔振器编号2的x,y,z轴向的安装数据为250 mm,125 mm,–38.5 mm;隔振器编号3的x,y,z轴向的安装数据为–250 mm,150 mm,–38.5 mm。冲击形式为半正弦波冲击激励取10.3 g,12 ms,频率参数取0.04,0.06,0,1。垂直安装隔振器,当受到垂直方向的非线性冲击时,非线性冲击隔振器静态力位移响应曲线图如图4所示,非线性冲击隔振器静态力加速度响应曲线图如图5所示。
|
图 4 非线性冲击隔振器静态力位移响应曲线图 Fig. 4 Static force displacement response curve of nonlinear impact isolator |
|
图 5 非线性冲击隔振器静态力加速度响应曲线图 Fig. 5 Static force acceleration response curve of nonlinear impact isolator |
本次实验采用3种不同刚度特性的隔振器进行实验,实验数据如下:渐软特性隔振器静变形–5.15 mm,重心偏移最大值为22.258 mm,重心速度最大值为0.357 4 m/s,重心加速度最大值为1.578 g;渐硬特性隔振器静变形–20.62 mm,重心偏移最大值为21.224 mm,重心速度最大值为0.117 m/s,重心加速度最大值为4.125 g;直线特性隔振器静变形–4.58 mm,重心偏移最大值为16.578 mm,重心速度最大值为0.541 m/s,重心加速度最大值为3.127 g。由此可见,渐硬特性隔振器的非线性冲击响应效果最佳。
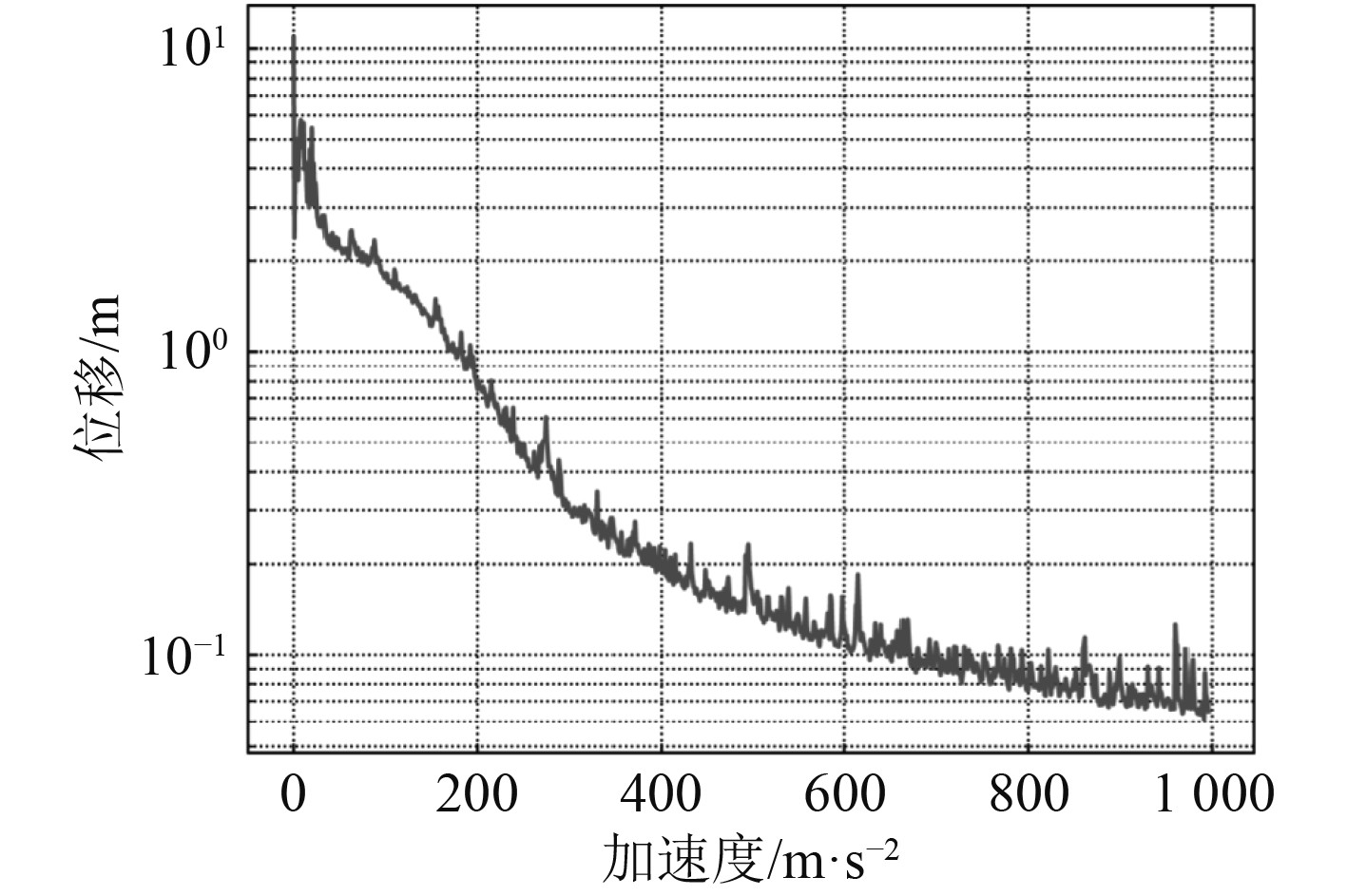
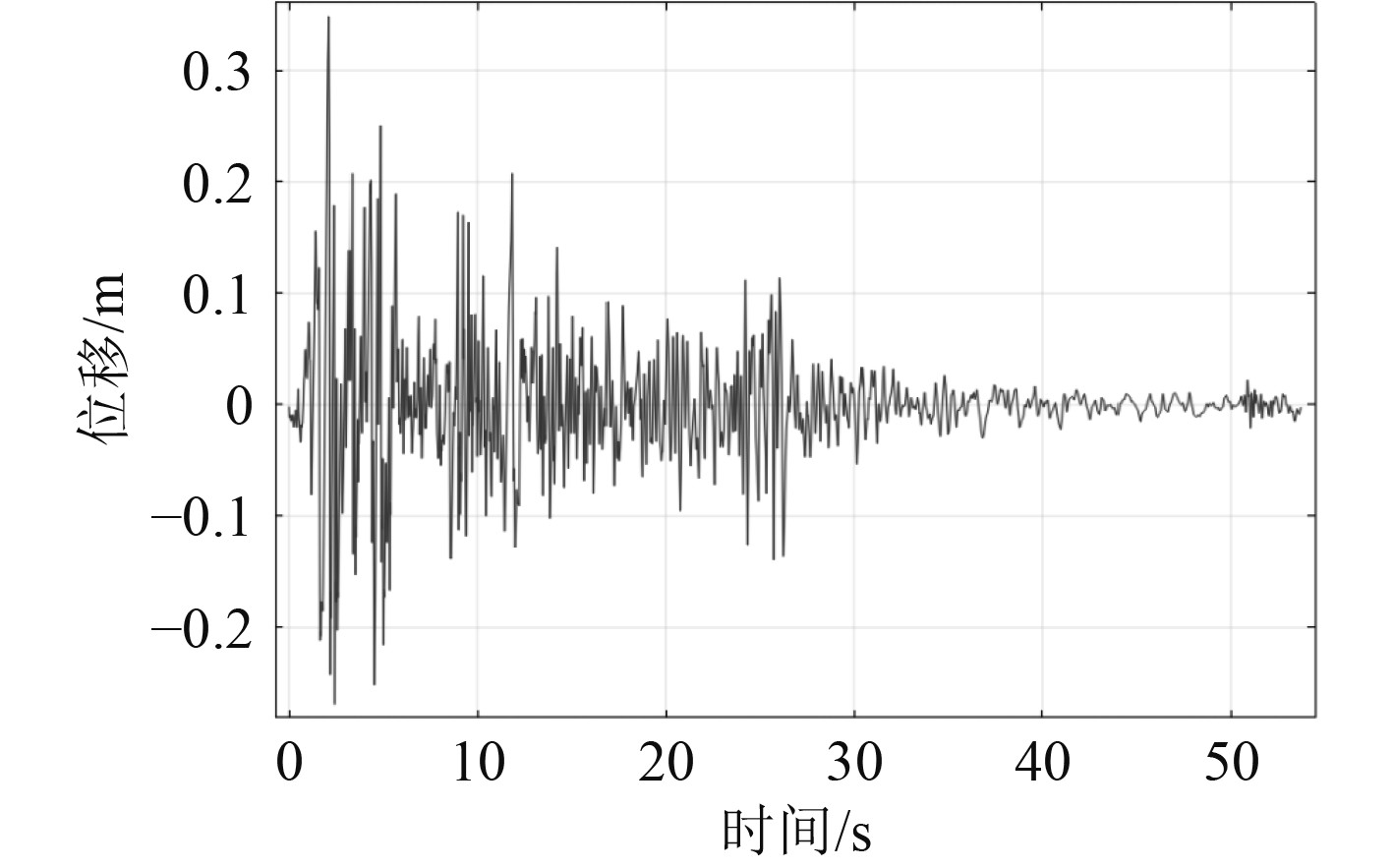
2.4 不同冲击激励下的响应结果比较采用上述仿真实验条件,将冲击持续时间改为8 ms,冲击激励形式采用衰减正弦波,机电设备非线性冲击下的位移响应曲线如图6所示,机电设备加速度响应曲线图如图7所示。
|
图 6 基于衰减正弦波冲击激励形式下的机电设备位移响应曲线图 Fig. 6 Displacement response curve of electromechanical equipment under shock excitation based on attenuated sine wave |
|
图 7 机电设备加速度响应曲线图 Fig. 7 Acceleration response curve of electromechanical equipment under shock excitation based on attenuated sine wave |
在实验软件中输入底座激励数据[0,0,6,100.12,41,0],计算出不同冲击激励波形的机电设备重心响应数据,具体包括:半正弦12 ms冲击激励下重心偏移最大值为22.287 mm,重心速度最大值为0.3571 m/s,重心加速度最大值为1.865 4 g;半正弦8 ms冲击激励下重心偏移最大值为15.548 mm,重心速度最大值为0.449 m/s,重心加速度最大值为1.351 8 g;半正弦16 ms冲击激励下重心偏移最大值为29.657 mm,重心速度最大值为0.809 5 m/s,重心加速度最大值为2.263 5 g;衰减正弦冲击激励下重心偏移最大值为9.277 9 mm,重心速度最大值为0.321 6 m/s,重心加速度最大值为0.924 3 g;三角波形冲击激励下重心偏移最大值为17.242 mm,重心速度最大值为0.514 4 m/s,重心加速度最大值为1.557 5 g。由此可见,半正弦16 ms冲击响应效果最佳。
3 结 语舰船机电设备要安装非线性冲击隔振器,以维护机电设备运行环境安全,减少爆炸冲击力对机电设备造成的破坏。在隔振器设计开发中,要考虑到弹性变形和阻尼影响因素,采用渐硬特性隔振器,运用理论模型对计算程序正确性进行验证,确定最终安装位置,以达到最佳的非线性冲击响应效果。
| [1] |
李俊南, 方臣富, 杨志东, 等. 船舶甲板感应加热矫平机电能变换及能量转换系统[J]. 电焊机, 2022, 52(5): 74-83+90. |
| [2] |
郭兆贤. 船舶机电设备振动采集系统的故障诊断技术[J]. 船舶物资与市场, 2021(3): 9-10. DOI:10.19727/j.cnki.cbwzysc.2021.03.004 |
| [3] |
罗自来, 常汉宝, 张晓怀. IETM在舰船机电设备信息化保障中的应用[J]. 船舶, 2009(4): 55-58. DOI:10.3969/j.issn.1001-9855.2009.04.013 |
| [4] |
杨正祥. 不同寿命阶段舰船机电设备运行能效检测系统设计[J]. 舰船科学技术, 2019(4): 100-102. YANG Zheng-xiang. Design of energy efficiency detection system for ship electromechanical equipment operation in different life stages[J]. Ship Science and Technology, 2019(4): 100-102. DOI:10.3404/j.issn.1672-7649.2019.04.019 |
| [5] |
石屹琳, 芦荻. 船舶机电一体化管理系统设计[J]. 船舶物资与市场, 2021(1): 25-26. DOI:10.19727/j.cnki.cbwzysc.2021.01.008 |
| [6] |
凌国建. 船舶机电设备故障诊断方法[J]. 船舶物资与市场, 2021(2): 29-30. DOI:10.19727/j.cnki.cbwzysc.2021.02.013 |
| [7] |
李新亮. 探讨船舶机电设备振动采集系统的故障诊断技术[J]. 珠江水运, 2020(21): 48-49. DOI:10.14125/j.cnki.zjsy.2020.21.021 |
 2022, Vol. 44
2022, Vol. 44
