舰船供电系统是舰船电力系统的重要组成部分。典型供电系统的数学模型用于模拟发电机组运行的物理过程,从而用于供电系统仿真和验证。结合虚拟现实技术,数学模型可用于电力系统相关的模拟训练[1]。
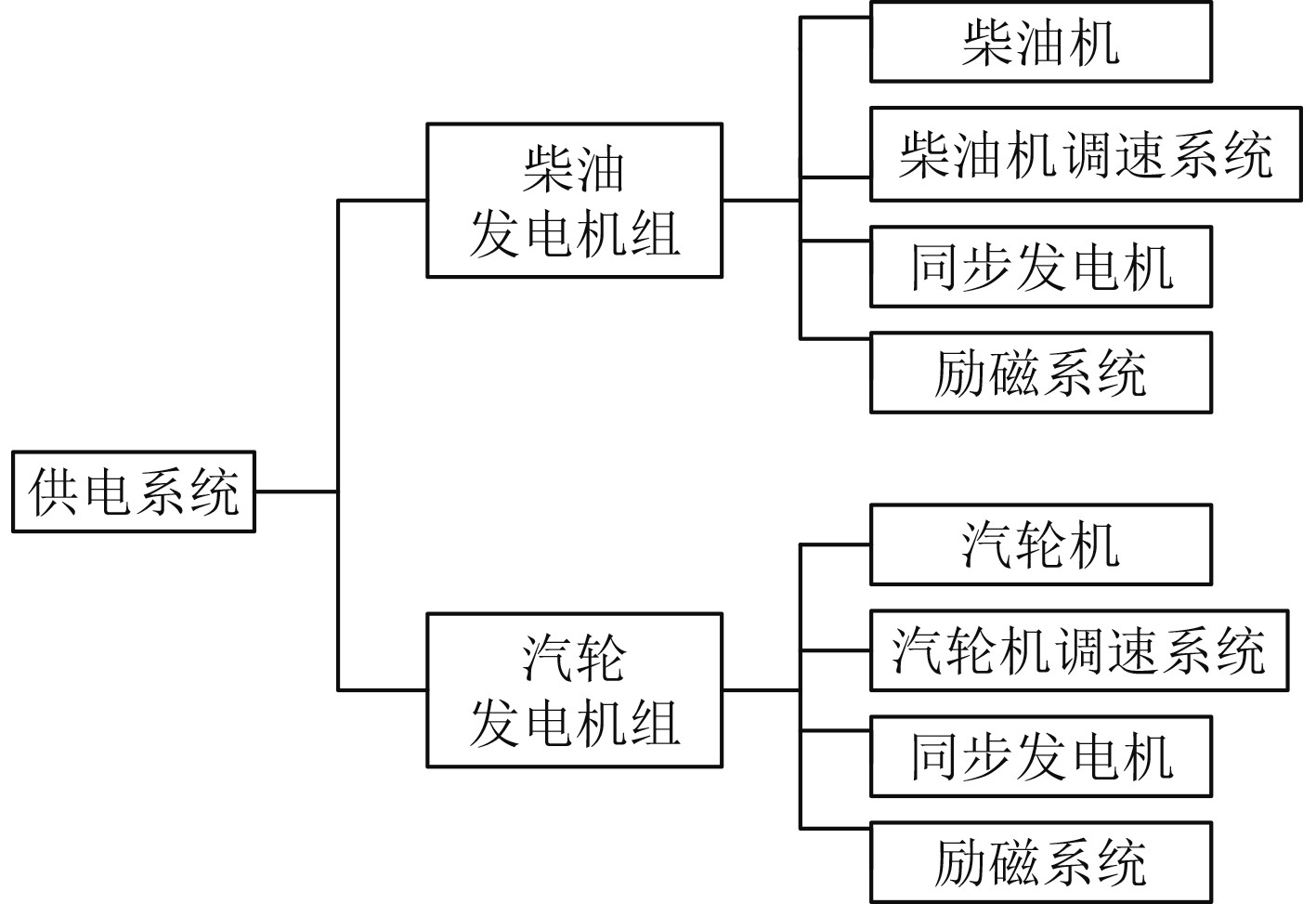
1 概 述 1.1 供电系统组成舰船供电系统一般包括汽轮发电机组和柴油发电机组。柴油发电机组主要由柴油机及其调速系统,同步发电机及其励磁系统组成。汽轮发电机组主要由汽轮机及其调速系统,同步发电机及其励磁系统组成,如图1所示。本文以柴油机、汽轮机、同步发电机及励磁系统为研究对象,开展供电系统数学建模分析。
|
图 1 舰船供电系统组成 Fig. 1 Composition of ship power supply system |
柴油机和汽轮机向同步发电机输出给定转速,达到动能转换为电能的目的。同步发电机是一种最常用的交流发电机。由于同步发电机一般采用直流励磁,当其单机独立运行时,通过调节励磁电流能方便的调节发电机的电压。励磁系统用于维持发电机端电压在给定值,当发电机负荷发生变化时,通过励磁电流调节磁场的强弱来恒定发电机端的电压[2-5]。
1.2 基本假设在建立供电系统数学模型时,需作如下假设:
1)选取发电机原动机模型输出的稳态值作为下一级的输入;
2)发电机组的启动和停机特性曲线,按照一阶段惯性方程模拟;
3)为便于表达,在不影响模块间逻辑关系的前提下,对数学模型传递函数进行近似和简化。
2 柴油发电机组模型 2.1 组成柴油发电机组由柴油机及其调速器、执行器、同步发电机及其励磁调压系统组成。
|
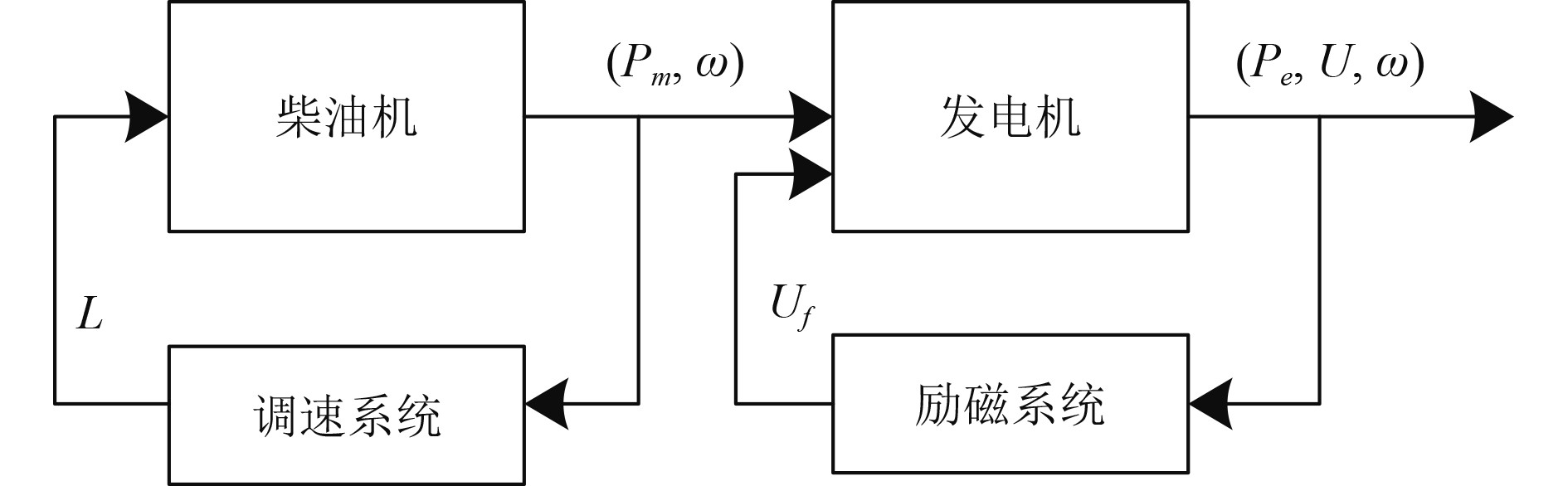
图 2 柴油发电机模块 Fig. 2 Diesel generator set modules |
模型输入:给定转速,机组转差率
模型输出:调整后的转速。
参数:执行器常数、PID控制器的比例、积分、微分系数。
关系模型:船舶电力系统的调速系统分为速度控制器、执行机构、原动机(柴油机)、转速反馈环节、发电机等重要部分,形成一个闭环控制系统,其框图如图所示。

|
图 3 柴油机及其调速系统的结构框图 Fig. 3 Diesel generator and speed regulation modules |
速度控制器采用经典的PID控制器,其传递函数模型为:
| $ \frac{{\eta (s)}}{{{{V}}(s)}} = {K_P} + {K_I}/s + {K_D}s 。$ |
式中:
执行机构是柴油机电子调速器实现对柴油机控制的最终手段。因为执行器的阶跃响应和一阶惯性环节的阶跃响应类似,因此可以采用阶跃响应实验法来建立一阶惯性环节的数学模型,其传递函数为:
| $ \frac{{\mu (s)}}{{\eta (s)}} = \frac{1}{{{\rm{}}T_ss + \beta }}。$ |
式中:
| $ \mu = \frac{{X - {\rm{}}X_0}}{{{\rm{}}X_e}}。$ |
式中:
转速反馈环节主要是由转速传感器和信号转换电路组成的,工作过程是将转速传感器获得的频率信号转换为方波脉冲信号,根据2个脉冲之间的时间间隔来测量速度,它的输入量是柴油机的转速,输出量是与转速度正比例的电压信号,定义它的增益为
模型输入:伺服活塞的相对位移
模型输出:机组转差率
参数:机组的平衡旋转惯量、转子角速度初
始值、活塞位置处于额定值时的转矩、原动机自调整系数。
关系模型:柴油机复频域下的传递函数为
| $ \frac{{S(s)}}{{\mu (s)}} = \frac{1}{{T_{\alpha} s + \beta_c}}。$ |
式中:
| $ T_\alpha = \frac{{J\omega_0}}{{M_e}}。$ |
式中:
为简化计算,柴油机组并网后只选取上述模型计算结果的稳态值作为后续模型的计算值。柴油发电机组模型模拟柴油机组起动特性曲线的变化趋势。
3 汽轮发电机组模型 3.1 组成汽轮发电机组由汽轮机及其调速器、执行器、同步发电机及其励磁调压系统组成。
|
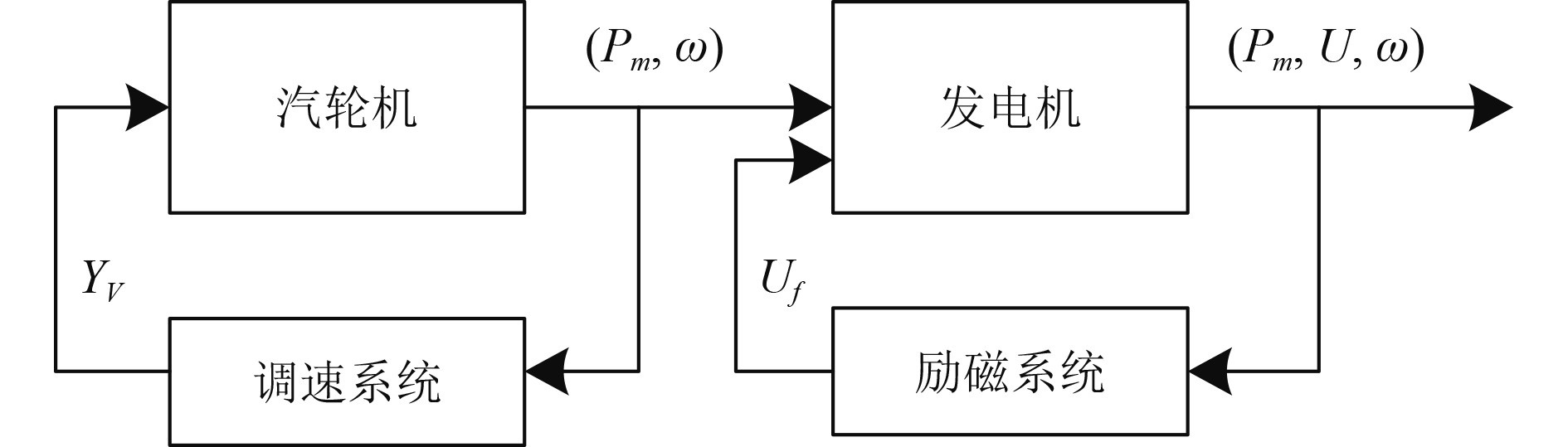
图 4 汽轮发电机模块 Fig. 4 Turbo generator set modules |
汽轮机调速模型以蒸汽流量阀门开度为控制目标。按照PID闭环控制原理开展建模。
模型输入:电磁功率参考,设定速度,实际速度。
模型输出:阀门开度。
参数:放大倍数、固态转速、阀门开度速度限制、阀门开度限制。
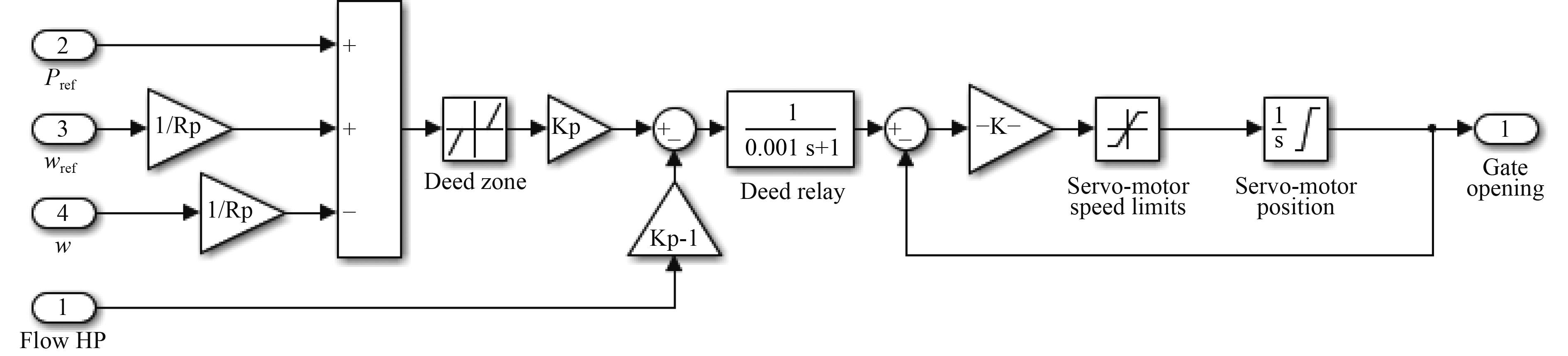
关系模型如图5所示。
|
图 5 汽轮机速度调节 Matlab模型 Fig. 5 Matlab model for turbo generator of speed regulation |
速度调节系统为液压调节,包括一个比例积分环节、一个速度延迟环节和一个伺服机构控制阀门开度。
图5中:
汽轮机组并网后只选取上述模型计算结果的稳态值作为后续模型的计算值。汽轮发电机组选取上述模型的汽轮机组起动特性曲线的变化趋势来模拟。
3.3 汽轮发电机组模型模型输入:蒸汽阀门开度与主汽压力。
模型输出:机械功率。
参数:高压缸功率所占比例、中压缸功率所占比例、低压缸功率所占比例、高压缸功率自然过调系数、高压缸蒸汽容积时间常数、再热蒸汽容积时间常数、低压连通管容积时间常数。
关系模型:汽轮机模型如图6所示。

|
图 6 汽轮机发电机组模型框图 Fig. 6 Model of turbo generator set |
其中,
| $ \frac{1}{{T_{ch}.s + 1}}。$ |
式中:
再热蒸汽容积传递函数为:
| $ \frac{1}{{T_{rh}.s + 1}}。$ |
式中:
低压连通管容积传递函数为:
| $ \frac{1}{{T_{co}.s + 1}}。$ |
式中:
同步发电机即转子转速与定子旋转磁场的转速相同的交流发电机。
模型输入:电机q轴瞬态电动势,为电机q轴超瞬态电动势,为电机d轴超瞬态电动势。
模型输出:发电机 d 轴电压、发电机q轴电压。
参数:q轴超瞬态电动势、q轴超瞬态电动势、定子每相绕组电阻、直轴超瞬态电抗、交轴超瞬态电抗、直轴瞬态开路时间常数、直轴同步电抗、直轴瞬态电抗、直轴超瞬态短路时间常数、直轴同步电抗、直轴瞬态电抗、交轴超瞬态短路时间常数。
关系模型:建立同步发电机五阶实用模型。
1)定子电压方程
| $ u_d = E''_d - X''_qi_q + R_si_d,$ |
| $ u_q = E''_q + X''_di_d + R_si_q。$ |
式中:
2)转子f绕组电压方程
| $ T'_{do}p E'_q = Ef - \left(\frac{{X''d - Xd}}{{X''d - X'd}}E'q + \frac{{Xd - X'd}}{{X''d - X'd}}E''q\right) 。$ |
式中:
3)转子D绕组电压方程
| $ T''_{do}pE''_q = - E''_q + E'_q + (X'_d - X''_d)i_d。$ |
式中:
4)转子 Q绕组电压方程
| $ T''_{qo}pE''_d = - E''_d - (X_q - X''_q)i_q。$ |
式中:
5)转子运动方程
| $ T_j\frac{{{\rm{d}}_\omega }}{{{\rm{d}}_t}} = T_m + [E''_qi_q + E''_di_d + (X''_d - X''_q)i_di_q] $ |
其中:
另有:
| $ \frac{{{\rm{d}}\delta }}{{{\rm{d}}t}} = \omega - 1,$ |
进一步推导[6]可得:
| $ \left[ \begin{gathered} u_d \\ u_q \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} \begin{gathered} 0 \\ 0 \\ \end{gathered} &\begin{gathered} 0 \\ 1 \\ \end{gathered} &\begin{gathered} 1 \\ 0 \\ \end{gathered} \end{array}} \right]\left[ \begin{gathered} E'_q \\ E''_q \\ E''_d \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}{c}} \begin{gathered} 0 \\ 0 \\ \end{gathered} &\begin{gathered} R_s \\ X''_q \\ \end{gathered} &\begin{gathered} - X''_q \\ R_s \\ \end{gathered} \end{array}} \right]\left[ \begin{gathered} E_f \\ i_d \\ i_q \\ \end{gathered} \right]。$ |
即为以
发电机组通常采用无刷励磁系统,励磁系统常用自并励励磁系统的PID控制模型。在自并励励磁系统中选择一级的超前-滞后补偿器完全可以满足励磁系统的各项性能指标[8]。
模型输入:给定电压、励磁电压初值、发电机d轴电压、发电机q轴电压、接地电压。
模型输出:励磁电压。
参数:励磁机时间常数、励磁机增益系数。
关系模型:励磁调压装置的主要任务时根据发电机不同运行工况向同步发电机提供一个可调的励磁电流,以保证同步发电机的输出电压为额定值。本模型针对无刷同步发电机励磁调压系统,其结构原理框图如图7所示。

|
图 7 励磁系统模型框图 Fig. 7 Model of excitation system |
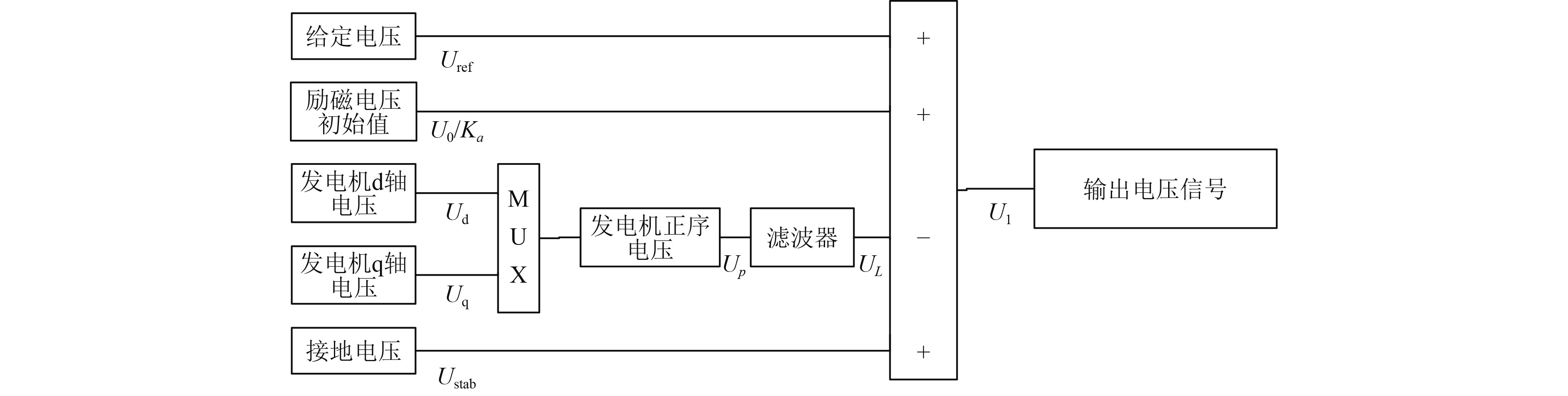
励磁系统输入电压的测取方式见图8。
|
图 8 励磁系统电压输入模型 Fig. 8 Model of excitation system input |
即输入电压为
| $ {U_1} = {U_{ref}} + {U_0}/{K_a} - {U_L} + {U_{stab}},$ |
放大单元传递函数为一阶惯性环节:
| $ \frac{{{k_a}}}{{{T_k}s + 1}},$ |
简化的励磁机输出数学模型可用一阶惯性环节表示如下式:
| $ \frac{1}{{{T_e}s + {k_e}}}。$ |
式中:
反馈单元传递函数为:
| $ \frac{{{k_m}s}}{{{T_m}s + 1}}。$ |
式中:
选取某型16V船用柴油机参数作为输入,对柴油发电机组输出的稳态值进行分析。
|
|
表 1 某船用柴油机基本参数 Tab.1 The parameters of marine diesel engine |
按照某柴油机起动特性曲线,柴油机从起动到达稳态额定转速1500 r/min的时间不大于9 s。柴油发电机组起动时间为机组从按下按钮至首次达到稳态额定电压400 V的时间,不大于10 s;
采用本柴油发电机组模型,柴油机备车达到稳态额定转速时间为 10±1s,发电机组起动达到稳态额定功率时间为 10±1s。起动成功后,发电机组的电压、频率、转速达到理论值:电压 400±10% V,频率 50±5% Hz,转速 1500±5% r/min。
6 结 语在分析发电机组闭环控制模型的基础上,通过简化模型结构、特性曲线拟合的优化方式,形成了一整套纯数学模型表达。通过测试表明,当前数学模型可以基本反映发电机组输出的基本变化趋势以及稳态值。作为仿真模型,可用于驱动以供电系统启停、调速等操作为科目的模拟训练系统。
| [1] |
谢辉, 卜乐平, 冯源. 船舶电力模拟训练评估系统的设计和开发[J]. 舰船科学技术, 2013, 35(11): 45-48. XIE Hui, BU Le-ping, FENG Yuan. Design and development of on-board power simulating training evaluation system[J]. Ship Science and Technology, 2013, 35(11): 45-48. |
| [2] |
KUNDUR P. Power systems stability and control[M]. New York: McGraw- Hill / EPRI, 1994.
|
| [3] |
薛学斌. 1000 MW 机组发电机励磁方式的选择[J]. 电工技术, 2008(1): 59-60. DOI:10.3969/j.issn.1002-1388.2008.01.028 |
| [4] |
冯旭. 大型汽轮发电机制造中的励磁方式选型[J]. 科技创新与应用, 2013(7): 74. |
| [5] |
刘取. 电力系统稳定性及发电机励磁控制[M]. 北京: 中国电力出版社, 2007.
|
| [6] |
倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
|
| [7] |
邓玲, 桂实, 王正风, 等. 同步发电机数学模型物理含义解析[J]. 东北电力技术, 2012, 12: 5-7. DENG Ling, GUI shi, WANG Zheng-feng, et al. Physics resolution for mathematics model of synchronous generator[J]. Northeast Electric Power Technology, 2012, 12: 5-7. |
| [8] |
李明强. 励磁系统PID 控制模型的选型探讨[J]. 四川电力技术, 2017, 40(4): 87-90. |
| [9] |
郝正航, 陈卓, 邱国跃, 等. 励磁机时间常数对电力系统动态稳定性的影响[J]. 电工电能新技术, 2006, 25(1): 26-29,43. HAO Zhenghang, CHEN Zhuo, QIU Guoyue, et al. Influence of excitation time constant on dynamic stability of power system[J]. Advanced Technology of Electrical Engineering and Energy, 2006, 25(1): 26-29,43. |
 2022, Vol. 44
2022, Vol. 44
