随着风电技术的不断发展,海上风电朝着深水化、风机单机容量大型化发展,固定式海上风机面临着施工难度高、经济成本急剧增加的困境,浮式海上风机具有明显优势。现阶段常见的浮式基础结构主要分为Spar浮式基础、半潜式浮式基础和张力腿浮式基础三大类,美国可再生能源实验室搭载5 MW风机的OC4半潜式浮式基础就是典型的半潜式浮式基础之一[1]。
随着风机单机容量朝着大型化发展,全球各大风机生产商纷纷推出了自己研发的10 MW风机,丹麦科技大学提出的DTU10 MW风机[2]成为市面主流的10 MW风机之一,风机容量增加的同时,整体结构随之增大,对应的浮式基础需要进一步进行结构调整,以满足其使用需求。
在海洋工程结构物的设计建造过程中,特别是浮式平台,因为要在海洋中长期作业,所以平台在波浪载荷下的水动力性能分析尤为重要。本文基于美国可再生能源实验室搭载5 MW风机的OC4半潜式浮式基础设计建立四浮筒半潜式浮式风机基础,对其进行水动力分析,通过计算来确定水动力性能,以此来判断浮式基础的水动力性能,为后续其结构研究奠定了基础。
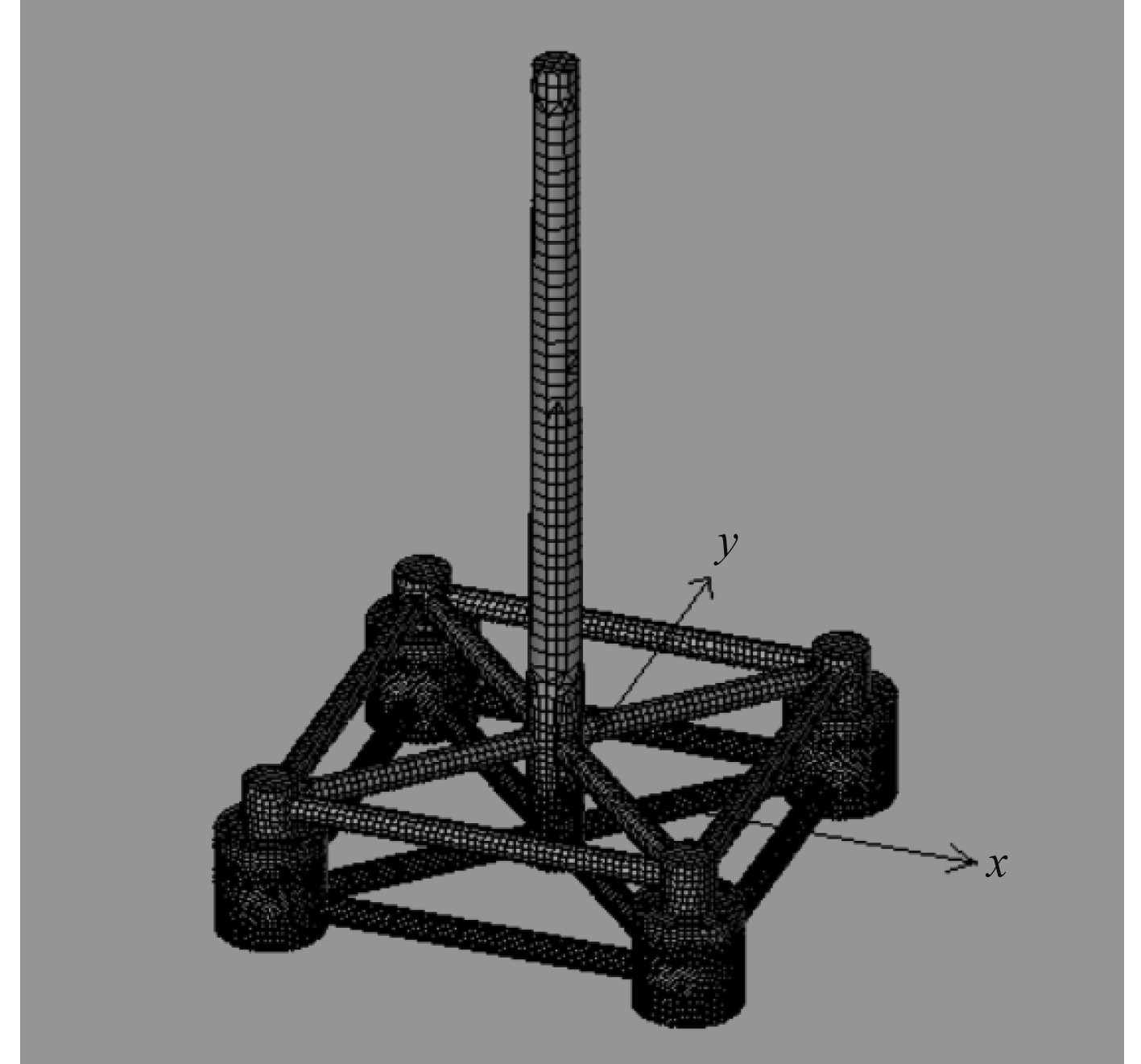
1 半潜式浮式基础建模及边界条件建立 1.1 基础结构设计及计算模型建立本文基于OC4基础[3]所建立的四浮筒半潜式浮式基础设计吃水为15 m,浮筒间距为80 m,主要由1个主浮筒、4个副浮筒、16根撑杆以及塔筒组成,基础参数如表1所示,水动力计算模型如图1所示。网格大小为1 m,共有14125个节点,17204个单元。
|
|
表 1 浮式基础主要参数 Tab.1 Main parameters of floating foundation |
|
图 1 半潜式浮式基础水动力模型 Fig. 1 Hydrodynamic model of semi-submersible floating foundation |
高强度钢AH36为该浮式基础材料,具体材料属性如表2所示。
|
|
表 2 浮式基础材料属性 Tab.2 Material properties of floating foundation |
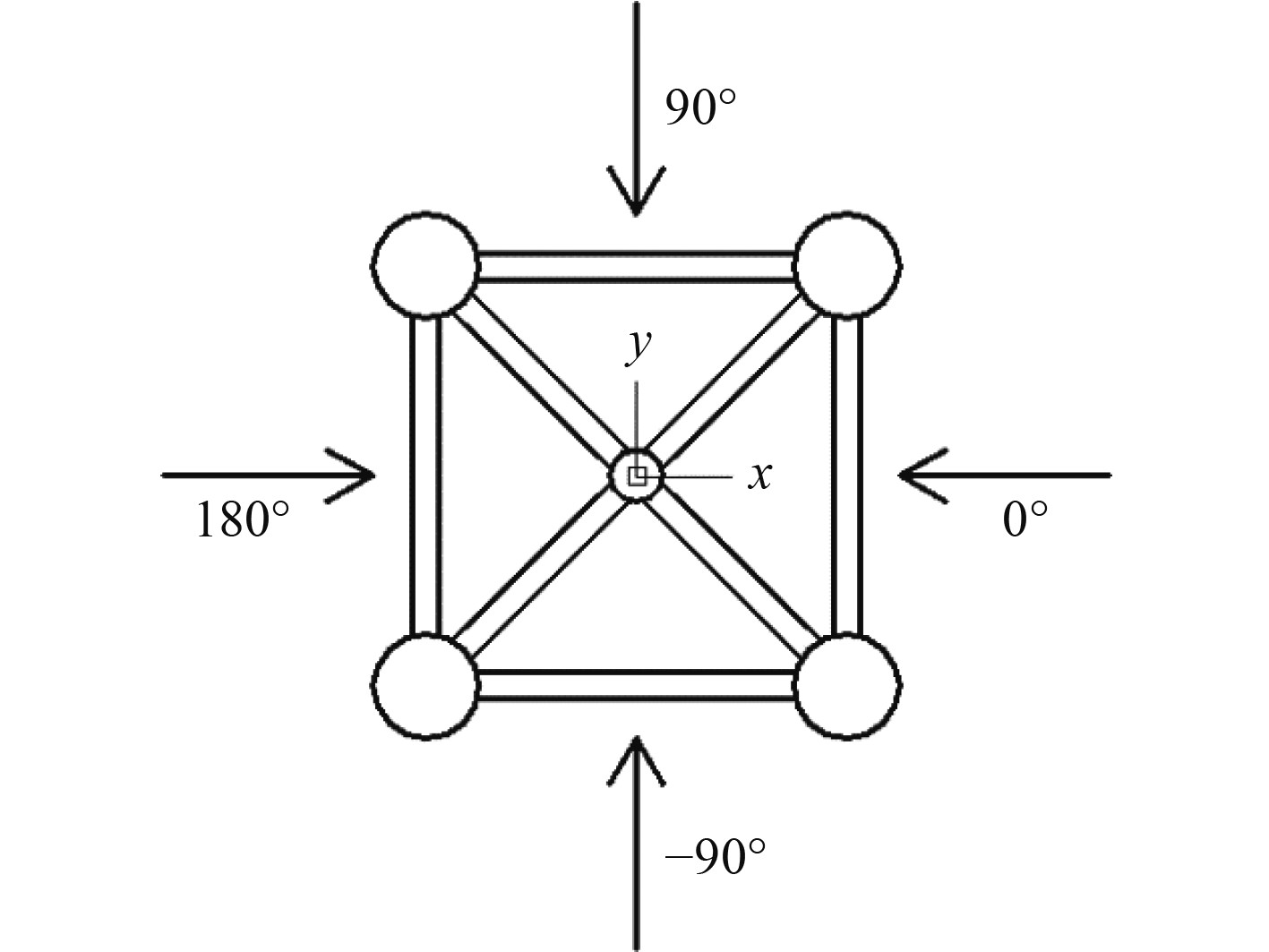
参考坐标系的选取如图2所示。其坐标原点是半潜式浮式风机中心线与水线面交点,xoy面与静水面重合,z轴与浮体中心线重合并垂直于静水面向上;波浪沿坐标系x轴正方向传播时,浪向角为0°,当波浪坐标系y轴正方向传播时,浪向角为90°,浪向角随着波浪逆时针变化而增加。
|
图 2 半潜式浮式基础坐标系 Fig. 2 Coordinate system of semi-submersible floating foundation |
在对半潜式浮式基础进行频域分析时,由于半潜式浮式基础没有设置系泊系统,因此分析时仅考虑半潜式浮式基础在波浪作用下的波频运动。在设置环境参数时,水深设为200 m;波浪频率范围为0.1~2.3 rad/s,步频数为23;浪向角范围为0~90°,间隔15°,浪向角数量7个。同时,在计算过程中,采用P-M谱和定常风。在计算过程中,波浪载荷采用P-M谱[4]、风载荷采用API风谱[5]。
2 水动力系数分析半潜式浮式基础会产生:纵荡、横荡、垂荡、横摇、纵摇以及首摇等6个自由度运动。本文分析浮式基础的附加质量系数、附加阻尼系数、一阶波浪力、二阶波浪力以及幅频响应函数等重要水动力参数,以验证浮式基础的水动力性能。
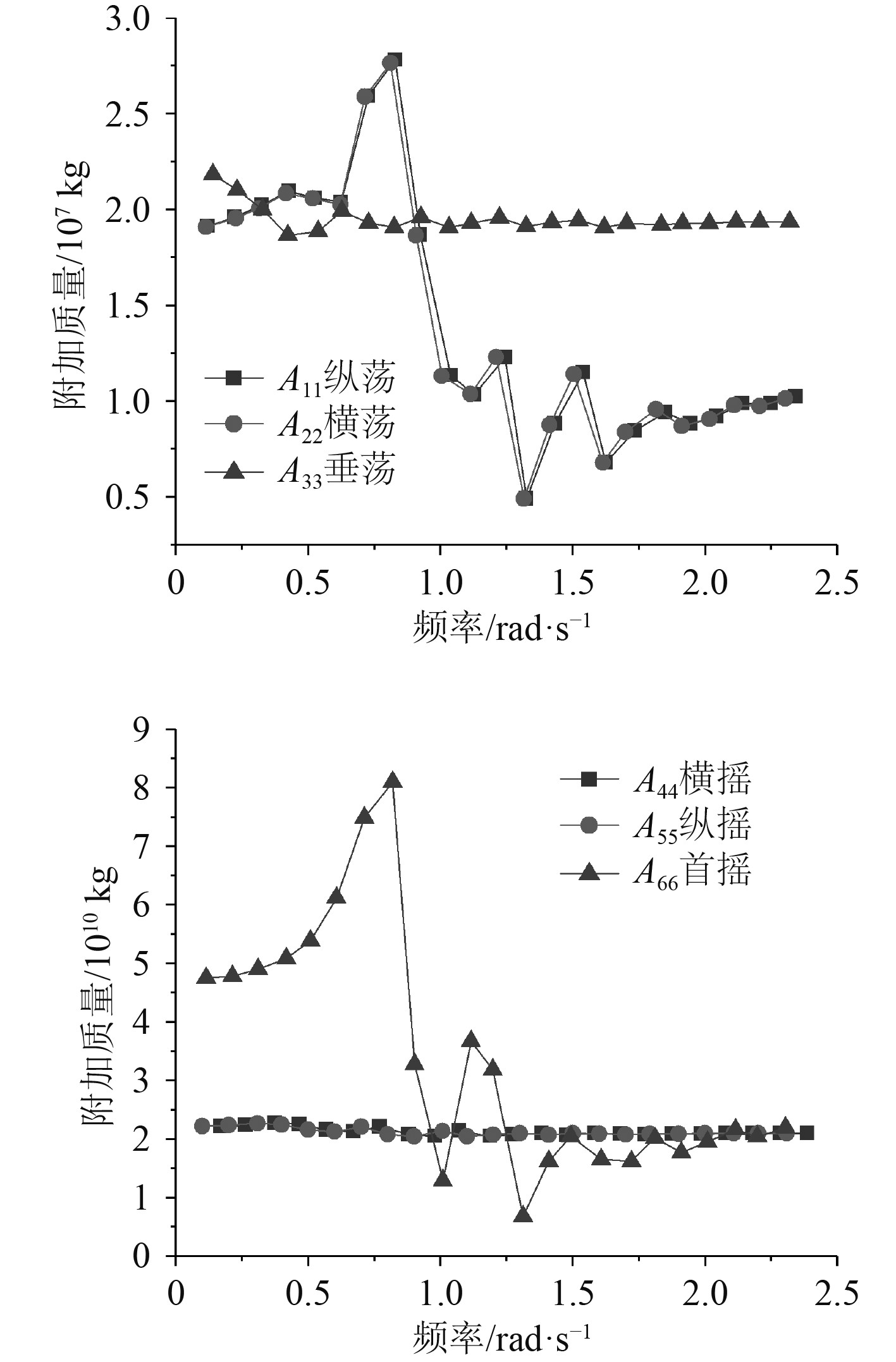
2.1 附加质量系数由图3分析可得,在纵荡和横荡方向上,浮式基础的附加质量A11与A22变化趋势几乎相同,随着频率的增加,附加质量先增加,在频率为0.8 rad/s时达到峰值,之后开始降低,在高频区间波动后趋于稳定,最终稳定在1.0×107kg;在横摇和纵摇方向上,浮式基础的附加质量A44与A55变化趋势也相近,同样是随着频率的增加,附加质量先增加,在频率为0.3 rad/s时达到峰值,之后开始降低,在高频区间波动后趋于稳定,最终稳定在2.0×1010 kg;在垂荡方向上,浮式基础的附加质量A33变化趋势呈现出随着频率的增加而减小的趋势,在0.4 rad/s时,附加质量降到最小值,在0.4~1.7 rad/s之间附加质量呈波动状态,之后稳定在1.9×107 kg附近;在首摇方向上浮式基础的附加质量A66的变化趋势为先增加到0.8 rad/s时达到峰值,随后附加质量出现波动,最后在高频区稳定在2.3×1010 kg。
|
图 3 附加质量系数 Fig. 3 Additional mass factor |
势流阻尼和粘性阻尼为海上浮式结构物水动力主要的阻尼,考虑到一般海上大型浮体的粘性阻尼相对很小,在频域分析时可以忽略,只考虑势流阻尼[6]。
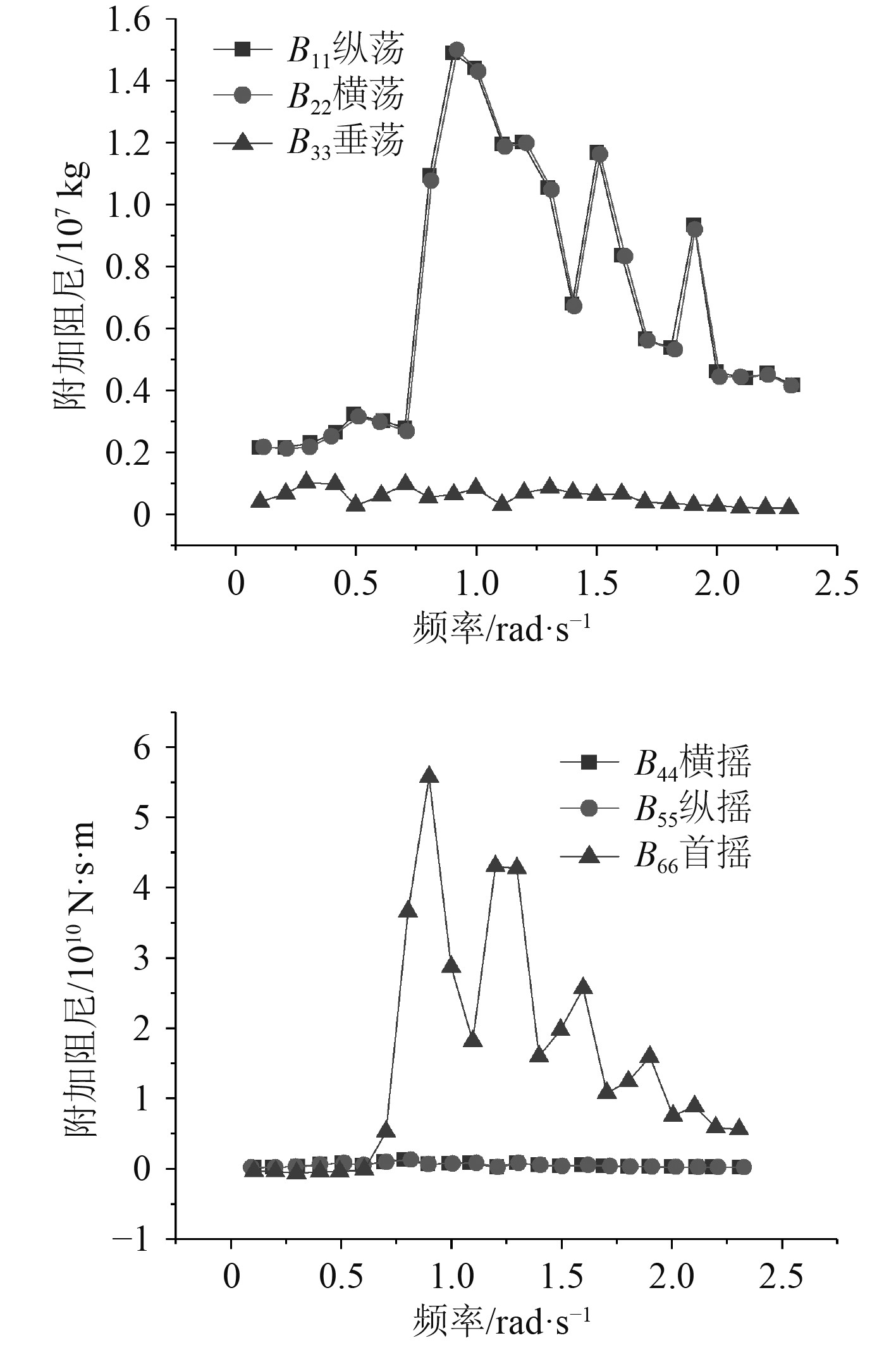
由图4可以看出,在纵荡和横荡方向上,浮式基础的附加阻尼变化较为相似,在0.1~0.7 rad/s的低频区域均处于较小数量级,之后迅速增加并在0.9 rad/s时达到峰值,随后降低,在高频区域出现波动,最后稳定在2.0×106 N·s/m;在垂荡方向上,附加阻尼在低频区域出现波动变化,出现多个波峰,在1.3 rad/s后逐渐减小,最后稳定在8.6×103 N·s/m左右;在横摇和纵摇方向上,附加阻尼变化较为相似,随着频率的增加,附加阻尼在0.8 rad/s时达到峰值,随后减小并出现波动,最后稳定在1.3×107 N·s·m左右;在首摇方向上,附加阻尼在频率小于0.6 rad/s时处于较小数量级,之后迅速增加,在0.9 rad/s时达到峰值,随后在高频区域波动并逐渐减小,最后稳定在6.2×109 N·s·m左右。
|
图 4 附加阻尼系数 Fig. 4 Additional damping coefficient |
总体来看,浮式基础在纵荡和横荡、纵摇和横摇上的附加质量和附加阻尼相同,证明该浮式基础结构具有良好的对称性。
2.3 一阶波浪力当波浪入射波在遭遇浮体时,会在浮体周围产生较为复杂的波浪绕射,一阶波浪力就是考虑了波浪绕射对浮体的影响,主要由F-K力(Froude-Kriloff力)与绕射力线性叠加而成[7]。因为浮体基础结构具有对称性,因此仅考虑波浪入射角为0°,30°,60°和90°时,浮式基础在六自由度上的一阶波浪力传递函数曲线。
如图5所示,对六自由度上的一阶波浪力进行比较可以得到,纵荡、横荡、纵摇和横摇自由度上一阶波浪力对波浪入射角的变化较为敏感,而垂荡自由度上的一阶波浪力对波浪入射角的改变最不敏感。在纵荡和横荡自由度上,一阶波浪力在低频区域逐渐增大,在0.5 rad/s时到达第一个小峰值,在0.8 rad/s时到达峰值,之后随着频率的增大出现波动,总体上逐渐减小。同时在纵荡自由度上随着入射角的增大一阶波浪力随之减小,在入射角为90°时一阶波浪力几乎为0,而在垂荡自由度上则完全相反在入射角为0°时一阶波浪力几乎为0;在垂荡自由度上,一阶波浪力随着频率的增加而减小,同时在低频区域一阶波浪力几乎不受波浪入射角的影响,只在0.5~2.0 rad/s之间出现小幅度的波动,之后在高频区间维持在较小数量级;在横摇和纵摇自由度上,一阶波浪力的变化趋势也基本相同,都是呈现出先增加再减小的趋势,在0.4 rad/s时达到峰值,之后出现波动并逐渐降低,在高频区间处于较小数量级,在纵摇自由度上,一阶波浪力随着入射角的增加逐渐减小,在90°时一阶波浪力几乎为0,相反在横摇自由度上,一阶波浪力随着入射角的增加逐渐增大,在0°时一阶波浪力几乎为0;在艏摇方向上,在波浪入射角为0°和90°时,其一阶波浪力变化趋势相同,数值都为较低数量级,与之相比,其它入射角下一阶波浪力数值都随着频率的增加呈先增加再减小的趋势,在0.9 rad/s时出现最大值,最后逐渐降低。
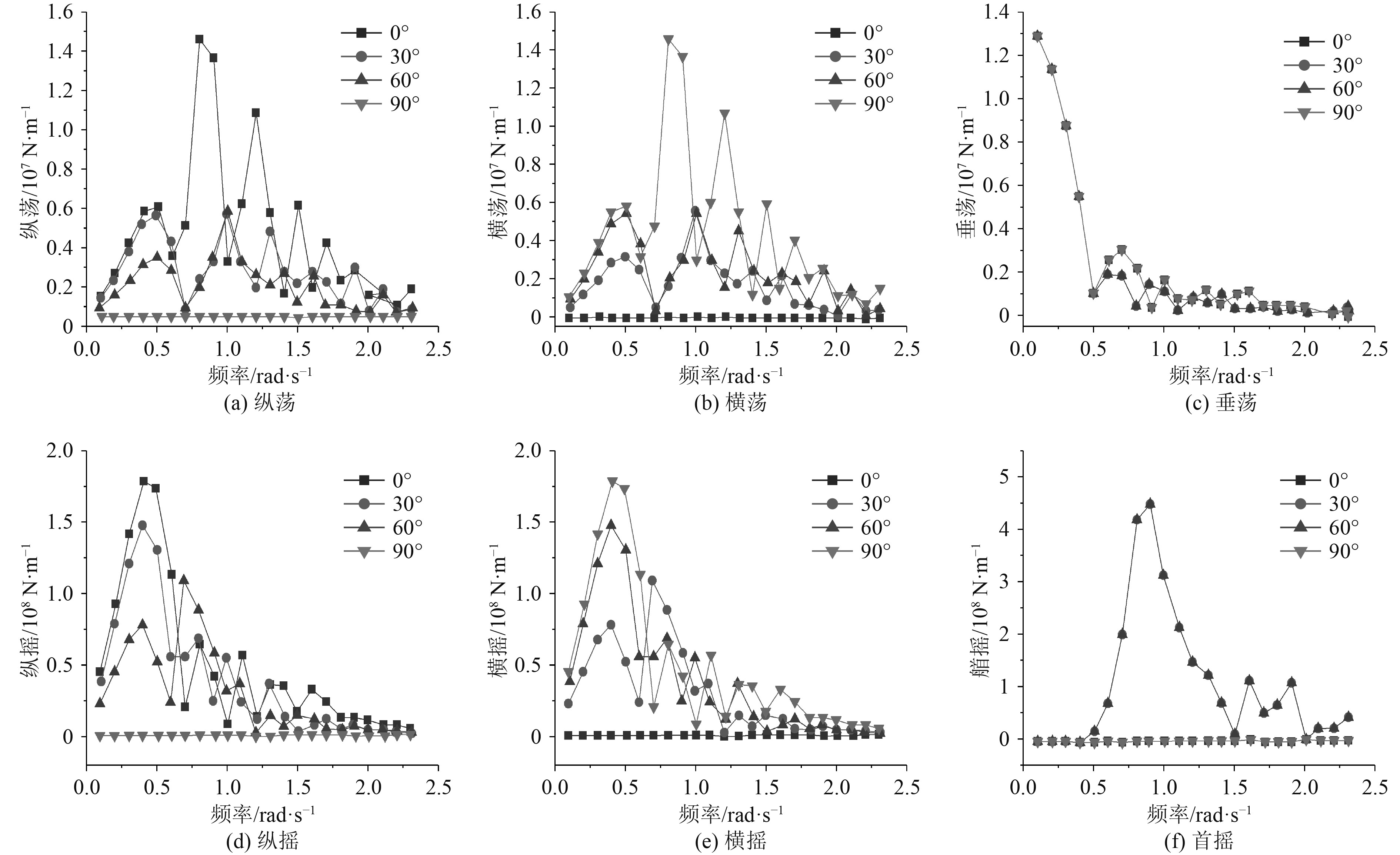
|
图 5 浮式基础一阶波浪力传递函数 Fig. 5 First order wave force transfer function of floating foundation |
基于远场理论,通过求解无穷远处的速度势来代替物面上的压力积分[8]进行二阶波浪力计算。由于浮式基础在纵摇,横摇和垂荡方向上的二阶波浪力很小,因此仅计算浮式基础在纵荡,横荡,摇3个自由度上的二阶波浪力。
由图6可以看出,在纵荡、横荡和首摇自由度低频区域,浮式基础所受的二阶波浪力较小且变化幅度不大;频率大于0.5 rad/s时,浮式基础所受的二阶波浪力开始增大,不同浪向角下的二阶波浪力数值变化较为明显,并且出现了多个峰值。在纵荡自由度上,浪向角为0°时所受二阶波浪力最大,二阶波浪力随浪向角的增大而减小,在浪向角为90°时二阶波浪力处于较小数量级;在横荡自由度上,二阶波浪力随浪向角的变化趋势与纵荡相反,浪向角为90°时二阶波浪力最大,0°时处于较小数量级。在首摇方向上,二阶波浪力在0°和90°时处于较小数量级,在30°和60°浪向角下二阶波浪力变化较大,相对应的数值互为倒数,在0.6 rad/s时达到峰值,并在高频区域出现波动。
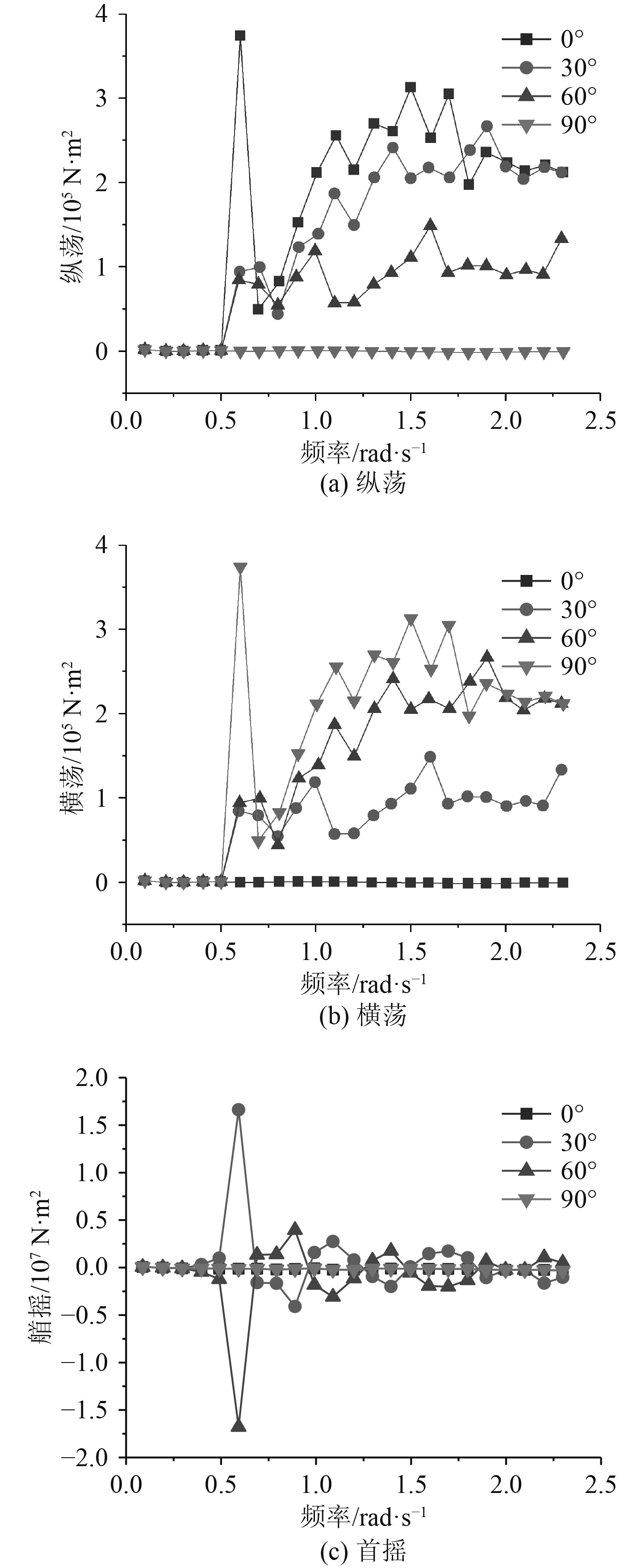
|
图 6 浮式基础二阶波浪力传递函数 Fig. 6 Second order wave force transfer function of floating foundation |
根据线性势流理论的假设,将一阶波浪力的大小与波幅的比例关系定义为波浪力的幅值响应函数RAO(response amplitude operators)[9]。由于在横荡、横摇和首摇等3个自由度上的幅值响应函数数值非常小,对风机的运动影响较小,因此本文仅列出纵荡、垂荡和纵摇等3个自由度的运算结果。
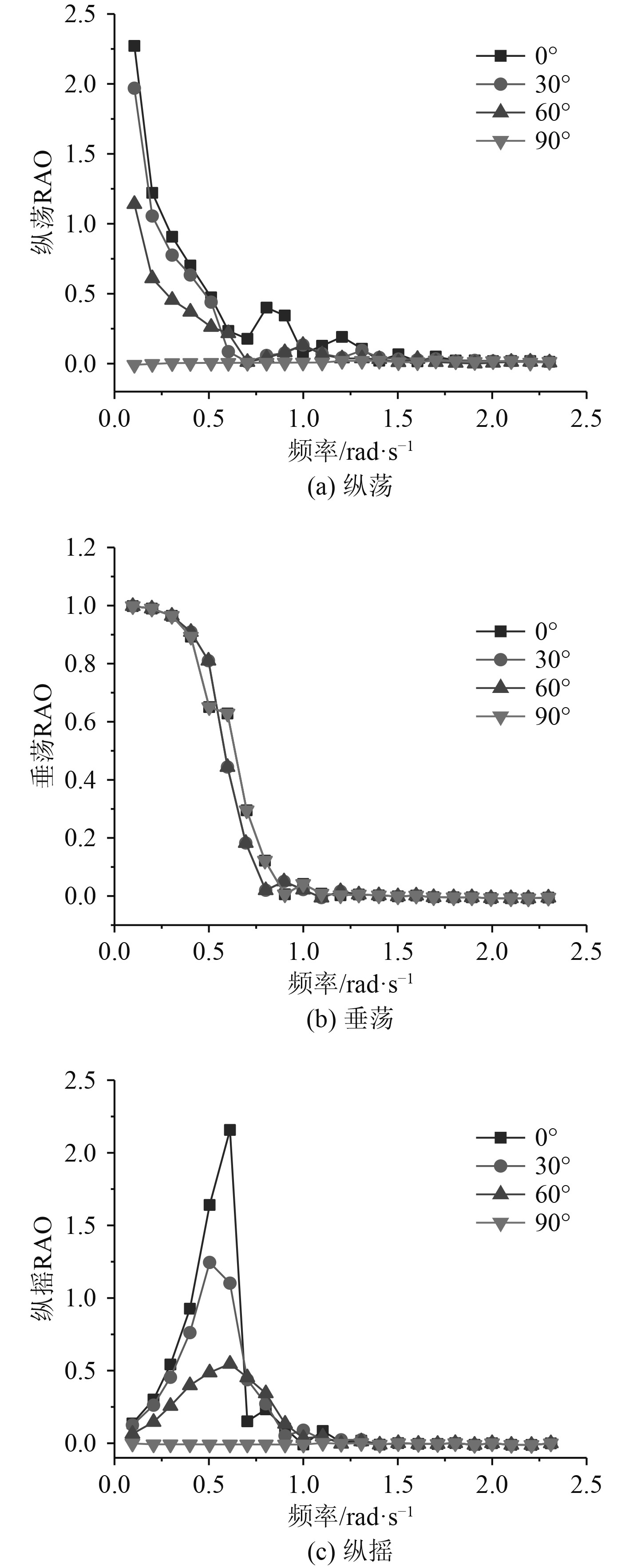
由图7分析可得,在纵荡自由度上,浮式基础的幅值响应函数随着频率的增加而快速减小,在1 rad/s后基本趋于0;在垂荡自由度上,浮式基础的幅值响应函数的变化趋势与纵荡类似,在低频区域RAO快速减小,在0.9 rad/s后基本趋于0;在纵摇自由度上,浮式基础的幅值响应函数随着频率的增加呈现出先增大再减小的趋势,在0.6 rad/s时幅值响应函数达到峰值,之后随着波浪频率的增加,运动幅值迅速下降并趋近于0。总体来说,浮式基础在低频区域的运动响应比较明显,可以避开绝大部分的短周期波浪,证明该浮式风机平台具有良好的水动力性能。

|
图 7 浮式基础幅频运动响应曲线 Fig. 7 Amplitude frequency response curve of floating foundation |
在频域分析计算中,设定不同的波浪入射角度,以此来研究波浪入射角度对于浮式基础运动响应的影响。由于浮式基础有良好的对称性,因此本文只设置了0°,30°,60°和90°等4个角度,具体数据如图8所示。
|
图 8 浮式基础幅频运动响应曲线 Fig. 8 Amplitude frequency response curve of floating foundation |
可知,不同的波浪入射角对于纵荡自由度和纵摇自由度上的浮式基础运动响应影响较大,在纵荡自由度上,随着波浪入射角的增大,浮式基础的幅值响应函数逐渐减小,且当波浪入射角为90°时,幅值响应函数最小,几乎为0;在纵摇自由度上,幅值响应函数的变化趋势与纵荡类似,在低频区域都是随着波浪入射角度的增加而减小,在高频区域,不同波浪入射角度下的幅值响应函数几乎都为0;在垂荡自由度上,不同波浪入射角对于浮式基础的幅值响应函数几乎没有影响,只在0.3~1.0 rad/s时略有区别。总的来说,不同的波浪入射角度对于浮式基础的幅值响应函数只在低频区域有一定影响,对于高频区域则基本没有影响。
3.3 水深对浮式基础运动响应的影响浮式风机在工作中可能会被放置在不同水深的海洋环境中,因此在频域计算中,本文考虑在100 m,200 m,500 m和1000 m等4种不同水深下对于浮式基础运动响应的影响。同样,只列出了纵荡、垂荡和纵摇等3个自由度的数据,如图9所示。

|
图 9 浮式基础幅频运动响应曲线 Fig. 9 Amplitude frequency response curve of floating foundation |
可知,在纵荡自由度上,水深对浮式基础的运动响应影响较为明显,主要体现在低频区域,随着水深的增加,浮式基础的幅值响应函数逐渐减小,而在高频区域,水深对于浮式基础的幅值响应函数几乎没有影响;在垂荡自由度上,水深的变化对于浮式基础的幅值响应函数几乎没有影响;在纵摇自由度上,水深变化在低频率时对于浮式基础的幅值响应函数有较小的影响,随着水深的增加,幅值响应函数的数值有小幅度的减小,在高频区域,水深对于幅值响应函数基本没有影响。总体来说,浮式风机工作海域的水深变化对于浮式基础的幅值响应函数只在低频区域有一定影响,对于高频区域则基本没有影响。
4 结 语本文基于OC4半潜式浮式基础建立半潜式四浮筒式海上风机基础模型,通过水动力计算软件AQWA对四浮筒式基础的水动力性能进行分析计算,得到了浮式基础在频域内的附加质量、附加阻尼、一阶波浪力和二阶波浪力,以及六自由度下的平台运动响应幅值算子RAO。之后又分析了波浪入射角度和水深的变化对浮式基础的幅值响应函数的影响,结果表明:
1)浮式基础在纵荡和横荡、纵摇和横摇上的附加质量和附加阻尼以及一阶波浪力基本相同,表明浮式基础结构具有良好的对称性。
2)浮式基础在低频区域的运动响应比较明显,在高频区域的运动响应相对较小,表明浮式基础在选设定的海洋环境下拥有良好的水动力性能。
3)波浪入射角度和水深的变化对浮式基础的运动响应仅在低频区域有一定的影响,在高频区域几乎没有影响。
| [1] |
赵志峰. 海上风电机组基础全寿命疲劳分析[D]. 大连: 大连理工大学, 2016.
|
| [2] |
徐应瑜, 胡志强, 刘格梁. 10MW级海上浮式风机运动特性研究[J]. 海洋工程, 2017, 35(3): 44-51. DOI:10.16483/j.issn.1005-9865.2017.03.006 |
| [3] |
ROBERTSON A , JONKMAN J , MASCIOLA M , et al. Definition of the semisubmersible floating system for phase II of OC4[J]. Scitech Connect Definition of the Floating System for Phase IV of Oc3, 2014.
|
| [4] |
施勇, 姜贞强, 任年鑫, 等. 三桩基础海上风电机组结构波浪载荷实验研究[J]. 风能, 2019, 4(7): 84-87. DOI:10.3969/j.issn.1674-9219.2019.07.027 |
| [5] |
严心宽, 陈超核, 樊天慧, 等. 风浪联合作用下5MW三桩固定式风机动力特性响应[J]. 中国海洋平台, 2020, 35(3): 33-37+42. DOI:10.3969/j.issn.1001-4500.2020.03.007 |
| [6] |
邓小康, 谢文会, 李阳, 等. 一种新型深水浮式平台及其系泊系统动力响应分析[J]. 舰船科学技术, 2021, 43(05): 95-101. DOI:10.3404/j.issn.1672-7649.2021.03.019 |
| [7] |
邓小康, 谢文会, 谢彬. 新型深水干树半潜平台水动力性能数值研究[J]. 中国造船, 2021, 62(2): 187-200. DOI:10.3969/j.issn.1000-4882.2021.02.017 |
| [8] |
王亮. 大开口防撞套箱的结构强度及耐撞性能研究[D]. 武汉: 华中科技大学, 2019.
|
| [9] |
陆佳颖, 刘振华, 朱云龙. 基于三维势流理论的新型养殖半潜平台水动力特性[J]. 船舶工程, 2021, 43(4): 12-16. DOI:10.13788/j.cnki.cbgc.2021.04.03 |
 2022, Vol. 44
2022, Vol. 44
