2. 浙江海洋大学 东海科学技术学院,浙江 舟山 316022;
3. 浙江海洋大学 船舶与海运学院,浙江 舟山 316022
2. Donghai Science and Technology College, Zhejiang Ocean University, Zhoushan 316000, China;
3. School of Naval Architecture and Maritime, Zhejiang Ocean University, Zhoushan 316022, China
多模块MOB动力响应的计算方法主要采用频域法和时域法,所采用的计算模型主要有RMFC,RMRC,FMFC和FMRC模型。余澜[4]对超大型海上移动基地进行了较为深入的研究,涉及MOB的动力响应,考虑了浮体水弹性的影响,并进行了实验验证。王永恒等[5]提出由3个相同模块组成的超大型浮体,研究了不同环境不同连接器刚度下连接器载荷并与试验结果进行了比较,通过比较提出了较为合理的连接器刚度值。宋斌等[6]提出了一种由多个浮式平台合围成的人工港湾式超大型海上基地VLFOB,设计了一种可分离式连接器装置将8个模块连接成整体。研究了不同连接器轴向刚度对VLFOB固有频率的影响,得出了连接器刚度的合理范围避免与海洋环境条件产生共振。鲁达[7]以铰接多浮体为研究对象,研究了浪向、波频、阻尼等因素对波浪能发电装置发电功率的影响,并提出了一种用于多浮体水弹性分析的简化计算方法。李志伟[8]以岛礁附近的超大型浮式结构物为研究对象,研究了海底变化对浮体运动响应和连接器载荷的影响,并将数值计算结果与试验结果进行了比较。L. Sun[9]计算了两铰接方形浮式结构物的水动力响应并与Newman的算例作比较以验证程序正确性,又计算了2艘大型液化天然气船并排停靠时在波浪中的运动响应和刚性连接器载荷响应。J.N. Newman[10]计算了2个铰接连接的驳船在波浪中的运动响应,2条驳船尺寸相同,长40 m,宽10 m,吃水5 m。J.N. Newman的论文中又提供了另外一个算例,以1,3,5,9,17个直线排列的圆柱形浮体阵列为研究对象,计算每个圆柱体的波浪力和水动力系数。
1 计算原理本文研究的MOB系统由7个模块组成,模块编号为M1~M7,共有12个连接器,连接器编号为C1~C12。整体坐标系和局部坐标系的定义如图1所示。

|
图 1 MOB(7MS)坐标系定义 Fig. 1 Coordinate system of MOB(7MS) |
当多个模块位于同一流场中时,总速度势表达为:
| $ \phi = {\phi _I} + {\phi _D} + i\omega \sum\limits_{k = 1}^n {\sum\limits_{j = 1}^6 {u_j^k\phi _j^k} }。$ | (1) |
式中:
忽略多体间相互影响的刚性浮体柔性连接器模型计算方法与考虑多体间相互影响的计算方法主要区别在于水动力系数矩阵的组成不同。当考虑浮体间相互影响时,第
| $ \begin{split} R_p^k =& \rho {\omega ^2}\left(\sum\limits_{j = 1}^6 {\iint\limits_{{S_k}} {u_j^k\phi _j^k}} n_p^k{\rm{d}}s + \sum\limits_{m \ne k}^n {\sum\limits_{j = 1}^6 {\iint\limits_{{S_k}} {u_j^k\phi _j^kn_p^k{\rm{d}}s}} } \right) = \\ &{\omega ^2}A_p^k - i\omega B_p^k,\end{split}$ | (2) |
第k模块的附加质量阵
| $ {\boldsymbol{A}}_p^k = {\left\{ {A_{p1}^{k,1},A_{p2}^{k,1},\cdots,A_{pj}^{k,k},\cdots,A_{pj}^{k,m},\cdots A_{p6}^{k,n}} \right\}_{6n \times 1}},$ | (3) |
| $ {\boldsymbol{B}}_p^k = {\left\{ {B_{p1}^{k,1},B_{p2}^{k,1},\cdots,B_{pj}^{k,k},\cdots,B_{pj}^{k,m},\cdots B_{p6}^{k,n}} \right\}_{6n \times 1}}。$ | (4) |
式中:
考虑浮体间相互影响时,认为第
将
| $ \begin{split} {{\boldsymbol{M}}_s} = \left[ {\begin{array}{*{20}{c}} {{M_1}}&0&0&0&0 \\ 0&{{M_2}}&0&0&0 \\ 0&0&{{M_k}}&0&0 \\ 0&0&0&{\cdots}&0 \\ 0&0&0&0&{{M_n}} \end{array}} \right],\\ {{\boldsymbol{K}}_w} = \left[ {\begin{array}{*{20}{c}} {{K_{w1}}}&0&0&0&0 \\ 0&{{K_{w2}}}&0&0&0 \\ 0&0&{{K_{wk}}}&0&0 \\ 0&0&0&{\cdots}&0 \\ 0&0&0&0&{{K_{wn}}} \end{array}} \right]。\end{split}$ | (5) |
式中:
连接器载荷为连接器总刚度矩阵乘以连接器位移矩阵,将连接器视为线性弹簧,表达式如下:
| $ F = {K_c}\Delta {u_{l,l + 1}} = \left[ {\begin{array}{*{20}{c}} {{K_x}}&0&0&0&0&0 \\ 0&{{K_y}}&0&0&0&0 \\ 0&0&{{K_z}}&0&0&0 \\ 0&0&0&0&0&0 \\ 0&0&0&0&0&0 \\ 0&0&0&0&0&0 \end{array}} \right]\Delta {u_{l,l + 1}},$ | (6) |
| $ \Delta {u_{l,l + 1}} = {N_i}{u^l} - {N_j}{u^{l + 1}} = {T_c}\left\{ {\begin{array}{*{20}{c}} {{u^l}} \\ {{u^{l + 1}}} \end{array}} \right\},$ | (7) |
位于第
| $ {{{K}}_{l,l + 1}} = {{T}}_c^{{T}}{{{K}}_c}{{{T}}_c},$ | (8) |
| $ {{\boldsymbol{K}}_s} = \sum\limits_{l = 1}^{n - 1} {{K_{l,l + 1}}},$ | (9) |
频域下多浮体运动方程的矩阵表达式:
| $ - {\omega ^2}({{\boldsymbol{M}}_S} + {\boldsymbol{A}}) + i\omega {\boldsymbol{B}} + ({{\boldsymbol{K}}_S} + {{\boldsymbol{K}}_W})\left\{ {\boldsymbol{u }}\right\} = \left\{ F \right\}。$ | (10) |
式中:
短期预报所采用的波浪谱为Bretshneider谱,北太平洋开敞海域7级海况(SS7)的特征波高为7.5 m,谱峰周期为13.8 s。
| $ S_{\eta}(\omega)=\frac{1.25}{4}\left(\frac{2 \text{π}}{\mathrm{T}_{p}}\right) \omega^{-5} H_{s}^{2} e^{-1.25\left(\frac{2 \text{π}}{\mathrm{T}_{p} \sigma}\right)^{4}}。$ | (11) |
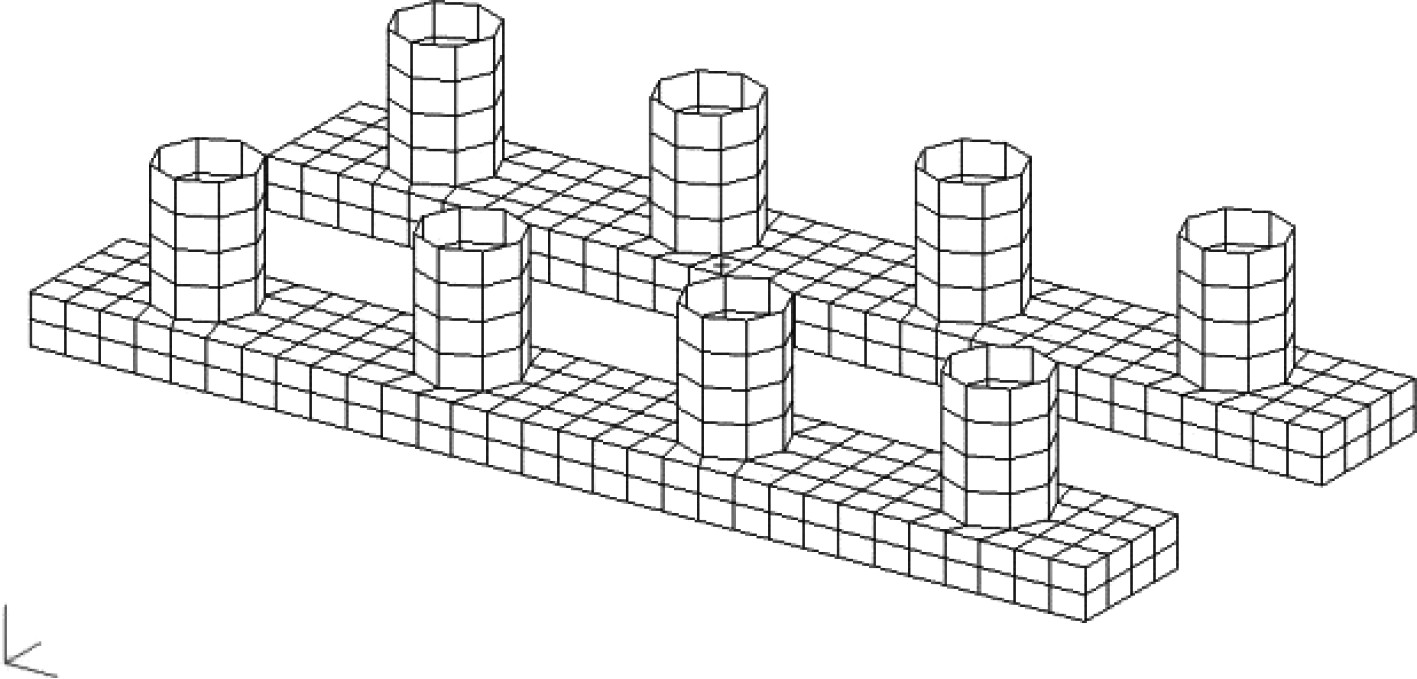
|
图 2 模块水动力计算网格 Fig. 2 Mesh of MOB module |
本文计算8个浪向角(0°,15°,30°,45°,60°,75°,85°,90°),46个波浪频率 (0.1~1.5 Hz),2种连接器刚度下浮体的运动响应和连接器载荷,并在北太平洋7级海况下进行短期预报。计算过程中,连接器刚度选择K5(Kx=
本文通过自主开发程序Multifloat计算MOB系统的波浪诱导响应。为了验证本程序的有效性,计算了5模块MOB系统在K6连接器刚度
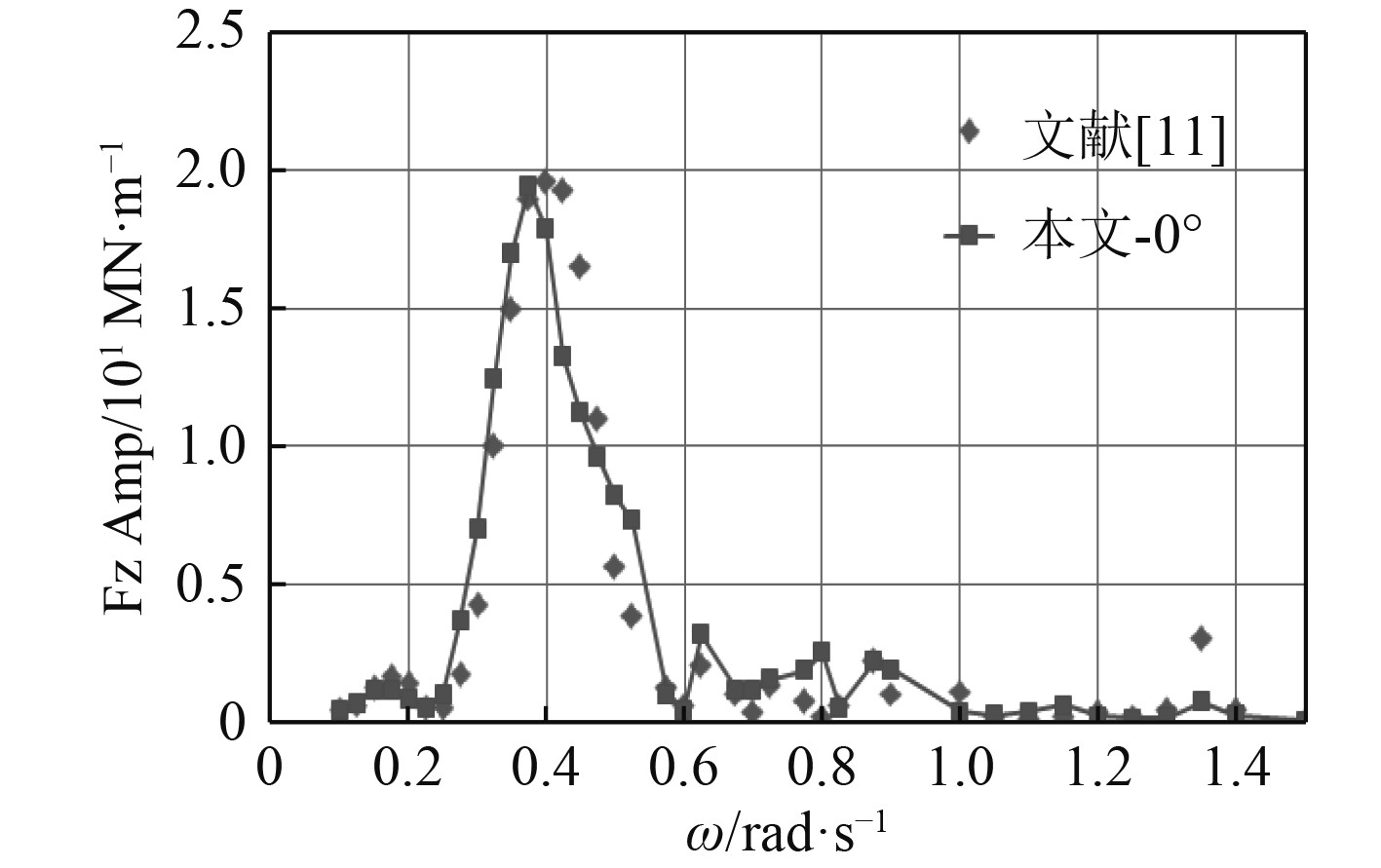
|
图 3 C3垂向载荷(5MS,K6) Fig. 3 RAO of Fz of C3 (5MS, K6) |
利用水动力计算软件SESAM计算出考虑浮体间水动力相互作用的波浪激励力矩阵和水动力系数矩阵(主要包括附加质量矩阵、阻尼系数矩阵、静水恢复力矩阵)。图4为波浪入射角为

|
图 4 各模块波浪力(矩)幅值 Fig. 4 RAO of force and moment |
将附加质量进行无因次化处理,图5(a)为M1~M4模块的垂荡运动导致的M1模块的纵荡运动附加质量系数。图5(b)为M1~M4模块的纵摇运动导致的M1模块的纵荡运动附加质量系数。由图5可知,附加质量系数和波浪频率有关。体现模块间相互影响的附加质量系数中,
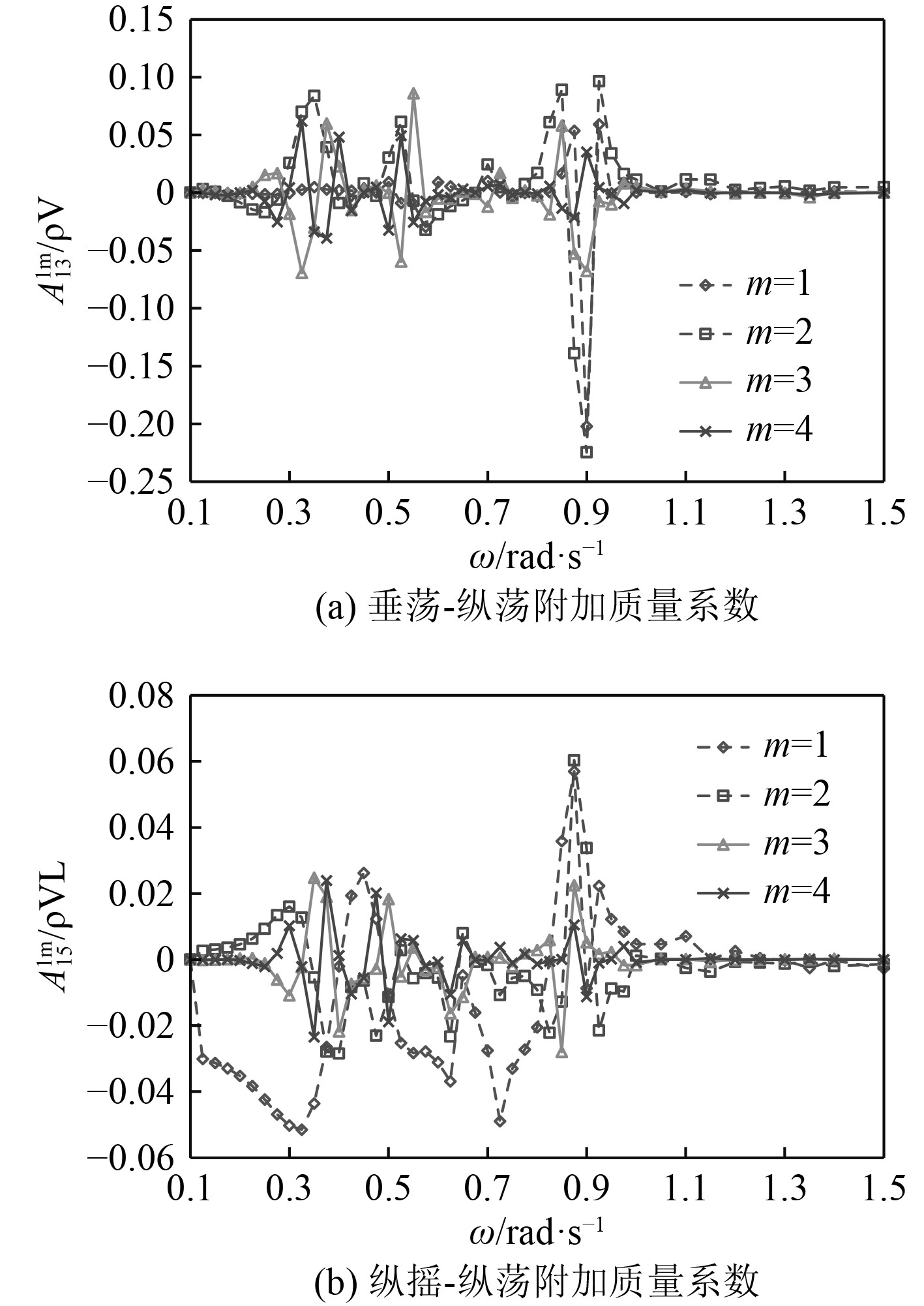
|
图 5 附加质量系数 Fig. 5 Added mass coefficients |
图6为K5和K11刚度下不同波频和波浪入射角度下C1连接器纵向和垂向载荷幅值图,计算过程中均考虑了模块间的相互作用。由图可知,K5连接器刚度下,波频在0.3~0.5之间时连接器载荷值较大,其余频率下连接器载荷较小。K11连接器刚度下,波频位于0.3~0.5时,连接器纵向和垂向载荷值较大,当波频为0.475,波浪入射角为

|
图 6 K5和K11刚度下C1连接器载荷幅值 Fig. 6 Load amplitude of C1 under K5 and K11 |
考虑浮体间相互作用时的计算结果是最为准确的,但是由于求解模块间相互作用的水动力系数矩阵过程较为复杂。为了简化计算,采用不考虑浮体间相互影响的方法进行水动力计算目前也是比较流行的。
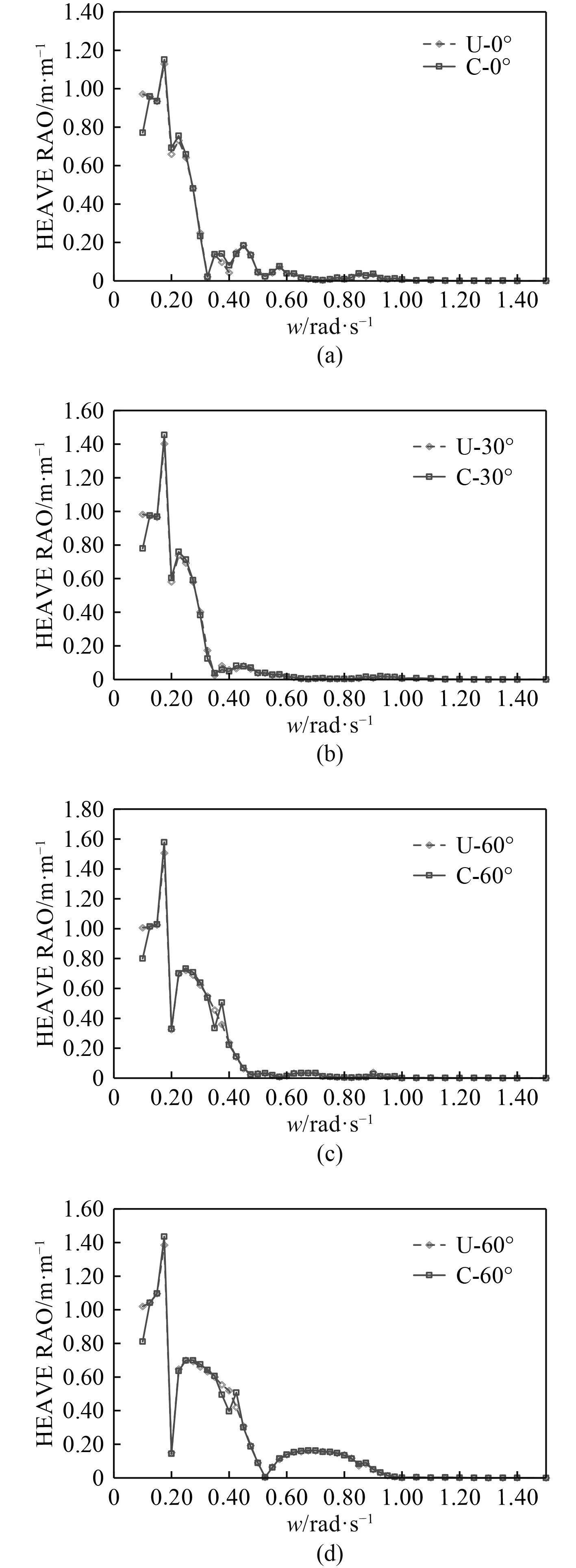
不考虑模块间相互作用时得到的计算结果与考虑模块间相互作用时的结果存在一定差别。图7和图8分别为K5连接器刚度下采用2种计算方法得到的M1模块纵荡和垂荡响应幅值。从图中可以看出2种方法得出的模块运动值存在一定差别,考虑水动力相互作用时M1模块的纵荡和垂荡响应极值略大于不考虑相互作用时的值,2种方法计算得出的M1模块纵荡响应极值最多相差27.1%。
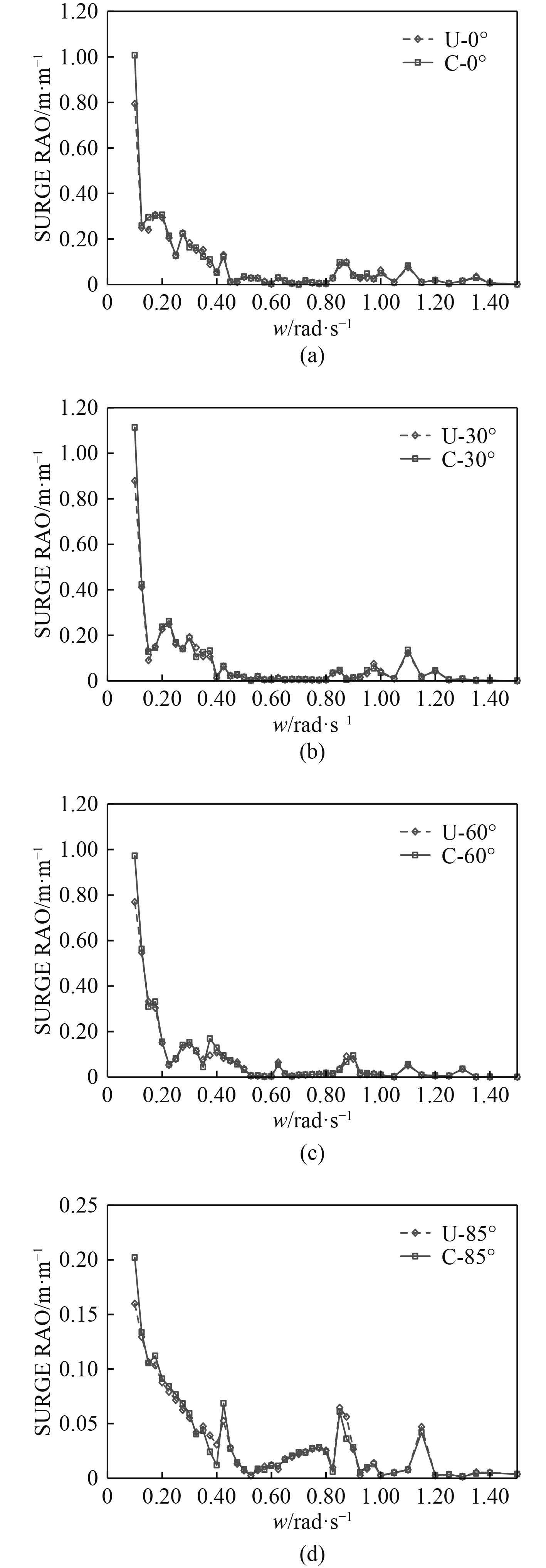
|
图 7 M1模块纵荡响应幅值(K5) Fig. 7 Surge RAO of M1(K5) |
|
图 8 M1模块垂荡响应幅值(K5) Fig. 8 Heave RAO of M1(K5) |
图9和图10分别为K5刚度下C1连接器纵向和垂向载荷。由图可知,不同波浪入射角度下连接器载荷极值差异较大。在同一个波频下使用2种计算方法得出的C1连接器纵向和垂向载荷值存在一定差别,但差别并不显著。

|
图 9 C1纵向载荷RAO(K5) Fig. 9 RAO of Fx of C1(K5) |

|
图 10 C1垂向载荷RAO(K5) Fig. 10 RAO of Fz of C1(K5) |
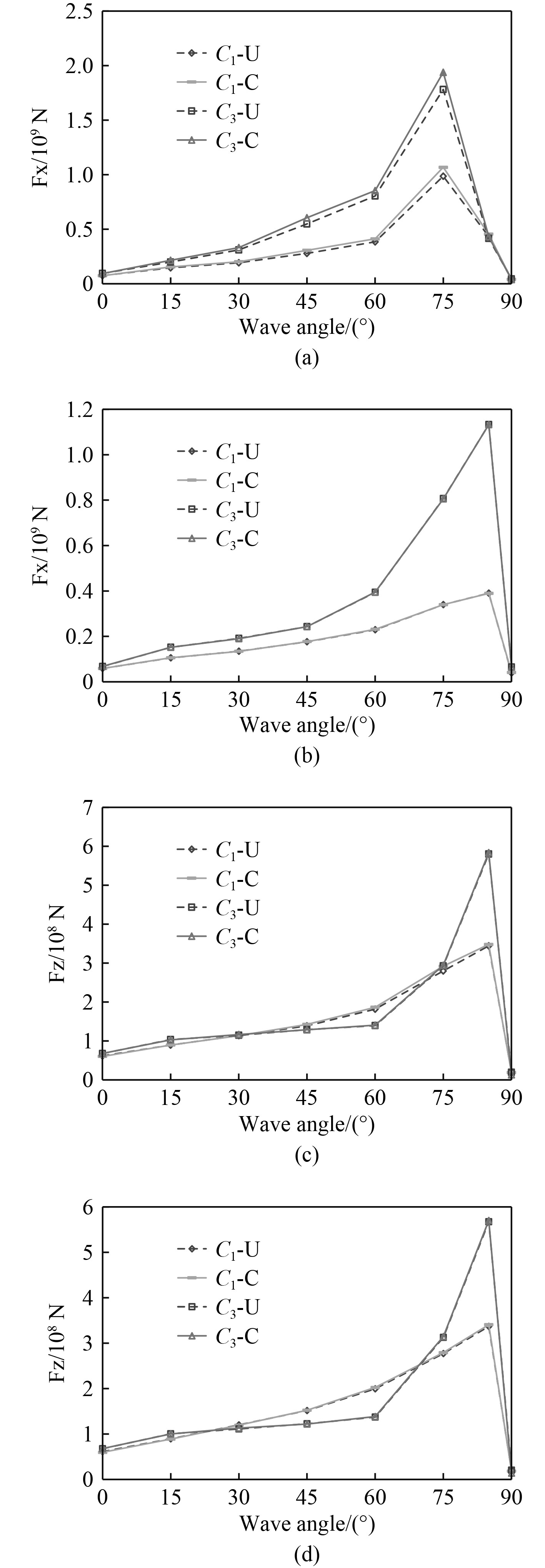
图11为K5和K11刚度时北太平洋7级海况下C1和C3连接器纵向和垂向载荷的短期预报值。由图可知,K11刚度下C1连接器纵向载荷极值比K5刚度时小,但K11刚度下C3连接器纵向载荷比K5刚度时大。当浪向角在
|
图 11 连接器载荷短期预报值 Fig. 11 Short response of connectors' load |
本文利用数值计算方法计算多浮体水动力系数,编程计算了多浮体动力响应,并分析了水动力相互作用对计算结果产生的影响。主要得出以下结论:
1)MOB系统中2个相邻浮体间的距离越近水动力相互作用越大,当浮体相距较远时相互作用明显减小。
2)模块间相互作用对MOB运动响应和连接器载荷存在一定程度的影响。对于不同刚度的连接器来说,模块间水动力相互作用对连接器载荷的影响程度不同。
3)将多浮体系统与波浪入射方向夹角保持在
4)连接器载荷和浮体的耐波性是MOB初步设计过程中的重要关注点,因此找到一种快速有效的预报方法至关重要。由于采用不考虑模块间相互作用的方法进行响应预报可以大大降低计算复杂程度,且偏差在可接受范围内,所以在MOB连接器初步设计时不失为一种更为简便的计算方法。
| [1] |
RIGGS H R, ERTEKIN R C. A comparative study of RMFC and FEA models for the wave-induced response of a MOB[J]. Matine Structure, 2000, 13: 217–232.
|
| [2] |
袁宇波. 船舶碰撞载荷对超大型浮式结构物连接器载荷的影响[D]. 镇江: 江苏科技大学, 2012.
|
| [3] |
余澜, 李润培, 舒志. 移动式海上基地连接器动力特性[J]. 上海交通大学学报, 2003, 37(8). YU Lan, LI Run-pei, SHU Zhi. Dynamic characteristics of mobile offshore base connectos[J]. Journal of Shanghai Jiaotong University, 2003, 37(8). |
| [4] |
余澜, 丁伟, 李润培. 移动式海上基地多模块间相互作用对连接器载荷的影响[J]. 海洋工程, 2004, 22(1): 25-31. YU Lan, DING Wei, LI Run-pei. Effect of the multiple modules interaction on MOB connector loads[J]. The Ocean Engineering, 2004, 22(1): 25-31. DOI:10.3969/j.issn.1005-9865.2004.01.004 |
| [5] |
王永恒, 汪学锋, 徐胜文, 等. 多模块超大型浮体中连接器刚度对其运动响应的影响[J]. 海洋工程, 2018, 36(4): 11-18. WANG Yongheng, WANG Xuefeng, XU Shengwen et al. Influence of multi-module VLFS connector stiffness on dynamic response performance[J]. The Ocean Engineering, 2018, 36(4): 11-18. |
| [6] |
宋斌. 超大型浮式海上基地连接件特性研究[D]. 上海: 上海交通大学, 2012.
|
| [7] |
鲁达. 带有连接器的多浮体结构的水动力研究[D]. 上海: 上海交通大学, 2016.
|
| [8] |
LI Zhi-wei, ZHANG Zheng-wei. A study on connector loads of very large floating structures near islands and reefs[J]. Ship Mechanics, 2017, 21(3): 329-338. |
| [9] |
L Sun. Responses of interconnected floating bodies[J]. The IES Journal Part A:Civil & Structural Engineering, 2012, 4(3): 143-156. |
| [10] |
NEWMAN J N. Wave effects on deformable bodies[J]. Applied Ocean Research, 1994, 16: 47-59. DOI:10.1016/0141-1187(94)90013-2 |
| [11] |
余澜. 移动式海上基地(Mobile Offshore Base-MOB)连接器动力响应研究[D]. 上海: 上海交通大学, 2004.
|
 2022, Vol. 44
2022, Vol. 44
