2. 国家深海基地管理中心,山东 青岛 266237
2. National Deep Sea Center, Qingdao 266237, China
水下无人航行器(UUV)是海洋资源开发、海洋环境监测及海洋生态保护等的关键装备之一。近年来,随着人类对深海资源开发的不断深入,UUV由于在军事与科研方面有重要应用,引起了广泛关注,研究价值和意义也日益凸显[1-2]。
操纵性能是UUV总体性能的主要指标之一,直接影响着航行器执行作业任务的能力,在航行器初步设计和运动控制参数选取时,操纵性能的预报尤为重要[3]。建立合理的空间运动数学模型是研究UUV操纵性及控制系统设计的基础,王波[4]、赵金鑫[5]等参考潜艇操纵性研究的方法搭建了非线性的UUV空间运动数学模型进行了仿真预报,段斐等[6]针对REMUS模型中的推力(力矩)和舵力(力矩)难于获取等问题,提出了一种修正的REMUS模型并完成了航行器的运动仿真预报。戴君锐等[7]采用六自由度模型完成了UUV操纵运动仿真,并与K-T模型的仿真结果进行了对比。徐得志等[8]参考舰船操纵性理论研究方法,采用四阶龙格-库塔算法对UUV垂向操纵运动进行了研究。聂为彪等[9]建立了UUV水平面内的动力学方程,应用Matlab编程对研究对象的水平面操纵运动进行了预报。
本文基于水下航行力学基本原理,参考鱼雷操纵性基本理论[10],在小冲角、小侧滑角、小机动运动条件下导出了UUV六自由度空间运动的线性数学模型,并搭建了操纵运动仿真预报平台,对某型UUV单平面典型操纵运动特性进行仿真预报,为UUV水动力布局和控制系统的设计提供一定的技术指导与理论支撑。
1 UUV空间运动数学模型 1.1 基本假设1)UUV是刚体,并关于
2)流体是无粘不可压缩的;
3)流体为无界流场,在航行体运动之前是静止的;
4)坐标原点与UUV浮心重合;
5)不考虑地球的自转和地球的曲率,近似认为地面坐标系为惯性坐标系。
1.2 坐标系选择与运动学参数采用如图1所示坐标系,包括地面坐标系
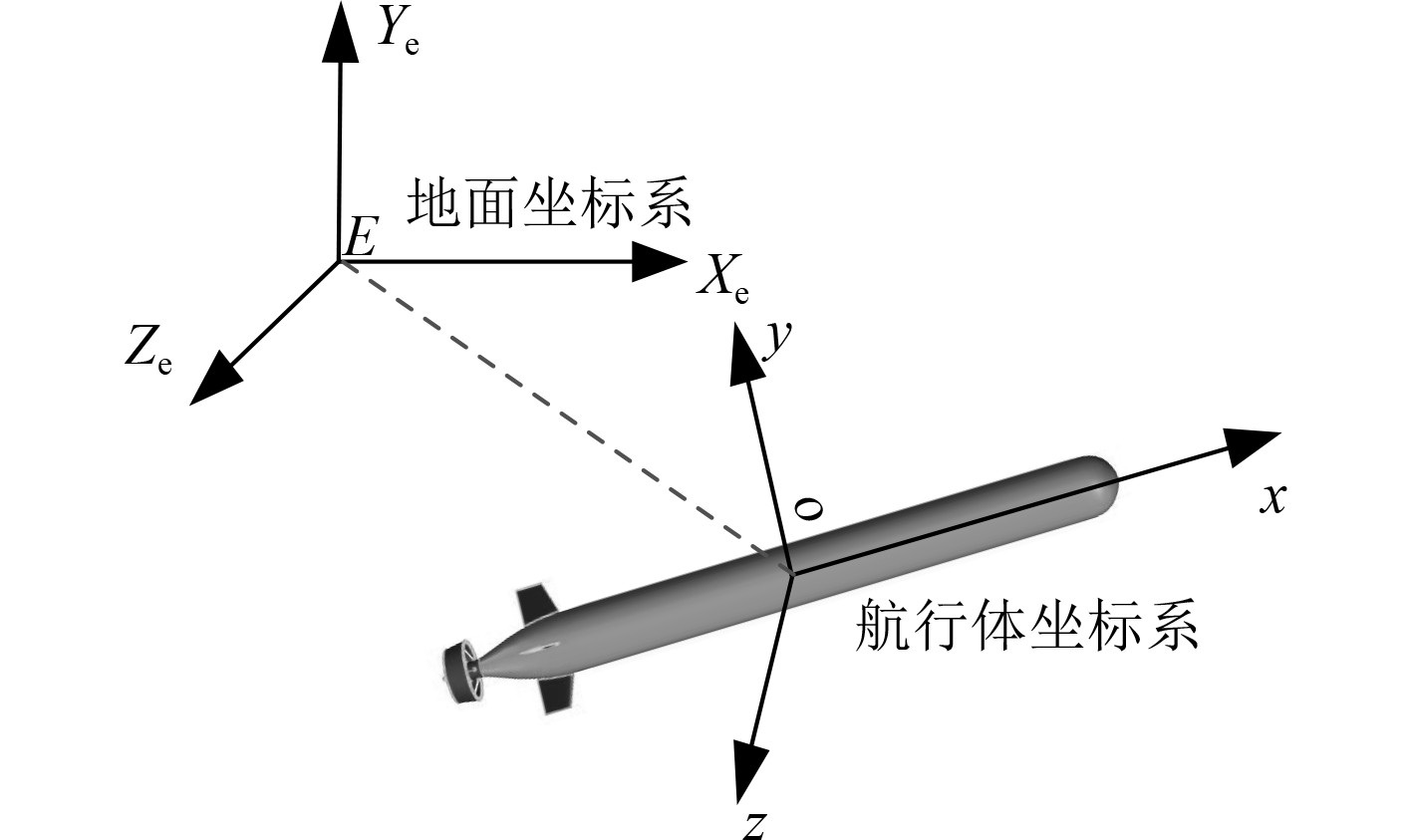
|
图 1 水下无人航行器坐标系 Fig. 1 Coordinate system of underwater unmanned vehicle |
地面坐标系
| $ \left[ \begin{gathered} {X_e} \\ {Y_e} \\ {Z_e} \\ \end{gathered} \right] = {\boldsymbol{C}}_{\mathbf{E}}^{\mathbf{O}} \left[ \begin{gathered} x \\ y \\ z \\ \end{gathered} \right],$ | (1) |
| $ \begin{split}{\boldsymbol{C}}_{\mathbf{E}}^{\mathbf{O}} =& \left[ \begin{array}{cc} \cos \theta \cos \psi & \sin \psi \sin \varphi - \sin \theta \cos \psi \cos \varphi \\ \sin \theta &\cos \varphi \cos \theta \\ - \cos \theta \sin \psi &\cos \psi \sin \varphi + \sin \theta \sin \psi \cos \varphi \end{array} \right. \\ & \left. \begin{array}{c} \sin \psi \cos \varphi + \sin \theta \cos \psi \sin \varphi \\ - \sin \varphi \cos \theta \\ \cos \psi \cos \varphi - \sin \theta \sin \psi \sin \varphi \end{array} \right] 。\end{split}$ | (2) |
运动参数包括:
1)UUV在地面坐标系中的位置(
2)航行体坐标系下的UUV速度(
3)UUV速度
| $ \left\{ \begin{gathered} v = \sqrt {{v_x}^2 + {v_y}^2 + {v_z}^2} ,\\ \alpha = \arctan ( - {v_y}/{v_x}),\\ \beta = \arctan ({v_z}/\sqrt {{v_x}^2 + } {v_y}^2)。\\ \end{gathered} \right. $ | (3) |
根据UUV速度在地面坐标系和航行体坐标系下的转换关系,可得平动运动学方程:
| $ {\left[ {{X_e}\;{Y_e}\;{Z_e}} \right]^{{\rm{T}}} } = {\boldsymbol{C}}_{\mathbf{E}}^{\mathbf{O}} {\left[ {{v_x}\;{v_y}\;{v_z}} \right]^{{\rm{T}}} }。$ | (4) |
式中:
由UUV旋转角在地面坐标系和航行体坐标系下的关系,可得转动运动学方程:
| $ \left[ \begin{gathered} {\dot \varphi } \\ {\dot \psi } \\ {\dot \theta } \\ \end{gathered} \right] = \left[ \begin{gathered} 1\;\;\;\; - \cos \varphi \tan \theta \;\;\;\;\;\;\sin \varphi \tan \theta \\ 0\;\;\;\;\;\cos \varphi /\cos \theta \;\;\; - \sin \varphi /\cos \theta \\ 0\;\;\;\;\;\;\;\;\;\;\;\sin \varphi \;\;\;\;\;\;\;\;\;\;\;\cos \varphi \\ \end{gathered} \right] \left[ \begin{gathered} {\omega _x} \\ {\omega _y} \\ {\omega _z} \\ \end{gathered} \right]。$ | (5) |
根据动量定理和动量矩定理[11],可以得到UUV在无流界中的动力学运动方程,并通过系列的推导,可表示为矩阵形式:
| $ \begin{split}\left[ \begin{array}{*{20}{c}} {{\dot v}_x} \\ {{\dot v}_y} \\ {{\dot v}_z} \\ {{\dot \omega }_x} \\ {{\dot \omega }_y} \\ {{\dot \omega }_z} \\ \end{array} \right] = {\left[ \begin{array}{*{20}{c}} m+{\lambda _{11}} & 0 & 0 & 0 & m{z_c} & - m{y_c} \\ 0 & m + {\lambda _{22}} & 0 & - m{z_c} & 0 & m{x_c} + {\lambda _{26}} \\ 0 & 0 & m + {\lambda _{33}} & m{y_c} & {\lambda _{35}} - m{x_c} & 0 \\ 0 & - m{z_c} & m{y_c} & {J_{xx}} + {\lambda _{44}} & 0 & 0 \\ m{z_c} & 0 & {\lambda _{35}} - m{x_c} & 0 & {J_{yy}} + {\lambda _{55}} & 0 \\ - m{y_c} & m{x_c} + {\lambda _{26}} & 0 & 0 & 0 & {J_{zz}} + {\lambda _{66}} \\ \end{array} \right]^{ - 1}}\times \left[ \begin{array}{c} {F_{sx}} + {F_{gx}} + {F_{tx}} + T \\ {F_{sy}} + {F_{gy}} + {F_{ty}} \\ {F_{sz}} + {F_{gz}} + {F_{tz}} \\ {M_{sx}} + {M_{gx}} + {M_{tx}} + \Delta {M_{xp}} \\ {M_{sy}} + {M_{gy}} + {M_{ty}} \\ {M_{sz}} + {M_{gz}} + {M_{tz}} \\ \end{array} \right]。\end{split} $ | (6) |
式中:
1)
2)
| $ \left[ \begin{gathered} {F_{gx}} \\ {F_{gy}} \\ {F_{gz}} \\ {M_{gx}} \\ {M_{gy}} \\ {M_{gz}} \\ \end{gathered} \right] = \left[ \begin{gathered} {\text{(}}B - G)sin\theta \\ {\text{(}}B - G)\cos \theta \cos \varphi \\ - {\text{(}}B - G)\cos \theta \sin \varphi \\ G\cos \theta ({y_c}\sin \varphi + {z_c}\cos \varphi ) \\ - G({x_c}\cos \theta \sin \varphi + {z_c}\sin \theta ) \\ G({y_c}\sin \theta - {x_c}\cos \theta \cos \varphi ) \\ \end{gathered} \right]。$ | (7) |
式中:
3)
| $ \begin{split}&\left[ \begin{gathered} {F_{tx}}\;\; \\ {F_{ty}}\;\; \\ {F_{tz}}\;\; \\ {M_{tx}} \\ {M_{ty}}\; \\ {M_{tz}} \\ \end{gathered} \right] = \\&\left[ \begin{gathered} - m\left[ {{v_z}{\omega _y} - {v_y}{\omega _z} + {y_c}{\omega _x}{\omega _y} + {z_c}{\omega _x}{\omega _z} - {x_c}({\omega _y}^2 + {\omega _z}^2)} \right]\;\; \\ - m\left[ {{v_x}{\omega _z} - {v_z}{\omega _x} + {x_c}{\omega _x}{\omega _y} + {z_c}{\omega _y}{\omega _z} - {y_c}({\omega _x}^2 + {\omega _z}^2)} \right]\; \\ - m\left[ {{v_y}{\omega _x} - {v_x}{\omega _y} + {x_c}{\omega _x}{\omega _z} + {y_c}{\omega _y}{\omega _z} - {z_c}({\omega _x}^2 + {\omega _y}^2)} \right]\;\; \\ - \left[ {m{y_c}({v_y}{\omega _x} - {v_x}{\omega _y}) + m{z_c}({v_z}{\omega _x} - {v_x}{\omega _z}) + ({J_{zz}} - {J_{yy}}){\omega _y}{\omega _z}} \right] \\ - \left[ {m{z_c}({v_z}{\omega _y} - {v_y}{\omega _z}) + m{x_c}({v_x}{\omega _y} - {v_y}{\omega _x}) + ({J_{xx}} - {J_{zz}}){\omega _z}{\omega _x}} \right]\; \\ - \left[ {m{x_c}({v_x}{\omega _z} - {v_z}{\omega _x}) + m{y_c}({v_y}{\omega _z} - {v_z}{\omega _y}) + ({J_{yy}} - {J_{xx}}){\omega _x}{\omega _y}} \right] \\ \end{gathered} \right]。\end{split}$ | (8) |
4)
| $ \left[ \begin{gathered} {F_{sx}}\; \\ {F_{sy}}\; \\ {F_{sz}}\; \\ {M_{sx}}\; \\ {M_{sy}}\; \\ {M_{sz}} \\ \end{gathered} \right] = \frac{1}{2}\rho {v^2}S\left[ \begin{gathered} {C_x}(0) \\ {C_y}(0) + C_y^\alpha \alpha + C_y^{{{\bar \omega }_z}}{{\bar \omega }_z} + C_y^{{\delta _e}}{\delta _e} \\ C_z^\beta \beta + C_z^{{{\bar \omega }_x}}{{\bar \omega }_x} + C_z^{{{\bar \omega }_y}}{{\bar \omega }_y} + C_z^{{\delta _r}}{\delta _r}\; \\ L\left[ {m_x^\beta \beta + m_x^{{{\bar \omega }_x}}{{\bar \omega }_x} + m_x^{{{\bar \omega }_y}}{{\bar \omega }_y} + m_x^{{\delta _r}}{\delta _r}\;} \right]\; \\ L\;\left[ {m_y^\beta \beta + m_y^{{{\bar \omega }_x}}{{\bar \omega }_x} + m_y^{{{\bar \omega }_y}}{{\bar \omega }_y} + m_y^{{\delta _r}}{\delta _r}} \right] \\ L\left[ {{m_z}(0) + m_z^\alpha \alpha + m_z^{{{\bar \omega }_z}}{{\bar \omega }_z} + m_z^{{\delta _e}}{\delta _e}} \right] \\ \end{gathered} \right]。$ | (9) |
式中:
搭建操纵性仿真预报平台[12-13],该平台将航行体空间运动数学模型分为姿态角模型、速度转化模型、粘性流体动力模型、静水力模型、其他力模型、坐标系转换模型等。
仿真预报过程中采用变步长四阶-五阶Runge-Kutta算法,输入UUV基本参数及水动力参数,并赋予初始速度、推力和舵角,运行程序后便可输出对应时刻UUV的姿态角、位置、速度等,生成对应曲线图,即可对UUV的操纵性能进行预报。
|
|
表 1 UUV总体参数 Tab.1 The parameters of underwater unmanned vehicle |
给定推力值T=95.96 N,对应设计航速4 kn,初始速度
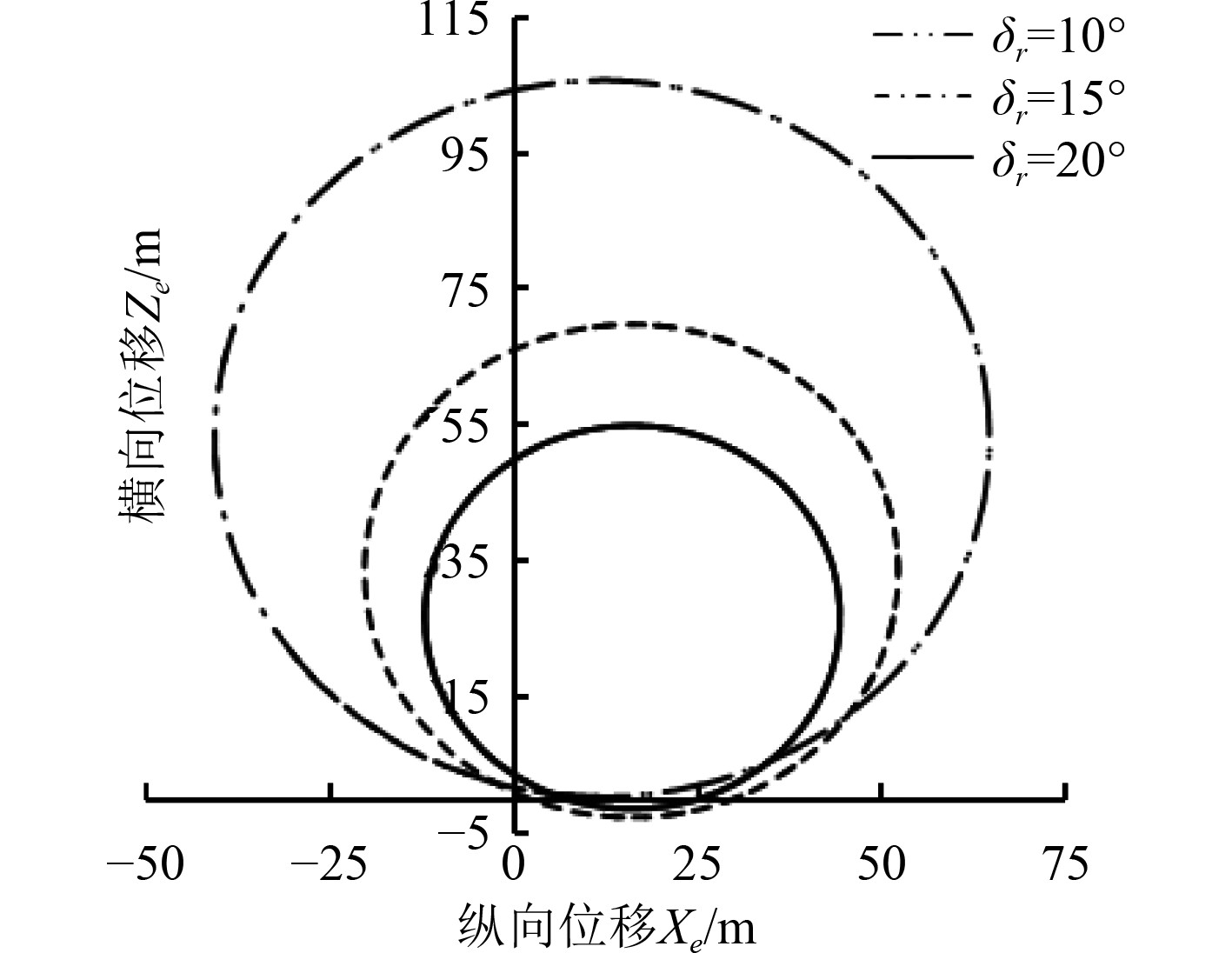
|
图 2 航速4 kn时,不同舵角的回转曲线 Fig. 2 Rotation curve of different rudder angles at 4 kn |
|
|
表 2 UUV回转运动特征参数 Tab.2 Rotary motion characteristic parameters of underwater unmanned vehicle |
可以看出,在设计航速为4 kn下,舵角越大,回转直径、回转周期和纵距越小。在操大舵角20°时,回转直径为56.3 m,约为航行体长(7 m)的8倍,可以看出该UUV具有较高的水平面回转性能。
3.1.2 水平面Z形操舵预报给定推力值T,初始速度,对应航速分别为4 kn和8 kn下,对于
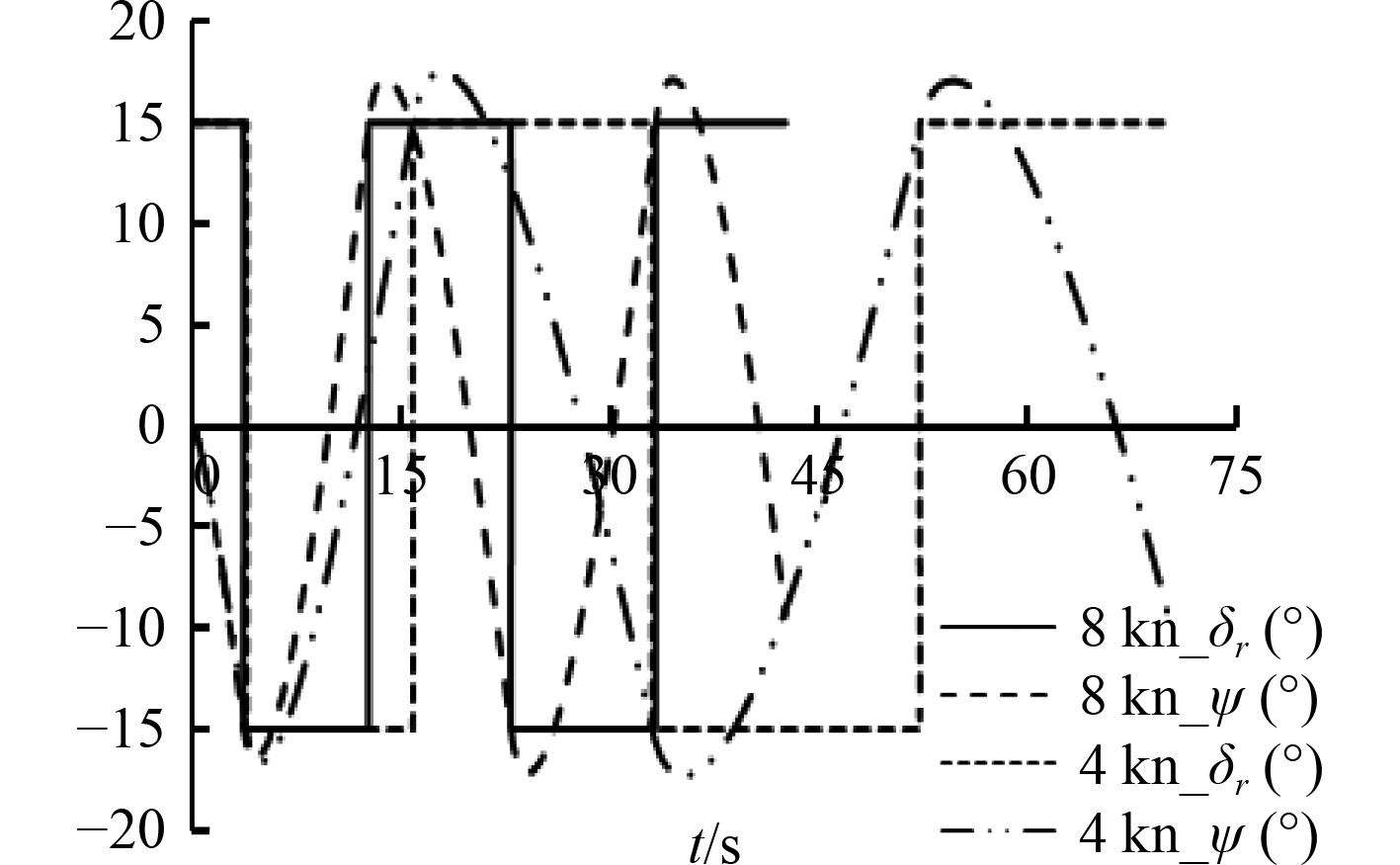
|
图 3
不同航速下,偏航角
|
从表3可以看出,航速8 kn时,UUV的初转期
|
|
表 3 UUV Z形操舵运动特征参数 Tab.3 Z-shape motion characteristic parameters of underwater unmanned vehicle |
给定推力值T,初始速度,对应航速分别为4 kn和8 kn下,操升降舵
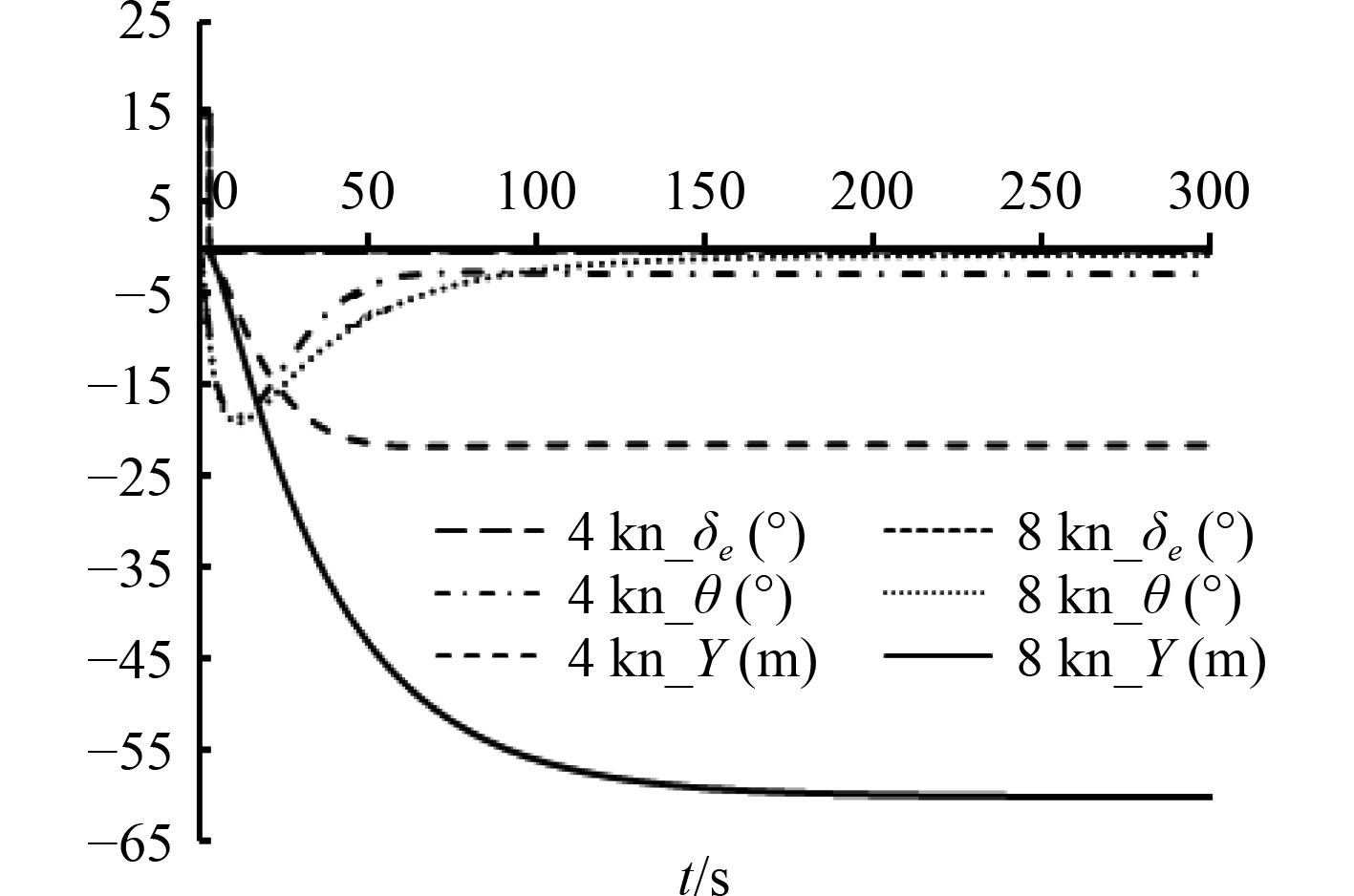
|
图 4
不同航速下,升降舵
|
从表4两个响应航速结果可以看出,航速越大,UUV的初转期
|
|
表 4 UUV T形操舵运动特征参数 Tab.4 T-shape motion characteristic parameters of underwater unmanned vehicle |
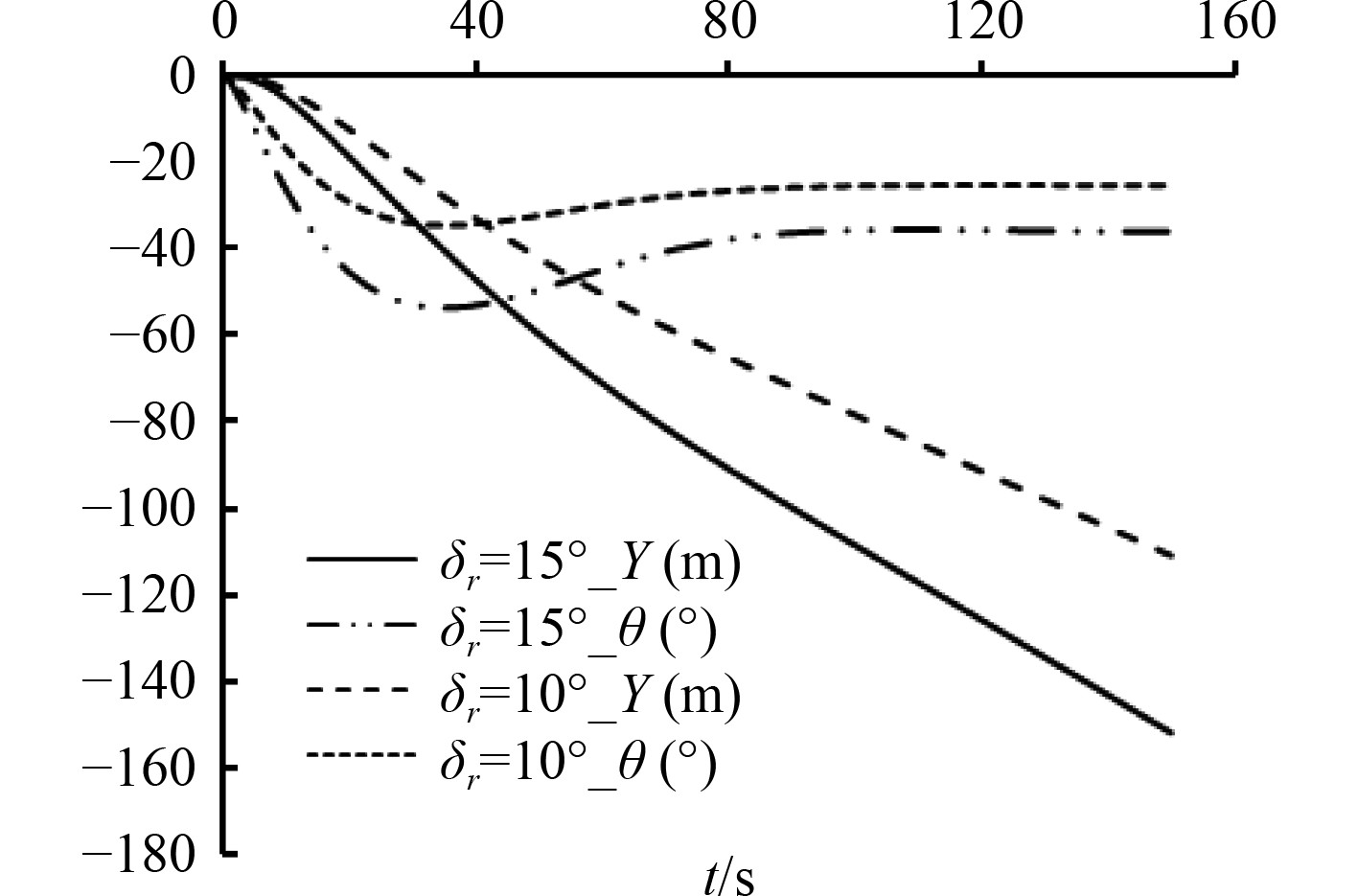
给定推力值T,初始速度,在设计航速4 kn下,分别操横舵
|
图 5
航速4 kn时,俯仰角
|
从图5可以看出,在同一航速为4 kn下,操横舵角越大,UUV转首性越好,下潜得也越快,但对应稳定后的俯仰角也越大,符合UUV的实际操纵运动特性。
4 结 语本文基于水下航行力学基本原理,参考鱼雷操纵性基本理论,导出了UUV六自由度空间运动线性数学模型,并搭建了操纵运动仿真预报平台,采用变步长四阶-五阶龙格-库塔(Runge-Kutta)算法,对某型UUV的水平面回转、Z形操舵运动以及垂直面T形操舵、纯下潜等运动进行了仿真预报。仿真结果表明,该UUV具备良好的应舵性和操纵性能,响应时间较快,能真实地反映研究对象的操纵运动特性,其结果可为UUV水动力布局和控制系统的设计提供一定的技术指导与理论支撑。
| [1] |
钟宏伟. 国外无人水下航行器装备与技术现状展望[J]. 水下无人系统学报, 2017, 25(3): 215-225. ZHONG H W. Review and prospect of equipment and techniques for unmanned undersea vehicle in foreign countries[J]. Journal of Unmanned Undersea Systems, 2017, 25(3): 215-225. |
| [2] |
王童豪, 彭星光, 潘光, 等. 无人水下航行器的发展现状与关键技术[J]. 宇航总体技术, 2017, 4(1): 52-64. WANG T H, PENG X G, PAN G, et al. Development and key technologies of unmanned underwater vehicles[J]. Astronautical Systems Engineering Technology, 2017, 4(1): 52-64. |
| [3] |
高婷. 基于空间拘束运动模拟的AUV动力学建模与操纵性优化设计[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [4] |
王波, 苏玉民, 秦再白. 微小型水下机器人操纵性能与运动仿真[J]. 系统仿真学报, 2009, 21(13): 4149-4158. WANG B, SUN Y M, QIN Z B. Research on maneuverability and simulation of small autonomous underwater vehicle[J]. Journal of System Simulation, 2009, 21(13): 4149-4158. DOI:10.16182/j.cnki.joss.2009.13.066 |
| [5] |
赵金鑫. 某潜器水动力性能计算及运动仿真[D]. 哈尔滨: 哈尔滨工程大学, 2011.
|
| [6] |
段斐, 庞硕. 基于修正的REMUS水下机器人模型的运动仿真[J]. 应用科技, 2012, 39(4): 83-88. DUAN F, PANG S. Motion simulation based on the modified remus model[J]. Applied Science and Technology, 2012, 39(4): 83-88. DOI:10.3969/j.issn.1009-671X.2012.04.017 |
| [7] |
戴君锐, 向先波, 于曹阳, 等. 六自由度水下航行器操纵性仿真及性能评估[J]. 华中科技大学学报(自然科学版), 2015, 43(I): 452−456. DAI R J, XIANG J B, YU C Y et al. Maneuverability simulation and performance evaluation of six degrees of freedom underwater vehicle[J]. Huazhong University of Science and Technology (Natural and Edition)43(I): 452−456. |
| [8] |
徐得志, 任晋宇. 水下航行器垂向操纵性运动数学仿真研究[J]. 中国水运, 2015, 15(12): 87-89. XUN D Z, REN J Y. Mathematical simulation of vertical maneuverability motion of underwater vehicle[J]. China Water Transport, 2015, 15(12): 87-89. |
| [9] |
聂为彪, 钱治强, 吴铭, 等. 水下航行器横向操纵运动预报设计与仿真[J]. 舰船科学技术, 2021, 43(1): 22-26. NIE W B, QIAN Z Q, WU M, et al. Design and simulation of horizontal maneuvering motion prediction for the underwater vehicle[J]. Ship Science and Technology, 2021, 43(1): 22-26. |
| [10] |
李天森. 鱼雷操纵性[M]. 北京: 国防工业出版社, 2007.
|
| [11] |
严卫生. 鱼雷航行力学[M] . 西安: 西北工业大学出版社, 2005.
|
| [12] |
沈建森, 朱书平, 周徐昌. 基于Matlab/Simulink的水下航行器建模与仿真[J]. 兵工自动化, 2012, 31(2): 24-27. SHEN J S, ZHU S P, ZHOU X C. A method for modeling and simulation of underwater vehicle based on Matlab/Simulink[J]. Ordnance Industry Automation, 2012, 31(2): 24-27. DOI:10.3969/j.issn.1006-1576.2012.02.007 |
| [13] |
王茂励, 赵国良. 鱼雷空间运动非线性数学模型的建立与仿真[J]. 系统仿真学报, 2007, 19(20): 4812-4814. WANG M L, ZHAO G L. Nonlinear mathematics modeling and simulation of torpedo move in space[J]. Journal of System Simulation, 2007, 19(20): 4812-4814. DOI:10.3969/j.issn.1004-731X.2007.20.051 |
 2022, Vol. 44
2022, Vol. 44
