水面舰船对海上作战有重要影响,对于水面舰船的防御手段也日益增加,因此对舰船的隐身性能提出了要求。隐身舰船通常采用内倾舷墙的船型设计,舭部与舷侧折角形式连接,能够有效地减少雷达的反射截面,降低被雷达探测的几率。
在研制某摇摆试验台时,根据项目要求,将用于承载舰载武器装备开展摇摆条件下的动态精度、可靠性以及高海清环境适应性试验等,需能够精确模拟舰船在波浪中纵摇和横摇2个自由度的摇摆运动。为研究舰船在波浪中的横摇、纵摇运动,通常采用试验水池的方法。为追求精确的试验结果,对试验者要求较高,且在模拟高海情舰船试验极易对船模造成毁损。随着计算机计算能力的提升,数值水池造波的应用越来越广泛,目前已基本能够模拟物理试验水池的主要功能。
参数横摇是当舰船航行于纵浪或接近纵浪,且所遭遇波浪波长与船长近似相等时,在短时间内出现大幅值的横摇运动。与横浪中的横摇运动有着本质上的不同,出现参数横摇的内部机理是,舰船与所遭遇波浪的相对位置随着时间发生改变,导致水线面面积由于吃水变化引起的周期性变动,从而导致了回复力矩的波动。隐身舰船为实现良好的隐身效果,采用的内倾舷墙式设计同样存在该隐患。目前国内外学者已经开始对舰船在迎浪中的大幅值横摇开展研究。William N. France等[1]提出引发参数横摇的条件:船舶横摇周期约为遭遇周期的2倍、舰船航行于近似纵浪条件下。赵春慧[2]通过进行参数横摇模型试验,得出结论:在试验开始时刻,给船模初始横向倾角,会缩短达到稳定参数横摇所需时间,且不影响参数横摇的稳定横摇幅值。葛文澎[3]采用粘性CFD方法对集装箱进行参数横摇模拟,通过与切片法以及试验数据的结果比对,验证了利用CFD方法进行参数横摇模拟具有更高的精度。
为准确全面地分析隐身舰船在波浪中的横摇运动,提出采用CFD方法,通过构建数值水池,模拟隐身舰船在波浪中的横摇运动以及甲板上浪对舰船运动的影响,为摇摆试验台的后续研究提供指导。
1 隐身舰船横摇运动模型与数值模拟 1.1 数值方法本文使用CFD方法,对隐身舰船进行数值模拟,对舰船在迎浪中的大幅值横摇运动及横摇过程中出现的强非线性现象进行研究,对于粘性流体,需满足连续性方程:
| $ \frac{\partial \rho }{\partial t}+\frac{\partial \left(\rho l\right)}{\partial x}+\frac{\partial \left(\rho m\right)}{\partial y}+\frac{\partial \left(\rho n\right)}{\partial z}=0 ,$ | (1) |
N-S方程:
| $ \begin{split}&\frac{\partial l}{\partial t} + l\frac{\partial l}{\partial x} + m\frac{\partial l}{\partial y} + n\frac{\partial l}{\partial z} = X - \frac{1}{\rho }\frac{\partial p}{\partial x} + v\left(\frac{{\partial }^{2}l}{\partial {x}^{2}} + \frac{{\partial }^{2}l}{\partial {y}^{2}} + \frac{{\partial }^{2}l}{\partial {z}^{2}}\right) + \\ &\frac{v}{3}\frac{\partial }{\partial x}\left(div\overrightarrow{v}\right)\frac{\partial m}{\partial t} + l\frac{\partial m}{\partial x} + m\frac{\partial m}{\partial y} + n\frac{\partial m}{\partial z} = Y - \frac{1}{\rho }\frac{\partial p}{\partial x} + \\ &v\left(\frac{{\partial }^{2}m}{\partial {x}^{2}} + \frac{{\partial }^{2}m}{\partial {y}^{2}} + \frac{{\partial }^{2}m}{\partial {z}^{2}}\right) + \frac{v}{3}\frac{\partial }{\partial y}\left(div\overrightarrow{v}\right) \frac{\partial n}{\partial t} + l\frac{\partial n}{\partial x} + m\frac{\partial n}{\partial y} + \\ &n\frac{\partial n}{\partial z} = Z - \frac{1}{\rho }\frac{\partial p}{\partial x} + v\left(\frac{{\partial }^{2}n}{\partial {x}^{2}} + \frac{{\partial }^{2}n}{\partial {y}^{2}} + \frac{{\partial }^{2}n}{\partial {z}^{2}}\right) + \frac{v}{3}\frac{\partial }{\partial x}\left(div\overrightarrow{v}\right) 。\end{split} $ | (2) |
式中:ρ为粘性流体的流体密度;l,m,n为3个相互垂直的速度分量;X、Y、Z为3个相互垂直的质量力;p为压力;v为粘性系数;div为散度。假设目标流体不可压缩,即密度为定值,且忽略散度项,则式(1)和式(2)可改写为:
| $ \frac{\partial l}{\partial x}+\frac{\partial m}{\partial y}+\frac{\partial n}{\partial z}=0 ,$ | (3) |
| $ \begin{split}& \frac{\partial l}{\partial t} + l\frac{\partial l}{\partial x} + m\frac{\partial l}{\partial y} + n\frac{\partial l}{\partial z} = X - \frac{1}{\rho }\frac{\partial p}{\partial x} + v\left(\frac{{\partial }^{2}l}{\partial {x}^{2}} + \frac{{\partial }^{2}l}{\partial {y}^{2}} + \frac{{\partial }^{2}l}{\partial {z}^{2}}\right)\\ &\frac{\partial m}{\partial t} + l\frac{\partial m}{\partial x} + m\frac{\partial m}{\partial y} + n\frac{\partial m}{\partial z} = Y - \frac{1}{\rho }\frac{\partial p}{\partial x} + v\left(\frac{{\partial }^{2}m}{\partial {x}^{2}} + \frac{{\partial }^{2}m}{\partial {y}^{2}} + \frac{{\partial }^{2}m}{\partial {z}^{2}}\right)\\ &\frac{\partial n}{\partial t} + l\frac{\partial n}{\partial x} + m\frac{\partial n}{\partial y} + n\frac{\partial n}{\partial z} = Z - \frac{1}{\rho }\frac{\partial p}{\partial x} + v\left(\frac{{\partial }^{2}n}{\partial {x}^{2}} + \frac{{\partial }^{2}n}{\partial {y}^{2}} + \frac{{\partial }^{2}n}{\partial {z}^{2}}\right)。\end{split} $ | (4) |
将式(4)简写为矢量形式:
| $ \frac{\partial \overrightarrow{v}}{\partial t}+\left(\overrightarrow{v}\cdot \nabla \right)\overrightarrow{v}=\overrightarrow{F}-\frac{1}{\rho }\nabla \rho +v{\nabla }^{2}\overrightarrow{v} \;。$ | (5) |
式中:
针对DTMB 5613型隐身舰船进行数值模拟,该船型由美国海军水面舰船研究中心提出,外观近似于DDG1000型内倾船,图1为DTMB 5613型隐身舰船三维模型。

|
图 1 DTMB 5613三维模型 Fig. 1 The 3D model of DTMB 5613 |
重叠网格基于动网格,在背景网格与重叠网格交界处采用插值计算,能够参照船体的自由度进行运动,即重叠网格的部分区域与船体共同运动,理论上讲任意方向、任意幅值的运动都能被精确捕捉,对大幅值运动的模拟有较好的精度,本文采用重叠网格对舰船的横摇运动模拟,采用VOF法对自由液面进行捕捉。
针对数值造波,在单个波长内保持不少于100层网格,波高范围内不少于12层网格,时间步长设定为波浪周期的1/500,自由液面采用多体控制以实现网格尺寸过渡均匀,减小网格体积突变所产生的计算误差,如图2所示。
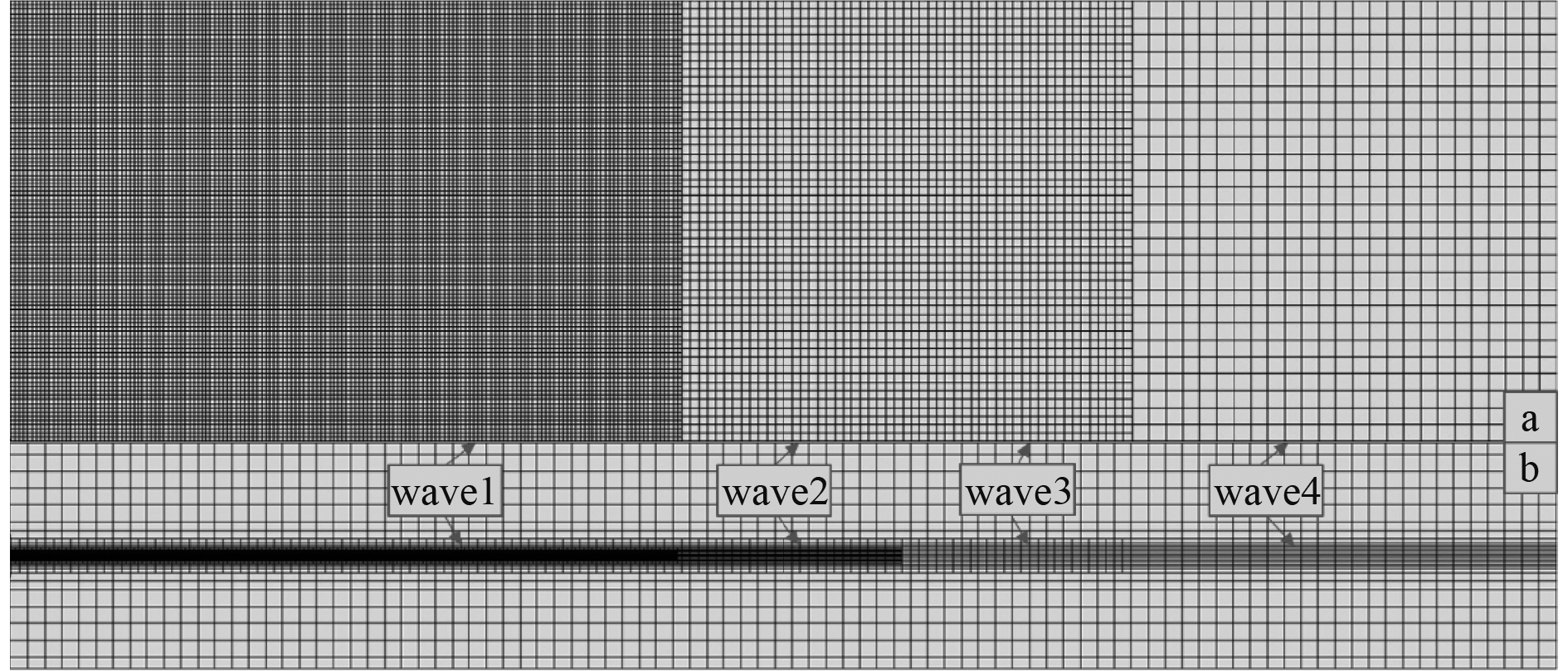
|
图 2 数值水池造波网格示意图 Fig. 2 Schematic diagram of gridding to the numerical wave tank |
全域数值模拟网格方案如图3所示。
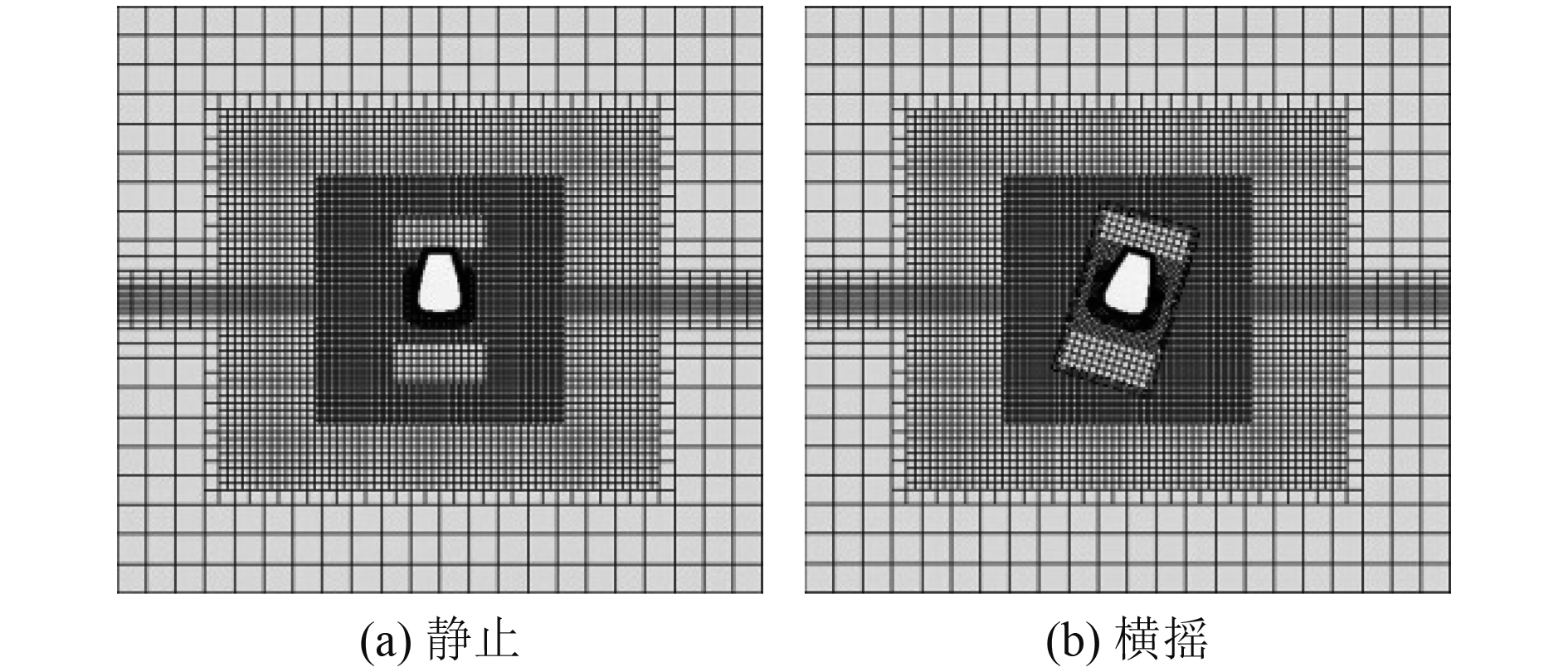
|
图 3 重叠网格 Fig. 3 Overlapping grid |
数值模拟计算域尺寸设置为22 m×9 m×6 m(长×宽×高),船体部分设置为不可滑移壁面,入口截面、顶部、底部设置为速度入口,出口截面设置为压力出口,左右两侧设置为对称面。针对舰船横摇运动存在的强非线性现象,选用

|
图 4 计算域与边界条件示意图 Fig. 4 Schematic diagram of computational domain and boundary conditions |
根据国内外文献研究以及数值模拟前期数据发现:舰船在确定工况下发生参数横摇通常需要经历数个横摇周期,过长的发展时间对网格量大、时间步长小、迭代次数多的CFD数值模拟非常不利。为了加速舰船达到稳定参数横摇的进程,首先在初始时刻对舰船施加不同程度扰动,分析初始扰动对参数横摇的影响。选取施加横摇角速度作为初始扰动,统计达到参数横摇稳定阶段所需周期、最大幅值和稳定幅值,分析初始扰动对参数横摇的影响。针对波陡0.04的迎浪规则波,设定傅氏数
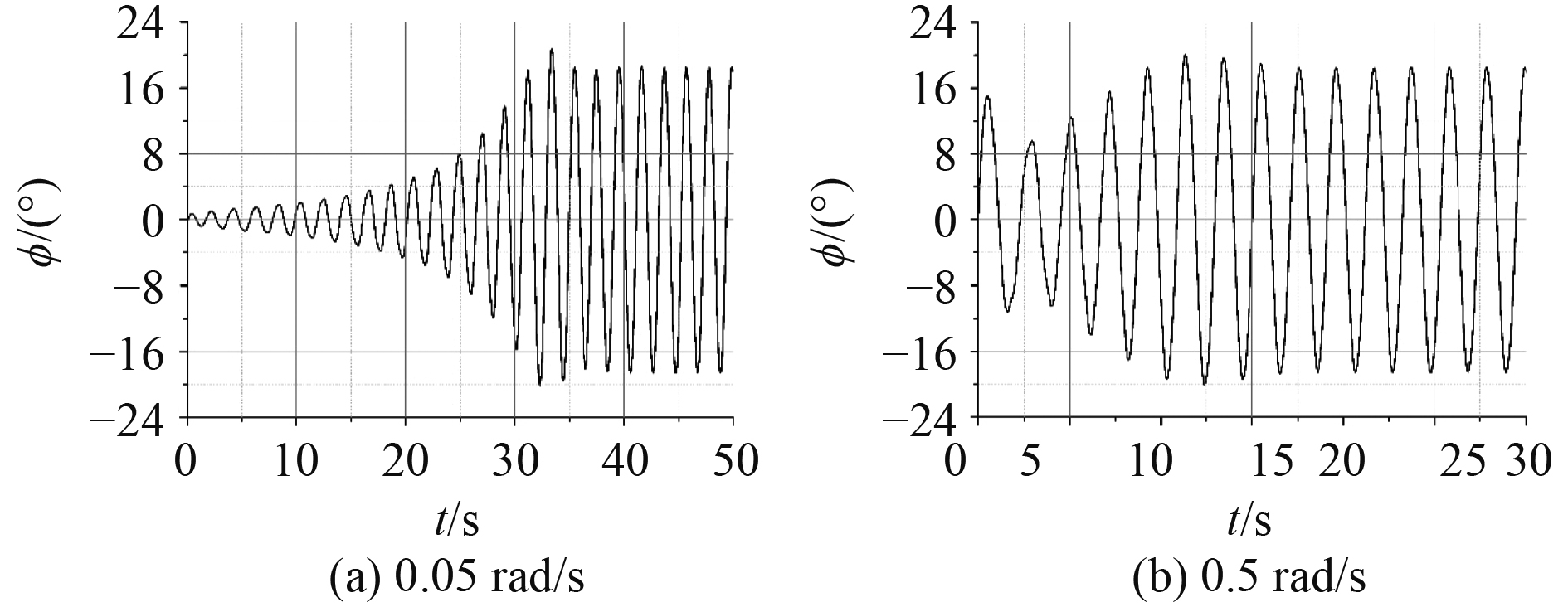
|
图 5 不同初始横摇角速度参数横摇时历曲线图 Fig. 5 Duration curve of different initial yaw velocity |
从表1和图5可以看出,在施加0.05 rad/s的初始横摇角速度的情况下,经历18个周期,达到了18.49°的稳定横摇幅值,其中最大横摇幅值为20.68°,而施加了0.5 rad/s的初始横摇角速度后,仅经历8个横摇周期,就达到了稳定横摇阶段,横摇幅值为18.54°,其中最大横摇幅值为20.11°。对比发现,施加0.05 rad/s与0.5 rad/s的横摇角速度在参数横摇线性稳定后无明显差异,仅缩短了参数横摇达到稳定所需时间,即初始扰动不影响参数横摇的最终结果,后续为减少计算用时,均在初始时刻对船模施加0.5 rad/s的横摇角速度。
|
|
表 1 不同初始扰动下参数横摇数据统计 Tab.1 Data statistics of parametric roll with different yaw velocity |
舰船发生参数横摇需满足特定的遭遇频率,当遭遇频率接近2倍舰船横摇固有频率时,存在发生参数横摇的风险。在确定遭遇波长的情况下,通过色散关系可以确定遭遇频率,计算公式如下:
| $ {\omega }_{e}=\omega -\frac{{\omega }^{2}}{g}V\mathrm{cos}\beta 。$ | (6) |
式中:
本文研究隐身舰船在迎浪中的横摇,数值模拟选用迎浪规则波,即
|
|
表 2 迎浪时航速与傅氏数及遭遇频率与横摇固有频率比值的对应关系 Tab.2 Matchup of velocity and ratio of encounter frequency to inherent frequency |

|
图 6 各航速下横摇运动时历曲线 Fig. 6 Duration curve of parametric roll with different yaw velocity |
可以看出,在
波陡对参数横摇的发生有重要影响。波高增加,会导致水线面面积变化加剧,由此复原力矩的周期性变化更加显著;当波长近似等于船长时,船波相对位置变化导致的水线面面积变化最剧烈。选取傅氏数
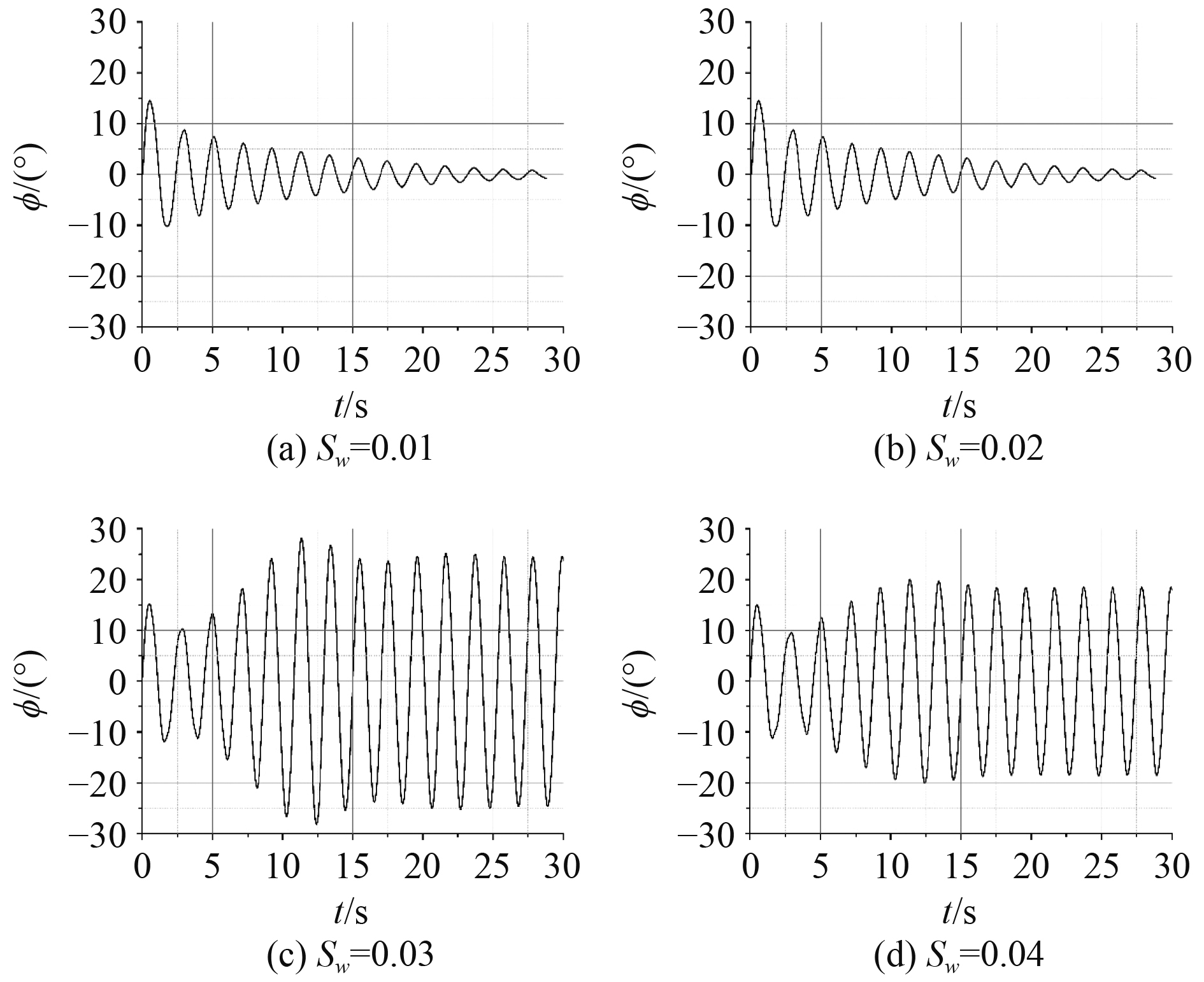
|
图 7 各波高下横摇运动时历曲线 Fig. 7 Duration curve of parametric roll with different wave height |
|
|
表 3 各波高下横摇模拟相关数据 Tab.3 Data statistics of parametric roll with different wave height |
由图7可知,在波长不变,仅改变波高的情况下,隐身舰船的横摇运动:波陡
|
|
表 4 各波长下横摇模拟相关数据(波陡Sw=0.04) Tab.4 Data statistics of parametric roll with different wave length (Sw=0.04) |
根据国内外学者对参数横摇的研究,指出参数横摇仅发生在波长船长比等于0.8~2.0的情况下,图8为固定波陡

|
图 8 各波长下横摇模运动时历曲线 Fig. 8 Duration curve of parametric roll with different wave length |
甲板上浪是因舰船与波浪之间的耦合作用而产生的一种非线性现象,尤其以迎浪中的上浪最为明显。图9为隐身舰船在

|
图 9 隐身舰船甲板上浪过程示意图 Fig. 9 Schematic diagram of the process of green water |
图9展示了DTMB 5613型隐身舰船航行于迎浪规则波中的上浪过程,由于隐身舰船向后倾斜的穿浪首,及采用低干舷、无舷墙的设计,极易产生爬浪。当舰船产生埋首时,大量水体涌上甲板,加剧了舰船的首部运动(见图9(a));当船首抬升,上层建筑阻挡水体流动,会产生 “爬浪”现象(见图9 (b));由于船首升高,爬升的水体向上的相对速度分量减小,部分水体顺着上层建筑侧壁离开船体(见图9(c));部分水体残留甲板,参与下一上浪过程(见图9(d))。
甲板上浪不仅与航速相关,还与波长船长比有关,一般波长船长比在1~1.3的情况下较容易出现甲板上浪。舰船发生参数横摇时波长近似等于船长,且多发生于迎浪条件下,这也表明甲板上浪在隐身舰船发生参数横摇时往往伴随发生。
模拟结果显示,波陡

|
图 10 波陡0.03(左)与波陡0.04(右)甲板上浪对比 Fig. 10 Comparison between Sw=0.03 (Left) and Sw=0.04 (Right) |
在此提出猜想:甲板上浪产生的积水一定程度上抑制了参数横摇的发生。相当体积的积水改变了舰船的横摇固有周期,使得在增加波陡后反而出现参数横摇幅值减小的情况,且甲板上流动的积水给船体提供了部分回复力矩。为排除甲板上浪的影响,研究参数横摇与波高的真实关系,设置舷墙以抑制甲板上浪。船模如图11所示。

|
图 11 增加舷墙船模 Fig. 11 Hull model with balwark |
设置与上层建筑平齐的舷墙,从而使得舰船在运动过程中,积水无法涌上甲板,从而不会对参数横摇的模拟起到影响。设置舷墙后运动情况如图12所示,所得横摇时历如图13所示。

|
图 12 设置舷墙运动情况 Fig. 12 Motion of hull with balwark |
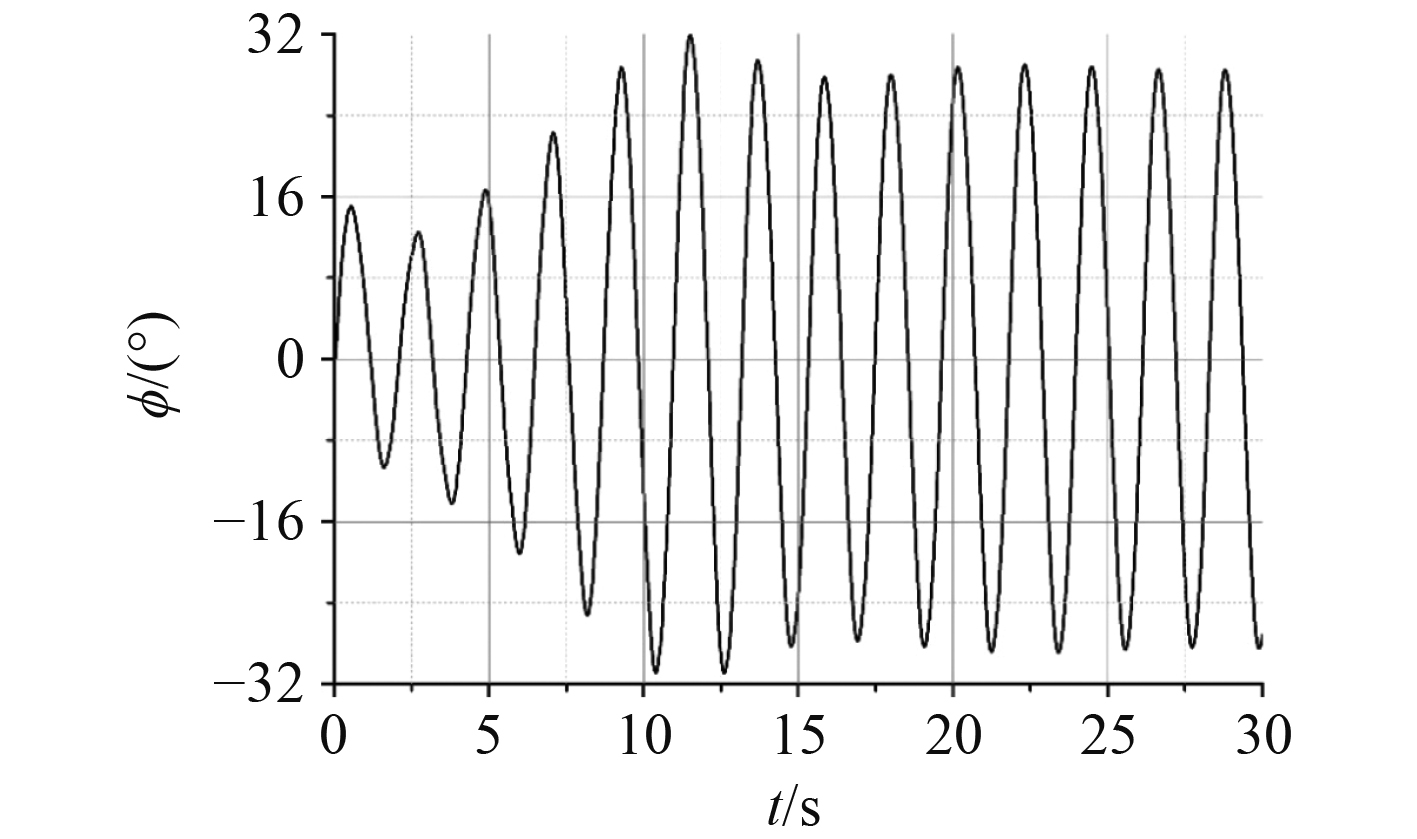
|
图 13 设置舷墙后参数横摇运动时历曲线 Fig. 13 Duration curve of parametric roll with balwark |
舷墙将波浪与甲板完全隔离开来,排除甲板上浪情况后,舰船经过7个周期形成稳定的参数横摇运动,最大幅值达31.87°,稳定阶段幅值为28.45°,如表5所示。
|
|
表 5 排除甲板上浪影响后系列波高下参数横摇数据 Tab.5 Data statistics of parametric roll with different wave height overlook green water |
当排除甲板上浪影响后可以得出:随着波高增加,隐身舰船达到横摇稳定阶段所需周期逐渐减少,达到的横摇最大幅值与稳定幅值都有所增加,且需在波陡达到某一临界值时才会发生参数横摇,与其他存在参数横摇隐患船型结论一致。
隐身舰船由于采用低干舷、无舷墙以及向后倾斜的穿浪首设计,在迎浪大波陡情况下极易出现爬浪导致甲板积水,相当体积甲板积水起到部分减摇水舱的作用,增加船舶横摇阻尼,改变船舶横摇固有周期,使得在大波陡(开始产生爬浪)情况下,出现波陡增加,参数横摇稳定幅值下降的情况。
3 结 语本文针对DTMB 5613型隐身舰船,研究舰船在波浪中的运动及甲板上浪对舰船运动的影响,建立波浪数值水池,模拟了隐身舰船在迎浪规则波下大幅值横摇,即参数横摇运动的发生,分析初始扰动、航速、波陡以及甲板上浪对参数横摇的影响。结果表明,隐身舰船在迎浪规则波下存在发生大幅值横摇,即参数横摇的可能,且横摇幅值达到28.16°,伴随参数横摇现象,往往会有甲板上浪的发生,且对参数横摇有一定的抑制作用。通过以上分析,证明利用CFD方法可以对舰船在波浪中的大幅值、强非线性运动进行较为准确的模拟,对后续舰船运动研究起到一定指导作用。
| [1] |
FRANCE W. N. LEVADOU M. TREAKLE T. W. An investigation of head-sea parametric rolling and its influence on container lashing systems[J]. Marine Technology and SNAME News, 2003, 40: 1-19. DOI:10.5957/mt1.2003.40.1.1 |
| [2] |
赵春慧. 集装箱船参数横摇试验与理论研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [3] |
葛文澎. 基于CFD技术的规则波中船舶参数激励横摇数值模拟研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [4] |
苏作靖. “育鲲”轮参数横摇的数值模拟及分析[D]. 大连: 大连海事大学, 2011.
|
| [5] |
CIHAN E U. Numerical and experimental study of parametric rolling of a container ship in waves[D]. Technical University of Lisbon, 2011.
|
| [6] |
刘乐. 内倾船型有航速纵向运动与甲板上浪粘性数值模拟[D]. 武汉: 武汉理工大学, 2017.
|
| [7] |
刘怡锦. 基于势流理论的穿梭船型性能特征研究[D]. 上海: 上海交通大学, 2013.
|
| [8] |
KERWIN, J. E. Notes on rolling in longitudinal waves[J]. International Shipbuilding Progress, 1955, 2(16): 597-614. DOI:10.3233/ISP-1955-21604 |
 2022, Vol. 44
2022, Vol. 44
