2. 上海船舶设备研究所,上海 200030;
3. 海洋石油工程股份有限公司,天津 300451
2. Shanghai Marine Diesel Engine Research Institute, Shanghai 200030, China;
3. Offshore Oil Engineering Co. Ltd., Tianjin 300451, China
船舶动力定位(dynamic positioning,DP)系统[1]是一种能够适用于复杂海况条件下,自动保持船舶位置、航向或者跟踪指定航迹的运动控制技术。动力定位船[2]在海上运动时受风、浪、流等环境载荷作用,其中波浪载荷主要包括一阶波浪载荷和二阶波浪载荷,进而使船体产生一阶波浪运动和二阶漂移运动。一阶高频运动是零均值的往复振荡运动,对动力定位性能影响较大。在传感器的测量运动信号输入DP控制器之前[3],必须将信号中的一阶高频运动和测量白噪声滤除。
针对船舶波浪运动滤波和控制问题,国内外的许多学者都做过相关研究。Fossen等[4]对船舶受环境扰动情况时运动控制系统展开研究。Hassani等[5]提出一个由递归优化过程组成的自适应波浪滤波系统。李杨等[6]在海浪干扰主频率辨识方法的基础上,设计扩展状态观测器及二次最优控制器。邓英杰等[7]提出一种动力定位的状态观测饱和控制算法。然而Kalman滤波由于参数较多和强耦合性,未能在DP控制中很好应用。
本文针对船舶动力定位系统的一阶波浪运动滤波与控制问题,建立船舶DPS系统非线性动力学模型和波浪运动的数学模型,对船舶DPS的非线性数学模型进行线性化理处;建立一种基于位置和航向输出的DPS状态观测器,研究如何利用基于连续Kalman滤波技术解决动力定位系统三自由度解耦滤波问题,并讨论DPS滤波器的噪声协方差矩阵参数的选择方法;构建一种包含状态估计和运动控制器的DPS系统仿真模型,并在Simulink中进行了动力定位仿真分析,进而探讨非线性无源滤波和Kalman滤波方法的滤波效果和船舶动力定位性能。
1 船舶动力学与一阶波浪运动建模 1.1 船舶动力学及运动学模型在海洋等外部环境的扰动下,船舶运动会产生6个自由度运动。对于动力定位系统来说,一般只控制水面上的3个自由度(纵荡、横荡、首摇)运动。定义在北东坐标系下[8]船舶三自由度向量
船舶在海面上的运动可分为由风、海流及二阶波浪力等引起的船舶低频漂移运动和由一阶波浪力引起的船舶高频运动。船舶真实的运动是二者运动的叠加,考虑到传感器的测量白噪声干扰,DP船舶三自由度低频非线性模型可以写为:
| $ \begin{split} \left\{ \begin{aligned} & {{\boldsymbol{\dot \eta }}= {\boldsymbol{R}}(\psi ){\boldsymbol{v}}}\;,\\ & {{\boldsymbol{M\dot v}} = - {\boldsymbol{Dv}} + {{\boldsymbol{R}}^{\text{T}}}{\text{(}}\psi {\text{)}}{\boldsymbol{b}} + {\boldsymbol{\tau }} + {{\boldsymbol{\tau }}_{\text{w}}} + {{\boldsymbol{\omega }}_{\boldsymbol{v}}}}\;,\\ & {\boldsymbol{\dot b}} = - {{\boldsymbol{T}}^{{{ - 1}}}}{\boldsymbol{b}} + {{\boldsymbol{\omega }}_b}{\text{(}}{\boldsymbol{\dot b}} = {{\boldsymbol{\omega }}_b}{\text{)}}\;。\end{aligned} \right. \end{split}$ | (1) |
式中:
一阶海浪干扰力作用到船体上表现为和波高成线性关系且同频的波浪运动,DP船舶所受的高频往复运动是一阶波浪干扰力引起的,且在横荡、纵荡和首摇3个自由度上互不影响,可看成是单独的运动,都看作是一个附加阻尼项的二阶谐波振荡器[9]:
| $ {h} (s) = \frac{{{K_\omega }s}}{{{s^2} + 2\lambda {\omega _0}s + \omega _0^2}}。$ | (2) |
式中:
| $ \begin{split} \left\{ {\begin{aligned} &{{\boldsymbol{\dot \xi }} = {{\boldsymbol{A}}_{\boldsymbol{\omega }}}{\boldsymbol{\xi }} + {{\boldsymbol{E}}_{\boldsymbol{\omega }}}{\boldsymbol{\omega }}} ,\\ &{{{\boldsymbol{y}}_{\boldsymbol{\omega }}} = {\boldsymbol{C}}_{\boldsymbol{\omega }}^{\text{T}}{\boldsymbol{\xi }}} 。\end{aligned}} \right. \end{split} $ | (3) |
式中:
| $ \begin{split} \left\{ {\begin{aligned} &{\left[ {\begin{aligned} {{{{\boldsymbol{\dot x}}}_{{\boldsymbol{\omega }}1}}} \\ {{{{\boldsymbol{\dot x}}}_{{\boldsymbol{\omega }}2}}} \end{aligned}} \right] = \left[ {\begin{aligned} 0&\;1 \\ { - \omega _0^2}&{ - 2\lambda {\omega _0}} \end{aligned}} \right]\left[ {\begin{aligned} {{{\boldsymbol{x}}_{{\boldsymbol{\omega }}1}}} \\ {{{\boldsymbol{x}}_{{\boldsymbol{\omega }}2}}} \end{aligned}} \right] + \left[ {\begin{aligned} 0 \\ {{K_\omega }} \end{aligned}} \right]{\boldsymbol{\omega }}} \;,\\ &{{{\boldsymbol{y}}_{\boldsymbol{\omega }}} = \begin{aligned} [ 0&\;1] \end{aligned} \left[ {\begin{aligned} {{{\boldsymbol{x}}_{{\boldsymbol{\omega }}1}}} \\ {{{\boldsymbol{x}}_{{\boldsymbol{\omega }}2}}} \end{aligned}} \right]} \;\text{。} \end{aligned}} \right. \end{split} $ | (4) |
DP船舶测量系统测量出的船舶位置以及首摇角度的信息是带有噪声干扰的[10],因此选用的系统测量模型为:
| $ {\boldsymbol{y}} = {\boldsymbol{\eta }} + {{\boldsymbol{\eta }}_{\boldsymbol{\omega }}} + {{\boldsymbol{\omega }}_{\boldsymbol{y}}} \;,$ | (5) |
在非线性无源估计滤波器中不再采用零转首率的假设,增加2个新的假设。
假设1 忽略均值为零的高斯白噪声。
假设2 即使在极端海况下,船舶对一阶波浪力响应后的首摇角度不超过5°,得到非线性无源估计滤波器的观测方程为:
| $ \begin{split} \left\{ \begin{aligned} &{{\boldsymbol{\dot {\hat \xi} }} = {{\boldsymbol{A}}_{\boldsymbol{\omega }}}{\boldsymbol{\hat \xi }} + {{\boldsymbol{K}}_1}{\boldsymbol{\tilde y}}} \;,\\ &{{\boldsymbol{\dot {\hat \eta} }} = {\boldsymbol{R}}{\text{(}}\psi {\text{)}}{\boldsymbol{\hat v}} + {{\boldsymbol{K}}_2}{\boldsymbol{\tilde y}}}\;,\\ &{{\boldsymbol{M\dot {\hat v}}} = - {\boldsymbol{D\hat v}} + {{\boldsymbol{R}}^{\text{T}}}{\text{(}}\psi {\text{)}}{\boldsymbol{\hat b}} + {\boldsymbol{\tau }} + {{\boldsymbol{\tau }}_{\text{w}}} + {{\boldsymbol{R}}^{\text{T}}}(\psi ){{\boldsymbol{K}}_3}{\boldsymbol{\tilde y}}}\;,\\ &{{\boldsymbol{\dot {\hat b}}} = - {{\boldsymbol{T}}^{{{ - 1}}}}{\boldsymbol{\hat b}} + {{\boldsymbol{K}}_4}{\boldsymbol{\tilde y}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\boldsymbol{\dot {\hat b}}} = {{\boldsymbol{K}}_4}{\boldsymbol{\tilde y}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} )}\;,\\ &{{\boldsymbol{\hat y}} = {\boldsymbol{\hat \eta }} + {{\boldsymbol{C}}_{\boldsymbol{\omega }}}{\boldsymbol{\hat \xi }}} \;。\end{aligned} \right. \end{split}$ | (6) |
式中:
为保证式(6)满足KYP引理,使得系统是严格无源系统,设计增益矩阵结构如下:
| $\begin{split} &{{\boldsymbol{K}}}_{1}=\left[\begin{array}{ccc} {k}_{11}&0&0\\ 0&{k}_{12}&0\\ 0& 0&{k}_{13}\\ {k}_{21}&0&0\\ 0&{k}_{22}&0\\ 0&0&{k}_{23}\end{array}\right]\text{,} {{\boldsymbol{K}}}_{2}\text=\left[\begin{array}{ccc} {k}_{31}&0&0\\ 0&{k}_{32}&0\\ 0&0&{k}_{33}\end{array}\right]\text{,}\\ &{{\boldsymbol{K}}}_{3}\text=\left[\begin{array}{ccc} {k}_{41}&0&0\\ 0&{k}_{42}&0\\ 0&0&{k}_{43}\end{array}\right]\text{,} {{\boldsymbol{K}}}_{4}\text=\left[\begin{array}{ccc} {k}_{51}&0&0\\ 0&{k}_{52}&0\\ 0&0&{k}_{53}\end{array}\right]\;。\end{split} $ | (7) |
非线性无源估计滤波器增益矩阵中的参数如下:
| $ \begin{split} \left\{ {\begin{aligned} & {{k_{1i}} = \dfrac{{ - 2{\omega _{ci}}({\zeta _{ni}} - {\zeta _i})}}{{{\omega _{oi}}}}}\;,\\ & {{k_{2i}} = 2{\omega _{oi}}({\zeta _{ni}} - {\zeta _i})}\;,\\ & {{k_{3i}} = {\omega _{ci}}} \;。\end{aligned}} \right. \end{split} $ | (8) |
式中:
滤波器增益选取理想情况下需要考虑到波谱的峰值频率,为了满足正实引理,重要的是3个解耦函数都有一个−90°相位滞后,系统参数必须满足:
| $ \frac{1}{{{T_i}}} \ll \frac{{{k_{5i}}}}{{{k_{4i}}}} < {\omega _{oi}} < {\omega _{ci}} 。$ | (9) |
式中:
建立线性连续时间系统的状态空间方程[11]:
| $ {\boldsymbol{\dot x}} = {\boldsymbol{Ax}} + {\boldsymbol{Bu}} + {\boldsymbol{E\omega }} 。$ | (10) |
式中:过程噪声
测量方程(传感器系统)为:
| $ {\boldsymbol{y}} = {\boldsymbol{Hx}} + {\boldsymbol{\upsilon }} 。$ | (11) |
式中:测量噪声
连续时间Kalman滤波算法及噪声方差阵如下:
| $ \begin{split} \left\{ {\begin{aligned} &{{\boldsymbol{Q}}(t) = {{\boldsymbol{Q}}^{\text{T}}}(t) > 0} ,\\ &{{\boldsymbol{R}}(t) = {{\boldsymbol{R}}^{\text{T}}}(t) > 0} ,\\ &{{\boldsymbol{\hat x}}(0) = {{\boldsymbol{x}}_0}} \end{aligned}} \right. \end{split}$ | (12) |
初始条件:
| $ P(0) = E[(x(0) - \hat x(0)){(x(0) - \hat x(0))^{\rm{T}}}] = {{\boldsymbol{P}}_0} 。$ | (13) |
卡尔曼增益矩阵迭代式:
| $ K(\text t) = {\boldsymbol{P}}(t){{\boldsymbol{H}}^{\text{T}}}(t){{\boldsymbol{R}}^{ - 1}}(t) ,$ | (14) |
状态估计迭代式:
| $ \dot {\hat x}(\text t) = {\boldsymbol{A}}(t){\boldsymbol{\hat x}}(t) + {\boldsymbol{B}}(t){\boldsymbol{u}}(t) + {\boldsymbol{K}}(t)[{\boldsymbol{y}}(t) - {\boldsymbol{H}}(t){\boldsymbol{\hat x}}(t)] \;,$ | (15) |
误差协方差迭代式:
| $\begin{split} \dot P(\text t) = &{\boldsymbol{A}}(t){\boldsymbol{P}}(t) + {\boldsymbol{P}}(t){{\boldsymbol{A}}^{\text{T}}}(t) + {\boldsymbol{E}}(t){\boldsymbol{Q}}(t){\boldsymbol{E}}(t) -\\ &{\boldsymbol{P}}(t){{\boldsymbol{H}}^{\text{T}}}(t){{\boldsymbol{R}}^{ - 1}}(t){\boldsymbol{H}}(t){\boldsymbol{P}}(t)。\end{split}$ | (16) |
选用的线性DP模型设计结果模型为15阶状态空间模型[12]:
| $ \begin{split} \left\{ {\begin{aligned} &{{\boldsymbol{\dot x}} = {\boldsymbol{Ax}} + {\boldsymbol{Bu}} + {\boldsymbol{E\omega }}} ,\\ &{{\boldsymbol{y}} = {\boldsymbol{Hx}} + {\boldsymbol{\upsilon }}} 。\end{aligned}} \right. \end{split} $ | (17) |
式中:
系统矩阵为:
| $\begin{split}&{\boldsymbol{A}}=\left[\begin{array}{cccc}{{\boldsymbol{A}}}_{\omega }& {0}_{6\times 3}& {0}_{6\times 3}& {0}_{6\times 3}\\ {0}_{3\times 6}& {0}_{3\times 3}& {{\boldsymbol{I}}}_{3\times 3}& {0}_{3\times 3}\\ {0}_{3\times 6}& {0}_{3\times 3}& {\boldsymbol{-M}}^{-1}{\boldsymbol{D}}& {{\boldsymbol{M}}}^{-1}\\ {0}_{3\times 6}& {0}_{3\times 3}& {0}_{3\times 3}& {\boldsymbol{-T}}^{-1}\end{array}\right]\text{,}\\ &{\boldsymbol{B}}=\left[\begin{array}{c}{0}_{6\times p}\\ {0}_{3\times p}\\ {{\boldsymbol{M}}}^{-1}{{\boldsymbol{B}}}_{u}\\ {0}_{3\times p}\end{array}\right]\text{,}{\boldsymbol{E}}=\left[\begin{array}{ccc}{{\boldsymbol{E}}}_{\omega }& {0}_{6\times 3}& {0}_{6\times 3}\\ {0}_{3\times 3}& {0}_{3\times 3}& {0}_{3\times 3}\\ {0}_{3\times 3}& {{\boldsymbol{M}}}^{-1}& {0}_{3\times 3}\\ {0}_{3\times 3}& {0}_{3\times 3}& {{\boldsymbol{I}}}_{3\times 3}\end{array}\right]。\end{split} $ | (18) |
在连续时间Kalman滤波器中:
| $ \begin{split} \left\{ \begin{aligned} &{\boldsymbol{\hat{\dot{x}}}}={\boldsymbol{A\hat{x}}}+{\boldsymbol{Bu}}+{\underset{K}{\underbrace{{\boldsymbol{P}}{{\boldsymbol{H}}}^{\text{T}}{\boldsymbol{R}}}}}^{-1}\left({\boldsymbol{y}}-{\boldsymbol{H\hat{x}}}\right),\\ &{\boldsymbol{\dot{P}}}={\boldsymbol{AP}}+{\boldsymbol{P{A}}}^{\text{T}}+{\boldsymbol{EQ{E}}}^{\text{T}}-{\boldsymbol{P{H}}}^{\text{T}}{{\boldsymbol{R}}}^{-1}{\boldsymbol{HP}}。\end{aligned} \right. \end{split}$ | (19) |
协方差矩阵
| $ {\boldsymbol{R}} = {\rm{diag}}\{ {\sigma} _{{\text{v}}1}^2,{\sigma} _{{\text{v}}1}^2, \cdots ,{\sigma} _{{\text{vp}}}^2\}。$ | (20) |
式中:
协方差矩阵
矩阵
通过以上的推导计算,可得到一个维度为
综上,可对DP船三自由度的运动进行解耦运算。即在实际计算过程中纵荡、横荡、首摇这三自由度各取增益
在每个自由度进行单独的滤波后,考虑到这3个自由度的耦合关系,仍需要进行一定程度的重组工作。在与质量矩阵的逆
对单自由度的滤波过程进行设计,具体DP运动滤波的内部原理如图1所示。
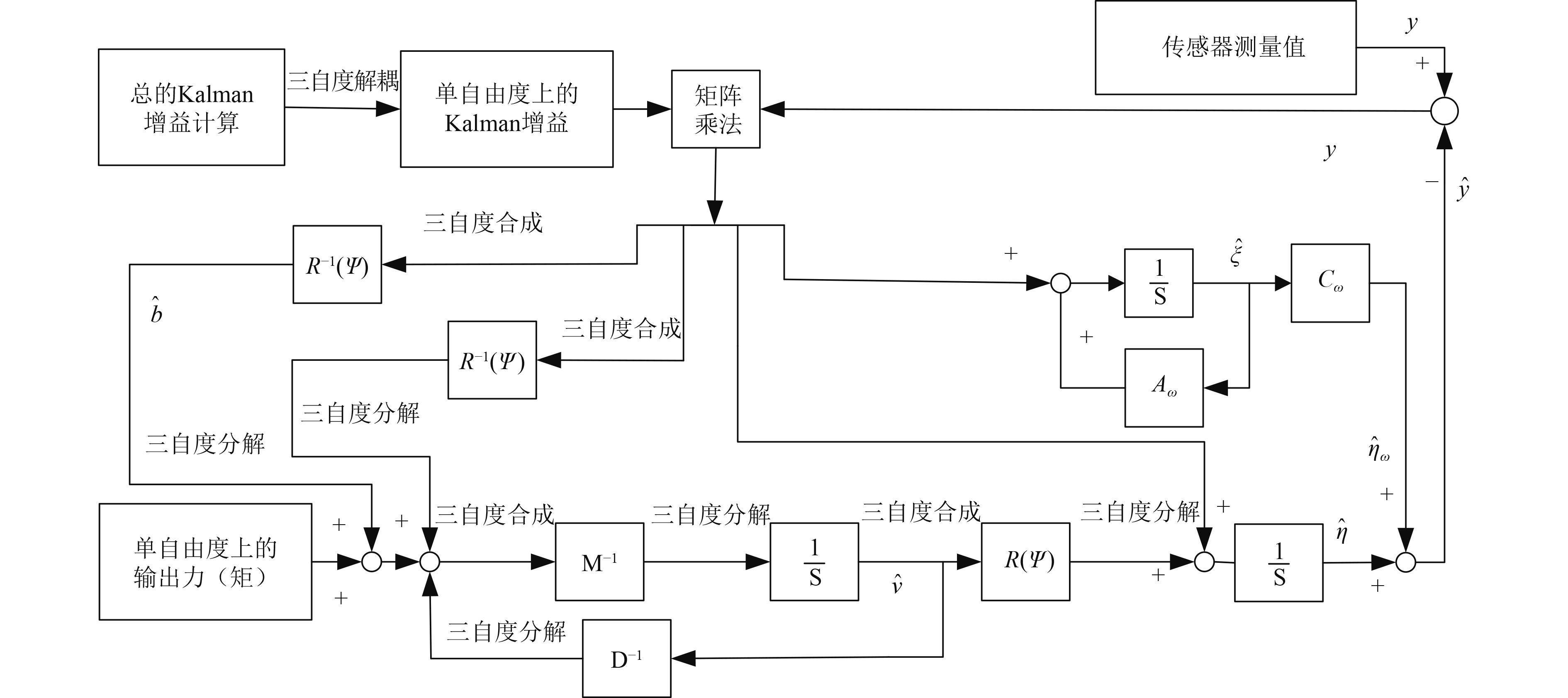
|
图 1 某单自由度运动滤波内部原理图 Fig. 1 Internal principle diagram of a single degree of freedom motion filter |
使用之前数学模型和滤波算法,以某DP实船模型为研究对象,通过经验公式的估算,该船舶模型的无因次质量矩阵
| $ \begin{split} {\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {25.800}&0&0 \\ 0&{33.800}&{1.0115} \\ 0&{1.0115}&{2.7600} \end{array}} \right],{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {2.0}&0&0 \\ 0&{7.0}&{0.1} \\ 0&{0.1}&{0.5} \end{array}} \right] 。\\ \end{split}$ | (21) |
取海浪强度的参数
| $ b = \left[ {\begin{array}{*{20}{c}} {100}&0&0 \\ 0&{100}&0 \\ 0&0&{100} \end{array}} \right],$ | (22) |
其中,在非线性无源估计滤波器中可以设定增益。
| $ \begin{array}{l}{k_{11}} = \left[ {\begin{array}{*{20}{c}} { - 2.34}&0&0 \\ 0&{ - 2.34}&0 \\ 0&0&{ - 2.34} \end{array}} \right],{k_{12}} = \left[ {\begin{array}{*{20}{c}} {1.44}&0&0 \\ 0&{1.44}&0 \\ 0&0&{1.44} \end{array}} \right],\\ {k_3} = {k_4} = \left[ {\begin{array}{*{20}{c}} {0.1}&0&0 \\ 0&{0.1}&0 \\ 0&0&{0.01} \end{array}} \right]\;。\\[-21pt]\end{array}$ | (23) |
在连续型Kalman滤波器中,取初始矩阵
在Matlab中构建船舶运动滤波及控制的仿真系统,船舶水动力参数和运动控制器取上文中的参数值,滤波器参数分别取非线性无源滤波器和Kalman滤波器的值,仿真时间200 s,设置N,E期望位置均为0,期望航向角为10°,得出船舶运动位置和航向角滤波的仿真结果如图2所示。
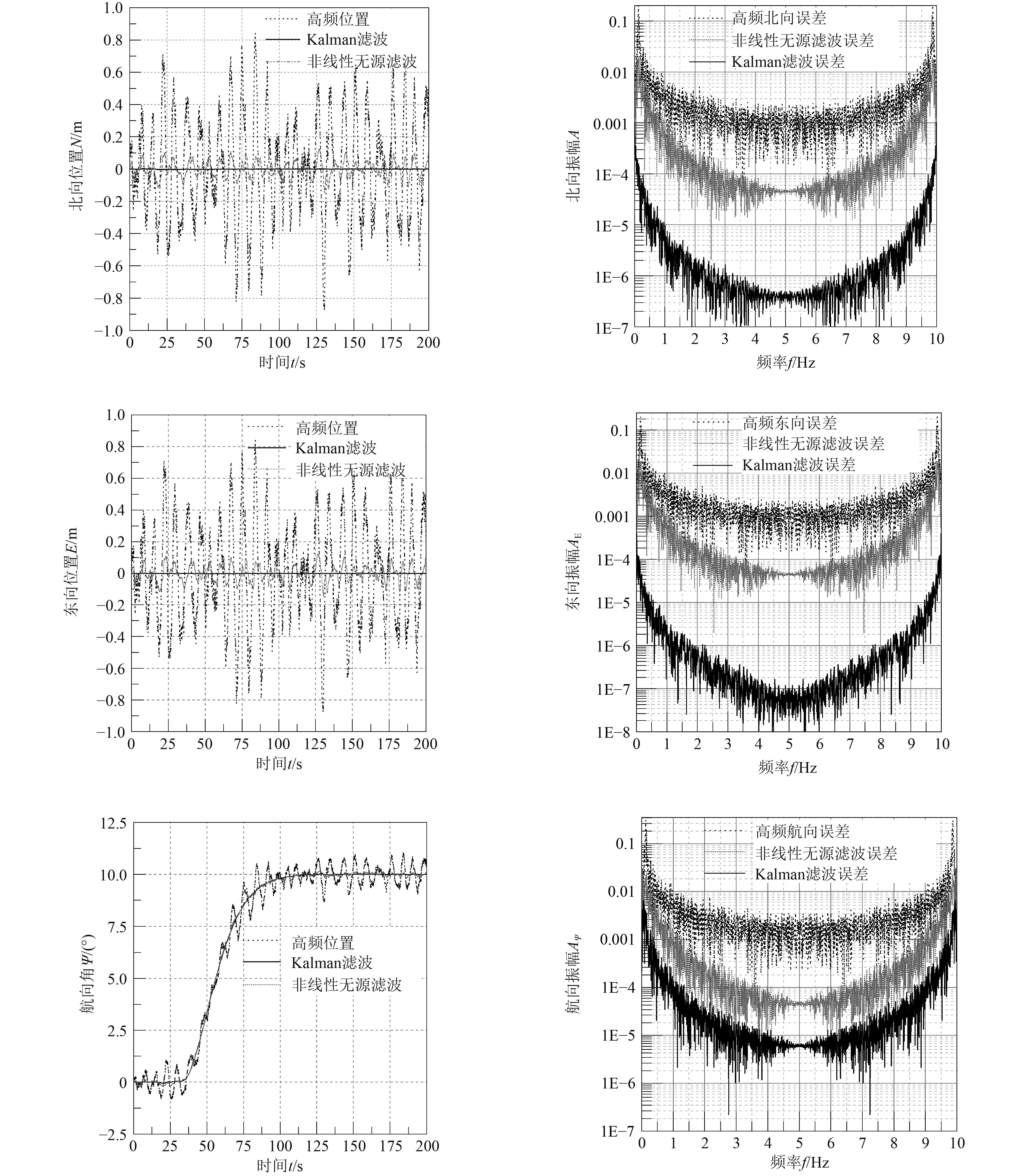
|
图 2 三自由度滤波效果对比图 Fig. 2 Comparison of filtering effect in three degrees of freedom |
通过对这三自由度的频率-振幅对应的面积可以展示滤波效果的好坏,如表1所示。
|
|
表 1 三自由度能量剩余表 Tab.1 Three degree of freedom energy residual table |
由表1可知,非线性无源估计滤波器在正北、正东上滤除了82%以上的一阶高频波浪运动;Kalman滤波器在正东和正北方向上滤除了99%以上的一阶波浪运动,而且对于传感器测量白噪声的抑制效果也很理想。亦可知,非线性无源估计滤波器在航向上滤除了83%的一阶高频波浪运动,Kalman滤波器在航向上滤除了超过98%的一阶波浪运动,而且传感器测量白噪声的滤波效果也较好。
由此看出,Kalman滤波器使得船舶的位置、航向的估计值和理想的低频漂移运动输出值基本一致,基本滤除了一阶波浪运动,其中航向角滤除了98%以上的一阶波浪运动,北东方向滤除了99%以上的一阶波浪运动。同非线性无源滤波器相比,Kalman滤波器的运动滤波效果更好,能够较好估计出船舶期望的低频运动。同时也较好抑制了传感器的测量白噪声信号,有利于减少控制器的设计难度和实现高精度运动控制。
5 结 语本文针对船舶动力定位系统设计中遇到的波浪运动滤波问题,提出一种动力定位系统三自由度解耦Kalman滤波方法,设计了动力定位系统的状态观测器和运动控制器,通过动力定位系统滤波与运动控制仿真,可以得到如下结论:
1)本文方法使得DP船舶在北东坐标系中的位置和航向上滤波效果和估计出的运动曲线更平滑稳定,有效滤除了一阶波浪运动的干扰,其中航向滤除了98%以上的一阶波浪运动,北东方向滤除了99%以上的一阶波浪运动,对传感器测量白噪声信号也有较好的抑制作用。
2)与非线性无源估计滤波器相比,本文方法所得到的运动曲线更平滑、稳定,可有效减小动力定位控制器的设计难度,对船舶动力定位高精度控制系统设计而言,本文方法是一种有效且实用的运动滤波方法。
| [1] |
SELIMOVIC D, LERGA J, PRPIC-ORSIC J, et al. Improving the performance of dynamic ship positioning systems: a review of filtering and estimation techniques[J]. Journal of Marine Science and Engineering, 2020, 8(4): 28. |
| [2] |
骆寒冰, 佟海兵, 谢芃, 等. 动力定位船舶循迹控制海上实测与数值模拟研究[J]. 中国造船, 2020, 61(1): 18-28. LUO H B, TONG H B, XIE F, et al. Marine measurement and numerical simulation of dynamic positioning ship tracking control[J]. Ship Building of China, 2020, 61(1): 18-28. DOI:10.3969/j.issn.1000-4882.2020.01.002 |
| [3] |
陈施奇. Kalman滤波器在船舶动力定位系统中的应用[J]. 舰船科学技术, 2019, 41(14): 73-75. CHEN S Q. Application of Kalman filter in ship dynamic positioning system[J]. Ship Science and Technology, 2019, 41(14): 73-75. |
| [4] |
FOSSEN T I, PEREZ T. Kalman filtering for positioning and heading control of ships and offshore rigs estimating the effects of waves, wind, and current[J]. IEEE Control Systems Magazine, 2009, 29(6): 32-46. DOI:10.1109/MCS.2009.934408 |
| [5] |
HASSANI V, PASCOAL A M, SORENSEN A J, et al. A novel methodology for adaptive wave filtering of marine vessels: theory and experiments[C]//Proceedings of the 52nd IEEE Annual Conference on Decision and Control (CDC). Florence, Italy, 2013: 6162–6167.
|
| [6] |
李杨, 徐雪峰, 赵光. 基于扩展状态观测器的海浪滤波算法及仿真[J]. 中国舰船研究, 2020, 15(S1): 1-5+33. LI Y, XU X F, ZHAO G. Wave filtering algorithm and aimulation based on extended state observer[J]. Chinese Journal of Ship Research, 2020, 15(S1): 1-5+33. |
| [7] |
邓英杰, 张显库, 张国庆. 水面舰船动力定位系统ESO输入饱和控制[J]. 系统工程与电子技术, 2019, 41(5): 1110-1117. DENG Y J, ZHANG X K, ZHANG G Q. ESO input saturation control for dynamic positioning system of surface ship[J]. Journal of Systems Engineering and Electronics, 2019, 41(5): 1110-1117. DOI:10.3969/j.issn.1001-506X.2019.05.25 |
| [8] |
李君. 非线性观测器在船舶动力定位系统DP的应用[J]. 舰船科学技术, 2021, 43(16): 208-210. LI J. Application of nonlinear observer in ship dynamic positioning system[J]. Ship Science and Technology, 2021, 43(16): 208-210. |
| [9] |
蒋帆, 徐海祥, 冯辉, 等. 基于模型预测扩展卡尔曼滤波的动力定位状态估计[J]. 船舶工程, 2019, 41(7): 86-91+132. JIANG F, XU H X, FENG H, et al. Dynamic positioning state estimation based on model predictive extended Kalman filter[J]. Ship Engineering, 2019, 41(7): 86-91+132. |
| [10] |
BENETAZZO F, IPPOLITI G, LONGHI S, et al. Advanced control for fault-tolerant dynamic positioning of an offshore supply vessel[J]. Ocean Engineering, 2015, 106: 472-484. DOI:10.1016/j.oceaneng.2015.07.001 |
| [11] |
朱楠, 方伟. 卡尔曼滤波在组合导航中的仿真与分析[J]. 智能计算机与应用, 2020, 10(6): 300-302+309. DOI:10.3969/j.issn.2095-2163.2020.06.074 |
| [12] |
边信黔, 付明玉, 王元慧. 船舶动力定位[M]. 北京: 科学出版社, 2011: 118–120.
|
 2022, Vol. 44
2022, Vol. 44
