0 引　言

船舶螺旋桨尾轴承常用橡胶材料作为支撑面和摩擦面。这类轴承由于润滑液是水，其粘度较低，通常为油的1/20以下，在低速、重载工况下难以得到流体润滑，可能造成运动副的直接接触，发生干摩擦现象，或者处于边界润滑状态^[1]。在启动、停机、低速运转等工况下，会产生异常摩擦振动与噪声，严重威胁舰船的安全性、隐蔽性及生存能力^[2]。

众多研究表明，螺旋桨尾轴承异常摩擦振动噪声产生的原因可能是由于螺旋桨轴的悬伸布置和螺旋桨的巨大重量，受载不均匀，给尾轴承造成很大的边缘载荷，导致尾轴承的局部比压巨大，使得尾轴承的润滑状态变得极其恶劣^[3]。姚世卫等^[4]认为水润滑橡胶轴承当载荷过高时，轴瓦与旋转轴之间的相互作用相当于汽车上刮水器与玻璃之间的刮水作用，会产生摩擦振动，从而发出尖叫。

自20世纪60年代，稀土永磁材料的发现与迅速发展，钐钴、钕铁硼等具有高磁能积、高矫顽力的永磁材料问世，永磁材料在电机、磁轴承、磁悬浮、大型起重设备等领域被广泛应用。相比使用线圈绕组产生磁场，永磁材料具有体积小、无需外部能源、无涡流损耗等优点。Halbach永磁阵列是一种新型永磁体排列方式，最早由美国劳伦斯伯克利国家实验室的Klaus Halbach教授提出^[5]。其通过将不同充磁方向的永磁体按照一定规律排列，能够在磁体的一侧汇聚磁力线，而在另一侧消弱磁力线，从而获得比较理想的单边磁场。文献[6]以某种径向激磁的电机为例，当采用Halbach永磁阵列后(在相同磁阵列体积情况下)，强侧气隙磁密幅值增大41%。Halbach阵列可以降低漏磁，一般普通磁体的漏磁严重，通常需要添加屏蔽装置，而Halbach即使不加任何屏蔽措施，磁体的漏磁也很小^[7]。

汪勇^[8]使用扇形磁瓦拼接而成的“吸盖式”卸载轴承，可以卸载轴系80%～90%重量，该设计结构简单紧凑，可靠性高，并指出磁场不均匀性对轴向卸载力影响可忽略。陈勇^[7]针对传统爬壁机器人体积庞大、结构复杂等问题，利用 Halbach 阵列的单边聚磁效应并通过外侧软铁磁轭进一步增强了爬壁机器人永磁吸附装置的吸附力，通过与传统H形磁吸附机构性能参数仿真比较，表明Halbach结构具有永磁利用率高、自重轻而负载能力强等特点。闫晨飞^[9]基于 Halbach 阵列提出了一种新型变磁化方向单元组合式的永磁吸附装置，并利用遗传算法对结构参数进行优化。相比普通Halbach装置，变磁化方向Halbach阵列的吸附力增幅在1倍以上，并且随着气隙厚度的增大，衰减速率较慢。Halbach永磁阵列作为吸引单元和卸载组件可满足高承载和稳定性好的需求，在大型卸载领域具有重大前景。将Halbach永磁轴承与水润滑橡胶轴承进行复合设计，有望减小橡胶轴承局部比压，从而消除水润滑橡胶轴承异常摩擦振动与噪声产生。对于永磁轴承与水润滑轴承复合后的静态力学性能研究还未见文献报道。

本文设计一种具有Halbach永磁阵列的磁复合型水润滑橡胶尾轴承，介绍其基本结构和工作原理，引入磁标势求解Maxwell方程建立Halbach永磁阵列的静磁场解析模型，同时利用Maxwell应力张量法推导Halbach永磁阵列对转轴的垂直吸力，最后通过有限元分析软件Comsol对磁复合轴承进行静力学分析，分析不同结构参数下Halbach永磁阵列的磁场分布、对转轴的吸引力和转轴与橡胶轴承的接触状况。

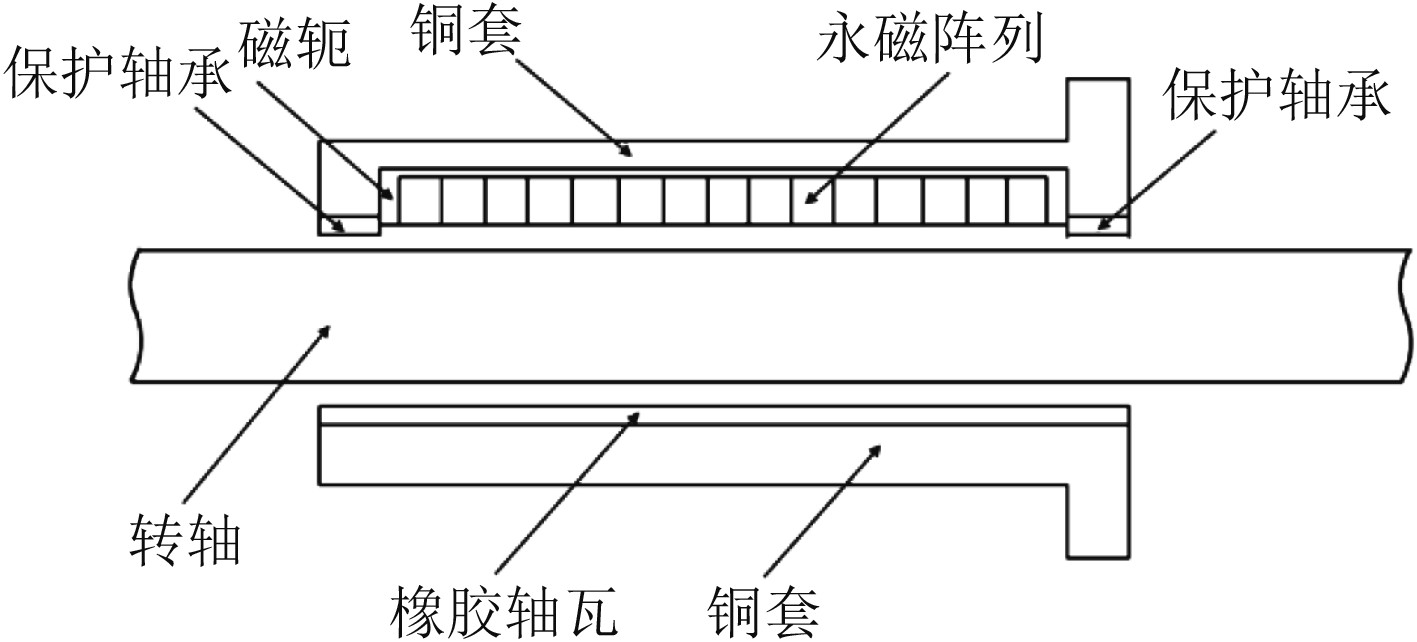
1 基本结构与工作原理

图1为具有Halbach阵列的磁复合型水润滑橡胶轴承的结构示意图。轴承由铜套、永磁体、磁轭、橡胶轴瓦和保护轴承组成。转轴和Halbach阵列之间存在空气间隙，通过Halbach阵列、气隙和转轴之间形成一个闭合的磁路，Halbach阵列对转轴产生垂直向上的吸引力，抵消部分转轴对橡胶轴瓦的压力。磁轭是导磁率较高金属材料制成的轭铁，均匀对称分布在Halbach阵列的上方和前后，通过与Halbach永磁阵列构成封闭的磁路，使永磁体产生的磁力线被封闭在内部，约束永磁体漏磁向外扩散，提高永磁体的工作效率。保护轴承作用是当转子受到各种瞬间载荷时，承载转子对轴承上方较大的冲击力，保护上方永磁体避免由于碰撞而退磁，延长Halbach永磁阵列使用寿命。

本文使用的Halbach永磁阵列由径向极化和轴向极化的磁环按一定规律排列，图2为不同极化磁环的磁场合成效果。图中，方块内箭头所指方向为永磁体充磁方向，方块外箭头所指方向为磁力线方向。从图2 (c)中可以看出Halbach磁体阵列的的磁场为垂向磁场与径向磁场的合成，在阵列上方发生抵消，形成弱磁侧，在下方发生叠加，形成强磁侧。

2 理论模型 2.1 静磁场解析模型

基于Halbach阵列磁复合水润滑橡胶轴承主要是通过Halbach永磁阵列与铁磁性转轴相互作用产生吸引力，从而降低转轴对橡胶轴瓦施加的载荷。通过对Halbach永磁阵列进行电磁场解析，分析不同磁环尺寸、轭铁厚度、气隙长度等因素对Halbach永磁吸附组件所产生磁场和转轴所受到吸引力的影响，为之后进行仿真、加工和实验提供可靠的理论依据。

在柱坐标系中，图3为圆筒型Halbach阵列沿平面的截面，阵列中只有沿 $\phi = {\text{π}} /2$ 轴向 $\overrightarrow {\boldsymbol{a}}$ 和径向 $\overrightarrow {\boldsymbol{r}}$ 磁化的永磁体，为二维磁场分布，磁化强度可以表示为：

$\overrightarrow M = {M_a}\hat a + {M_r}\hat r \;。$

(1)

图3为Halbach永磁阵列沿 $\overrightarrow {\boldsymbol{a}}$ 和 $\overrightarrow {\boldsymbol{r}}$ 向磁化强度分布，前面假设不考虑端部效应，使用傅里叶级数得到Halbach阵列的磁化强度表达式为：

$\overrightarrow M = \frac{{{B_r}}}{{{\mu _0}}}\mathop \sum \limits_{k = 1}^\infty \left[ {\begin{array}{*{20}{c}} {{m_k}\cos (k\omega a)} \\ { - {n_k}\sin (k\omega a)} \end{array}} \right] \;。$

(2)

其中：

$\omega = 2{\text{π}} /l \;，$

(3)

${m_k} = \frac{4}{{k{\text{π}} }}\sin \frac{{k{\text{π}} }}{2}\cos \frac{{k\omega \tau }}{2} \;，$

(4)

${n_k} = \frac{4}{{k{\text{π}} }}\sin \frac{{k{\text{π}} }}{2}\sin \frac{{k\omega \tau }}{2} \;。$

(5)

式中： $k$ 为谐波数， ${B}_{r}$ 为磁铁剩余磁化强度， ${\mu }_{0}$ 为真空磁导率。

由前面假设不考虑铜套和轭铁对磁场的影响，可将Halbach永磁阵列划分为3个区域，区域Ⅰ和Ⅲ为空气，相对磁导率 ${\mu }_{r}\approx 1$ ，区域Ⅱ为Halbach阵列。由于是无电流的静磁场分析，引入磁标势和磁高斯定理计算Halbach阵列的磁场强度。由Maxwell方程组，各区域应满足下列方程：

${\nabla ^2}{\varPsi _{I,III}} = 0 \;，$

(6)

${\nabla ^2}{\varPsi _{II}} = \nabla \frac{{\overrightarrow M }}{{{\mu _r}}} = - \frac{{{B_r}}}{{{\mu _0}{\mu _r}}}\mathop \sum \limits_{k = 1}^\infty {m_k}k\omega \sin (k\omega a) \;。$

(7)

式中： ${\mathrm{\varPsi }}_{I,II,III}$ 分别是区域 $\text{Ⅰ}$ 、区域 $\text{Ⅱ}$ 和区域 $\text{Ⅲ}$ 的磁标势， ${\mu }_{r}$ 为相对磁导率。

根据磁场中不同磁介质分界面上的边值关系，得到如下边界条件：

${\left. {{\Psi _I}} \right|_{r = + \infty }} = 0 \;，$

(8)

${\left. {{\Psi _{III}}} \right|_{r = - \infty }} = 0 \;，$

(9)

${\left. {{H_{Ia}}} \right|_{r = {h_1}}} = {\left. {{H_{IIa}}} \right|_{r = {h_1}}} \;，$

(10)

${\left. {{B_{Ir}}} \right|_{r = {h_1}}} = {\left. {{B_{IIr}}} \right|_{r = {h_1}}} \;，$

(11)

${\left. {{H_{IIa}}} \right|_{r = {h_2}}} = {\left. {{H_{IIIa}}} \right|_{r = {h_1}}}\;，$

(12)

${\left. {{B_{IIr}}} \right|_{r = {h_1}}} = {\left. {{B_{IIIr}}} \right|_{r = {h_1}}} \;。$

(13)

式中： ${H}_{Ia}，{H}_{IIa}，{H}_{IIIa}$ 分别为区域 $\text{Ⅰ}$ 、区域 $\text{Ⅱ}$ 和区域 $\text{Ⅲ}$ 磁场强度的 $\overrightarrow {\boldsymbol{a}}$ 向分量； ${{{B}}_{Ir}}$ ， ${{{B}}_{IIr}}$ 和 ${{{B}}_{IIIr}}$ 分别为区域 $\text{Ⅰ}$ 、区域 $\text{Ⅱ}$ 和区域 $\text{Ⅲ}$ 磁感应强度的 $\overrightarrow {\boldsymbol{r}}$ 向分量。使用分离变量法结合边界条件求解式（6）和式（7），在区域Ⅲ中有如下关系：

${\overrightarrow H _{III}} = - \nabla {\Psi _{III}}\;，$

(14)

${\overrightarrow B _{III}} = {\mu _0}{\overrightarrow H _{III}}\;。$

(15)

得到区域Ⅲ处磁感应强度的表达式为：

${\overrightarrow B _{III}} = - {\mu _0}\mathop \sum \limits_{k = 1}^\infty \lambda {K_{III}}{e^{\lambda r}}\left[ {\begin{array}{*{20}{c}} {\cos \lambda a} \\ {\sin \lambda a} \end{array}} \right]\;。$

(16)

其中：

$\lambda = k\omega \;，$

(17)

${K_{III}}({\mu _r} = 1) = - \frac{{{B_r}}}{{2{\mu _0}\lambda }}\left( {{e^{ - \lambda {h_2}}} - {e^{ - \lambda {h_1}}}} \right)({m_k} + {n_k}) \;。$

(18)

2.2 吸引力模型

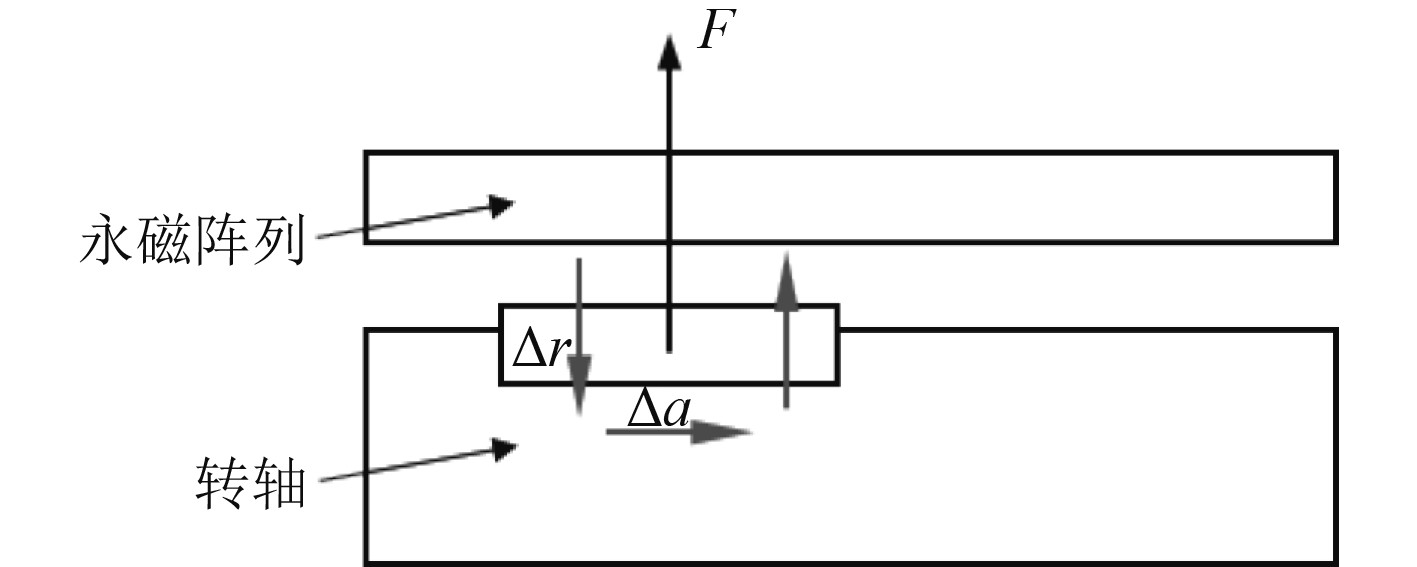
铁磁材料在磁场中的受力通常使用麦克斯韦应力张量法或者虚功原理法计算。采用Maxwell应力张量（Stresstensor）法求解Halbach阵列对转轴的吸引力/吸引力。假设转轴的相对磁导率 ${\mu }_{r}\gg {\mu }_{0}$ ，且无漏磁，即空气中仅气隙处有磁场分布，在此假设下气隙磁场沿轴向的分量可以忽略不记，转轴下表面磁感应强度为0。如图4所示，在Halbach阵列与转轴的气隙 $\varphi$ 处考虑以长 $\mathrm{d}a$ ，宽 $r\mathrm{d}\varphi$ ，高 $\mathrm{d}r$ 的微元，宽度方向未标出，微元上表面紧邻转轴外表面外侧，下表面紧邻转轴内表面外侧。根据应力张量法，在此长方体 $V$ 中磁场作用于铁磁材料的力可表示为：

${{\boldsymbol{F}}_\phi } = \frac{1}{{{\mu _r}}}\int_V {\nabla \cdot \rm{T}} {\text{d}}v \;。$

(19)

根据散度定理，该体积分可改写为面积分：

${{\boldsymbol{F}}_\phi } = \frac{1}{{{\mu _r}}}\oint_S {\rm{T}} \cdot \widehat {\boldsymbol{n}} {\text{d}}s \;。$

(20)

式中：S为长方体表面， $\widehat{\boldsymbol{n}}$ 为S的法向外矢量，根据假设沿轴向的磁场分量可忽略，则式（20）可改写为：

${{\boldsymbol{F}}_\phi } = \frac{1}{{2{\mu _0}}}\oint_S {{{B}}_n^2\widehat {\boldsymbol{n}}} {\text{d}}s\;。$

(21)

式中： ${B}_{n}$ 为磁感应强度垂直于表面S的分量，显然只有气隙中的平行于转轴的表面有贡献，即

${{\boldsymbol{F}}_\phi } = \frac{r}{{2{\mu _0}}}{{B}}_n^2{\text{d}}\phi {\text{d}}a \;。$

(22)

则Halbach阵列对转轴产生的垂直向上的吸引力可通过积分得到：

${\boldsymbol{F}} = \iint_{\phi ,a} {{{{F}}_{\phi ,a}}\cos \phi {\text{d}}\phi {\text{d}}a}\;。$

(23)

3 有限元分析 3.1 静磁场分析 3.1.1 Halbach磁吸组件静磁场分析

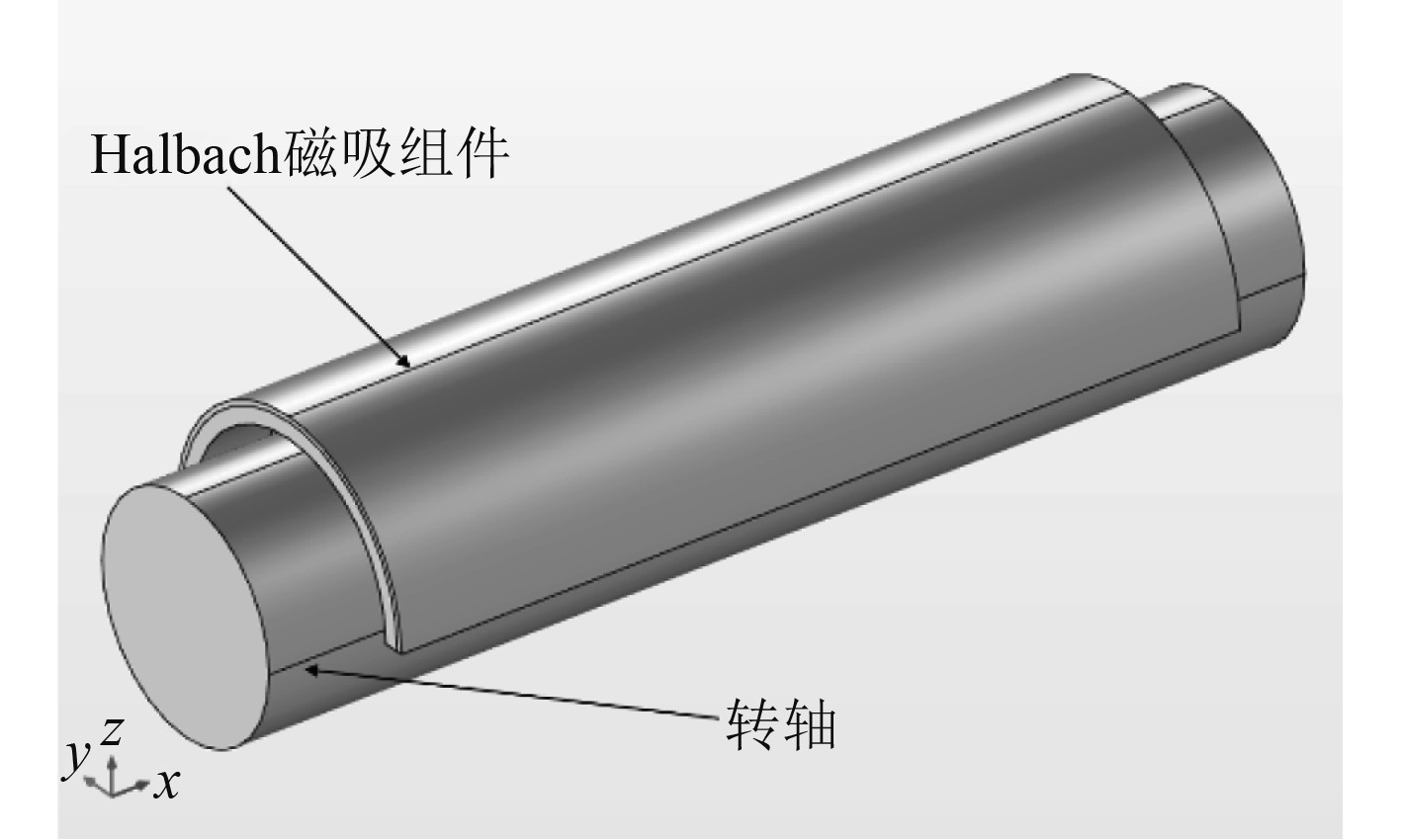
图5为使用有限元仿真分析软件Comsol建立的Halbach阵列静磁场分析模型，在这部分计算中，忽略了转轴外铜套和轴承外铜套的影响。模型各结构和材料参数如表1所示。

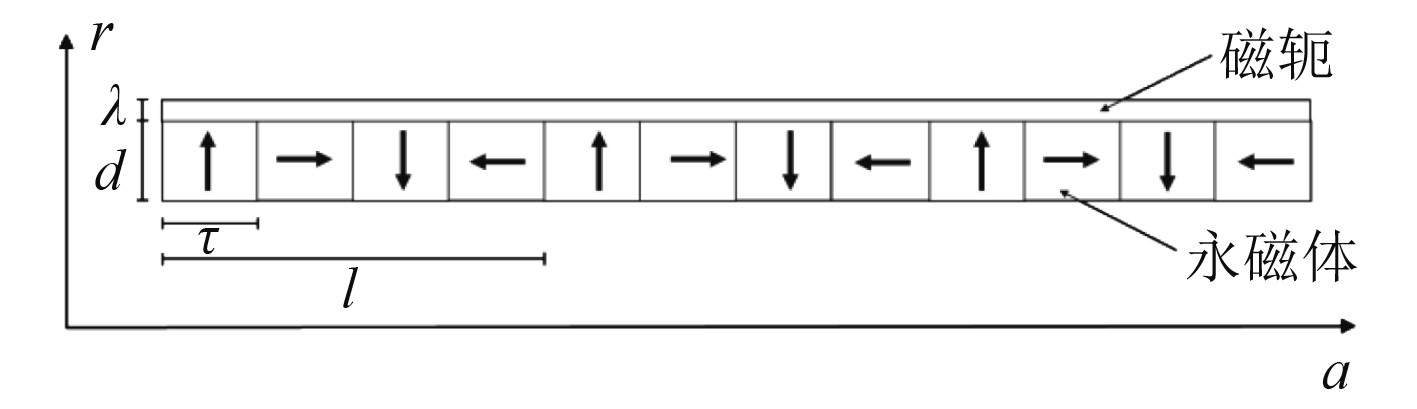
磁复合型水润滑橡胶艉轴承所用的Halbach永磁阵列为3单元12模块结构，每单元包含4对半圆弧磁环，各磁环极化方向和参数如图6所示，具有不同极化方向的磁环沿轴向排布，形成Halbach阵列，其参数如下： $\lambda$ 为磁轭厚度， $\tau$ 为磁环沿轴向的长度， $l$ 为四模块的长度，有 $l=4\tau$ 。

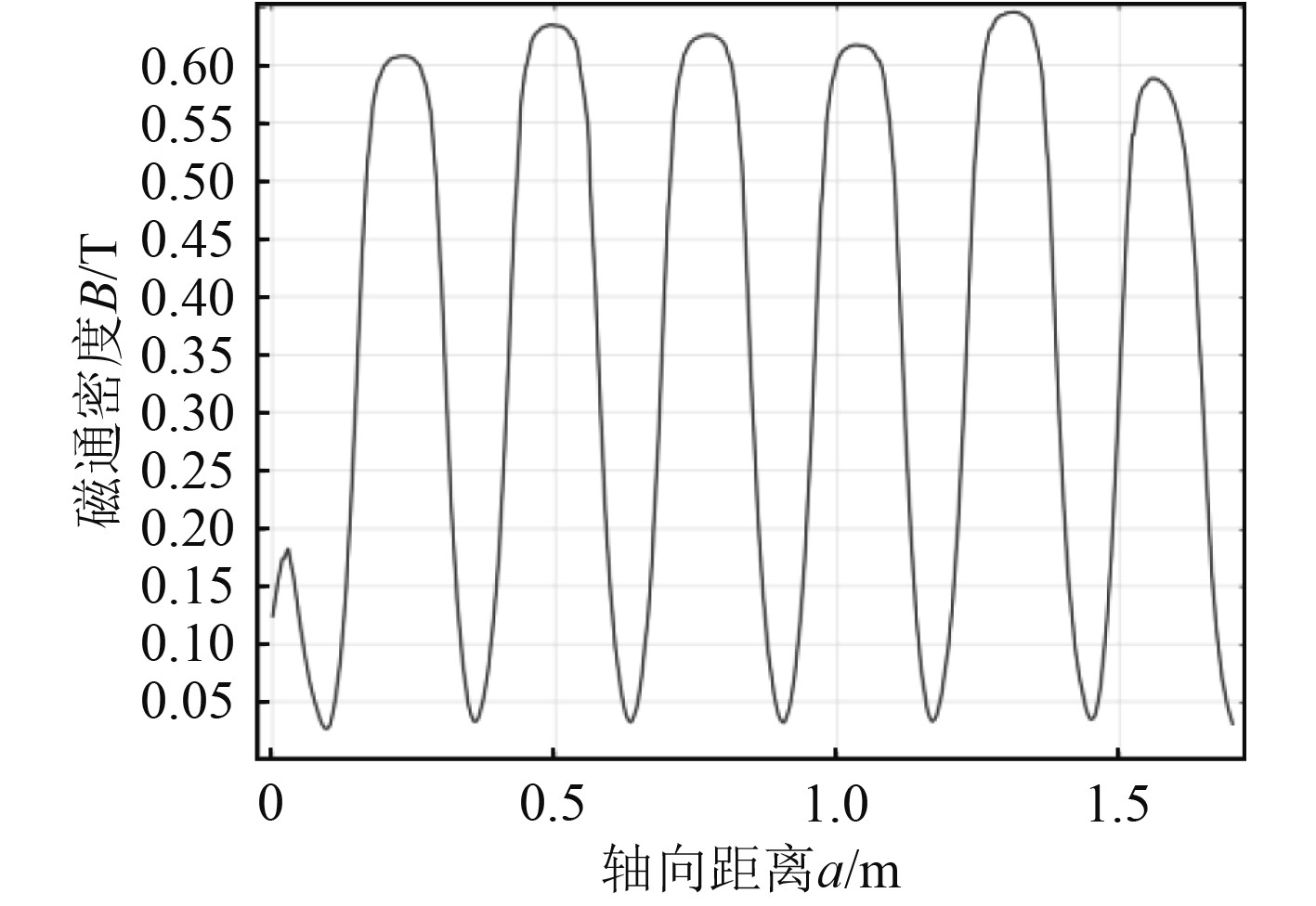
图7为距转轴钢材表面2 mm处磁通密度B的轴向分布，如果忽略Halbach的端部效应，在Halbach阵列在近轴侧的气隙中，磁通密度呈较明显的正弦分布，磁通密度最大值在0.65 T左右。

图8为 $\varphi =\dfrac{{\text{π}} }{2}$ 处的磁通密度云图，Halbach阵列中轴向极化的磁环与径向极化的磁环的磁感线在空间发生叠加，在近轴一侧的磁通密度得到增强，在背轴一侧的磁通密度得到减弱。这说明Halbach永磁阵列具有明显的聚磁性，磁力线主要集中在近轴一侧，提高了永磁体利用率，结合磁轭的导磁作用进一步降低了永磁体的漏磁。

3.1.2 相关参数对磁吸组件静态性能影响

Halbach组件对转轴产生的吸引力取决于Halbach组件的几何参数，考察Halbach阵列单元数、轭铁厚度和磁环弧度对组件性能的影响。

1） Halbach阵列单元数对磁吸组件性能的影响

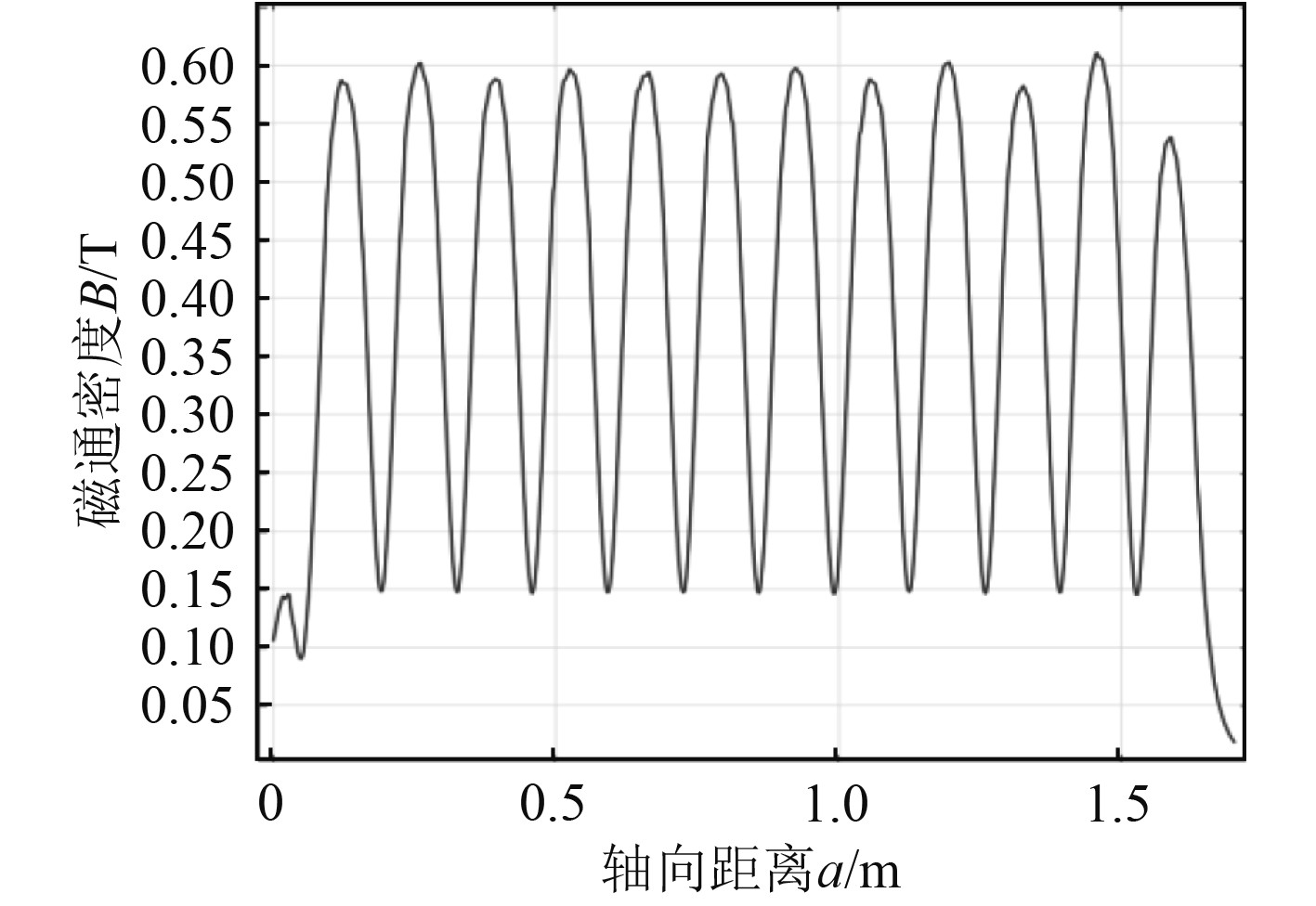
固定组件中Halbach阵列轴向长度为1600 mm，轭铁与磁环的总厚度为40 mm，磁环弧度为180°，阵列单元数决定了阵列中磁化方向变化的频率，图9为6单元24模块Halbach阵列强磁侧的磁通密度分布图，对比图7可看出轴向长度固定的情况下，6单元阵列的磁通密度变化频率是3单元阵列的2倍。

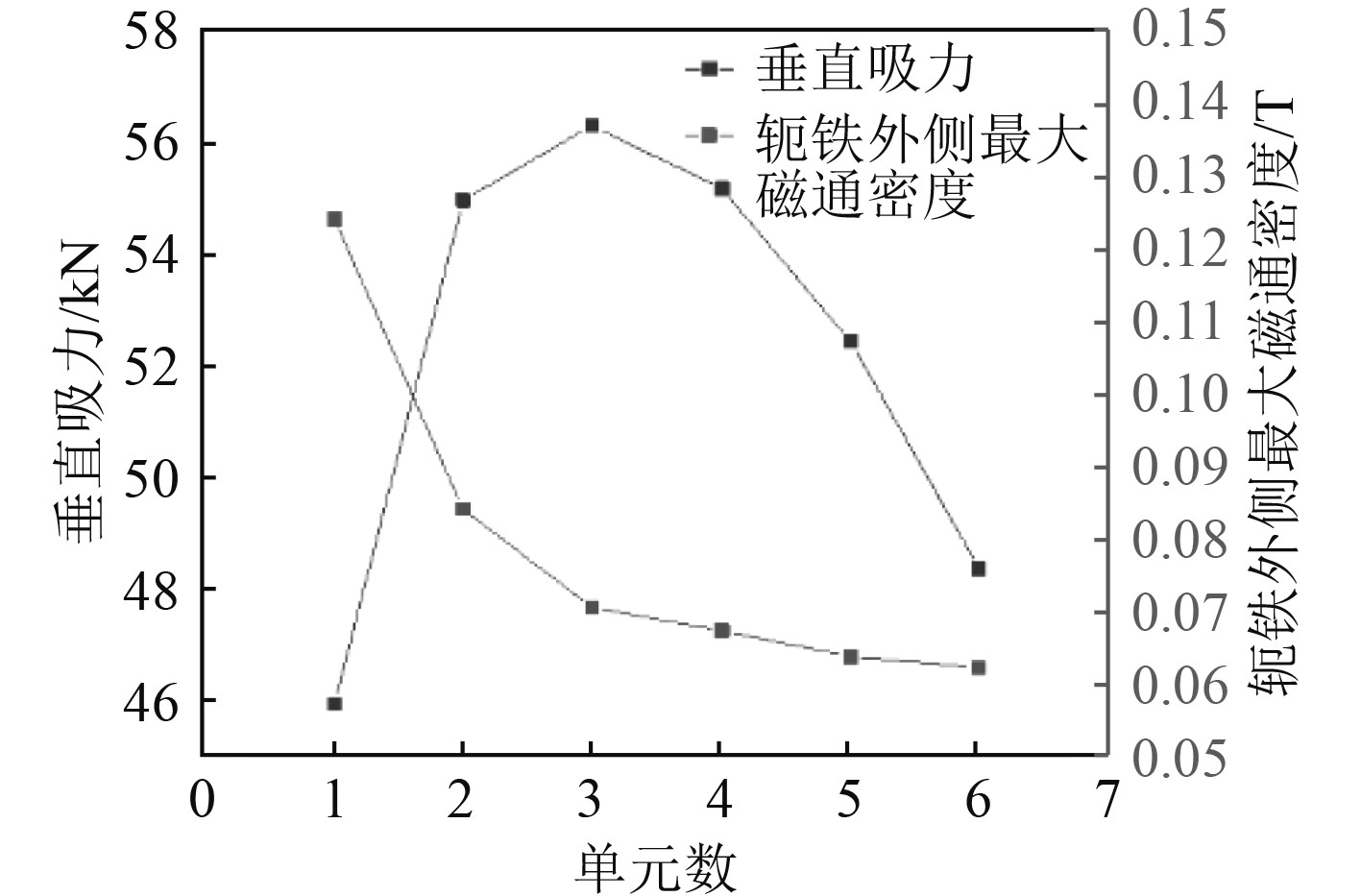
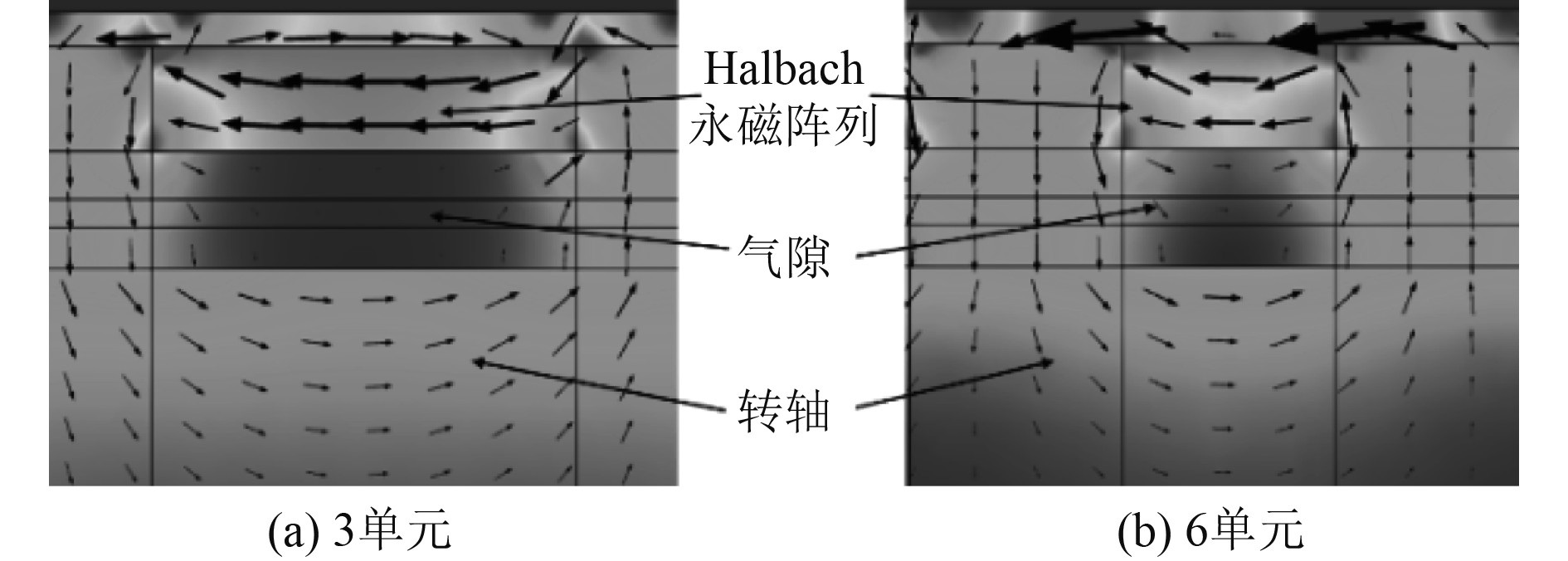
从图10可以看出，在轴向长度不变的情况下，随着Halbach永磁阵列单元数的增加，转轴获得的垂向吸引力先增大后减小。经分析得到，当单元数较少时，此时Halbach阵列的单边聚磁作用较不明显，阵列对转轴主要的磁通密度贡献来自于沿径向极化的磁环。随着单元数的增多，导致气隙中磁通密度的变化频率变大，从图11可以看出,气隙中磁环极面产生的磁力线不经过转轴铁磁材料直接进入磁环极面增多，导致距转轴铁磁材料表面2 mm处的最大磁通密度减小。

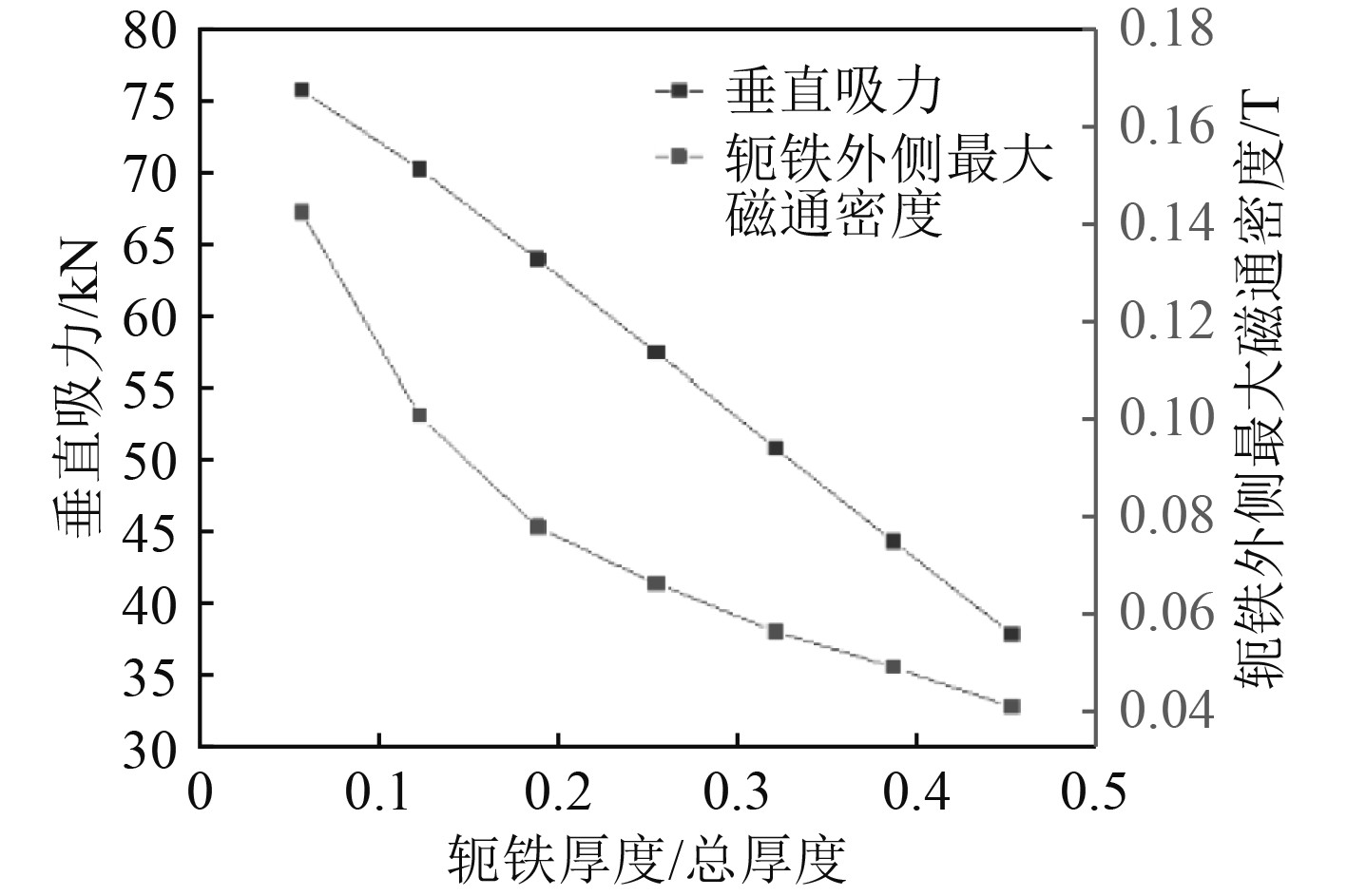
如果用轭铁上表面外侧10 mm处的最大磁通密度表征Halbach组件的漏磁程度，从图12可以看出，随着单元数的增加，轭铁外最大磁通密度从0.125 T逐渐减小到0.061 T，漏磁程度逐渐减小。

2）轭铁厚度对磁吸组件性能的影响

固定轭铁与磁环的总厚度为40 mm，轭铁厚度与总厚度比值越大表示Halbach阵列磁环的厚度越小，永磁材料体积越小。从图12可以看出，随着轭铁厚度的增大，转轴获得的垂向吸力逐渐减小，总体呈线性关系，永磁材料体积减小对Halbach阵列产生吸引力的影响较大。另一方面，随着轭铁厚度与总厚度比值的增大，组件的漏磁程度逐渐减小，但减小的趋势总体变缓。设计过程中，在满足垂向吸力需求的同时，也要考虑到轭铁厚度过小容易在永磁材料的作用下发生变形。

3）磁环弧度对磁吸组件性能的影响

磁环弧度一方面影响了永磁材料的体积和Halbach阵列与转轴的气隙面积，另一方面，考虑到水润滑橡胶轴承在转轴运转时，通过产生流体动压来产生承载力，转轴会产生一定的偏心，大小不超过气隙宽度，而转轴具有水平偏心量时，磁吸组件会对其产生水平方向的差分力。考察不同磁环弧度对转轴获得的垂向吸力，以及转轴发生最大水平偏心0.75 mm时，转轴受到的水平差分力的影响。

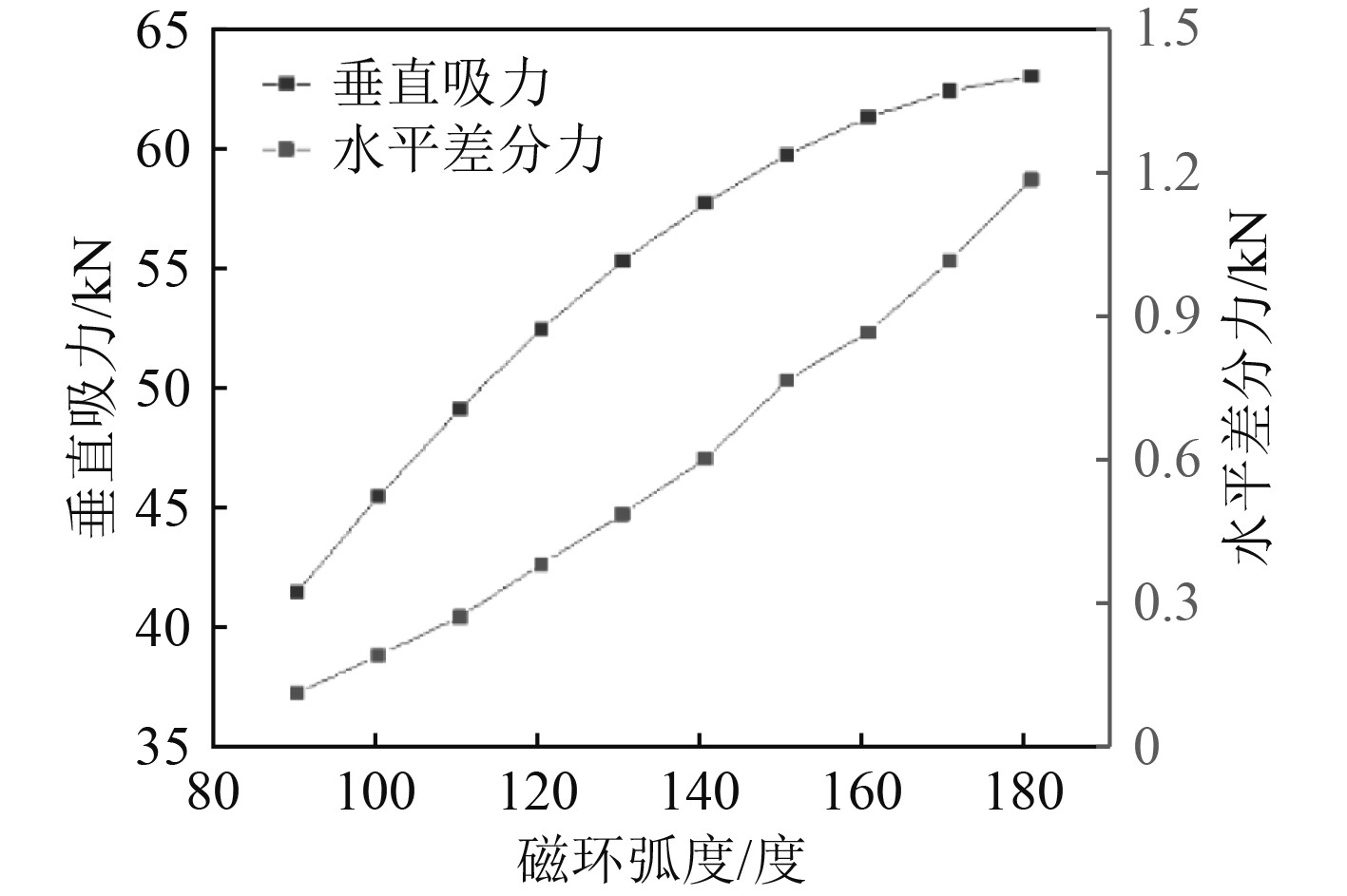
从图13可以看出，随着磁环弧度的增加，转轴获得的垂向吸力逐渐增大，这是因为永磁材料的体积与Halbach阵列与转轴的气隙面积增大的原因，但增大的趋势总体变缓，这是由于磁环靠近两侧的永磁材料对垂向吸力的贡献较小。另一方面，转轴所受的最大水平差分力随着磁环弧度增加同步增大，这是由于磁环靠近两侧的永磁材料对水平差分力的贡献较大。因此在设计过程中可以牺牲一定垂向吸力以降低转轴发生偏心时受到的最大水平差分力，从而提高转轴在水平方向的稳定性。

3.2 载荷作用下接触状况分析 3.2.1 均匀载荷作用下接触状况分析

在螺旋桨轴低转速或轴承受重载荷时，轴与轴承间由于发生直接接触，导致轴与轴承间无法形成流体动压润滑膜，而产生了粘-滑运动，产生振动；尖叫声是在轴承与螺旋桨轴摩擦面处于半干摩擦或干摩擦时出现，此时局部比压太大，无法建立润滑膜。可见粘-滑现象的产生与轴承接触状况有着密切关系，将磁复合型水润滑橡胶轴承与普通型轴承作为对比，通过研究二者在不同均匀载荷下的发生的形变和应力分布，以此分析Halbach永磁吸引组件对橡胶轴瓦在重载下接触状况的影响，降低轴承比压的效果。

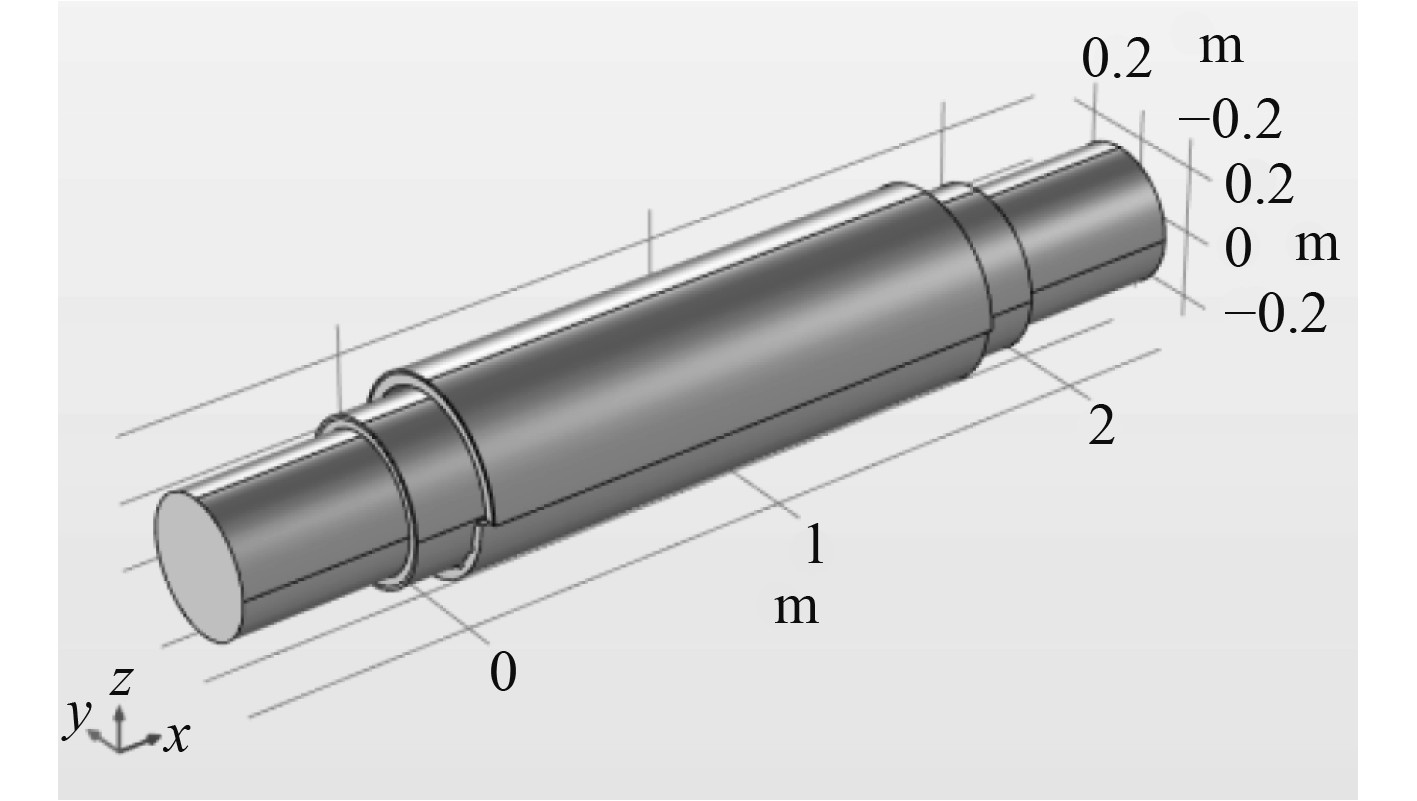
图14为使用有限元分析软件Comsol建立的橡胶轴承应力应变分析模型，模型忽略了橡胶轴承的铜套等其他无关结构。水润滑轴承轴瓦为橡胶材料，是一类非线性超弹性材料，但一般用于水润滑轴承的橡胶轴瓦变形量小于轴瓦厚度的50%，所以采用二参数的Moone-Rivlin本构模型作为橡胶材料的本构模型。Mooney-Rivlin 系数为C_10 =0.7066 MPa，C_01 = 0.3704 MPa，弹性模量7.8 MPa，泊松比为设为0.47，体积模量设为43.3 MPa。

橡胶轴瓦条固定在铜套上，铜套是固定约束的，在进行轴与橡胶轴瓦条的静态接触分析时，可忽略铜套结构。转轴通过设置体载荷实现均匀加载，研究磁复合型和普通型轴承在不同均匀载荷下的接触应力和橡胶发生的最大形变。

图15分别是载荷为180 kN时普通型、磁复合型橡胶轴承的接触应力分布云图。通过比较，可以看出磁复合型的平均接触应力（0.23 MPa）明显小于普通型（0.32 MPa）。

图16分别是载荷为180 kN时普通型和磁复合型橡胶轴瓦的表面应变分布云图。通过比较，可以看出磁复合型橡胶轴瓦在180 kN下发生的最大形变（0.38 mm）明显小于普通型（0.57 mm）。

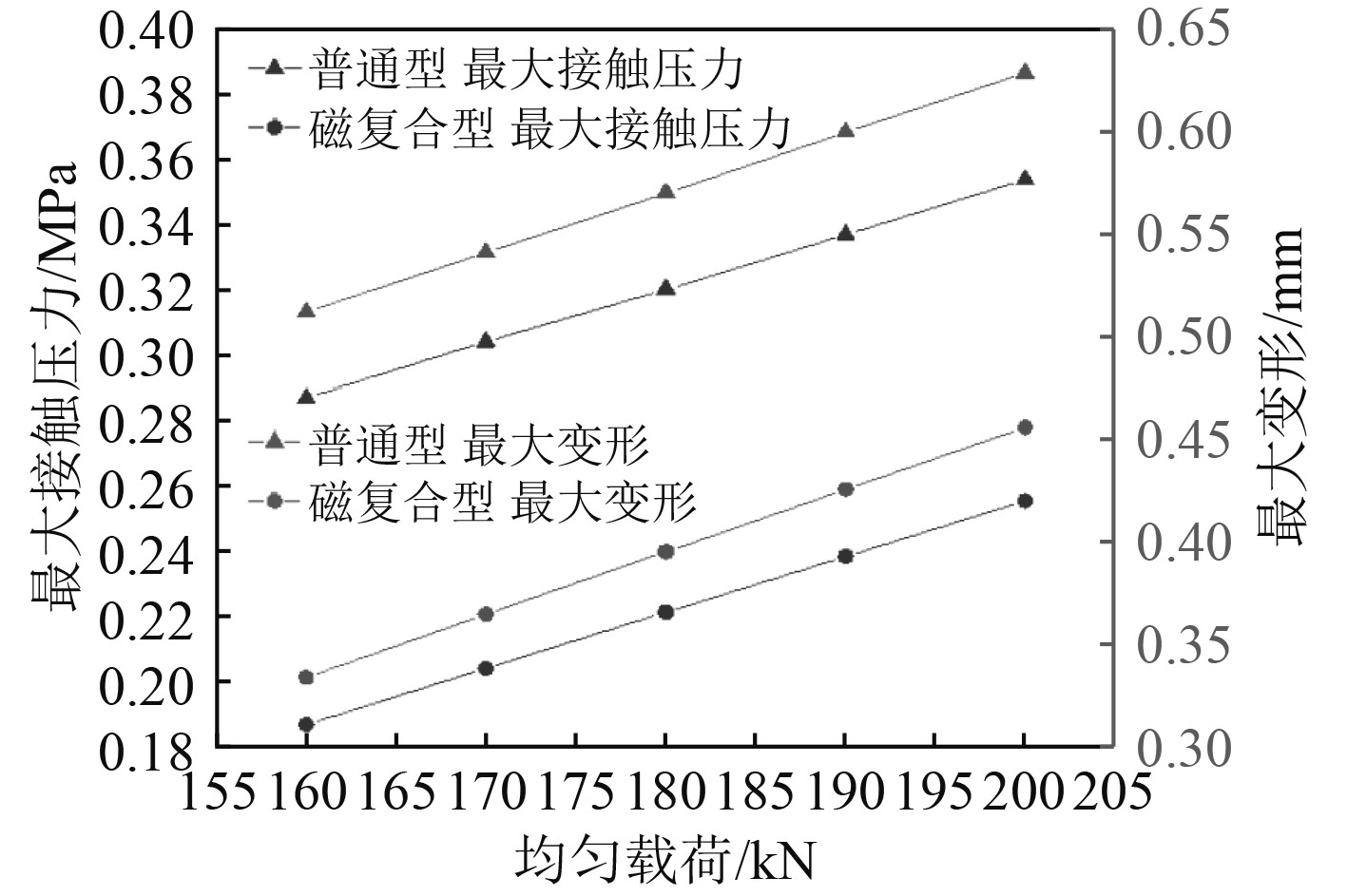
图17是普通型、磁复合型橡胶轴承随载荷逐渐增大时，载荷与橡胶轴瓦最大接触应力和表面最大形变的关系。可以看出，磁复合型在所有载荷工况下，其橡胶轴瓦的最大接触压力与最大变形均明显小于普通型。通过静态均匀载荷接触状况分析，Halbach永磁吸引组件通过对转轴产生磁吸力，橡胶轴瓦产生的表面形变和接触应力都明显小于普通型。以上工况下磁复合型橡胶轴承可以明显降低橡胶轴瓦承受的比压。

3.2.2 尾端偏载下接触状况分析

选用的研究模型与上节基本一致，所不同的是转轴所受载荷为均匀载荷与尾端偏载共同作用。选择转轴所受的均匀体载荷为150 kN，尾端偏载从10 kN到50 kN变化，研究磁复合型和普通型在不同尾端载荷下的接触应力和橡胶轴瓦发生的最大形变。

图18分别是载荷为180 kN时普通型、磁复合型橡胶轴承的接触应力分布云图。通过比较，可以看出磁复合型的总体接触应力分布明显小于普通型。在尾端不平衡载荷的作用下，普通型轴承的边缘应力达到了0.52 MPa，而由于Halbach永磁吸引组件的吸引力作用，磁复合型轴承的边缘应力为0.37 MPa，橡胶轴瓦承受的边缘载荷得到了显著降低。

图19分别是尾端载荷为30 kN时普通型和磁复合型橡胶轴承的表面应变分布云图。通过比较，可以看出磁复合型在尾端偏载30 kN下发生的最大形变（0.68 mm）明显小于普通型（1.02 mm）。

图20为普通型、磁复合型橡胶轴承随尾端载荷逐渐增大时，载荷与橡胶轴瓦最大接触应力和表面最大形变的关系。可以看出磁复合型在所有载荷工况下，其橡胶轴瓦的最大接触压力与最大变形均明显小于普通型。通过静态尾端偏载接触状况分析，Halbach永磁吸引组件通过对转轴产生磁吸力，橡胶轴瓦产生的表面形变和接触应力都明显小于普通型。以上工况下磁复合型橡胶轴承可以明显降低橡胶轴瓦承受的比压。

4 结　语

具有Halbach永磁阵列的磁复合型水润滑橡胶尾轴承相比普通型水润滑橡胶尾轴承可明显降低轴承比压。通过静磁场分析得到Halbach磁吸组件性能受Halbach阵列单元数、磁轭厚度、磁环弧度影响，且具有明显的非线性。通过应力应变分析得到磁复合型橡胶尾轴承在转子承受均匀载荷或尾端偏载工况下，接触应力和表面形变均明显小于普通型橡胶尾轴承。