0 引　言

为了降低水下航行器的辐射噪声，需要识别出整个机械振动辐射系统中起主要辐射作用的噪声源，从而有针对性地采取有效减振降噪措施，成为安静型水下航行器研制的一项关键技术^[1]。Brooks等^[2]利用阵列元素信号的混合特征，通过控制旁瓣的高度来提高了空间分辨率。B.Barsikow^[3]利用29个麦克风组成一维和二维阵列，实现了对运动声源的有效识别和定位。王斌等^[4]提出一种结构噪声源辐射声场快速预报方法——单元辐射叠加法，给出了矩形活塞辐射声场表达式。毛晓群等^[5]通过麦克风阵列测量得到声场信息，使用波束形成方法对声场信号进行处理，能够对宽带声源进行有效的识别。时洁等^[6]提出MVDR聚焦波束形成方法，根据最小方差无畸变原理，实现了简单单极子声源的高分辨识别定位。

本文提出一种基于振声传递矩阵的广义逆波束形成方法^[7-9]，根据规则障板表面活塞辐射声场的解析表达式建立目标结构表面声源与接收基阵之间的声传递矩阵，代替传统点源球面波扩展传递矩阵，克服了传统点源球面扩展声传播模型的局限性，解决了复杂结构声源声传播模型的精细化表征问题；利用基于振声传递矩阵的广义逆波束形成方法实现了对矩形板结构噪声源的识别。理论分析与仿真结果表明，该方法具有更高的空间分辨率，有效提高矩形板结构声源的识别定位性能。

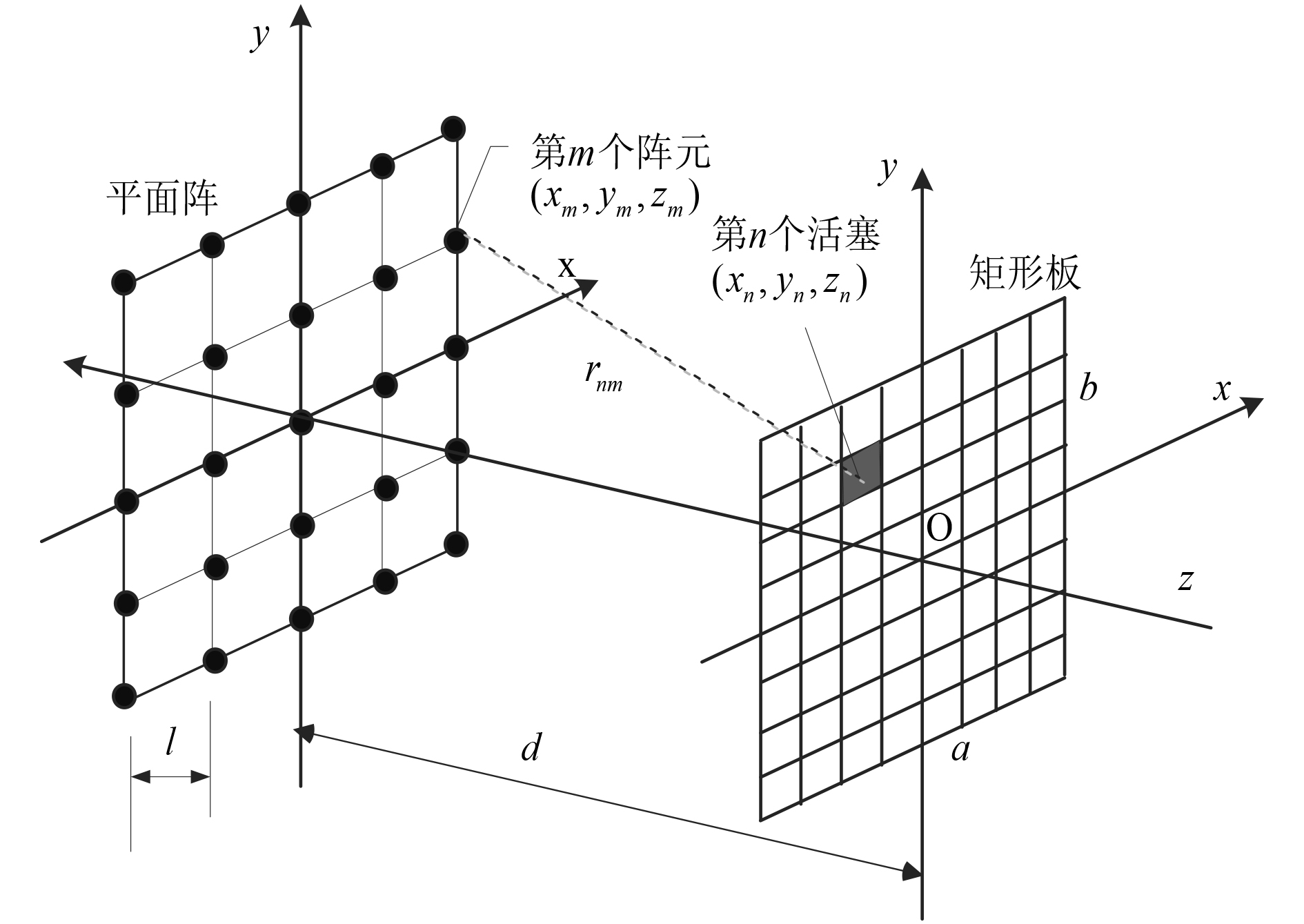
1 矩形板测量模型

矩形板测量模型如图1所示，矩形板四边条件简支，镶嵌于无限大平面刚性障板中，测量阵采用平面阵，阵元数为M，长度为 $ a $ ，宽度为 $ b $ ，厚度为 $ h $ ，板面均匀划分为N个矩形活塞，第 $ n $ 个结构表面活塞的几何中心坐标为 $ \left( {{x_n},{y_n},{z_n}} \right) $ ，第 $ m $ 个阵元的空间坐标位置为 $ \left( {{x_m},{y_m},{z_m}} \right) $ ，阵元间距为 $ l $ ，板面到平面阵的垂直距离为 $ d $ 。

2 广义逆波束形成 2.1 广义逆波束形成原理

广义逆波束形成技术是一种基于阵列接收信号处理的噪声源识别定位技术。通过阵列接收数据处理以及声场传递矩阵逆向求解方法，可以得到噪声源声压分布。

对于矩形板结构声源，首先将结构辐射面划分为很多均匀规则表面障板活塞，将每个活塞看作一个独立辐射声源。矩形板结构声源测量模型如图1所示，第 $ n $ 个活塞到第 $ m $ 个阵元的空间距离为 $ {r_{mn}} = \sqrt {{{\left( {{x_m} - {x_n}} \right)}^2} + {{\left( {{y_m} - {y_n}} \right)}^2} + {{\left( {{z_m} - {z_n}} \right)}^2}} $ ，根据广义逆波束形成基本理论，建立声源表面活塞到阵元的传递函数，通过该方程可准确描述声场空间信息，可得：

$ \begin{aligned} & {{\boldsymbol{A}}} \cdot x = {\boldsymbol{p}} \text{，} \\ & {{\boldsymbol{B}}} \cdot v = {\boldsymbol{p}} \text{。} \end{aligned} $

(1)

式中： ${\boldsymbol{A}}$ 为辐射面到阵列面的点源格林函数传递矩阵； ${\boldsymbol{B}}$ 为辐射面到阵列面的单元辐射法振声传递矩阵； $ \left[ x \right] $ 表示声源表面声压矢量； $ \left[ v \right] $ 为声源表面法向振速矢量； $ {\boldsymbol{p}} $ 为M元阵列接收声压矢量；M，N分别为阵元个数和结构辐射面离散活塞个数。为达到更好地识别效果，往往要求辐射面离散活塞尺寸尽可能小，因此活塞个数M远大于阵元个数N。

由于活塞个数大于阵元个数，矩阵 ${\boldsymbol{A}}$ 和 ${\boldsymbol{B}}$ 的行数小于列数，式(1)为欠定方程组，不能对矩阵 ${\boldsymbol{A}}$ 和 ${\boldsymbol{B}}$ 直接求逆。在这种情况下，声学响应传递方程是具有不适定性的，无法通过直接对传递矩阵求逆得出满意的声源面成像结果。为此，需要采用结合正则化方法的广义逆方法在消除这种不适定性的同时近似求解上述方程。经典的正则化方法是Tikhonov正则化方法，该方法是基于上式逆问题解的残余范数和解范数之间的联合加权以达到最小的思想，即

$ {\boldsymbol{q}} = \arg \min \left\{ {\left\| {{\boldsymbol{p}}{{ - }}{\boldsymbol{Gq}}} \right\|_2^2 + {\varepsilon ^2}\varOmega {{\left( {\boldsymbol{q}} \right)}^2}} \right\}\text{。} $

(2)

式中： $ {\boldsymbol{q}} $ 为声源表面物理量； $\varOmega \left( {\boldsymbol{q}} \right) = {\left\| {{{\boldsymbol{L}}^{{{ - }}1}}{\boldsymbol{q}}} \right\|_2}$ ， $\varOmega \left( {\boldsymbol{q}} \right)$ 为离散平滑范数； $ {{\boldsymbol{L}}^{ - 1}} $ 为正则化方阵。

在传统的广义逆波束形成方法中，是令 $ {{\boldsymbol{L}}^{-1}} = {{\boldsymbol{I}}_{\text{N}}} $ ，通过最小二乘法结合Tikhonov正则化方法可得解最终声源表面声压矢量和声源法向振速矢量。

$ \begin{split} &x = {{\boldsymbol{A}}^{\text{H}}}{\left( {{\boldsymbol{A}}{{\boldsymbol{A}}^{\text{H}}} + \varepsilon {\boldsymbol{I}}} \right)^{-1}}{\boldsymbol{p}} \text{，}\\ &v = {{\boldsymbol{B}}^{\text{H}}}{\left( {{\boldsymbol{B}}{{\boldsymbol{B}}^{\text{H}}} + \varepsilon {\boldsymbol{I}}} \right)^{-1}}{\boldsymbol{p}}\text{。} \end{split} $

(3)

式中： ${{H}}$ 为矩阵的共轭转置； $ {\boldsymbol{I}} $ 为对角单位矩阵； $ \varepsilon $ 为Tikhonov正则化参数。

对于广义逆波束形成的声源识别问题，其经验值为 $ {\boldsymbol{A}}{{\boldsymbol{A}}^{\text{H}}} $ 和 $ {\boldsymbol{B}}{{\boldsymbol{B}}^{\text{H}}} $ 的最大特征值1%～10%。通过式(3)就可以重构声源表面声压 $ {\boldsymbol{p}} $ 和振速 $ v $ 。

2.2 建立传递矩阵

根据点源球面波扩展模型，构建自由场格林函数传递矩阵 ${\boldsymbol{A}}$ ，第 $ \left( {m,n} \right) $ 个元素的表达式为:

$ {{\text{A}}_{mn}} = \frac{{{e^{ - jk{r_{mn}}}}}}{{4{\text{π}} {r_{mn}}}} \text{，}$

(4)

根据矩形障板活塞辐射声场解析式，构建振声传递矩阵 ${\boldsymbol{B}}$ ，第 $ \left( {m,n} \right) $ 个元素的表达式为：

$ {{\text{B}}_{mn}} = \frac{{ - 2j\rho ck{L_x}{L_y}{e^{jk{r_{mn}}}}}}{{{\text{π}} {r_{mn}}}}{j_0}\left( {k{L_x}\frac{{{x_m}}}{{{r_{mn}}}}} \right){j_0}\left( {k{L_y}\frac{{{y_m}}}{{{r_{mn}}}}} \right) \text{。}$

(5)

式中： $ {L_x} $ 和 $ {L_y} $ 分别为矩形活塞的长和宽； $ {j_0}\left( * \right) $ 为零阶球贝塞尔函数。

为了比较2种传递矩阵广义逆波束形成方法识别误差，定义重构误差为：

$ {{error}} = \frac{{{{\left\| {{P_{re}} - {P_{th}}} \right\|}_2}}}{{{{\left\| {{P_{th}}} \right\|}_2}}} \times 100 \text{%。}$

(6)

式中： $ {P_{re}} $ 为重构声压； $ {P_{th}} $ 为对应的理论声压； $ {\left\| * \right\|_2} $ 为矩阵2-范数。

2.3 结构噪声源识别流程

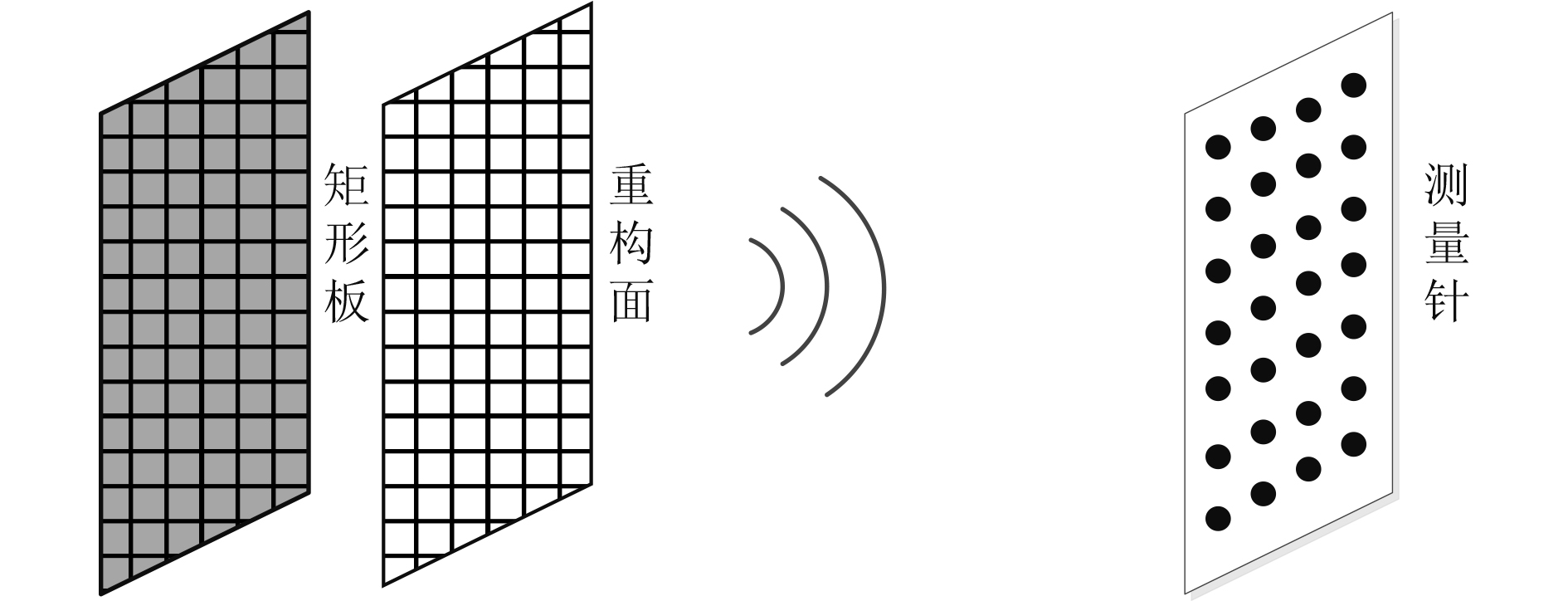
利用GFTM-GIB和VATM-GIB方法，对矩形板结构噪声源进行识别，图2为结构噪声源识别示意图。由于GFTM-GIB方法传递矩阵为结构表面声压到声场声压的传递矩阵，VATM-GIB方法为结构表面法向振速和声场声压的传递矩阵，为了方便比较，选取距离结构表面很近的重构面，识别重构面声压分布。首先，利用解析法计算测量阵的辐射声压数据。其次，将测量数据代入广义逆波束形成器，其中GFTM-GIB方法可以直接得到重构面声压分布，VATM-GIB方法先计算得到结构表面法向振速，再利用结构表面法向振速计算重构面声压分布。最后，将这2种方法得到的重构面声压分布于理论值对比，并分析2种方法识别性能。

3 仿真分析

仿真中选取简支钢板作为目标声源，钢板表面的尺寸为 $ 0.6 \times 0.6{\text{ }}{{\text{m}}^2} $ ，厚度为0.008 m，矩形活塞的尺寸为 $ 0.015 \times 0.015{\text{ }}{{\text{m}}^2} $ ，钢板的弹性模量为 $ 2.1 \times {10^{11}}\;{\text{N}}/{{\text{m}}^2} $ ，泊松比为0.3，取钢板几何中心为坐标原点，在钢板表面 $ \left(-0.2，-0.2\right) $ 处施加简谐激励力，激励钢板向外辐射噪声，激励力幅值为1N，测量面的大小为 $ 2 \times 2{\text{ }}{{\text{m}}^2} $ ，阵元数目为 $ 11 \times 11 $ ，阵元间距为 $ 0.2{\text{ m}} $ ，测量距离为 $ 0.5{\text{ m}} $ ，重构面距离板面 $ 0.01{\text{ m}} $ ，水中的声速为 $ 1\;500{\text{ m/s}} $ ，水的密度为 $ 1\;000{\text{ kg/}}{{\text{m}}^{\text{3}}} $ ，参考声压为 $ 1 \times {10^{ - 6}}{\text{ Pa}} $ 。

图3和图4给出了250 Hz和500 Hz时钢板表面法向振速分布，通过对比可得，VATM-GIB方法计算的表面法向振速分布与理论分布基本一致，说明该方法可以实现对钢板表面法向振速的重构。

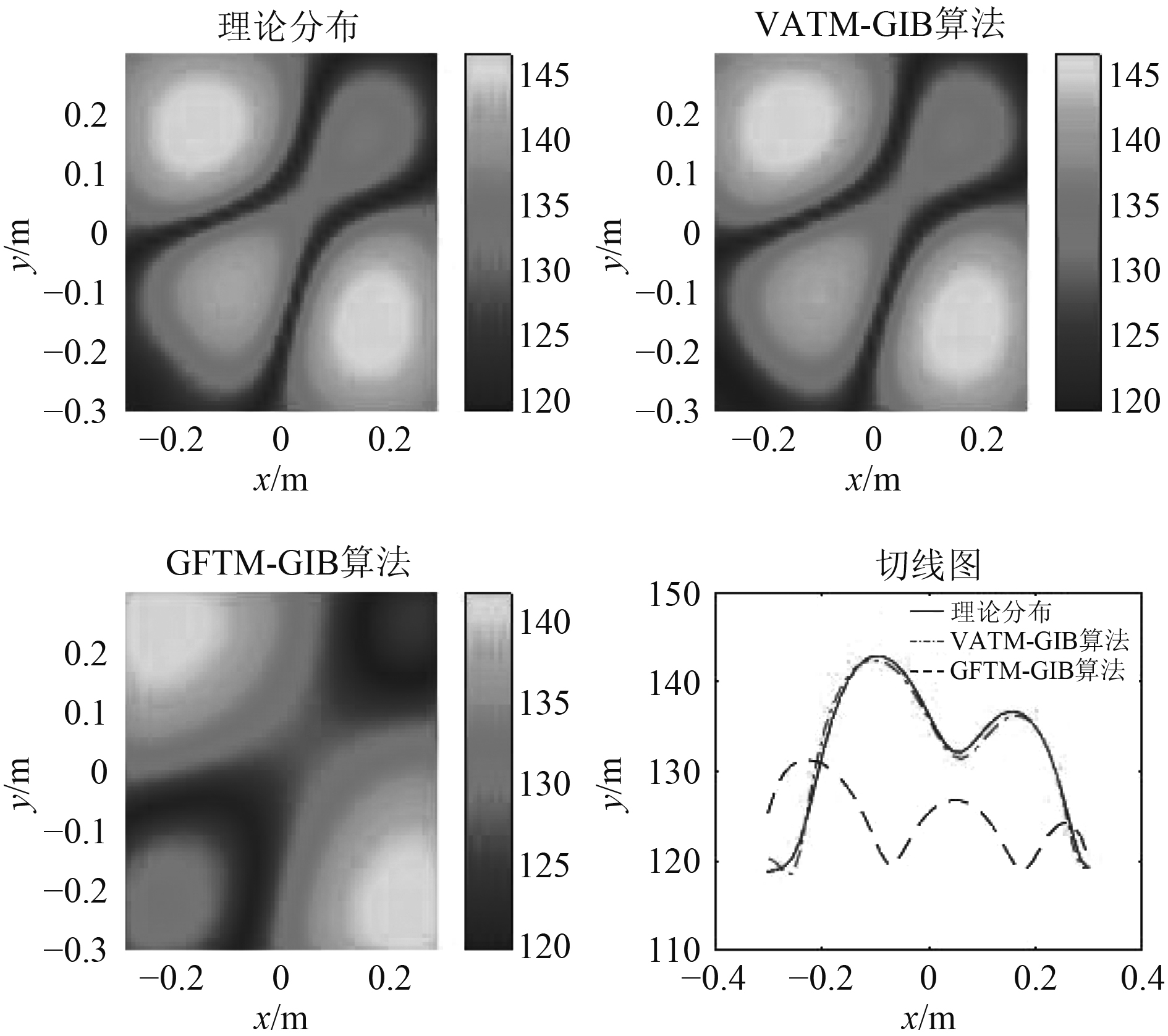
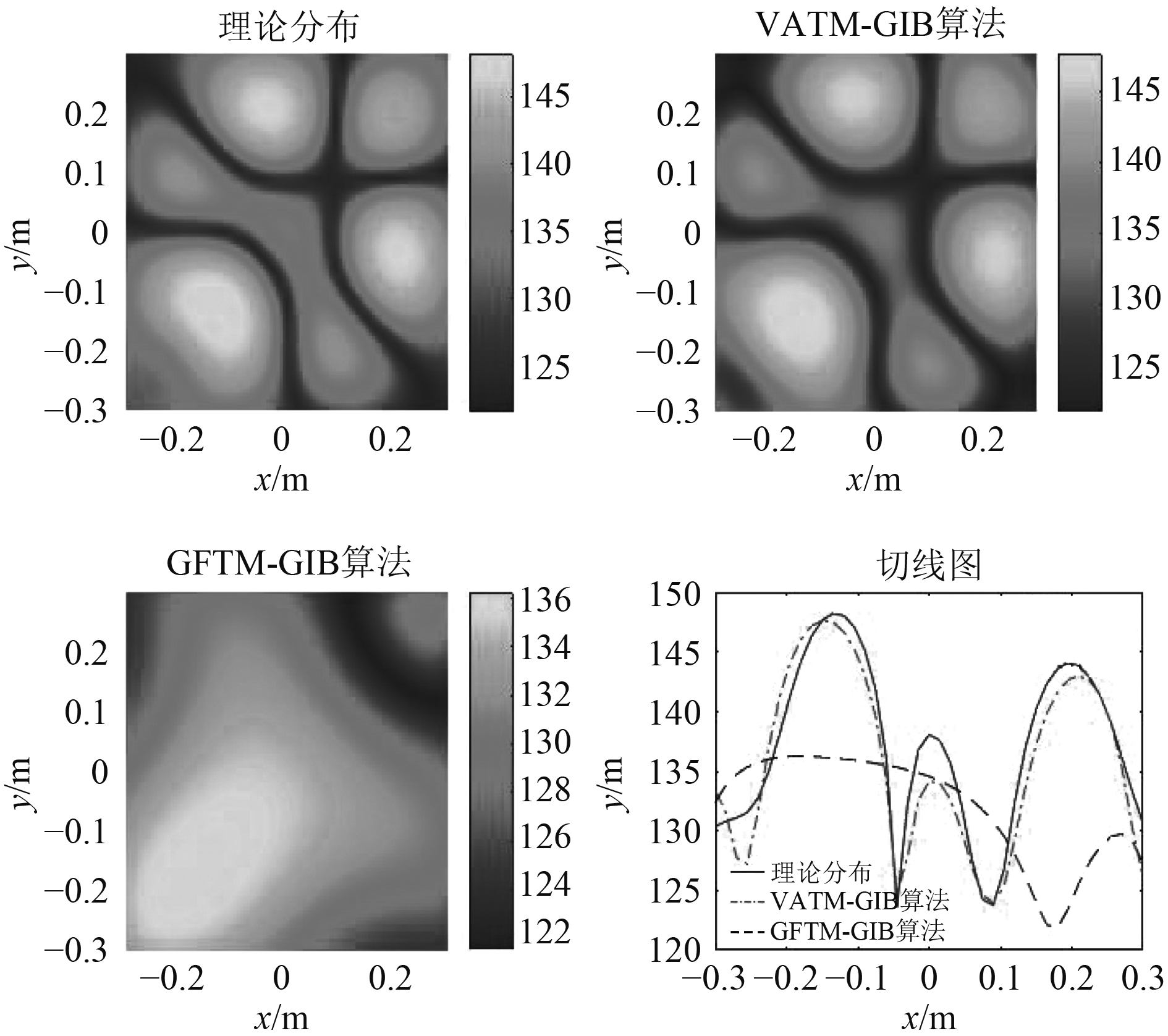
图5和图6给出了250 Hz和500 Hz时重构面声压分布，通过声压分布以及对角线声压切线值对比可以看出，VATM-GIB方法可以实现对钢板表面声压的识别重构，而GFTM-GIB方法不能完全识别重构，VATM-GIB方法较GFTM-GIB方法提高了结构噪声源识别定位的空间分辨率。

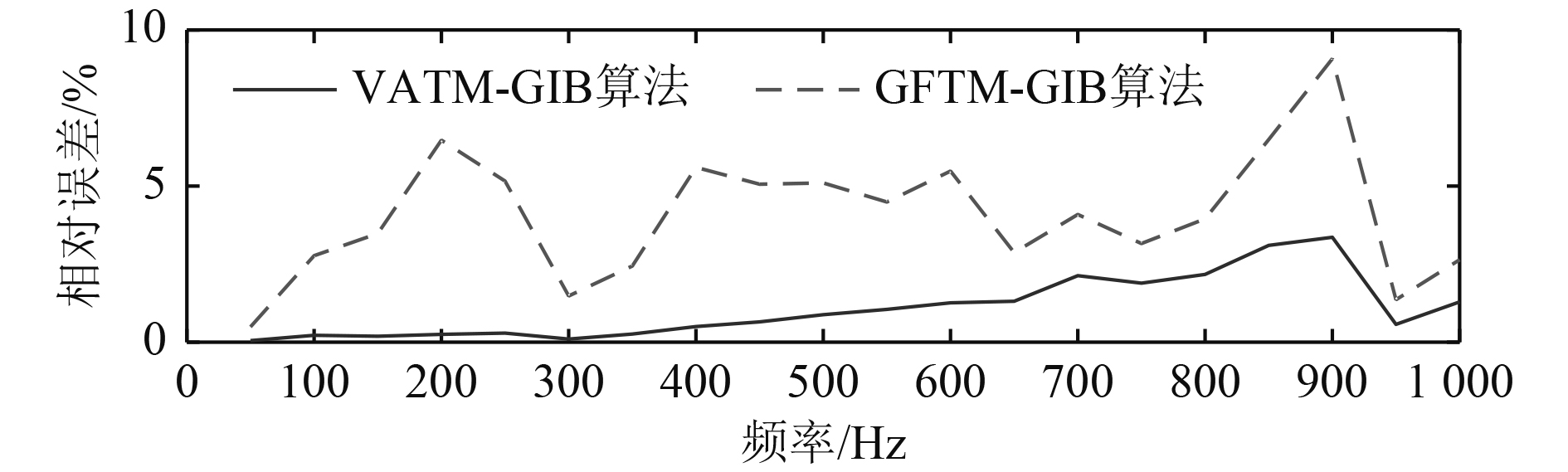
图7给出了频率10～1 000 Hz，GFTM-GIB方法和VATM-GIB方法的重构声压与理论声压的相对误差大小。可以看出，VATM-GIB方法重构相对误差远小于GFTM-GIB方法，声压重构误差基本在小于4%，VATM-GIB方法重构声压相对误差基本上随着频率的增大而增大。

4 结　语

本文提出基于振声传递矩阵的广义逆波束形成方法，克服了传统点源球面扩展声传播模型描述结构声源的局限性理，理论仿真验证了该方法对矩形板结构声源识别定位的有效性，从仿真结果可以看出，该方法较基于点源格林函数传递矩阵的广义逆波束形成方法提高了结构声源识别定位的空间分辨率，实现对结构表面法向振速和辐射声压的重构，并可得结构表面振速和声压的绝对大小。可用于水下近场结构噪声源测试与结构噪声源减振降噪，具有较好的应用前景。