2. 金陵科技学院 机电学院,江苏 南京 211169;
3. 航空工业成都飞机工业(集团)有限责任公司,四川 成都 610092
2. College of Mechanical & Electrical Engineering, JINLING Institute of Technology, Nanjing 211169, China;
3. AVIC Chengdu Aircraft Industrial (GROUP) Co. Ltd., Chengdu 610092, China
长期处于振动环境的机械结构,其振动疲劳性能不容忽视。工程结构振动疲劳计算以Dirlik[1]基于蒙特卡罗算法提出的统计模型使用最为广泛。曹明红等[2-3]用多种频域算法分别计算不同带宽下结构振动疲劳寿命,并结合实验结果对比各方法计算精度,结果表明Dirlik模型普遍使用窄带响应和宽带响应,计算精度稳定。王明珠等[4-5]提出样本法估算振动疲劳寿命,样本法是兼顾频域和时域的算法,计算精度和计算时间随样本容量增加而提升。张晓飞等[6]基于频域谱密度Dirlik模型对船舶减振支架进行振动疲劳寿命预测,并分析连接刚度对振动疲劳寿命的影响。张翼[7]和罗杨阳等[8]用Dirlik模型计算导弹吊挂振动疲劳寿命,并从应力响应均方根角度考虑振动疲劳寿命分布规律。黄军等[9]设计实验和仿真研究了不同振动谱型对电焊结构振动疲劳寿命的影响,结果表明结构低阶固有频率处的振动激励对振动疲劳寿命有决定性影响。
本文以全垫升气垫船空气导管螺旋桨后支撑为研究对象,主要考虑危险点应力响应和材料疲劳性能对振动疲劳寿命影响,横向对比各因素对外接头振动疲劳寿命影响大小,最后结合导管后支撑工作环境和结构特征,对比各优化方案实际可行性。本文较为系统研究了影响振动疲劳的诸多因素,同时提出薄壁结构提高振动疲劳寿命的一种可行的思路,对提高工程结构振动疲劳寿命有一定借鉴意义。
1 振动疲劳理论 1.1 振动理论基础n自由度系统自由振动,其运动方程为:
| $ {\boldsymbol{M}}\ddot X(t) + {\boldsymbol{C}}\dot X({\text{t}}) + {\boldsymbol{K}}X(t) = 0。$ | (1) |
式中:M为质量;C为阻尼;K为刚度,均为n×n阶矩阵。X(t)为位移向量。一般金属材料阻尼系数很小,可以忽略不计,式(1)简化为
| $ {\boldsymbol{M}}\ddot X(t) + {\boldsymbol{K}}X(t) = 0 ,$ | (2) |
对式(2)傅里叶变换可得:
| $ ( - {\omega ^2}{\boldsymbol{M}} + {\boldsymbol{K}})X(\omega ) = 0。$ | (3) |
n自由度系统受迫振动,其运动方程为:
| $ {\boldsymbol{M}}\ddot X(t) + {\boldsymbol{C}}\dot X({\text{t}}) + {\boldsymbol{K}}X(t) = F(t)。$ | (4) |
式中:M为质量,C为阻尼,K为刚度,均为n×n阶矩阵。X(t)是位移向量,F(t)是外部激励。对式(3)傅里叶变换可得:
| $ X(\omega)=H(j \omega) F(\omega) ,$ | (5) |
式中
| $ H(j \omega)=\left(-\omega^{2} {\boldsymbol{M}}+j \omega {\boldsymbol{C}}+{\boldsymbol{K}}\right)^{-1} 。$ | (6) |
由式(6)发现频响函数由质量矩阵、刚度矩阵、结构固有频率和阻尼矩阵确定,而结构固有频率是受质量分布和刚度分布影响的非独立变量,因此频响函数可认为仅受阻尼和结构固有频率影响。
1.2 随机振动疲劳计算方法频域谱密度方法计算的核心是获得应力响应功率谱密度,对该功率谱密度分布曲线通过概率统计方法获得应力峰值期望和正向0穿期望,再结合S-N曲线和Miner线性损伤累计理论估算结构振动疲劳寿命。应力响应功率谱和输入谱满足[10]:
| $ G_{\text {out }}(f)=\left.H(j \omega)\right|^{2} G_{\text {in }}(f) 。$ | (7) |
式中:
Dirlik将宽带随机过程的幅值概率密度函数定义为1个指数分布和2个瑞利分布,由此近似给出的雨流幅值概率密度表达式为:
| $ P(S) = \dfrac{{\dfrac{{{D_1}}}{Q}{e^{\tfrac{{ - Z}}{Q}}} + \dfrac{{{D_2}Z}}{{{R^2}}}{e^{\tfrac{{ - {Z^2}}}{{2{R^2}}}}} + {D_3}Z{e^{\tfrac{{ - {Z^2}}}{2}}}}}{{2\sqrt {{m_0}} }} ,$ | (8) |
式中各变量表达式为:
| $ \begin{split}&{D_1} = \frac{{2({\chi _m} - {\gamma ^2})}}{{1 + {\gamma ^2}}}\text{,} {D_2} = \frac{{1 - \gamma - {D_1} - {D_1}^2}}{{1 - R}}\text{,}\\ &{D_3} = 1 - {D_1} - {D_2}\text{,}Z = \frac{S}{{2\sqrt {{m_0}} }},\end{split}$ |
| $ \begin{split}&Q = \frac{{1.25(\gamma - {D_3} - {D_2}R)}}{{{D_1}}}\text{,}R = \frac{{\gamma - {\chi _m} - {D_1}^2}}{{1 - \gamma - {D_1} + {D_1}^2}}\text{,}\\ &\gamma = \frac{{{m_2}}}{{\sqrt {{m_0}{m_4}} }}\text{,}{\chi _m} = \frac{{{m_1}}}{{{m_0}}}\sqrt {\frac{{{m_2}}}{{{m_4}}}} 。\end{split}$ |
其中:
n阶谱矩计算方法为:
| $ {m_n} = \int_{ - \infty }^{ + \infty } {{f^n}G(f){\rm{d}}f} ,$ | (9) |
式中:
| $ D=\int_{0}^{+\infty} \frac{n_{S}}{N_{S}} 。$ | (10) |
式中:
| $ T = \frac{{{N_S}}}{{{E_P}P(S)}} = \frac{C}{{{E_P}\int {{S^m}P(S){\rm{d}}S} }} 。$ | (11) |
式中:
导管后支撑具有对称性,提取1/5后支撑作为有限元分析模型。轴套内侧节点刚性耦合到轴套中心,约束X,Z方向平动和转动4个自由度,外接头底座与导管内蒙皮铆钉连接位置设置固支边界,由于铆钉位置未出现裂纹,因此未建实体铆钉模型,有限元模型如图1所示。5083铝合金力学性能为:杨氏模量70.3 GPa、泊松比0.33、屈服强度214 MPa、抗拉强度303 MPa、密度2660 kg/m3。需要说明的是子模型局部坐标X,Y,Z方向分别对应空气导管内蒙皮圆周切向、内蒙皮圆周轴线方向和内蒙皮圆周径向。

|
图 1 有限元模型 Fig. 1 Finite element model |
图2(a)~图2(c)为前3阶固有频率对应的模态振型,图2(d)为外接头1阶模态应力分布。模态应力的大小虽然没有实际意义,但是模态应力反映在该频率共振时应力集中位置,也是振动疲劳裂纹萌生重要参考,实际裂纹出现在外接头倒角和计算结果吻合。固有频率计算结果如表1所示,误差满足精度需求。

|
图 2 模态分析 Fig. 2 Modal analysis |
|
|
表 1 模态分析结果 Tab.1 Modal analysis results |
利用模态叠加法,在外接头边界处施加X方向单位加速度激励,即可求得激励与结构应力间的传递函数,将关注区域节点传递函数与波高功率谱密度相乘,便可获得该节点处应力响应功率谱密度,如图3(a)所示。采用Dirlik雨流幅值概率模型计算该模型振动疲劳寿命,最终计算振动疲劳寿命为809.1 h,寿命分布云图如图3(b)所示。振动疲劳危险点出现在外接头前缘倒角处,与1阶模态应力集中位置一致。加速度功率谱是根据该船舶适航某工况实测数据,经过处理后,截取的20~60 Hz值为2 (m/s2)2/Hz的平直谱,每1 h作用60 s。
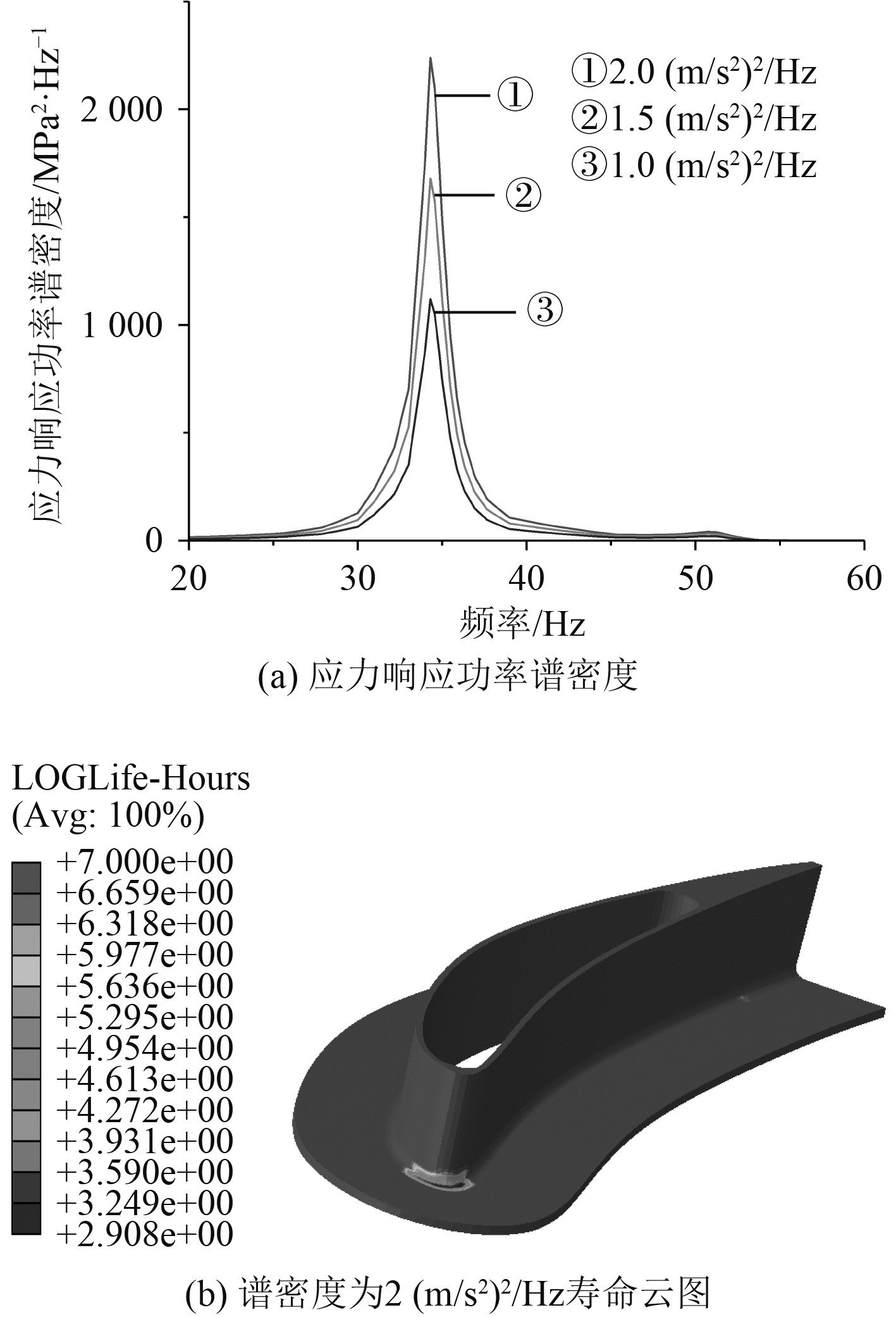
|
图 3 应力功率谱密度和寿命云图 Fig. 3 Stress power spectral density and life prediction |
结构振动疲劳分析主要包括4部分内容:危险点应力响应、振动疲劳算法、材料疲劳性能和损伤累计理论。主要考虑危险点应力响应和材料疲劳性能对振动疲劳寿命的影响。根据式(5)~式(7),降低振动激励下危险点应力响应可以从2个角度出发:1)通过隔振方法降低外接头处的振动激励峰值;2)改变结构固有参数,降低应力响应。
3.1 降低振动激励采取适当隔振措施,使加速度功率谱密度降低为1.5 (m/s2)2/Hz和1 (m/s2)2/Hz时,应力均方根σRMS分别为72.69 MPa和59.35 MPa,振动疲劳寿命分别为5308.8 h和100000 h,危险点仍在外接头前缘倒角位置。计算结果表明,降低振动激励确实可以有效提高振动疲劳寿命;当振动激励水平较低时,对结构产生的疲劳损伤有限,只有当振动激励超过某个阈值时,才会引起较为严重的振动疲劳问题。
3.2 降低应力响应根据式(6),频响函数是关于结构刚度、固有频率、质量和阻尼的函数,而结构的固有频率又是由质量分布矩阵和刚度矩阵共同决定的非独立变量,因此研究固有频率和阻尼变化对降低结构振动响应的影响。
3.2.1 调整固有频率根据振动理论基础,结构共振发生在以共振频率点为中心,半功率点为半径的频带。在载荷无法改变时可以通过调整结构固有频率避开共振区间。根据式(3),频率主要由刚度质量比决定,大幅提升结构刚度使其1阶固有频率高于60 Hz很难实现,一般采用附加大质量块将结构固有频率降低来避振。集中质量法对低阶模态计算精度影响不大,在支臂中段耦合2个大质量点各12 kg,1阶固有频率降至16 Hz,振动疲劳寿命如图4所示,寿命仅有38 h,危险点转移至外接头后缘,与2阶模态应力集中位置一致。因此在增加大质量后,虽然避开1阶共振,但是由于负载提高,2阶模态共振疲劳损伤远大于原结构1阶共振损伤,寿命减小。
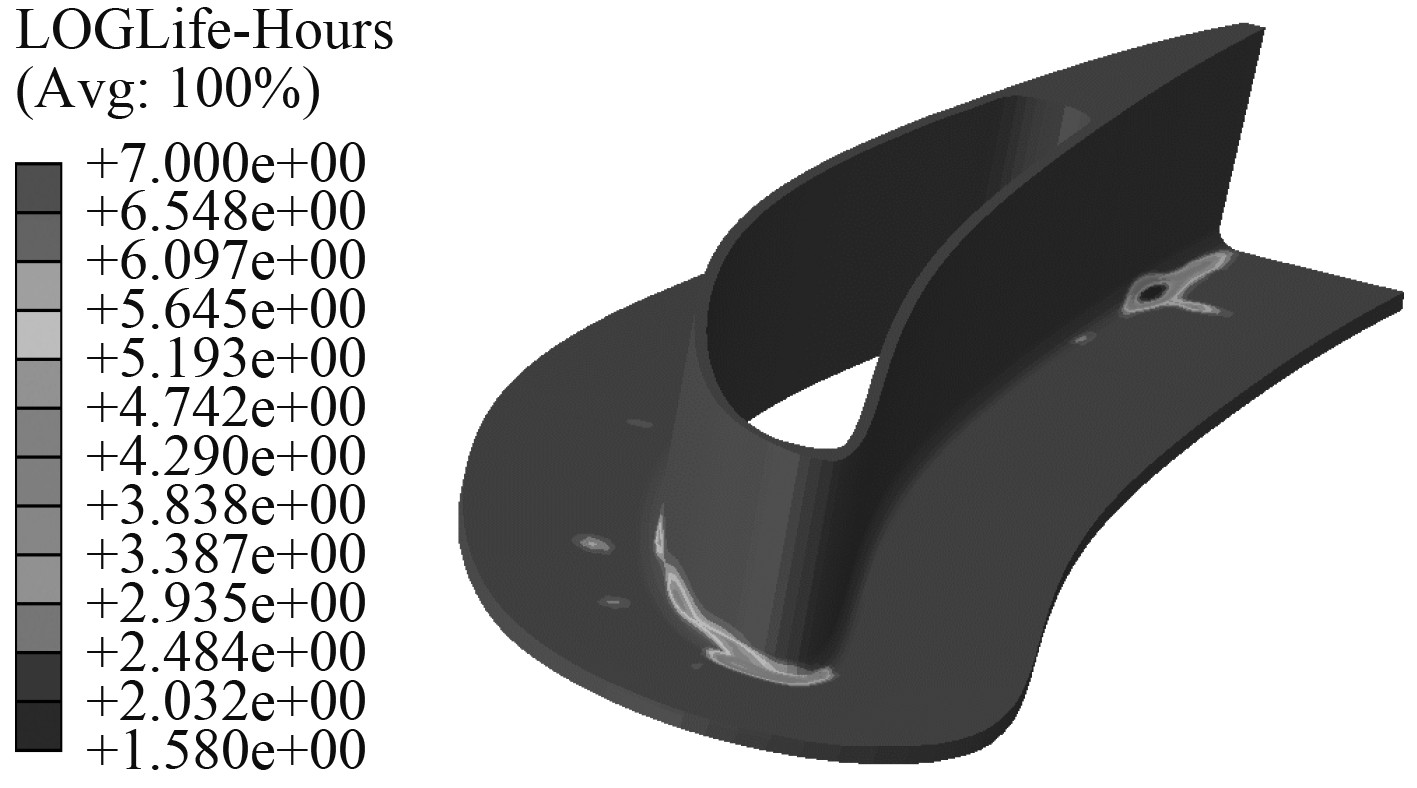
|
图 4 配重后寿命云图 Fig. 4 Life prediction with added mass |
模态阻尼是影响振动的重要物理量,目前对该参数研究还不够透彻,工程计算中一般将其视作标量,其数值可以通过实验测量。描述模态阻尼一般与临界阻尼系数比较,定义二者比值为模态阻尼比,以此描述该结构阻尼特性。原结构阻尼比为0.03,此处以0.01,0.05和0.07的阻尼比研究不同阻尼比下振动疲劳寿命变化趋势,计算结果如图5所示。阻尼比ξ=0.03,应力均方根σRMS=83.95 MPa。容易发现危险点应力响应集中于1阶模态处,2阶模态处几乎为0。
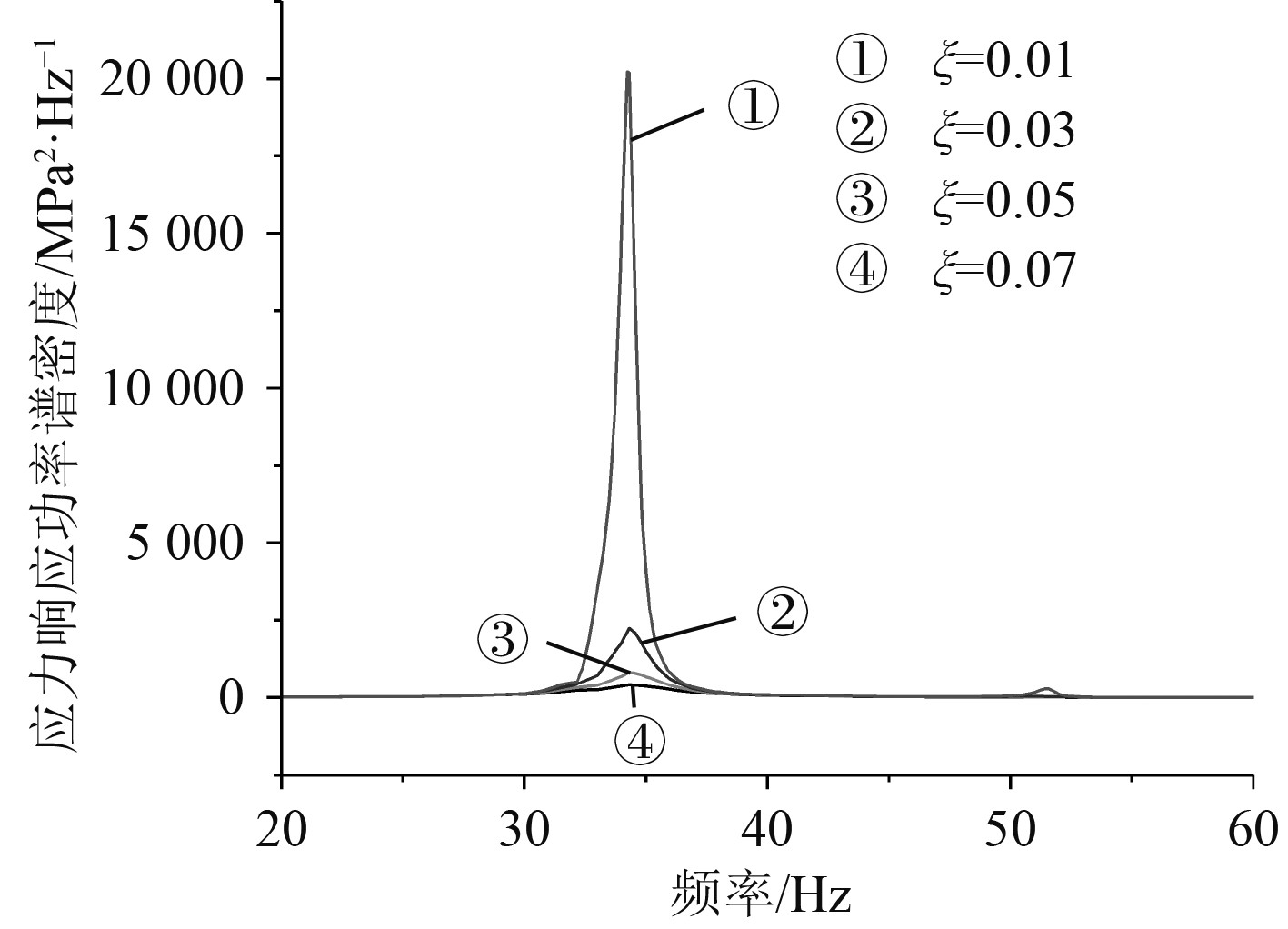
|
图 5 危险点应力响应功率谱密度 Fig. 5 Power spectral density of stress response at critical points |
根据图5,阻尼比0.01~0.03之间,危险点应力功率谱密度变化剧烈,随着阻尼比提升,应力响应功率谱峰值急剧减小,结构振动疲劳寿命显著提升。各阻尼比下危险点应力均方根σRMS分别为169.48 MPa,64.15 MPa和53.71 MPa,其振动疲劳寿命计算结果分别为0.027 h,31622.8 h和426579 h。阻尼比变化0.02会使振动疲劳寿命改变1~2个数量级,因此阻尼对结构振动疲劳寿命影响极大,对长期处于振动环境的机械结构应在设计阶段充分考虑结构的阻尼效应并合理利用。
3.3 提高疲劳性能 3.3.1 材料影响结构疲劳性能最直观的体现在材料的疲劳性能,40CrNiMoA材料力学性能为:杨氏模量209 GPa、泊松比0.3、屈服强度835 MPa、抗拉强度980 MPa、密度7830 kg/m3。5083铝合金和40CrNiMoA材料[11]的疲劳性能如表2所示。根据表中数据发现,40CrNiMoA的杨氏模量和密度约为原结构的3倍,但由于外接头处存在边界约束,质量对固有频率的影响远不如刚度,整个结构固有频率上移。危险点应力响应功率谱密度如图6(a)所示,由于40CrNiMoA的杨氏模量远大于铝合金材料,危险点处应力响应峰值明显提升,其应力均方根σRMS=110.62 MPa,但是并未产生振动疲劳。
|
|
表 2 材料疲劳性能曲线 Tab.2 Fatigue property curve of materials |
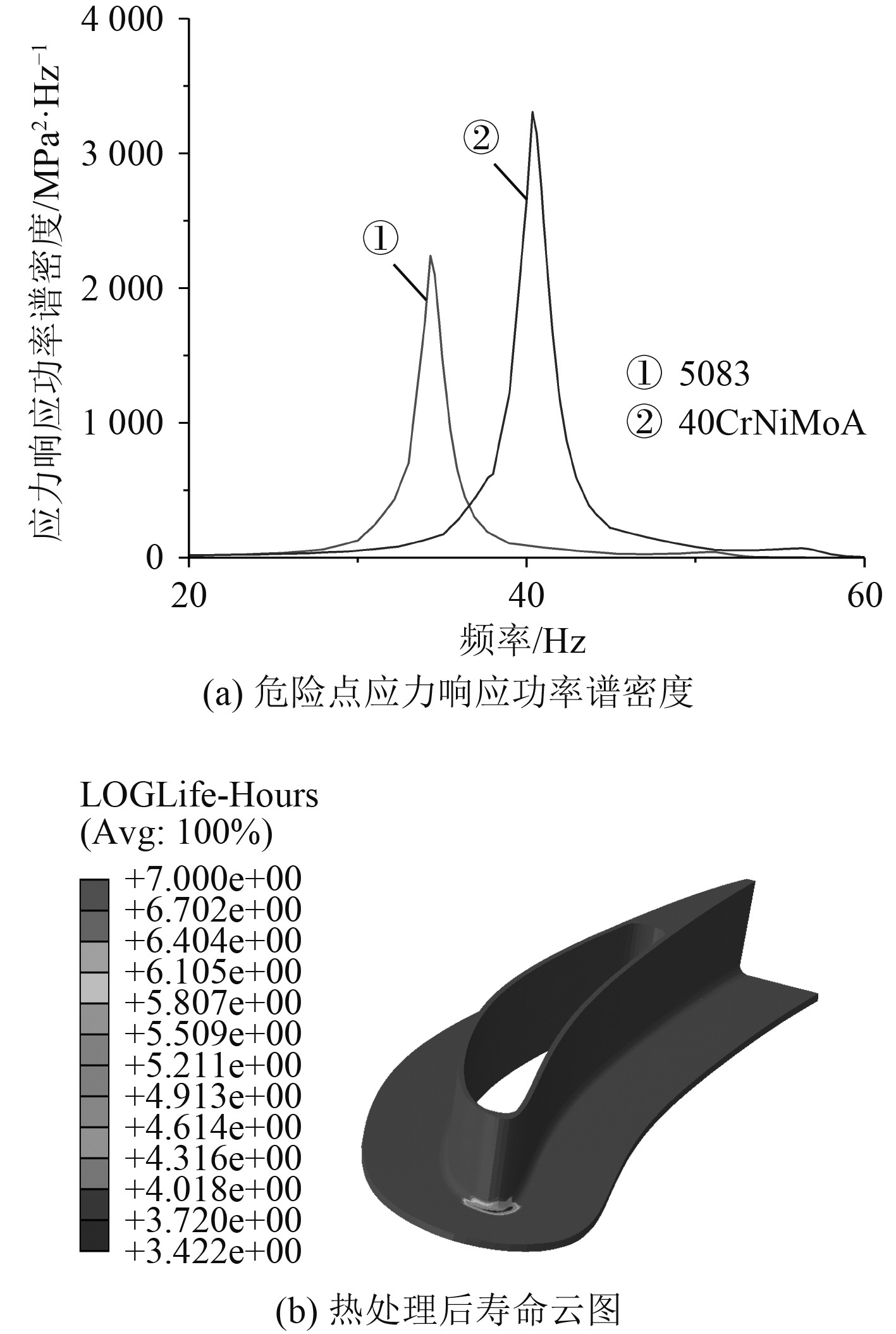
|
图 6 位移-应力响应及寿命云图 Fig. 6 Displacements - stress response and life prediction |
考虑温湿的海上工作环境使得不同材料之间的电化学腐蚀严重,此处以经过热处理的5083铝合金材料代替,其S-N曲线数值见表2,计算结果如图6(b)所示,寿命为2642.4 h,相较于原材料的振动疲劳寿命有明显改善。
3.3.2 局部强化根据材料力学基础知识,应力与结构的传力路线和截面形状是不可分割的。后支撑承担部分空气螺旋桨转动产生的载荷,是动力系统传力的重要一环,而外接头作为后支撑与导管框架连接的唯一零件,其前缘薄壁端极易因刚度不足和应力集中产生疲劳问题。在不改变传力路线的前提下,试图通过在外接头外侧增加补强片支撑,变相提高有效截面面积,降低前缘倒角处应力水平。补强片网格与支臂蒙皮和外接头基座网格部分绑定,模拟铆接。
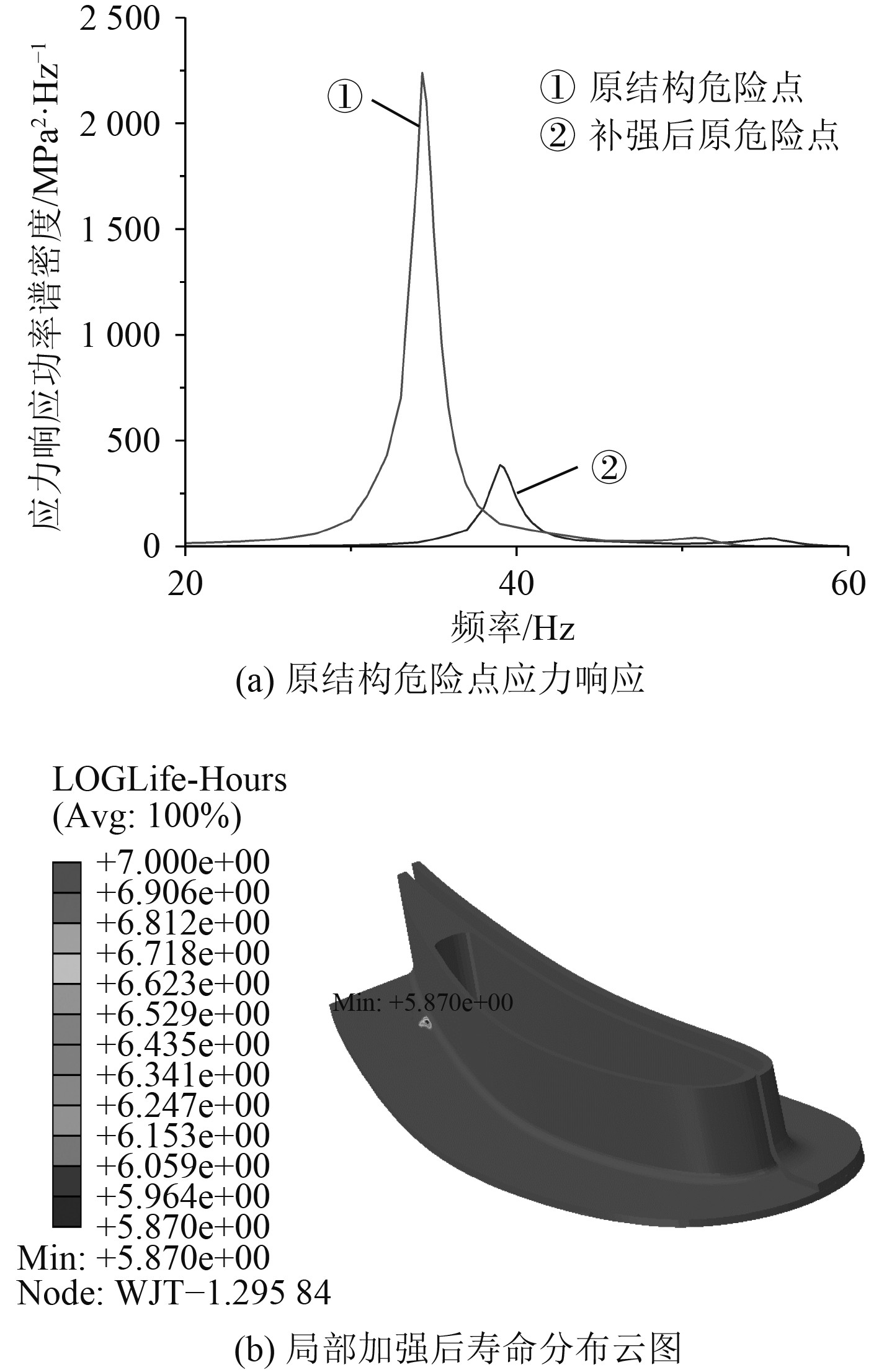
局部补强后,原结构的危险点应力响应功率谱密度如图7(a)所示,由于增加补强片后结构刚度提升,模型固有频率有所上升,但原模型的危险点应力水平明显下降,应力均方根σRMS=39.377 MPa。最终寿命计算结果如图7(b)所示,振动疲劳寿命为741310.2 h,危险位置转移至后缘倒角处,说明该强化方案有效。因此,工程薄壁结构的振动疲劳可以在薄弱位置适当加强,降低危险点应力水平从而提高振动疲劳寿命。
|
图 7 局部补强计算结果 Fig. 7 Calculation results of local reinforcement |
1) 降低振动激励,可有效提高振动疲劳寿命,较低水平的振动不会引起振动疲劳;2) 模态阻尼对振动响应影响极大,提高阻尼比可以有效提升振动疲劳寿命;3) 薄壁结构振动疲劳可以从局部加强的角度,改善危险点应力响应水平,延长振动疲劳寿命;4) 疲劳性能优越的材料可以有效提升振动疲劳寿命,但要注意电化学腐蚀等问题,可适当采取热处理等方式提升材料疲劳性能;5)调整固有频率避开共振频带的方法,对解决共振疲劳问题可能效果明显,但对于平直功率谱加载,效果可能适得其反。
| [1] |
DIRLIK T. Application of computers in fatigue analysis[J]. University of Warwick, 1985.
|
| [2] |
曹明红, 葛森, 齐丕骞. 随机振动疲劳频域分析方法的对比研究[C]//中国振动工程学会. 中国航空结构动力学专业组第十六届学术交流会论文集, 2008: 5. CAO M R, GE S, QI P S. Comparative study of random vibration fatigue analysis methods in frequency domain[C]// Chinese Society of Vibration Engineering. Proceedings of the 16th Symposium of China Aeronautical Structural Dynamics Specialized Group, 2008: 5. |
| [3] |
曹明红, 邵闯, 齐丕骞. 宽带随机振动疲劳寿命的频域分析与试验对比研究[J]. 机械科学与技术, 2013, 32(6): 839-844. CAO M R, SHAO C, QI P S. Comparison of the frequency-domain analysis and the test results for a wide-band random vibration fatigue problem[J]. Mechanical Science and Technology, 2013, 32(6): 839-844. |
| [4] |
王明珠, 姚卫星, 孙伟. 结构随机振动疲劳寿命估算的样本法[J]. 中国机械工程, 2008(8): 972-975. WANG M Z, YAO W X, SUN W. Sample Approach for fatigue life prediction of structures under random vibration[J]. China Mechanical Engineering, 2008(8): 972-975. DOI:10.3321/j.issn:1004-132X.2008.08.021 |
| [5] |
王明珠. 结构振动疲劳寿命分析方法研究[D]. 南京: 南京航空航天大学, 2009.
|
| [6] |
张晓飞, 李良碧, 谷晓梅. 连接刚度对船舶减振支架振动疲劳寿命的影响[J]. 江苏科技大学学报(自然科学版), 2018, 32(4): 472–476, 502. ZHANG X F, LI L B, GU X M. Influence of connector stiffness on vibration fatigue life of vibration damping bracket in ship [J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition) 2018, 32(4): 472–476, 502. |
| [7] |
张翼, 杨晨, 罗杨阳. 随机振动载荷下导弹吊挂疲劳寿命分析[J]. 机械科学与技术, 2013, 32(11): 1675-1679. ZHANG Y, YANG C, LUO Y Y. Fatigue life analysis of missile hanging in random vibration load[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(11): 1675-1679. |
| [8] |
罗杨阳, 倪樵, 陈铎民, 等. 吊挂随机振动疲劳影响因素分析[J]. 机械科学与技术, 2016, 35(6): 821-825. LUO Y Y, NI Q, CHEN D M, et al. Effect factor analysis of random vibration fatigue of missile hanging[J]. Mechanical Science and Technology, 2016, 35(6): 821-825. |
| [9] |
黄军, 王瑞杰, 毛志亮. 点焊结构在随机振动环境下的疲劳寿命研究[J]. 机械科学与技术, 2017, 36(12): 1838-1842. HUANG J, WANG R J, MAO Z L. Studying fatigue life of spot welded structure under random vibration environment[J]. Mechanical Science and Technology, 2017, 36(12): 1838-1842. |
| [10] |
CLOUGH R W, PENZIEN J. Dynamics of structures [M]. 3rd ed. Berkeley, USA: Computer & Structures, Inc, 1995: 427−538.
|
| [11] |
姚卫星. 结构疲劳寿命分析[M]. 北京: 科学出版社, 2019
|
 2022, Vol. 44
2022, Vol. 44
