2. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
输流管道系统广泛应用于船舶海洋工程领域,其振动特性对于保证船舶正常工作而言是不可忽视的关键部分,由液体压力脉动等交变载荷引发的管道振动,极有可能导致管道疲劳破坏,影响船舶设备的安全运行[1]。对于石油钻井平台、LNG-FPSO(浮式天然气生产储卸设备)等结构物,其管道系统中存在气液两相流,相较单相流其运动过程更为复杂[2],产生的流体激振力会导致管道显著的振动。因此,对典型管道结构中两相流诱导振动特性进行深入研究对于工程应用十分必要。
目前国内外针对气液两相流诱导振动主要研究管道外横向两相流和轴向两相流,对管道内流的研究相对较少[3]。张涛等[4]计算了不同含气率下气液两相流对管道内壁产生的流场作用力,表明当含气率大于50%时,长圆管内两相流流型转变为层状流,流场作用力随之减小。Riverin等[5]测量了多种两相流流型下U型管道结构的流场激励力,表明两相流激励力由窄带和周期性分量组成,且激励力的主频随着两相流折算流速的增加而成比例增加。张红艳等[6]基于流固耦合方法研究了管道振动峰值与不同气液组分参数的段塞流的关系。马晓旭等[7]利用ADINA对水平管内气液两相流诱导振动进行数值仿真,研究了两相流流型、体积含气率和分相折算速度对激振力的影响,总结了水平管道多相流流激振动的机理。蔡标华等[8]基于流固耦合算法,应用有限体积和有限元方法研究了注水管道的流激振动特性,对振动产生的噪声进行了数值模拟。
气液两相流诱导管道振动由于流动的复杂性以及流固耦合的特殊性,对计算资源有较高的要求,数值仿真的相关研究相对较少。因此,本文使用Ansys Fluent与Ansys Mechanical进行竖直弯管内的气液两相流诱导振动分析[9],主要研究竖直弯管的转弯角度对气液两相流流型变化以及管道动态响应的影响,为涉及气液两相流的船舶管道系统设计提供参考。
1 两相流管道数学模型 1.1 流固耦合控制方程流固耦合问题的控制方程包括流体域、固体域、流固耦合交界面3个部分。
对于流体域,其遵循的守恒定律包括质量守恒定律、动量守恒定律以及能量守恒定律。在研究气液两相流诱导管道振动时,不考虑气液两相的相变过程,即在整个流体域内不发生能量传递,因此仅给出粘性不可压缩流体质量和动量的控制方程,即Navier-Stokes方程。
质量控制方程:
| $ \nabla \cdot V = 0 ,$ | (1) |
动量控制方程:
| $ \rho \left( {\frac{{\partial V}}{{\partial t}} + V \cdot \nabla V} \right) = - \nabla p + \rho f + \mu {\nabla ^2}V 。$ | (2) |
式中:
气液两相流在运动过程中产生的激励力作用在管道内壁,并诱导管道振动。固体域即管道在该激励力作用下的结构动力学基本方程如下:
| ${{ {\boldsymbol{M}}}}\left\{ {\ddot u} \right\} + {{{\boldsymbol{C}}}}\left\{ {\dot u} \right\} + {{{\boldsymbol{K}}}}\left\{ u \right\} = \left\{ F \right\}。$ | (3) |
式中:
在流固耦合交界面处遵循最基本的物理守恒原则,在不考虑热效应的情况下,应满足流体域与固体域应力
| $ {d_f} = {d_s}, $ | (4) |
| $ {\tau _f} \cdot {n_f} = {\tau _s} \cdot {n_s}。$ | (5) |
式中:
目前流固耦合问题的主流求解方法为分离解法,即无需求解耦合控制方程,而是按照规定好的顺序在求解器中分别求解流体域和固体域的控制方程,并在流固耦合交界面处实现计算数据的互相传递,待当前时间步计算达到收敛,再进行下一时间步的计算,依次而行,直至得到最终结果。对于气液两相流诱导管道振动这一典型的流固耦合振动问题,本文采取分离解法中的单向流固耦合分析方法[11]。
1.2 两相流相关参数气液两相流的流动形态有别于单相流动,其两相交界面的形状不断变化,因此引入描述气液两相流流动特征的相关参数[12-13]。
|
|
表 1 气液两相流的相关参数 Tab.1 Related parameters of gas-liquid two-phase flow |
上述参数间存在以下关系:
| $ {u_{sl}} = \frac{{{Q_l}}}{A} {u_{sg}} = \frac{{{Q_g}}}{A} ,$ | (6) |
| $ {u_m} = \frac{{{Q_l} + {Q_g}}}{A} = {u_{sl}} + {u_{sg}} ,$ | (7) |
| $ \beta = \frac{{{Q_g}}}{{{Q_l} + {Q_g}}} = \frac{{{u_{sg}}}}{{{u_m}}}。$ | (8) |
选取竖直平面内的弯管作为研究对象,将弯管转弯角度记作
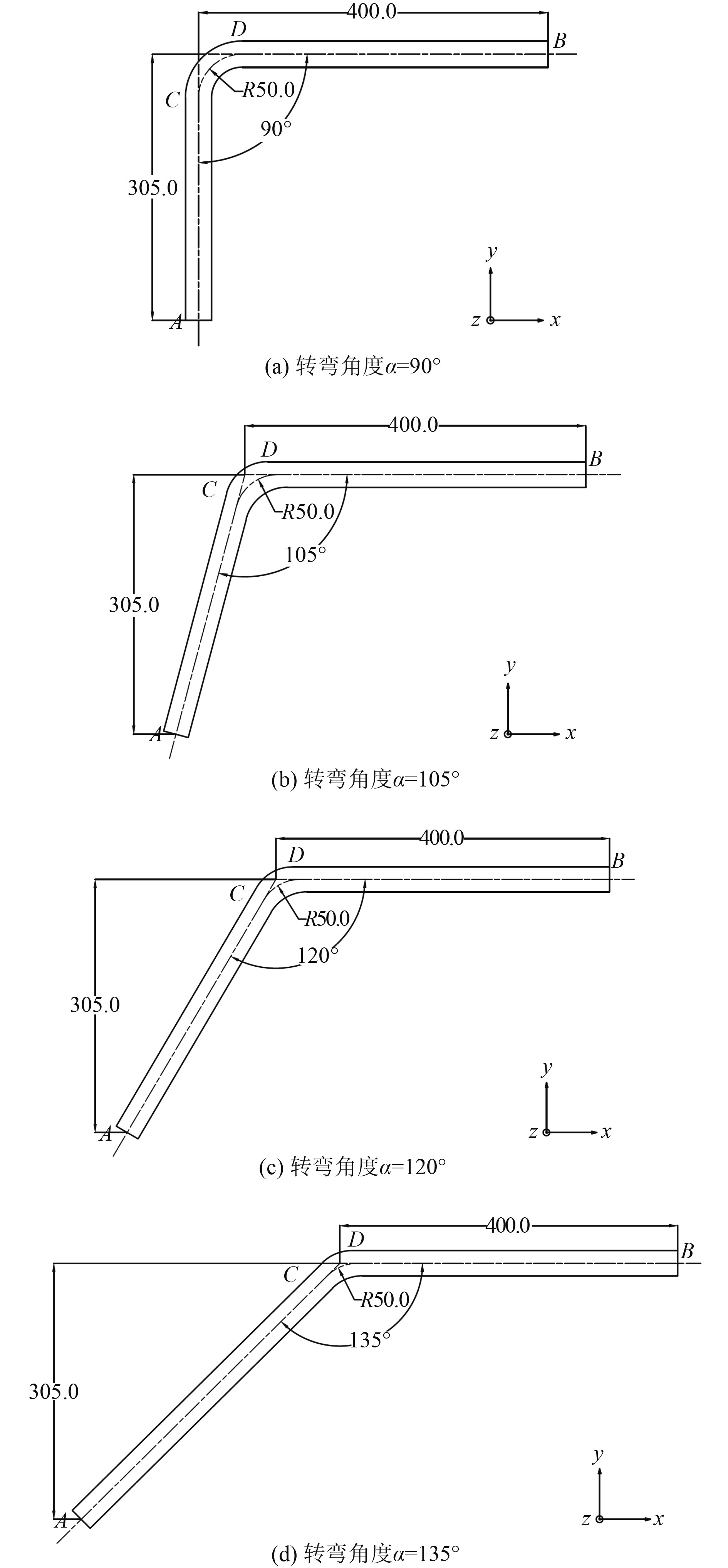
|
图 1
不同转弯角度的竖直弯管示意图
Fig. 1
The diagrammatic drawing of vertical elbows with different turning angel
|
竖直弯管及管道内流的物性参数如表2所示。
|
|
表 2 竖直弯管及管道内流的物性参数 Tab.2 Physical parameters of vertical elbows and internal flow of pipes |
进行气液两相流仿真与管道瞬态响应的耦合计算,分别使用扫掠网格和四面体网格进行结构和流体的网格剖分。在进行数值仿真之前,为获取本文建立的数值模型求解精度受网格密度的影响,以转弯角度
数值仿真工况设置如下:
1)入口采用速度入口边界,气相速度为2 m/s,液相速度为0.8 m/s,气相的入口截面为与管道横截面圆同心且直径为内径一半(即12.7 mm)的圆截面,其体积分数的值为1.0,液相的入口截面为气相入口圆周和管道内径圆周之间的圆环截面,其体积分数的值为1.0,图2为气液两相入口截面示意图。可计算得到仿真入口处气相折算速度

|
图 2 气液两相入口示意图 Fig. 2 The diagrammatic drawing gas-liquid two-phase flow inlet |
出口采用压力出口边界;施加沿Y轴负方向的重力加速度,其值取为9.81 m/s2;管道两端为简支约束,限制其在空间3个自由度的平动运动;管道和流体相互接触的壁面设置为流固耦合交界面。
2)采用标准
在3种网格划分方案下,得到管道结构在弯头监测点的位移响应、速度响应以及加速度响应,并将三者的均方根值作为网格无关性验证的衡量参数。位移响应、速度响应和加速度响应的均方根值分别依照式(9)~式(11)进行计算,90°竖直弯管的网格无关性验证结果如表3所示。
|
|
表 3 转弯角度
|
| $ {d_{RMS}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^n {{d_i}^2} }, $ | (9) |
| $ {v_{RMS}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^n {{v_i}^2} }, $ | (10) |
| $ {a_{RMS}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^n {{a_i}^2} }。$ | (11) |
根据表3,采用3种不同的网格剖分方案,管道结构在两相流激励力作用下的位移响应和速度响应的均方根值差别不大,相对误差均落在13%以内。网格方案2和网格方案3在位移响应这一计算结果上相差仅有1%~2%左右,即当前网格密度下数值计算已达收敛。综合考虑数值计算精度和计算资源,最终采用网格剖分方案2,在该方案下流体域和固体域的有限元模型如图3所示。对于其他转弯角度的竖直弯管均采用了相同方法进行网格无关性验证来选择相对合适的网格密度。
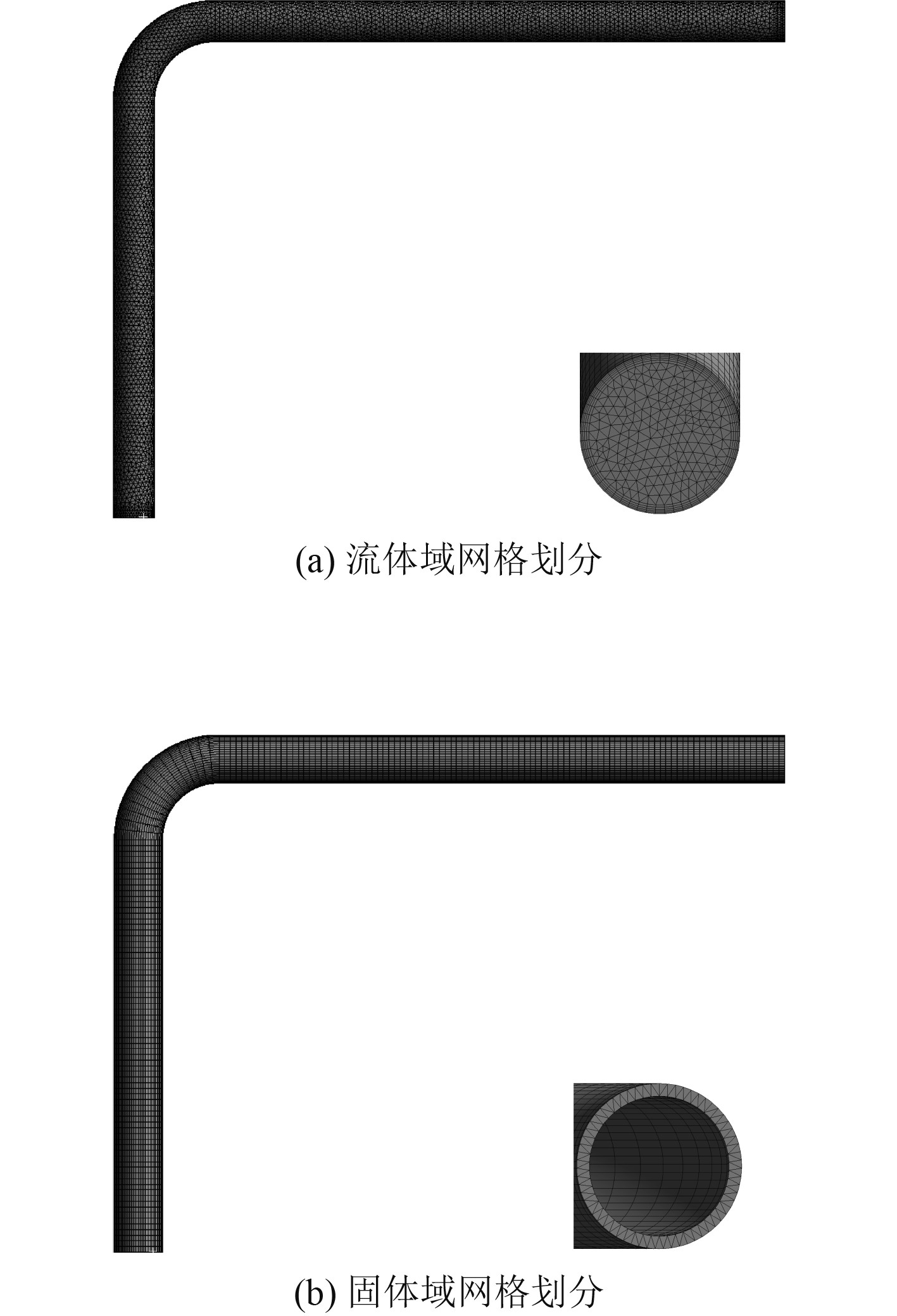
|
图 3 90°竖直弯管有限元模型 Fig. 3 Finite element model of vertical elbows with α=90° |
对于气液两相流诱导振动而言,流型是重要的影响因素,通常情况下气相和液相的速度以及管道实际的布置形式决定了管道内气液两相的分布以及特定流型的产生和发展。为了更直观地观测管道内气液两相流的流型特征,提取不同时刻下管道中剖面上液相的相体积分数云图,如图4所示。
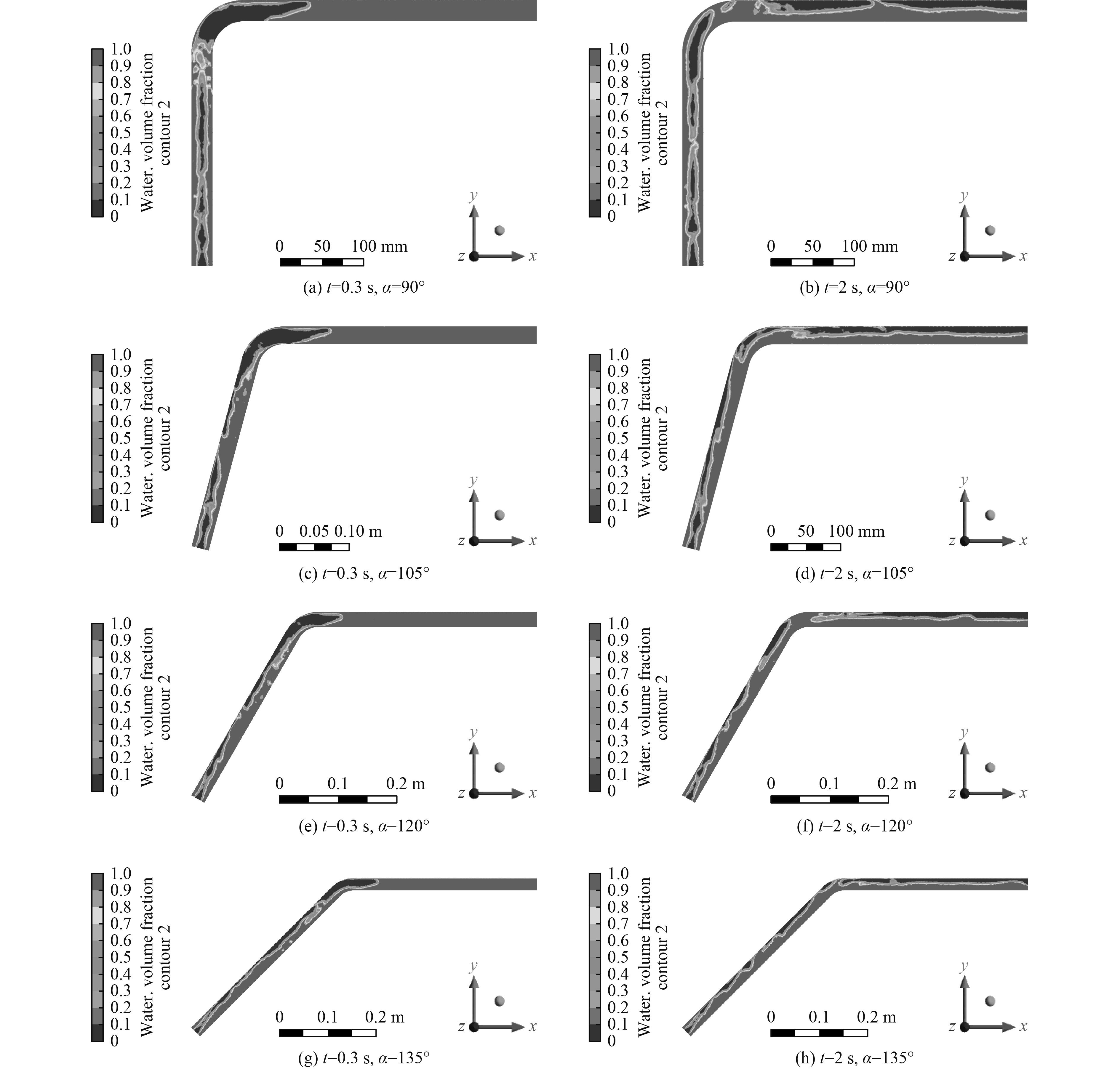
|
图 4 不同转弯角度竖直弯管在不同时刻下管道中剖面液相体积分数云图 Fig. 4 Contour plots of water volume fraction in the middle section of vertical elbows with different turning angles at different times |
可以看出,在气液两相折算速度确定的情况下,相界面的波动与管道布置形式即竖直弯管的转弯角度密切相关。仿真工况的入口边界为环形流边界,由于气相进入管道的实际速度相对较大,是液相进入管道实际速度的2.5倍,在初始时刻产生较大的两相间冲击力,导致相界面产生波动变化。以90°弯管在0.3 s时刻的相体积分数云图(见图4(a))为例,管道竖直管段中产生了多段头部较钝、尾部扁平形如子弹的气泡,由于气相速度较快,在通过弯头区域时快速挤压液相,形成一段较为完整的气泡,气泡在管壁之间则形成很薄的一层液膜。这种气液两相的流动特征在其他转弯角度的竖直弯管中同样清晰可见,不同的是随着转弯角度
气液两相在完全流经竖直弯管后呈现的流型特征也较为统一,在水平管段随着时间推移在重力的作用下逐渐形成波动相界面的分层流;在竖直管段,随着转弯角度
对于不同转弯角度下的竖直弯管,选取管壁弯头区域中间一点作为监测点,提取其振动响应时域数据并得到时域分布曲线。不同转角竖直弯管的振动响应时域分布曲线相类似,以90°竖直弯管为例,其振动位移响应的时域曲线如图5所示。
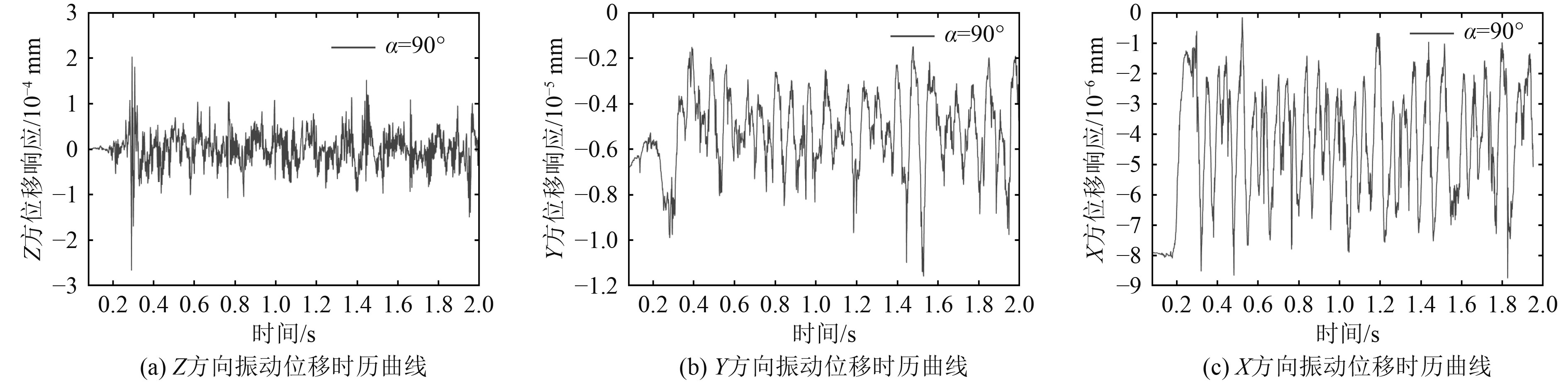
|
图 5 90°竖直弯管弯头监测点处的振动位移时域分布曲线 Fig. 5 Curve of the displacement and time at the monitoring point of vertical elbows with α=90° |
可知,气液两相流在竖直弯管中诱导产生的振动具有高度不稳定特性,在弯头区域会产生较为剧烈的振动,且主要表现为垂向(Z方向)振动。
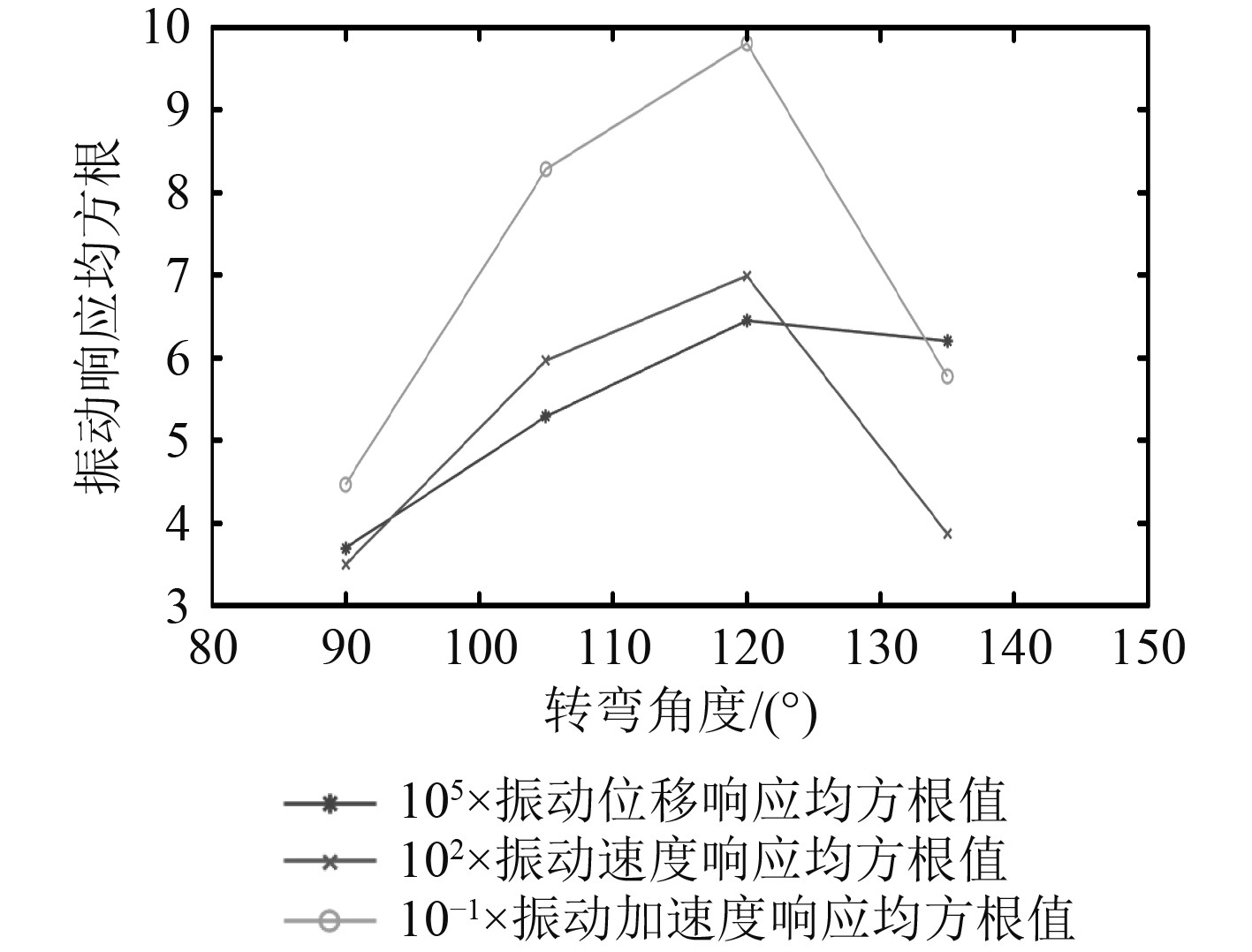
计算不同转弯角度竖直弯管监测点处的振动位移、振动速度以及振动加速度的均方根值,结果如表4所示。图6给出了管道振动响应均方根值随管道转弯角度变化的趋势。
|
|
表 4 不同转弯角度竖直弯管的振动响应均方根值 Tab.4 Root mean square value of vibration response of vertical elbows with different turning angles |
|
图 6 管道振动响应随转弯角度变化曲线 Fig. 6 Curve of the flow-induced vibration response and time at the monitoring point |
根据表4和图6的仿真计算结果可以得出,随着转弯角度的增大,竖直弯管的振动响应即位移、速度和加速度响应幅值的均方根值均呈现出先增大后减小的趋势,这也与气液两相流在不同转弯角度竖直弯管中的流型分布特征相吻合。
4 结 语本文基于流固耦合方法针对气液两相流在竖直弯管内的诱导振动进行数值仿真和研究,探讨管道布置形式即管道转弯角度对于气液两相流流型以及管道振动响应的影响,可以得到以下结论:
1)通过CFD仿真以及结构瞬态响应仿真的耦合计算对气液两相管道内流诱导振动进行模拟是可行的,流固耦合计算可以实现对两相流的流型进行判断以及对结构的振动响应进行前期预判。
2)竖直弯管转弯角度增大幅度较小时,如从90°增大到105°和120°,气液两相流相界面的波动会更为剧烈,在倾斜管段更易产生不连续的气泡,在弯头处气液两相之间的挤压冲击作用更加显著;当转弯角度继续增大,气液两相在整个管段均相对连续,弯头处的相间挤压冲击作用相对平缓。
3)气液两相流在竖直弯管中诱导产生的振动具有高度随机性和不稳定性,随着转弯角度的增大,管道振动响应均方根值均呈现出先增大后减小的趋势,这与气液两相流的流型转化密切相关。
| [1] |
徐丽琼. 船舶输流管道系统的振动研究[D]. 武汉: 武汉理工大学, 2009.
|
| [2] |
卢嘉伟. LNG管内流体诱导振动以及影响因素分析研究[D]. 武汉: 武汉理工大学, 2018.
|
| [3] |
MIWA S, MORI M, HIBIKI T. Two-phase flow induced vibration in piping systems[J]. Progress in Nuclear Energy, 2015, 78(jan.): 270-284. |
| [4] |
张涛, 方舟, 董皓, 等. 含气率对长圆管内气液两相流流场特性的影响[J]. 西安工业大学学报, 2019, 39(3): 273-277. DOI:10.16185/j.jxatu.edu.cn.2019.03.006 |
| [5] |
RIVERIN J L, PETTIGREW M J. Vibration excitation forces due to two-phase flow in piping elements[J]. 2007.
|
| [6] |
张红艳, 白长青, 吴伟阳, 等. 气液两相段塞流作用下管道流固耦合动力学分析[J]. 应用力学学报, 2017, 34(146): 63-67+215-216. |
| [7] |
马晓旭, 田茂诚, 张冠敏, 等. 水平管内气液两相流诱导振动的数值研究[J]. 振动与冲击, 2016, 35(16): 204-210. DOI:10.13465/j.cnki.jvs.2016.16.033 |
| [8] |
蔡标华, 方超, 马士虎, 等. 流固耦合作用下的注水管路流激振动噪声数值模拟[J]. 舰船科学技术, 2020, 42(7): 118-122. DOI:10.3404/j.issn.1672-7649.2020.04.023 |
| [9] |
宋学官, 蔡林, 张华. ANSYS流固耦合分析与工程实例[M]. 北京: 中国水利水电出版社, 2012.
|
| [10] |
ZHANG H, BATHE K J. Direct and iterative computing of fluid flows fully coupled with structures[C]//Computational Fluid and Solid Mechanics, 2001.
|
| [11] |
BATHE K J , HOU Z , JI S . Finite element analysis of fluid flows fully coupled with structural interactions[J]. Computers & Structures, 1999, 72(s 1–3): 1–16.
|
| [12] |
国丽萍, 刘承婷, 刘保君. 石油工程多相流体力学[M]. 北京: 中国石化出版社, 2011.
|
| [13] |
BRENNEN C E . Fundamentals of Multiphase Flow[M]. Cambridge University Press, 2005.
|
 2022, Vol. 44
2022, Vol. 44
