2. 中国船舶科学研究中心,江苏 无锡 214082
2. China Ship Scientific Research Center, Wuxi 214082, China
入水冲击问题具有广泛的工程应用背景,如船舶航行受浪砰击,海洋工程结构物下水安装,救生艇自由降落释放,导弹、鱼雷入水等。随着海洋工程计算和武器装备的发展,入水冲击问题的研究受到持续关注。入水冲击作为一个复杂的物理现象[1],伴随着流固耦合作用,而高速入水大大加剧了流固耦合的复杂程度,同时结构物撞水瞬间受到的砰击载荷可能导致结构运动变化和结构变形失效。因此有必要考虑流固耦合作用,分析入水结构的动态响应,为结构物高速入水设计提供参考。
对于入水冲击问题,国内外学者做了大量研究。1929年,Von Karman[2]首先引入附加质量的概念,推导计算出二维楔形体入水冲击载荷,奠定了入水冲击理论计算的基础。Wagner[3]在1932年,针对楔形体入水冲击问题提出了小倾角平板近似理论,通过求解伯努利方程计算出二楔形体入水过程中的压力分布。后续学者在二者的研究基础上,通过试验、数值计算等方式对入水冲击问题开展了广泛研究。Worthington[4]采用高速摄影技术,最早记录了小球入水的流场演变情况,分析了空泡的变化规律。MAY[5- 6]开展了不同形状参数和入水速度的试验,研究了结构物入水过程中的载荷特征。顾建农[7]开展了弹体高速入水试验,分析了形状参数和入水初速度对弹道特征和运动特性的影响。张伟[8]通过试验分析了不同头型弹体入水的弹道稳定性,得到了弹体入水速度衰减公式。
数值计算成本较低且不受场地、设备等现实条件限制,可较为准确地预报入水过程中结构和流场的变化情况,逐渐成为研究入水冲击问题的关键方法之一。陈震[9]开展了船舶在波浪中出入水的数值模拟,分析了入水运动参数对抨击压力的影响。何春涛[10]采用有限体积法,建立了结构物垂直入水的计算模型,对比试验结果分析了入水的运动轨迹和空泡闭合规律。马庆鹏[11]采用VOF方法开展了不同入水速度下回转体的数值计算,研究了入水冲击载荷变化规律以及侵水深度和空泡发展的关系。李强[12]基于Ls-dyna软件计算了鱼雷入水过程,分析了不同头型参数对鱼雷水下运动的影响。杨力[13]采用ALE方法,分析了平底结构入水过程中质量、刚度对砰击压力的影响。路丽睿[14]基于RANS方程采用动网格技术,模拟了凹形体入水过程,分析了液体喷溅对角运动的影响。
目前针对结构入水的研究多集中于刚体低速入水,主要关注入水运动轨迹和空泡演变规律,考虑流固耦合的高速入水研究较少。本文进行回转体高速入水流固耦合数值计算,分析回转体高速入水的运动特性和结构响应,其结果可以为结构物高速入水的预报提供参考。
1 流固耦合计算模型采用光滑粒子流体动力学(SPH)和有限元(FEM)耦合方法对高速入水过程进行模拟,其中模回转体模型采用有限元Lagrange网格,水域采用SPH粒子。FEM 方法在计算结构运动和动力响应方面, 具有更高的精度和效率;SPH 方法中计算域使用粒子形式表示,无需网格划分,在此计算介质大变形,可以有效避免有限元方法中网格畸变等情况。FEM/SPH 耦合可发挥两者优势,在计算入水冲击等介质大变形的动力问题上,具有较好的准确性和较高计算效率。
1.1 SPH方法基本理论SPH方法使用粒子分布表达计算域,采用核函数近似的方式将求解的偏微分方程转换为积分形式,使用粒子近似的方式将核函数方程离散化,通过求解离散方程得到粒子场内变量。
在SPH方法中,给定任意一个函数f(x),其积分表达形式如下:
| $ f(x) = \int\limits_\varOmega {f(x')} \delta (x - x'){{\rm{d}}x}', $ | (1) |
式中:
| $ \delta (x - x'){\text{ = }}\left\{ \begin{gathered} 1,{\text{ }}x = x{'} , \\ 0,{\text{ }}x \ne x{'}。\\ \end{gathered} \right. $ | (2) |
由上式可知,任意连续函数f (x)采用狄拉克函数可以表示为以下积分形式:
| $ \left\langle {f(x)} \right\rangle = \int\limits_\varOmega {f(x')} W(x - x',h){{\rm{d}}x}' 。$ | (3) |
式中:
根据分布积分和散度定理,可以将上式进行变换:
| $ \left\langle {\nabla \cdot f(x)} \right\rangle = - \int\limits_\varOmega {f(x')} W(x - x',h){{\rm{d}}x}' 。$ | (4) |
最后,将变换后的函数进行离散化处理,得到域内所有粒子叠加的离散形式:
| $ \left\langle {\nabla \cdot f({x_i})} \right\rangle {\text{ = }}\sum\limits_{j = 1}^N {\frac{{{m_j}}}{{{\rho _j}}}} f({x_j}) \cdot \nabla {W_{ij}} 。$ | (5) |
式中:i和j为粒子编号;m和ρ为粒子的质量和密度;N为粒子总数 。
| $ {W_{ij}} = W({x_i} - {x_j},h) = W(\left| {{x_i} - {x_j}} \right|,h) 。$ | (6) |
所以,在SPH方法中对于基本控制方程可以表示为如下离散形式:
| $ \left\{ \begin{gathered} \frac{{{\rm{d}}{\rho _i}}}{{{\rm{d}}t}} = \sum\limits_{j = 1}^N {{m_j}\left(\nu _i^\beta - \nu _j^\beta \right)\frac{{\delta {W_{ij}}}}{{\delta x_i^\beta }}} , \\ \frac{{{\rm{d}}\nu _i^\alpha }}{{{\rm{d}}t}} = \sum\limits_{j = 1}^N {{m_j}\left(\frac{{\sigma _i^{\alpha \beta }}}{{\rho _i^2}} + \frac{{\sigma _j^{\alpha \beta }}}{{\rho _j^2}} + \prod\nolimits_{ij} {} \right)\frac{{\delta {W_{ij}}}}{{\delta x_i^\beta }}} , \\ \frac{{{\rm{d}}e_i^{}}}{{{\rm{d}}t}} = \frac{1}{2}\sum\limits_{j = 1}^N {{m_j}\left(\frac{{p_i^{}}}{{\rho _i^2}} + \frac{{p_j^{}}}{{\rho _j^2}} + \prod\nolimits_{ij} {} \right)\left(\nu _i^\beta - \nu _j^\beta \right)\frac{{\delta {W_{ij}}}}{{\delta x_i^\beta }}} , \\ \frac{{{\rm{d}}x_i^\alpha }}{{{\rm{d}}t}} = \nu _i^\alpha 。\\ \end{gathered} \right. $ | (7) |
在入水过程中, 实现结构体和水中介质耦合作用,需要在SPH-FEM耦合方法中,将网格和粒子之间的界面进行处理。结构体网格和水粒子之间需要采用接触算法进行相应的计算处理。
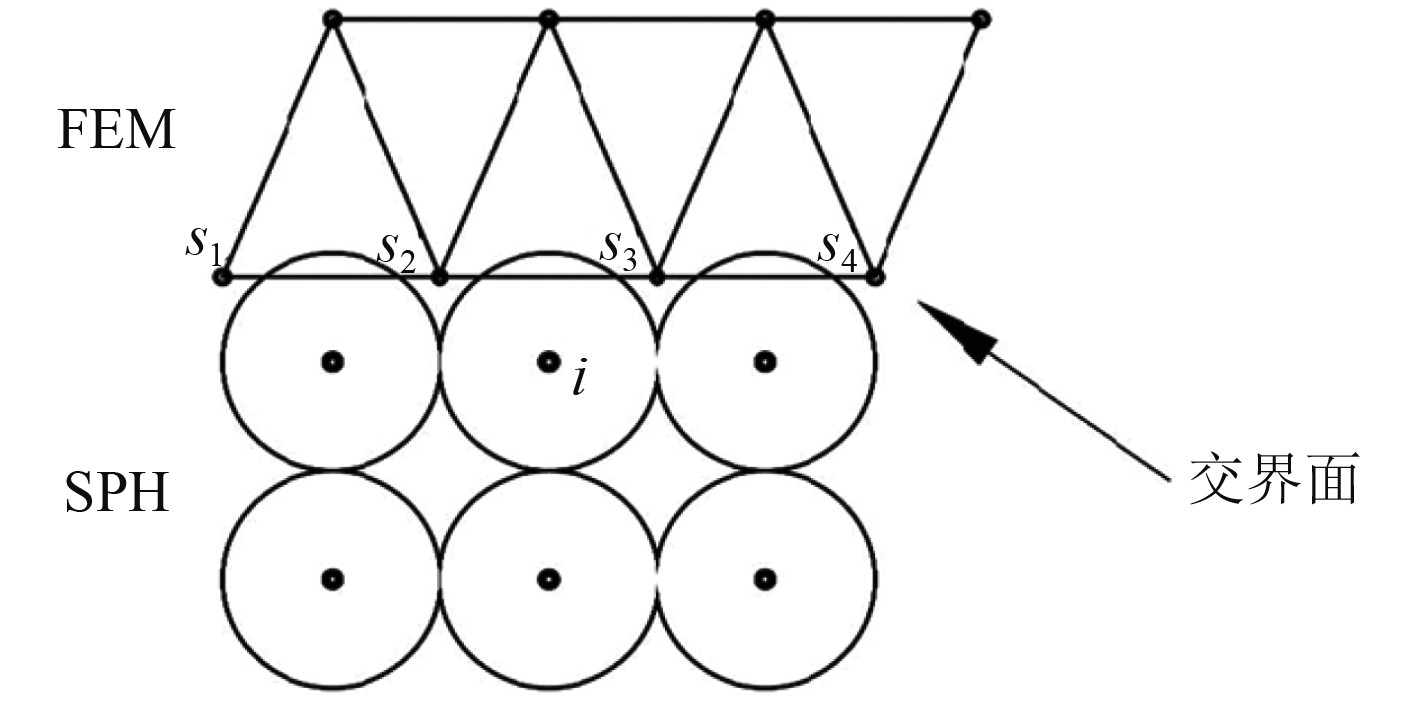
|
图 1 有限元网格和SPH粒子耦合界面 Fig. 1 Coupling interface of FEM and SPH |
在接触算法中,每一时间步内计算有限元网格节点穿过SPH粒子的距离,罚函数根据有限元网格和SPH粒子间的穿透距离计算出两者之间的接触力,通过接触力实现两者之间的相互作用,接触力将SPH粒子拉出交界面,避免SPH粒子穿越有限元网格,导致计算失效。
1.3 计算模型设置在计算模型中,回转体最大直径 120 mm,头部直径 100 mm,回转体长度为0.5 m,结构厚度为5 mm,其首端倾斜斜面与回转体头部平面所呈角度为 93.18°,入水速度为100 m/s,采用有限元网格进行划分。水域尺寸为 1.2 m×1.2 m×3.6 m,采用SPH粒子表示,回转体外形及流域如图2所示。

|
图 2 计算域设置 Fig. 2 Computational domain settings |
SPH粒子数为1536000,使用 Gruneisen 状态方程控制,回转体采用4节点壳单元,网格数量为520000,材料模型考虑弹性和塑形,材质为45号钢材,材料性能参数见表1。
|
|
表 1 材料模型参数 Tab.1 Material parameters |
首先进行回转体入水速度变化分析并与理论公式对比,验证计算方法的准确性。假设物体在入水过程中空泡内部和外部压力差保持一致,在空化数不为定值的情况下,存在如下规律:
| $ \sigma {\text{ = }}\frac{{\Delta p}}{{{\rho _w}\nu _p^2/2}} = \frac{{{\rho _w}gh + {C_a}{\rho _{\text{a}}}v_0^2/2}}{{{\rho _w}\nu _p^2/2}} = \frac{{{C_a}{\rho _a}}}{{{\rho _w}}}\frac{{v_0^2}}{{\nu _p^2}} = {\sigma _0}\frac{{v_0^2}}{{\nu _p^2}} 。$ | (8) |
式中:Δp 为空泡内外压力差;Ca为气流压力降系数;σ0 为初始空化数;σ0 = 0.006−0.018 ;ρa为空气密度;ρw为水密度;v0为入水初速度;vp为入水后速度。
阻力系数与空化数关系:
| $ {C_d} = {C_p}(1 + \sigma ) ,$ | (9) |
忽略重力的情况下,入水运动方程为:
| $ {m_p}{\text{ = }}\frac{{{\rm{d}}{v_p}}}{{{\rm{d}}t}} = - \frac{1}{2}{\rho _w}{A_0}{C_d}v_p^2 。$ | (10) |
式中:mp为物体的质量;A0为触水面积。
通过式(9)和式(10),可得到速度衰减公式:
| $ {v_p} = \sqrt {{\sigma _0}} {v_0}\tan \left( {\arctan \left( {\frac{1}{{\sqrt {{\sigma _0}} }}} \right) - k\sqrt {{\sigma _0}} {v_0}t} \right) 。$ | (11) |
式中:衰减系数 k = ρwA0C0/ 2mp 。
图3为衰减公式与数值计算得到的速度曲线。可以看出,触水瞬间回转体高速撞击水面受到极大的瞬间冲击载荷,速度衰减剧烈,随着入水进程加深,速度衰减减弱,最后近似线性衰减。计算得到的速度曲线与公式曲线具有好的一致性,验证了SPH-FEM 耦合计算模型在计算高速入水方面的有效性。
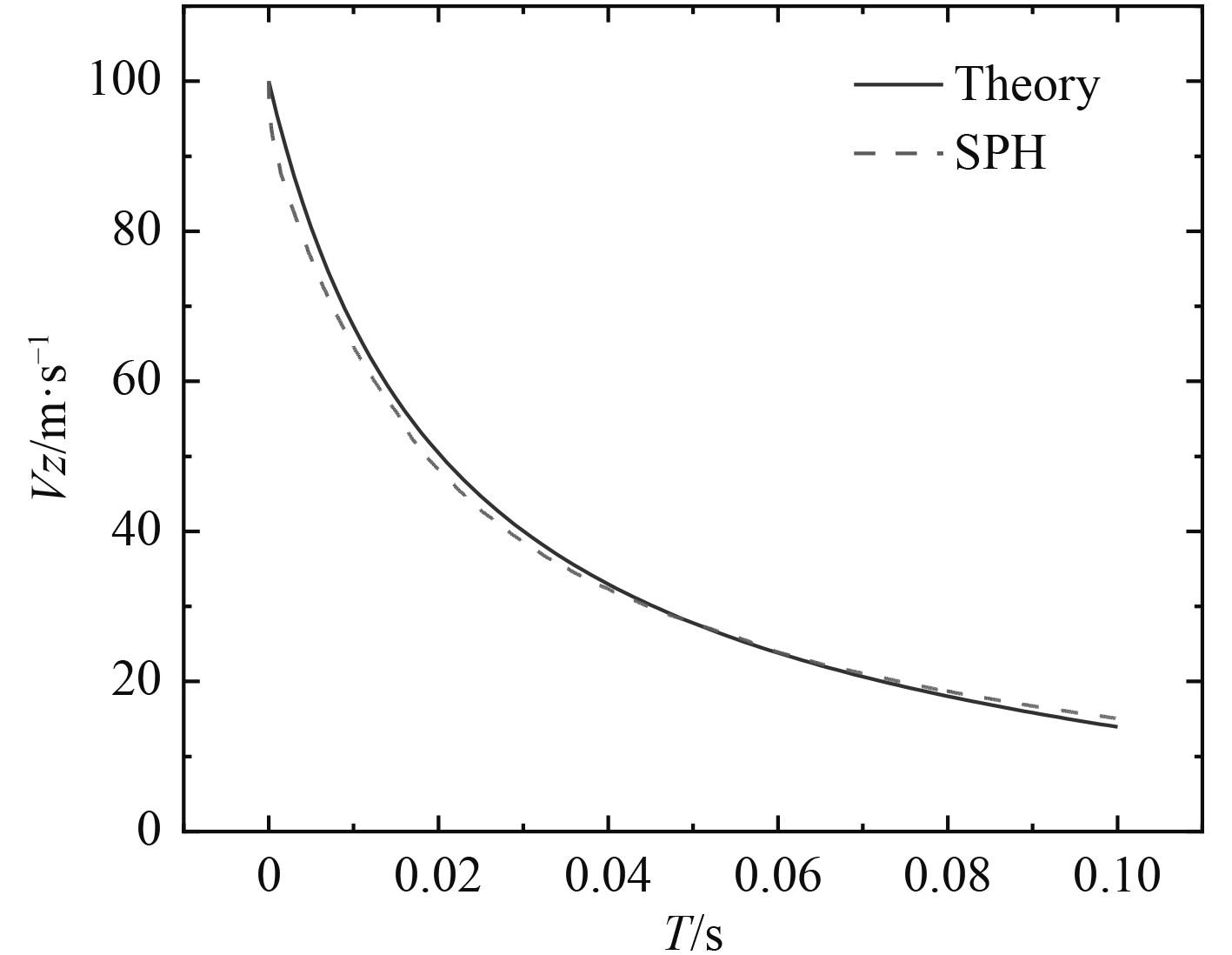
|
图 3 回转体速度衰减曲线对比图 Fig. 3 Curve of velocity attenuation comparison |
王珂[15]拟合了回转体入水抨击压强峰值,入水过程中回转体头部中心处峰值压强可以表示为:
| $ p = {\rho _w}{k_d}{k_e}{k_v} 。$ | (12) |
式中:
由式(11)可以计算出回转体入水头部中心错误压力峰值为1.73×108 Pa,采用SPH-FEM耦合计算得到的回转体头部中心处压力情况如图4所示,其峰值为 1.92×108 Pa。可以看出,数值计算得到的回转体头部中心处压力峰值与文献公式计算结果接近,数值计算结果稍大。在数值计算过程中未充分考虑高速入水过程中压缩空气的影响,导致结果略微偏大。高速入水是一个涉及气-液-固三相耦合的瞬时冲击问题,空气高速压缩带来的空气垫效应一直作为数值计算中的难点,在未来具有广阔的研究空间。
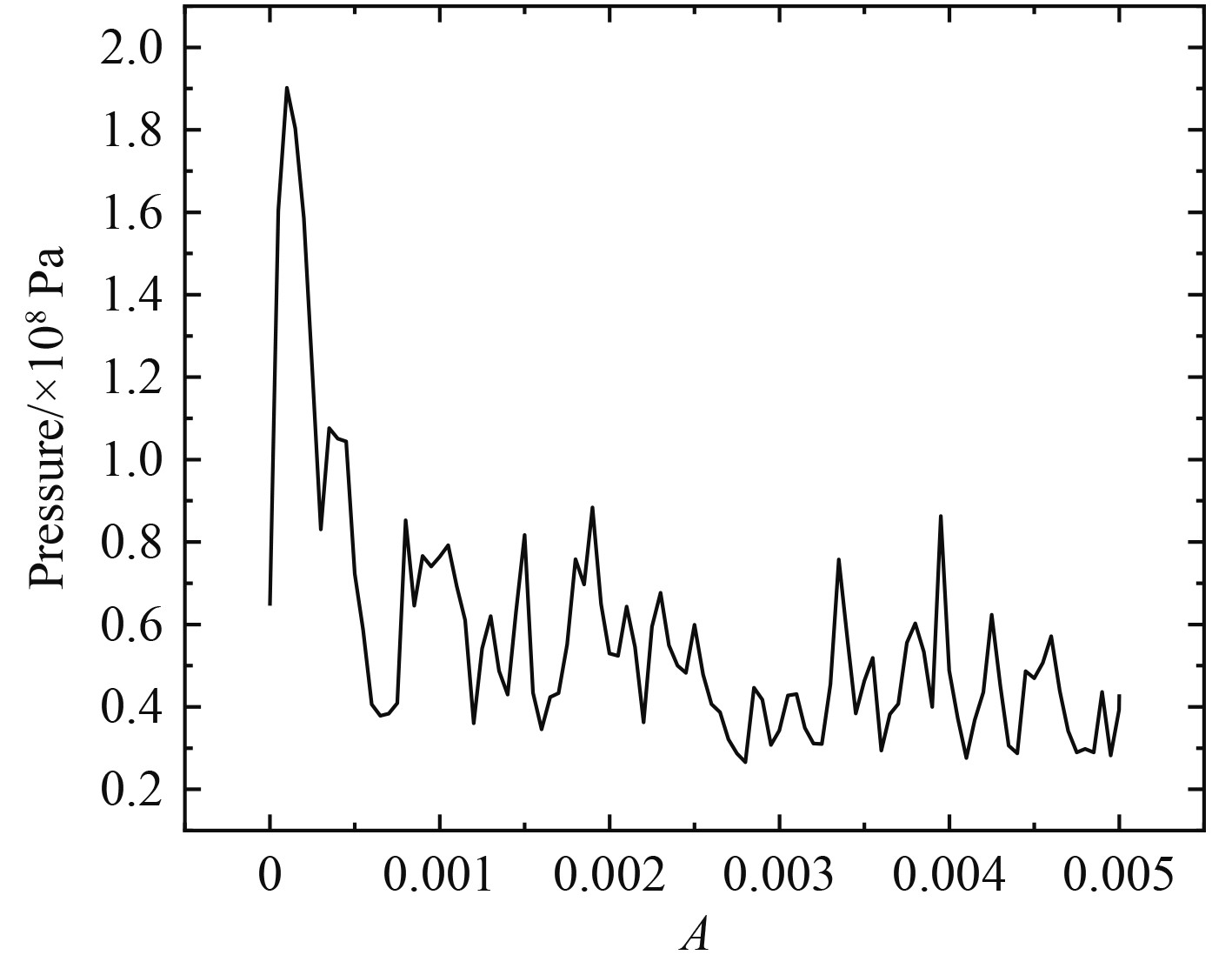
|
图 4 回转体中心单元压力图 Fig. 4 Pressure intensity curve in the central head region of the revolution body |
图5给出了入水过程中回转体垂直方向受力情况。从图中可以看出,撞水瞬间回转体头部受到的冲击力急剧增加,在毫秒量级时间达到峰值,峰值为1.37×108 N ,头部触水后,峰值迅速下降,随着回转体完全进入水面,冲击力呈小幅度震荡衰减,逐渐趋于稳定。
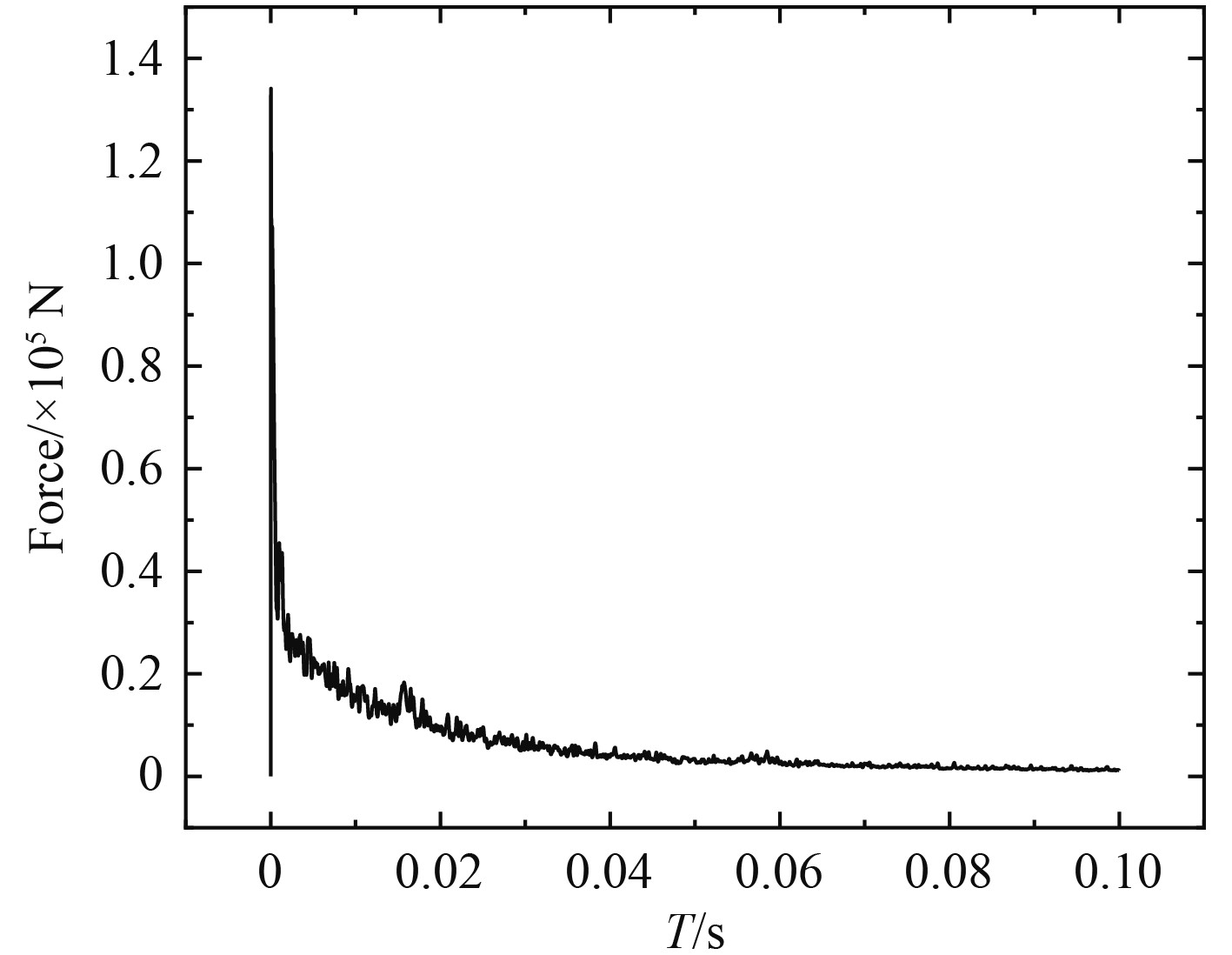
|
图 5 回转体沿轴向受力图 Fig. 5 Curve of the axial force of the revolution body |
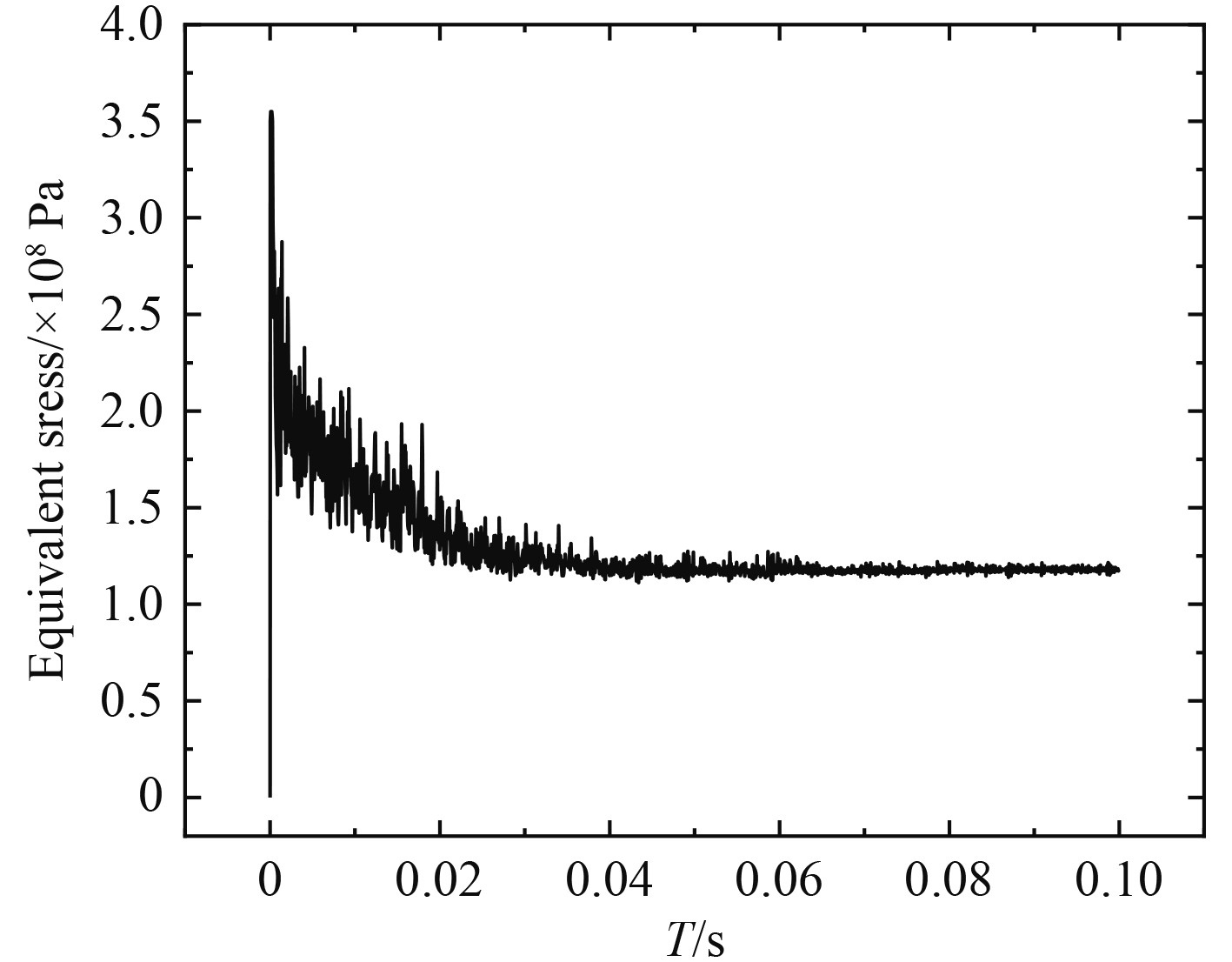
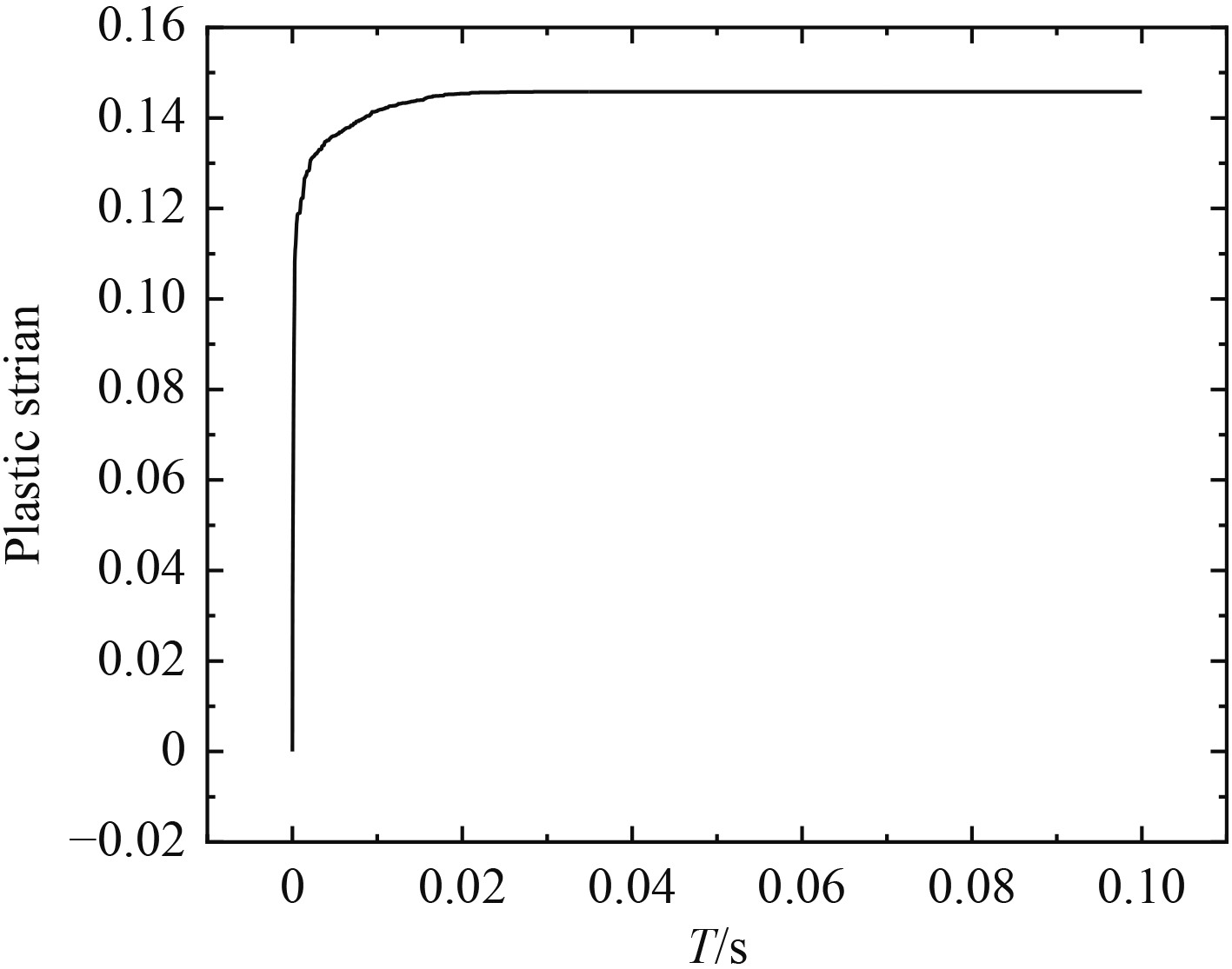
高速入水过程中,撞水初期会产生瞬时巨大冲击力,可能导致结构变形甚至失效,因此有必要研究入水冲击的结构强度问题。图6为回转体头部中心单元的等效应力曲线,图7给出了回转体头部中心单元的塑形应变曲线。本次计算考虑流固耦合效应,物体撞水后会产生变形缓冲抨击,变形呈反复状态。在应力曲线上表现为:出现瞬时峰值后,应力衰减呈现波动震荡形式,随着入水进程加深,震荡的频率和幅度减小,伴随着整个入水进程。在100 m垂直入水情况下,回转体头部中心处应力峰值迅速达到材料的屈服应力 355 MPa,材料发生塑形应变,塑性应变值0.146,虽然未出现破坏现象,但是在设计过程中有必要加强结构物触水位置处的结构强度,避免结构失效。
|
图 6 回转体头部单元等效应力曲线 Fig. 6 Equivalent stress curve of the central element of the revolution body head |
|
图 7 回转体头部单元塑形应变曲线 Fig. 7 Plastic strain curve of the central element of the revolution body head |
入水空泡形态是研究空泡问题的关键,研究入水空泡动力学问题在基于一定的假设条件下可以推导出在入水过程中的侵彻距离与空泡半径的函数关系。此时假定入水过程中的能量流失转化为回转体周围空泡区域的流体动能和空泡介质势能。利用分布点源理论推导出回转体周围流体动能为:
| $ {\rm{d}}{E}_{k}=\pi {\rho }_{w}N{(R\stackrel{·}{R})^{2}}{\rm{d}}x 。$ | (13) |
式中:R为空泡半径;N为无量纲系数,在忽略重力作用下,对有限长度的平头回转体,其空泡内势能
| $ \begin{split}{\rm{d}}{E}_{p}=&\left({\displaystyle {\int }_{{t}_{0}}^{t}\Delta p2\pi R\stackrel{·}{R}{\rm{d}}t}\right){\rm{d}}x=\left({\displaystyle {\int }_{{t}_{0}}^{t}\Delta p\stackrel{·}{S}}dt\right){\rm{d}}x=\\ &\Delta p\left({S}_{t}-{S}_{{t}_{0}}\right){\rm{d}}x 。\end{split} $ | (14) |
式中:
| $ \frac{{{\rm{d}}E}}{{{\rm{d}}{x_p}}} = - m{v_p}\frac{{{\rm{d}}{v_p}}}{{{\rm{d}}{x_p}}} = \frac{1}{2}{\rho _w}{A_0}{C_d}(v){v_p}^2 。$ | (15) |
在忽略入水初始阶段入水速度的影响下,同时根据能量守恒原理有:
| $ {\text π} {\rho }_{w}N{(R\stackrel{·}{R})}^{2}+\Delta p\left({S}_{t}-{S}_{{t}_{0}}\right)=\frac{1}{2}{\rho }_{w}{A}_{0}{C}_{d}{v}_{p}^{2}。$ | (16) |
通过式(12)~式(16),同时应用入水速度关系式
| $ R(x) = {\left[ {R_0^2 + 2{R_0}\sqrt {\frac{{{C_d}}}{{2N}}} \left( {x - {x_0}} \right) - \frac{\sigma }{{2N}}{{\left( {x - {x_0}} \right)}^2}} \right]^{1/2}}。$ | (17) |
式中:
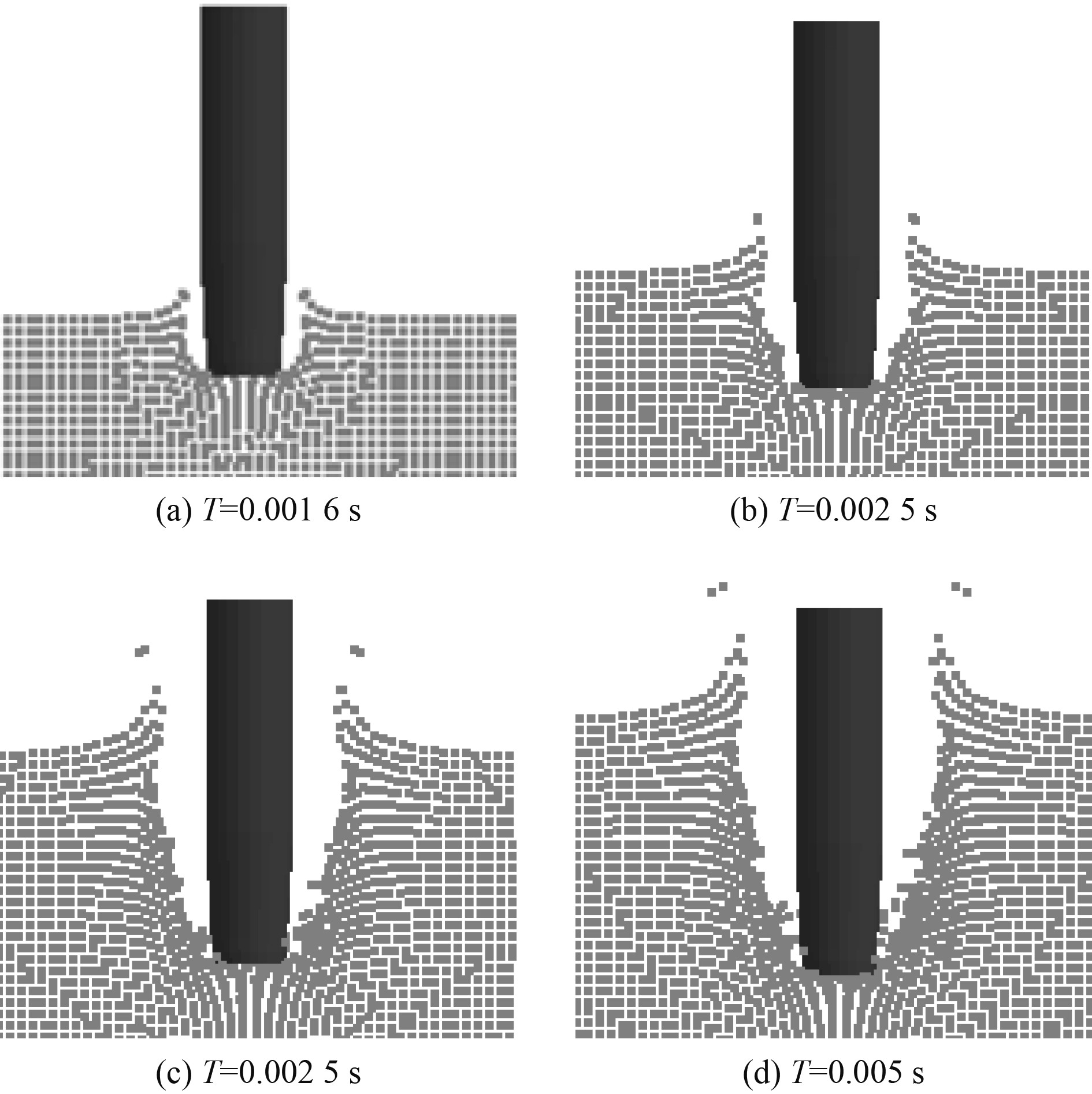
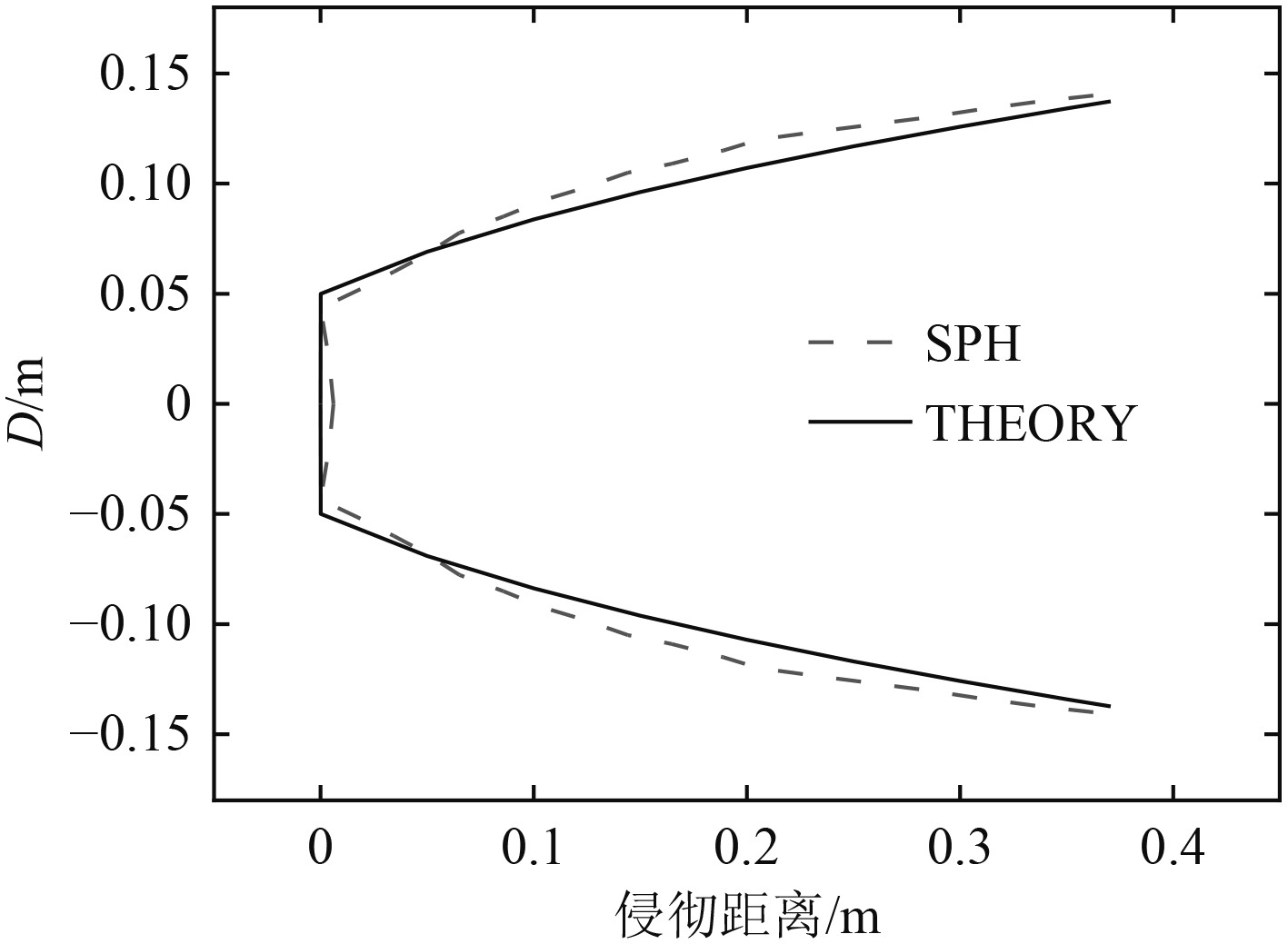
在得到图8各个时刻回转体入水空泡体积分数的前提下,提取回转体入水的最终状态即0.005 s时刻的空泡气-液交界面轮廓,同时利用式(17)的空泡半径与侵彻距离公式关系,取变量数值N=2。对比数值模拟和理论计算得到的空泡尺寸轮廓如图9所示。从图中可以看出2条曲线表征的空泡尺寸吻合较好,证明了数值模拟中计算空泡的准确性。
|
图 8 回转体入水开空泡过程 Fig. 8 Cavity feature during the water-entry process |
|
图 9 回转体泡轮廓与理论模型对比 Fig. 9 Comparison of the cavity model with the simulation |
另一方面,理论公式为刚体入水计算结果,而本次数值计算考虑到材料的弹塑性,更加接近于实际情况。由于回转体在入水过程中存在变形,可以看出2条空泡轮廓曲线存在一定的差别。弹性体入水的首端空泡尺寸相比刚体结果较小,回转体头部为入水过程中变形最明显的区域,在入水过程中,头部的变形使流体进入内凹区域,导致弹性体的入水空泡形状首部区域不再是平面,使其首部的直径变小,随着入水进程加深,后体区域的尺寸差异随空泡直径的增大逐渐减小。
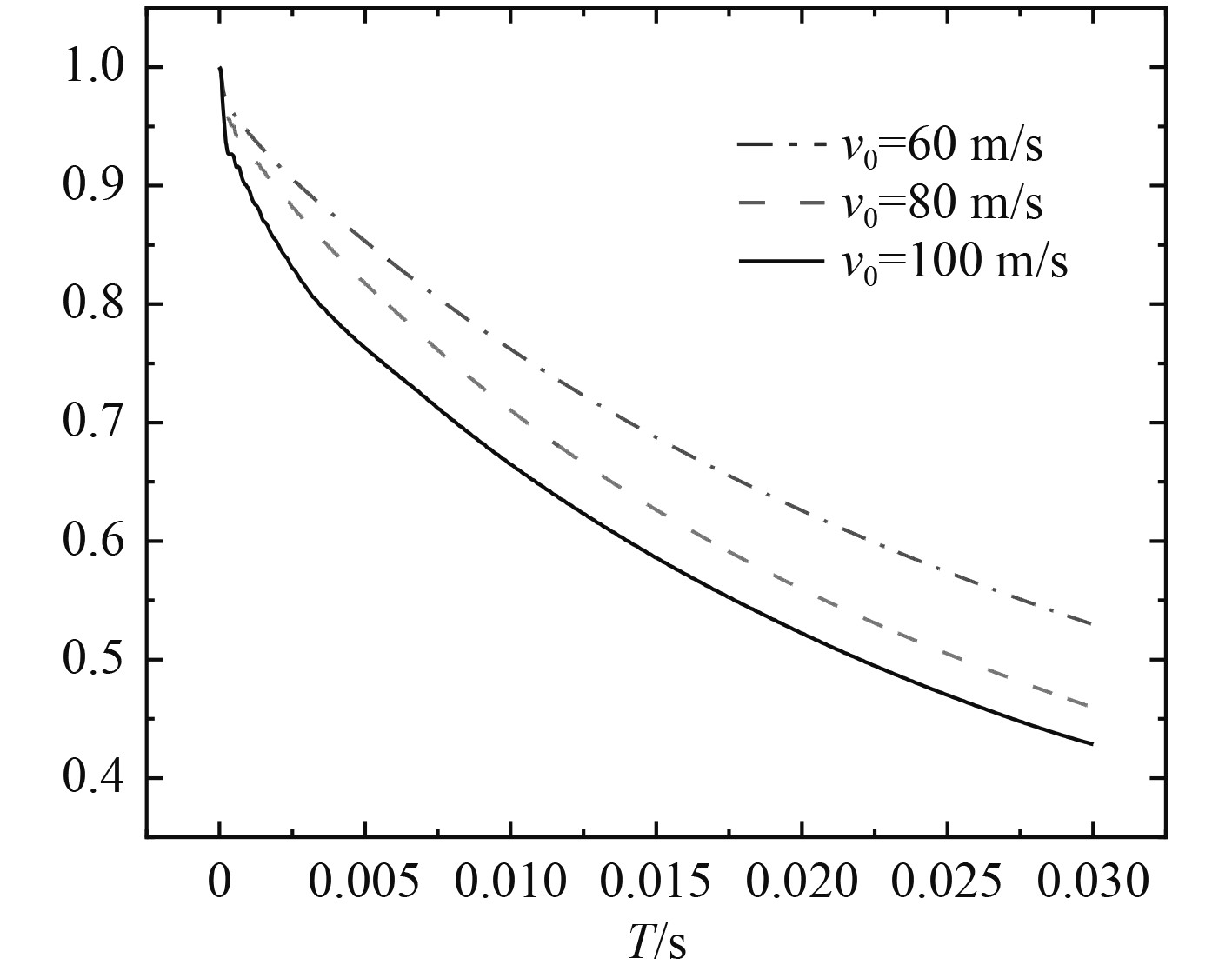
2.4 入水速度对入水进程的影响为进一步探究入水速度的影响,开展回转体以60 m/s,80 m/s,100 m/s速度条件下的计算。表2给出了不同入水速度下回转体头部中心处压力峰值,图10为不同入水初速度下的归一化速度曲线。可以看出,回转体入水初期受到极大的冲击力,速度衰减剧烈,之后冲击力迅速降低,回转体速度衰减程度放缓明显,最后速度衰减表现为类似线性变化。回转体速度衰减情况受初速度影响,初速度越大速度衰减程度越大,随着入水进程加深,不同初速度下的回转体速度衰减程度接近,趋于稳定。
|
|
表 2 回转体头部中心压力峰值 Tab.2 Results of pressure peak of cylinders head central point |
|
图 10 归一化速度衰减曲线 Fig. 10 Curve of normalizes velocity attenuation |
回转体入水阻力系数计算公式[17]为:
| $ {C_d}{\text{ = }}\dfrac{F}{{\dfrac{1}{2}\rho {v^2}A}}。$ | (18) |
其中:
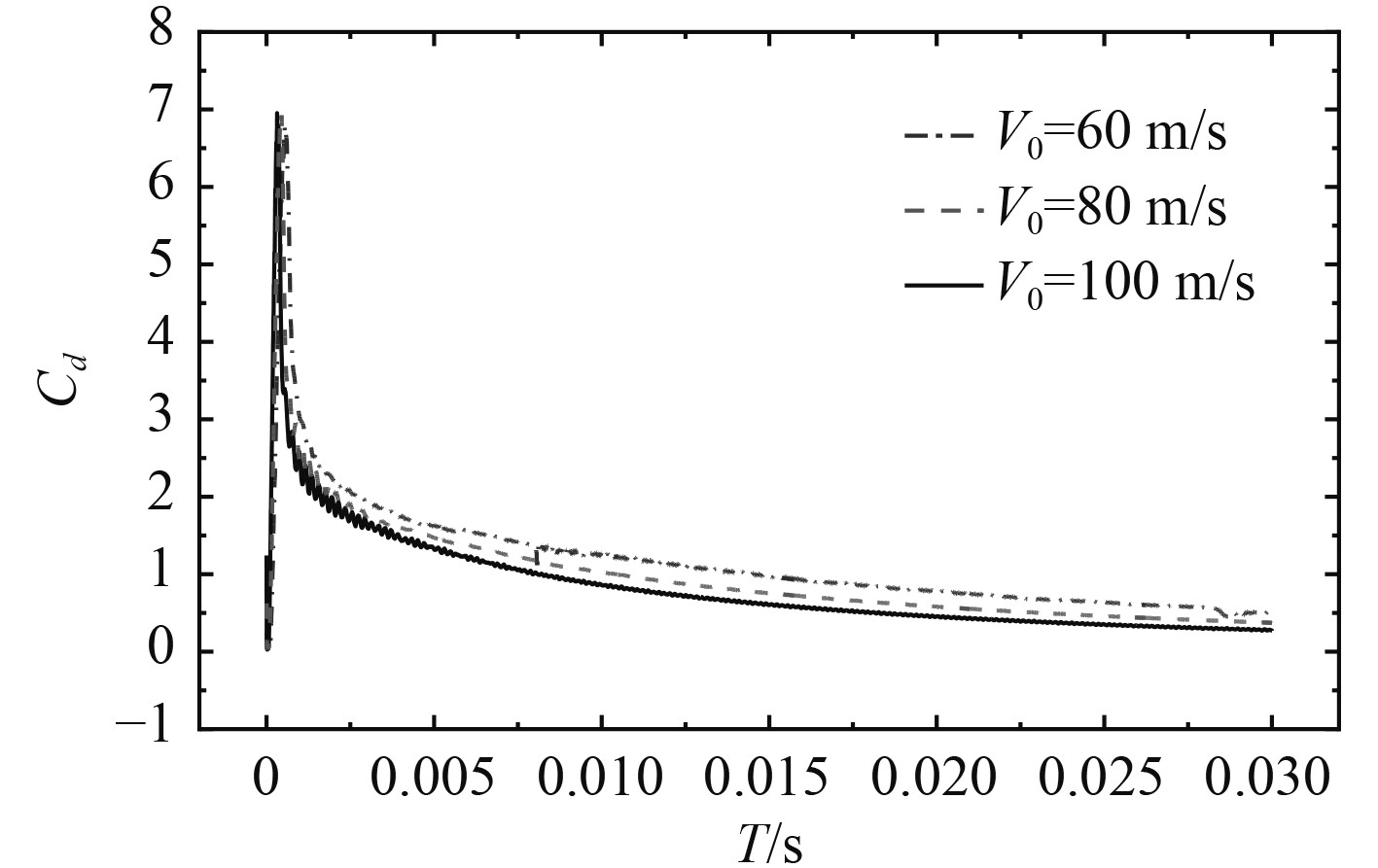
图11为初速下回转体入水的阻力系数曲线。可以看出,在不同入水速度下回转体阻力系数变化情况趋于一致,阻力系数峰值接近,入水速度越大,峰值持续时间越短,随着入水进程发展,流动稳定,3种情况的阻力系数值保持接近。由此可见,入水初速度对回转体阻力系数的影响不明显。
|
图 11 阻力系数曲线 Fig. 11 Curve of Cd with different velocity |
本文采用SPH-FEM耦合方法对回转体高速入水过程进行数值分析,得到以下结论:1)通过与速度衰减和回转头部压力峰值的理论公式对比,表明SPH-FEM耦合方法可以较为准确地预报回转体高速入水过程中的运动及动力特征,可以较好地解决数值计算过程中由于流体介质不连续变形带来的计算困难等问题。
2)回转体触水瞬间产生应力峰值,出现时间极短,受变形影响,随后应力衰减呈现波动震荡形式,其头部中心处应力峰值超过了材料的屈服应力,材料发生塑形应变,在设计上可考虑对头部结构进行加强。
3)数值计算中得到的入水空泡轮廓尺寸数据与刚性回转体的理论空泡尺寸结果总体吻合良好,由于弹性变形的影响,在空泡轮廓头部存在一定的差异,后体区域的尺寸差异随空泡直径的增大逐渐减小。
4)回转体速度衰减受入水初速度影响,初速度越大速度衰减程度越大,随着入水进程加深,不同初速度下的回转体速度衰减程度接近,入水速度对阻力系数变化影响不大。
| [1] |
王永虎, 石秀华. 入水冲击问题研究的现状与进展[J]. 爆炸与冲击, 2008, 28(3): 276-282. DOI:10.3321/j.issn:1001-1455.2008.03.014 |
| [2] |
Von KARMAN T. The impact of seaplane floats during landing[J]. Technical Report Archive & Image Library, 1929(321): 309-313. |
| [3] |
WAGNER H. Phenomena associated with impacts and sliding on liquid surfaces[J]. Z Angew Math Mesh, 1932, 4(12): 193-215. |
| [4] |
WORTHINGTON A M, COLE R S. Impact with a liquid surface, studied by the aid of instantaneous photography. Paper II.[J]. Proceedings of the Royal Society of London, 1899, 65(1): 153-154. |
| [5] |
MAY A, WOODHULL J C. The virtual mass of a sphere entering water vertically[J]. Journal of Applied Physics, 1950, 21(12): 1285-1289. DOI:10.1063/1.1699592 |
| [6] |
MAY A, ALBERT. Effect of surface condition of a sphere on its water‐entry cavity[J]. Journal of Applied Physics, 1951, 22(10): 1219-1222. DOI:10.1063/1.1699831 |
| [7] |
顾建农, 张志宏, 范武杰. 旋转弹丸入水侵彻规律[J]. 爆炸与冲击, 2008, 4(25): 55-63. |
| [8] |
张伟, 郭子涛, 肖新科, 等. 弹体高速入水特性实验研究[J]. 爆炸与冲击, 2011, 31(6): 579-584. |
| [9] |
陈震, 肖熙. 二维楔形体入水砰击仿真研究[J]. 上海交通大学学报, 2007, 41(9): 1425-1428. DOI:10.3321/j.issn:1006-2467.2007.09.008 |
| [10] |
何春涛, 王聪, 闵景新, 等. 回转体匀速垂直入水早期空泡数值模拟研究[J]. 工程力学, 2012, 29(4): 237-243. |
| [11] |
马庆鹏, 魏英杰, 王聪, 等. 锥头圆柱体高速入水空泡数值模拟[J]. 北京航空航天大学学报, 2014, 34(2): 174-180. DOI:10.13700/j.bh.1001-5965.2014.02.022 |
| [12] |
李强, 石秀华, 曹银萍. 鱼雷头部形状对人水影响的数值模拟研究[J]. 弹箭与制导学报, 2009, 4(29): 173-176. |
| [13] |
杨力, 周勇, 李华峰, 等. 基于ALE方法的平底结构入水冲击动力特性研究[J]. 舰船科学技术, 2017, 39(12): 125-133. DOI:10.3404/j.issn.1672-7649.2017.12.027 |
| [14] |
路丽睿, 魏英杰, 王聪, 等. 凹形运动体三自由度入水运动特性数值研究[J]. 舰船科学技术, 2018, 40(9): 13-20. DOI:10.3404/j.issn.1672-7649.2018.09.003 |
| [15] |
王珂, 陈刚, 袁洪涛. 弹性回转体入水砰击载荷预报[J]. 船海工程, 2011, 40(5): 27-32. DOI:10.3963/j.issn.1671-7953.2011.05.006 |
| [16] |
SHI H H, TAKAMI T. Some progress in the study of the water entry phenomenon[J]. Experiments in Fluids, 2001, 30(4): 475-477. DOI:10.1007/s003480000213 |
| [17] |
宣建明, 缪弋, 程军, 等. 返回舱水上冲击特性的试验研究与理论计算[J]. 水动力学研究与进展, 2000(3): 276−286.
|
 2022, Vol. 44
2022, Vol. 44

