2. 招商局金陵船舶(南京)有限公司,江苏 南京 210015
2. China Merchants Jinling Shipbuilding (Nanjing) Co., Ltd., Nanjing 210015, China
极地运输船,在冰区航行时,其破冰能力远差于破冰船。船体在与冰体接触时会受到冰阻力,伴随着冰激振动响应。振动加速度的大小与船体所受冰阻力的大小呈正相关。在冰区航行中,船体振动会直接影响到船上船员的工作与生活,且对船体设备的寿命有一定的损害。因此,对于冰区运输船的冰激振动的研究亟需深入。
目前冰激振动的研究对象多是海洋平台。在海洋平台上出现的冰激振动影响较大不可忽略,而对于在冰区航行的船舶,之前的研究考虑较少,所以缺乏参考。但随着地球气温上升,北极融化的大背景下,对极地航行的研究亟需加快。现今的国内外学者主要以北极实地考察和冰区模拟对此课题进行研究。
张鹏[1]获得破冰船水线区船肩受力分析的数据后,简化了船肩结构,为探究冰载荷及冰激振动对冰体结构破坏的影响,选用了合理的冰体强度参数与冰载荷计算公式后研究了船肩处冰载荷与冰激振动响应的关系,为研究冰区破冰船的破冰航行提供了一定的参考。季顺迎等[2]测定了在南极破冰航行的“雪龙”号极地科考船实时冰激振动加速度,确定了船速、外界荷载及外界因素对船体振动的影响关系。蔡柯[3]模拟了破冰船在层冰区的破冰航行,使用离散元方法去建立了冰体模型,求得船体周围的压力变化及冰载荷导致的冰激船体结构振动效应。应用北极实地科考过程中破冰船上测得的数据,分析了3个方向上船体局部冰激振动的数值,研究了航速及冰体力学性质对船首局部振动的变化规律,获得了冰载荷的时程曲线和冰激振动加速度的时程曲线。
1 极地运输船冰区航行过程分析 1.1 模型及计算域的建立本文的研究对象为某型16万吨级的油船。使用Ansys建立简化船首模型,再使用有限元软件Ls-dyna,单元网格取1 m×1 m。
船体结构材料选用普通船用钢,选Ls-dyna中的3号塑性随动材料模型作为钢材料本构模型,并在船首后建立平行中体,使用刚体建立中体。虽然以刚体作为材料的平行中体并不会参与船首结构的计算,但会使船体的重心偏移,从而使计算结果出现偏差,因此本文在关键字*part_inertial修改船体重心位置至实船的实际重心位置。最后对所有节点设置Y方向和Z方向上的位移约束和3个方向上旋转自由度的全约束。此外,在船舶破冰仿真计算中,使用附加质量法时,水的附连质量系数К取为0.05[4],钢材料参数如表1所示。
|
|
表 1 钢材料参数 Tab.1 Material parameter |
船体有限元模型如图1所示。

|
图 1 船首有限元模型 Fig. 1 Bow finite element model |
使用体单元建立层冰模型,尺寸为140 m×80 m×1 m。网格尺寸选用区间为200~300 mm,冰层前端面约束为六自由度完全自由,后、左、右端面的约束为六自由度固定。在Ls-dyna的材料库中选取MAT_PLASTICITY_COMPRESSION_TENSION (MAT_124)作为冰体材料[5],冰体材料参数如表2所示。
|
|
表 2 海冰材料参数 Tab.2 Sea ice material parameters |
船冰接触处使用侵蚀接触(Eroding)算法,通过定义速度时程曲线,让船体匀速行驶,将计算的总用时设置为6 s。
在计算船体结构的振动响应时,需要在船体接触断面上施加激振力,而在本文的计算条件下,船首最主要的振源是与冰体碰撞产生冲击力。因此为了计算出船首冰带区结构的振动响应,用有限元方法模拟冰区船破冰过程。选用振动加速度作为局部结构的振动响应指标,它能直观体现振幅的大小,也能作为船员舒适度的参考指标。
船冰计算域模型如图2所示。

|
图 2 船冰计算域模型 Fig. 2 Ship-ice calculation domain |
设置冰层厚度为1 m,船舶航速为4 m/s的工况进行船舶航行的计算,其典型的船冰相互作用状态示意图如图3所示。

|
图 3 船体与海冰相互作用 Fig. 3 The hull interacts with the sea ice |
船首型线通常为尖瘦形,其中破冰船和球鼻首船更为典型,因此在船舶行驶过程中,船首不大会和冰体发生直接碰撞,反而是舷侧会与冰体发生直接碰撞,像是一个人的肩膀,因此也被叫做船肩。在船肩处冰带区附近的的舷侧纵桁上选取适当数量的测点测量振动响应。
在冰带区附近的一根纵桁上选取5个点作为观测点,分别以A,B,C,D,E命名,同时再选2个同一肋位上但在不同水线位置上的10个点作为参照组,区别命名为A1-E1,A2-E2,观测点的位置及命名如图4所示。

|
图 4 测点 Fig. 4 Test points' |
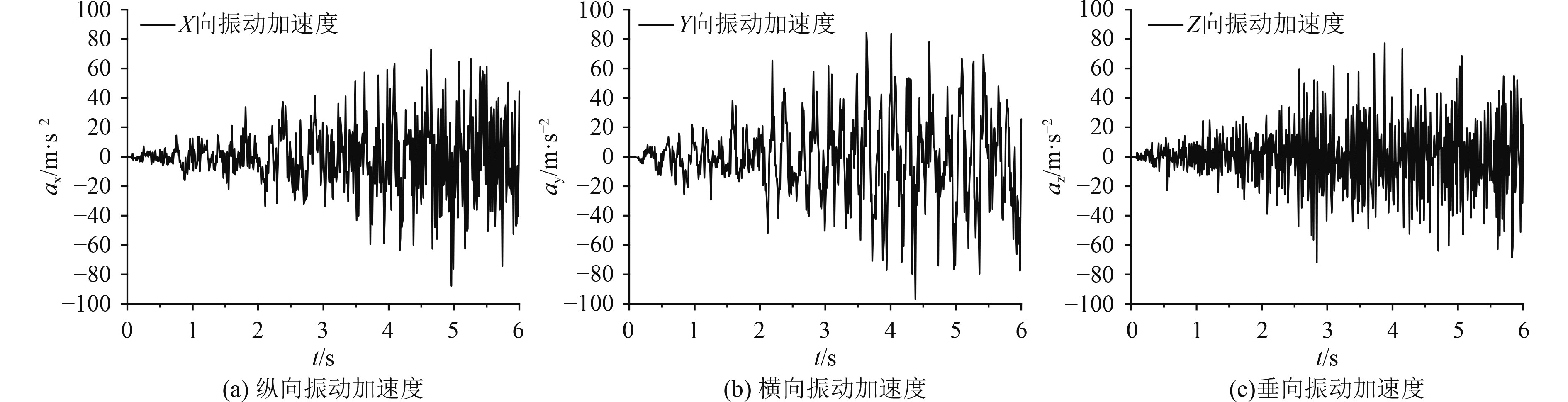
测出6 s内各观测点的振动时程曲线。计算步长为0.01 s,出图步长为0.01 s。图5仅展示对C点的加速度数据,在船肩处3个方向上的振动加速度的时程曲线如图5所示。
|
图 5 C点在3个方向上振动加速度时程曲线 Fig. 5 Time history curve of vibration acceleration of point C in three directions |
可知,在破冰航行时,船体在3个方向上皆出现了显著的振动加速现象,且皆无规律特征,表明船舶航行时船冰振动具有较大的随机性。同时,还可以注意到Z轴方向振动的频率较高,这是因为船肩处与XY平面平行的纵桁,在Z轴方向上较易出现振动加速。
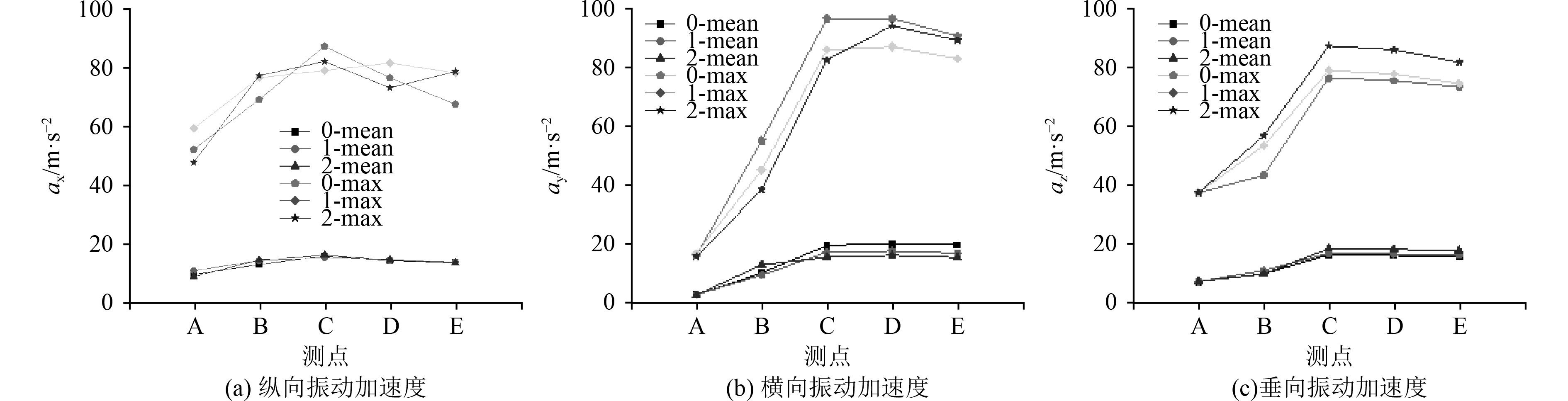
5个观测点在X方向、Y方向、Z方向上的振动加速度平均值及最大值如图6所示。
|
图 6 各测点振动加速度平均值及最大值 Fig. 6 Average value and maximum value of vibration acceleration at each measuring point |
图中后缀max和mean分别对应该点的最大振动加速度和平均振动加速度,前缀0是在A-E点,前缀1是在A1-E1点,前缀2是A2-E2点。
显然,尽管处于不同水线,但其振动加速度的值接近。3组测点的振动加速度平均值十分接近,且靠近撞击点的测点值,在纵向和垂向的振动加速度明显偏大,尤其是横向的差距更为显著,其最大值为97.6 m/s2,平均值为20 m/s2。
纵向振动加速度其最大值的数值随机性很强,测点距水线越近,垂向振动加速度会越小,反之则越大。这是因为冰带区沿水平方向延伸,垂直于纵桁,因此垂向的振动加速度相较于其他方向上的更小。
2 极地航行船抗冰激振动新型结构形式研究船舶破冰过程中产生振动不可忽视,使用夹层结构对船体进行局部加强,验证夹层结构是否对抗冰激振动有效。
2.1 夹层板夹层板结构在提高结构的强度、降低结构的损伤等方面有着显著的效果,因此受到国内外结构领域学者的关注。Stephen等[6]构造了一种不同于普通桥面板的Sandwich Plate System(SPS)结构,SPS结构在静载测试环节上对比普通桥面板,展现出了其在强度上的优点。
王自力等[7]构造了FCT和IFP两种舷侧板结构,进行对比静载测试,结果证明了2种结构在强度上的优势。为探究应用夹层结构在极地航行船上对抗冰激振动是否有效,在上述数据基础上,优选4种夹层板,对船肩进行局部结构加强。
2.2 夹层板对冰激振动的影响为了避免局部结构重量对强度的影响,选用夹层板的厚度时保证与对照组的质量误差在1%以内。同时为了选出最佳方案,选取4种夹层板结构I型、V型、X型和四边蜂窝型等分别对船肩处进行加强。
把船的外板和肋骨替换成夹层板结构,夹层板的内、外面板的厚度之和与原方案厚度相等,夹芯层高度与肋骨高度持平,夹芯层厚度由等重量计算得到。图7为4种夹层板I型、V型、X型和四边蜂窝型的结构示意图。

|
图 7 四种夹层板 Fig. 7 Four sandwich plates |
4种夹层板I型、V型、X型和四边蜂窝型的结构尺寸见表3。
|
|
表 3 夹层板尺寸 Tab.3 Sandwich plate size |
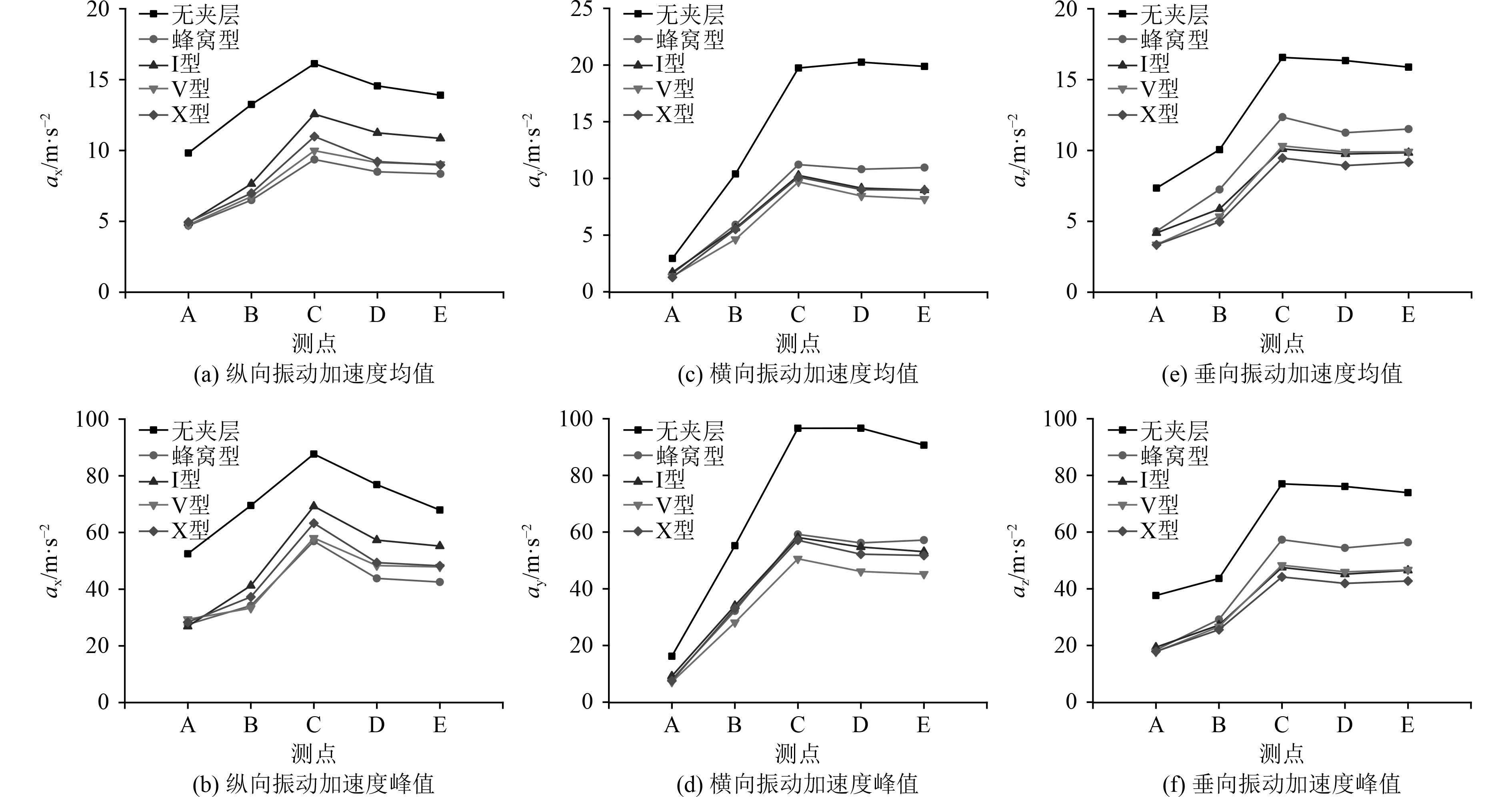
选取航速为4 m/s,冰厚为1m。计算的测点选择也是位于水线附近桁材上的5个测点A~E,5类船肩处5个测点的振动加速度均值及峰值如图8所示。
|
图 8 五类船肩处的振动加速度 Fig. 8 Five types of ship shoulder vibration acceleration |
可以看到,4种夹层板对抗振均十分有效,对3个方向上的振动均削减超20%,特别是对横向振动的削减更是接近40%。其中在纵向减振效果,四边蜂窝型夹层结构好于其他类型结构,V型夹层结构横向减振效果好,X型夹层结构纵向减振效果好。尽管经过大量实验证明,四边蜂窝型夹层板的抗冲击效果优良[8],但在计算后发现,四边蜂窝型夹层板并不是在所有工况下都是最优方案,因此在选择优化结构时要考虑船舶实际航行中主要受力的形式再去选择较为合适的局部结构强化方案。
为了更直观比较优化效果,通过比较测点B和测点D的2组数据,计算减少的振动,便于直接和成本进行比较,具体对比数据如表4所示。
|
|
表 4 B点和D点三方向振动优化对比 Tab.4 Comparison of three-direction vibration optimization at points B and D |
从表4可知,使用夹层板结构优化后,3个方向上的减振十分显著,尤其是在测点B的优化效果,纵向减幅接近50%,且测点D在纵向和横向上的减振减幅也达到了40%,说明使用蜂窝型夹层板减振处理十分有效,在横向上的减振优化尤其优异。该结果表明夹层板结构对抗冰激振动减振效果也不逊色于抗冲击领域。
尽管夹层板结构对于船肩抗冰激振动的效果十分优异,尤其是蜂窝型夹层板,但夹层板结构的工艺要求远高于普通板,因此要结合经济效益适当使用夹层板结构优化。
3 结 语本文使用有限元软件Ls-dyna,建立有限元船体模型和冰体模型,模拟冰区运输船在层冰区进行破冰航行的过程。根据计算结果,比较船肩在纵向、横向、垂向3个方向上的冰激振动加速度。为了强化船肩的抗振能力,尝试I型、V型、X型和四边蜂窝型4种夹层板结构,计算4种结构强化方案下船肩振动加速度,并与未优化的结构数据进行对比,再计算出4种方案的振动减幅,最后对比4种结构强化方案的优劣,可以得到以下结论:
1)船体不同水线处振动加速度的值接近,且靠近撞击点的测点值,在纵向和垂向的振动加速度明显偏大,纵向方向上的振动加速度的波动性很强,横向振动加速度随着离水线的距离增加而削弱。
2)使用夹层板对船肩进行结构优化,对于3个方向上的抗冰激振动的效用都非常好。比对4种夹层板结构的减振效果可发现,在纵向减振效果,四边蜂窝型夹层结构好于其他类型结构,V型夹层结构横向减振效果好,X型夹层结构纵向减振效果好。从总体减振效果而言,应优选三方向抗冰激振动能力均衡的四边蜂窝型夹层结构。但夹层板(尤其是蜂窝型夹层板)的制作工艺较普通外板的要求高,如果要使用夹层板结构会增加造价,且影响船体船肩结构(如重心,主要受力区域)。夹层板结构的减振效果数据可以给冰区船在抗冰激振动结构优化上提供技术参考数据,结合经济效益适当使用夹层板结构优化。
| [1] |
张鹏. 内河破冰船的冰激船体结构振动与舱室噪声试验研究[D].哈尔滨: 哈尔滨工程大学, 2017.
|
| [2] |
季顺迎, 雷瑞波, 李春花, 等. “雪龙”号科考船在冰区航行的船体振动测量研究[J]. 极地研究, 2017, 29(4): 427-435. DOI:10.13679/j.jdyj.2017.4.427 |
| [3] |
蔡柯. 船体结构冰荷载的离散元数值计算及船体冰激振动测量分析[D]. 大连: 大连理工大学, 2016.
|
| [4] |
DALEY C, KENDRICK A. Safe speed in ice [R]. Final Report, Prepared for BMT Fleet Technology, 2011.
|
| [5] |
ZHANG Jian, GAIDAI Olcg, WANG Kaimin, et al. A stochastic method for the prediction of icebreaker bow extreme stresses[ J], Applied Ocean Research, 2019(87): 95−102.
|
| [6] |
STEPHEN J. K, THOMAS M. M. Ultimate strength of an SPS bridge [R]. Annual Conference of the Transportation Association of Canada, 2004.
|
| [7] |
王自力, 姜金辉. 一种基于内充泡沫塑料薄壁方管的单壳舷侧耐撞结构[J]. 中国造船, 2004, 45(2): 51-56. DOI:10.3969/j.issn.1000-4882.2004.02.007 |
| [8] |
何文心. 破冰船首部冰载荷计算及结构强度研究[D].镇江: 江苏科技大学, 2017.
|
 2022, Vol. 44
2022, Vol. 44
