0 引　言

近年来，3D造型设计在计算机技术进步的基础上也得以迅速发展，3D造型技术作为工业领域的关键环节，在整个工业产品的生命周期中占有重要地位。目前，计算机辅助设计成为主流趋势，辅助设计软件不断在图形绘制、3D建模、仿真等方面有所突破，并在多学科融合背景下逐渐发展成熟。

3D造型技术发展也体现了工业产品设计的历程，尤其是船舶工业领域，零部件的设计在初期只能利用计算机进行简单的线条绘图，随着3D软件的优化升级，船舶零部件设计从点到线，从面到体，经历了跨越式的发展，计算机辅助设计技术也提高了船舶工业领域产品的设计效率，提高了设计水平。

在此背景下，本文基于交互设计技术的舰船零部件智能制造，从交互设计中造型元素出发，结合角点检测技术、图形几何变换和NURBS曲线造型技术，对船舶智能制造过程的零部件3D造型过程进行优化，具有重要的现实意义。

1 舰船零部件交互设计中3D造型元素研究

船舶零部件设计过程的3D造型元素，主要包括线框模型、曲面模型、实体模型以及特征模型等。

1）线框模型

线框模型是船体3D造型的基础，从二维程图衍生而来，也是最简单和基本的元素，可以表征产品的外部轮廓。

2）曲面模型

曲面模型是通过拼接、拟合等多种形式生成曲面片，包括自由曲面、Bezier曲面、几何曲面等，曲面模型元素在3D造型中占有重要地位，图1为某自由曲面模型的示意图。

3）实体模型

船舶产品的实体建模是通过几何逻辑模拟产品实际结构的建模过程，实体模型能够清晰地显示复杂零部件的外在和内在特性，目前，大量实体建模软件平台采用体素法进行实体建模，利用最基本的体素如长方体、球体、椎体等元素构建复杂的三维模型。

4）特征模型

特征建模是在实体建模的基础上进一步提炼而来的，特征建模将整个产品生产过程中的多种特征描述添加进实体模型中，比如产品的型号、规格、几何信息等，特征模型是零部件由设计转向实际生产的重要步骤。

2 舰船零部件交互设计的关键环节 2.1 基于角点检测法的曲线特征优化

在船舶零部件建模过程中，曲线特征建模主要通过软件搭建草图轮廓，这是零部件设计的基础环节，也直接决定了后续产品设计的效果。本文为了提高船舶零部件曲线设计效果，结合角点检测法对曲线进行优化^[1]。

角点检测可以提取曲线特征点的坐标和斜率信息，当曲线特征点的坐标和斜率出现较大变化时，将该位置特征点定义为角点，角点附近区域特征点的自相关函数如下：

$ Z(u,v) = \sum\limits_{x,y} w (x,y){[I(x + u,y + v) - I(x,y)]^2} \text{。} $

式中： $ u,v $ 为曲线上特征点在 $ x,y $ 两个方向上的偏移量， $ I(x + u,y + v) $ 为偏移后的特征点向量， $ I(x,y) $ 为偏移前的特征点向量， $ w(x,y) $ 为滤波器。

自相关函数的泰勒展开式为：

$ T(u,v) \approx \begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{l}} u \\ v \end{array}} \right]}&{ \cdot \displaystyle\sum\limits_{xy} w (x,y)\left[ {\begin{array}{*{20}{c}} {I_x^2}&{{I_y}} \\ {{I_x}}&{I_y^2} \end{array}} \right]} \end{array} \text{。} $

式中： $ {I_x} $ 和 $ {I_y} $ 分别为特征点在 $ x,y $ 两个方向的梯度，定义矩阵 $ \left[ {\begin{array}{*{20}{c}} {I_x^2}&{{I_y}} \\ {{I_x}}&{I_y^2} \end{array}} \right] $ 的特征值为 $ \omega_1 $ 和w₂，则特征值反映了曲线特征点的图像特征。

船舶零部件曲线设计过程的角点检测概况步骤为：

步骤1　输入零部件产品的特征曲线，获取每个关键特征点的坐标。

步骤2　使用角点检测算法进行特征曲线的边缘检测，获取非边缘特征点和边缘特征点的强度值。

步骤3　提取边缘特征点坐标。

步骤4　计算边缘特征点的曲率，评定特征曲线的优劣，并根据曲率进行特征曲线的优化。

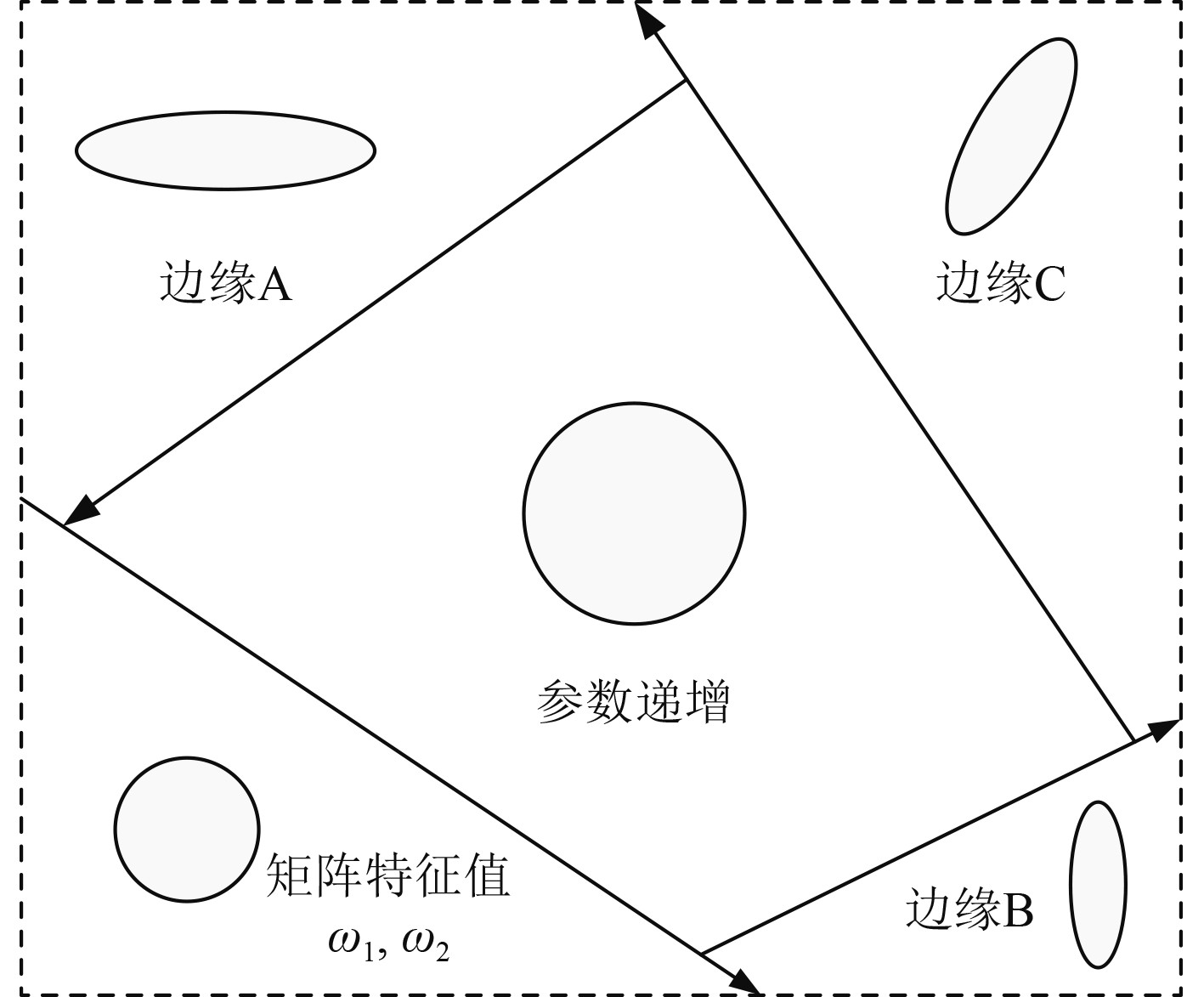
图2为基于角点检测的特征曲线优化示意图。

2.2 零部件产品2D特征的几何空间变换

根据交互设计理论，用户可以向计算机平台输入零部件产品的2D特征图，计算机平台对零部件2D特征进行优化，然后初步建立3D轮廓。

为了提高2D特征图像的配准精度，必须要进行图像的几何空间变换，主要包括：

1）刚体变换

主要是指2D特征图像的平移、旋转等变换，刚体变换能够提高角点检测的效率，变换如下式：

$ \left( {\begin{array}{*{20}{l}} {{x^\prime }} \\ {{y^\prime }} \end{array}} \right) = \left( {\begin{array}{*{20}{l}} {\cos \theta }&{\sin \theta } \\ { - \sin \theta }&{\cos \theta } \end{array}} \right)\left( {\begin{array}{*{20}{l}} x \\ y \end{array}} \right) + \left( {\begin{array}{*{20}{l}} {{\Delta _x}} \\ {{\Delta _y}} \end{array}} \right) \text{。} $

式中： $ \left( {\begin{array}{*{20}{l}} {{x^\prime }} \\ {{y^\prime }} \end{array}} \right) $ 为刚体变换后的特征点坐标， $ \left( {\begin{array}{*{20}{l}} {{\Delta _x}} \\ {{\Delta _y}} \end{array}} \right) $ 为特征点的平移量， $ \theta $ 为2D特征图像的旋转角度。

2）投影变换

特征图像的投影变换如下：

$ \left( {\begin{array}{*{20}{l}} {{x_0}} \\ {{y_0}} \end{array}} \right) = M\left( {\begin{array}{*{20}{l}} x \\ y \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{a_1}} \\ {{a_2}} \\ {{a_3}} \end{array}} \right) \text{。} $

式中： $ {a_1},\,{a_2},\,{a_3} $ 分别为投影夹角，M为特征图像的坐标转换矩阵。

2.3 基于NURBS样条曲线的船舶零部件交互设计

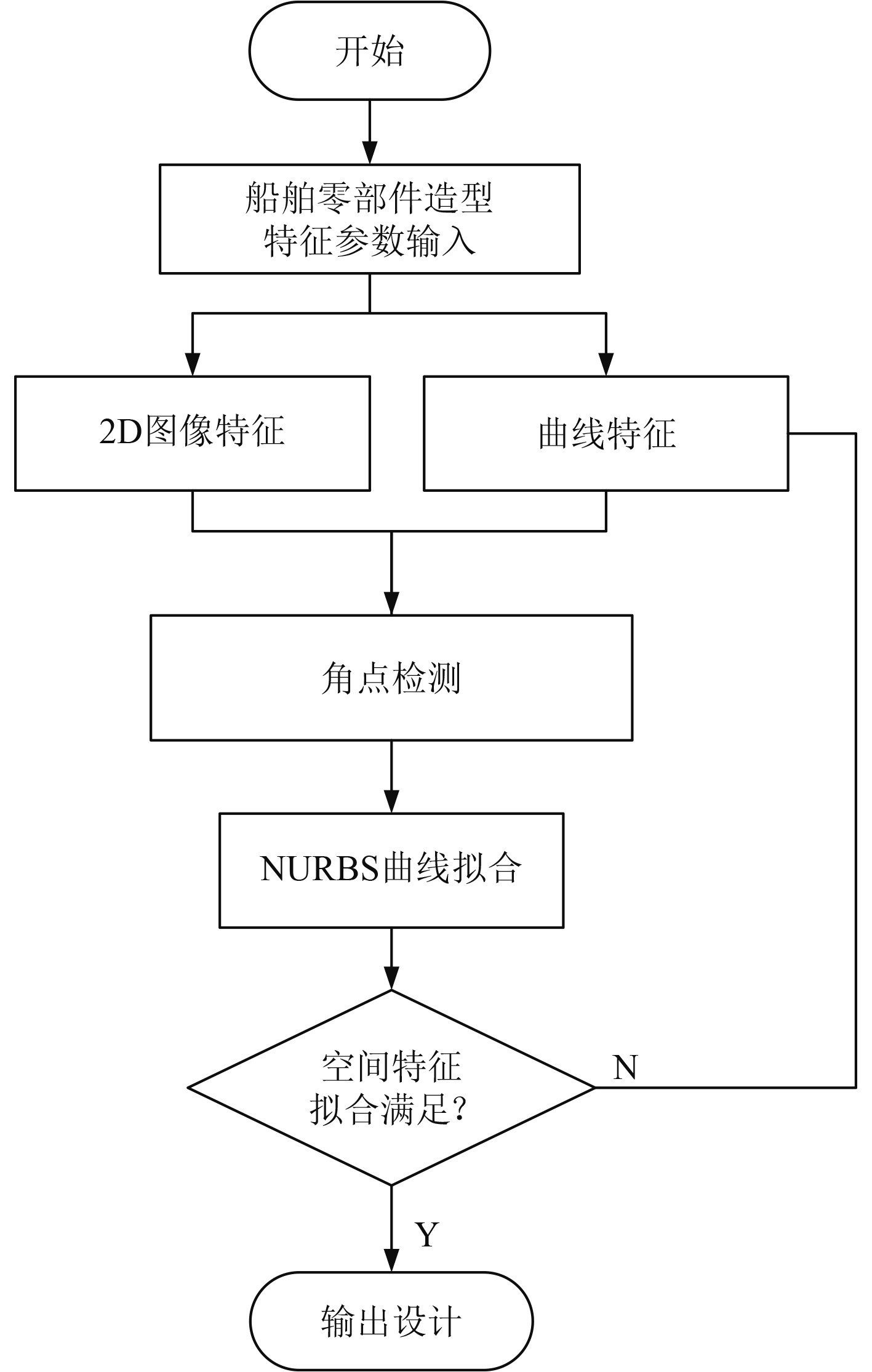
结合2D图像特征和角点检测算法^[2]，研究了基于NURBS样条曲线的船舶零部件交互设计，整体流程图如图3所示。

非均匀有理B样条(NURBS样条)具有良好的局部寻优特性，能较准确的表达空间自由曲面，非均匀有理B样条是在B样条曲线的基础上发展而来，因此，首先定义B样条曲线。

定义特征点矢量为：

$ T\left( {{t_0},{t_1},\cdots ,{t_n}} \right) {t_i} < {t_{i + 1}} \text{，} $

则第i个p次B样条基函数定义如下：

$ \left\{ {\begin{array}{*{20}{l}} {{{{N}}_{i,0}}({{t}}) = \left\{ {\begin{array}{*{20}{l}} {1,{{{t}}_i} \leqslant {{t}} < {{{t}}_{i + 1}}}，\\ {0,{\rm{else}}} \end{array}} \right.}，\\ {{{{N}}_{i,p}}({{t}}) = \dfrac{{{{t}} - {{{t}}_i}}}{{{{{t}}_{i + p}} - {{{t}}_i}}}{{{N}}_{i,p - 1}}({{t}}) + \dfrac{{{{{t}}_{i + p + 1}}}}{{{{{t}}_{{{i}} + 1}}}}{{{N}}_{i + 1,p - 1}}(t)}，\\ {{\rm{else}}}。\end{array}} \right. $

式中： $ {{{N}}_{i,p}}({{t}}) $ 为分段函数，共有P个特征点。

非均匀有理B样条(NURBS样条)曲线方程为：

$ \begin{gathered} p(u) = \displaystyle\sum\limits_{i = 0}^n {{d_i}} {R_{i,p}}(u)，\\ {R_{i,p}}(u) = \frac{{{\omega _i}{N_{i,p}}(u)}}{{\displaystyle\sum\limits_{j = 0}^n {{\omega _i}} {N_{i,p}}(u)}} 。\\ \end{gathered} $

式中：p为非均匀有理B样条的幂次^[3]， $ {R_{i,p}}(u) $ 为基函数。

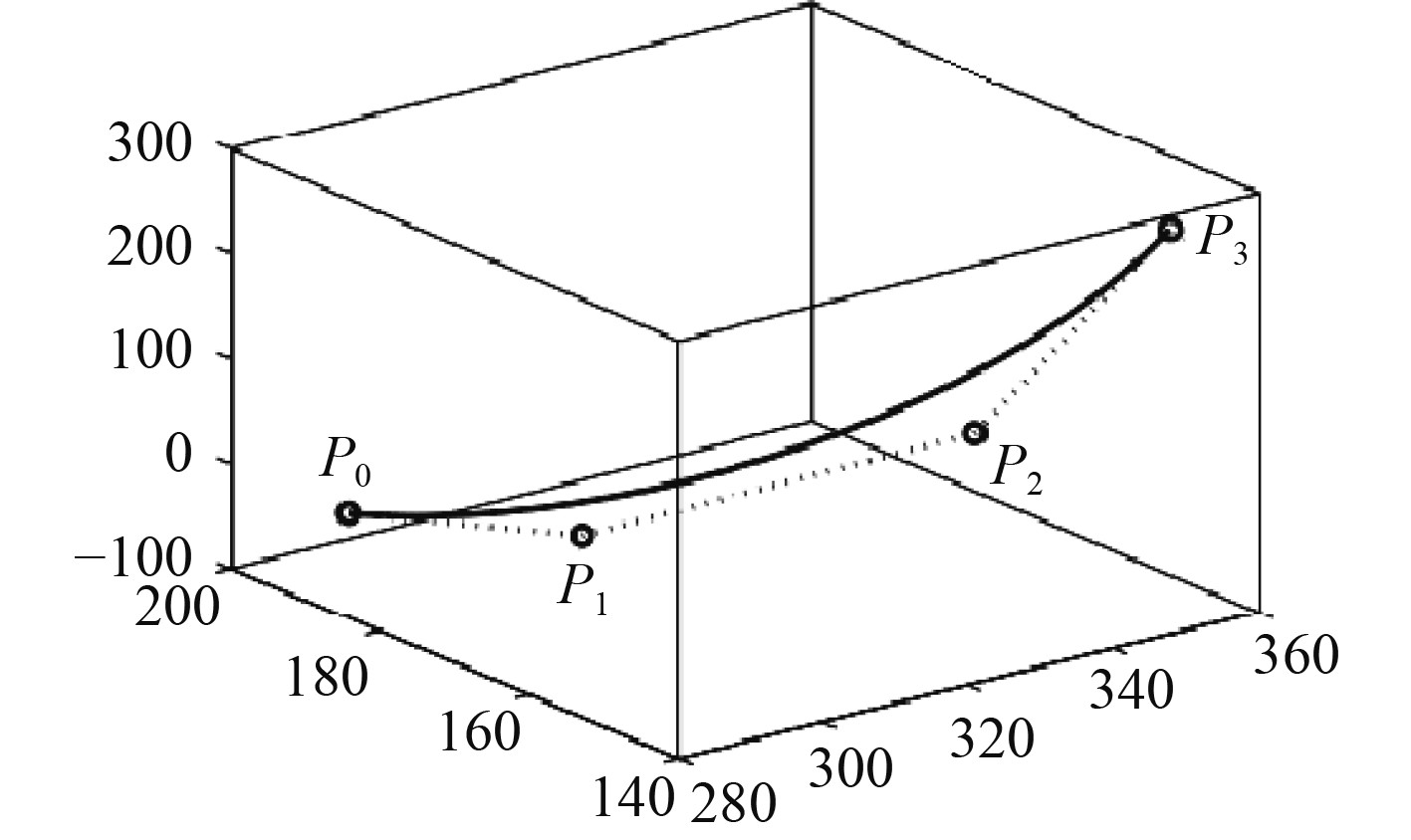
图4为非均匀有理B样条空间曲线示意图。

在研究舰船零部件的交互设计时，使用NURBS样条进行船体曲面的光顺设计优化，整个过程如下：

1）将船体外表面的曲面划分为首部、中体、尾部和底部等部分，获取初始的设计型线，定义初始设计型线的特征点为：

$ {V_{i,j}}\left( {i = 0,1,\cdots,m;j = 0,1,\cdots,n} \right) \text{。} $

2）建立特征点的方向矢量为：

$ \begin{gathered} F = \{ \underbrace {0,{t_{p + 1}}, \cdots ,{t_n},1}_{p + 1}\} ，\\ K = \{ \underbrace {0,{w_{q + 1}}, \cdots ,{w_n},1}_{q + 1}\} 。\\ \end{gathered} $

3）建立货舱轮廓曲线主尺寸型线方程如下：

$ \left\{ {\begin{array}{*{20}{c}} {x = \dfrac{L}{{{L_x}}}{x_0}}，\\ {y = \dfrac{B}{{{B_y}}}{y_0}}。\end{array}} \right. $

式中： $ L $ 和 $ B $ 分别为轮廓的长度、宽度，其剖面轮廓型线方程为：

$ \delta \left( {x,y} \right) = \alpha \left( {1 - x} \right)\left( {1 - y} \right) \text{。} $

式中： $ \alpha $ 为剖面的形变系数，对剖面轮廓方程进行积分得：

$ f\left( {x,y} \right) = \int\limits_s {\delta \left( {x,y} \right) = \int\limits_s^{} {\alpha \left( {1 - x} \right)\left( {1 - y} \right)} } = x\frac{{\alpha {C_o}}}{{1 - {C_o}}} \text{。} $

式中， $ {C_o} $ 为棱形系数。

4）建立光顺曲面^[4]如下：

$ S(F,K) = \sum\limits_{i = 0}^n {\sum\limits_{j = 0}^n {{N_{i,p}}(F)} } {N_{j,p}}(K){V_{i,j}} \text{。} $

式中： $ {N_{j,p}}(K) $ 和 $ {N_{i,p}}(F) $ 分别为B样条基函数。

定义优化参数方程为：

$ q\left( t \right) = {q_0} + t{q_d} \text{。} $

可得光顺曲面的优化目标函数为：

$ d = \frac{{\left| {n\left( {F,K} \right) \cdot {q_d}} \right| \cdot \left( {{q_0} - S\left( {F,K} \right)} \right)}}{{\left\| {n\left( {F,K} \right) \cdot {q_d}} \right\|}} 。$

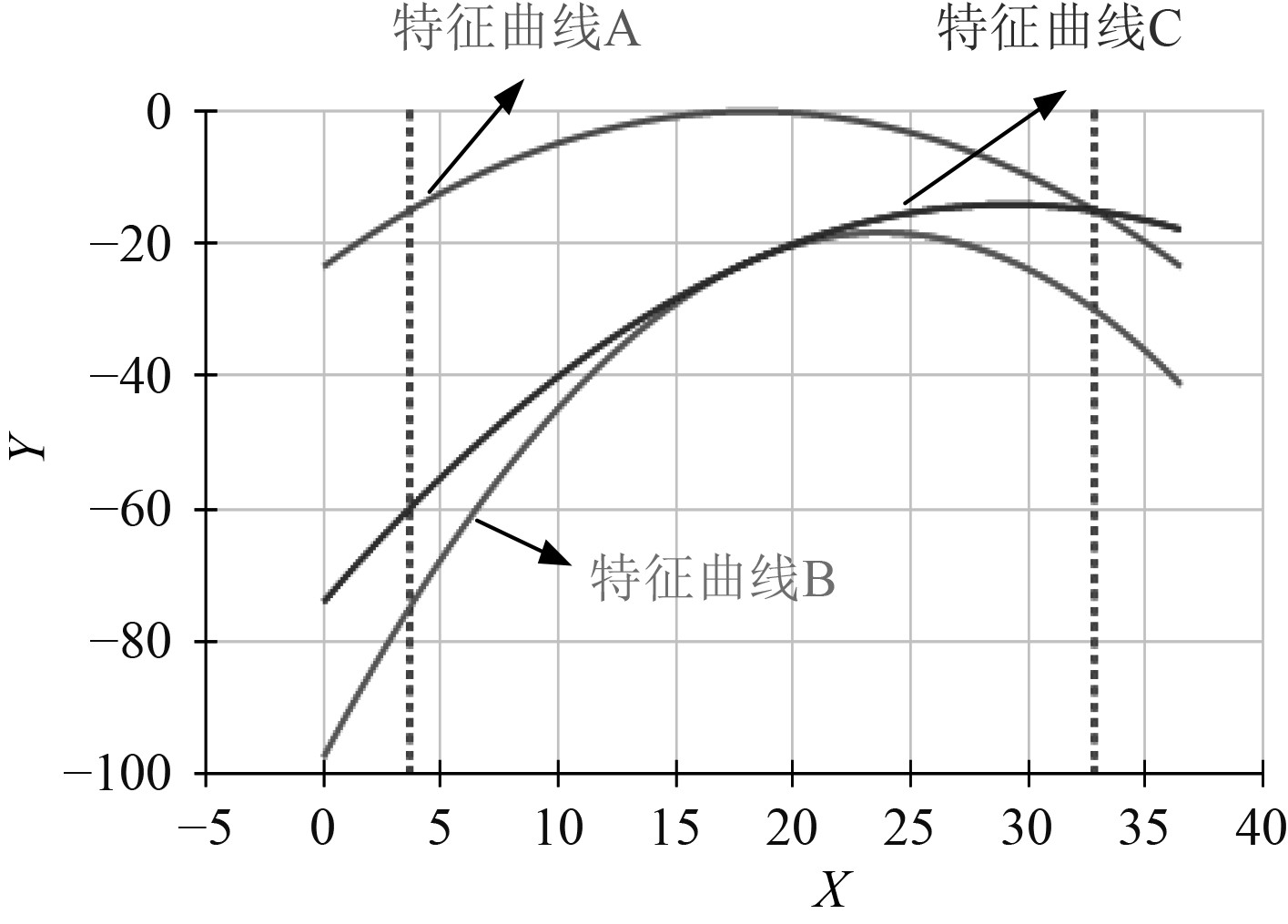
以船首处吃水线轮廓的型线为例，使用NURBS样条进行交互设计，图5为船舶吃水线轮廓处特征曲线的交互设计示意图。

3 结　语

船舶零部件的交互设计有助于提高船舶工业的智能化、自动化设计水平，本文对船舶零部件设计的关键要素进行梳理，结合角点检测技术、几何空间变换技术和非均匀B样条曲线造型技术进行船舶部件特征曲线、曲面优化，对于船体零部件3D造型智能化有重要的参考价值。