0 引　言

舰船设备逐渐向复杂化与智能化方向发展，造成其出现故障的概率不断提升。当下，舰船维修方式主要为定期维修和故障发生后维修，前者工作效率低，后者不能防止事故发生^[1-3]。为提升维修效率，避免事故发生，需实时估计舰船故障发展趋势，确定设备故障时间^[4]，及时展开维修，防止出现安全事故。例如，韩敏等^[5]利用卡尔曼滤波器估计舰船故障趋势，通过改进的序贯概率比分析估计残差，提升估计效果，该方法可有效估计舰船故障趋势，降低估计误差。王恒等^[6]通过分层狄利克雷与隐马尔科夫模型，构造设备故障趋势估计模型，该方法具备较优的故障趋势估计鲁棒性。这2种方法均能有效描绘舰船故障趋势变化情况，但均具有一定的局限性，估计结果稳定性差，不能为维修人员提供精准的故障信息。为此研究基于大数据的舰船故障趋势估计方法，提升故障趋势估计效果。

1 舰船故障趋势估计方法

基于大数据的舰船故障趋势估计方法的步骤为：

步骤1　在舰船历史数据库内选择各设备历史运行数据；

步骤2　归一化处理各设备历史运行数据，引入滑动窗口，将舰船故障趋势估计问题变更成监督学习问题^[7]；

步骤3　以处理完成的各设备历史运行数据为样本，将其分成训练集与测试集；

步骤4　对于训练集，分析训练次数是否达到需求，如果未达到需求，那么继续步骤5，反之，继续步骤6；

步骤5　利用改进的注意力机制在训练集内提取各设备历史运行数据的多变量时间序列；

步骤6　以改进的注意力机制的输出，为自回归预测模型与小波神经网络的输入，输出对应的舰船故障趋势估计结果，处理2个预测结果，获取训练集的最终估计结果；

步骤7　调整参数，同时优化自回归预测模型与小波神经网络，返回步骤4；

步骤8　在自回归预测模型与小波神经网络内输入训练集，输出舰船故障趋势估计结果。

1.1 舰船历史数据的注意力处理

利用改进的注意力机制，在归一化处理后的舰船各设备历史运行数据样本内，自适应选取和舰船故障趋势估计有关的时间序列。令已知窗口中舰船各设备历史运行数据是 $X = \left\{ {{x^1},{x^2}, \cdots ,{x^n}} \right\}$ ，其中，n为舰船设备属性数量； ${x_t}$ 为t时刻舰船设备历史运行数据观测值；T为滑动窗口尺寸， $t = 1,2, \cdots ,T$ ； ${x^i},i = 1,2, \cdots ,n$ 为第i个时间序列的观测值；t时刻， $x_t^i$ 为时间序列i的观测值。改进的注意力机制仅考虑舰船设备历史运行数据时间序列，即行向量 ${x^i}$ ，解决各时间步内包含数个变量时，不能提取变量间繁琐的关联性问题。改进的注意力机制，自适应选取和舰船故障趋势估计有关的时间序列具体步骤如下：

1） 计算t时刻，第i个舰船设备历史运行数据时间序列的重要性 $z_t^i$ ，公式如下：

$z_t^i = v_m^{\rm{T}}\tanh \left[ {\left( {{W_m}{h_{t - 1}};{W_m}{s_{t - 1}}} \right) + {Q_m}{x^i}} \right]。$

(1)

其中，h_t−1和S_t−1分别为t−1时刻的隐藏状态、单元状态是； ${W_m}$ 为第m个状态的权重； $v_m^{\rm{T}}$ 和 ${Q_m}$ 为需要学习的参数。

2）通过 $z_t^i$ 获取舰船设备历史运行数据的多变量时间序列 $\hat X = \left\{ {{{\hat x}_1},{{\hat x}_2}, \cdots ,{{\hat x}_T}} \right\}$ ，公式如下：

$\begin{split} {\hat x_t} =& \Big( soft\max \left( {z_t^1} \right)x_t^1,soft\max \left( {z_t^2} \right)x_t^2, \cdots ,\\ & soft\max \left( {z_t^n} \right)x_t^n \Big)^{\rm{T}}。\end{split}$

(2)

1.2 基于自回归预测的舰船故障趋势估计方法

以获取的舰船设备历史运行数据的多变量时间序列 $\hat X = \left\{ {{{\hat x}_1},{{\hat x}_2}, \cdots ,{{\hat x}_T}} \right\}$ 为输入，通过自回归预测模型输出舰船故障趋势估计结果。

p阶自回归预测模型 $AR\left( p \right)$ 的定义为：

$AR\left( p \right) = {u_0} + {u_1}{\hat x_{t - 1}} + {u_2}{\hat x_{t - 2}} + \cdots + {u_p}{\hat x_{t - p}} + {\varepsilon _t}。$

(3)

式中： ${u_0},{u_1} \cdots ,{u_p}$ 为回归系数； ${\varepsilon _t}$ 为 $AR\left( p \right)$ 的残差。

令t-1时刻， ${\hat x_t}$ 的估计值是 ${x'_t}$ ，公式如下：

${x'_t} = {u_0} + {u_1}{\hat x_{t - 1}} + {u_2}{\hat x_{t - 2}} + \cdots + {u_p}{\hat x_{t - p}} + {\varepsilon _t}。$

(4)

以矩阵形式描绘式(4)，公式如下：

${\boldsymbol{{{X}}}}' = {\boldsymbol{{{A}}}}{\boldsymbol{\varPhi}} + R。$

(5)

式中： ${\boldsymbol{{{X}}}}' = \left( {{{x'}_{p + 1}},{{x'}_{p + 2}}, \cdots ,{{x'}_T}} \right)$ ； ${\boldsymbol{\varPhi}} = \left( {{u_1}, \cdots ,{u_p},{u_0}} \right)$ ； $R = \left( {{\varepsilon _{p + 1}},{\varepsilon _{p + 2}}, \cdots ,{\varepsilon _T}} \right)$ ； $\boldsymbol{A} = \left[ \begin{array}{*{20}{c}} {{\hat x}_p}&{{\hat x}_{p - 1}}& \cdots & {{\hat x}_1}& 1 \\ {{\hat x}_{p + 1}}& {{\hat x}_p}&\cdots &{{\hat x}_2}&1 \\ \vdots &\vdots & \cdots &\vdots & \vdots \\ {{\hat x}_{T - 1}}& {{\hat x}_{T - 2}}& \cdots & {{\hat x}_{T - p}}&1\end{array} \right]$ 。

通过最小二乘法确定 $\varPhi$ ， $\varPhi$ 的估计结果如下：

$\hat \varPhi = \frac{{{A^{{\rm{T}}'}}X'}}{{{A^{{\rm{T}}'}}A}}。$

(6)

其中， ${\rm{T}}'$ 为转置符号。

将式(6)代入式(5)，获取舰船故障趋势估计结果 $X'$ 。

1.3 基于小波神经网络的舰船故障趋势估计方法

利用小波变换凸显提取的舰船设备历史运行数据多变量是时间序列 $\hat X = \left\{ {{{\hat x}_1},{{\hat x}_2}, \cdots ,{{\hat x}_T}} \right\}$ 内的特征，公式如下：

${f_{\hat x}}\left( {a,\tau } \right) = \frac{{\displaystyle\int_{ - \infty }^\infty {{{\hat x}_t}\frac{{\phi t - \phi \tau }}{a}{\rm{d}}t} }}{{\sqrt a }}。$

(7)

其中： $\phi$ 为小波函数；τ为 $\phi$ 的平移量；a为常数， $a > 0$ 。

以小波基函数为神经网络隐含层节点的传递函数，以向前传播方式传递 $\hat X$ ，以反向传播方式传递误差。网络输入是 $\hat X = \left\{ {{{\hat x}_1},{{\hat x}_2}, \cdots ,{{\hat x}_T}} \right\}$ ；网络输出是 $Y = {Y_1}, {Y_2}, \cdots ,{Y_M}$ ，其中，M为输出层节点数量。隐含层的输出公式为：

$g\left( j \right) = {r_j}\left( {\frac{{\displaystyle\sum\limits_{t = 1}^T {\sum\limits_{j = 1}^N {{\omega _{tj}}{{\hat x}_t} - {b_j}} } }}{{{q_j}}}} \right),j = 1,2, \cdots ,N$

(8)

式中： ${\omega _{tj}}$ 为输入层与隐含层间的权重；j为隐含层节点编号；N为节点数量； ${r_j}$ 为小波基函数； ${b}_{j}$ 和 ${q_j}$ 分别为 ${r_j}$ 的平移、伸缩因子。

以Morlet母小波函数为 ${r_j}$ ，输出层公式如下：

$y\left( k \right) = \sum\limits_{j = 1}^N {\sum\limits_{k = 1}^M {{\omega _{jk}}g\left( j \right)} } ,k = 1,2, \cdots ,M 。$

(9)

式中： ${\omega _{jk}}$ 为隐含层与输出层间的权重；k为输出层节点编号； $y\left( k \right)$ 为舰船故障趋势估计结果。

通过梯度修正法调整网络权重ω， ${b_j}$ ， ${q_j}$ ，舰船故障趋势估计结果在ω， ${b_j}$ ， ${q_j}$ 持续调整时，会不断近似期望估计结果。小波神经网络预测误差如下：

$E = \sum\limits_{k = 1}^M {\hat y\left( k \right) - y\left( k \right)}。$

(10)

其中： $\hat y\left( k \right)$ 为舰船故障趋势估计结果的期望输出； $y\left( k \right)$ 为舰船故障趋势估计结果。

通过E调整ω， ${b_j}$ ， ${q_j}$ ，调整公式如下：

$\omega \left( {j + 1} \right) = \omega \left( j \right) - \eta \frac{{\partial E}}{{\partial \omega \left( j \right)}}，$

(11)

$q\left( {j + 1} \right) = q\left( j \right) - \eta \frac{{\partial E}}{{\partial q\left( j \right)}}，$

(12)

$b\left( {j + 1} \right) = b\left( j \right) - \eta \frac{{\partial E}}{{\partial b\left( j \right)}}。$

(13)

式中，η为学习速率。

将自回归预测模型和小波神经网络输出的舰船故障趋势估计均值，O为舰船故障趋势估计的最终结果，公式如下：

$O = \frac{{X' + Y}}{2}。$

(14)

2 实验结果分析

以某舰船为实验对象，该舰船历史数据库内主要包含6种关键设备的历史运行数据，分别是主柴油机、主辅锅炉与主机冷却水系统等，舰船设备间彼此影响，共选择10000个数据点的舰船设备历史运行数据为样本集。

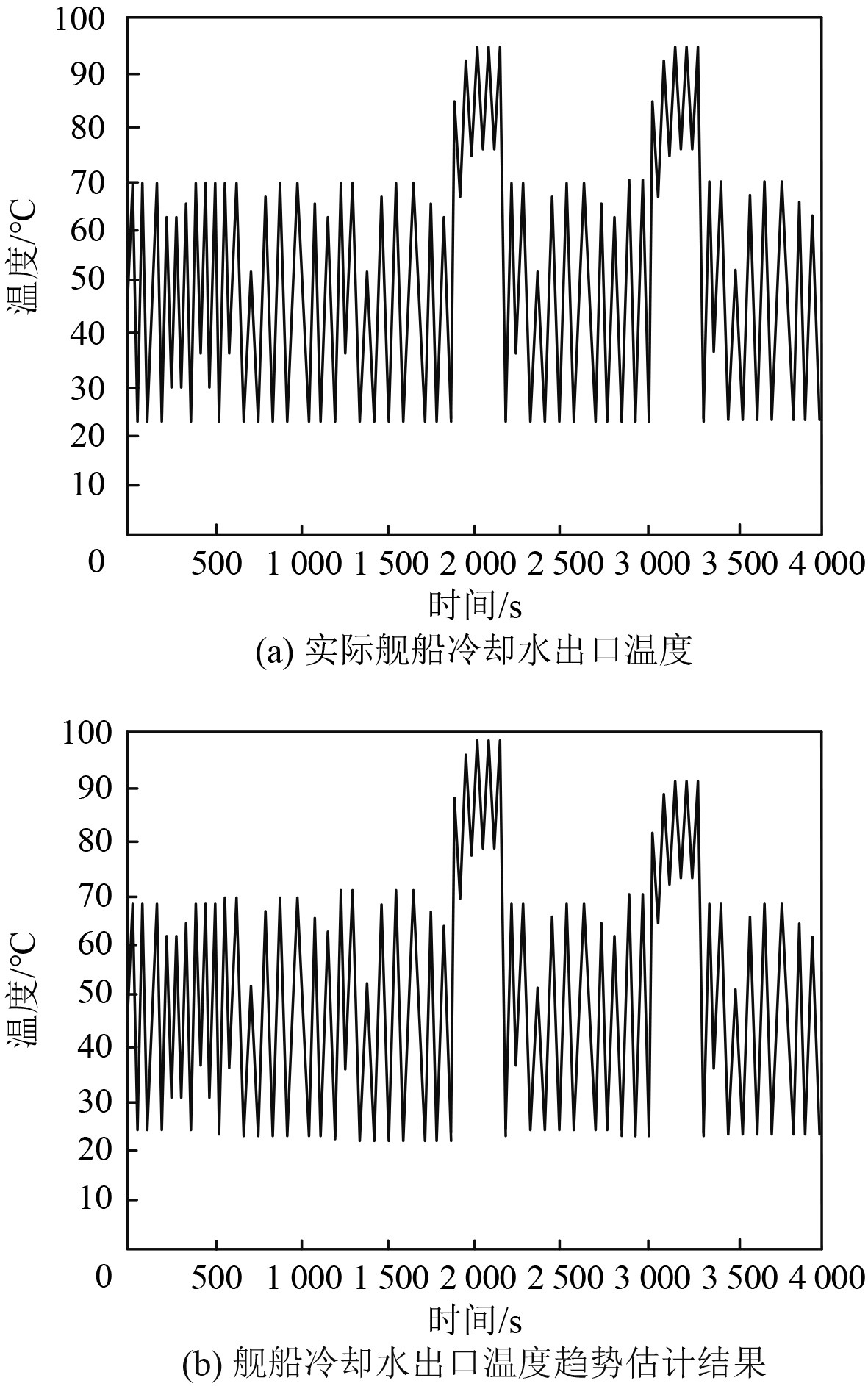
以舰船主机冷却水系统的冷却水出口温度为例，利用本文方法估计舰船故障趋势，当出口冷却水温度波动幅度较大时，说明舰船处于故障状态，舰船冷却水出口温度趋势估计效果如图1所示。可知，当时间在2000～3000 s左右时，该舰船冷却水出口温度出现异常波动，说明此时舰船存在故障，本文方法可有效估计舰船冷却水出口温度。本文方法估计温度变化趋势，与实际舰船冷却水出口温度仅有微小的差距，当时间在2000～3000 s左右时，冷却水出口温度出现异常波动，与实际情况相符。实验证明：本文方法可精准估计舰船冷却水出口温度变化趋势，即精准估计舰船故障趋势，为维修人员提供精准的数据支持，及时维修舰船，避免故障事件发生，提升舰船航行的安全性。

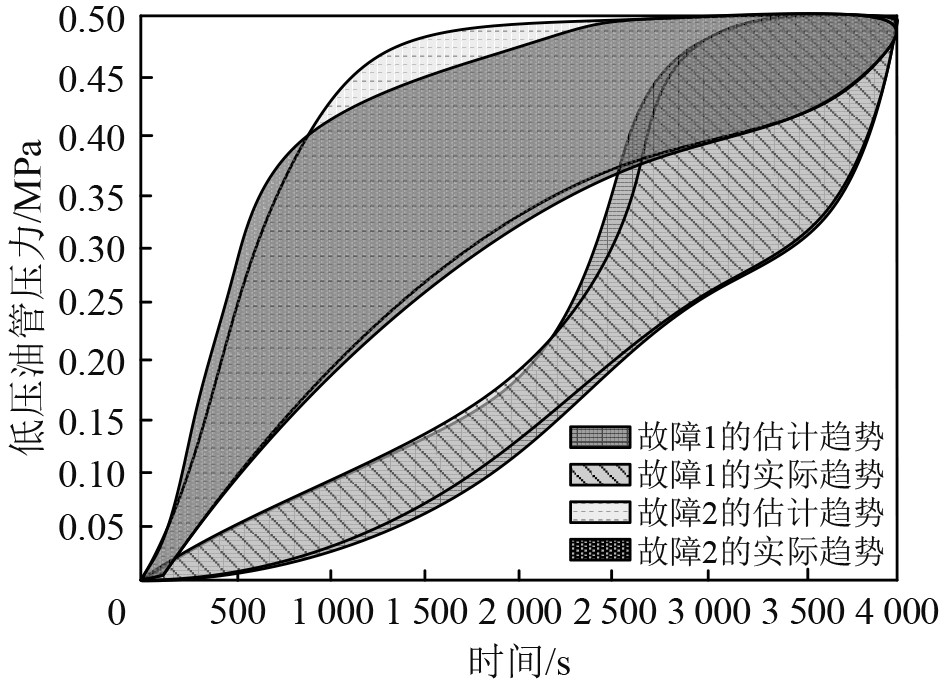
以舰船主柴油机的低压油管压力为例，该舰船主柴油机共有磨损与腐蚀2处故障，记作故障1与故障2，这2处故障发生后，利用本文方法估计舰船主柴油机的故障趋势，低压油管压力最大值是0.5 MPa，估计结果如图2所示。可知，当舰船主柴油机出现不同故障时，本文方法均可有效估计舰船主柴油机低压油管压力变化趋势，完成故障趋势估计。发生故障1时，前期低压油管压力上升速度较慢，在3000 s左右时会达到最大值，与实际趋势非常接近；发生故障2时，低压油管压力在2500 s左右时会达到最大值，且发生故障2时，低压油管压力上升速度较快，近似实际趋势。实验证明，在舰船出现不同故障时，本文方法均可精准估计舰船故障趋势。

利用赤池信息准则(akashi information criterion，AIC)衡量本文方法舰船趋势估计的优劣，ACI值越小，说明本文方法的趋势估计结果与实际趋势间的拟合精度越高，最大ACI值为80，在不同滑动窗口大小时，本文方法估计不同舰船设备故障趋势时的AIC值分析结果如表1所示。可知，在不同滑动窗口大小时，本文方法均可有效估计舰船各设备故障趋势，随着滑动窗口的提升，AIC值呈先上升后下降的趋势；在滑动窗口大小为8时，本文方法估计舰船各设备故障趋势时的AIC值降至最低，说明此时本文方法估计结果与实际结果的拟合精度最高。不同滑动窗口大小时，本文方法估计舰船各设备故障趋势时的AIC值均未超过80，说明本文方法具备较优的舰船故障趋势估计效果。

3 结　语

舰船维修过程中，故障趋势估计至关重要。舰船故障类型各式各样，且无规律性，为快速维修舰船故障，需精准估计舰船故障趋势，为此研究基于大数据的舰船故障趋势估计方法，精准估计舰船故障趋势，帮助维修人员快速修复故障，确保舰船航行安全。