2. 江西机电职业技术学院,江西 南昌 330013;
3. 中国船舶集团有限公司第七〇七研究所 九江分部,江西 九江 332007
2. Jiangxi Vocational College of Mechanical and Electrical Technology, Nanchang 330013, China;
3. Jiujiang Branch of the 707 Research Institute of CSSC, Jiujiang 332007, China
随着信息技术的快速发展,运用信息技术实现舰船航行安全性预测已经成为重点研究领域,对促进航海事业发展起着重要作用。在舰船安全性预测中,国外学者采用BP神经网络、贝叶斯理论、SVM算法等研究舰船航行安全的影响因素,这些算法得出的预测结果准确性偏低[1-3]。基于此,本文提出一种改进ELM算法,借助卡尔曼滤波、粒子群算法对传统ELM算法进行改进,针对舰船安全性构建起预测模型,能够保证预测结果的准确性。
1 改进极限学习机算法 1.1 极限学习机原理极限学习机(ELM)是针对单隐含层前馈神经网络的一种新型算法[4-6]。在ELM算法中,随机产生输入层与隐含层的连接权值,以及隐含神经元的阈值,无需在训练中调整数据便可以获得唯一最优解。ELM算法采用3层前馈神经网络结构。
在ELM算法内,每个节点的隐含层输出后合并形成矩阵式:
| $ {\boldsymbol{H}}\beta =T \text{。} $ |
矩阵式中的H为隐含层输出矩阵:
| $ {\boldsymbol{H}}({a_1} \cdots {a_L},{b_1} \cdots {b_L},{x_1} \cdots {x_L}) \text{。} $ |
在ELM算法中,训练前随机设置初始权值,通过求解广义逆矩阵得出最小化权值,不需要采用迭代调整。在安全性预测中,安全风险包括结构性风险和经验性风险,运用ELM算法预测时要兼顾结构风险最小化和经验误差最小化。而BP神经网络在安全性预测中只会考虑到训练误差最小化,产生过拟合问题,难以得到最优测试结果。因此,ELM算法与BP神经网络算法相比具备泛化性能好、学习速度快、参数敏感度低、分类效果好、计算复杂度低的优势。
1.2 改进极限学习机算法ELM算法通过对隐含层输出矩阵的广义逆计算构建线性网络结构,属于回归与分类算法。但是,由于ELM算法需要随机选取输入权值和隐含层偏置值,所以会出现输出矩阵条件数过大的情况,影响隐含层泛化性,这使得ELM算法的输出结果会忽略有价值的输出信息。因此需要对ELM算法进行改进,本文提出基于拉尔曼滤波思想的改进ELM算法。
卡尔曼滤波算法采用高斯白噪声理论、随机估计理论和状态空间理论,在描述含有白噪声信号的输入输出关系时采用状态变量法,通过输出方程和状态方程得到关系式,无需估计频域信息,使得算法可以处理非平稳输出数据。在ELM算法改进中运用卡尔曼滤波,能够解决均方误差最小化带来的问题,优化建立状态空间模型和观测方程式,更新估算观测值,得出最优化的计算结果。在算法中,受噪声干扰的状态量为随机量,很难保证测算的精确值,只能促使估计值接近真实值。当输入当前估计值后,能够通过滤波算法得出输出估计值,再利用反馈修正系数建立起输入与输出值之间的关系式。卡尔曼滤波主要采用预估和修正2种方法,利用系统方程和观测方程建立起预估模型,再利用观测方程估计当前状态,修正后反馈测量结果,按照顺序恢复系统数据。
1.3 改进极限学习算法的网络训练改进ELM算法是单隐层前馈神经网络,能够提高传统ELM算法的泛化性能,对实际输出值进行优化,在输入层添加实际输出值和期望值,利用前馈神经网络不断学习输出数据误差值,进一步提高预测精度。在改进的ELM算法模型训练中,输入神经元数为X,通过模型运算得出期望输出变量Y,再将输入值和输出值之间的误差反馈到训练层中继续学习,优化最终的输出结果。
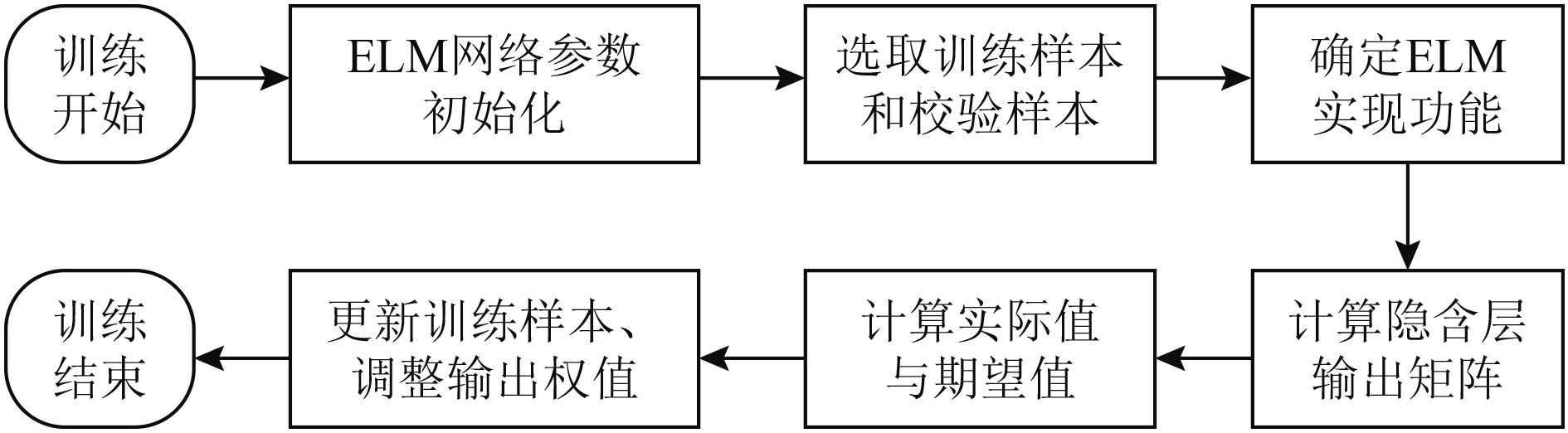
具体训练流程如图1所示。训练操作步骤如下:输出值为实际预测值y,在输入层的反馈阶段利用公式进行归一化处理,公式为:
|
图 1 改进极限学习机算法的网络训练流程图 Fig. 1 Network training flow chart of improved extreme learning machine algorithm |
| $ {e_k} = \frac{{{e_k} - {e_{\min }}}}{{{e_{\max }} - {e_{\min }}}} \text{。} $ |
将训练样本划分为3种数据集,分别为训练集、测试集和校验集,反馈值设定为0,在输入层内输入实际值与期望值误差,设置隐含层内的偏置值和连接权值;根据反馈参数修改输入权值和隐含层偏置值,得出修正后的公式,通过矩阵运算出结果。
2 改进极限学习机算法在舰船安全性预测中的应用 2.1 改进极限学习机算法的预测流程改进ELM算法要结合采用粒子群算法完成对舰船安全性的预测,在粒子群算法内,随机设定执行问题的初始值,根据粒子群的位置向量解释迭代结果。粒子群算法要采用适应度函数表示任意粒子与最优解的接近程度,根据每一次迭代获取的速度向量搜索出粒子朝向的最优解。在最优解空间中,设置自适应惯性权值,限制粒子速度,避免粒子飞出最优解的空间限制。
改进ELM算法流程如图2所示。训练过程如下:对粒子群进行初始化,优化ELM算法中粒子群参数,使粒子群内每个离子对应输入权值和偏置值,使粒子群内的初始值处于[−1,1]之间;根据粒子的适应值训练得出输出权值和误差值,随机选取训练集,更新粒子群中的偏置值,训练输入权值集合,校验训练集误差,根据误差值计算出偏置值的调整值;更新位置向量、个体极值和群体极值,更新后对每个粒子的适应度排序,选取排名前几的粒子构建组合模型,测试样本集;提取出输入权值和偏置值,建立极限学习机组合预测模型,预测数据结果。

|
图 2 改进极限学习机算法在安全性预测中的执行流程图 Fig. 2 Execution flow chart of improved limit learning machine algorithm in security prediction |
采用本文提出的改进ELM算法作为舰船航行安全性预测分类器,建立改进ELM模型,对舰船航行安全影响因素进行分析,优选影响因素子集。具体步骤为:
步骤1 利用因素和染色体个数的关联性编制二进制编码,表示第m个因素状态,用0代表因素不被采纳,用1代表因素被采纳。
步骤2 随机选择群体中的多条染色体,初始群体根据空间异同进行选择,确保初始群体中包含各子集因素。
步骤3 精确处理适合度函数,利用适合度函数与ELM分类的正比关系,求出影响因素的数量。按照从高到底的顺序对初始群体因素的适合度进行排序,再结合舰船航行安全影响的外部环境条件,确定子集因素,计算出个体适合度值。
步骤4 根据运算规则选取染色体,按照由高到低的原则对适合度值进行排序,保证染色体顺利进入到下一阶段遴选。
步骤5 判断适合度值是否都达到阈值要求,选择因素进行异化,产生下一代群体。
步骤6 重复步骤3,准确计算出群体的个体因素,从各项因素中选取出适合度最高的个体因素,停止其他数据训练,形成最终的筛选结果。
3 仿真实验 3.1 实验条件因改进ELM算法对数据资料信息量的要求偏低,在综合考虑舰船航行事故影响因素的基础上,剔除年度跨度大、非权威性信息,尽量保证数据资料信息的准确性。本次仿真实验采用2010~2020年海上舰船事故统计资料作为实验数据,对157起舰船安全事故原因进行分析,将其作为改进ELM算法的验证依据。
安全事故等级分类。根据舰船航行事故造成的直接经济损失、人员伤亡严重程度以及海洋污染程度划分为5个安全等级,分别为:对无人员伤亡,经济损失小于100万元,海洋环境污染程度小于1 t溢油的安全事故认定为“微小事故”;对人员死亡在1~3人或重伤人数在1~10人,经济损失在100~1000万元,海洋环境污染程度在1~100 t之间的安全事故认定为“一般事故”;对人员死亡在4~10人或重伤人数在11~50人,经济损失在1000~5000万元,海洋环境污染程度在100~500 t之间的安全事故认定为“大事故”;对人员死亡在11~30人或重伤人数在51~100人,经济损失在5000万元~1亿元,海洋环境污染程度在500~1000 t之间的安全事故认定为“重大事故”;对人员死亡在30人以上或重伤人数在100人以上,经济损失在1亿元以上,海洋环境污染程度在1000 t以上的安全事故认定为“特大事故”。
舰船航行安全影响因素识别。共包括7大类影响因素,28项因素子项,分别为:类别1−外部条件,下设助航设备外部条件、航标故障、能见度低、浅水效应、风浪、航区范围等因素子项;类别2−技术设备,下设助航仪器、通信设备、舰船技术、舵机和推进器等因素子项;类别3−航行因素,下设海图、舰船通信、驾驶台设置、人员配备等因素子项;类别4−航行过失,下设误认物标、设备使用、操作行为、通信情况判断等因素子项;类别5−违反规章,下设人为行动、值班配备、紧急避险等因素子项;类别6−他船行为,下设设备情况、海上避碰规格、瞭望、信号灯等因素子项;类别7−信息交流,下设舰船之间、船岸之间等因素子项。
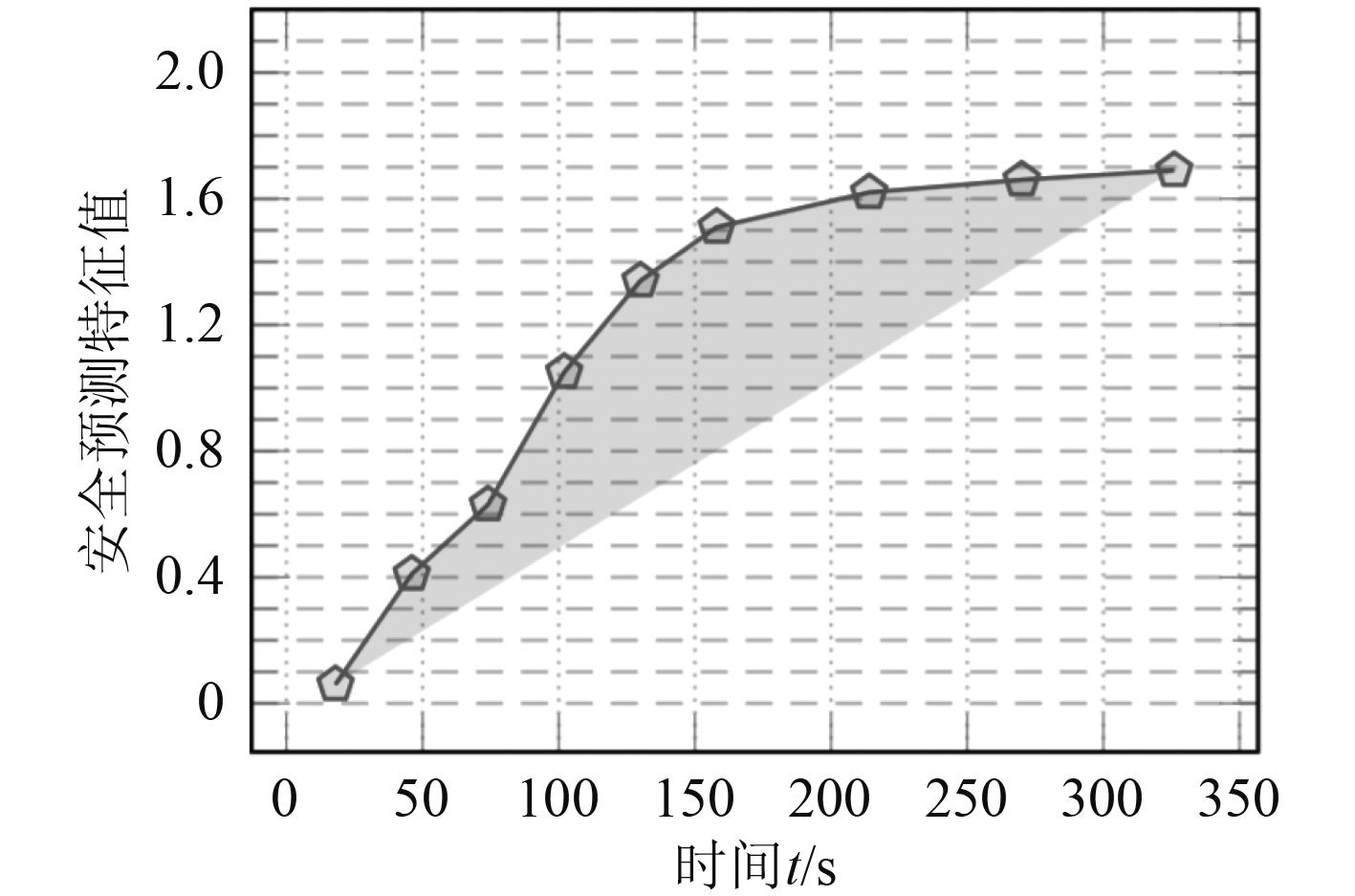
3.2 样本数据选择在5个等级的安全事故中随机抽取10%样本,将其作为改进ELM算法类别筛选试验集,其余90%作为操作集,通过测验得到理想类别精准度模型,设置改进ELM算法模型参数。初始群体数确定为350个,适合度阈值为1.7。改进ELM算法的测试结果如图3所示。选定SVM算法模型作为对比研究模型,用以验证改进ELM算法模型在安全性预测中的有效性。当优化效能处于最佳状态时,设定进化代数最大值为300,选取ELM激活函数sigmoid,设置50个隐藏点数。对比实验SVM算法模型采用RBF函数,计算出相关参数。
|
图 3 改进极限学习机算法的适合度进化代数渐变过程图 Fig. 3 Gradient process of fitness evolution algebra of improved limit learning machine algorithm |
实验采用Matlab软件,输入实验数据,得出进化代数变化的适合度,根据适合度分析影响航行安全性的影响因素和类别。在改进ELM算法模型中,共识别出10个影响因素,分别为助航仪器、浅水、能见度、瞭望、操纵行为、人员配备、航标、航区范围、海图、他航航行等影响因素,识别准确率为81.5%,识别时长为87.3 s;在SVM算法模型中,共识别出13个影响因素,包括紧急避险、风浪、人员配备、舵机和推进器、设备使用、航行情况、舰船间通信、遵守避让规则、船舶技术等,识别准确率为79.9%,识别时长为1562.7 s。可以看出,改进ELM算法模型与SVM算法模型相比,其在识别准确率和时效性上的优势较为明显。
4 结 语舰船安全性预测是保障舰船航行安全的重要工具,在安全性预测中要优选算法,构建起泛化性能好、学习速度快的预测模型,保证预测结果的准确性,为舰船航行决策提供依据。舰船安全性预测要采用改进的ELM算法,弥补传统ELM算法在输出值识别上的不足,建立起安全性预测模型,优化预测流程,进而提高预测时效性。
| [1] |
周书仁, 曹思思, 蔡碧野. 基于改进极限学习机算法的行为识别[J]. 计算机工程与科学, 2017(9): 1749-1757. ZHOU Shu-ren, CAO Si-si, CAI Bi-ye. Behavior recognition based on improved extreme learning machine algorithm[J]. Computer Engineering and Science, 2017(9): 1749-1757. DOI:10.3969/j.issn.1007-130X.2017.09.023 |
| [2] |
李巧君. 基于蚁群算法和极限学习机的舰船电子装备备件优化模型[J]. 舰船科学技术, 2022, 44(5): 158-161. LI Qiao-jun. Optimization model of ship electronic equipment spare parts based on ant colony algorithm and extreme learning machine[J]. Ship Science and Technology, 2022, 44(5): 158-161. DOI:10.3404/j.issn.1672-7649.2022.05.034 |
| [3] |
唐延强, 李成海, 宋亚飞. 基于改进粒子群优化和极限学习机的网络安全态势预测[J]. 计算机应用, 2021(3): 768-773. TANG Yan-qiang, LI Cheng-hai, SONG Ya-fei. Network security situation prediction based on improved particle swarm optimization and extreme learning machine[J]. Computer Applications, 2021(3): 768-773. DOI:10.11772/j.issn.1001-9081.2020060924 |
| [4] |
屈力刚, 杨忠文, 杨野光, 等. 采用改进粒子群算法的铣削参数优化研究[J]. 机械设计与制造, 2022(7): 187-191. QU Li-gang, YANG Zhong-wen, YANG Ye-guang, et al. Research on optimization of milling parameters using improved particle swarm optimization[J]. Mechanical Design and Manufacturing, 2022(7): 187-191. DOI:10.19356/j.cnki.1001-3997.2022.07.011 |
| [5] |
寇英信, 奚之飞, 杨爱武. 基于改进核极限学习机和集成学习理论的目标机动轨迹预测[J]. 国防科技大学学报, 2021(5): 23-35. KOU Ying-xin, XI Zhi-fei, YANG Ai-wu. Prediction of target maneuvering trajectory based on improved nuclear extreme learning machine and ensemble learning theory[J]. Journal of National University of Defense Technology, 2021(5): 23-35. DOI:10.11887/j.cn.202105003 |
| [6] |
赵坤, 覃锡忠, 贾振红. 采用改进的布谷鸟算法优化极限学习机[J]. 计算机仿真, 2018(11): 236-241. ZHAO Kun, QIN Xi-zhong, JIA Zhen-hong. Optimizing extreme learning machines with improved cuckoo algorithm[J]. Computer Simulation, 2018(11): 236-241. DOI:10.3969/j.issn.1006-9348.2018.11.050 |
 2022, Vol. 44
2022, Vol. 44
