2. 苏州科技大学 电子信息与工程学院,江苏 苏州 215009;
3. 苏州科技大学 地理科学与测绘工程学院,江苏 苏州 215009
2. School of Electronic and Information Engineering, Suzhou University of Science and Technology, Suzhou 215009, China;
3. School of Geography Science and Geomatics Engineering, Suzhou University of Science and Technology, Suzhou 215009, China
目前,光学遥感卫星影像技术发展迅速,遥感图像的分辨率已达厘米级,色彩信息也变得更加丰富,尤其是多光谱遥感影像技术,在进行海上目标识别时已经能够在真彩色条件下完成,使用人工肉眼就能相对准确和直观地判断舰船的类型、级别等信息。遥感多光谱图像技术不论在民用还是军事领域都具有非常重要的现实意义。在民用领域,多光谱遥感技术可以辅助进行海域的交通监控,进行船舶救援,辅助打击海事管理部门进行非法捕鱼打击、走私等违法活动的打击;在军事领域,可以准确获取敌方船舶、潜艇、军事基地的信息,分析敌方军事实力和作战意图,提升军事实力。
在多光谱遥感技术的图像中,每个遥感目标对象都有其特定的光谱特征,相同光照、分辨率等因素下,海洋背景、船舶、陆地、岛屿等目标的光谱特征各不相同,利用这一特性,可以通过光谱的分解和降维技术,利用光谱特性的差异快速识别目标物体。
本文首先介绍多光谱遥感技术的基本理论,结合多光谱降维处理技术和小波融合技术,研究了多光谱遥感图像的海上船舶目标识别技术和航行位置自动估计技术。
1 遥感多光谱图像技术简介不同被测目标或者相同被测目标的不同状态下,其电磁波特性具有明显的差异,多光谱遥感技术正是利用这一目标物体的电磁波差异性进行成像。
一幅多光谱遥感图像可同时记录不同电磁波波长物体的反射或辐射情况,对应的图像像素值[1]也存在差异,多光谱遥感技术的传感器可视为一个光谱数据立方体,具有多个空间维信息和特征维信息(见图1)。
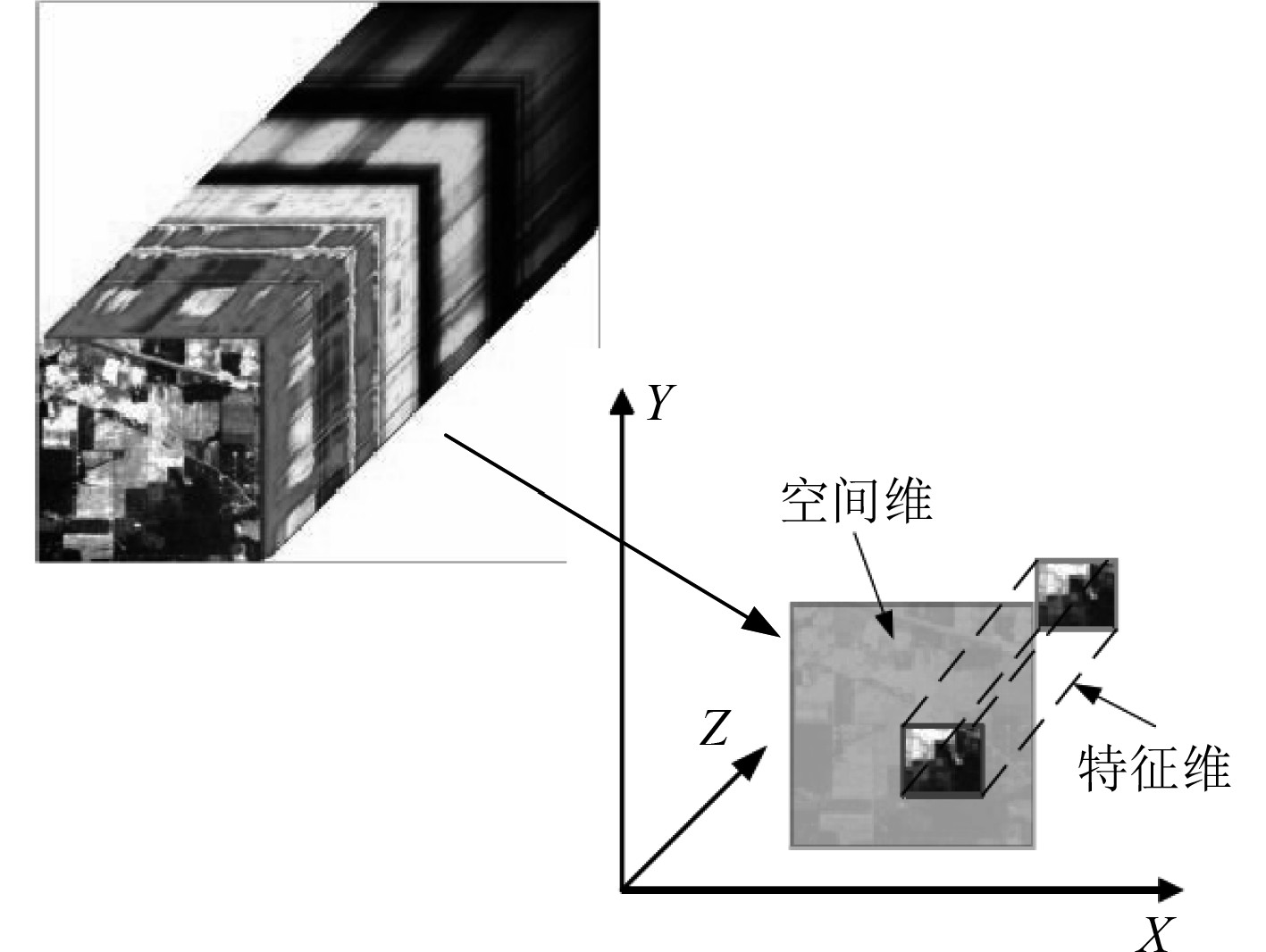
|
图 1 多光谱遥感图像信息的示意图 Fig. 1 Schematic diagram of multispectral remote sensing image information |
多光谱遥感技术的核心数据模型包括图像模型、光谱曲线模型和特征向量模型,分别如下:
1)图像模型
图像模型是最直接的多光谱遥感技术数据表现方式,基于图像模型可以确定被测目标在图像中的空间位置,包括每个像元的地面坐标信息,有利于帮助工作人员掌握目标的位置信息、形状信息,在分辨率足够的情况下,工作人员可直接从图像模型获取目标类别等更深层次信息。但由于图像模型只能表现出多光谱的部分信息,如果想进行批量的快速识别,还需要进一步的处理。
2)光谱曲线模型
光谱曲线模型与目标的光谱响应、电磁波波长等信息有关,在光谱空间信息的分析中应用非常多。光谱曲线模型中,每个目标的像元表示一条连续光谱曲线,曲线的特性反映了目标的反射特性。目前,基于光谱曲线模型可以实现目标类别的分类算法[2],有效提高图像处理的效率。
3)特征向量模型
特征向量模型表征遥感图像中每个像元对应着多个波段的反射值。在遥感图像的特征空间中,不同目标的统计分布特性不同,利用特征向量模型可以获取目标的光谱辐射特性,从而进行目标物体的特征识别。
2 基于遥感多光谱图像的舰船航行位置自动检测与估计技术研究 2.1 船舶遥感多光谱图像的降维处理技术多光谱遥感图像的处理过程中,降维预处理的主要作用是降低多光谱数据的复杂性和谱间相关性,去除遥感图像的冗余信息。多光谱遥感图像的降维预处理采用Green提出的最大噪声分量变换MNF方式,将原始光谱波段按照评估参数SNR进行波段分组,然后将分组的波段逐一提取特征,最后进行特征融合。
图2为多光谱遥感系统的降维技术原理图。

|
图 2 多光谱遥感系统的降维技术原理图 Fig. 2 Schematic diagram of dimensionality reduction technology for multispectral remote sensing system |
多光谱图像的谱间相关性是进行遥感图像降维处理的关键,遥感图像中同一空间位置的相邻波段具有较高的相关性,其原因在于相邻波段的波长相近,光谱反射值也相近。
遥感图像的光谱波段X和Y的相关系数定义为:
| $ {R_{XY}} = \frac{{\displaystyle\sum\limits_m {\left( {{X_m} - \overline X } \right)\left( {{Y_m} - \overline Y } \right)} }}{{\sqrt {\displaystyle\sum\limits_m {{{\left( {{X_m} - \overline X } \right)}^2}} } \sqrt {\displaystyle\sum\limits_m {{{\left( {{Y_m} - \overline Y } \right)}^2}} } }} \text{。} $ |
式中:
遥感多光谱图像的降维处理流程包括:
1)根据相关系数的公式计算相邻光谱波段的相关系数,构造相关系数矢量矩阵[3]。
2)对相关系数矢量矩阵进行处理,提取局部相关系数的极小值,将多光谱遥感图像空间按照极小值的个数划分为K+1个数据子集。
3)通过对比波段子集个数与阈值,基于MNF进行波段分组,确定最终的波段分组个数,并将剩余的波段单独作为一个单元。
4)进行波段特征提取和融合。
图3为提取的多光谱遥感图像波段之间的相关系数曲线。
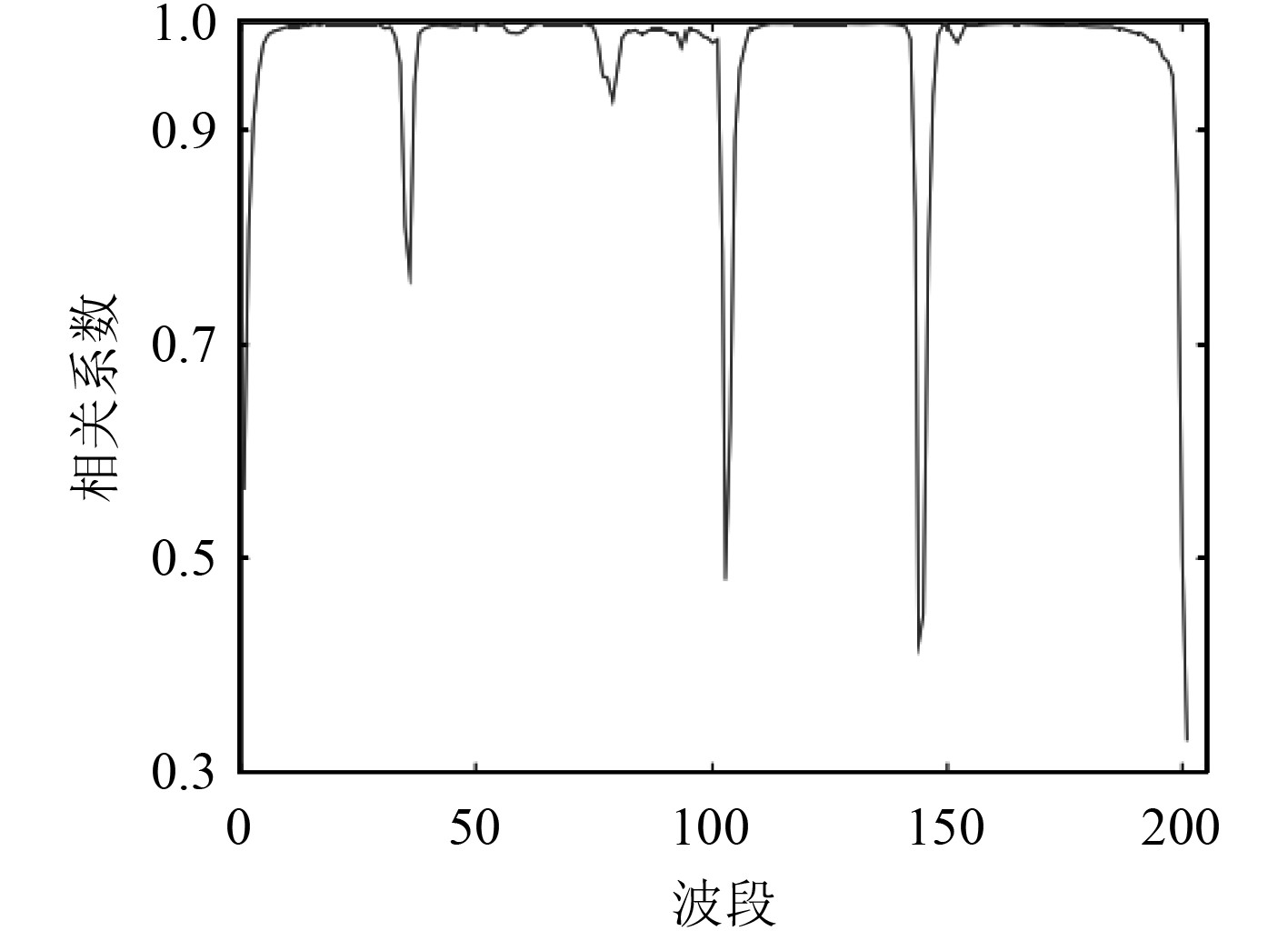
|
图 3 多光谱遥感图像波段之间的相关系数曲线 Fig. 3 Correlation coefficient curve between bands of multispectral remote sensing image |
图像融合技术在海上遥感多光谱图像的处理中也是重要的环节,其目的是对多个传感器阵列的图像信息进行综合处理,使同一目标、同一场景下的特征提取更加准确和全面。
小波变换融合的基本思想是利用小波变换算法,将船舶多光谱图像转化为多尺度的分解量,然后在不同尺度下进行融合。在小波变换融合算法中,图像信号的分解空间相互独立,分解过程中不会产生图像信息的丢失和多余信息,图4为遥感图像小波融合算法的原理图。

|
图 4 遥感图像小波融合算法的原理图 Fig. 4 Schematic diagram of remote sensing image wavelet fusion algorithm |
融合算法首先将得到的遥感图像从RGB空间转换至HIS彩色空间,把具有高分辨率的I分量进行小波变换,得到遥感图像的高频部分,然后利用I分量的小波变换结果与S分量进行融合计算。
通常在遥感图像中,船舶目标是图像的高频部分,与背景有明显区别,表示为:
| $ f\left( t \right) = s\left( t \right) + n\left( t \right) \text{。} $ |
信号的小波展开方程为:
| $ \begin{gathered} f(t) = \sum c (m,n){\psi _{mn}}(t) ,\\ {\psi _{mn}}(t) = {2^{ - \frac{m}{2}}}\psi \left( {{2^{ - m}}t - n} \right)。\\ \end{gathered} $ |
式中:
在遥感多光谱图像中,小波变换采用的尺度对于噪声过滤、边缘处理有较大的影响,当小波变换的尺度较小时,遥感图像处理时边缘细节较为丰富,船舶位置信息的精度高,但此时图像噪声干扰较大,图像处理的速度也相对较慢;当小波变换的尺寸较大时,图像边缘的细节较粗糙,但是具有较好的噪声抑制效率。
结合小波尺度的特点,本文使用多维连续小波变换算法MCWT算法进行图像的小波融合,对于二维图像的MCWT算法可以表示为:
| $\begin{split} &w\left( {a,\theta ,{b_x},{b_y}} \right) = \int_{ - x}^{ + \infty } g (x,y){\psi _{a,h}}\left( {{r_\theta }\left( {\frac{{x - {b_x}}}{a},\frac{{y - {b_y}}}{a}} \right)} \right){\rm{d}}x \text{,} \\ &{r_\theta }(x,y) = (x\cos (\theta ) - y\sin (\theta )){(x\sin (\theta ) + y\cos (\theta ))^{\rm{T}}} \text{。} \end{split}$ |
式中:a为图像的能量密度,
MCWT的逆变换为:
| $ \iint |g(x,y){|^2}{\rm{d}}x{\rm{d}}y = \iiint {\int {{{\left| {w\left( {a,\theta ,{b_x},{b_y}} \right)} \right|}^2}} }{\rm{d}}{b_x}{\rm{d}}{b_y}{\rm{d}}a{\rm{d}}\theta 。$ |
在实际船舶目标检测领域,可以将较难识别的遥感图像大致分为:1)对比度较低的遥感图像,目标的灰度较弱;2)是目标像素较少的遥感图像,目标的能量较弱[4]。
灰度弱的船舶目标图像信噪比定义为:
| $ SNR = \frac{{{{\left( {s - \mu } \right)}^2}}}{{{\sigma ^2}}} \text{。} $ |
式中:
能量弱的船舶目标图像信噪比定义为:
| $ SNR = \frac{{\displaystyle\sum {{t^2}} }}{{\displaystyle\sum {b^2}}} \text{。} $ |
式中:
基于船舶多光谱图像的船舶航行位置检测流程如下:
1)多光谱遥感图像的预处理
结合最大噪声分量变换MNF方式,将原始光谱的波段进行波段分组和降维处理,定义观测图像信号为:
| $ g\left( {x,y} \right) = A\left( {x,y} \right) + h\left( {x,y} \right) \text{,} $ |
式中:
2)计算遥感多光谱图形的信噪比SNR
设定连续小波变换和逆变换的尺度,匹配船舶遥感图像的信噪比等级[5]。
3)基于小波融合算法建立船舶目标检测公式
| $ s(x,y) = \sum\limits_{{x^\prime } = 1}^{Mx} {\sum\limits_{{y^\prime } = 1}^{My} {{g^2}} } \left( {{x^\prime },{y^\prime }} \right) \text{。} $ |
其中,
4)输出船舶目标检测结果
基于遥感多光谱图像的船舶目标位置检测流程如图5所示。
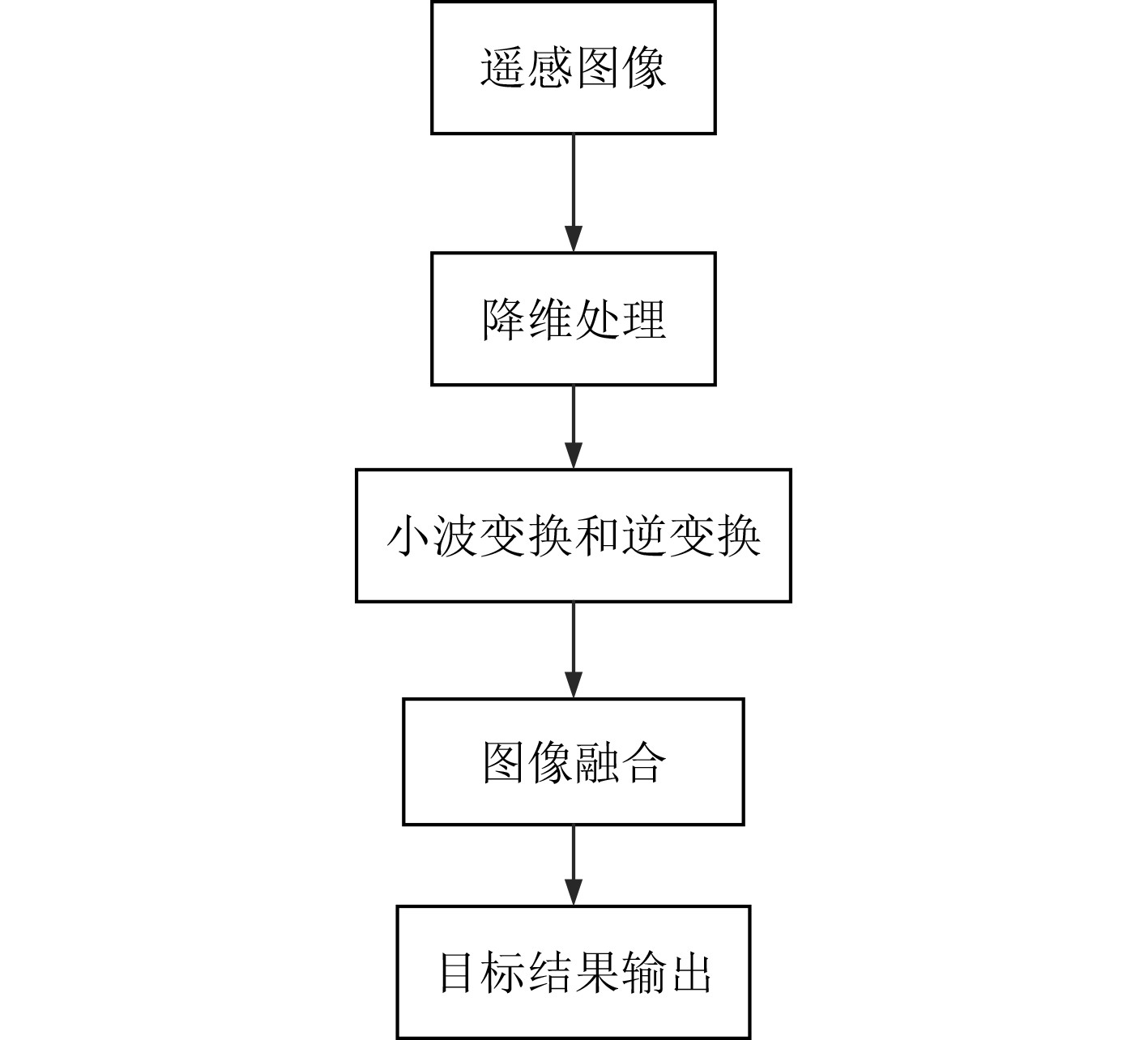
|
图 5 基于遥感多光谱图像的船舶目标位置检测流程 Fig. 5 Ship target location detection process based on remote sensing multispectral images |
图6为基于遥感多光谱图像的船舶目标位置检测示意图。

|
图 6 基于遥感多光谱图像的船舶位置检测示意图 Fig. 6 Schematic diagram of ship position detection based on remote sensing multispectral images |
海上船舶遥感多光谱图像的分辨率高,能够获取船舶目标的精确信息,但图像处理过程相对复杂,针对这一问题,本文提出多光谱图像的降维处理技术和小波变换融合算法,能够显著提高船舶多光谱图像的目标位置检测效果。
| [1] |
刘婷, 程建. 小波变换和稀疏表示相结合的遥感图像融合[J]. 中国图象图形学报, 2013, 18(8): 1045-1053. LIU Ting, CHENG Jian. Remote sensing image fusion based on wavelet transform and sparse representation[J]. Chinese Journal of Image and Graphics, 2013, 18(8): 1045-1053. DOI:10.11834/jig.20130820 |
| [2] |
邓书显, 曹殿立. 基于小波变换的全色多光谱高空间图像数据双源融合算法处理技术研究[J]. 西华大学学报:自然科学版, 2008(4): 7-12+1. DENG Shu-xian, CAO Dian-li. Research on dual source fusion algorithm processing technology of panchromatic multispectral hyperspace image data based on wavelet transform[J]. Journal of Xihua University:Natural Science Edition, 2008(4): 7-12+1. |
| [3] |
郑永安, 陈玉春, 宋建社, 等. 基于提升机制小波变换的SAR与多光谱图像融合算法[J]. 计算机工程, 2006, 32(6): 195-197. ZHENG Yong-an, CHEN Yu-chun, SONG Jian-she, et al. SAR and multispectral image fusion algorithm based on lifting mechanism wavelet transform[J]. Computer Engineering, 2006, 32(6): 195-197. |
| [4] |
林卉, 杜培军, 肖剑平. 利用小波变换进行遥感多光谱图像融合的算法及实现[J]. 地球科学与环境学报, 2006(1): 75-78+100. LIN Hui, DU Pei-jun, XIAO Jian-ping. Algorithm and implementation of remote sensing multispectral image fusion using wavelet transform[J]. Journal of Geoscience and Environment, 2006(1): 75-78+100. DOI:10.3969/j.issn.1672-6561.2006.01.016 |
| [5] |
奚祥书, 夏凯, 杨垠晖, 等. 结合多光谱影像降维与深度学习的城市单木树冠检测[J]. 遥感学报, 2022, 26(4): 711-721. XI Xiang-shu, XIA Kai, YANG Yin-hui, et al. Urban single tree crown detection combined with multi spectral image dimension reduction and deep learning[J]. Journal of Remote Sensing, 2022, 26(4): 711-721. DOI:10.11834/jrs.20220163 |
 2022, Vol. 44
2022, Vol. 44
