自20世纪30年代起,海上运输产业逐渐发展起来,海上集装箱运输成为国际之间大宗国际贸易最主要的运输方式[1,2]。海上集装箱运输便于港口作业机械化管理,提升货物运输时的装卸效率与海上货物运输量。但由于海上运输路径错综复杂,而遇到特殊海域状况时,集装箱货船需更改既定航线。为节省海上货运船舶航行时间成本,提升货物运输效率,很多学者提出集装箱船舶货物运输路径选择方法。母柏松[3]提出联运最优路径选择方法,该方法从集装箱船舶运输的经济角度入手,通过分析船舶运输环境影响因素,建立运输路径优化选择模型,利用该模型获得集装箱船舶航行路径。但该方法角度较为单一,并未考虑集装箱船舶航行的时间成本,因此存在片面性。潘伟[4]等提出智能船舶航线规划选择方法,该方法通过计算船舶航行时海域水深、浪高等数值,分析集装箱船舶航行风险,并选择相对安全的集装箱船舶航行路径。但该方法获取海域环境数据质量不高,使其选择的集装箱船舶航行路径存在偏差。D-S证据推理算法是多属性选择分析算法,目前被应用在选择和寻优等相关领域,在描述信息存在不确定性时使用区间估计方式获得选择结果。由于集装箱船舶在运输货物过程中,影响航行路径的因素较多且存在模糊性,因此将D-S证据推理算法与模糊理论相结合,提出基于模糊证据推理的集装箱船舶货物运输路径选择方法。
1 集装箱船舶货物运输路径选择 1.1 船舶货物运输运营成本计算集装箱船舶货物运输时的航线成本由总资本成本和管理费用构成,但由于船舶航行时日租金以及货物装卸费用均随着市场需求呈现波动变化趋势,且波动较为频繁,为此本文不考虑集装箱船舶进行海上运输时的经济成本,仅从其海上运输的时间成本入手。
以相同吨位船舶市场价值作为参考,设
| $ {T_t} = \frac{1}{{n \cdot {v_z}}}\cdot\sum\limits_u {\sum\limits_e {O_{ue}^k} }。$ | (1) |
式中:
集装箱船舶在运输过程中其时间成本也包括在出发港口、中转港口以及终点港口排队等待时间,
| $ {T_{md}} = \sum\limits_u {{t_u} + \left[ {\frac{{\displaystyle\sum\limits_u {\displaystyle\sum\limits_e {({G_{ue}} + {G_{eu}})} } }}{{{r_u}}}} \right]} /{f_k} 。$ | (2) |
式中:
依据公式(1)和公式(2)计算集装箱船舶货物运输时的总时间运营成本,具体公式如下:
| $ \begin{split} T = &\frac{1}{{n \cdot {v_z}}}\cdot\sum\limits_u {\sum\limits_e {O_{ue}^k} } +\sum\limits_u {t_u} + \left[ {\frac{{\displaystyle\sum\limits_u {\displaystyle\sum\limits_e {({G_{ue}} + {G_{eu}})} } }}{{{r_u}}}} \right] /{f_k} 。\end{split} $ | (3) |
模糊集是通过构建适当的隶属度函数,通过模糊集合之间的相关转换和计算后,对模糊对象进行实时分析的方法,其特征函数可描述某个元素是否存在特定集合内。由于集装箱船舶航线存在不确定性,依据得到的港口航线间时间运营成本,建立集装箱船舶货物运输路径模糊子集,其详细步骤如下:
假设
| $ {\varphi _R} = \left\{ \begin{array}{ll} 1&({Y_1}, \cdots ,{Y_n}) \in R({X_1}, \cdots ,{X_n}) ,\\ 0& {\rm{others}} 。\end{array} \right. $ | (4) |
可知,集装箱船舶运输路径精确集合特征函数取值仅为1或者0,而对于模糊集合来说,其取值区间为[0,1],因此需对集装箱船舶运输路径运营成本变量集合的论域进行关联处理,则集装箱船舶运输路径模糊子集
| $ F = \frac{{\displaystyle\sum\nolimits_i {{\varphi _i}} }}{{\displaystyle\sum\nolimits_i {{Y_i}} }} 。$ | (5) |
以集装箱船舶运输路径模糊子集作为输入,构建基于模糊证据推理的集装箱船舶货物运输路径选择模型,利用该模型输出集装箱船舶货物运输路径选择结果,其详细过程如下:
步骤1 以集装箱船舶运输路径模糊子集为基础,评价该子集内的集装箱船舶运输路径风险因子,并设定其评价模糊集合为
步骤2 构建模糊置信选择矩阵。假设
| $ {\varpi _l} = \sum\limits_{k = 1}^K {{\lambda _k}\varpi _l^k} 。$ | (6) |
对公式(6)进行归一化处理,则有:
| $ {\bar \varpi _l} = \frac{{{\varpi _l}}}{{\displaystyle\sum\limits_{l = 1}^L {\varpi _l^{}} }} 。$ | (7) |
假设
| $ {U_{ij}}({Z_n},R{F_l}) = \sum\limits_{k = 1}^K {{\lambda _k}U_{ij}^k({Z_n},R{F_l})} 。$ | (8) |
依据式(8)结果,则在
| $ \tilde X = \left[ \begin{array}{*{20}{c}} {Z_1} \\ {Z_2} \\ \vdots \\ {Z_3} \end{array} \right] = \left[ \begin{array}{*{20}{c}} {{\tilde X}_1}(1)& \cdots & {{\tilde X}_1}(L) \\ {{\tilde X}_2}(1)& \cdots& {{\tilde X}_2}(L) \\ {} & \cdots &{} \\ {{\tilde X}_N}(1)& \cdots & {{\tilde X}_N}(L) \end{array} \right] 。$ | (9) |
步骤3 去模糊化处理。为获取更为精准的集装箱运输路径,对公式(9)进行去模糊化处理。
假设
| $ {h_{ij}} = \frac{{\displaystyle\sum\limits_{i = 0}^n {({b_i} - {c_i})} }}{{\displaystyle\sum\limits_{i = 0}^n {({b_i} - {c_i})} - \sum\limits_{i = 0}^n {{a_i} - {d_i}} }} 。$ | (10) |
式中:
| $ {X_n}(l) = \sum\limits_{i = 1}^5 {\sum\limits_{j = 1}^5 {{h_{ij}}{U_{ij}}({Z_n},R{F_l})} } 。$ | (11) |
利用式(11),计算明确的集装箱船舶航行路径置信选择矩阵,其表达公式如下:
| $ {\boldsymbol{X}} = \left[\begin{array}{*{20}{c}} {Z_1} \\ {Z_2} \\ \vdots \\ {Z_3} \end{array} \right] = \left[ \begin{array}{*{20}{c}} {X_1}(1)& \cdots & {X_1}(L) \\ {X_2}(1)& \cdots & {X_2}(L) \\ {}& \cdots {} \\ {X_N}(1)&\cdots & {X_N}(L) \end{array} \right] 。$ | (12) |
利用式(12)即可得到集装箱船舶货物运输路径选择结果。
2 实验分析以某海运公司集装箱运输船舶为实验对象,使用本文方法选择其集装箱运输船舶运送货物航行路径,验证本文方法实际应用效果。将一批货物自始发地运输到港口C,其航行路径共4条,如图1所示。
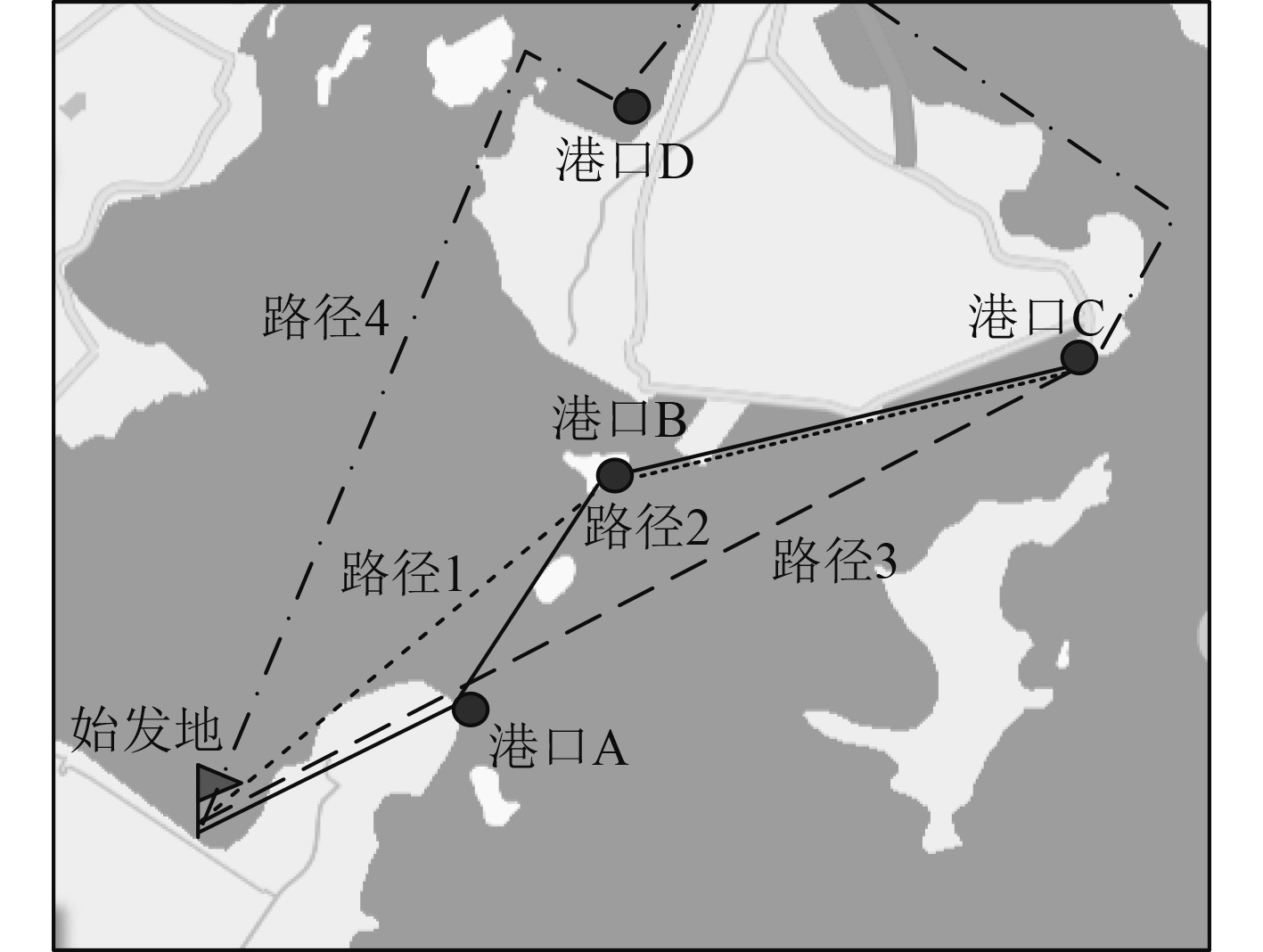
|
图 1 集装箱运输船舶航行路径 Fig. 1 Navigation route of container transport vessel |
使用本文方法计算集装箱船舶载重分别为5000 t、2万吨、5万吨和10万吨情况下的时间成本,结果如图2所示。
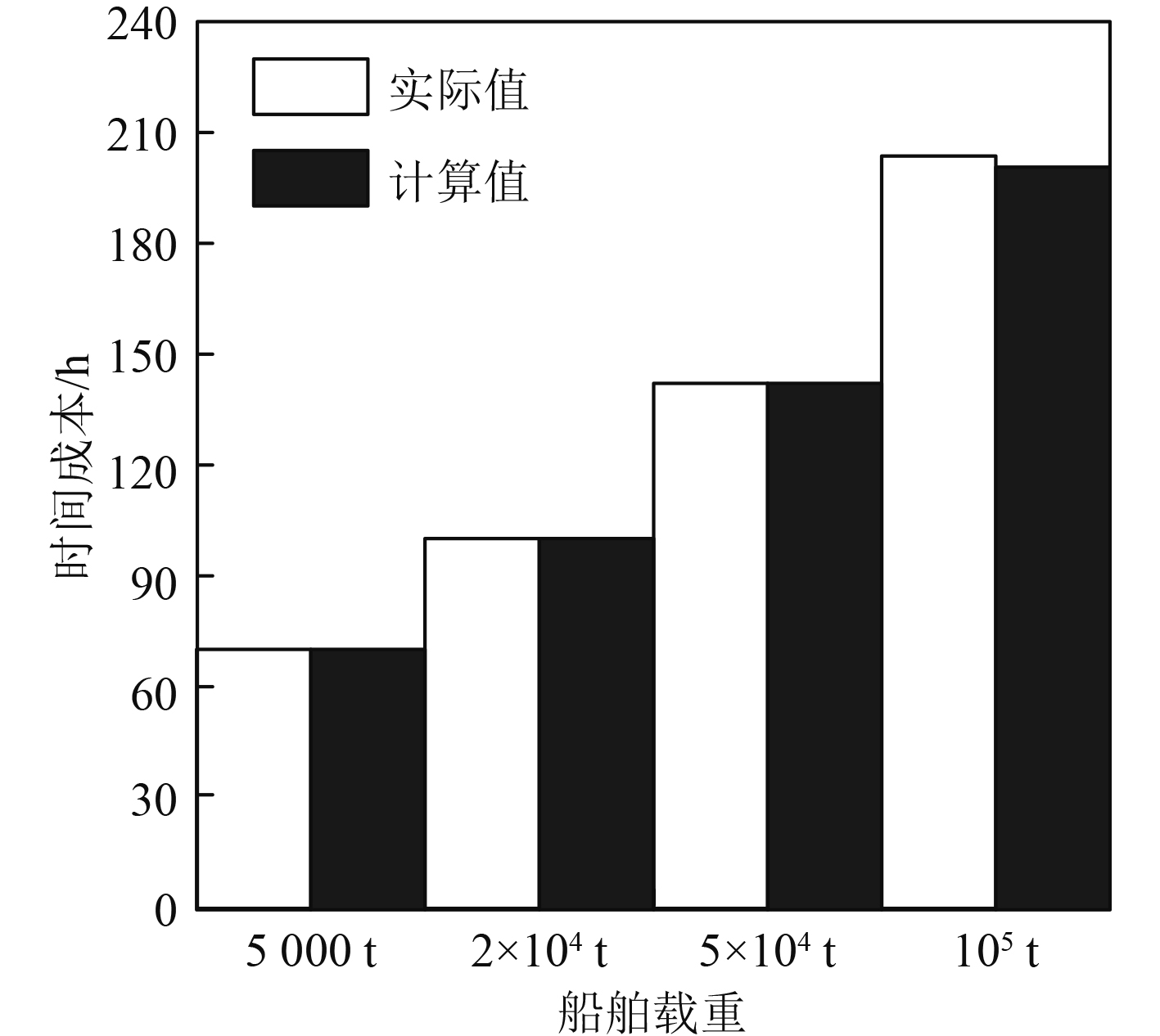
|
图 2 船舶货物运输运营成本计算测试结果 Fig. 2 Calculation and test results of ship cargo transportation operation cost |
分析可知,船舶载重吨数越大,在特定航行路径上所消耗的时间越长。在船舶载重为5万吨以下时,本文计算得出的船舶航行运营时间成本与其实际时间成本数值完全相同。当船舶载重为10万吨时,航行时的运营时间成本数值较大,本文方法计算得出的运营时间成本和实际值仅相差3 h左右。该数值在船舶总航行时长中占比极小,说明本文方法计算船舶航行运营时间较为准确,为选择集装箱船舶航行路径提供较好的数据基础。
2.2 运输路径选择测试以图1内4条集装箱船舶航行路径作为实验对象,使用本文方法选择由始发地发往港口C的航行路径,结果如图3所示。
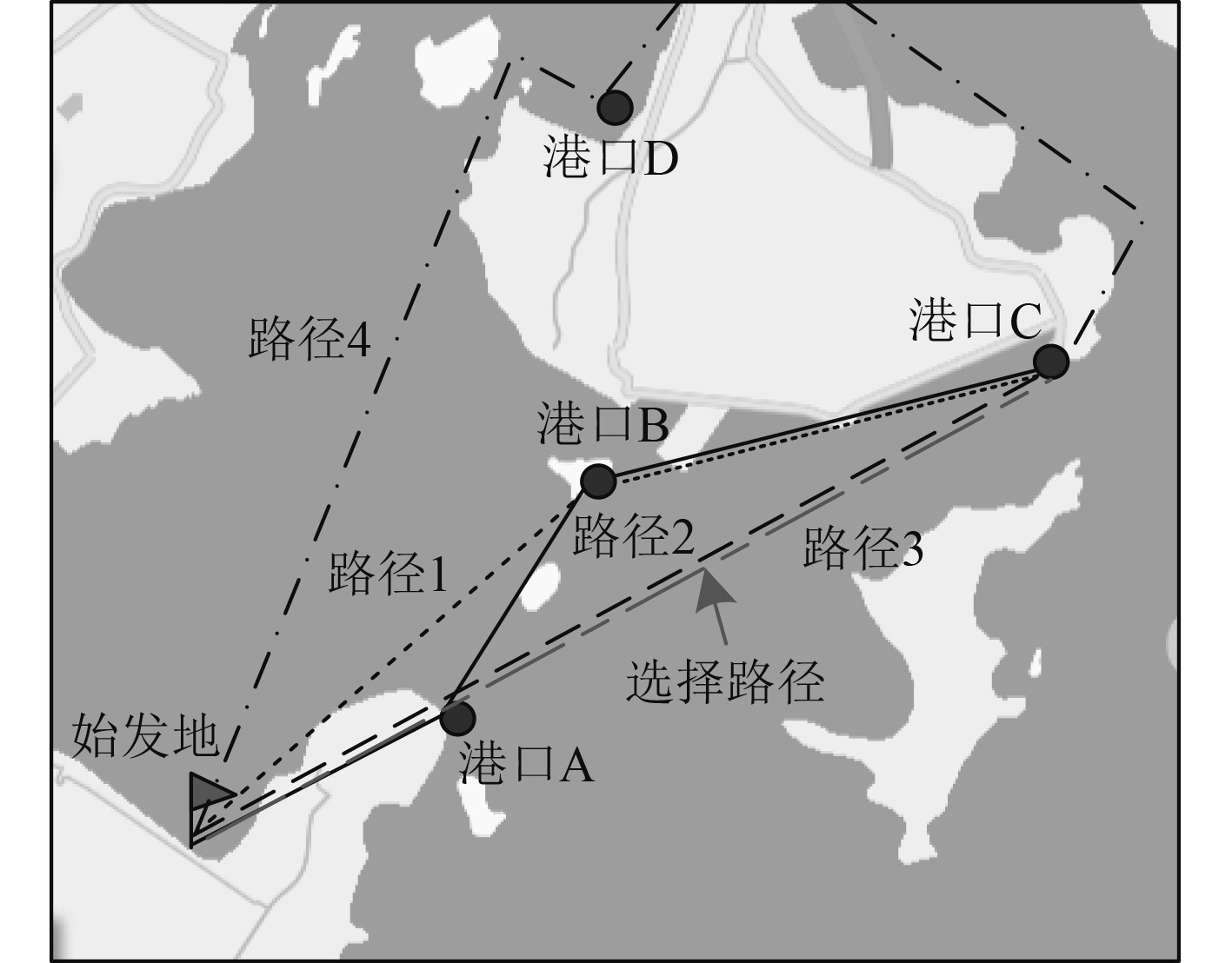
|
图 3 集装箱船舶航行路径选择结果 Fig. 3 Results of container ship navigation route selection |
分析可知,本文方法选取的集装箱船舶航行路径为由始发地发往港口A,再由港口A发往港口C,该路径与路径3相重合,说明本文方法可有效在4条船舶运输路径内选择合适的航行路径,应用效果好。
进一步验证本文方法选取集装箱船舶运输路径能力,以该海运公司小型、中型、大型集装箱船舶作为实验对象,使用本文方法选择运输路径后,计算运输时节省的时间成本数值,结果如图4所示。
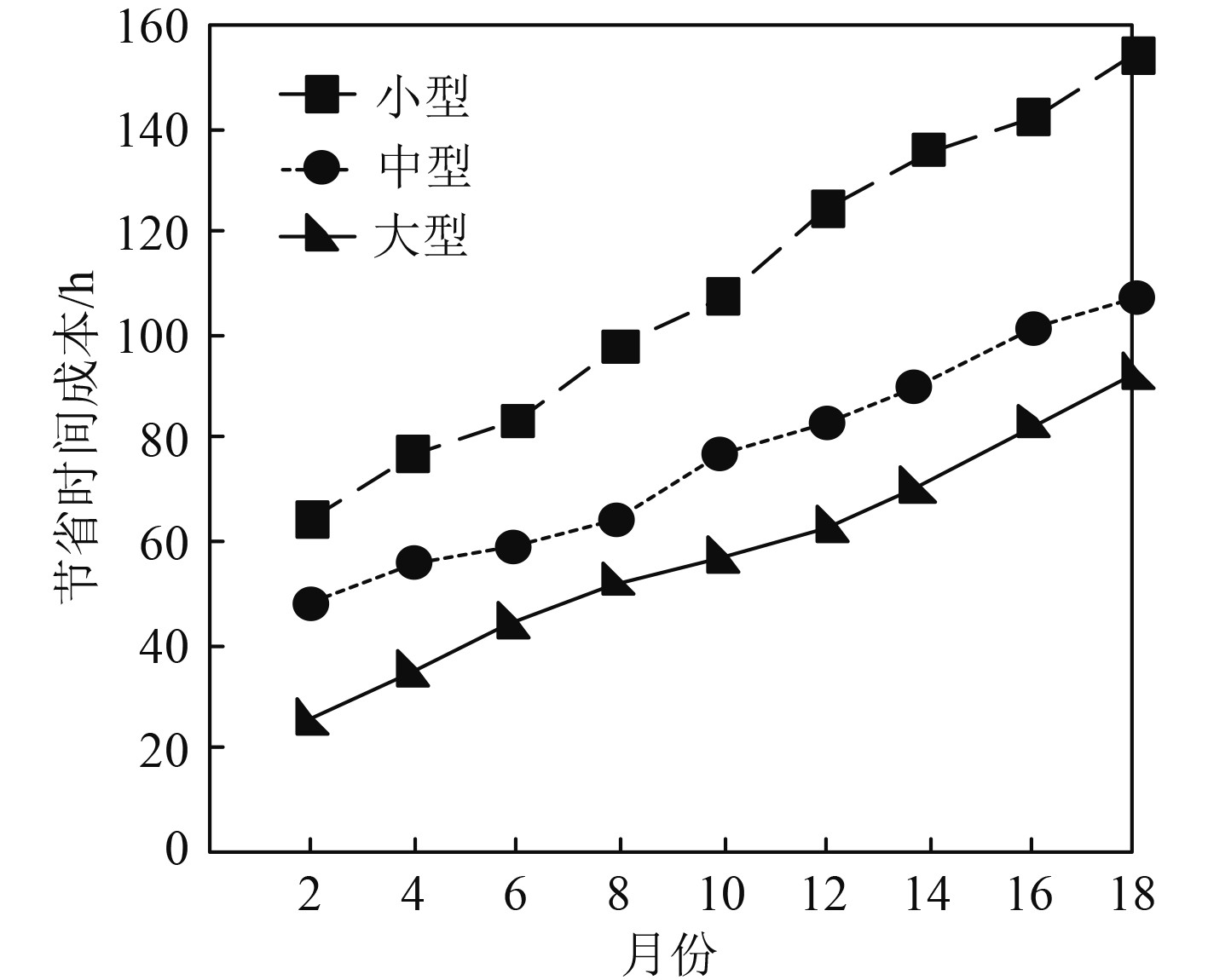
|
图 4 船舶航行节省时间成本数值 Fig. 4 Time saving cost value of ship navigation |
分析可知,应用本文方法后,该公司不同类型的集装箱船舶运输时节省的时间成本数值均随时间的增加而增加。其中小型集装箱船舶运输时节省的时间成本数值最大达到155 h左右。该数值说明,本文方法可有效降低集装箱船舶运输时间成本,提升其货物运输效率。
3 结 语本文提出基于模糊证据推理的集装箱船舶货物运输路径选择方法,以某公司船舶为实验对象对本文方法进行了多角度验证。从验证结果可知,本文方法计算集装箱船舶时间成本较为准确,且可有效在多个运输路径内选取最佳的运输路径,应用效果较佳,未来可应用于船舶运输路径选择领域。
| [1] |
王洋洋, 朱瑾. 集装箱码头装卸运输路径轨迹规划研究[J]. 计算机仿真, 2019, 36(5): 450-455. DOI:10.3969/j.issn.1006-9348.2019.05.092 |
| [2] |
蒋美芝, 吕靖. 基于Pareto蚁群算法的船舶风险规避路径优化[J]. 交通运输系统工程与信息, 2019, 19(1): 192-199. DOI:10.16097/j.cnki.1009-6744.2019.01.029 |
| [3] |
母柏松. 单OD对间集装箱多式联运最优路径选择研究[J]. 铁道运输与经济, 2019, 41(7): 99-105. DOI:10.16668/j.cnki.issn.1003-1421.2019.07.18 |
| [4] |
潘伟, 董其林, 许小卫, 等. 考虑通航环境因素的智能船舶航线规划[J]. 上海海事大学学报, 2021, 42(3): 76-84. DOI:10.13340/j.jsmu.2021.03.013 |
 2022, Vol. 44
2022, Vol. 44
