由于海底界面的存在,尤其在浅海环境中,水中声波的传播就不再适用无限空间声场计算模型,声波会在海底界面处产生反射与透射等声学现象,了解海底的声反射特性有助于水中目标探测、水声通信以及海洋声场的研究,因此有必要对海底界面的声反射特性进行分析与讨论。对于理想流体介质中声场的仿真有基于线性波动方程的边界元、有限元等比较成熟的数值计算方法,有大量的理论模型用于参考分析[1-2]。在海底声反射模型的建模分析中关键是对水下沉积物的模拟,目前水下沉积物分析主要有3类模型,分别为等效密度流体模型(EDFM)、弹性体模型与多孔介质模型。等效密度流体模型将沉积物等效为均匀的流体介质,于盛齐[3]根据等效密度流体近似反射模型得到不同掠射角下的海底反射损失,并反演海底介质参数,通过反演结果与部分实测参数值的比较验证了反演方法的可行性。弹性体模型将海底介质视为均匀的弹性结构,但实际水下沉积物应是液体介质与固体颗粒的混合物,经典的Biot多孔弹性介质模型[4-5]同时考虑了其弹性与多孔特性,更好的模拟了海底介质的真实状态。Stoll[6]在Biot多孔介质理论的基础上进行了大量的理论分析,给出了沙和软质沉积物的介质参数并计算分析了平面声波在水-沉积物界面的反射与透射。彭临惠[7]利用Biot-Stoll多孔介质声传播理论和分析方法对声波在沙质界面的声能透射与声波反射进行了理论计算和分析。基于多孔弹性介质模型的海底介质参数波动对声波反射的影响目前还缺少相关研究。利用Biot多孔介质模型,结合COMSOL压力声学-多孔弹性波多物理场计算模型,在沙质介质参数的基础上,对部分海底介质参数进行分析,研究其值的波动对界面处平面声波反射系数的影响规律。
1 计算模型 1.1 分层介质模型首先考虑2层理想流体介质界面的声传播问题。声波从介质1入射到介质2时会在界面处发生声波的反射、折射与透射,对于平面声波在2种特性阻抗不同的理想流体中的传播,可以根据入射波和界面处的边界条件求解出散射波和透射波的解析解[8]。
设介质1与介质2的特性阻抗分别为
介质1中声波为入射声波与反射声波之和:
| $ {p}_{1}={P}_{i}{e}^{i\left(\omega t-{k}_{1}x\right)}+{P}_{r}{e}^{i\left(\omega t+{k}_{1}x\right)} ,$ | (1) |
介质2中声波为透射声波:
| $ {p}_{2}={P}_{t}{e}^{i\left(\omega t-{k}_{2}x\right)} ,$ | (2) |
2种介质中质点速度分别为:
| $ {v}_{1}=\frac{{P}_{i}}{{\rho }_{1}{c}_{1}}{e}^{i\left(\omega t-{k}_{1}x\right)}-\frac{{P}_{r}}{{\rho }_{1}{c}_{1}}{e}^{i\left(\omega t+{k}_{1}x\right)}, $ | (3) |
| $ {v}_{2}=\frac{{P}_{t}}{{\rho }_{2}{c}_{2}}{e}^{i\left(\omega t-{k}_{2}x\right)}{\text{。}} $ | (4) |
结合分界面
| $ {\left({p}_{1}\right)}_{x=0}={\left({p}_{2}\right)}_{x=0} , {\left({v}_{1}\right)}_{x=0}={\left({v}_{2}\right)}_{x=0}, $ |
可以求得反射声波的大小并计算声压反射系数为:
| $ {r}_{p}=\frac{{\rho }_{2}{c}_{2}-{\rho }_{1}{c}_{1}}{{\rho }_{2}{c}_{2}+{\rho }_{1}{c}_{1}} 。$ | (5) |
同理对于平面声波斜入射时,计算得反射系数为:
| $ {r}_{P}=\frac{m\mathit{{\rm{cos}}}{\theta }_{i}-\sqrt{{n}^{2}-{\mathit{{\rm{sin}}}}^{2}{\theta }_{i}}}{m\mathit{{\rm{cos}}}{\theta }_{i}+\sqrt{{n}^{2}-{\mathit{{\rm{sin}}}}^{2}{\theta }_{i}}} ,$ | (6) |
其中
根据反射系数式(5)与式(6)可以在Matlab软件中绘制反射系数曲线,直观看出反射系数随介质参数的变化结果。
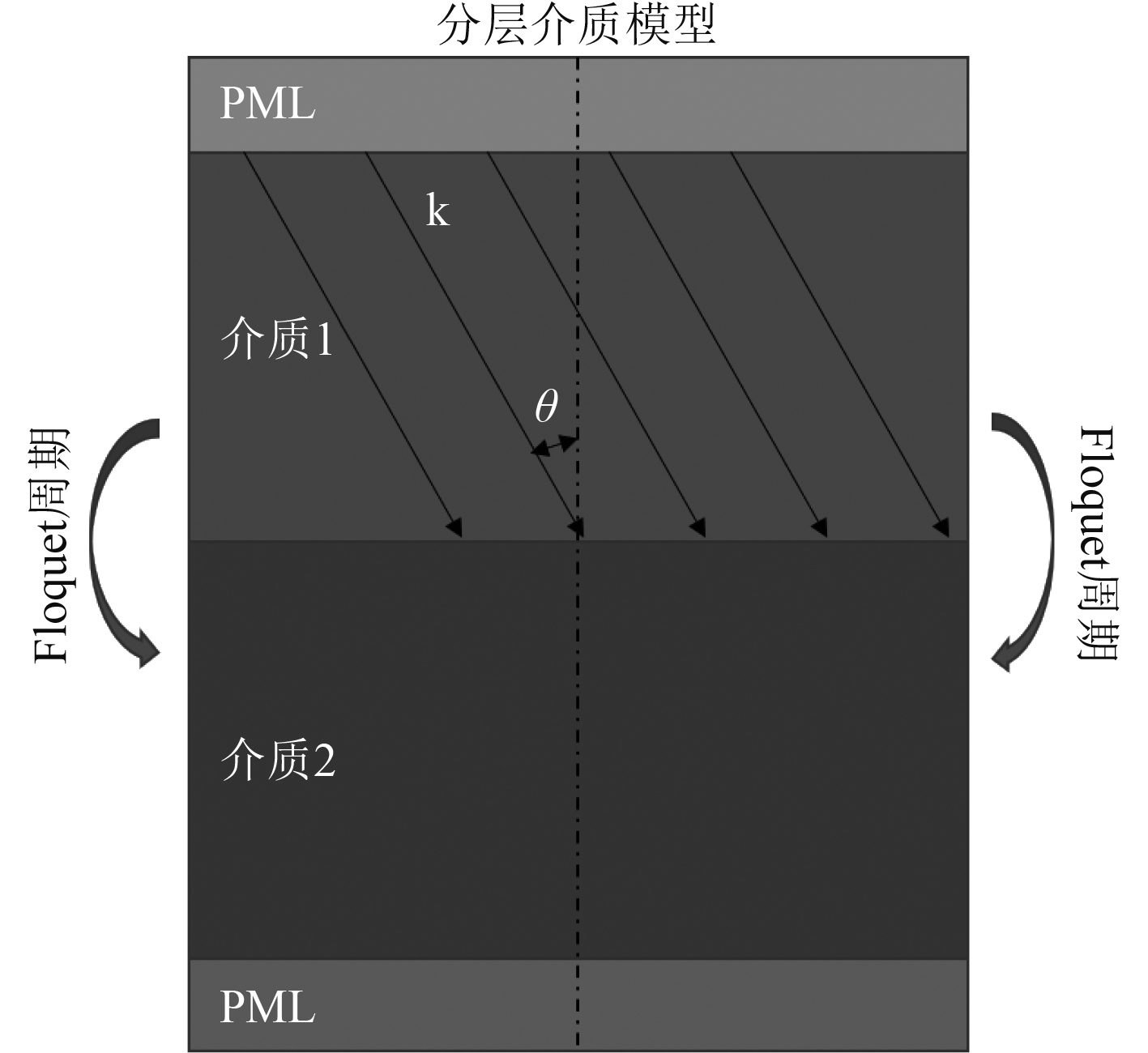
同时还进行此问题的仿真计算,在Comsol软件中建立分层介质声场仿真计算模型,将数值解与上述解析解进行对比,验证理想流体分层介质模型建模方法与流程的正确性,为后续水-多孔介质的分层介质建模提供参考。计算模型如图1所示,这里使用声学有限元建立模型,由于有限单元不能建立无限大计算域,故此模型的上下边界用完美匹配层(PML)来模拟无限远吸收边界条件,左右边界使用Floquet周期性边界条件用来表达无限大的分层介质界面。模型中上下层介质都是均匀的理想流体介质,改变其特性阻抗
|
图 1 模型示意图 Fig. 1 The diagram of the model |
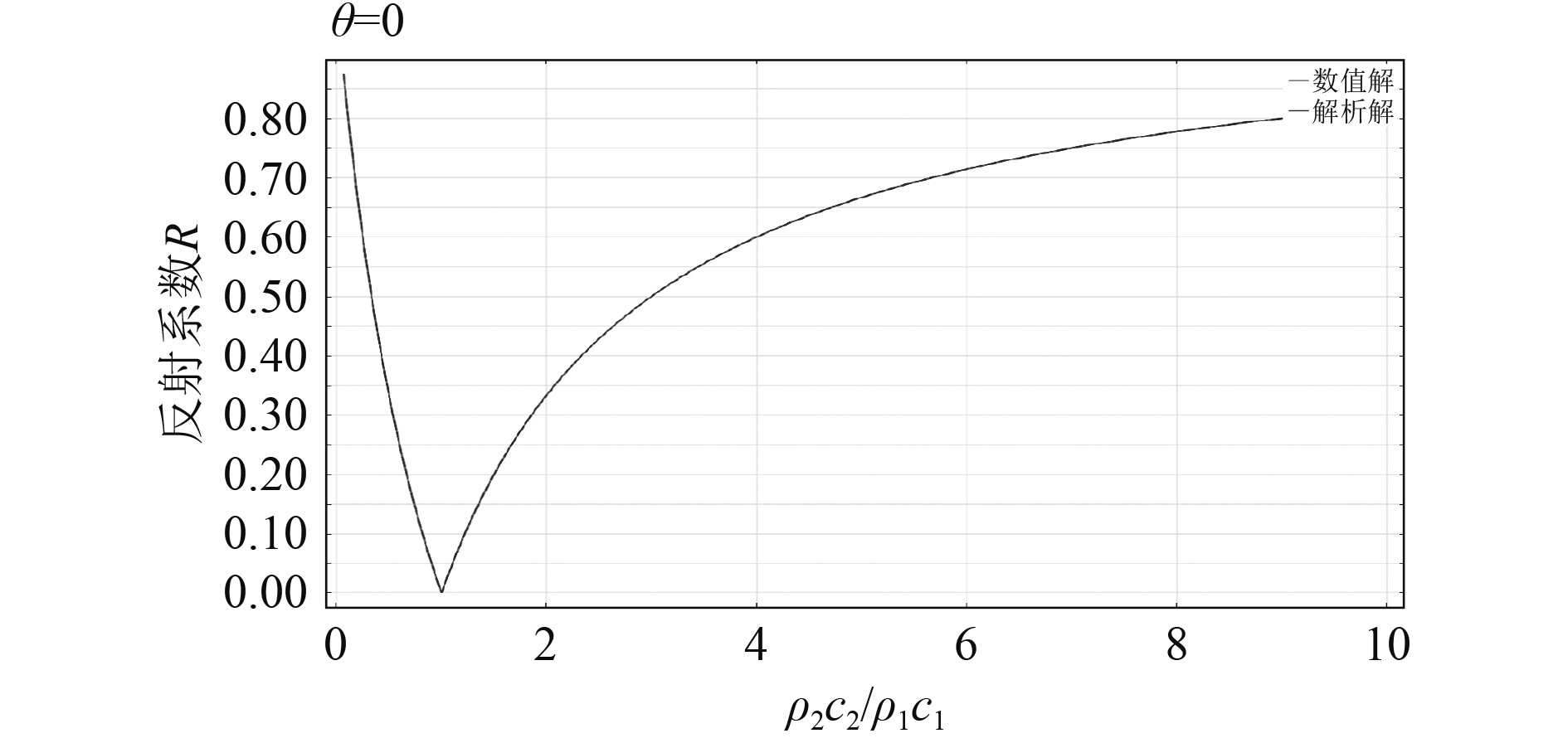
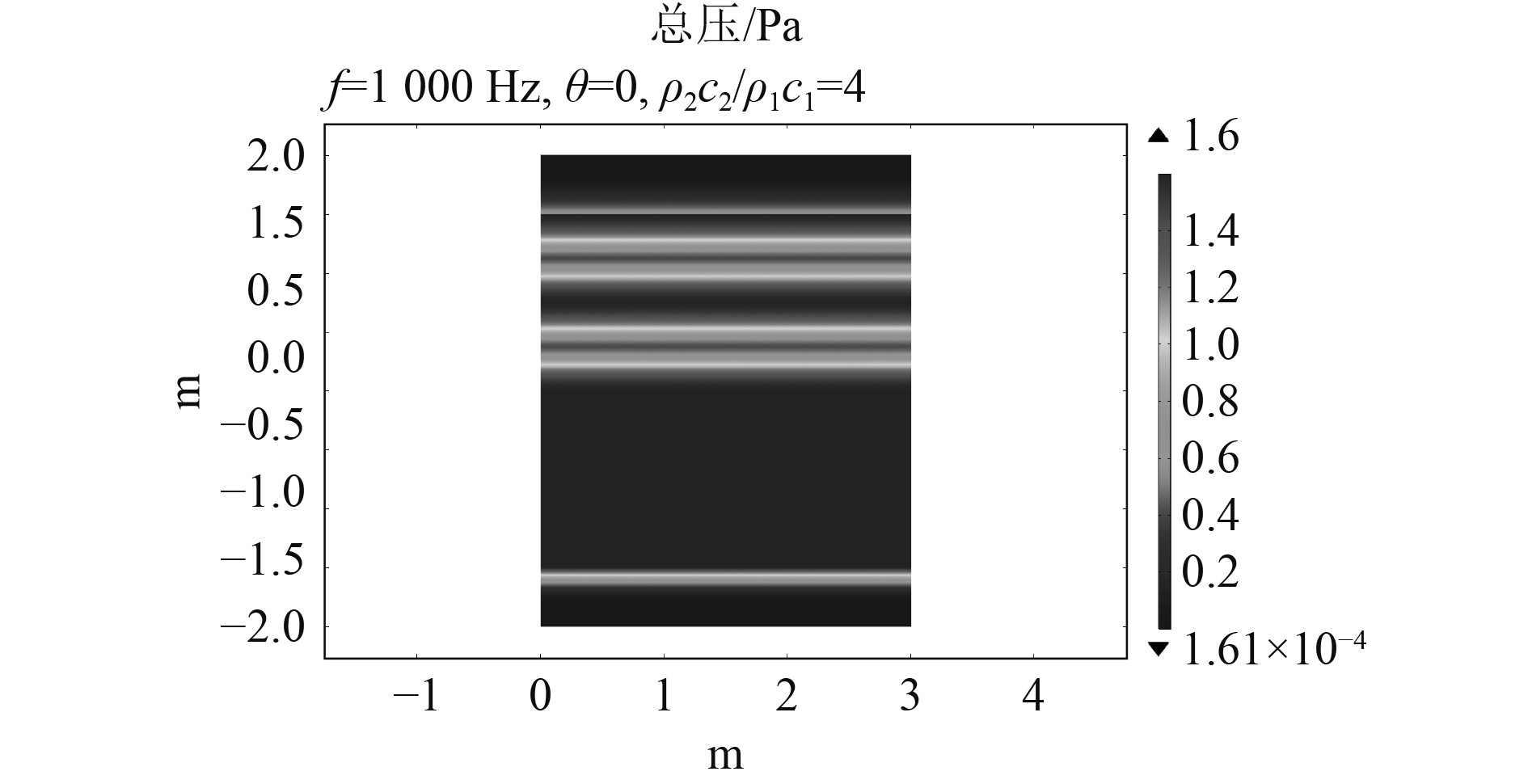
平面声波垂直界面入射时的反射系数随2种介质特性阻抗比的变化曲线如图2所示。结果显示由式(5)计算的理论值曲线与有限元仿真计算的数值解曲线一致重合,在特性阻抗比为1时反射系数为零,说明此时界面如同不存在,无声波的反射。特性阻抗比为4时的总声场如图3所示,可见在理想流体介质中平面声波的传播无衰减。
|
图 2 反射系数随特性阻抗比变化曲线 Fig. 2 Curve of reflection coefficient with characteristic impedance ratio |
|
图 3 总声压场 Fig. 3 The acoustic pressure field |
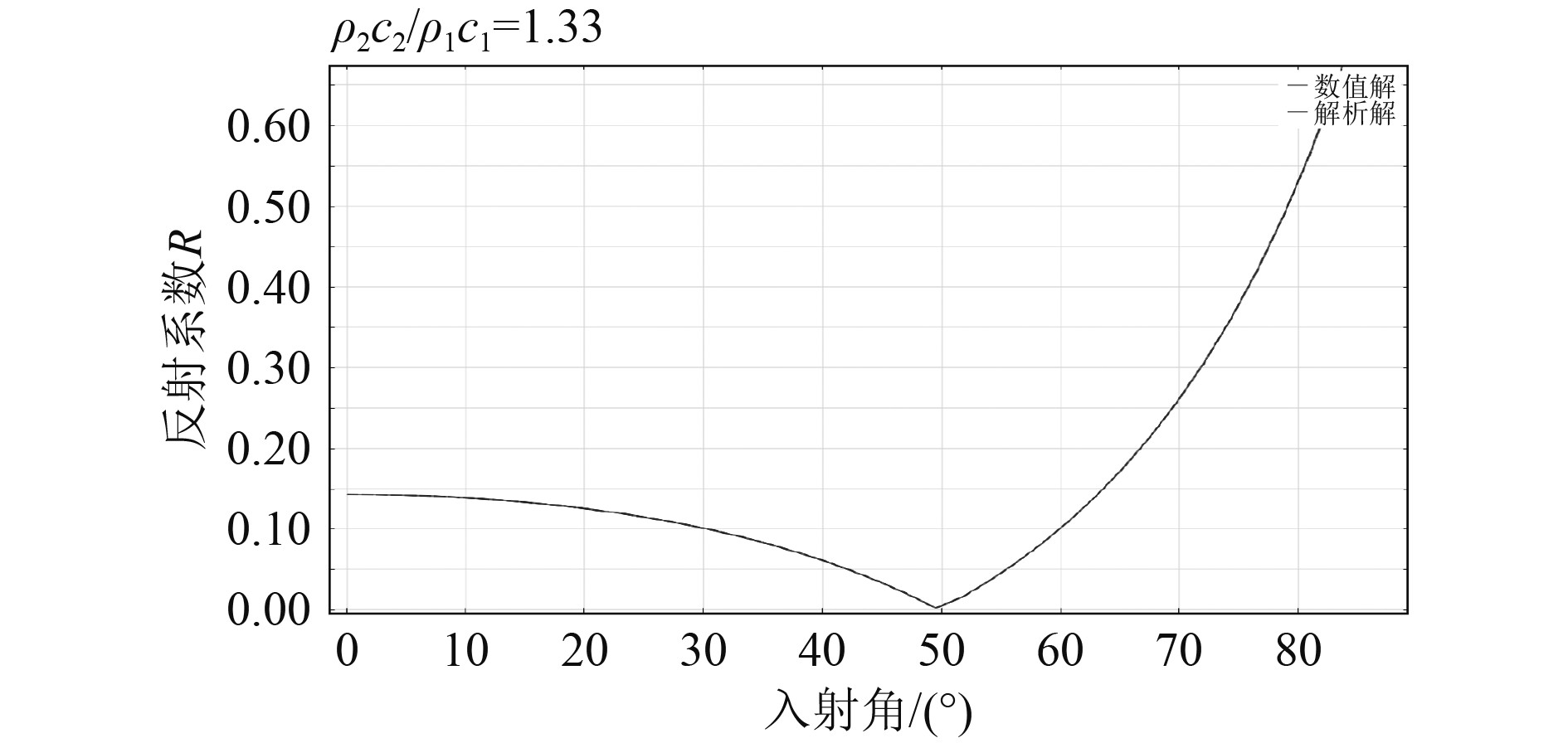
特性阻抗比分别为0.67与1.33时的反射系数随声波入射角的变化曲线如图4所示。结果显示解析解与数值解一致,可以表明分层介质声场计算模型的建立方法与数据处理是正确的。
|
图 4 反射系数随入射角变化曲线 Fig. 4 Curve of reflection coefficient with incident angle |
基于上述分层介质计算模型的方法建立水-沉积物模型,水下沉积物采用Biot多孔弹性介质模型来建立,其中包含流体介质中压力波与多孔基体中弹性波的相互作用,同时考虑孔隙流体的黏滞损耗。
对于水-多孔介质模型的声场仿真计算,下层沉积物采用多孔弹性波物理场建模,材料参数采用文献[6]中沙的多孔材料参数,如表1所示。
|
|
表 1 沙的多孔材料参数 Tab.1 Material parameters of sand |
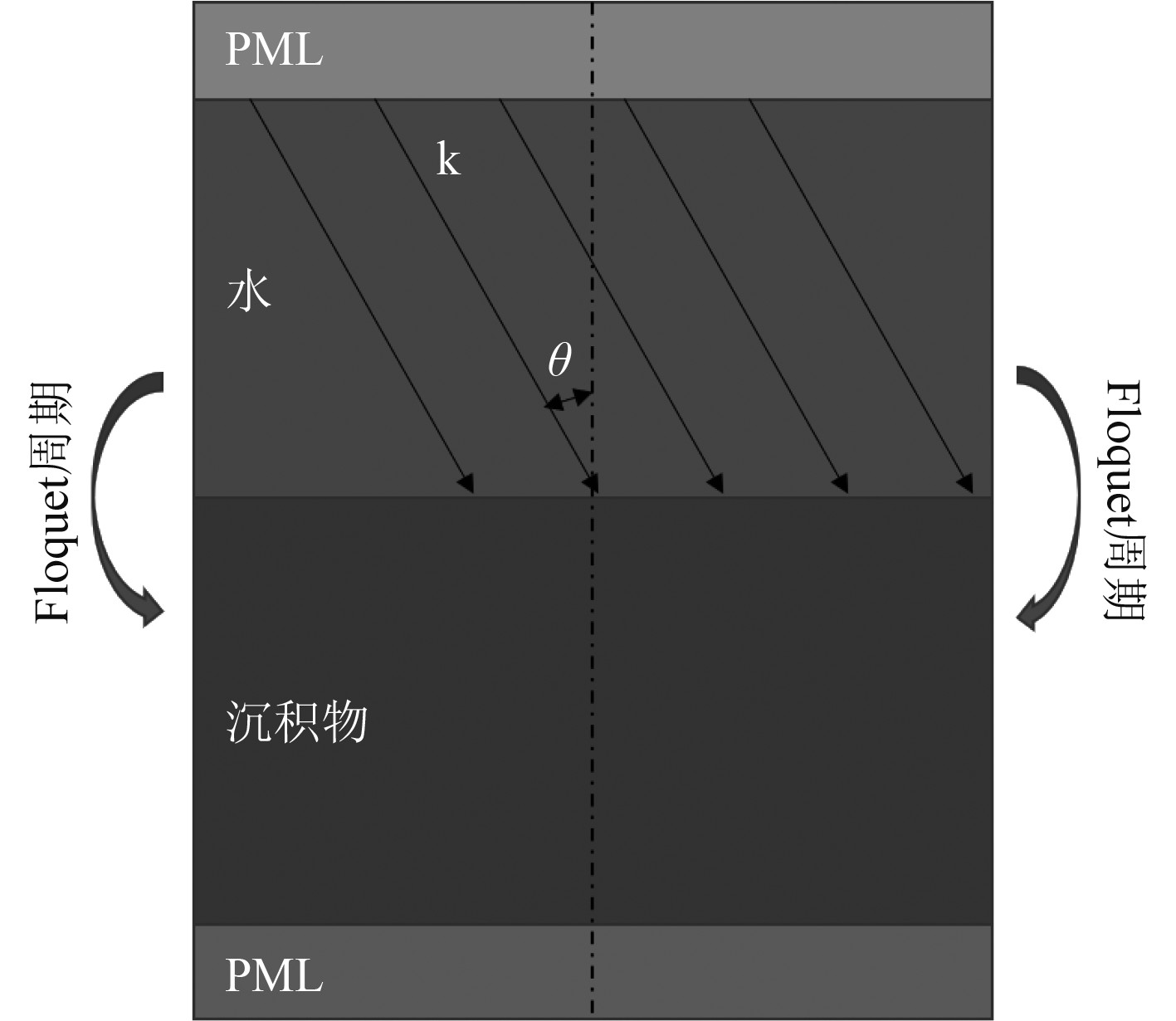
计算模型如图5所示,上层介质为水,下层介质为多孔弹性材料,上下边界设置PML模拟无限吸收边界条件,模型宽度定义为2倍波长,左右边界为Floquet周期性边界模拟无限大界面。
|
图 5 水-多孔介质计算模型 Fig. 5 Computational model for water-porous media |
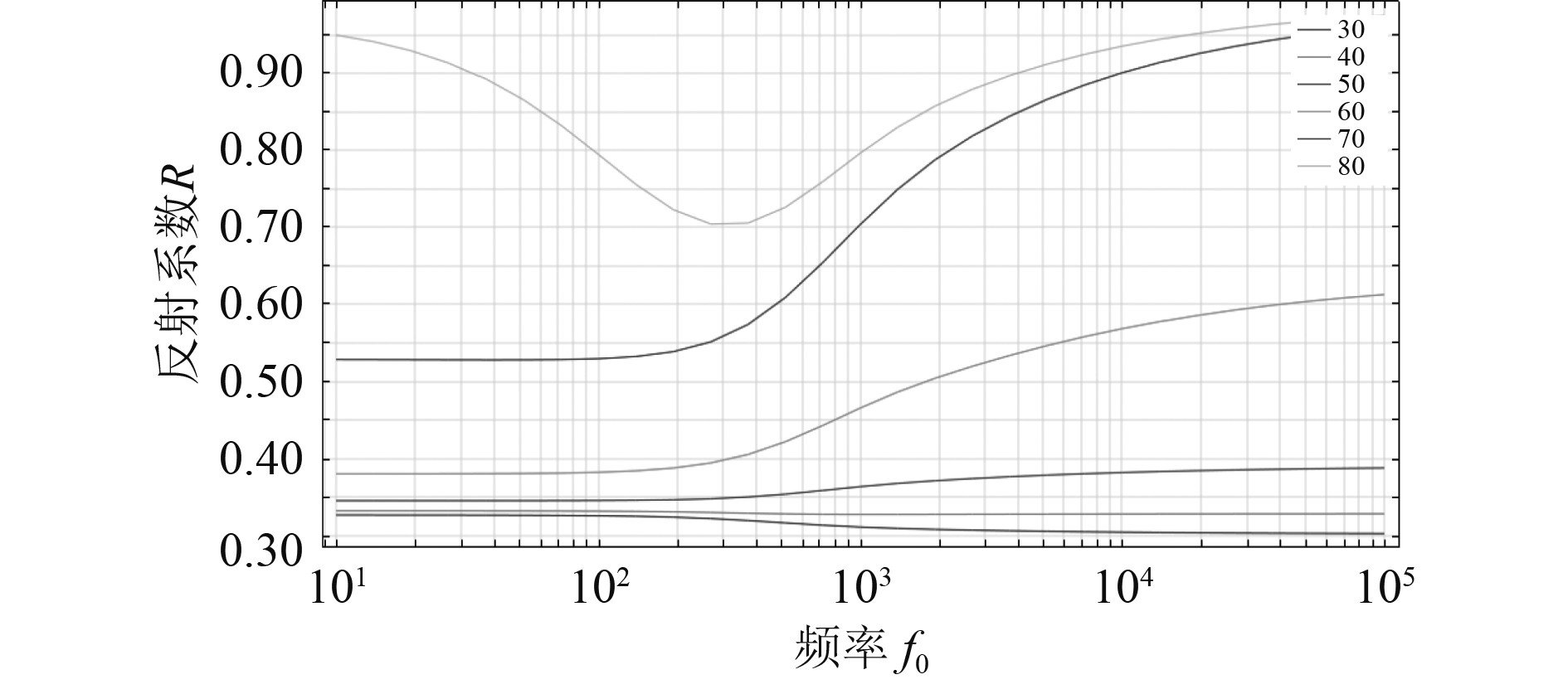
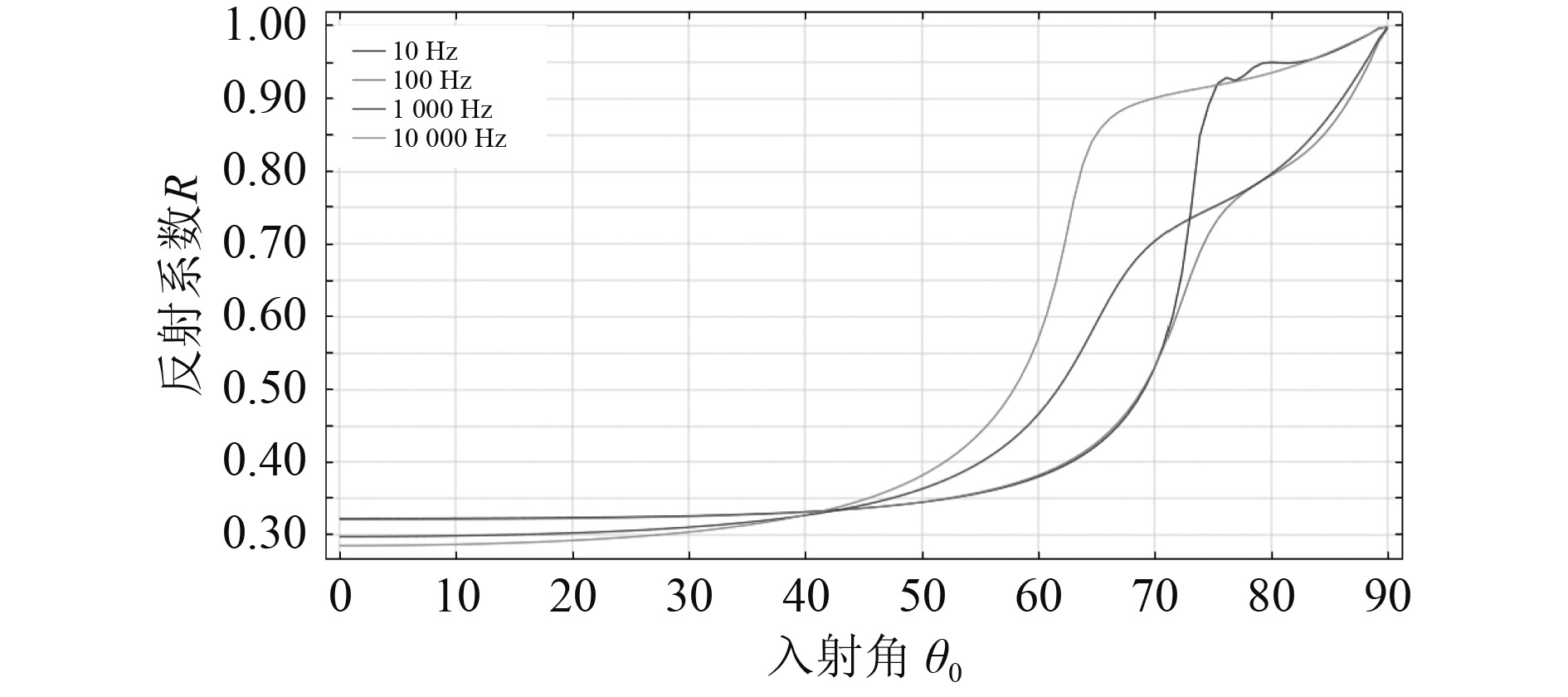
由表1给出的参数计算水-多孔介质模型在平面波从水中入射界面时的反射与透射声场,得到不同入射角下反射系数随频率的变化曲线如图6所示,不同频率下反射系数随入射角的变化曲线如图7所示。计算结果与文献[6]中的结果直观对比吻合的很好,表明有限元数值计算模型的建立方法正确。
|
图 6 不同入射角下反射系数随频率变化曲线 Fig. 6 Curve of reflection coefficient with frequency for different incident angles |
|
图 7 不同频率下反射系数随入射角变化曲线 Fig. 7 Curve of reflection coefficient with incident angle for four different frequencies |
为了探究水下沉积物介质参数变化对平面波反射系数的影响,基于上述计算模型对其3个参数进行参数化分析,分别为多孔介质孔隙率
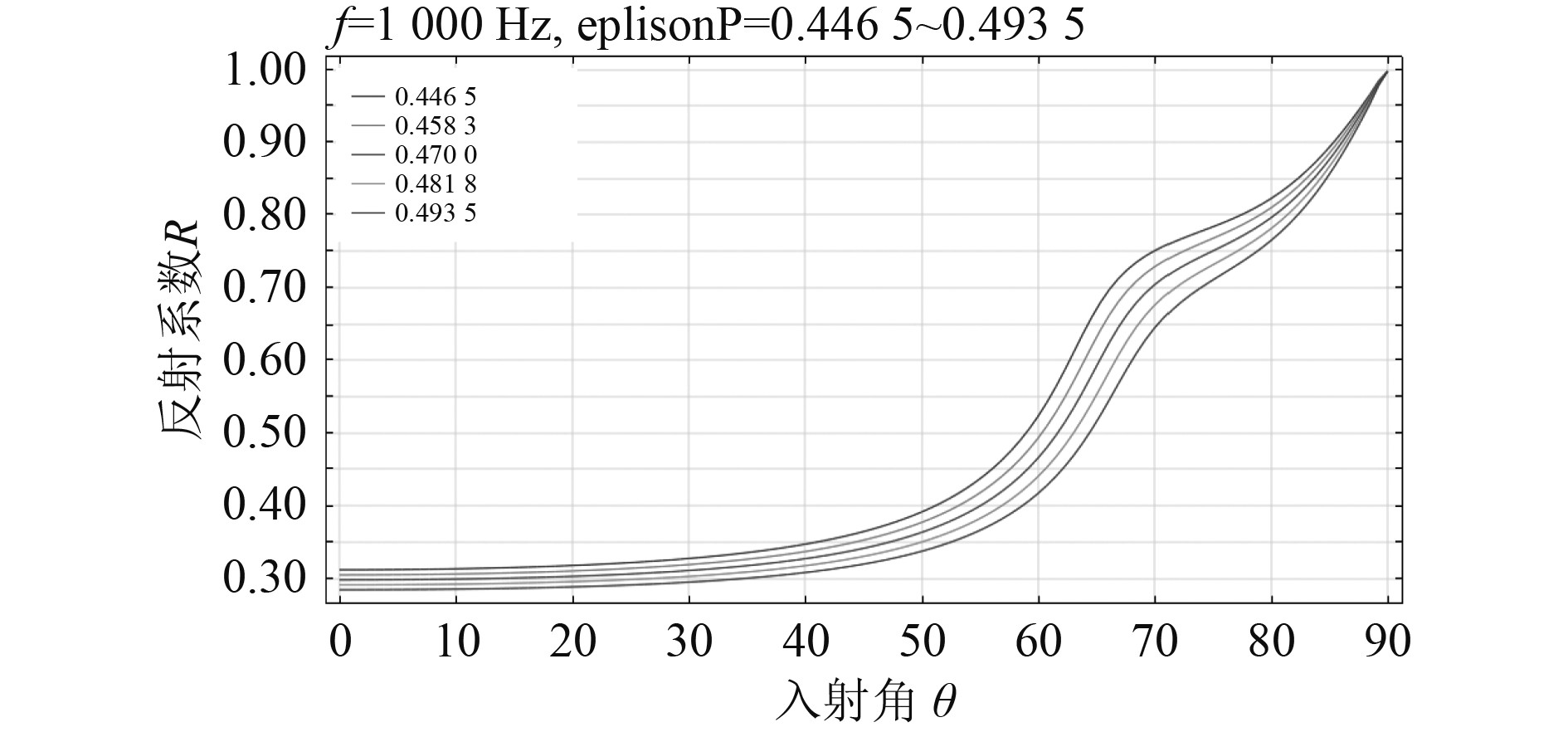
1)对于多孔介质孔隙率
|
图 8 不同孔隙率下反射系数随入射角变化曲线 Fig. 8 Curve of reflection coefficient with incident angle for different porosity |
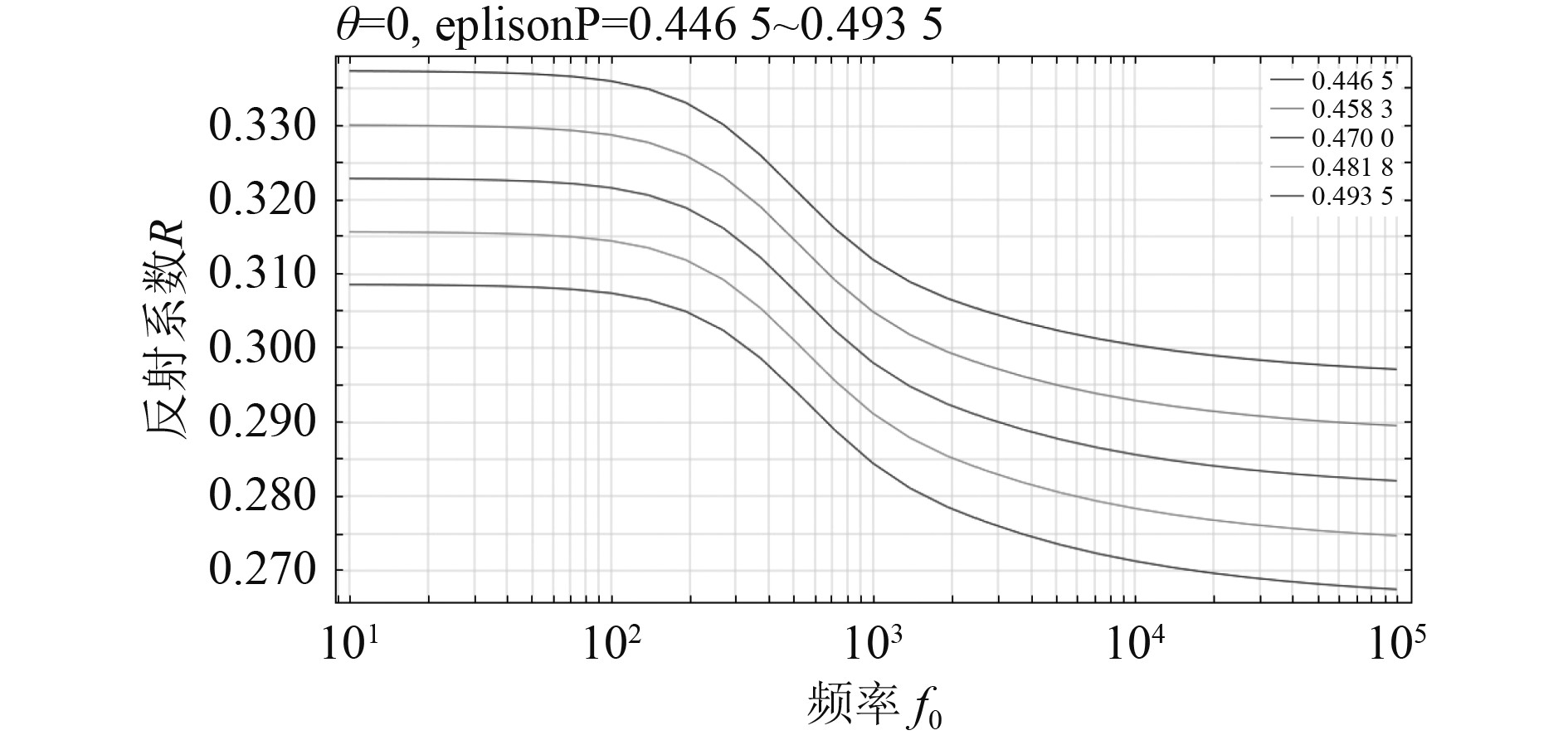
|
图 9 不同孔隙率下反射系数随频率变化曲线 Fig. 9 Curve of reflection coefficient with frequency for different porosity |
2)对于流体密度
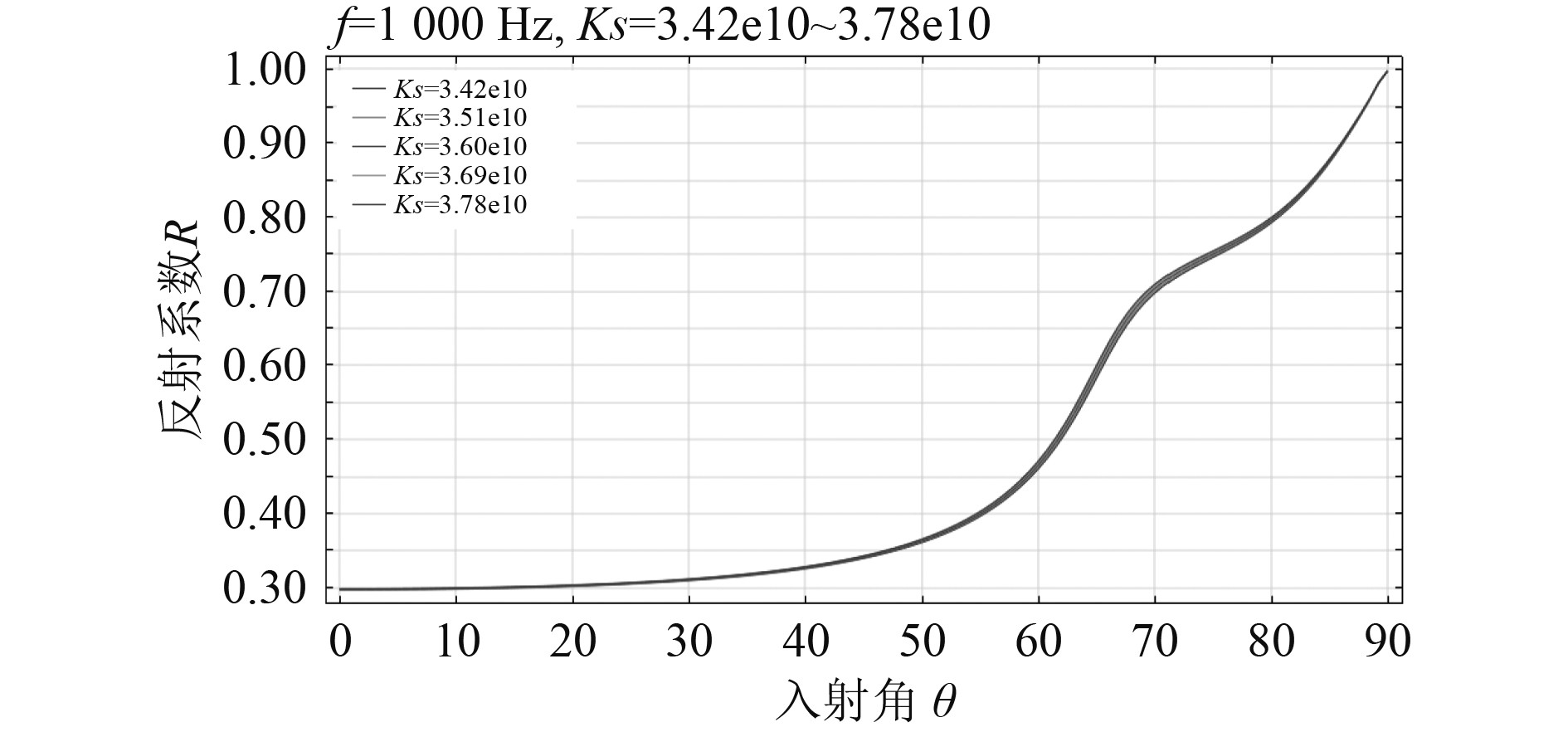
|
图 10 不同流体密度下反射系数随入射角变化曲线 Fig. 10 Curve of reflection coefficient with incident angle for different fluid density |
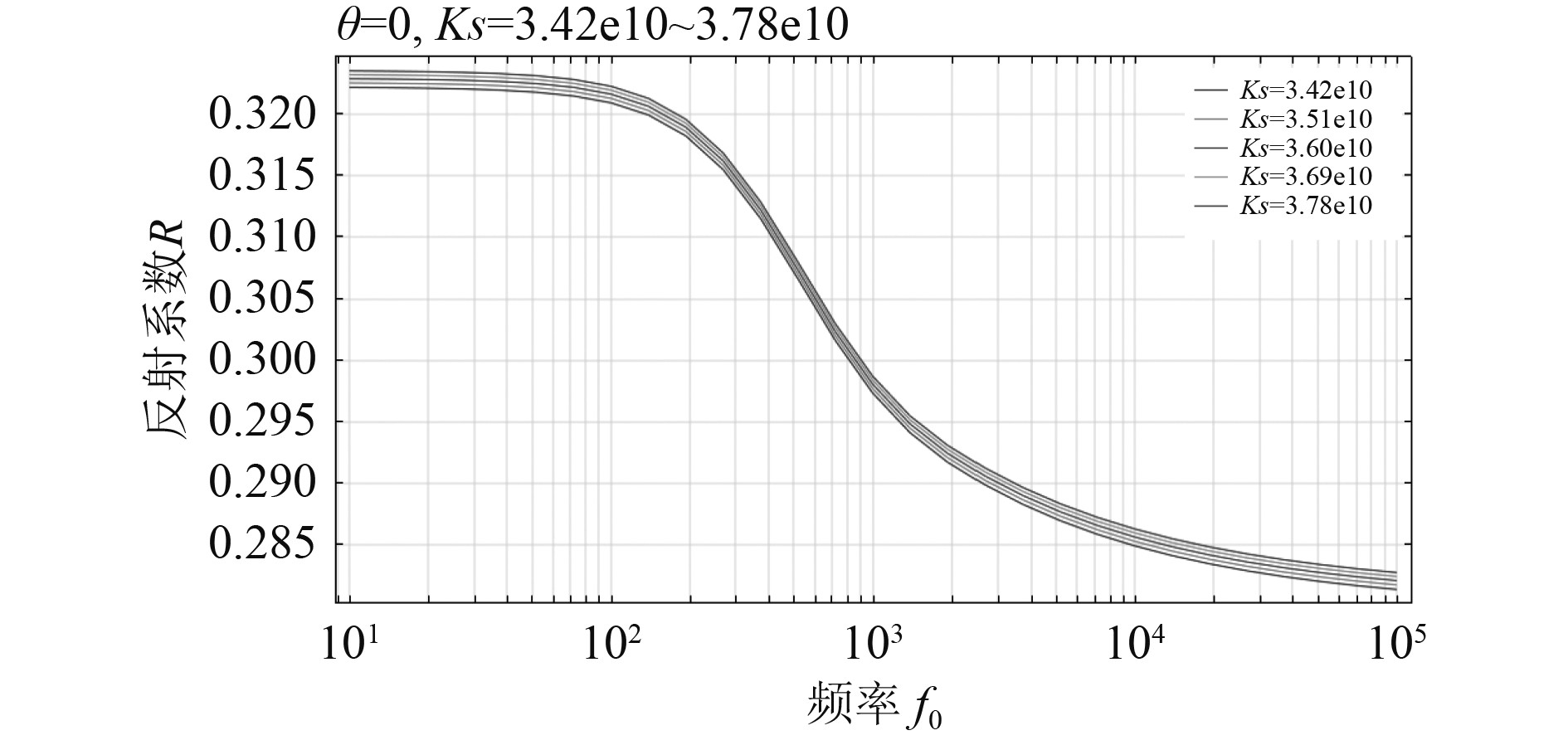
|
图 11 不同流体密度下反射系数随频率变化曲线 Fig. 11 Curve of reflection coefficient with frequency for different fluid density |
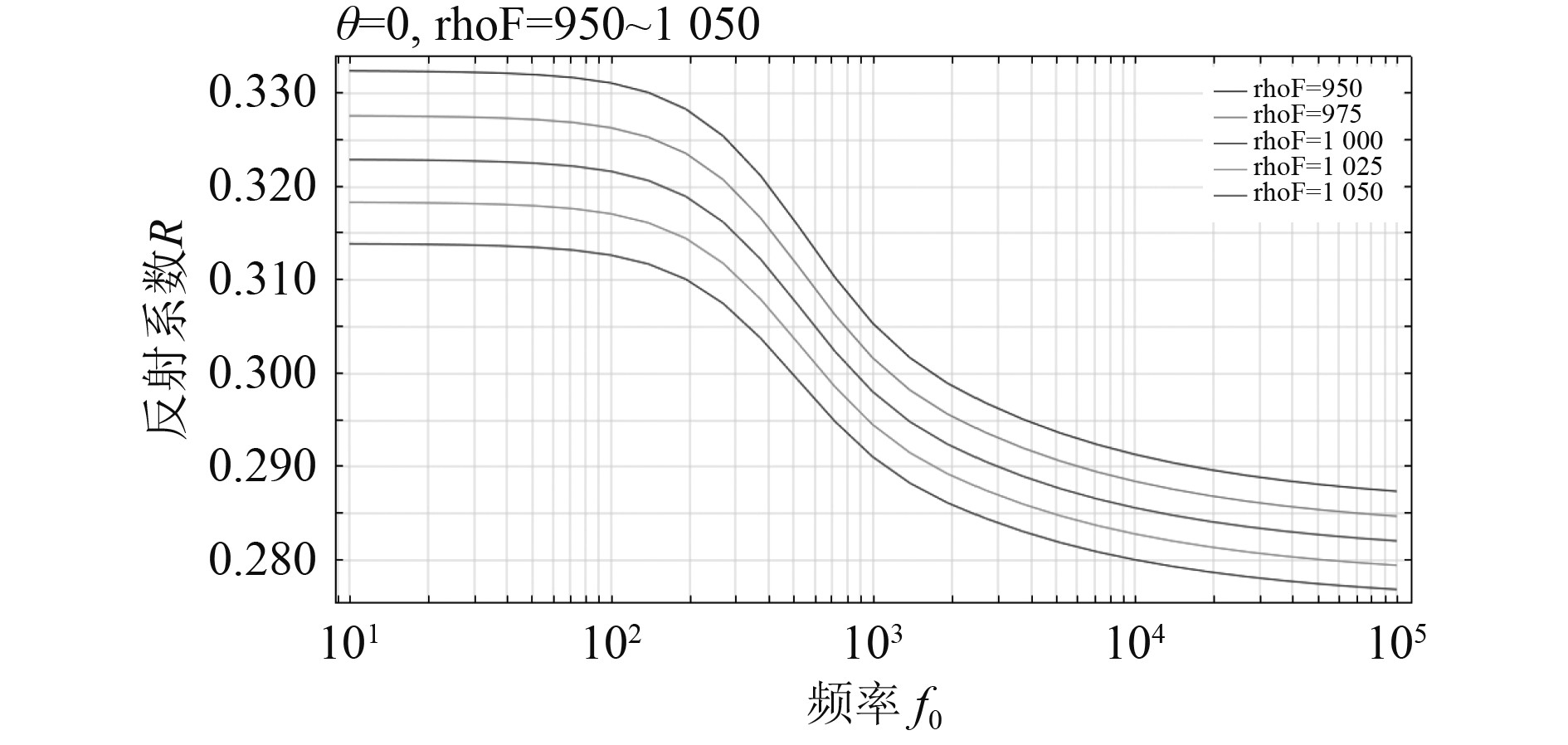
3)对于固体颗粒密度
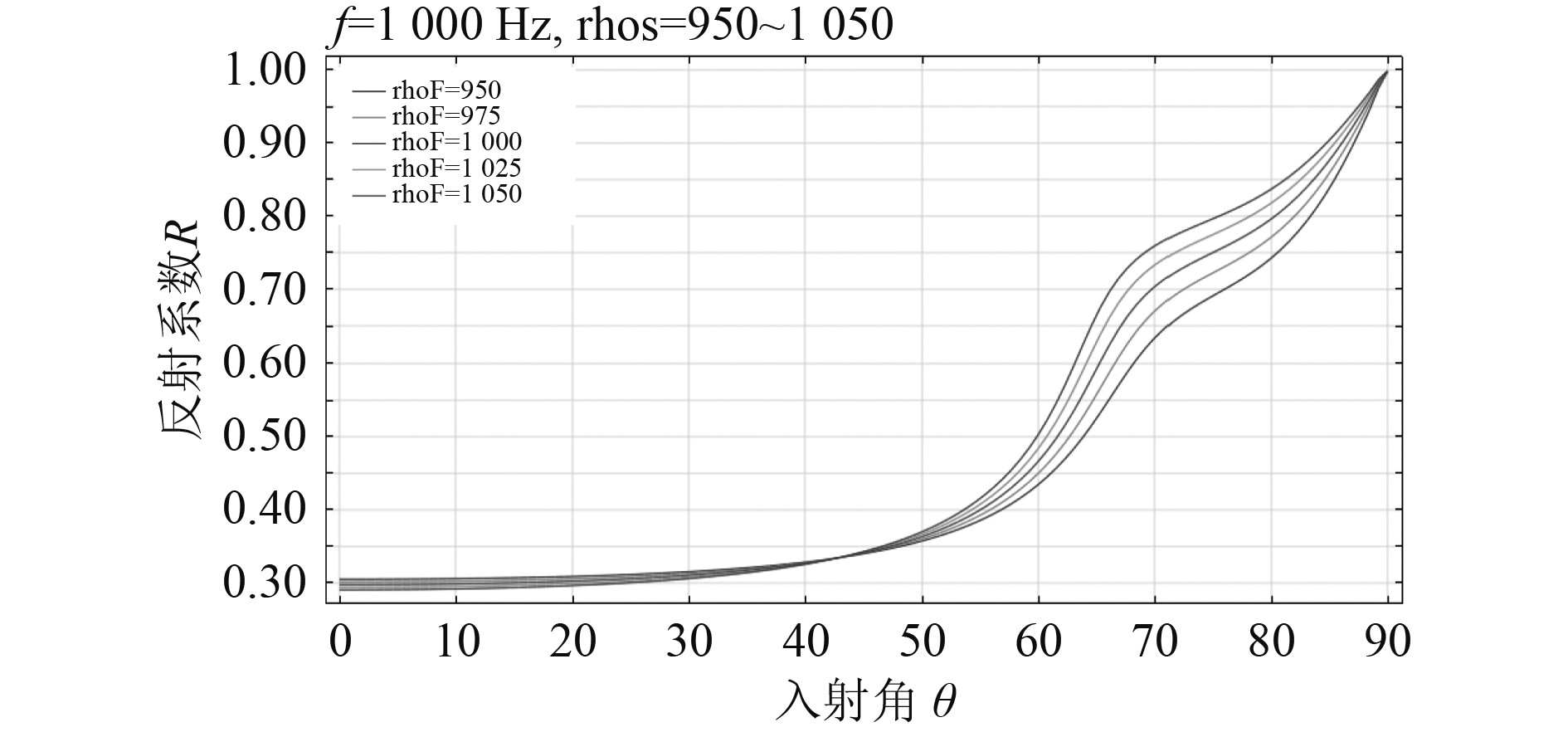
|
图 12 不同固体密度下反射系数随入射角变化曲线 Fig. 12 Curve of reflection coefficient with incident angle for different solid density |
|
图 13 不同固体密度下反射系数随频率变化曲线 Fig. 13 Curve of reflection coefficient with frequency for different solid density |
本文在理想流体分层介质界面声波反射系数解析解的基础上,建立其有限元计算模型,通过对比验证仿真计算方法的正确性。随后在此分层介质模型中将采用下层流体多孔弹性介质,计算的结果与参考文献中结果很好的吻合,表明水-多孔介质多物理场计算模型的正确性。根据此模型分别进行多孔介质孔隙率、流体密度、固体颗粒密度的参数化计算分析。在声波垂直入射时,结果表明孔隙率减小、流体密度减小、固体颗粒密度增大相应会导致平面声波反射系数(10~105Hz)的增大。同时得到在1 000 Hz时,任意入射角下孔隙率的增加会导致反射系数减小,而流体密度与固体颗粒密度变化对反射系数的影响规律会随着入射角增加而出现反转,在小入射角时,流体密度减小、固体密度增大相应会使海底界面的反射系数增大。
| [1] |
FARAN J J. Sound scattering by solid cylinder and spheres[J]. Journal of the Acoustical Society of America, 1951, 23(4): 405-418. DOI:10.1121/1.1906780 |
| [2] |
汤渭霖, 范军, 马忠成. 水中目标声散射[M]. 北京: 科学出版社, 2018.
|
| [3] |
于盛齐, 黄益旺, 吴琼. 基于等效密度流体近似反射模型反演海底参数[J]. 声学学报, 2014, 39(4): 417-427. |
| [4] |
BIOT. M. A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅰ. Low frequency range[J]. Journal of the Acoustical Society of America, 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [5] |
BIOT. M. A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅱ. Higher frequency range[J]. Journal of the Acoustical Society of America, 1956, 28(2): 179-191. DOI:10.1121/1.1908241 |
| [6] |
STOLL. R.D. Ka T.-K. n, Reflections of acoustic waves at a water-sediment interface[J]. Journal of the Acoustical Society of America, 1981, 70(1): 149-156. DOI:10.1121/1.386692 |
| [7] |
彭临慧, 赵燕鹏, 郁高坤. 声波在水-多孔介质海底界面上的反射与透射[J]. 中国海洋大学学报, 2007, 37(4): 671-675. |
| [8] |
杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 南京: 南京大学出版社, 2001.
|
 2022, Vol. 44
2022, Vol. 44
