2. 中国人民解放军91388部队,广东 湛江 524002
2. No. 91388 Unit of PLA, Zhanjiang 524002, China
DFB光纤激光水听器是光电子技术与水声工程技术相结合的新型传感器,因其灵敏度高、抗电磁干扰能力强、易于成阵等优势而在海上作战、海洋环境监测等领域被广泛应用[1-2]。相位噪声是影响DFB光纤激光水听器系统探测性能的重要因素之一[3-4],环境温度的变化作用于干涉仪进而影响系统的相位噪声,因而成为解调系统研究过程不可忽视的部分。
干涉仪中光纤由于热膨胀效应,受到温度波动影响后,会引起干涉仪的相位漂移,这种相位漂移最终会转化为系统的相位噪声,影响系统的探测性能。叶欣[5]为了分析环境温度对干涉系统相位检测的影响,建立了温度传感理论模型,得出温度对系统的影响与干涉仪的非平衡路径和系统传输光路都有直接关系,温度干扰与传输光路的长度成正增长趋势。王力求等[6]通过对干涉仪进行抽真空处理,对外部环境温度波动,噪声干扰进行隔绝控制达到了很好的降噪效果。陈文静[7]通过建立理论模型分析了温度变化对双偏振光纤干涉仪的影响并对其进行了测试。因此研究温度变化对DFB光纤光栅水听器系统中迈克尔逊干涉仪的影响极为重要,为后期系统降噪提供理论与实验支撑。
本文推导了迈克尔逊干涉仪将温度波动的影响通过激光器谐振腔转化为频率噪声的理论过程,并进行了理论仿真。通过设计搭建测试系统,测得温度波动对系统相位噪声的影响规律,进而验证了理论分析结果的正确性。
1 温度影响理论分析迈克尔逊干涉仪是光纤解调仪中的核心元件,外界温度波动会引起光纤的热光系数发生改变,导致光纤折射率改变,在激光器的谐振腔中形成频率噪声,从而通过干涉仪转化为相位噪声,影响解调过程。单模光纤的激光场可以写为[8]:
| $ E(r,t) = A(t){e^{ivt + \varphi (t)}}e(r) 。$ | (1) |
式中:
光纤受局部热平衡波动的影响,改变介质折射率,导致相位波动,根据式(1)和文献[9]中推导的激光方程给出局部热平衡波动引起的频率噪声为:
| $ \dot \varphi \left( t \right) = - vq\int {\Delta T} \left( {t,r} \right){\left| {e\left( r \right)} \right|^2}{\rm{d}}z。$ | (2) |
式中:
| $\begin{split} \left\langle {\dot \varphi \left( t \right)\dot \varphi \left( {t'} \right)} \right\rangle =& {v^2}{q^2}\times \int {\int {\left\langle {\Delta T\left( {t,r} \right)\Delta T\left( {t',r'} \right)} \right\rangle } } \times \\ & {\left| {e\left( r \right)} \right|^2}{\left| {e\left( {r'} \right)} \right|^2}{{\rm{d}}^3}x{{\rm{d}}^3}x', \end{split} $ | (3) |
积分下的期望值可以看做是热平衡波动的相关函数,将式(3)进行傅里叶变换得:
| $ \begin{split} \left\langle {\dot \varphi \left( \omega \right){{\dot \varphi }^*}\left( {\omega '} \right)} \right\rangle = &{v^2}{q^2} \times \int {\int {\left\langle {\Delta T\left( {\omega ,r} \right)\Delta {T^*}\left( {\omega ',r'} \right)} \right\rangle } } \times \\ & {\left| {e\left( r \right)} \right|^2}{\left| {e\left( {r'} \right)} \right|^2}{d^3}x{d^3}x'。\end{split} $ | (4) |
在10 MHz以下,由于热耗散波数远小于布拉格波数,
| $ \left\langle {\dot \varphi \left( t \right)\dot \varphi \left( {t'} \right)} \right\rangle = {v^2}{q^2}{L^{ - 1}}\left\langle {\Delta T\left( t \right)\Delta T\left( {t'} \right)} \right\rangle,$ | (5) |
其中,
| $ {S_\varphi }\left( \omega \right) = {v^2}{q^2}{L^{ - 1}}{S_{\Delta T}}\left( \omega \right),$ | (6) |
其中,
| $ \left\{ \begin{gathered} {S_{\Delta T}}\left( \omega \right) = \frac{{K{T^2}}}{{4{\text{π} ^2}{k_t}^2}}{Re} [{e^{i{k_1}^2{a^2}/2}}{E_1}(i{k_1}^2{a^2}/2)],\\ {E_1}\left( x \right) = \int_x^\infty {\left( {{e^{ - t}}/t} \right)} {\rm{d}}t。\\ \end{gathered} \right. $ | (7) |
式中:
| $ {S_\varphi }\left( \omega \right)\frac{{{c^2}{q^2}{L^{ - 1}}K{T^2}}}{{4{\text{π} ^2}{\lambda ^2}{k_t}^2}}{{\rm{Re}}} \left[{e^{i{k_1}^2{a^2}/2}}\int_{i{k_1}^2{a^2}/2}^\infty {\frac{{{e^{{{ - }}t}}}}{t}{\rm{d}}t} \right]。$ | (8) |
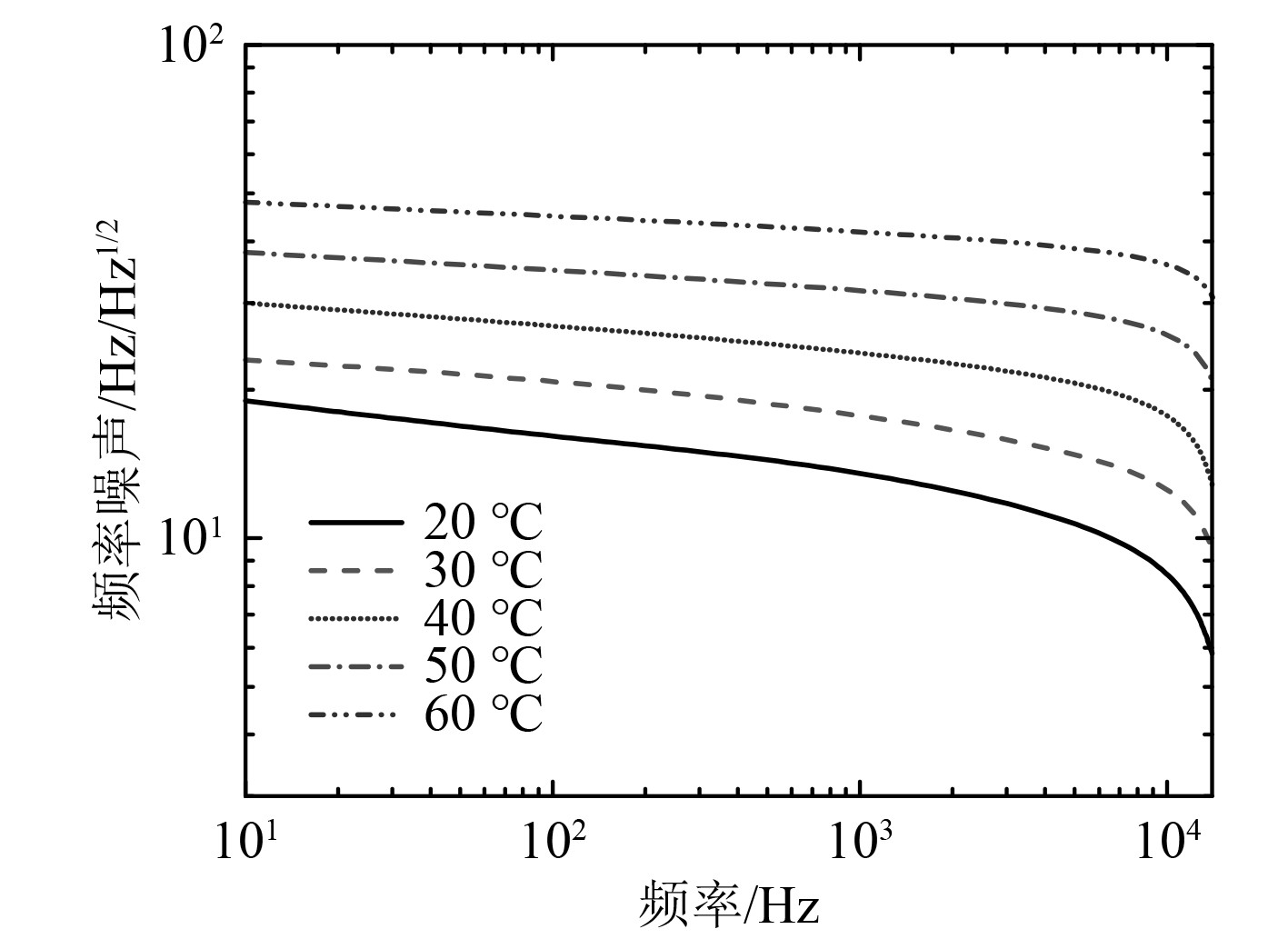
图1为利用式(8)对频率噪声随温度变化的仿真结果。其中光速为
|
图 1 频率噪声与温度变化关系图 Fig. 1 The relationship between frequency noise and temperature changes |
可知,当频率一定时,频率噪声会随着温度的升高而增大,对于各温度点而言,低频带的频率噪声较大,高频带的噪声相对变小,频率噪声随频率增加呈缓慢下降趋势。
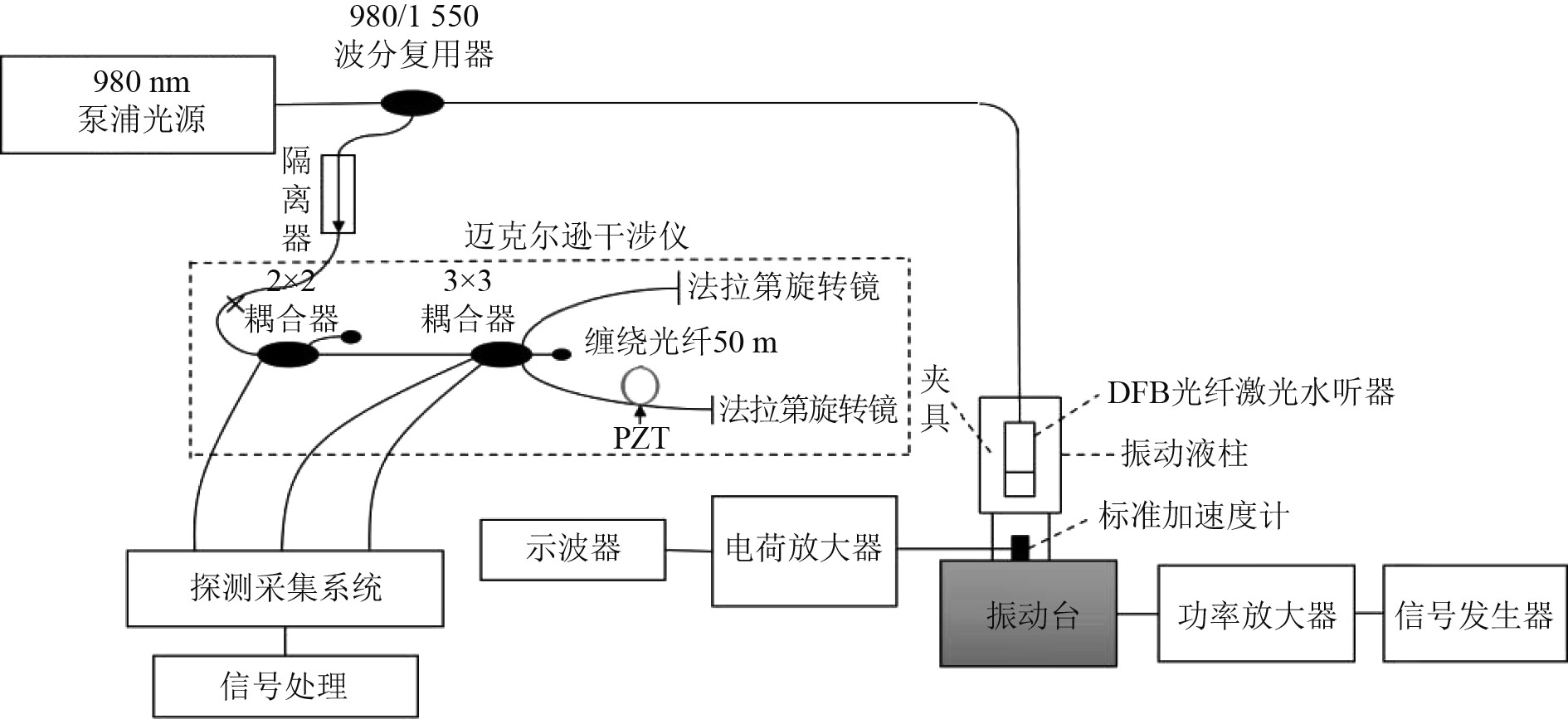
2 实验分析搭建振动液柱实验测试系统如图2所示。系统中泵浦光源发出980 nm波长的激光,为DFB光纤激光水听器提供持续稳定的光源激励,在此激励的作用下,DFB光纤激光水听器将反射特定波长为1550 nm的激光输出[11]。经过波分复用器到隔离器,再传输到迈克尔逊干涉仪中进行干涉,图中虚线框内为迈克尔逊干涉仪的结构,由2×2耦合器、3×3耦合器,压电陶瓷(PZT),法拉第旋转镜组成,其中2×2耦合器和3×3耦合器一臂空置。输出的3路光经过探测器,信号采集,到电脑主机进行信号处理,最终经过一系列解调算法,解调出待测信号。
|
图 2 振动液柱法测试系统 Fig. 2 Vibrating liquid column method test system |
采用振动液柱法进行实验,图2右下部分为水声振动部分,该部分由标准加速度计、振动台和振动罐组成。用夹具将水听器竖直放在罐中心处,使水听器完全处于水中,当对振动台加载振动信号时,使水听器处于水声振动环境,感知振动信号。将标准加速度计用495胶粘与振动罐底部,再将整个振动罐固定于振动台上,标准加速度计测量的是振动罐的加速度,经过电荷放大器放大后,通过示波器显示读数,此结果用于计算水听器的声压灵敏度信号发生器通过功率放大器给振动台提供激励。
实验中采用的温控装置温控范围为室温至100℃,控温精度小于等于0.5℃,温控装置没有水冷功能,当温度高于65℃时,会对干涉仪中的器件和光纤造成损害,室温为20℃左右,本次实验在20℃~60℃范围内,每隔10℃采1次数据,测试迈克尔逊干涉仪的相位噪声与温度的关系。
选择深夜安静环境进行实验,避免外界环境噪声的影响。水浴锅下面安装隔振棉避免外界环境振动对干涉仪的影响,不考虑电路噪声,解调噪声,此时可以认为系统的相位噪声的增加是由干涉仪所处环境的热平衡波动引起的,即实验所测系统的相位噪声等效为干涉仪的相位噪声。将迈克尔逊干涉仪放置在恒温箱铁架中央,铁架下面水覆盖加热棒,首先在室温20℃的环境温度下,通过信号发生器对振动台加载800 Hz频率的振动信号,振动幅值均为5 V。调节数显恒温箱温度为60℃,在加热过程中,分别在20℃和60℃两个温度点进行解调处理。
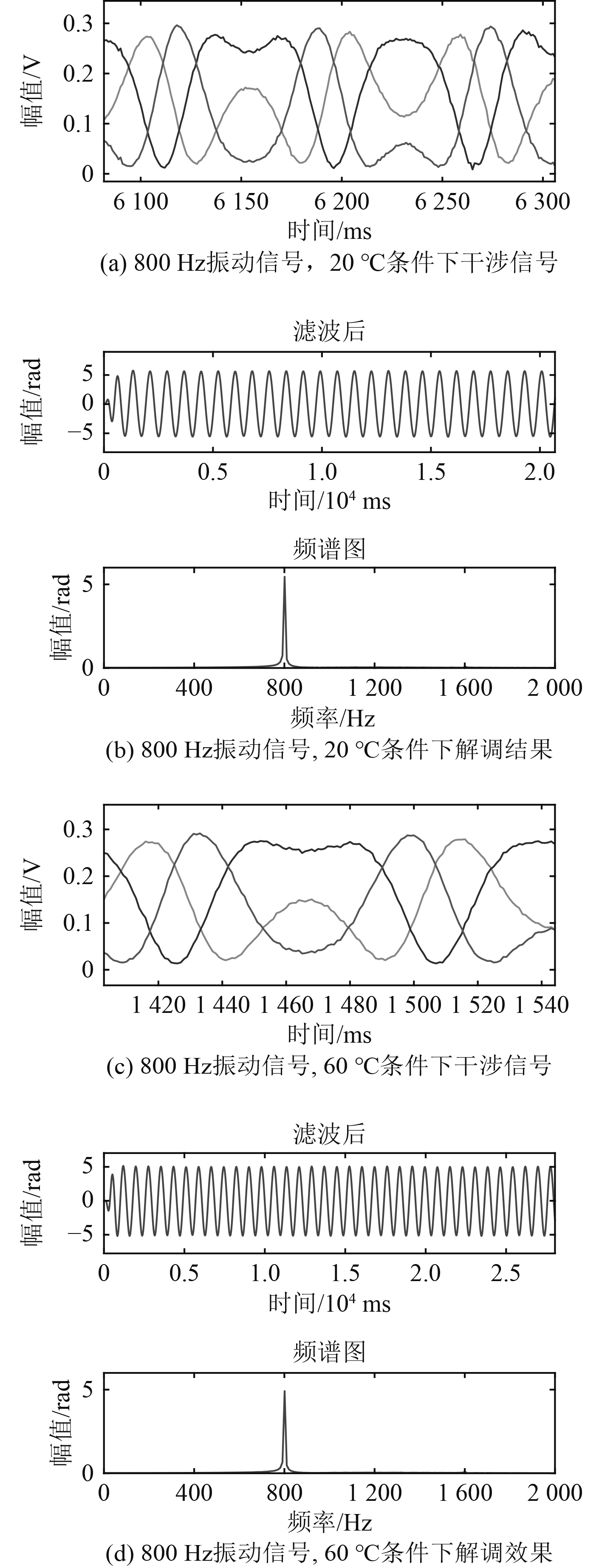
通过Matlab处理得水声振动信号为800 Hz时,干涉与解调效果如图3所示。
|
图 3 20℃和60℃温度点,800 Hz振动信号条件下的干涉与解调效果 Fig. 3 Interference and demodulation effect under the conditions of 20℃, 60℃ temperature and 800Hz vibration signal |
可以看出在室温20℃以及60℃的条件下,系统都能进行正常解调,干涉信号中存在少许噪声,能够准确的解调出外加的800 Hz的水声振动信号,说明温度增加到60℃时,系统可以维持正常的解调。
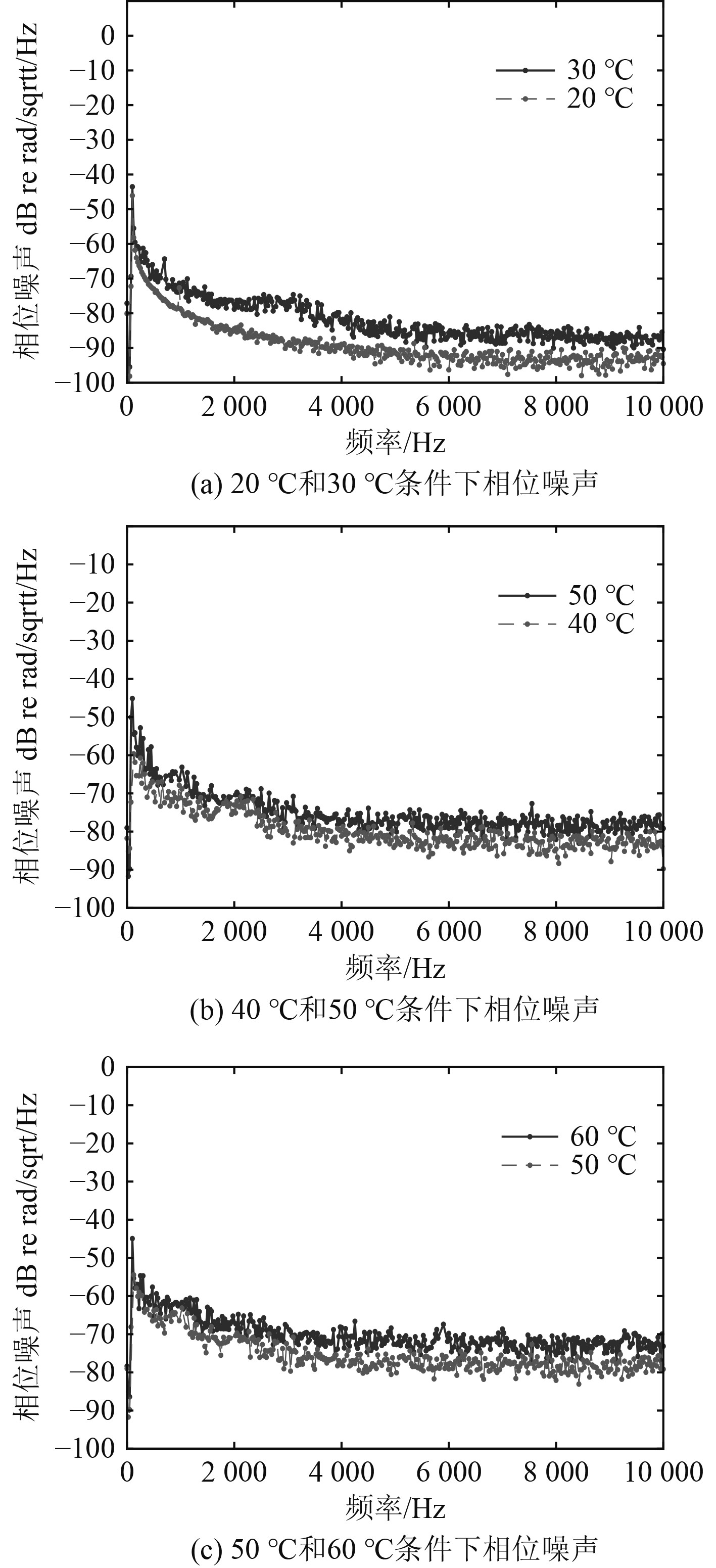
为了尽量避免外界环境对系统的干扰,将水听器用夹具置于振动液柱中心处,水面高于激光器的谐振腔部分,将水听器完全放置在水中,不施加振动信号,通过振动台的隔振装置和水的传声效率低等特性降低环境中的振动和声波经水听器引入的噪声,选择深夜进行实验,保持实验室安静的环境,调节恒温箱温度从20℃升至60℃,分别在20℃,30℃,40℃,50℃,60℃温度点测量系统的相位噪声,如图4所示。
|
图 4 温度影响相位噪声对比 Fig. 4 Temperature influence phase noise comparison |
通过图4可知,温度从20℃增加到60℃,在0~10 kHz频带范围内,系统相位噪声随温度增加而增加,温度每升高10℃,相位噪声增加约5 dB。但是从图4(a)中可以得知温度为30℃时,在0~3 kHz内,相位噪声明显被抬高,是因为在这个温度点采集数据时,混入了采集卡噪声,采集卡噪声的频点大概在3 kHz左右,在3~10 kHz范围内相位噪声水平正常。将上述数据整和得各个温度条件下系统的相位噪声对比如图5所示。
|
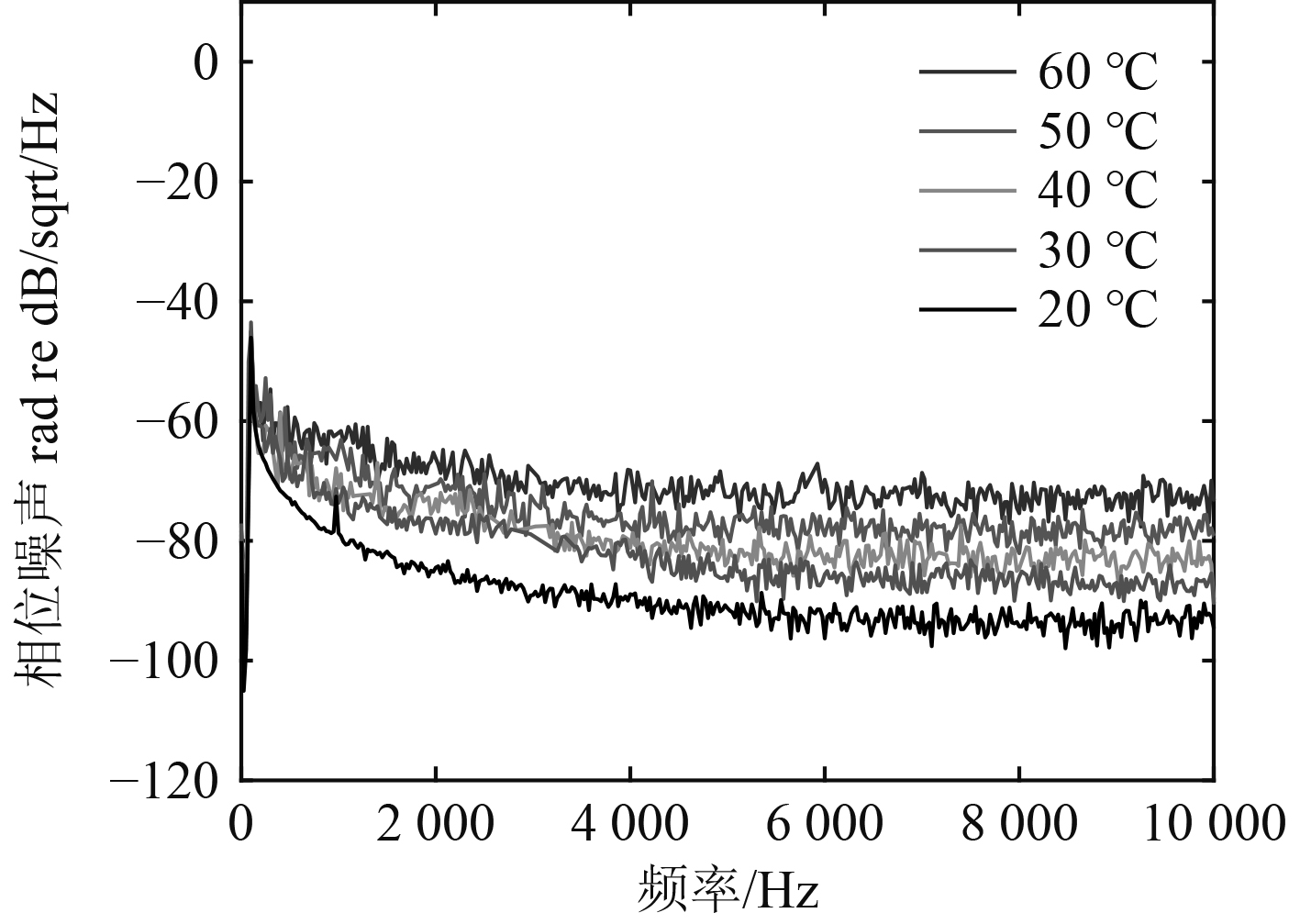
图 5 各温度条件下相位噪声对比 Fig. 5 Phase noise comparison under various temperature conditions |
可知,0~10 kHz频带范围内,系统的相位噪声随温度升高呈正增长趋势。由于存在无法避免的低频噪声和1/f噪声,每个温度条件下,0~3 kHz频带内的相位噪声相比3~10 kHz频带内的相位噪声都高。20℃条件下系统的相位噪声最小,在3~10 kHz范围内相位噪声约为–90 dB;温度为60℃时,系统的相位噪声最大,在3~10 kHz范围内相位噪声在–70 dB左右,相比20℃系统的相位噪声增加约20 dB左右,验证了理论仿真分析的结论。
3 结 语本文针对DFB光纤激光水听器系统在实际应用中迈克尔逊干涉仪受环境温度影响进行实验研究,推导了温度波动经干涉仪转化为相位噪声的传递过程,并对其进行仿真分析。设计搭建了实验测试系统,采用振动液柱法进行实验,实验测得当对水听器施加水声信号时,对干涉仪加热,系统依旧可以进行正常的解调。不加水声信号时,温度由20℃升至60℃,在3~10 kHz范围内,温度每升高10℃,相位噪声增加约5 dB,20℃条件下相位噪声约为–90 dB;60℃条件下,相位噪声约为–70 dB。在0~10 kHz频带范围内,系统的相位噪声与温度波动呈正增长关系,与仿真结果相符。后续会对干涉仪做隔温控温处理,降低干涉仪受所处环境温度波动的影响,对降低系统的等效噪声压,拓展水听器系统的探测距离具有重要意义。
| [1] |
张仁和, 倪明. 光纤水听器的原理与应用[J]. 物理, 2004(7): 503-507. DOI:10.3321/j.issn:0379-4148.2004.07.007 |
| [2] |
高学民. 光纤水听器及阵列的发展概况[J]. 光纤与电缆及其应用技术, 1996(1): 48-53. DOI:10.19467/j.cnki.1006-1908.1996.01.013 |
| [3] |
KOO K P, KERSEY A D. Bragg grating-based laser sensors systems with interferometric interrogation and wavelength division multiplexing[J]. Journal of Lightwave Technology, 1995, 13(7): 1243-1249. DOI:10.1109/50.400692 |
| [4] |
梁迅. 光纤水听器系统噪声分析及抑制技术研究[D]. 长沙: 国防科学技术大学, 2008.
|
| [5] |
叶欣. 干涉型光纤传感器低频信号检测技术研究[D]. 长沙: 国防科学技术大学, 2010.
|
| [6] |
王力求, 王巍, 李东明, 等. 光纤水听器解调干涉仪减振降噪技术[J]. 声学与电子工程, 2012(3): 1-3+17. |
| [7] |
陈文静. 双偏振光纤干涉仪噪声与温度的影响及其抑制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [8] |
FOSTER S. Dynamical noise in single-mode distributed feedback fiber lasers[J]. Quantum Electronics IEEE Journal of, 2004, 40(9): 1283-1293. DOI:10.1109/JQE.2004.833240 |
| [9] |
WANSER K H. Fundamental phase noise limit in optical fibers due to temperature fluctuations[J]. Electronics Letters, 1992, 28(1): 53-54. DOI:10.1049/el:19920033 |
| [10] |
FOSTER S, TIKHOMIROV A, MILNES M. Fundamental thermal noise in distributed feedback fiber lasers[J]. IEEE Journal of Quantum Electronics, 2007, 43: 378-384. DOI:10.1109/JQE.2007.894744 |
| [11] |
李日忠. DFB光纤激光器水听器关键技术研究[D]. 武汉: 华中科技大学, 2014.
|
 2022, Vol. 44
2022, Vol. 44

