滑动轴承作为旋转机械的主要支撑部件,其性能的好坏直接关系到整个机组的安全稳定运行[1],对转子稳定性起着至关重要的作用[2-3]。
随着计算机技术的发展,国内外学者越来越多的采用CFD方法研究滑动轴承的油膜流场特性。张艾萍等[4]建立不同滑动轴承间隙模型,通过CFD数值模拟分析,得到不同轴承间隙对转子稳定性的影响;涂林等[5]利用Fluent软件直接求解油膜轴承力学方程的方法对油膜轴承力场进行模拟,分析了轴承在不同转速下油膜力场的三维分布,得到了转速对油膜压力场分布的影响;CANG MC[6]分别采用单相流模型和两相流模型,研究滑动轴承油膜在液态以及含有气泡的气液两相流2种情况下,油膜润滑特性的变化规律。MERUANE V等[7]建立了滑动轴承流固模型,分析了不同转速和不同偏心率下轴向的压力分布,得到了转速及偏心率对油膜稳定性的影响。
本文以某型船用柴油机连杆轴承为模型,采用Fluent软件进行流动分析,以轴颈转速和轴承进油压力为变量,分析了转速和进油压力对滑动轴承油膜压力场分布的影响规律,对滑动轴承的润滑性以及油膜的稳定性研究具有一定的理论意义和工程实践价值。
1 工作原理流体动压润滑主要是利用动压效应[8],使轴承间隙内润滑油膜产生压力,以此平衡外载荷,避免摩擦表面相互接触,从而减小摩擦阻力和保护摩擦表面[9],滑动轴承动压润滑原理如图1所示。
|
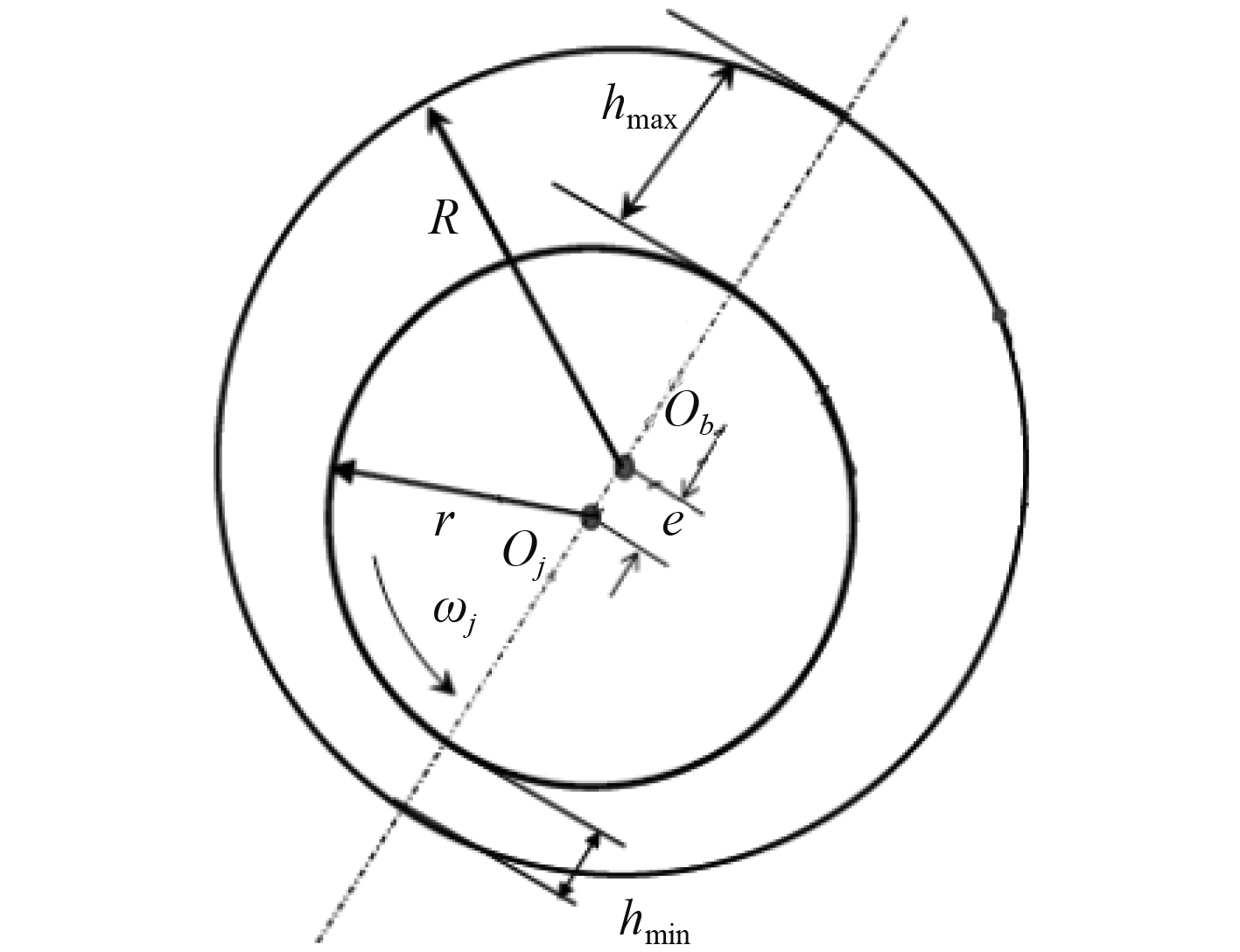
图 1 动压滑动轴承 Fig. 1 Hydrodynamic sliding bearing |
轴颈沿逆时针ωj方向转动,轴颈中心Oj相对于轴承中心Ob位置发生了偏移,偏心距为e,在OjOb连心线上,最大间隙为hmax,,hmax=c+e,最小间隙为hmin>,hmin=c−e。其中c为半径间隙c=R−r,R为轴承半径,r为轴颈半径。
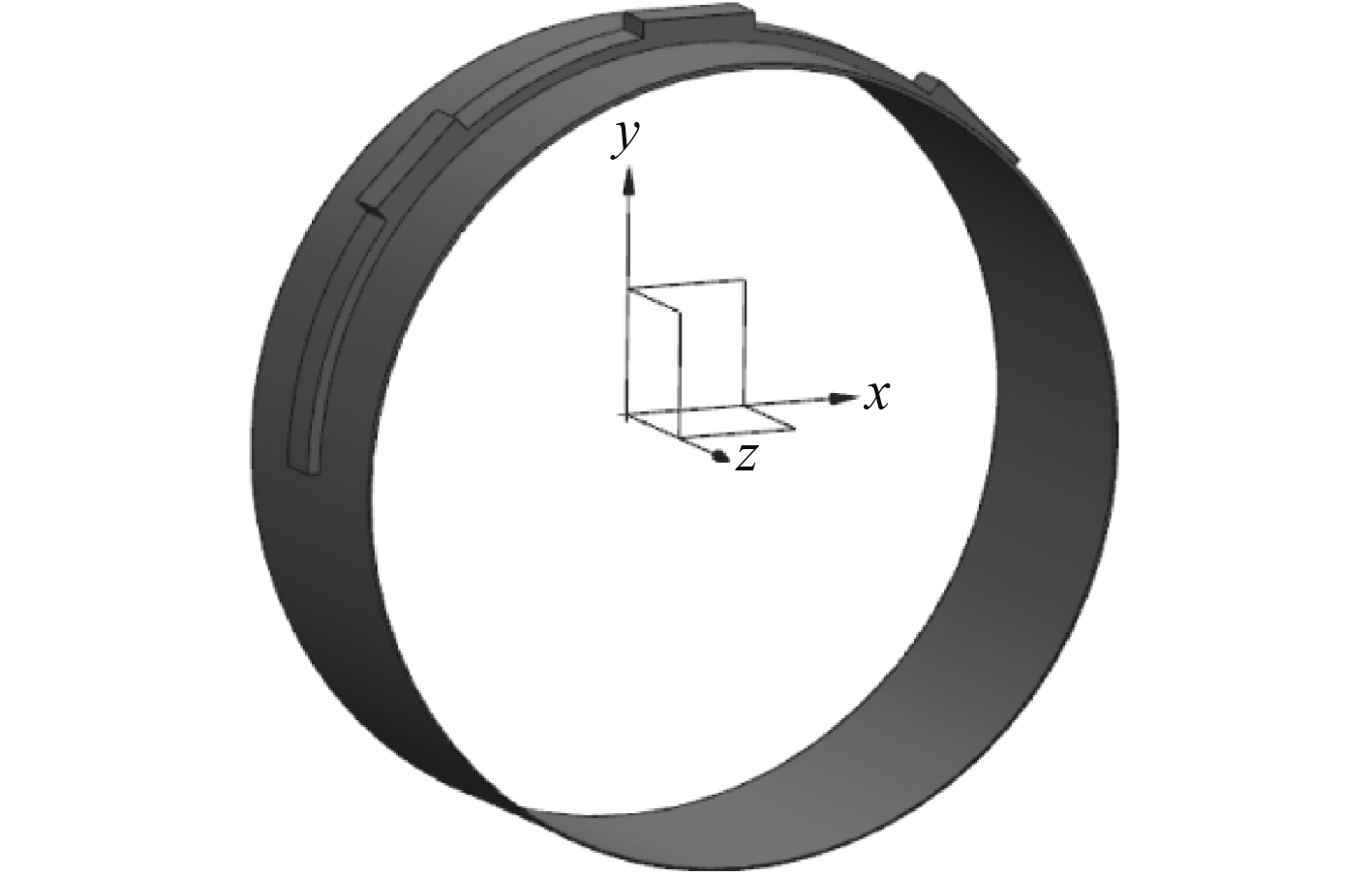
2 数值计算与分析 2.1 几何模型本文所采用的主轴承模型和润滑油的主要参数为:轴颈直径D=100 mm,半径间隙C=0.42 mm,偏心率ε=0.5,轴承宽度B=35 mm,润滑油密度ρ=860 kg/m3,动力黏度η=0.02 Pa·s。使用三维软件UG进行建模,油膜几何模型如图2所示。
|
图 2 油膜几何模型 Fig. 2 Geometric model of oil film |
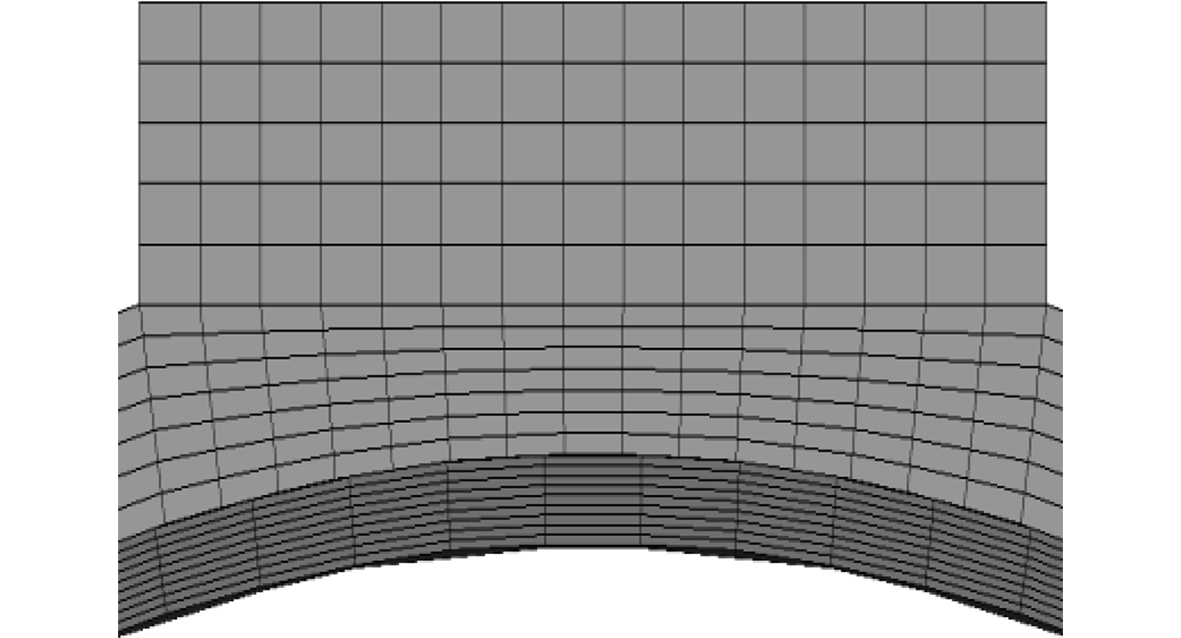
由于油膜结构简单、厚度薄,为得到高质量网格提高计算稳定性,采用全结构化六面体网格,油膜整体网格如图3所示。由于油膜厚度与其他位置尺寸相差很大,综合考虑计算精度和计算量,经网格无关性验证,在油膜厚度方向设置10层网格,网格质量在0.7以上,油膜局部网格放大如图4所示。采用SIMPLEC速度压力耦合算法,选择压力进出口边界条件,采用RNG κ-ε湍流模型进行数值模拟,采用滑移网格方法处理轴颈的旋转区域。

|
图 3 油膜整体网格 Fig. 3 Oil film global mseh |
|
图 4 油膜局部网格放大 Fig. 4 Local mesh enlargemengt of oil film |
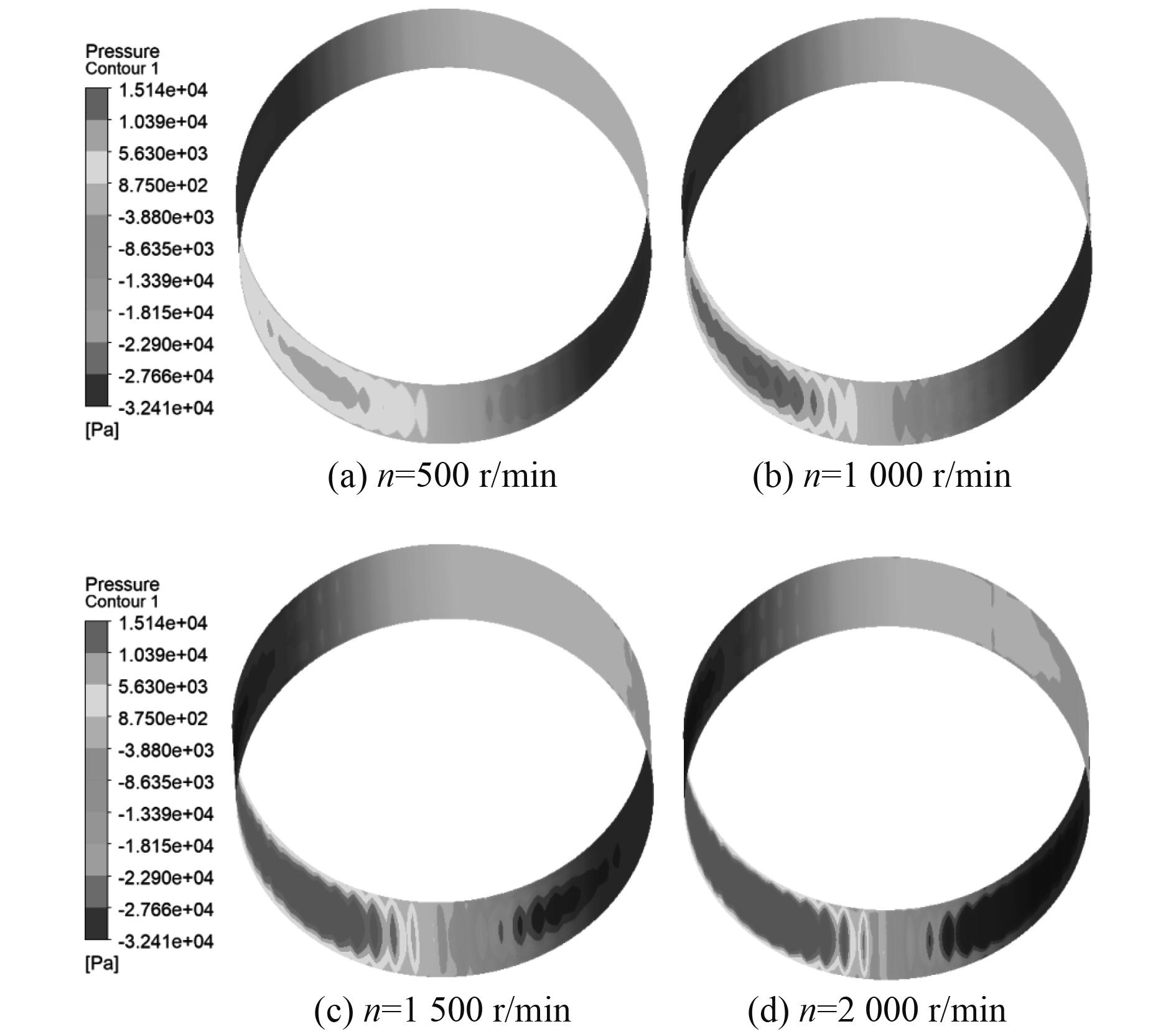
对油膜模型进行CFD数值模拟,转速分别取500 r/min,1000 r/min,1500 r/min,2 000 r/min时油膜压力场分布如图5所示。在最小油膜厚度处两侧分别呈现高压区和低压区,即楔形收敛区和发散区。当润滑油从进油口进入,随轴颈逆时针旋转,进入楔形收敛区,油膜压力逐渐增大,当达到最小油膜厚度处,进入发散区,油膜压力迅速减小,形成低压区后逐渐稳定,随转速逐渐增加,高压区和低压区逐渐在增大。
|
图 5 不同转速下油膜压力场分布 Fig. 5 Distribution of oil film pressure at different rotating speeds |
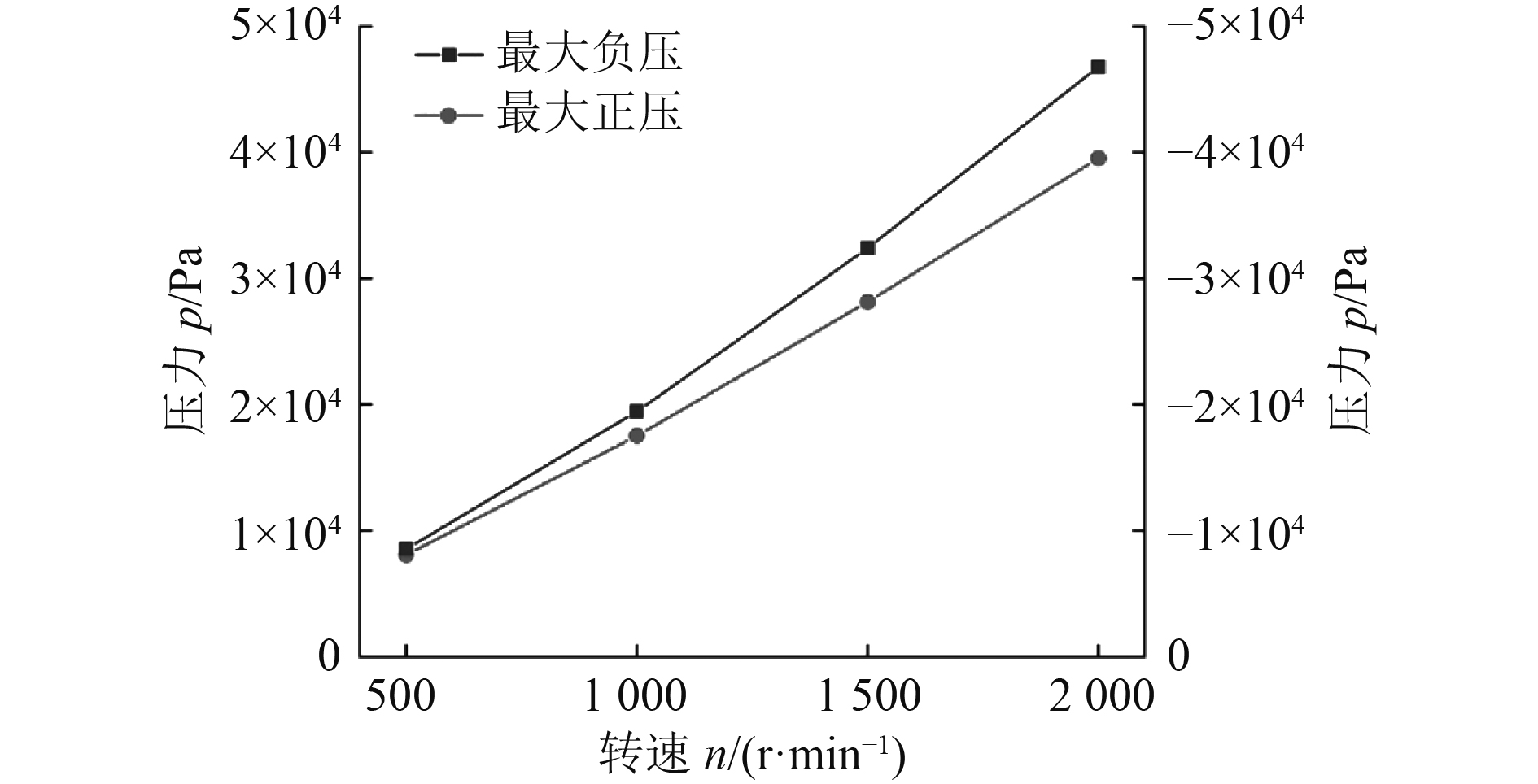
图6为不同转速下最大、最小压力变化曲线图。随转速增加,最大正压和最大负压均逐渐增大,两者增长速率均趋于稳定,呈线性增长,最大负压的增长速率高于最大正压。
|
图 6 不同转速下压力极值变化 Fig. 6 Variation of pressure extremum at different speeds |
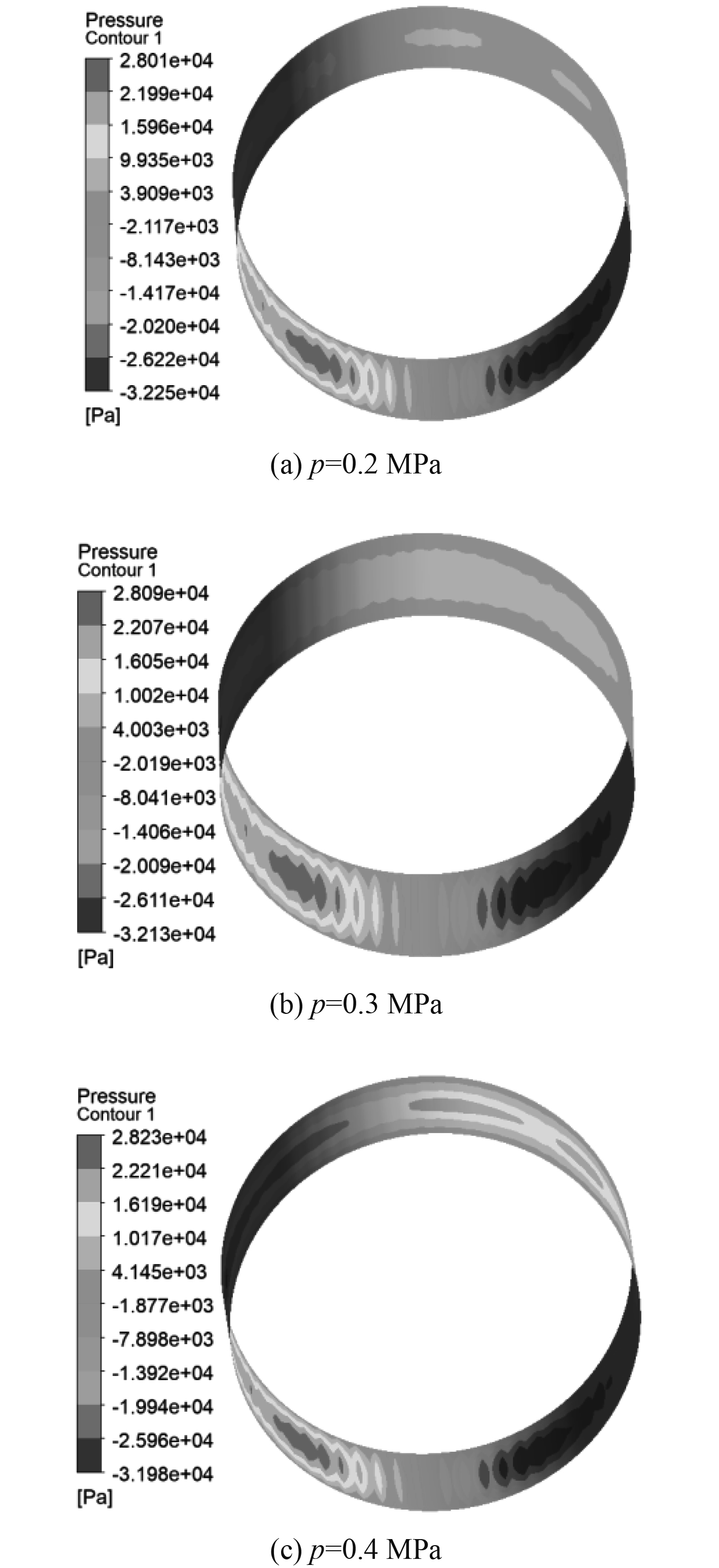
图7为轴颈转速n取1500 r/min不同进油压力下油膜压力场变化图。进油压力分别取0.2MPa,0.3 MPa,0.4 MPa,随着进油压力的不断增大,油膜整体压力和最大压力逐渐增加,高压区与低压区的分布逐渐分散,高压区逐渐向进油孔位置扩散,直至与低压区相接,且进油压力越大,与进油口相对应位置的压力越大,最大高压和最大负压位置基本保持不变
|
图 7 不同进油压力下油膜压力场分布 Fig. 7 Distribution of oil film pressure at different inlet pressure |
1)对油膜模型进行CFD数值模拟,得到油膜压力场的分布,在最小油膜厚度处两侧分别呈现高压区和低压区,即楔形收敛区和发散区。随轴颈逆时针旋转,润滑油从进油口进入楔形收敛区,油膜压力逐渐增大,当到达最小油膜厚度处,进入发散区,油膜压力迅速减小,形成低压区后逐渐稳定。
2)随转速增加,高压区和低压区逐渐在增加,最大正压和最大负压均逐渐增大,两者增长速率均趋于稳定,呈线性增长,最大负压的增长速率高于最大正压。
3)随进油压力增加,高压区逐渐向进油孔位置扩散,直至与低压区相接,且进油压力越大,与进油口相对应位置的压力越大,最大高压和最大负压位置基本保持不变。
| [1] |
NELSON H D. Rotor dynamic modeling and analysis procedures: a revive [J]. JSME International Journal, 1998, 41(1): 1−12.
|
| [2] |
韩清凯, 任云鹏, 刘柯,等. 转子系统油膜失稳故障的振动实验分析[J]. 东北大学学报, 2003(10): 959-961. |
| [3] |
杨金福, 哈三电厂3号机汽轮发电机组轴系稳定性的研究与分析 [J], 黑龙江电力, 2000, 22(4): 8.
|
| [4] |
张艾萍, 林圣强,等. 滑动轴承间隙对转子稳定性的影响 [J], 汽轮机技术, 2013, 55(2): 86−89.
|
| [5] |
涂林, 李多民, 段兹华. 基于Fluent的动压径向轴承油膜力场模拟研究[J], 润滑与密封, 2011, 36(4): 82−86.
|
| [6] |
S M CHUN. Aeration effects on the performance of a turbocharger journal bearing[J]. Tribology International, 2008, 41(4): 197−306.
|
| [7] |
MERUANE V, PASCUAL R. Identification of nonlinear dynamic coefficients in plain journal bearings[J]. Tribology International, 2008, 41(8): 743-754. DOI:10.1016/j.triboint.2008.01.002 |
| [8] |
张直明, 张言羊, 谢友柏,等. 滑动轴承的流体动力润滑理论[M]. 北京: 高等教育出版社, 1998.
|
| [9] |
温诗铸. 摩擦学原理[M]. 清华大学出版社. 2005.
|
 2022, Vol. 44
2022, Vol. 44

