0 引　言

近年来，深水沉船事故频发，这些沉船往往携带大量燃油，且沉船位置水域较深，一旦发生泄漏，对于海洋环境的影响巨大。所以在打捞沉船前需将沉船装载的大量燃油回收，以尽可能降低燃油泄漏对海洋环境造成的影响。目前，浅水沉船一般采用由潜水员或在水面布放水下开孔与抽液设备，来完成对沉船内部燃油的抽取。但当水深超过500 m后上述方法很难实施^[1]，除水深影响外，恶劣的海况与有限的潜水作业时间使得在打捞深水沉船时，只能采用专用的开孔抽液装备在ROV(remote operated vehicle, ROV)辅助下协同开展应急处置，通常是ROV在水下与不同装备对接后并为其提供动力，去完成沉船外层表面的基盘安装、外层钢板开孔、基盘对接、内层表面开孔及船内抽液等一些列复杂作业。

在沉船应急处置过程中，ROV在不确定的情况下（如沉船状态未知、海底水流变化等）协同不同的开孔抽液装备与沉船特定位置及其表面安装的基盘进行对接。协同对接的装备无论在质量、惯量还是水动力作用尺度上与ROV都比较接近，所以对接后的整个ROV系统动力学参数与对接前的单独ROV系统动力学参数会发生较大改变，特别是绕z轴的转动惯量，可能会增大5～6倍，而ROV常采用PID控制，且ROV的运动具有大惯性、多干扰、时变性等特点，所以在对接打捞沉船所需装备后，整体ROV的运动控制精度会大幅衰减，甚至可能使控制系统变得不稳定，特别是对首向角的控制，严重影响工作效率，增加工作成本^[2]。而ROV在一次作业中需要对接多个不同的装备，如外层船壳开孔机、内层船壳开孔机与抽液机等，且ROV在对接不同装备后都需要保持较高的控制精度才能完成精细化作业，所以需要切换到自适应性能强大的控制器才能满足ROV的精细化作业的要求。

Hernándezalvarado R ^[3]利用神经网络对PID控制器的增益进行在线调整以应对时变的外界干扰，杨淼^[4]通过RBF神经网络补偿ROV动力学模型中的不确定项达到更好的滑模控制效果，但上述2种控制器针对的是未知环境与系统内部较小的干扰。祁翔^[5]利用广义最小二乘法来对ROV的动力学模型进行在线辨识，随后为控制器的设计提供依据，但该种方法辨识参数收敛速度较慢。

本文针对ROV对接特殊装置后系统动力学参数变化较大但需快速保持良好控制性能与需对接多个不同装置这2个特点，设计了一种自校正控制器。该控制器利用ROV在运动过程中所产生的运动动态数据与推进器数据，采用带可变遗忘因子递推最小二乘法(variable forgetting factor recursive least-squares，VFFRLS)辨识得到ROV在携带不同工具状态下的整个系统的动力学参数，该种方法可以在2 s内快速且准确地识别ROV新的系统动力学参数。识别出新系统动力学参数后会对滑模控制算法里对应的参数进行更新，使得控制器的控制精度满足实际工程需要。由于对接装备后ROV绕z轴的转动惯量变化最为明显，对于ROV首向角的控制影响最为严重，所以最后利用Matlab/Simulink软件进行控制器首向角跟踪的仿真实验。

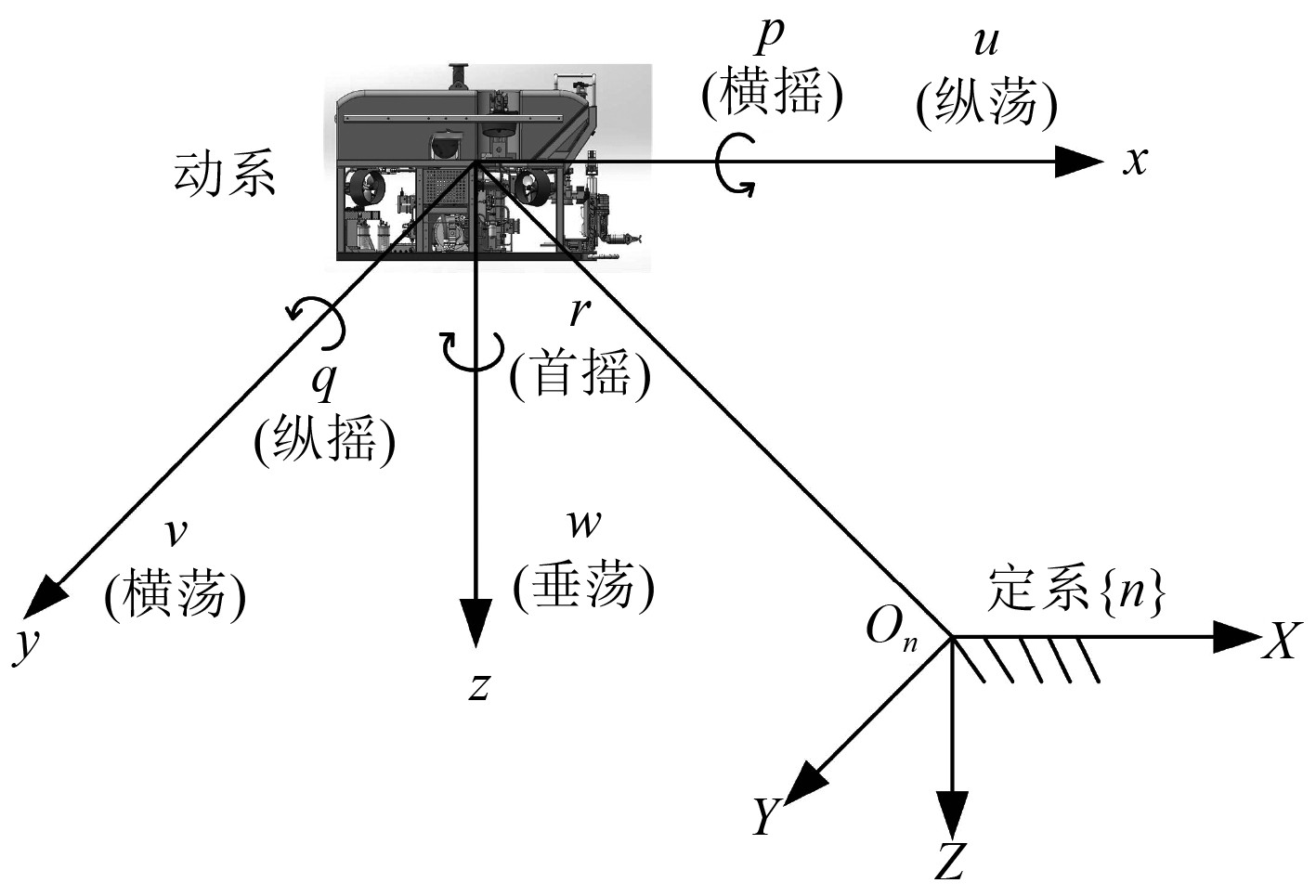
1 ROV动力学模型

在研究ROV的6自由度运动（横荡、纵荡、垂荡、首摇、横摇、纵摇）时，通常会建立ROV运动的两种参考坐标系^[6]，即大地参考坐标系 $ {O_n} - XYZ $ （定系）与随体参考坐标系 $ O - xyz $ （动系），如图1所示。

在随体坐标系下ROV的6自由度动力学模型可以写为^[7]：

$ M\dot v + C(v)v{\text{ + }}D(v)v + g(\eta ) = \tau 。$

(1)

式中： $ \tau $ 为推进器产生的力向量或力矩向量， $ \eta $ 为固定坐标系下ROV的位置与姿态向量， $ v $ 为运动坐标下ROV的线速度或角速度向量， $ M $ 为ROV的惯性有关系数矩阵； $ C(v) $ 为ROV的科氏与向心力有关系数矩阵； $ D(v) $ 为ROV在水中受到的阻力系数矩阵； $ g(\eta ) $ 为ROV所受的重力与浮力(力矩)所产生的回复力矩； $ \tau $ 为ROV所受到的力或力矩。

由于深海打捞作业ROV在运行时速度较小，科氏力与向心力可以忽略，结构对称，且各个自由度的运动之间耦合度较小，因此随体坐标系下ROV的6自由度的动力学模型可以写为：

$ M\dot v + D(v)v + g(\eta ) = \tau ，$

(2)

$ M = {\rm{diag}}\{ m - {X_{\dot u}}{\text{ }}0{\text{ }}m - {Z_{\dot w}}{\text{ }}0{\text{ }}{M_{\dot q}}{\text{ }}{I_z} - {N_{\dot r}}\}，$

(3)

$ D = - {\rm{diag}}\{ {X_u}{\text{ 0 }}{Z_w}{\text{ 0 }}{M_q}{\text{ }}{N_r}\}，$

(4)

$ g(\eta ) = {[0{\text{ }}0{\text{ }} - W{\text{ }}0{\text{ }} - WB{G_z}\sin (\theta ){\text{ }}0]^{\rm{T}}}。$

(5)

其中： $ m $ 为ROV的质量， $ {X_{\dot u}} $ ， $ {Z_{\dot w}} $ ， $ {M_{\dot q}} $ ， $ {N_{\dot r}} $ 为惯性水动力系数， $ {X_u} $ ， $ {Z_w} $ ， $ {M_q} $ ， $ {N_r} $ 为粘性水动力系数， $ {I_z} $ 为ROV绕z轴的转动惯量， $ W $ 为ROV重力与浮力的合力， $ B{G_z} $ 为浮心与重心z坐标的差值， $ \theta $ 为大地坐标系下ROV的俯仰角。

根据上述简化公式，可以得到首向角的动力学模型为：

$ ({I_z} - {N_{\dot r}})\dot r - {N_r}r = {\tau _N}，$

(6)

根据式(6)可得首向角的二阶Nomoto模型为^[8]：

$ \tau \dot r(t) + r(t) = Ku(t - {T_d}) , \dot \varphi (t) = r(t)，$

(7)

式中： $ \tau $ 为时间常量， $ \tau = \dfrac{{{I_z} - {N_{\dot r}}}}{{ - {N_r}}} $ ， $ K $ 为稳态增益， $K = \dfrac{1}{{ - {N_r}}}$ ， $ {T_d} $ 为纯时延时间。

经过拉氏变换后为：

$ G(s) = \frac{{{\varphi _s}}}{{{u_s}}} = \frac{K}{{\tau {s^2} + s}}{e^{ - {{{T}}_d}s}} 。$

(8)

可以看出，时间常量 $ \tau $ 、稳态增益 $ K $ 与纯时延时间 $ {T_d} $ 为影响整个首向角控制系统的关键参数。

2 水下机器人基于VFFRLS的自校正滑模控制 2.1 可变遗忘因子的递推最小二乘法

VFFRLS算法是基于最小二乘法原理的一种改进算法，具有对于参数的识别速度较快，对于参数的变化敏感，计算量较最小二乘法小，适合于工程使用，且对于噪声的抗扰能力较强的特点，其算法原理如下^[9-10]：

$ e(n) = d(n) - {x^{\rm{T}}}(n)w(n - 1) ，$

(9)

$ k(n) = \frac{{p(n - 1)x(n)}}{{\lambda (n) + {x^{\rm{T}}}(n)p(n - 1)x(n)}}，$

(10)

$ w(n) = w(n - 1) + k(n)e(n)，$

(11)

$ p(n) = \frac{1}{{\lambda (n)}}\left[ {p(n - 1) - k(n){x^{\rm{T}}}(n)p(n - 1)} \right]，$

(12)

$ \lambda (n) = {\lambda _{\min }} + (1 - {\lambda _{\min }}){2^{L(n)}} ，$

(13)

$ L(n) = - {\rm{round}}[\mu {e^2}(n)] 。$

(14)

在首向角控制器设计中： $x(n) = {[\dot r(n){\text{ }}r(n)]^{\rm{T}}}$ ； $w(n) = {[{I_z} - {N_{\dot r}}, - {N_r}]^{\rm{T}}}$ ； $d{\text{(n) = }}\tau {{(n)}}$ ，为推进器所产生的力或力矩； $ e(n) $ 为先验误差； $ k(n) $ 为卡尔曼增益矢量； $ p(n) $ 为 $ n $ 时刻及之前的输入信号矩阵的逆； $ \lambda (n) $ 表示 $ n $ 时刻的遗忘因子，通常 $ \lambda (n) $ 的上下限设置为1与0.95， ${\rm{round}}[]$ 表示最接近 $ \mu {e^2}(n) $ 的整数。

当系统动力学参数改变时， $ e(n) $ 变大， $ \lambda (n) $ 会快速减小，趋近下限，使得前面的 $ x(n) $ 与 $ d(n) $ 对于 $ w(n) $ 贡献值的权重变得非常小，当 $ e(n) $ 逐渐变小后， $ \lambda (n) $ 会迅速增大趋近上限直至稳定，之后的 $ x(n) $ 与 $ d(n) $ 对于 $ w(n) $ 贡献值的权重变得正常，使得系统动力学参数能够被快速辨识。

2.2 控制系统结构

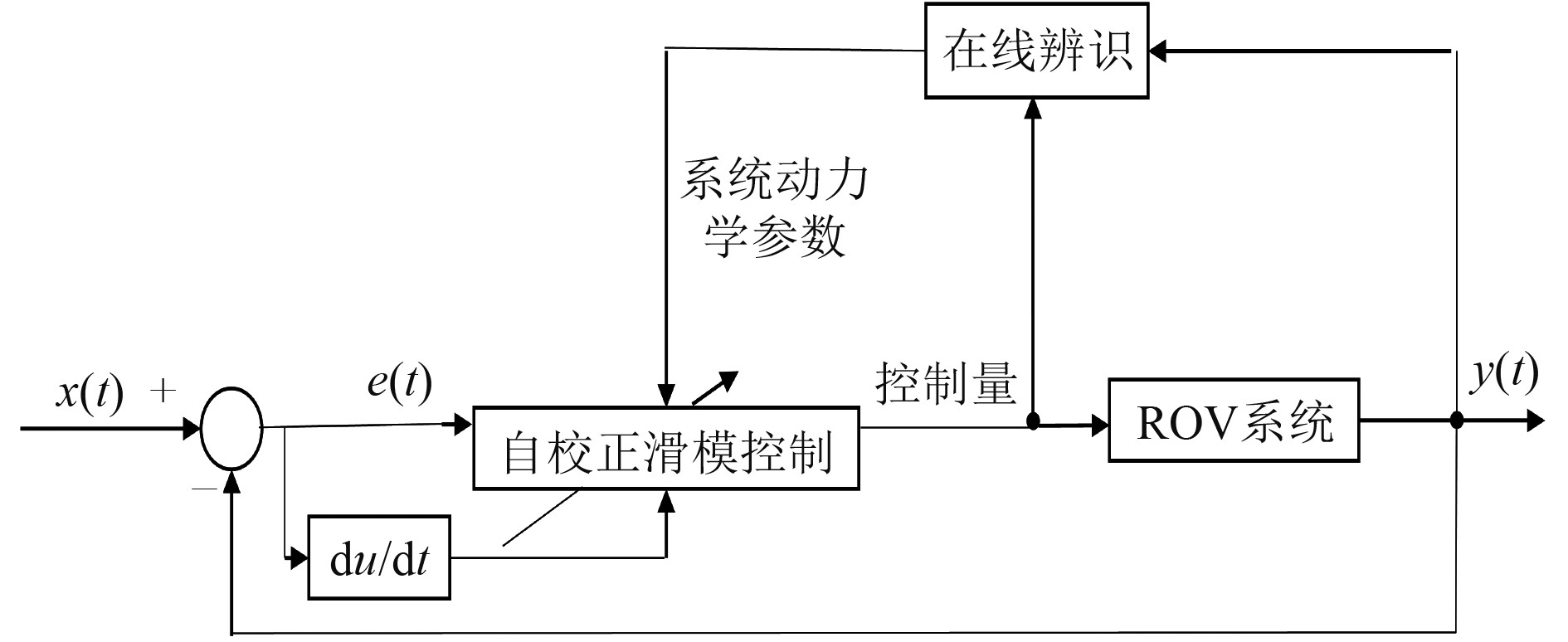
ROV在对接特殊装置后系统动力学参数会发生较大改变，由于滑模控制参数与ROV系统水动力参数具有较强的相关性，所以需要实时调整滑模控制器的参数，才能够获得满足工程精度要求的控制性能。ROV基于VFFRLS的自校正滑模控制器结构设计如图2所示，当系统动力学参数发生较大变化后，VFFRLS算法的遗忘因子会先趋向于最小值，当辨识参数稳定后，遗忘因子会趋向于最大值，此时的自校正滑模系统的控制率能取得最佳控制效果。

2.3 自校正滑模控制

根据式(8)，常见的ROV首向角动力学模型可以看作一个二阶系统，经变形可写作：

$ \ddot \varphi = \frac{{{N_r}}}{{{I_z} - {N_{\dot r}}}}\dot \varphi + \frac{1}{{{I_z} - {N_{\dot r}}}}{\tau _N}，$

(15)

令滑模面为：

$ s = c\dot \varphi + (\varphi - {\varphi _d}) = c\dot \varphi + {\varphi _e} ，$

(16)

其中： $ {\varphi _e} $ 为输出 $ \varphi $ 与参考输入 $ {\varphi _d} $ 的差值。

两边求导得：

$ \dot s = c\ddot \varphi + {\dot \varphi _e} = \left(c\frac{{{N_r}}}{{{I_z} - {N_{\dot r}}}} + 1\right){\dot \varphi _e} + c\frac{1}{{{I_z} - {N_{\dot r}}}}{\tau _N} ，$

(17)

取指数趋近率：

$ \dot s = - \varepsilon {{\rm{sgn}}} (s) - ks{\text{ }}(\varepsilon > 0,k > 0)，$

(18)

根据式（17）与式（18），得到：

$ {\tau _N} = \frac{{{I_z} - {N_{\dot r}}}}{c}\left( - \varepsilon {{\rm{sgn}}} (s) - ks\right) - \left({N_r} + \frac{{{I_z} - {N_{\dot r}}}}{c}\right){\dot \varphi _e} ，$

(19)

$ {\tau _N} $ 即控制输入。

现构造Lyapunov函数：

$ V(s,t) = \frac{1}{2}{s^2} ，$

(20)

对式子（20）求导得：

$ V'(s,t) = s\dot s = s( - \varepsilon {{\rm{sgn}}} (s) - ks)。$

(21)

易知， $ V(s,t) $ 满足Lyapunov第二法，且 $ s \ne 0 $ 时， $ V'(s,t) < 0 $ ，所以系统在李雅普诺夫意义下是渐进稳定的。

通过VFFRLS算法在线辨识ROV系统运动学参数可以在线调整滑模控制的参数，进一步调整输出。

3 首向角速度跟踪仿真对比

以“海龙Ⅲ” ROV和沉船抽液开孔机为研究对象，通过仿真实验模拟ROV与开孔机进行对接前后的传统PID控制、传统滑模控制、基于VFFRLS的自校正PID控制与基于VFFRLS的自校正滑模控制角度跟踪效果对比，从而验证控制方法的有效性。

开孔机参数如表1所示。

仿真实验中，ROV的航行速度设定为1 kn，由于采样频率与实验效果有较强相关性，将采样频率设置为100 Hz。为了尽可能地模拟真实情况，在ROV的控制系统里加入白噪声信号与阶跃信号来分别模拟传感器干扰、推进器非线性干扰与水流干扰，在信号传输环节加入0.1 s的延迟模块来模拟真实系统的信号传递，跟踪幅值为30°、频率为0.3 rad/s的正弦信号。

开始时传统PID与自校正PID参数经调试设定为 ${K_p} = 12\;700$ ， ${K_i} = 3\;615$ ， ${K_d} = 13\;967$ 。自校正PID控制的 $ {K_p} $ ， $ {K_i} $ ， $ {K_d} $ 会随着VFFRLS识别的系统动力学参数迭代而更新。根据频域分析法^[11]可整定得到合适的 $ {K_p} $ ， $ {K_i} $ ， $ {K_d} $ ，公式如下：

$ {K_p} = \frac{{w_n^2\tau }}{K} ，$

(22)

$ {K_d} = \frac{{2\xi \sqrt {K{K_p}\tau } - 1}}{K} = \frac{{2\xi {w_n}\tau - 1}}{K}，$

(23)

$ {K_i} = \frac{{{w_n}}}{\text{π} }{K_p} = \frac{{w_n^3\tau }}{{\text{π} K}} 。$

(24)

式中： $\tau = \dfrac{{{I_z} - {N_{\dot r}}}}{{ - {N_r}}}$ ， $K = \dfrac{1}{{ - {N_r}}}$ ， $ {w_n} $ 与 $ \xi $ 分别为系统的固有频率与阻尼系数，可设定为模型变换前控制系统的固有频率与阻尼系数。

传统滑模控制律的 $ {N_r} $ ， $ {I_z} $ 与 $ {N_{\dot r}} $ 不随时间而改变，经调试， $ \varepsilon $ ， $ c $ ， $ k $ 分别设定为51，3，2能达到较好的控制效果。自校正滑模控制律的 $ {N_r} $ ， $ {I_z} $ 与 $ {N_{\dot r}} $ 随着VFFRLS识别的系统动力学参数迭代而更新，见式（19）。

对接特殊装置后的ROV总体质量增加1050 kg，占ROV本身质量的30.43%，系统动力学参数也进行了相应的更新，模型变化前与模型变化后ROV的系统动力学参数分别如表2所示。将数据代入式(6)，可得ROV的首向角动力学模型。

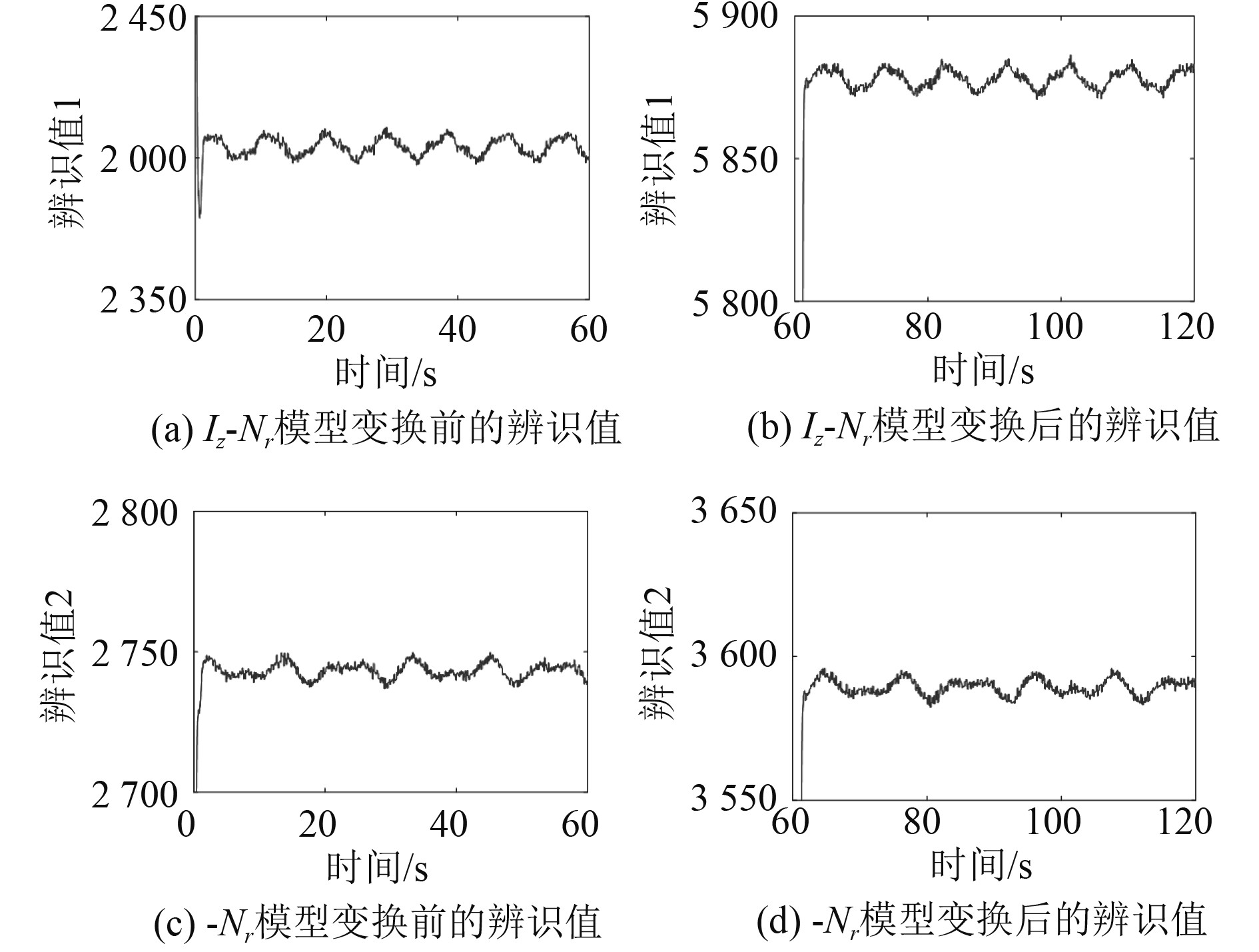
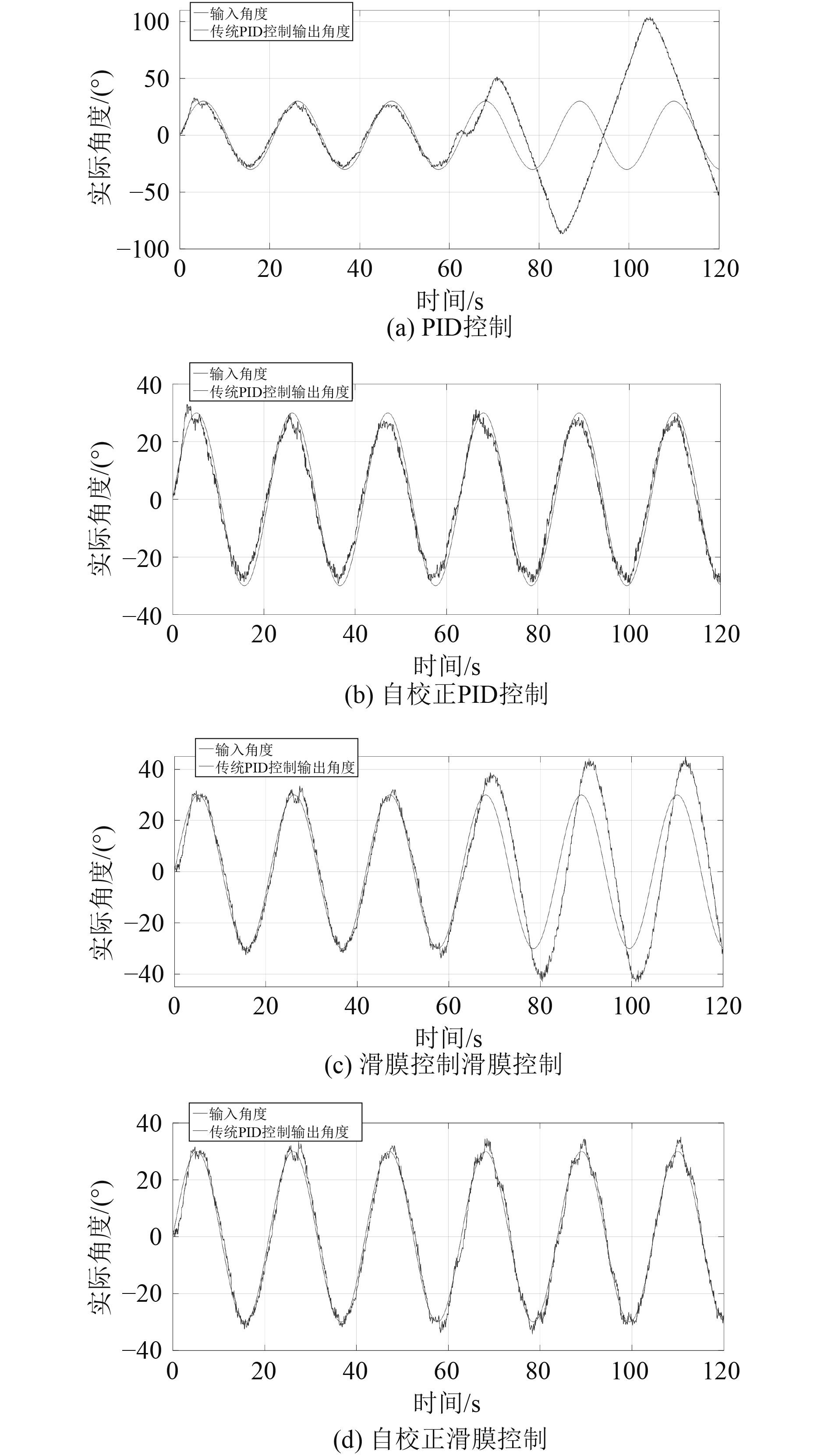
VFFRLS在仿真实验过程中识别出来的参数如图3所示，平均误差率如表3所示。可以看出，基于该种方法得到的在线辨识参数准确且迅速，误差率在5%以下，在采样率为100 Hz的条件下2 s内可以得到较稳定结果。在角度跟踪的仿真中，60 s的时候ROV对接了重量为1050 kg的内层开孔机，并改变了其系统特性，即系统动力学参数。传统PID控制、基于VFFRLS的自校正PID控制、传统滑模控制与基于VFFRLS的自校正滑模控制效果见图4。

从图4与表4可以看出：

1）当ROV系统动力学参数发生比较大改变后，对于传统PID控制器与传统滑模控制的影响比较大，PID控制器跟踪首向角时甚至出现了发散，但自校正滑模控制与自校正PID控制在跟踪角度正弦信号仍然保持着良好的跟踪效果。

2）在模型变换前，自校正滑模控制参考输入与输出的标准差比自校正PID参考输入与输出的标准差小68.57%，模型变换后，自校正滑模控制参考输入与输出的标准差比自校正PID控制参考输入与输出的标准差小34.80%。所以自校正滑模控制比自校正PID控制效果更好。

3）在模型变换后，自校正滑模控制参考输入与输出的标准差比传统滑模控制参考输入与输出的标准差要小72.31%，所以基于VFFRLS的在线辨识算法可以有效地提升滑模控制的跟踪效果。

4 结　语

本文以需水下协同作业的ROV为研究对象，针对该类ROV需多次对接不同特殊装置后系统动力学参数发生较大改变，导致原本的控制器性能无法满足工程精度要求的情况，设计了一种基于VFFRLS的自校正滑模控制器，并利用首向角跟踪控制的仿真实验，通过基于VFFRLS的自校正滑模控制与传统的PID控制、传统滑模控制以及自校正PID控制进行了跟踪效果的对比。仿真结果表明VFFRLS算法能够快速且准确地识别变化的系统动力学参数，并能提供切换控制系统的时间点，且基于VFFRLS的滑模自校正控制效果比传统的PID控制、传统滑模控制以及自校正PID控制效果更好，能够满足快速、稳定且自适应性强大的控制需求，从而验证了该方法的有效性。本文基于VFFRLS的自校正滑模控制法对于需要对接特殊装置的ROV控制具有参考意义。