为了提高水下机器人水中作业的时间和效率,布放回收技术是当前研究的热点和关键技术。如中国科学院沈阳自动化研究所研制的“CR-OIA0”型水下机器人,其布放回收主要以水面起吊为主[1];苏联科学院海洋研究所研制了一款水下机器人吊臂回收系统,该系统体积小,可通过液压缸驱动吊臂的伸缩,灵活性较强[2]。不同于较深水域的环境状况,近岸船舶受到岸边波浪、近岸回流等的作用,因此水下机器人布放回收方式会受到一定的限制。双体无人船作为一种新型船舶,其稳定性以及良好的操控性、定位性等方面受到科研人员的关注,同时双体船中间部分为安装通信、定位设备以及安装水下机器人布放回收设备提供了良好的布置空间[3]。设计了以双体船为载体的水下机器人布放回收系统三维模型,基于三维势流理论,结合 Ansys-AQWA 软件,对风、浪、流荷载的联合作用下双体船的水动力特性进行研究,得出双体船在近岸海况的环境下的运动响应特性。建立双体无人船-水下机器人运动学模型,运用Matlab/Simulink进行运动学分析,计算水下机器人在起吊过程中的摇摆情况。
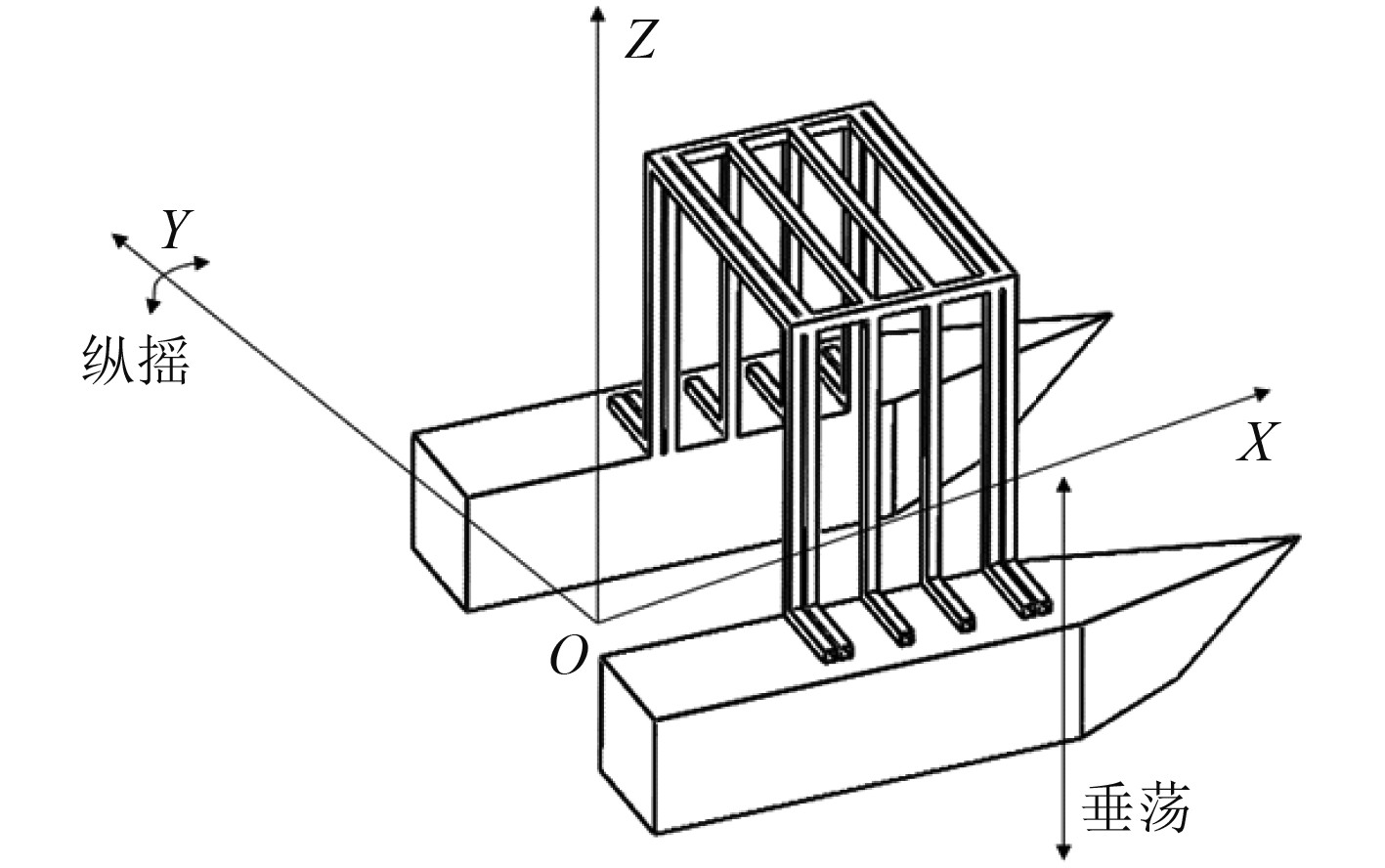
1 计算原理和方法 1.1 坐标系为了更好地描述船舶在水中6自由度运动状态,定义船体坐标系如图1所示[4]。
|
图 1 船体坐标系 Fig. 1 Hull coordinate system |
在坐标系中,定义纵荡、横荡、垂荡分别是沿着
假设船舶所处流域内的流体为理想流体,即无粘性、分布均匀的、不可压缩、无旋的流体,并且流域内的波浪频幅度非常小[5]。在这种情况下速度与速度势的关系是:
| $ q(x,y,z,t) = {Re} \{ u(x,y,z){e^{ - i\omega t}}\} ,$ | (1) |
| $ F(x,y,z,t) = f(x,y,z){e^{ - i\omega t}} ,$ | (2) |
式中:
速度势函数可以使用的拉普拉斯方程求出,用线性的边界条件代替非线性的自由表面条件,可以求得速度势[6]:
拉普拉斯方程:
| $ {\nabla ^2}\phi (x,y,z) = 0 ,$ | (3) |
线性化的自由表面:
| $ \frac{{\partial \phi _j^R}}{{\partial n}} - \frac{{{\omega ^2}}}{g}\phi _j^R = 0 ,$ | (4) |
物面条件:
| $ {\left. {\frac{{\partial \phi _j^R}}{{\partial n}}} \right|_S} = {n_j},$ | (5) |
海底条件:
| $ {\left. {\frac{{\partial \phi _j^R}}{{\partial n}}} \right|_{Z = - H}} = 0,$ | (6) |
无穷远处:
| $ \mathop {\lim }\limits_{x \to \infty } \sqrt R \left( {\frac{{\partial \varPhi }}{{\partial R}} - ik\varPhi } \right) = 0 。$ | (7) |
式中:
| $ \varPhi (x,y,z,t) = {\varPhi ^I}(x,y,z,t) + {\varPhi ^D}(x,y,z,t) + {\varPhi ^R}(x,y,z,t) ,$ | (8) |
其中,入射势是入射波对流场的作用,绕射势是船舶对流体扰动的作用,辐射势是船舶运动对流场的作用。
根据波浪理论,入射势
| $ {\Phi ^I} = - \frac{{Ag}}{\omega }\frac{{\cosh k(z + h)}}{{\cosh kh}}\exp [ik(x\cos \beta + y\sin \beta )],$ | (9) |
式中,
辐射势和绕射势也可以根据波浪理论,结合边界条件求得。得出速度势函数之后,可以用伯努利方程算出作用于船体的流体力。
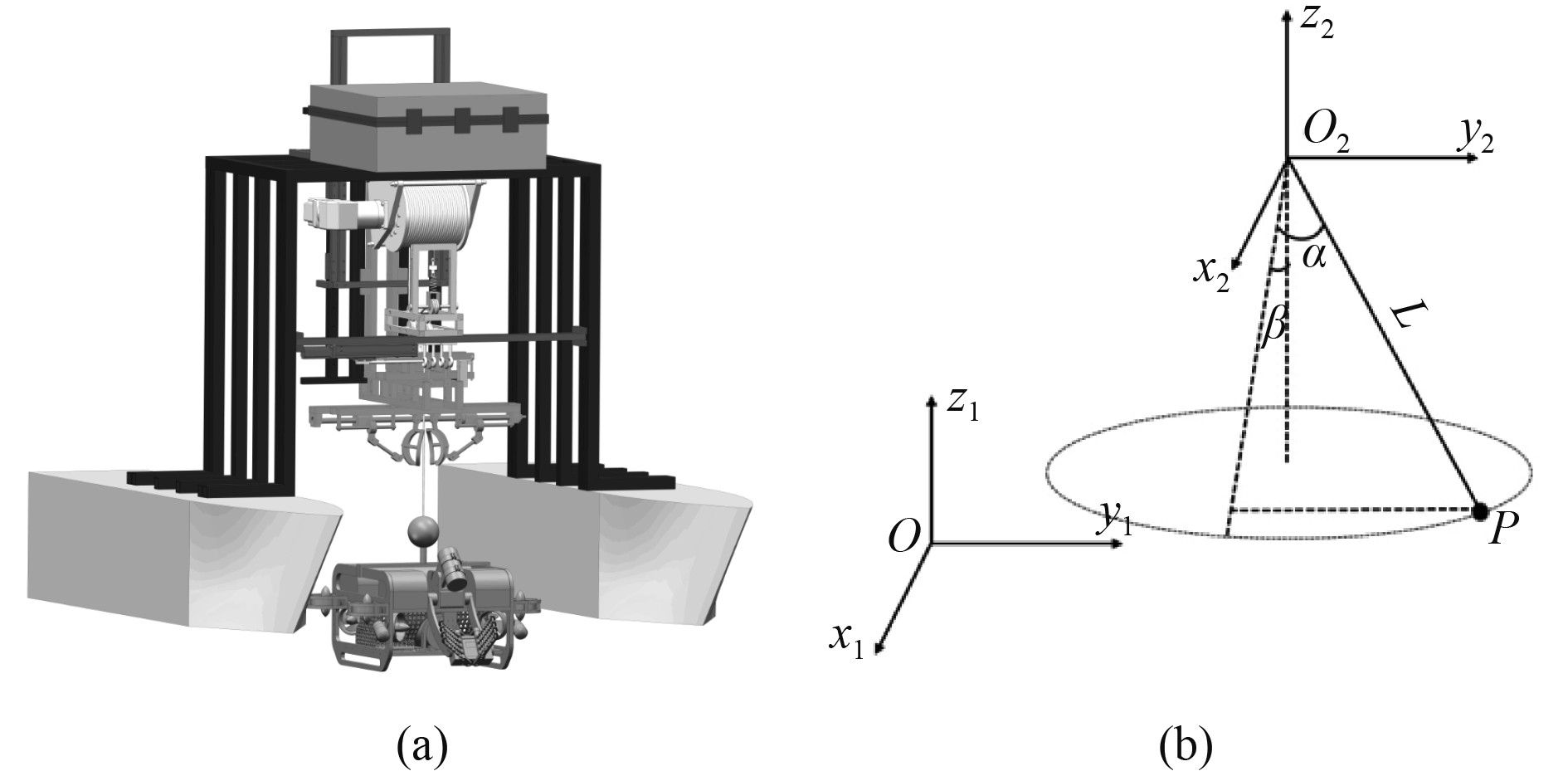
1.3 动力学建模在对水下机器人进行布放回收作业时,机器人本身是没有动力的,在进行收绳和放绳作业时,可以将其看成一个简单的球摆模型,类似于船用起重机起吊重物,将绞车看成吊点,机器人看作是吊重,其简化模型如图2所示,吊绳的长度为
|
图 2 简化模型图 Fig. 2 Simplified model diagram |
重物在绞车坐标系的位置坐标为:
| $ \begin{aligned} & {x_p} = {x_2} + l\cos \alpha \sin \beta ,\\ & {y_p} = {y_2} + l\sin \alpha ,\\ & {z_p} = {z_2} - l\cos \alpha \cos \beta ,\end{aligned} $ | (10) |
对式(10)求导,得到吊重的速度:
| $ \begin{aligned} & {{\dot x}_p} = {{\dot x}_2} + l\cos \alpha \cos \beta \dot \beta - l\sin \alpha \sin \beta \dot \alpha ,\\ & {{\dot y}_p} = {{\dot y}_2} + l\cos \alpha \dot \alpha ,\\ & {{\dot z}_p} = {{\dot z}_2} + l\cos \beta \sin \alpha \dot \alpha + l\cos \alpha \sin \beta \dot \beta ,\end{aligned} $ | (11) |
系统的动能
| $ \begin{aligned} & T = \frac{1}{2}{m_p}({{\dot x}_p}^2 + {{\dot y}_p}^2 + {{\dot z}_p}^2) ,\\ & V = {m_p}g{z_p},\end{aligned} $ | (12) |
式中:
拉格朗日方程为:
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial T}}{{\partial {{\dot q}_j}}}} \right) - \frac{{\partial T}}{{\partial {{\dot q}_j}}} + \frac{{\partial V}}{{\partial {q_j}}} = 0,$ | (13) |
式中:
联合式(11)~式(13),经过简化后,可以得到水下机器人球摆的动力学模型的数学微分方程:
| $ \begin{split} &\;\ddot \alpha = \frac{{ - \cos \beta (g + {{\ddot z}_2})\sin \alpha - \cos \alpha ({{\ddot y}_2} + l{{\dot \beta }^2}\sin \alpha ) + {{\ddot x}_2}\sin \alpha \sin \beta }}{l} ,\\ &\;\ddot \beta = - \frac{{\cos \beta {{\ddot x}_2} - 2l\dot \alpha \dot \beta \sin \alpha + (g + {{\ddot z}_2})\sin \beta }}{{l\cos \alpha }} 。\\[-15pt] \end{split} $ | (14) |
式中有关球摆的相关参数如表1所示。
|
|
表 1 球摆模型参数 Tab.1 Ball-pendulum model parameters |
通过Solidworks三维建模软件对双体船进行建模,其中双体船是一种通过中间支架连接两端船体的船型。双体船的排水量主要集中在支架的两侧船体上,在水中的阻力也主要来源于两侧的船体。双体船模型和模型网格划分如图3和图4所示,双体船的主要参数如表2所示。

|
图 3 双体船模型 Fig. 3 Catamaran model |

|
图 4 网格划分 Fig. 4 Mesh division |
|
|
表 2 双体船主要参数 Tab.2 Main parameters of catamaran |
运动响应幅值算子是一项可以精确地描述船舶运动情况的参数,这个参数是海洋波浪到船体本身的一种传递函数[10]。
| $ R(\omega ,\beta ,t) = A{Re} [\left| {\left. {H(\omega ,\beta )} \right|{e^{i(\omega t + \varphi )}}} \right.],$ | (15) |
式中:
在描述船舶运动的过程中,横摇、纵摇、垂荡是最重要的一项参数。这是船舶在自然载荷的作用下造成的,也很大程度上和粘性阻尼有关系。三维流势理论是将流体视为理性流体,忽略水的粘性,因此仿真计算的RAOs会比真实值偏大。当考虑粘性阻尼系数,取粘性阻尼系数为一阶阻尼系数的10%,每隔30°设置一次浪向角,可以得出12个不同浪向角下的RAO值。由于双体船为对称结构,因此只选用0°~180°一侧的浪向角,求解结果如图5所示。

|
图 5 各自由度下的运动响应 Fig. 5 Motion response under each degree of freedom |
图5充分地描述了双体船的频率-浪向角-RAOs之间的关系,因为船舶是对称结构,所以在不同浪向角下的运动响应呈对称分布。可以看出,双体船的运动幅值基本上随着波浪频率的增加而减小。由于双体船质量轻,因此横荡和纵荡在波浪频率较低的时候运动响应比较大,随着频率的增加,运动响应逐渐趋近于0;双体船在的横摇和纵摇0.46 Hz时出现最大值,首摇在0.6 Hz左右出现最大值,这与双体船的结构以及固有周期有关系。
由表3可知,双体船纵荡运动响应随着浪向角的增加呈先减小后增大的趋势;横荡运动响应随着浪向角的增加呈先增加后减小的的趋势;垂荡运动在不同浪向角之间的变化不大。
|
|
表 3 双体船在各个浪向角下移动运动响应的极值 Tab.3 The extreme values of the catamaran's movement at each wave direction angle |
由表4可知,双体船的横摇运动幅值随着浪向角的增加呈先增加后减少的趋势,当浪向角为90°时横摇角度最大;纵摇运动幅值随着浪向角的增加呈现先减小后增大的趋势,当浪向角为0°和180°时最大。
|
|
表 4 双体船在各个浪向角下转动运动响应的极值 Tab.4 Extreme values of the catamaran's rotational motion at each wave direction angle |
船舶在水面上航行时,总会受到波浪的作用,而且这种波浪总是不规则的,波浪的流向也是没有方向的。本文采用JONSWAP谱模拟不规则波[11]。
| $ S(\omega ) = \alpha {g^2}{\omega ^{ - 5}}\exp \left[ { - \frac{5}{4}{{\left( {\frac{\omega }{{{\omega _p}}}} \right)}^{ - 4}}} \right]{\gamma ^{\exp \left[ { - 0.5{{\left( {\frac{{\omega - {\omega _p}}}{{\sigma {\omega _p}}}} \right)}^2}} \right]}} 。$ | (16) |
在海况条件设置中,选取某沿海海况的参数。模拟仿真时设定海况如表5所示。
|
|
表 5 环境载荷参数 Tab.5 Environmental load parameters |
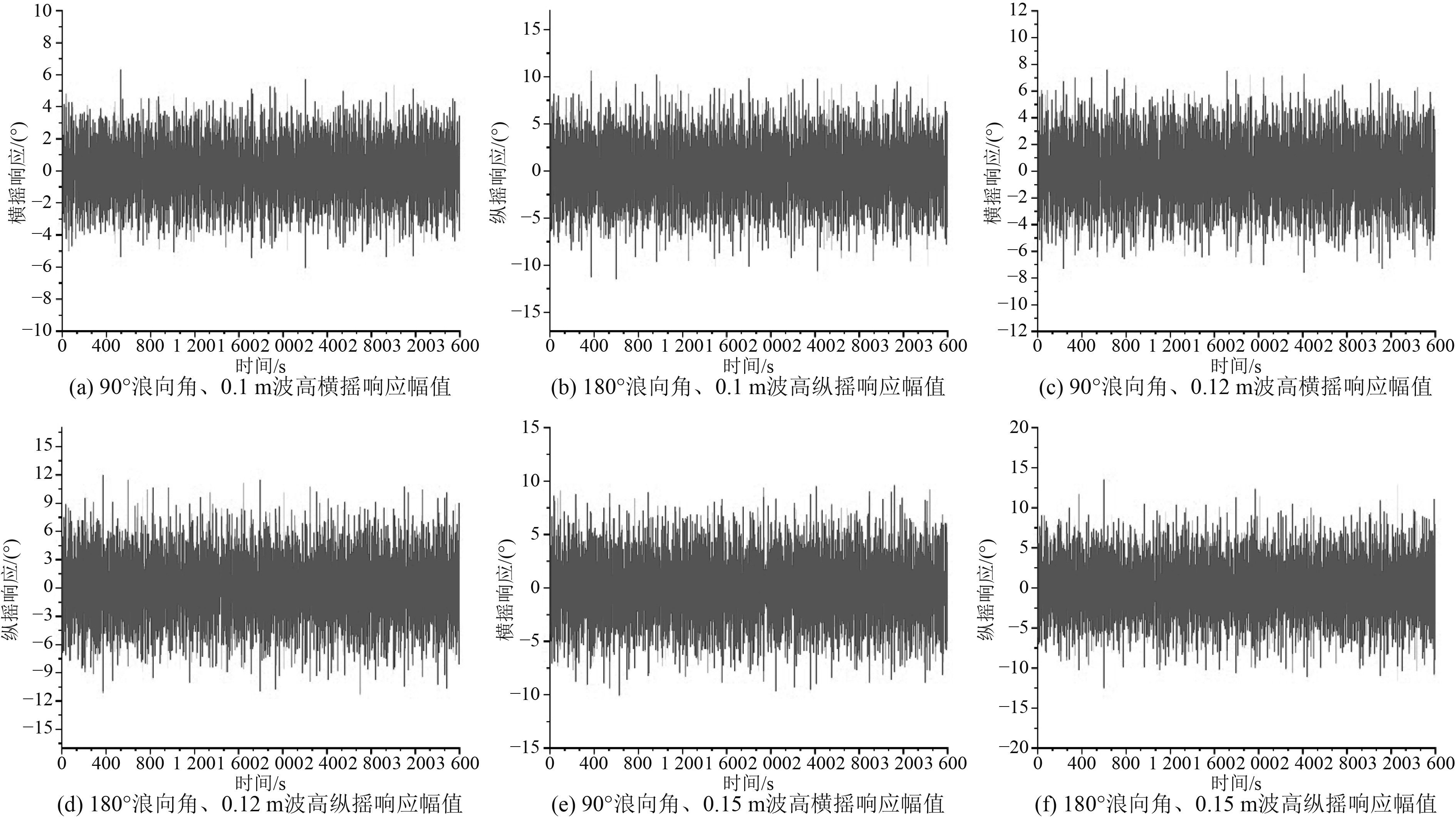
在时域分析中,分别模拟船体在浪向角为90°和180°时的运动情况,设置计算时长3600 s,考虑到真实环境条件下当风、浪、流相同方向时,船体的运动幅值最大,所以在计算中将风、浪、流载荷设置相同的方向[12],求解得出的各个方向的运动幅值的统计数据如表6所示,选取一些运动响应较大的曲线如图6所示。可以看出:
|
|
表 6 运动响应最大值 Tab.6 Maximum motion response |
|
图 6 不同浪向角和波高下的响应曲线 Fig. 6 Response curves under different wave direction angles and wave heights |
1)双体船的运动响应与弹簧振子的简谐运动类似,曲线整体呈现规律性。双体船在不同方向下的3个运动的响应幅值随着波浪高度的增加而逐渐变大。
2)在不同海况条件下,根据作用在双体船的浪向角不同,最大的运动响应分别是横摇和纵摇。当浪向角为90°时,双体船的横摇运动响应最大,其横摇的运动响应最大可以达9.821°;当浪向角为180°时,双体船的纵摇运动响应最大,最大可达13.429°。
3 布放回收装置动力学分析在进行船舶运动学仿真时,将船舶运动看作周期和复制给定的正弦运动,分别取绳长

|
图 7 不同浪向角下面外角、面内角、横向位移变化曲线 Fig. 7 Variation curves of external angle, in-plane angle and transverse displacement under different wave direction angles |
|
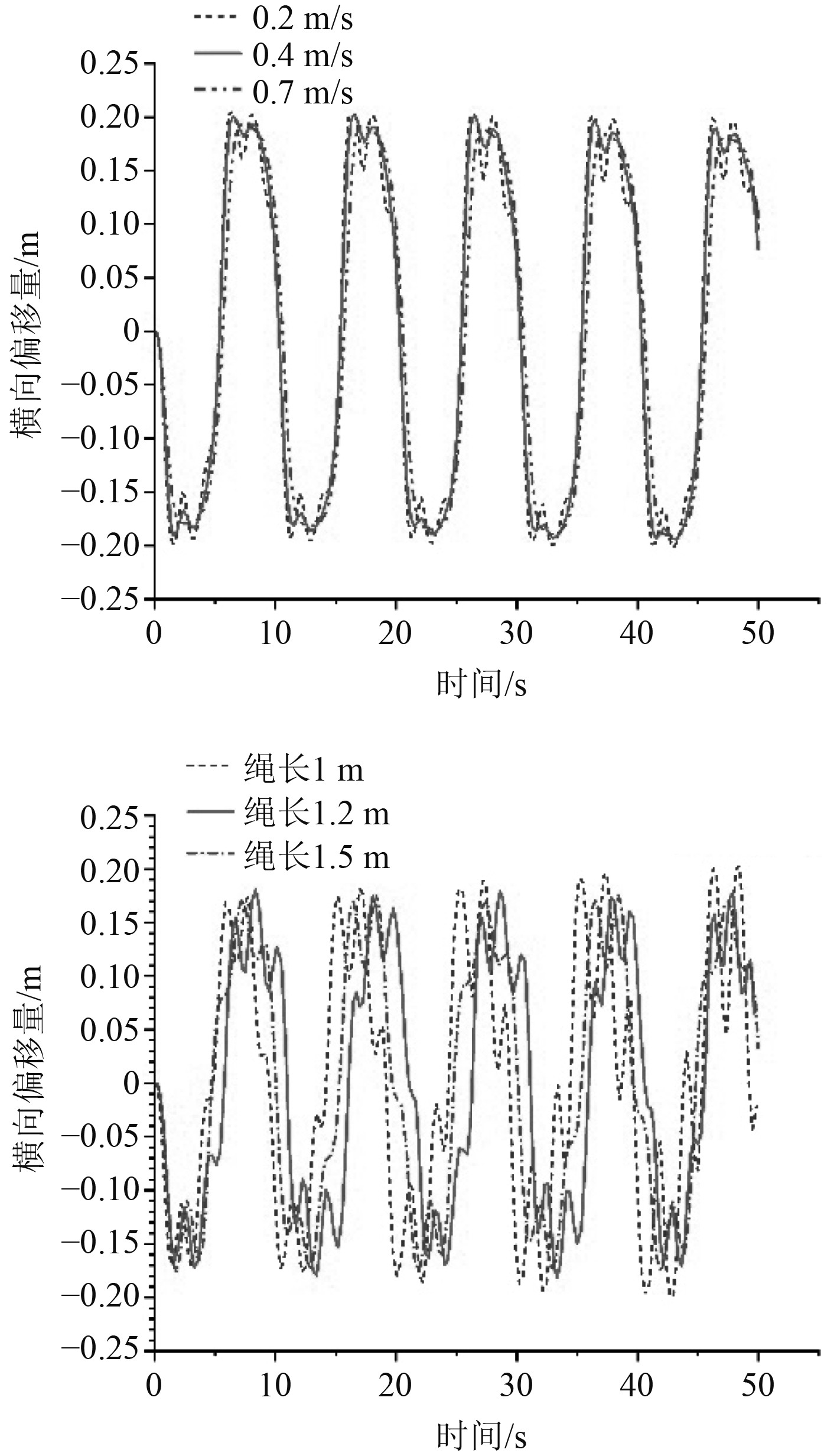
图 8 不同收绳速度以及不同绳长横向位移曲线 Fig. 8 Transverse displacement curves of different retracting speeds and rope lengths |
可以看出:
双体船在不同的浪向角作用下,面外角和面内角幅值之间相差很大。当浪向角为90°时,面外角
根据双体船浪向角的不同,面外角和面内角摆动的最大角度变化很大,且周期略大于激励的周期,且在摆动变化的过程中,会伴随着抖动现象出现。
随着收绳速度的增加,横向偏移量的抖动现象减弱,横向偏移量也逐渐减小。随着绳长的改变,横向偏移量的变化范围相差不大。因此要在允许的范围内,选取合适的收绳速度可以有效地减少回收机器人的摇晃幅度。
4 结 语分析双体船水动力曲线可知,环境载荷的方向性对双体船的运动响应对具有较大的影响,根据不同的波浪方向要及时调整双体船的姿态。回收机器人过程中,机器人的摇晃程度和收绳速度有很大的关系,在允许的范围内,选取合适的收绳速度可以有效地减少机器人的摇晃幅度。本文提出的一种以无人船为载体的水下机器人布放回收系统,提高了自动化程度,减少人工干预,船体具有良好的水动力性能,满足水下机器人布放回收的设计要求。在沿岸海域和浅海水域有很好的应用前景。
| [1] |
王雪峰, 吕汝信. 水下航行体位置指示及打捞、回收新技术研究[J]. 船舶工程, 2002(4): 52-55. DOI:10.3969/j.issn.1000-6982.2002.04.013 |
| [2] |
石宇超. AUV回收系统结构设计及关键技术研究[D]. 杭州: 中国计量大学, 2019.
|
| [3] |
王丹. 双体无人船运动建模及自主航行控制设计[D]. 成都: 西南交通大学, 2019.
|
| [4] |
CAO Ai-xia, SANG Song, SHENG Jing, et al. Numerical simulation of twin-barge float-over installation on AQWA software[J]. Cluster Computing: The Journal of Networks, Software Tools and Applications, 2019, 22(4).
|
| [5] |
XU Jin-hao, LIU Yue-qin, CHEN Chao-he. Dynamic response analysis of small oil tanker based on AQWA[J]. Advanced Materials Research, 2013, 2592. |
| [6] |
纪仁玮, 张亮, 王树齐, 等. 振荡浮子式双浮体波浪能装置的频域和时域分析[J]. 上海船舶运输科学研究所学报, 2019, 42(3): 19-27. DOI:10.3969/j.issn.1674-5949.2019.03.004 |
| [7] |
冷彦霖. 多体浮式防波堤的水动力性能及系泊系统分析研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [8] |
魏枭, 陈徐均, 苗玉基, 等. 有航速纵向连接多联浮体频域特性分析[J]. 舰船科学技术, 2019, 41(21): 37-41. |
| [9] |
王生海. 船用起重机吊重系统动力学分析与防摆控制研究[D]. 大连: 大连海事大学, 2018.
|
| [10] |
曹宇, 刘安东, 贾巧娇, 等. 一种新型海洋能发电轮机的水动力特性[J]. 船舶工程, 2020, 42(8): 16-22. |
| [11] |
李鸿, 张斐斐, 李莉, 等. 系泊多浮体耦合系统水动力特性数值分析[J]. 舰船科学技术, 2019, 41(5): 8-12. |
| [12] |
吕鸿冠, 黄技, 黄斯慧. 基于AQWA的游艇耐波性数值模拟[J]. 上海船舶运输科学研究所学报, 2016, 39(4): 22-25+48. DOI:10.3969/j.issn.1674-5949.2016.04.005 |
 2022, Vol. 44
2022, Vol. 44
