陆地资源不断被开采应用,许多专家开始将研究重心转移至资源丰富的海洋[1]。由于海洋的开发利用技术还不够成熟,为此,适应复杂水生环境的水下机器人逐渐被广泛熟知与应用[2]。遥控式水下机器人为手动操作的有缆型,无人无缆水下机器人是需要事先编程的半自主型,自主式水下机器人是能够感应水中环境并自主变换自身状态的全自主型,其主要的区别是供电、通信。有缆式水下机器人通常采用高压供电的方式,需要借助母船,且工作范围受限,无缆式采用的蓄电池供电存在工作时间短的问题,水声通信对环境要求高[3-4],可靠性较低。为解决水下机器人的上述缺点,半潜式航行体应时而生。
半潜式航行体的基本构造分为主航行体、拖体,主航行体在通航时沉入水底,在其上部安装了作为柴油引擎进排气的船桅,不但保证了航行体的动力稳定[5],还使其作业时间、范围得以加强,而拖体则可布放于较深层水域。
通过半潜式航行体的应用可有效为船舶提供合适的航道,确保其任务的正常推进,具有多样的种类及功能,信息实时效果较好。但是其航行过程中流场受多方因素扰动,因此需要对半潜式航行体的控制进行研究。王永涛[6]通过粒子群改进反步法设计控制策略,张涛等[7]采用闭环增益成形算法设计控制策略,但是以上已有的方法计算过程较为繁琐。为此,本文提出应用关联规则的半潜式航行体稳态控制技术,通过关联规则挖掘到半潜式航行体的数据潜在关联,提升控制的精准度。
1 半潜式航行体稳态控制 1.1 半潜式航行体空间运动数学模型 1.1.1 坐标系已知半潜式航行体的基本结构多为回转形式,结合动力、运动学理论为其构建空间运动方程[8]。在半潜式航行体浮心横截面交轴线中心坐标系
地面坐标系转换为流体坐标系的矩阵为:
| $ \begin{split} {\boldsymbol{C}}_b^0 =\;& \left( \begin{array}{*{20}{c}} {\cos \theta \cos \psi }&{\sin \theta } \\ { - \sin \theta \cos \psi \cos \varphi + \sin \psi \sin \varphi }&{\cos \theta \cos \varphi }\\ {\sin \theta \cos \psi \cos \varphi + \sin \psi \cos \varphi }&{ - \cos \theta \sin \varphi }\end{array}\right.\\ &\left. \begin{array}{*{20}{c}} { - \cos \theta \sin \psi }\\ { \sin \theta \sin \psi \cos \varphi + \cos \psi \sin \varphi } \\ { - \sin \theta \sin \psi \sin \varphi + \cos \psi \sin \varphi } \end{array} \right) 。\end{split}$ | (1) |
流体坐标系转换为地面坐标系的矩阵为式(1)的转置矩阵:
| $ \begin{split} {\boldsymbol{C}}_0^b =\;& \left( \begin{array}{*{20}{c}} {\cos \theta \cos \psi }&{ - \sin \theta \cos \psi \cos \varphi + \sin \psi \cos \varphi }\\ {\sin \theta }&{\cos \theta \cos \varphi }\\ { - \sin \psi \cos \theta }&{\sin \theta \sin \psi \cos \varphi + \cos \psi \sin \varphi }\end{array}\right.\\ &\left. \begin{array}{*{20}{c}} {\sin \theta \cos \psi \sin \varphi + \sin \psi \cos \varphi } \\ { - \cos \theta \sin \varphi } \\ { - \sin \theta \sin \psi \sin \varphi + \cos \psi \cos \varphi } \end{array} \right)。\end{split} $ | (2) |
分析航行体的动力学特性,结合动量、动量矩定理在流体坐标系中构建的空间运动方程组[10],得到:
| $\begin{split} & \left( {m + {\lambda _{11}}} \right){{\dot v}_x} - m{y_c}{{\dot \omega }_z} + m{z_c}{{\dot \omega }_y} + \\ & m\left[ {{v_z}{\omega _y} - {v_y}{\omega _z} - {x_c}\left( {\omega _y^2 + \omega _z^2} \right) + {y_c}{\omega _x}{\omega _y} + {z_c}{\omega _z}{\omega _x}} \right] \\ & = - \left( {G - B} \right)\sin \theta + T + X\left( {m + {\lambda _{22}}} \right){{\dot v}_y}+ \\ & \left( {m{x_c} + {\lambda _{26}}} \right){{\dot \omega }_z} - m{z_c}{{\dot \omega }_x} + \\ & m\left[ {{v_x}{\omega _z} - {v_z}{\omega _x} + {x_c}{\omega _x}{\omega _y} + {z_c}{{\dot \omega }_y}{\omega _z} - {y_c}\left( {\omega _x^2 + \omega _z^2} \right)} \right] \\ & = - \left( {G - B} \right)\cos \theta \cos \varphi + Y ,\end{split}$ | (3) |
| $\begin{split} & \left( {m + {\lambda _{33}}} \right){{\dot v}_z} - \left( {m{x_c} - {\lambda _{35}}} \right){{\dot \omega }_y} + m{y_c}{{\dot \omega }_x} + \\ & m\left[ {{v_y}{\omega _x} - {v_x}{\omega _y} - {x_c}{\omega _z}{\omega _x} + {y_c}{\omega _y}{\omega _z} + {z_c}\left( {\omega _x^2 + \omega _z^2} \right)} \right] \\ & = \left( {G - B} \right)cos\theta \sin \varphi + Z\left( {{J_{xx}} + {\lambda _{44}}} \right){{\dot \omega }_x} + m{y_c}{{\dot v}_z} - \\ & m{z_c}{{\dot v}_y} + m{y_c}\left( {{v_y}{\omega _x} - {v_x}{\omega _y}} \right) + m{z_c}\left( {{v_z}{\omega _x} - {v_x}{\omega _z}} \right) + \\ & \left( {{J_{zz}} - {J_{yy}}} \right){\omega _y}{\omega _z} = G\cos \theta \left( {{y_c}\sin \varphi + {z_c}\cos \varphi } \right)- \\ & B\cos \theta \left( {{y_b}\sin \varphi + {z_b}\cos \varphi } \right) + {M_x} ,\end{split} $ | (4) |
| $ \begin{split} & \left( {{J_{yy}} + {\lambda _{55}}} \right){{\dot \omega }_y} + m{z_c}{{\dot v}_x} - \left( {m{x_c} - {\lambda _{35}}} \right){{\dot v}_z}+ \\ & m{z_c}\left( {{v_z}{\omega _y} - {v_y}{\omega _z}} \right) + m{x_c}\left( {{v_x}{\omega _y} - {v_y}{\omega _x}} \right)+ \\ & \left( {{J_{xx}} - {J_{zz}}} \right){\omega _z}{\omega _x} = - G\left( {{x_c}cos\theta \sin \varphi + {z_c}\sin \varphi } \right) + \\ & B\left( {{x_b}\cos \theta \sin \varphi + {z_b}\sin \varphi } \right) + {M_y} ,\end{split} $ | (5) |
| $ \begin{split} & \left( {{J_{zz}} + {\lambda _{66}}} \right){{\dot \omega }_z} + m{y_c}{{\dot v}_x} - \left( {m{x_c} - {\lambda _{26}}} \right){{\dot v}_y}+ \\ & m{x_c}\left( {{v_x}{\omega _z} - {v_z}{\omega _x}} \right) + m{y_c}\left( {{v_y}{\omega _z} - {v_z}{\omega _y}} \right)+ \\ & \left( {{J_{zz}} - {J_{yy}}} \right){\omega _x}{\omega _y} = G\left( {{y_c}\sin \theta - + {x_c}cos\theta cos\varphi } \right) - \\ & B\left( {{y_b}\sin \theta - + {x_b}cos\theta \cos \varphi } \right) + {M_z}。\end{split} $ | (6) |
其中:
| $ \left[ {\begin{array}{*{20}{c}} {\dot \psi } \\ {\dot \theta } \\ {\dot \varphi } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{\sec \theta \cos \varphi }&{\sec \theta \sin \varphi } \\ 0&{\sin \varphi }&{\cos \varphi } \\ 1&{ - {\rm{tg}}\theta \cos \varphi }&{{\rm{tg}}\theta \sin \varphi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\omega _x}} \\ {{\omega _y}} \\ {{\omega _z}} \end{array}} \right] ,$ | (7) |
半潜式航行体的空间位置取决于:
| $ \left( {\begin{array}{*{20}{c}} {{\rm{d}}{x_0}/{\rm{d}}t} \\ {{\rm{d}}{y_0}/{\rm{d}}t} \\ {{\rm{d}}{z_0}/{\rm{d}}t} \end{array}} \right) = C_0^b\left( {\begin{array}{*{20}{c}} {{v_x}} \\ {{v_y}} \\ {{v_z}} \end{array}} \right),$ | (8) |
攻角
| $ \alpha = - {\rm{arctg}}\left( {{v_y}/{v_x}} \right), $ | (9) |
| $ \beta = {\rm{arctg}}\left( {{v_z}/\sqrt {v_x^2 + v_y^2} } \right), $ | (10) |
| $ v = \sqrt {v_x^2 + v_y^2 + v_z^2}。$ | (11) |
应用最为广泛的关联规则算法为Apriori算法,通过该算法挖掘分析可获取到庞大数据中所蕴含的关联关系。该算法的主要内容如下:
1)项目和项集
设项集
2)事务和事务数据库
设
3)项集的支持度
设
| $ {\rm support} \left( X \right) = \frac{{{\rm{count}}\left( {X \subseteq T} \right)}}{{\left| D \right|}}。$ | (12) |
4)项集最小支持度与频繁集
关联规则查找时,项集中存在一最小支持度
5)关联规则
关联规则形式为:
| $ R:X \Rightarrow Y。$ | (13) |
其中:
6)关联规则的支持度
关联规则
| $ {\rm support} \left( {X \Rightarrow Y} \right) = \frac{{{\rm{count}}\left( {X \cup Y} \right)}}{{\left| D \right|}}。$ | (14) |
7)关联规则的可信度
关联规则
| $ {\rm{confidence}} \left( {X \Rightarrow Y} \right) = \frac{{{\rm support} \left( {X \cup Y} \right)}}{{{\rm support} \left( X \right)}}。$ | (15) |
8)连接和剪枝
若同长度的2个频道项集中仅存在一个差异项,对其进行组装获取候选频繁集的操作为连接[13],对候选频繁集进行修剪的操作为剪枝。
1.2.2 基于矩阵的Apriori算法由于Apriori算法在实际运行过程的效率较低,所以将矩阵的思想代入该算法进行改进,并将
针对随机给定
| $ {M_{ij}} = \left\{ {\begin{array}{*{20}{c}} {1,\mathop {}\nolimits_{} {I_i} \in {T_j}},\\ {0,\mathop {}\nolimits_{} {I_i} \notin {T_j}}。\end{array}} \right. $ | (16) |
其中,
| $ {L_i} = \left( {{m_{i1}},{m_{i2}}, \cdots ,{m_{in}}} \right),$ | (17) |
其中,
| $ {\rm{{support}}} \_{\rm{count}}\left( {{I_i}} \right) = \sum\limits_{i = 1}^n {{m_{ij}}}。$ | (18) |
2项集
| $ {L_{ij}} = {L_i} \wedge {L_j} = \left( {{m_{i1}} \wedge {m_{j1}},{m_{i2}} \wedge {m_{j2}}, \cdots ,{m_{in}} \wedge {m_{jm}}} \right)。$ | (19) |
其中,
| $ \begin{split} & {{\rm{support}}} \_{{\rm{{count}}}}\left( {{L_{ij}}} \right) = \sum\limits_{i = 1}^n {\left( {{m_{ik}} \wedge {m_{jk}}} \right)} =\\ & {m_{i1}} \wedge {m_{j1}} + {m_{i2}} \wedge {m_{j2}} + \cdots + {m_{in}} \wedge {m_{jm}}。\end{split}$ | (20) |
| $ {{\rm{support}}} \_{\rm{count}}\left( {{L_{1,2, \cdots k}}} \right) = \sum\limits_{i = 1}^n {\left( {{m_{1i}} \wedge {m_{2i}} \wedge \cdots {m_{ki}}} \right)}。$ | (21) |
基于矩阵的Apriori算法的步骤为:转化
应用引入矩阵改进的关联规则挖掘半潜式航行体空间运动数学模型选取控制参数,利用该控制参数设计一个可调权值的PID控制器,该控制器包括PID控制以及卷积神经网络训练网络参数两部分,利用PID控制器完成半潜式航行体控制,通过卷积神经网络预测获取准确性较高的PID控制器参数,利用该参数不断优化PID控制器,完成半潜式航行体的稳态优化控制。
通过该算法控制半潜式航行体的姿态,同时采用Hebb权值学习规则,以
| $ \Delta {w_{ij}}\left( k \right) = \eta \left( {{d_j}\left( k \right) - {o_j}\left( k \right)} \right){o_i}\left( k \right){o_j}\left( k \right)。$ | (22) |
其中:
| $ \Delta u\left( k \right) = k\left( {{{\omega '}_1}{x_1} + {{\omega '}_2}{x_2} + {{\omega '}_3}{x_3}} \right),$ | (23) |
| $ {w'_i}\left( k \right) = \frac{{{w_i}\left( k \right)}}{{\displaystyle\sum\limits_{i = 1}^3 {\left| {{w_i}\left( k \right)} \right|} }},$ | (24) |
| $ \left\{ {\begin{array}{*{20}{c}} {{w_1}\left( k \right) = {w_1}\left( {k - 1} \right) + {\eta _I}z\left( k \right)u\left( k \right){x_1}\left( k \right)},\\ {{w_2}\left( k \right) = {w_2}\left( {k - 1} \right) + {\eta _P}z\left( k \right)u\left( k \right){x_2}\left( k \right)},\\ {{w_3}\left( k \right) = {w_3}\left( {k - 1} \right) + {\eta _D}z\left( k \right)u\left( k \right){x_3}\left( k \right)}。\end{array}} \right. $ | (25) |
其中:
单卷积神经元的控制算法和学习方法为:
| $ u\left( k \right) = u\left( {k - 1} \right) + K\sum\limits_{i = 1}^3 {{{w'}_i}\left( k \right){x_i}\left( k \right)}。$ | (26) |
其中:K为改进关联规则获取控制参数;
以Matlab软件为仿真环境,搭建半潜式航行体模型,该航行体长7 m,质量7000 kg,航行深度低于5 m,初始为2.5 m,回转深度设为3 m,航行速度为8 kn,垂直舵角为3°~12°。
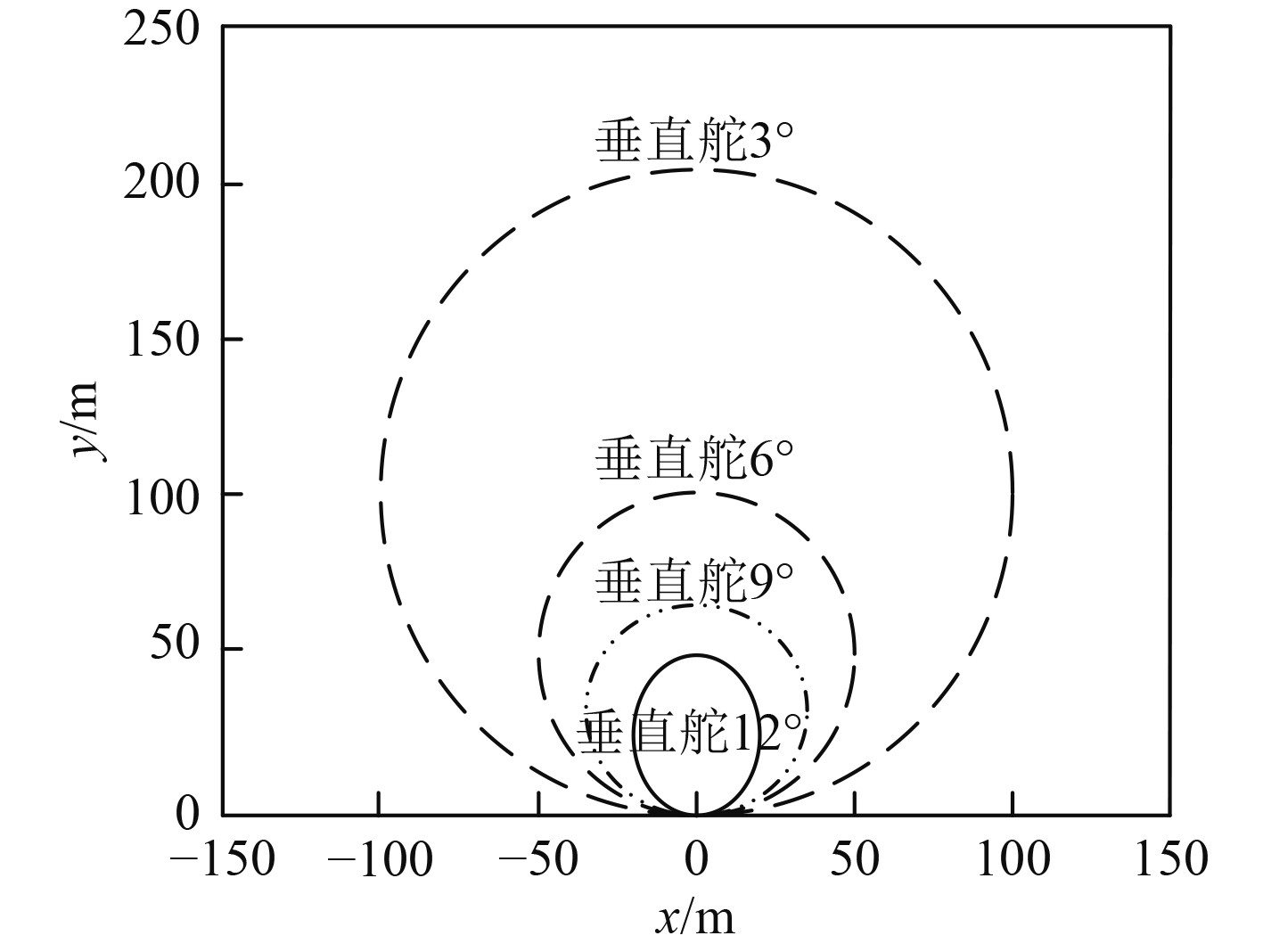
半潜式航行体的水平面轨迹、深度及姿态角变化如图1~图3所示。
|
图 1 半潜式航行体水平面航迹 Fig. 1 Horizontal track of semi-submersible vehicle |
|
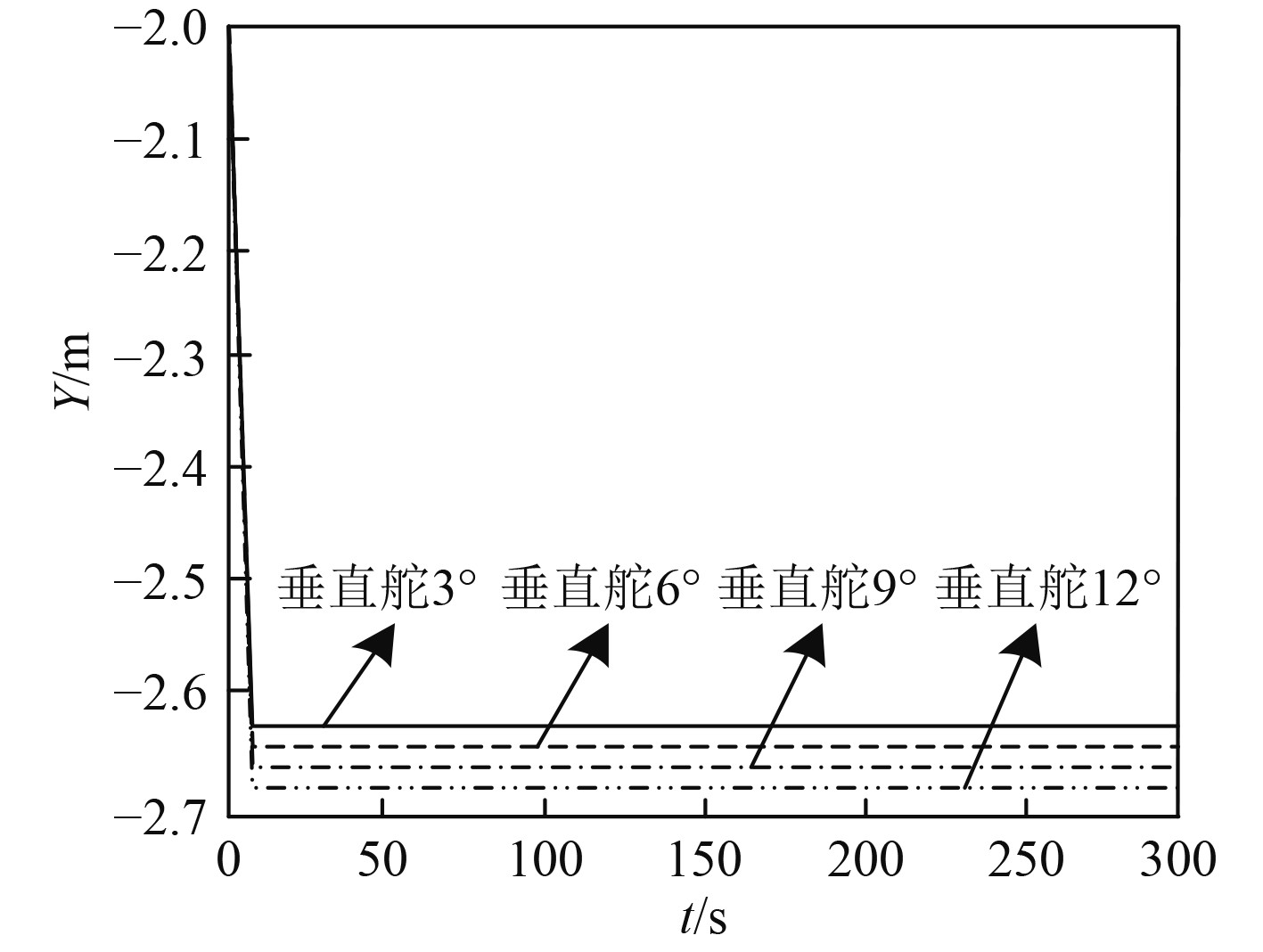
图 2 半潜式航行体深度 Fig. 2 Depth of semi-submersible vehicle |
|
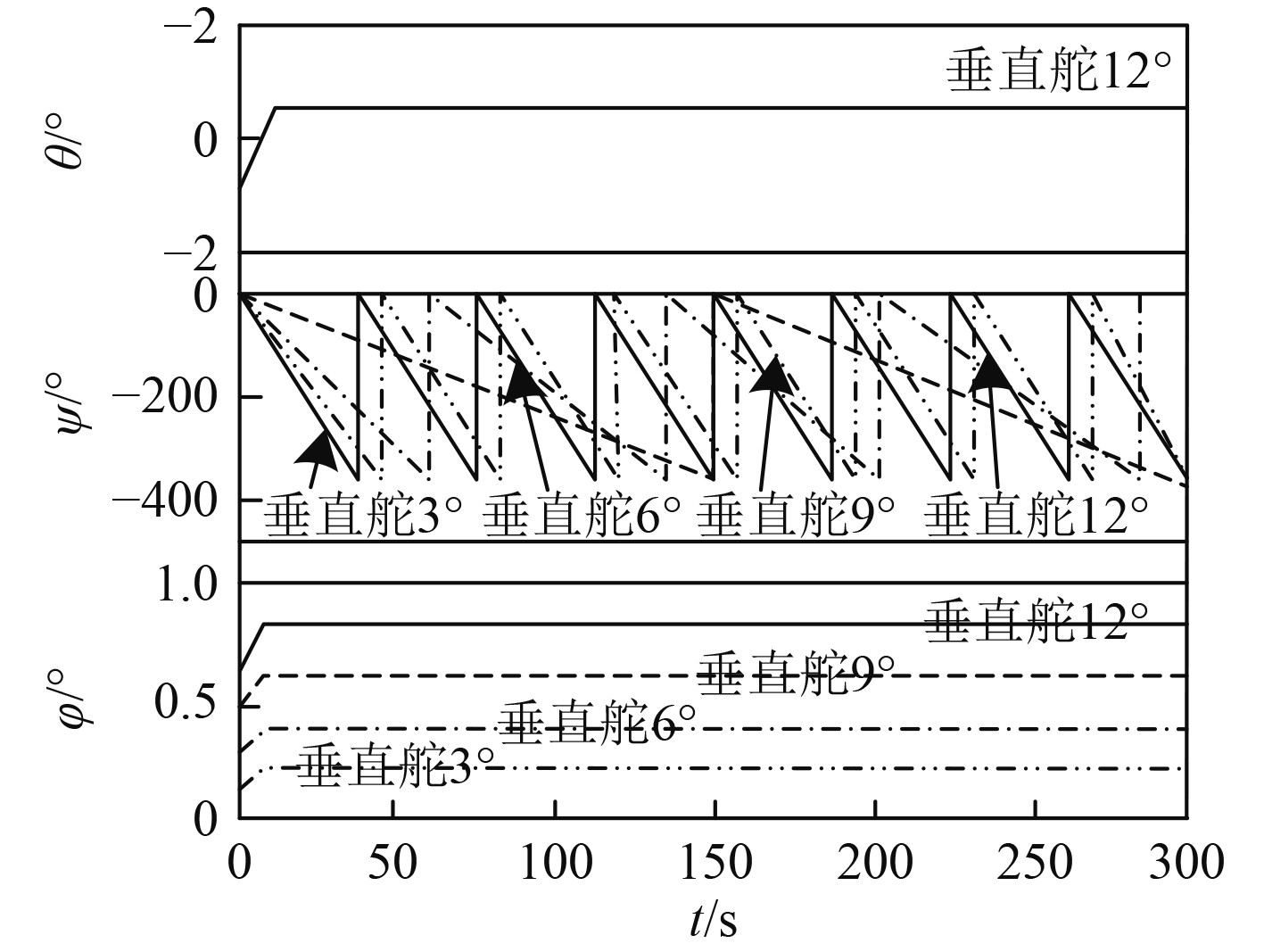
图 3 半潜式航行体姿态角 Fig. 3 Attitude angle of semi-submersible vehicle |
可以看出,半潜式航行体的回转半径与垂直舵角成负相关关系,最大、最小回转半径分别约为100 m和25 m;航行体回转过程中,航行深度同垂直舵角、航速成正比,但是变化程度较小;姿态角中横滚角与垂直舵角呈正比例关系。
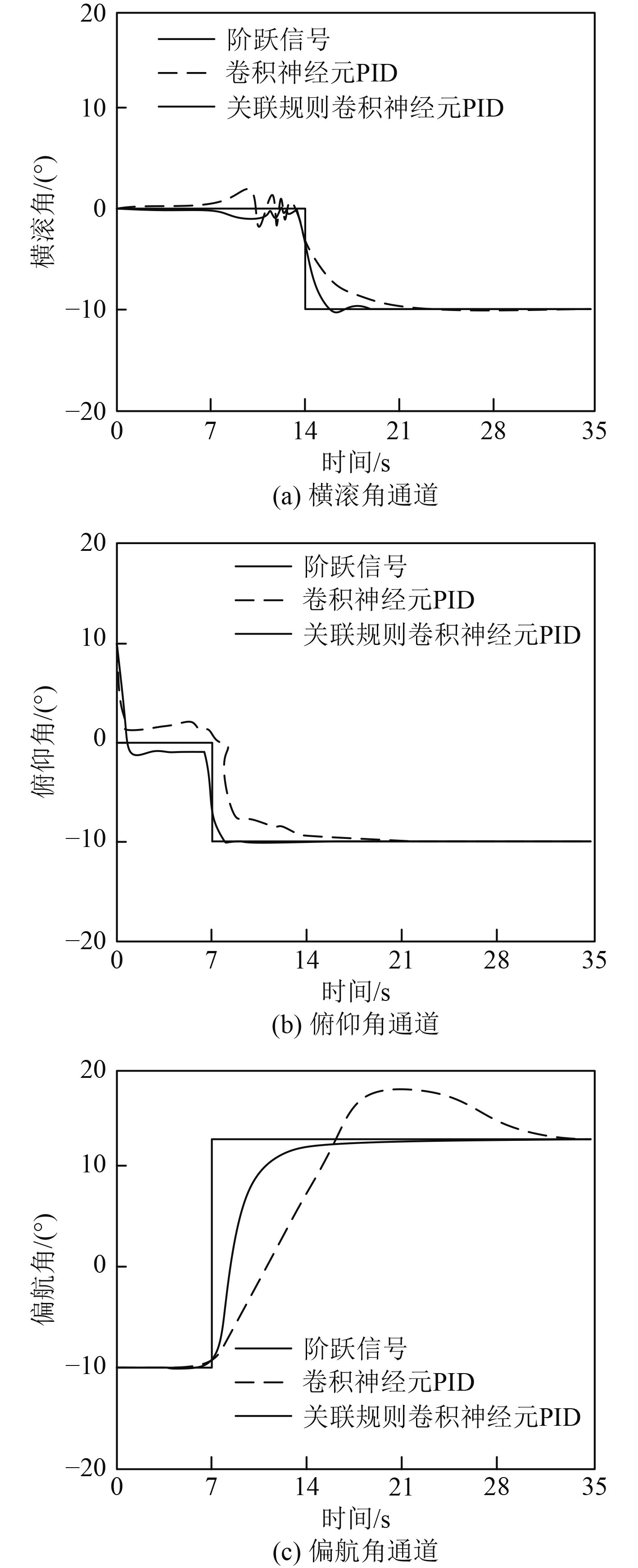
为验证本文方法的稳态控制性能,统计半潜式航行体在应用关联规则挖掘后加入卷积神经网络控制的自适应情况,对比3个通道的姿态控制通道响应情况,结果如图4所示。
|
图 4 姿态控制通道响应 Fig. 4 Attitude control channel response |
由图4可以看出,半潜式航行体的横滚角通道在14 s处出现阶跃信号,单卷积神经网络的PID控制与加入关联规则的卷积神经网络PID控制的超调量都较小,基本保持平稳。俯仰角通道与偏航角通道均在7 s处出现阶跃信号,前者单卷积神经网络的PID控制的响应速度加快、加入关联规则的卷积神经网络PID控制的超调量最小,后者中加入关联规则的卷积神经网络PID控制效果最明显,在明显减小系统超调量的同时加快了其响应速度。
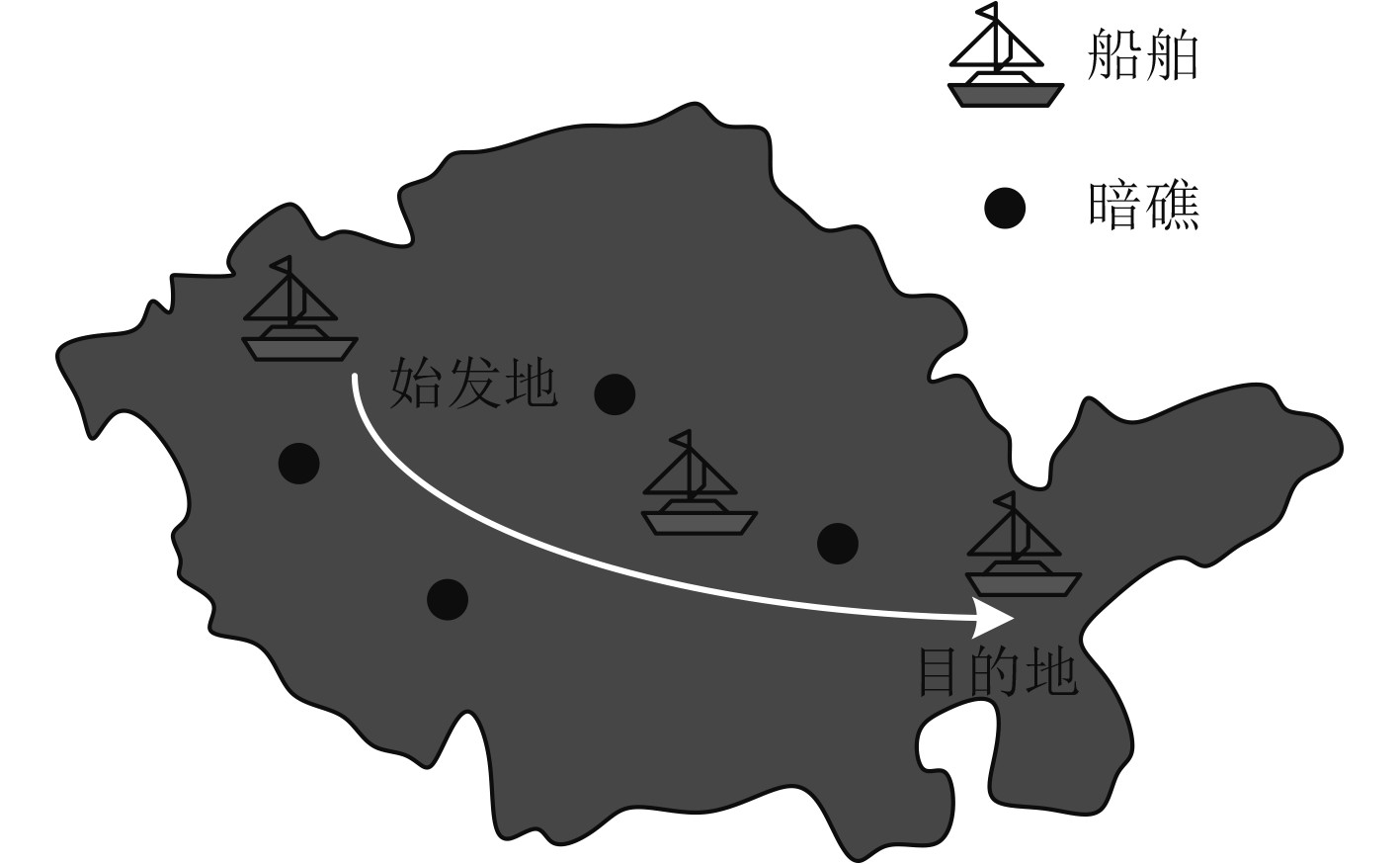
为分析该技术应用后的效果,将半潜式航行体搭载于某船舶,在实验环境中设置4处障碍,测试该技术应用后,搭载半潜式航行体的船舶对于障碍物的躲避情况,衡量本文技术控制效果,结果如图5所示。
|
图 5 船舶行驶控制效果 Fig. 5 Control effect of ship driving |
分析可知,搭载应用本文技术控制后的船舶,能够在通航时躲避所有障碍,说明本文技术的稳态控制效果较好,可有效保障船舶的通航安全情况。
3 结 语根据半潜式航行体的运动数学模型构建地面及流体坐标系以及二者之间的转换,结合关联规则设计基于卷积神经网络的PID控制器,完成半潜式航行体的稳态控制。最后通过实验验证得出,半潜式航行体航行时的回转半径受垂直舵角的影响较大,而且在高航速回转时,半潜式航行器的深度会增加。
| [1] |
甄荣, 石自强. 一种基于高斯混合模型的船舶航迹聚类方法[J]. 船舶工程, 2021, 43(11): 139-143. DOI:10.13788/j.cnki.cbgc.2021.11.24 |
| [2] |
陈再发, 刘彦呈, 庄绪州. 基于自抗扰控制的船舶永磁电机无位置传感器混合控制[J]. 电机与控制应用, 2020, 47(10): 24-32. |
| [3] |
王润芝, 李学民, 袁志国, 等. 曲轴转角域ADRC在船舶柴油机中的应用[J]. 哈尔滨工程大学学报, 2020, 41(1): 116-124. DOI:10.11990/jheu.201901110 |
| [4] |
朴在吉, 郭晨. 一种无人船动力定位跨平台实时控制模型[J]. 控制与决策, 2021, 36(4): 909-916. DOI:10.13195/j.kzyjc.2019.0960 |
| [5] |
陈晓寒, 牛小兵. 基于改进扩张状态观测器的船舶动力定位系统控制[J]. 上海海事大学学报, 2020, 41(4): 25-29,102. DOI:10.13340/j.jsmu.2020.04.005 |
| [6] |
王永涛. 基于粒子群优化反步法的船舶航向控制器设计[J]. 中国航海, 2020, 43(1): 78-82. DOI:10.3969/j.issn.1000-4653.2020.01.015 |
| [7] |
张涛, 关巍, 苏作靖, 等. 基于闭环增益成形算法的船舶减摇鳍控制器设计与分析[J]. 上海海事大学学报, 2020, 41(1): 27-33,56. DOI:10.13340/j.jsmu.2020.01.005 |
| [8] |
徐海祥, 李超逸, 余文曌, 等. 智能船舶循迹控制方法研究[J]. 华中科技大学学报(自然科学版), 2020, 48(8): 103-108. DOI:10.13245/j.hust.200818 |
| [9] |
宋吉广, 王继铭, 梁利华, 等. 舵鳍联合自抗扰主从控制策略设计[J]. 控制理论与应用, 2021, 38(2): 264-274. DOI:10.7641/CTA.2020.00301 |
| [10] |
王威, 王聪, 宋武超, 等. 侧滑角对超空泡航行体转弯运动沾湿区域的影响[J]. 振动与冲击, 2020, 39(12): 135-141. DOI:10.13465/j.cnki.jvs.2020.12.018 |
| [11] |
谢鸿伟, 张英俊, 邢胜伟, 等. 基于模型预测控制的船舶自主避碰方法[J]. 船舶工程, 2021, 43(8): 23-28,95. DOI:10.13788/j.cnki.cbgc.2021.08.05 |
| [12] |
李英, 汤庸. 基于关联规则与相似度的数据挖掘算法研究[J]. 华南师范大学学报(自然科学版), 2021, 53(5): 121-127. |
| [13] |
李纪强, 张国庆, 尚洪达. 基于鲁棒自适应扰动观测器的船舶航向保持控制器设计[J]. 中国航海, 2020, 43(4): 15-19. DOI:10.3969/j.issn.1000-4653.2020.04.003 |
| [14] |
吕国华, 胡学先, 张启慧, 等. 基于联邦学习的船舶AIS轨迹谱聚类算法研究[J]. 计算机应用研究, 2022, 39(1): 70-74,89. DOI:10.19734/j.issn.1001-3695.2021.06.0221 |
| [15] |
陈海力, 任鸿翔, 李源惠, 等. 基于反推滑模的船舶动力定位有限时间控制[J]. 计算机仿真, 2021, 38(12): 182-187,479. DOI:10.3969/j.issn.1006-9348.2021.12.038 |
 2022, Vol. 44
2022, Vol. 44
