水面无人艇(unmanned surface vessel,USV)作为一种新型的无人作战平台,具备火力打击,救援搜索,敌情侦察等多种功能。随着人工智能的发展和未来作战模式的不断改变,无人艇势必会在海上作战系统中发挥更重要的作用[1]。
无人艇的路径规划可以分为全局路径规划和局部路径规划。对于障碍物已知的全局路径规划,国内外的科研人员做了大量的研究。而无人艇在海面航行时,最容易发生危险的是碰到动态的障碍物。
到目前为止,局部路径规划常用的方法有很多。文献[2]汽车避障局部路径规划中采用改进RRT的方法,文献[3]采用改进的遗传算法进行船舶局部路径规划,文献[4]采用高斯伪谱法进行智能车局部路径规划,文献[5]采用人工势场法进行移动机器人局部路径规划。因人工势场法计算简单,易于实现而得到了广泛的应用。但同时也存在局部极小和目标不可达等问题,因此不一定能找到问题的解。文献[6]提出了一种低震荡人工势场-ARRT混合算法,先采用低震荡人工势场法进行搜索,当遇到局部极小、碰撞等情况时在切回ARRT算法进行搜索。文献[7]采用切线法、搜索法解决局部极小问题,提出了自适应步长调节算法。文献[8]设计了一种沿目标900移动的方法来跳出局部极小点。
本文在传统人工势场法的基础上,通过引入一阈值对引力场进行改进,到指定距离时无人艇与目标点的引力为一定值,避免引力过大导致无人艇与障碍物相撞。通过引入模糊界点,当无人艇与障碍物距离较近而产生的斥力过大时,可引导无人艇向前运动,防止来回震荡而造成目标不可达。通过与模拟退火算法相结合,利用Metropolis准则使无人艇脱离局部极小点,顺利到达目标点。
1 人工势场法人工势场法路径规划是由Khatib提出的一种虚拟力法。它的基本思想是将无人艇在周围运动的环境设计成为一个抽象的引力场,目标点对无人艇产生“引力”,引导物体朝向其运动。障碍物对无人艇产生“斥力”,避免物体与之发生碰撞。引力和斥力共同对无人艇产生作用,使无人艇避开障碍物到达目标点[9-15]。
1.1 引力场假设目标点当前的位置为qgoal,无人艇的位置为q,则引力势场函数可定义为:
| $ \mathop U\nolimits_{{{att}}} \left( q \right) = \frac{1}{2}\varepsilon \mathop \rho \nolimits^2 \left( {q,\mathop q\nolimits_{goal} } \right)。$ | (1) |
式中:Uatt(q)为目标点对无人艇产生的引力场;ε为引力增益系数,引力增益系数越大说明目标点的吸引力越大;ρ(qgoal,q)表示无人艇当前状态与目标的距离。目标点对无人艇的引力为引力势场函数的负梯度,即
| $ \mathop F\nolimits_{{{att}}} \left( q \right) = - \nabla \mathop U\nolimits_{att} \left( q \right) = \varepsilon \left( {\mathop q\nolimits_{goal} - q} \right)。$ | (2) |
假设无人艇的位置为q,障碍物的位置为qobs,则斥力势场函数定义为:
| $ \mathop U\nolimits_{{{rep}}} \left( q \right) = \left\{ {\begin{array}{*{20}{l}} \dfrac{1}{2}\eta \left( {\dfrac{1}{{\rho \left( {q,\mathop q\nolimits_{obs} } \right)}} - \dfrac{1}{{\mathop \rho \nolimits_0 }}} \right),{\rm{i}}{\rm{f}}\;\rho \left( {q,\mathop q\nolimits_{obs} } \right) \leqslant \mathop \rho \nolimits_0 ,\\ 0,{\rm{i}}{\rm{f}}\rho \left( {q,\mathop q\nolimits_{obs} } \right) > \mathop \rho \nolimits_0 。\end{array}} \right. $ | (3) |
式中:Urep(q)为障碍物对无人艇产生的斥力场;η为斥力增益系数 ;ρ(q,qobs)表示无人艇当前状态与障碍物的距离;ρ0为障碍物的影响半径,离开一定的距离,障碍物就对无人艇没有斥力影响。障碍物对无人艇的斥力为:
| $ \begin{gathered} \mathop F\nolimits_{{\text{rep}}} \left( q \right) = - \nabla \mathop U\nolimits_{rep} \left( q \right) = \\ \left\{ {\begin{array}{*{20}{l}} \eta \left( {\dfrac{1}{{\rho \left( {q,\mathop q\nolimits_{obs} } \right)}} - \dfrac{1}{{\mathop \rho \nolimits_0 }}} \right)\dfrac{1}{{\mathop \rho \nolimits^2 \left( {q,\mathop q\nolimits_{obs} } \right)}}\dfrac{{\partial \rho \left( {q - \mathop q\nolimits_{obs} } \right)}}{{\partial q}},\\ {\rm{i}}{\rm{f}}\;\rho \left( {q,\mathop q\nolimits_{obs} } \right) \leqslant \mathop \rho \nolimits_0 ,\\ {0,{\rm{i}}{\rm{f}}\;\rho \left( {q,\mathop q\nolimits_{obs} } \right) > \mathop \rho \nolimits_0 } 。\end{array}} \right. \\ \end{gathered} $ | (4) |
当无人艇所处的位置有m个障碍物时,对引力势场函数和斥力势场函数求负梯度可得无人艇受到的合力为:
| $ F\left( {{q}} \right) = \mathop F\nolimits_{att} \left( q \right) + \sum\limits_{i = 1}^m {\mathop F\nolimits_{rep} } \left( q \right)。$ | (5) |
为了解决局部最优解问题,Kirkpatrick等提出了模拟退火算法。“退火”是指对物体加温在冷却的一个过程,模拟退火算法起源于自然界中晶体冷却的过程。分子和原子在高温状态下是不稳定的,如果温度下降过快,原子可能缺少足够的时间排列成晶体的结构形成能量较高的非晶体,这就相当于算法中的局部最优解。如果温度缓慢下降,固体中的原子按照一定形状排列,形成高密度、低能量的有规则晶体,这就得到了全局最优解。
模拟退火算法的基础是Metropolis准则,即以一定的概率来接受新的状态,而不是使用完全确定的规则。假设前一个状态为x(n),系统根据梯度下降的能量,状态变为x(n+1)。与此同时,系统的能量由E(n)变为E(n+1),定义系统由x(n)变为x(n+1)的接受概率为:
| $ \begin{gathered} P= \left\{ {\begin{array}{*{20}{l}} 1\text{,}E\left(\text{n}+1\right) < E\left(n\right),\\ {{\displaystyle e}}{-\dfrac{E\left(n+1\right)-E\left(n\right)}{T}},E\left(\text{n}+1\right)\geqslant E\left(n\right)。\end{array}} \right. \\ \end{gathered}$ | (6) |
由式(6)可以看出,如果能量降低,那么这种转移就可以被接受(概率为1)。如果能量升高,这种转移也不会立刻结束,而是会以一定的概率选择:首先在区间[0, 1]产生一个均匀分布的随机数ε,如果ε<p,则接受此种转移,否则进入下一步[16-18]。
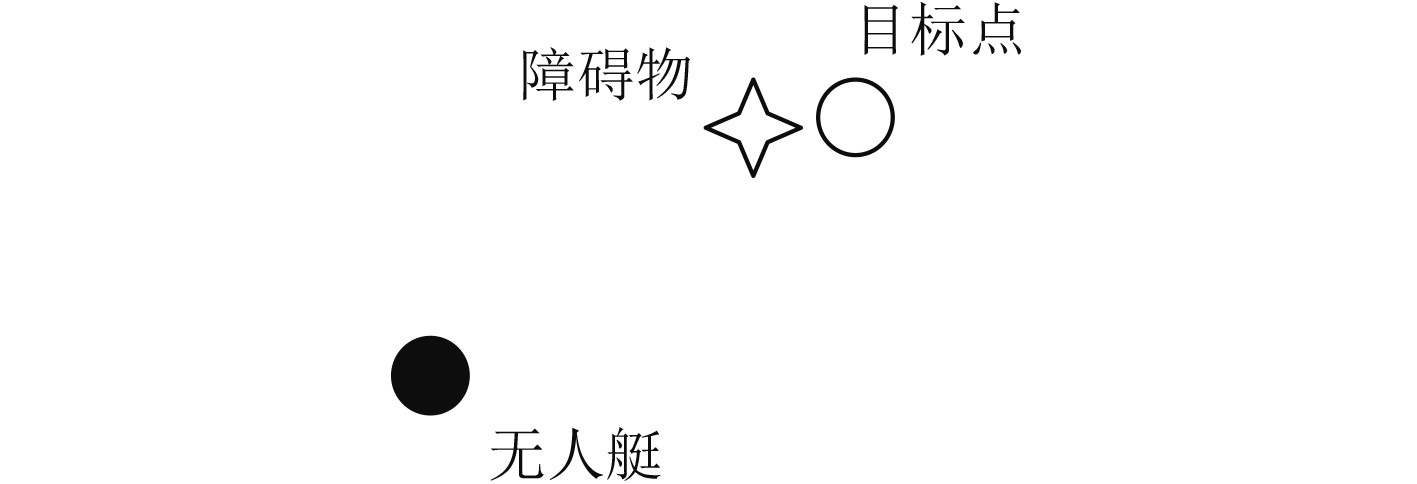
3 人工势场法存在的问题1)当目标点与障碍物的距离较远时,无人艇与目标点的引力较大,与障碍物的斥力较小。此时,障碍物产生的引力远大于目标点产生的引力,则无人艇易与障碍物产生碰撞,如图1所示。

|
图 1 无人艇与障碍物的距离较远 Fig. 1 The distance between the target point and the obstacle is far |
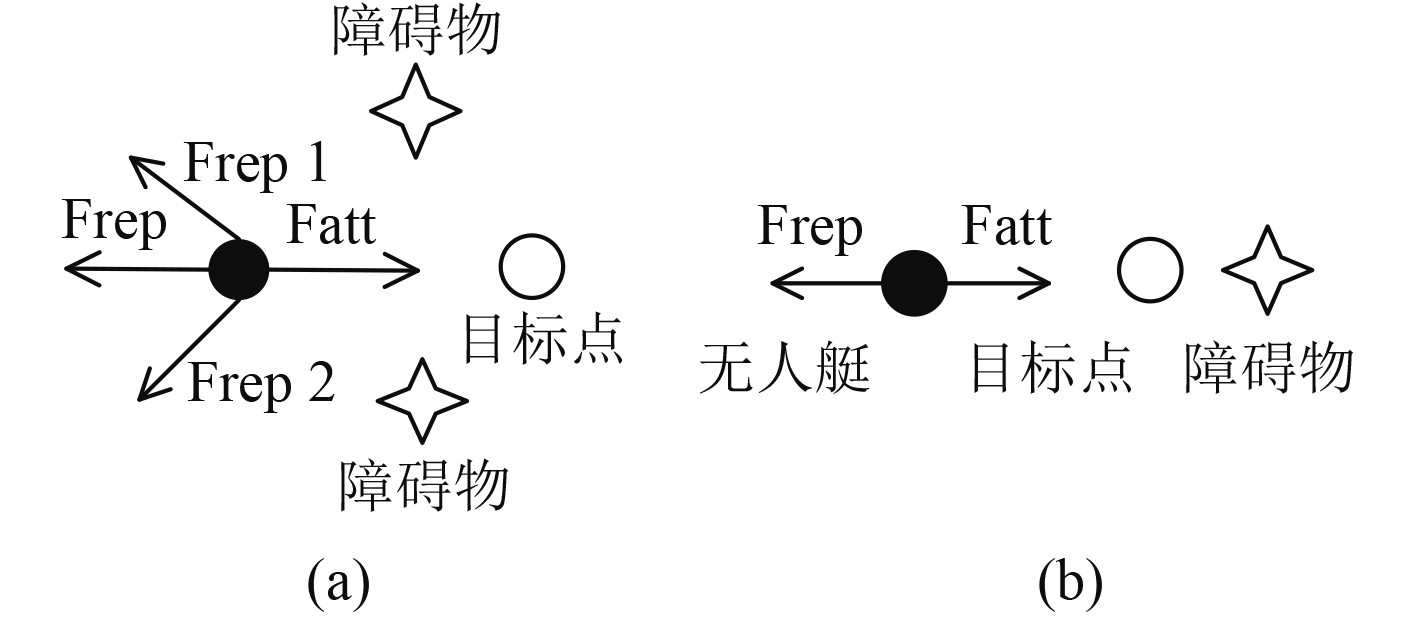
2)当障碍物距离目标点较近时,无人艇因受到的斥力作用较大但引力作用较小而导致无人艇在障碍物周围震荡,无法到达目标点,如图2所示。
|
图 2 无人艇与障碍物的距离较近 Fig. 2 The target point is closer to the obstacle |
3)由于无人艇在运动空间中是受到斥力和引力的共同作用而向前推进的,当在某一位置斥力和引力的合力为0时,无人艇会误以为已经到达目标点而停止运动,如图3所示。
|
图 3 无人艇受到的合力为0 Fig. 3 The unmanned boat receives a combined force of 0 |
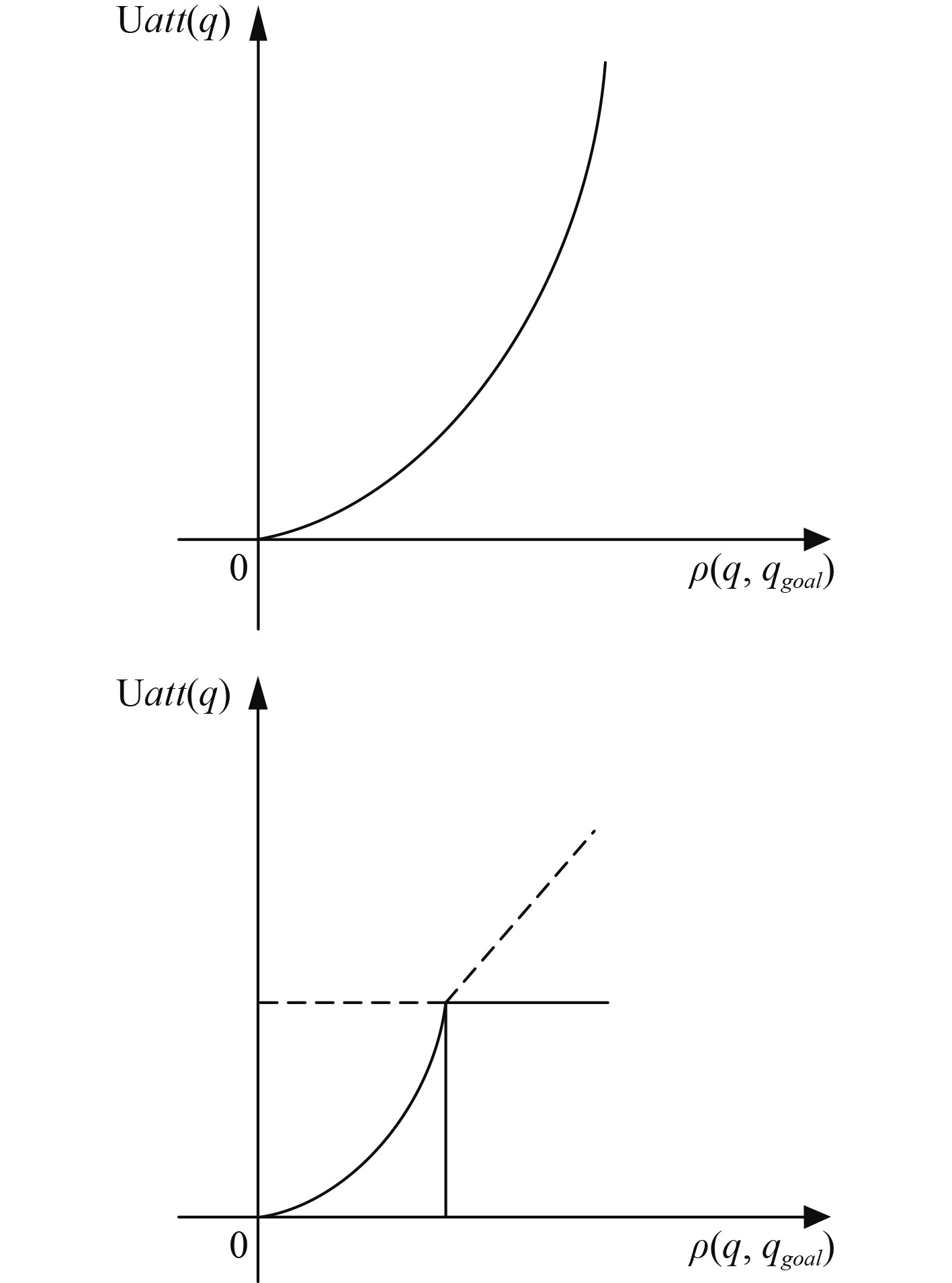
由式(1)可知,引力势场强度随着无人艇和目标点距离的增大而成指数增长,当无人艇与目标点距离较大时,引力势场强度过大,斥力势场强度较小。如图1所示,可能导致无人艇与障碍物碰撞。现引入一阈值d,当目标点与无人艇的距离小于等于d时,引力势场大小与距离的关系不变。当目标点与无人艇的距离大于d时,将引力势场大小视为一常数,如图4所示。将引力改进的引力场公式如下:
|
图 4 势场强度与无人艇和目标点距离的关系曲线 Fig. 4 Relationship curve between potential field strength and distance |
| $ \mathop U\nolimits_{{\text{att}}} = \left\{ {\begin{array}{*{20}{l}} \dfrac{1}{2}\varepsilon \mathop \rho \nolimits^2 \left( {q,\mathop q\nolimits_{goal} } \right),&{\rm{i}}{\rm{f}}\;\rho \left( {q,\mathop q\nolimits_{goal} } \right) \leqslant d ,\\ \mathop d\nolimits^{} \varepsilon \rho \left( {q,\mathop q\nolimits_{goal} } \right),&{\rm{i}}{\rm{f}}\;\rho \left( {q,\mathop q\nolimits_{goal} } \right) > d。\end{array}} \right. $ | (7) |
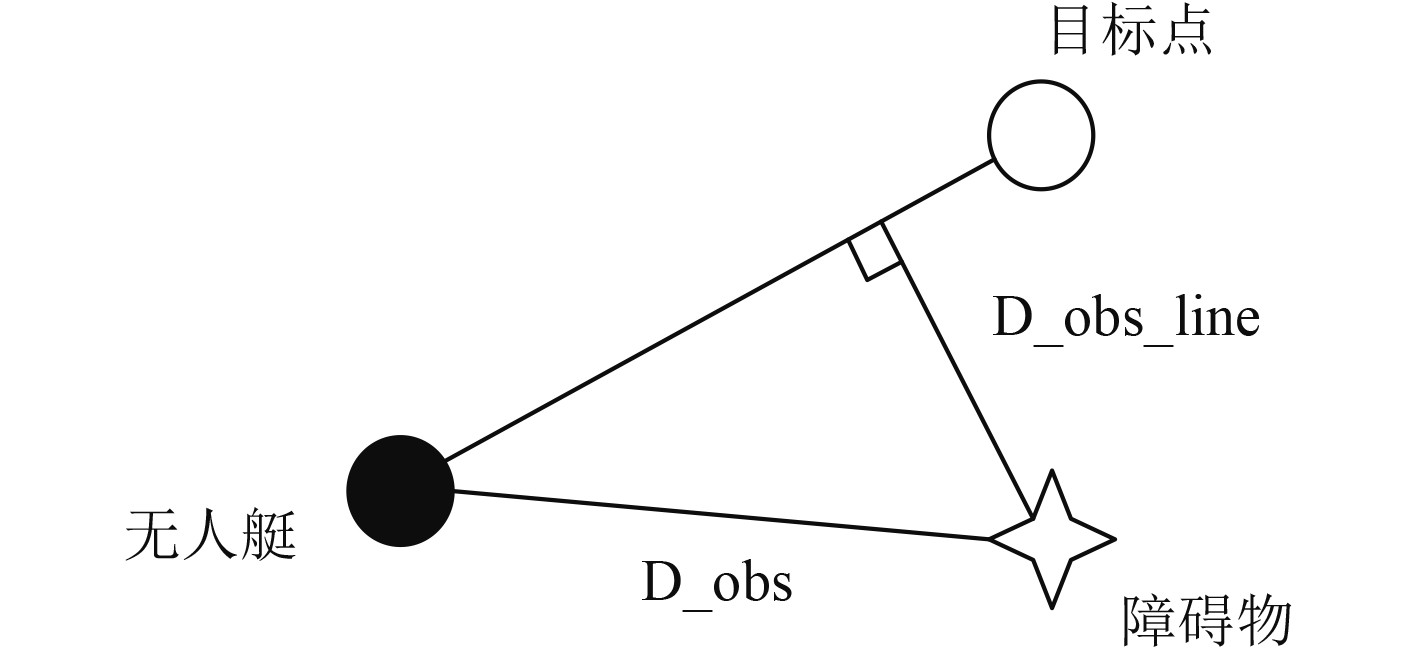
设置D_obs为无人艇到最近障碍物的距离(模糊界点)。D_obs_line为无人艇到机器人和目标连线的距离。在考虑靠近目标点的情况下,尽量保持直线运动,防止来回震荡。判断是否到达目标点,在距离一个步长之内认为到达目标点。设置D_obs_line=0.8;当靠近目标点,D_obs>0.8时认为机器人应该直线运动。
|
图 5 模糊远近界点的判断关系图 Fig. 5 Judgment relationship diagram of fuzzy far and near boundary points |
人工势场法优点是方法简单,规划路线平滑。缺点是容易陷入局部最小值,无法应对复杂环境。模拟退火法优点是可以找到全局最优解,缺点是收敛速度慢。
当利用人工势场法进行局部路径规划陷入局部最小值时,可以在当前点x的附近选择一个点x1,由上述势场函数公式计算x和x1点的势场u(x)和u(x1)。如果u(x)>u(x1),则接受x1作为下一个要移动的点。如果u(x)<u(x1),则根据Metropolis准则进行选择。计算概率
|
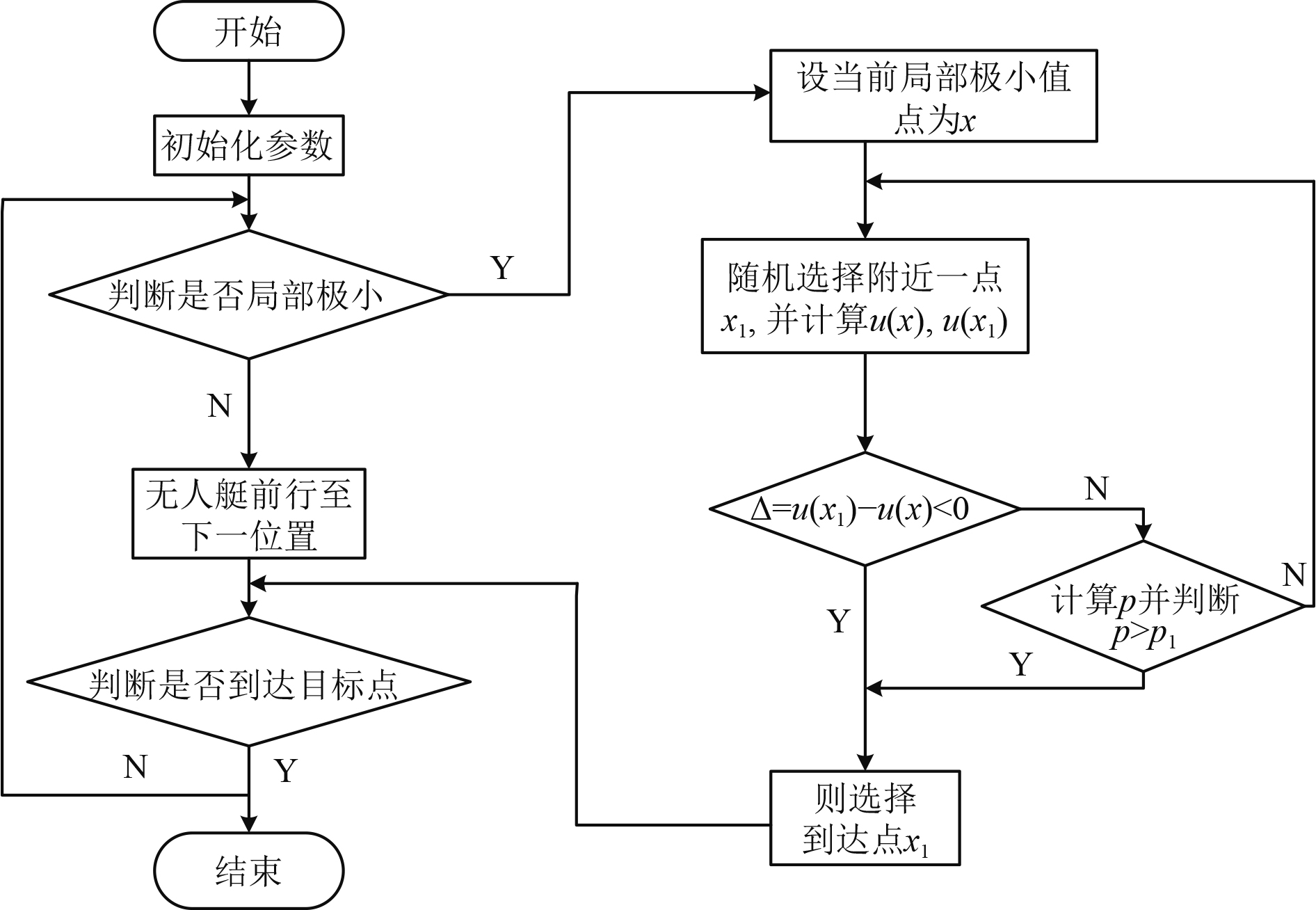
图 6 局部路径规划流程图 Fig. 6 Partial path planning flowchart |
结合模拟退火法的算法步骤如下:
步骤1 初始化参数,确定初始温度T和随机概率p1。
步骤2 判断是否到达局部极小,在这里的判断依据是无人艇所受的合力是否为0或者陷入震荡状态。
步骤3 选择x附近一个随机点x1。
步骤4 计算u(x)和u(x1),Δ= u(x1)−u(x),Δ<0则输出x1。
步骤5 Δ>0则根据Metropolis准则计算概率p,若p>p1,则输出x1,若p<p1,则选择新的随机点。
步骤6 到达x1后判断是否脱离局部极小点,若是则返回成功。否则,继续迭代。
在实际操作过程中,判断是否陷入震荡是根据无人艇当前所在位置与上一次的位置判断,若2个点的距离小于步长的0.2倍,则认为陷入震荡。判断无人艇脱离局部极小值的依据是计算当前点与局部极小值点的距离,若距离大于步长的2倍,则认为脱离局部极小点。
5 仿真实验及分析为了对改进后算法的效果进行验证,通过Matlab平台进行仿真验证。针对无人艇在实际海域中遇到的障碍物情况,将传统的障碍物换为具有一定半径的障碍物,更贴合实际情况。
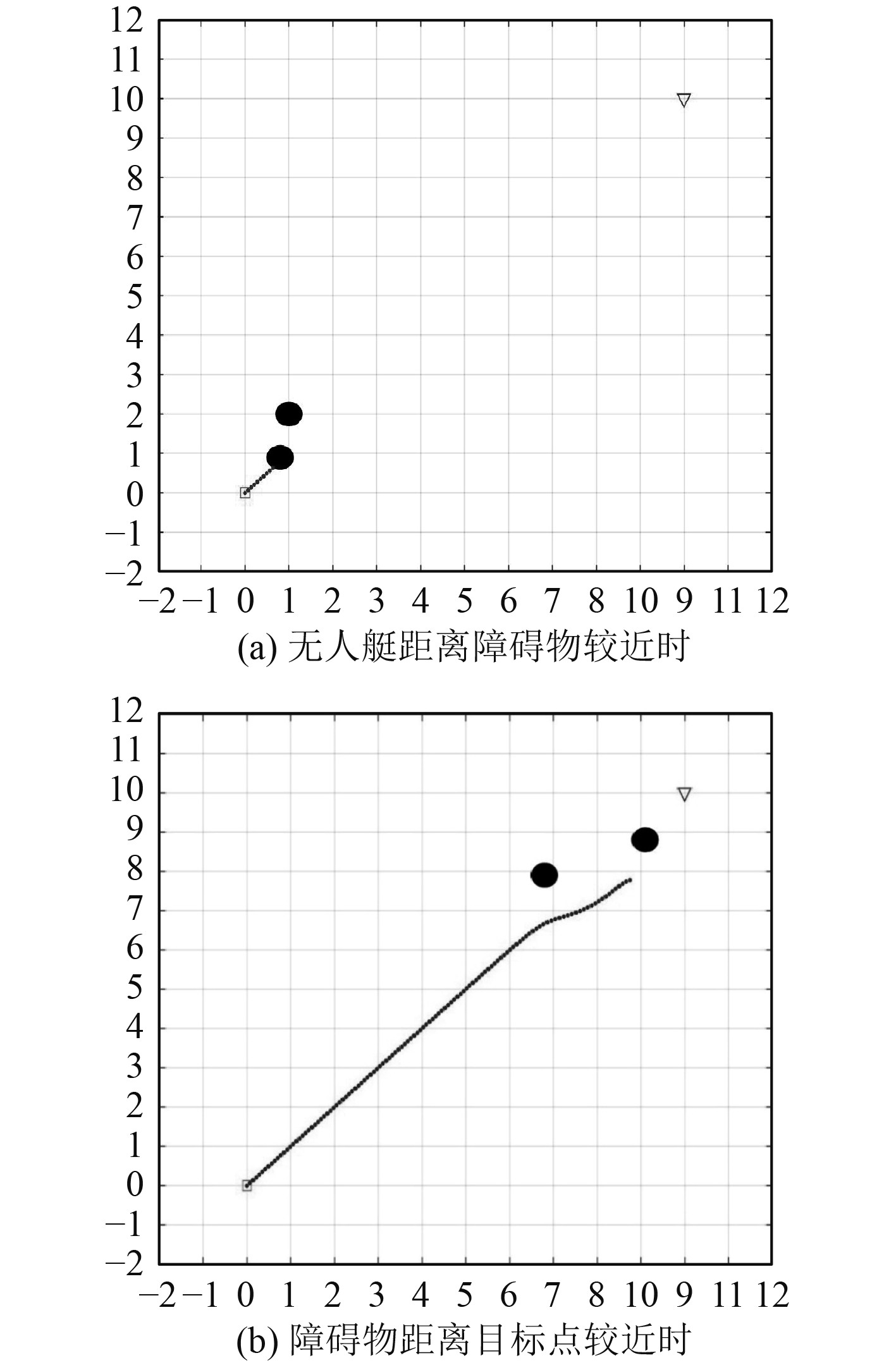
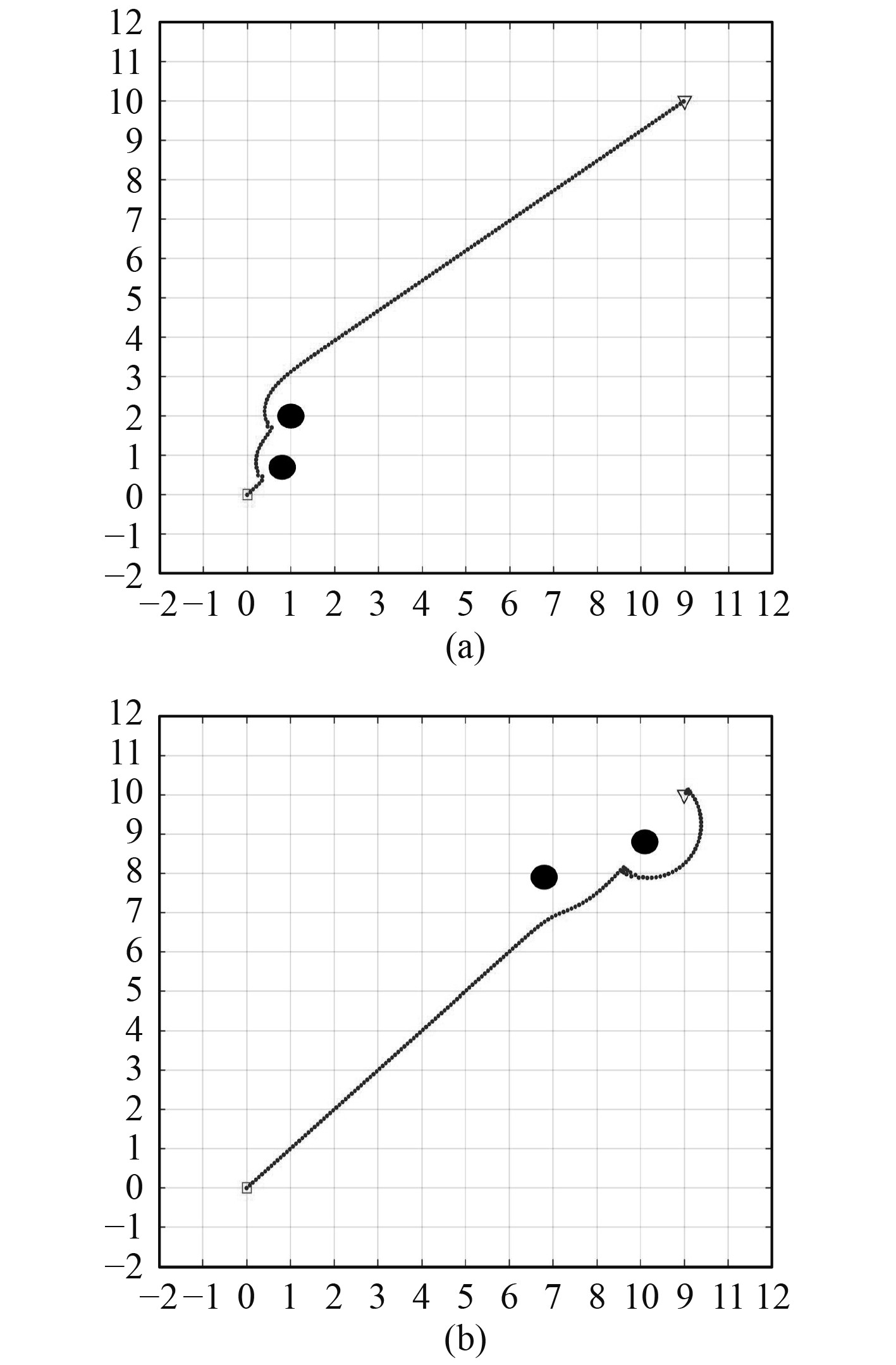
仿真结果如图7所示。从图7(a)可以看出,当无人艇距离障碍物较近且距目标点较远时易发生碰撞。这是因为传统人工势场法中的引力势场强度随着距离的增大而指数增加,斥力相对忽略不计,导致发生碰撞。由图8(a)可以看出,不论无人艇距离目标有多远,当大于一定距离时,引力势场强度始终为一定值,避免了安全事故的发生。
|
图 7 传统人工势场法仿真情形 Fig. 7 Simulation of traditional artificial potential field method |
|
图 8 改进后的仿真结果 Fig. 8 Improved simulation results |
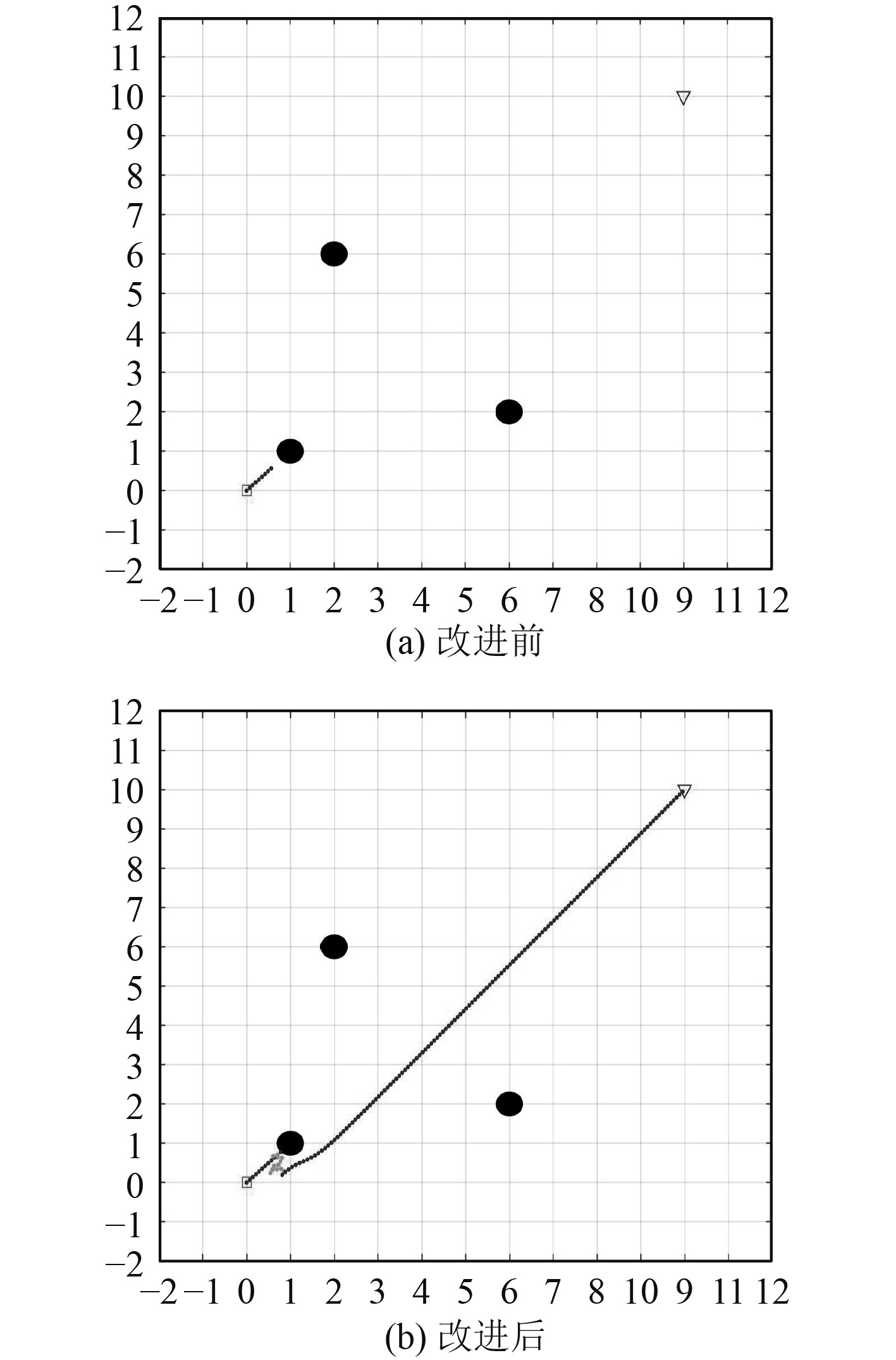
由图9可以看出,当无人艇受到的合力为0时就会陷入局部极小点而停止运动。结合模拟退火法改进后,虽然还有一定的震荡,但无人艇最终摆脱了局部极小点到达目标点。
|
图 9 局部极小点情形改进前后的仿真情况 Fig. 9 The simulation situation before and after the improvement of the local minimum situation |

|
图 10 复杂环境下的仿真结果 Fig. 10 Simulation results under complex environment |
人工势场法作为一种经典的算法非常适用于无人艇的局部路径规划,但由于算法本身的局限性,在路径规划的过程中会出现一定的问题。本文针对人工势场法在路径规划中的问题,通过改进引力势场函数、引入一阈值、结合模拟退火算法进行改进,并利用Matlab仿真软件对优化后的算法进行验证,由图10可以看出优化后的人工势场法对上述的问题具有较好的改进效果,在复杂的情况下也能安全到达目标点。
| [1] |
宋洋, 毛建舟. 多无人艇协同作战智能指挥控制系统研究[J]. 舰船电子工程, 2020, 40(10): 1-4+57. |
| [2] |
宋晓琳, 周南, 黄正瑜, 等. 改进RRT在汽车避障局部路径规划中的应用[J]. 湖南大学学报, 2017, 44(4): 30-37. |
| [3] |
卢昌宇. 基于改进遗传算法的船舶局部路径规划研究[D]. 大连: 大连海事大学, 2020.
|
| [4] |
郭泉成. 基于高斯伪谱法的智能车局部路径规划研究[D]. 广州: 华南理工大学, 2018.
|
| [5] |
王迪, 李彩虹, 郭娜, 等. 改进人工势场法的移动机器人局部路径规划[J]. 山东理工大学学报, 2021, 35(3): 1-6. |
| [6] |
陈满意, 张桥, 张弓, 等. 多障碍环境下机械臂避障路径规划的研究[J]. 计算机集成制造系统, 2021, 27(4): 990-998. |
| [7] |
罗强, 王海宝, 崔小劲, 等. 改进人工势场法自主移动机器人路径规划[J]. 控制工程, 2019, 26(6): 1091-1098. |
| [8] |
谵海云, 陈华胄, 刘强. 基于改进人工势场法的多无人机三维编队路径规划[J]. 系统仿真学报, 2020, 32(23): 414-420. |
| [9] |
KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[J]. The International Journal of Robotics Research, 1986, 5(1): 90-98. DOI:10.1177/027836498600500106 |
| [10] |
庄雷雨. 典型路况下无人驾驶车辆局部路径规划方法研究[D]. 武汉: 武汉理工大学, 2017.
|
| [11] |
崔靓, 朱学军. 基于ROS的服务机器人智能导航系统研究与仿真[J]. 传感器与微系统, 2020, 39(2): 22-25. |
| [12] |
徐小强, 祝亚兰. 基于YimaEnc海图的无人艇局部路径规划研究[J]. 武汉理工大学学报, 2017, 39(5): 521-524. |
| [13] |
郭蓬, 吴学易, 戎辉, 等. 基于代价函数的无人驾驶汽车局部路径规划算法[J]. 中国公路学报, 2019, 32(6): 79-85. |
| [14] |
伊戈, 刘忠, 张建强, 等. 基于改进终端滑模控制的USV航向跟踪控制方法[J]. 电光与控制, 2020, 27(10): 12-16+21. |
| [15] |
刘冰雁, 叶雄兵, 方胜良, 等. 基于Frenet和改进人工势场的在轨规避路径自主规划[J]. 北京航空航天大学学报, 2021, 47(4): 731-741. |
| [16] |
臧益鹏, 许振宇, 黄安, 等. 基于改进模拟退火算法的非均匀燃烧场分布重建[J]. 物理学报, 2021, 70(13): 229-240. |
| [17] |
刘娜, 谭亦炆, 莫伟强, 等. 基于模拟退火算法的Halbach直线发电机优化设计[J]. 电工技术学报, 2021, 36(6): 1210-1218. |
| [18] |
韩露露. 基于模拟退火算法的多相序列搜索[J]. 长江信息通信, 2021, 34(2): 52-55. |
 2022, Vol. 44
2022, Vol. 44
