2. 船舶振动噪声重点实验室,湖北 武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China
颗粒阻尼技术原理,是一种利用填充于结构体内部空腔或附属结构中微小颗粒之间的摩擦和冲击作用来消耗振动能量的被动减振技术,具有耐久好、稳定性和可靠性高、对温度变化不敏感等优点。颗粒阻尼器是一个强非线性系统,颗粒体间的碰撞与摩擦以及颗体与主体结构间的耦合作用非常复杂,因此国内外学者提出了一些简化的数值模拟方法,比如多相流理论[1]、回归模型法[2]、分数导数理论[3]、恢复力曲面法[4]、功率输入法[5]和神经网络法[6]等。虽然这些简化模型和实验研究已经取得了很大的成果,但这些毕竟是基于现象的方法,其结论很难推广到除实验之外的其他情况。近年来,离散元法已被广泛用于研究颗粒流问题,由于该方法可模拟颗粒-颗粒,颗粒-内壁之间的相互作用,因此可以更合理地分析颗粒阻尼器的性能。
本文基于离散单元法,将颗粒间的接触模型用振动运动方程进行模拟,研究了颗粒阻尼器在简谐振动条件下的颗粒耗能特性,分析了简谐振动的幅值、频率及填充率对颗粒体损耗功率的影响。
1 颗粒介质细观模型
|
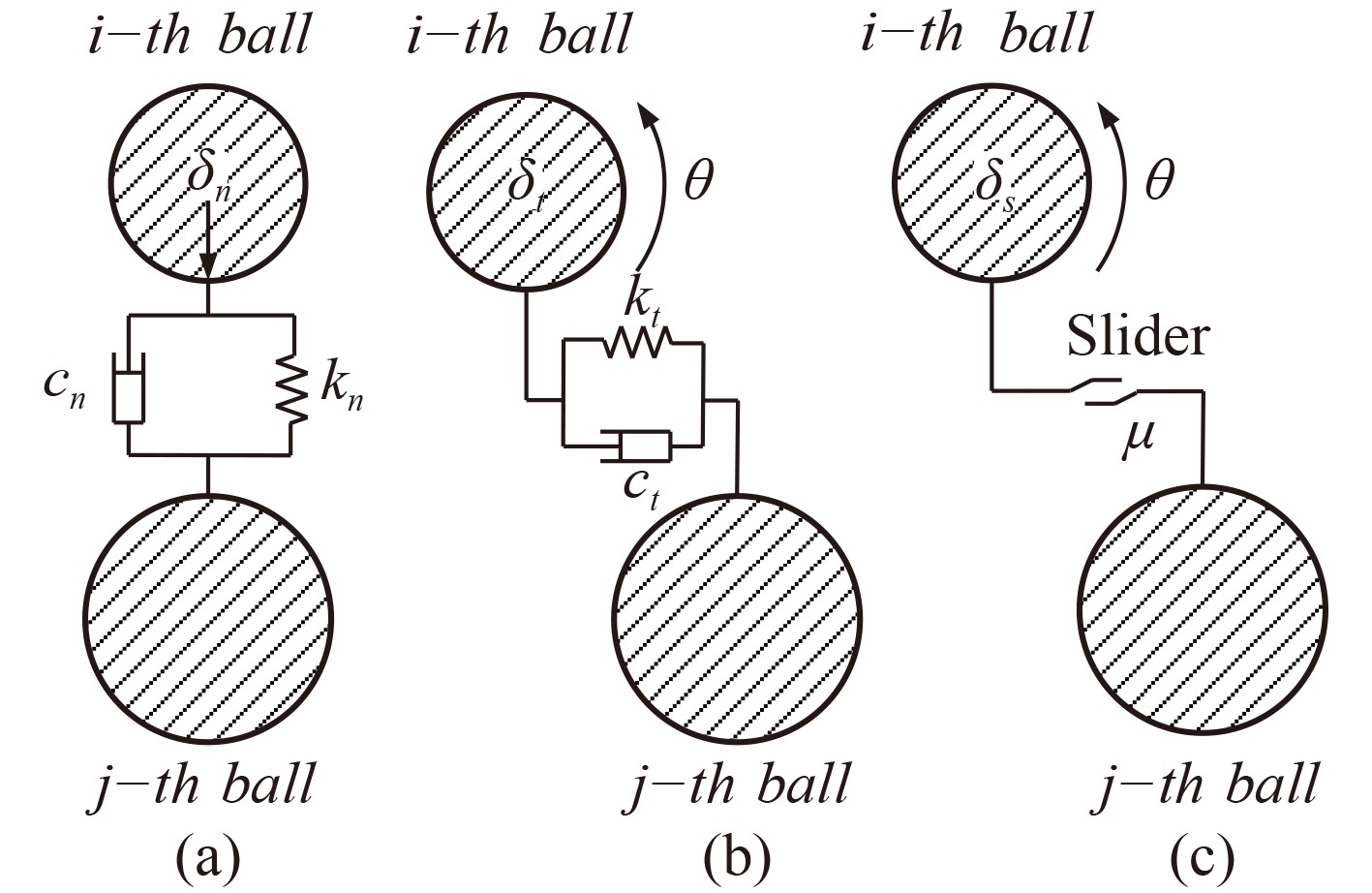
图 1 法向振动、切向振动和滑动模型 Fig. 1 Normal vibration,tangential vibration and sliding model |
将颗粒体之间的碰撞用振动运动方程描述,则法向上的运动方程为:
| $ {m^*}{{\rm{d}}^2}{\delta _n}/{\rm{d}}{t^2} + {c_n}{\rm{d}}{\delta _n}/{\rm{d}}t + {k_n}{\delta _n} = {F_N}。$ | (1) |
在切向方向上有可能发生切向滑动或滚动,运动方程表示如下:
| $ {m^*}\frac{{{\rm{d}}^2}{\delta _t}}{{\rm{d}}{t^2}} +\frac{ {c_t}{\rm{d}}{\delta _t}}{{\rm{d}}t} + {k_t}{\delta _t} = {F_T},$ | (2) |
| $ {I^*}\frac{{{\rm{d}}^2}\theta }{{\rm{d}}{t^2}} + \left(\frac{{c_t}{\rm{d}}{\delta _t}}{{\rm{d}}t} + {k_t}{\delta _t}\right)s = M 。$ | (3) |
式中:
根据Hertz接触理论计算法向接触力
颗粒运动过程中任意颗粒
| $ \left. \begin{gathered} {m_i}{{\ddot \delta }_i} = \sum F \\ {I_i}{{\ddot \theta }_i} = \sum M \\ \end{gathered} \right\} ,$ | (4) |
利用欧拉法对式(4)两边同时积分,则可得下一时间步长颗粒的速度表达式:
| $ \left. \begin{gathered} {({{\dot \delta }_i})_N} = {({{\dot \delta }_i})_{N - 1}} + {\left[\sum {F/{m_i}} \right]_N}{\Delta _t} \\ {({{\dot \theta }_i})_N} = {({{\dot \theta }_i})_{N - 1}} + {\left[\sum {M/{I_i}} \right]_N}{\Delta _t} \\ \end{gathered} \right\},$ | (5) |
式中:
对式(5)两边再次积分,即可得到颗粒的位移表达式:
| $ \left. \begin{gathered} {({\delta _i})_{N + 1}} = {({\delta _i})_N} + {({{\dot \delta }_i})_N}{\Delta _t} \\ {({\theta _i})_{N + 1}} = {({\theta _i})_N} + {({{\dot \theta }_i})_N}{\Delta _t} \\ \end{gathered} \right\}。$ | (6) |
根据上述计算过程可以在每个时间步更新颗粒的位置,再根据颗粒的位置来计算颗粒之间的作用力,不断重复该计算过程,则可实时跟踪每个颗粒的运动情况。
在颗粒接触过程中,法向上的阻尼力耗能为:
| $ {E_{nLos}} = \sum\limits_{i = 1}^{IC} {( - {c_n}{{\dot \delta }_{in}} \cdot {{\dot \delta }_{in}}\Delta t)}。$ | (7) |
式中:
在颗粒接触的切线方向,切向上的阻尼力耗能为:
| $ {E_{tLos1}} = \sum\limits_{i = 1}^{IC} {( - {c_t}{{\dot \delta }_{it}} \cdot {{\dot \delta }_{it}}\Delta t)}。$ | (8) |
颗粒的切向滑动与颗粒的滚动同时受颗粒之间摩擦力的影响,由滑动模型可以建立颗粒的切向滑动与滚动的极限判断条件[11]:
| $ {F_t} = \mu {k_n}{\delta _n}{{\rm{sgn}}} [{k_t}({\delta _t} + {\rm{d}}\theta /2)]。$ | (9) |
式中:
若
| $ {E_{tLos2}} = \sum\limits_{i = 1}^{IC} {( - {\mu _t}{F_{ti}} \cdot {{\dot \delta }_{it}}\Delta t)}。$ | (10) |
若
| $ {E_{tLos3}} = \sum\limits_{i = 1}^{IC} {( - {\mu _r}R{F_{ti}} \cdot {{\dot \theta }_i}\Delta t)}。$ | (11) |
式中:
阻尼器在一个振动周期中,颗粒在2个方向上耗能之和即为颗粒的损耗功率:
| $ P = \sum {{E_{nLos}} + } \sum {{E_{tLos}}}。$ | (12) |
振动的容器与其中的颗粒体之间构成了一个耦合封闭的动力学系统,鉴于颗粒耦合运动系统的复杂性,忽略颗粒冲击对结构运动的影响,在此基础上研究阻尼器简谐振动的频率、幅值以及填充率对颗粒耗能特性的影响规律。计算时间取阻尼器自振周期的75倍以消除瞬态振动的影响,并取后25个周期的平均损耗功率作为衡量耗能效果的最终指标[12]。
算例模型如图2所示,阻尼器尺寸36 mm×75 mm,材料为铝,密度

|
图 2 颗粒阻尼器 Fig. 2 Test rig of particle damper |
5种不同填充率(50%,60%,70%,80%和90%)对颗粒阻尼器等效阻尼比的影响试验已经开展[13],研究发现当颗粒填充率为90%时,颗粒阻尼器表现出较好的阻尼性能,针对90%以上的颗粒阻尼器的阻尼性能还未开展。本文选定测试填充率的变化区间为90%~100%,阻尼器简谐振动的频率50 Hz,幅值1 mm。
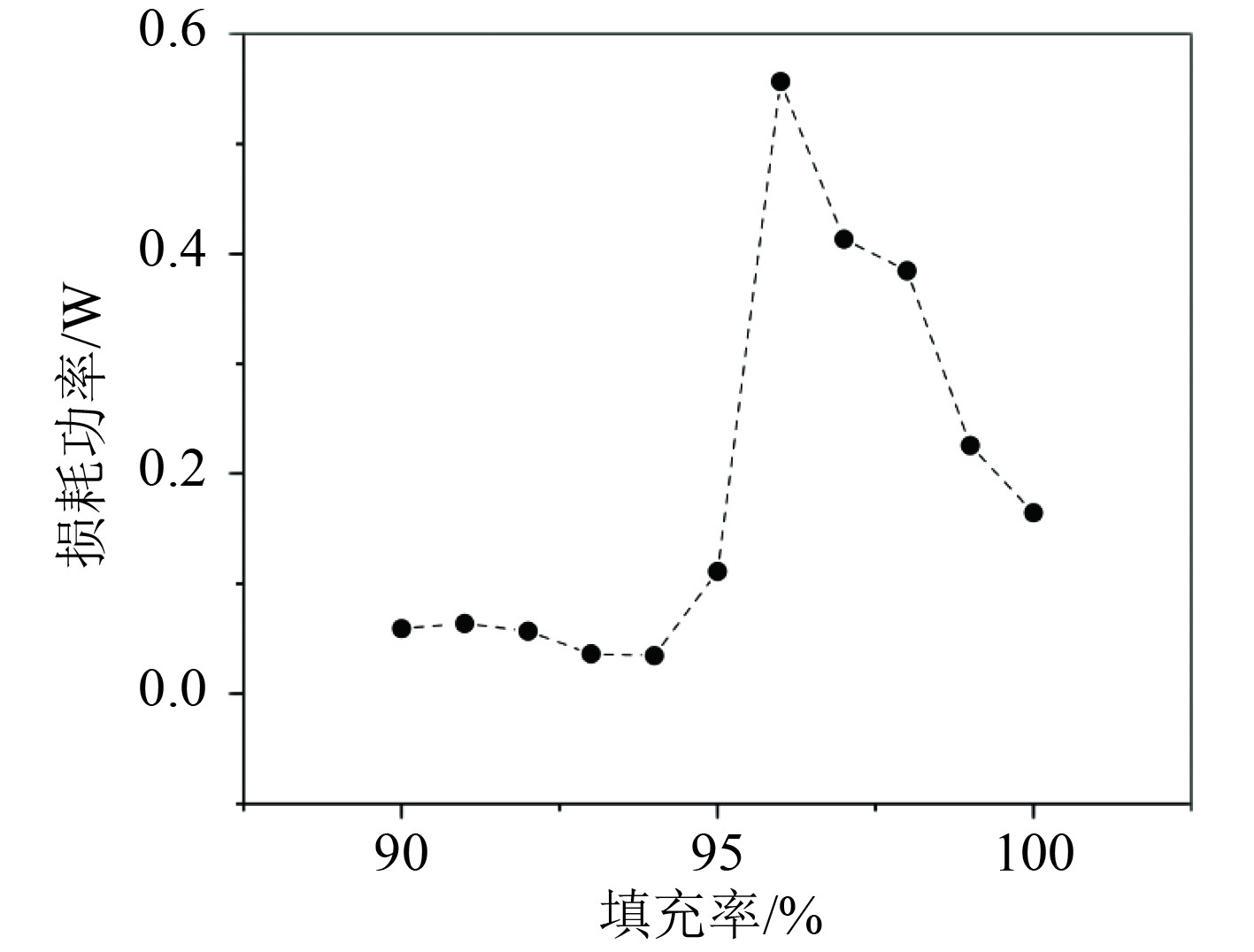
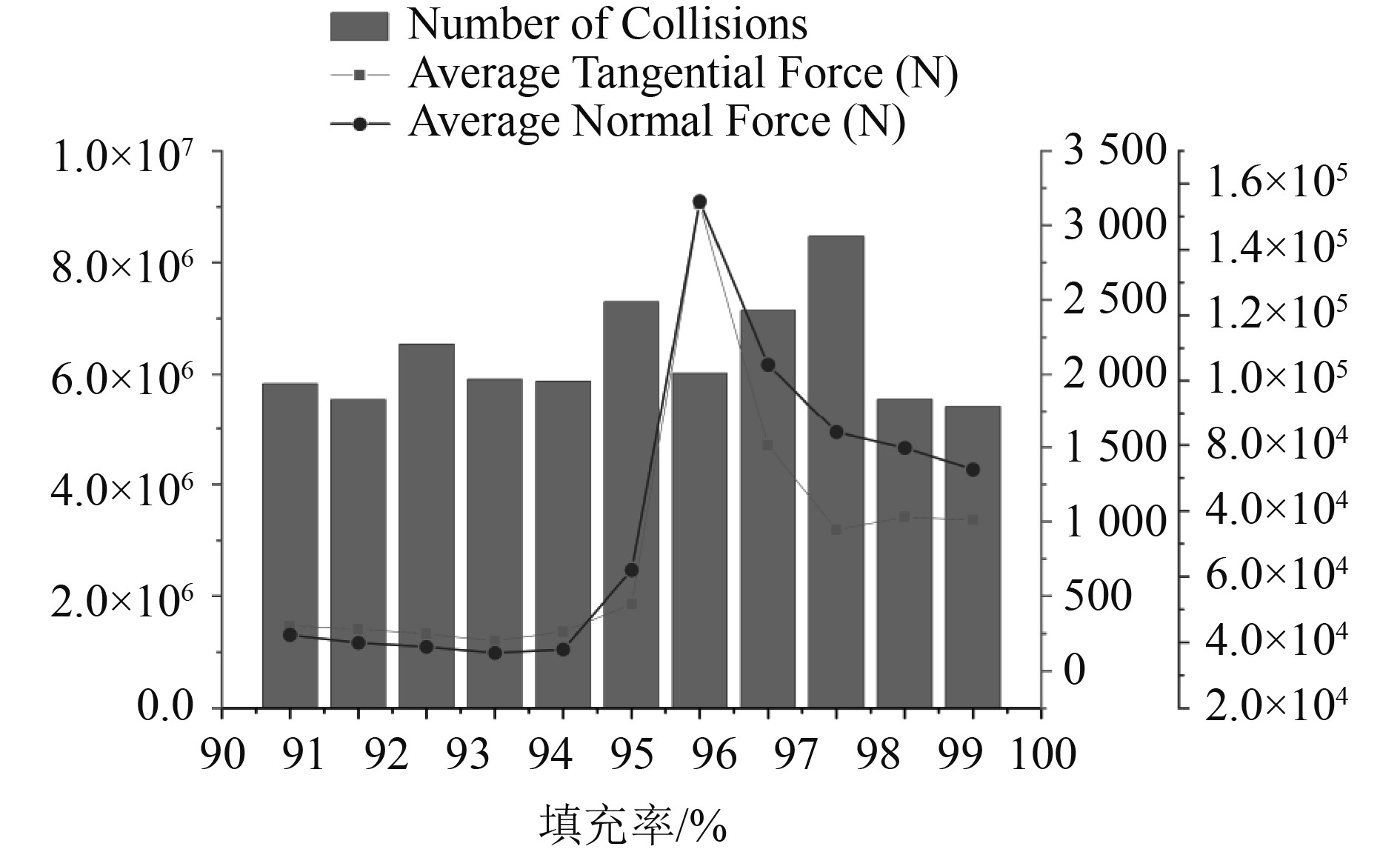
图3为颗粒损耗功率随填充率的变化曲线。随着填充率的增加,损耗功率有先增大后减小的趋势,当填充率约为96%时,损耗功率达到最大值。由图4可以看出,随着填充率的增加,在一个振动周期中颗粒间的总碰撞次数表现为小幅度的上下波动,而平均切向力和平均法向力与损耗功率有着几乎相同的变化趋势,当填充率约为96%时,两者同时达到最大值,此时内部颗粒的碰撞最激烈。当填充率较低时,顶部颗粒层仅受重力作用向下运动,随着填充率的增加,颗粒层与容器之间的空隙会逐渐变小,在阻尼器简谐振动的过程中能够与容器顶部接触的颗粒数量逐渐增多,由容器顶部给颗粒系统施加向下的冲击力,将振动能量输入颗粒系统,因此颗粒系统的碰撞程度会增加,而当容器内填充满颗粒时,在运动的过程中颗粒处于集聚态,犹如一块质量做整体运动,因此损耗功率会降低。
|
图 3 损耗功率随填充率的变化 Fig. 3 Change of the loss power varing with filling rate |
|
图 4 碰撞元素的属性随填充率变化图 Fig. 4 The properties of the collision element change with the filling rate |
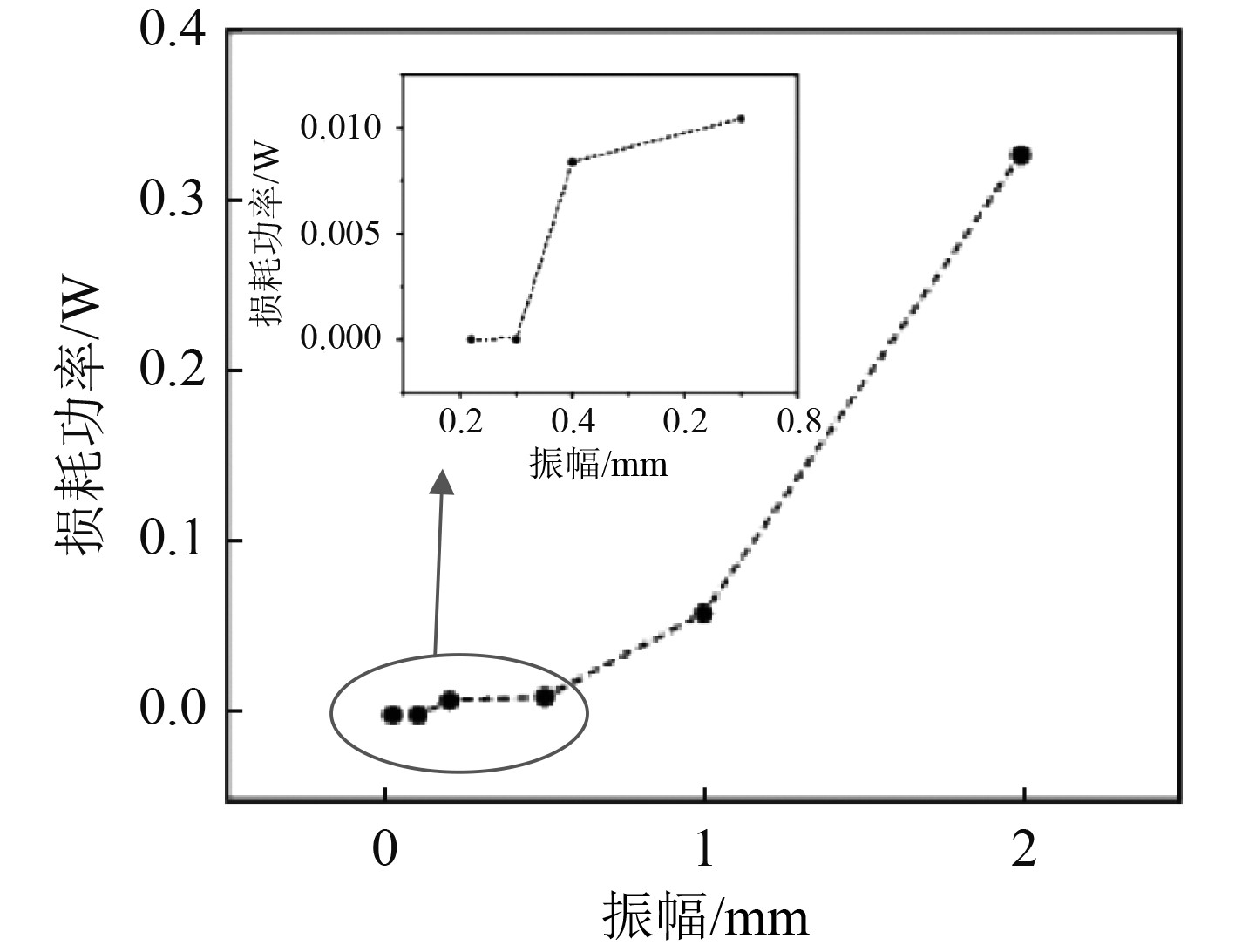
图5表示阻尼器简谐振动频率50 Hz,颗粒填充率90%时,损耗功率与位移幅值的关系曲线。当振幅在临界点之前(<0.1 mm),颗粒的损耗功率几乎为0,临界点之后,损耗功率随着振动位移幅值的增大而增大。
|
图 5 损耗功率与位移幅值的关系 Fig. 5 The relationship between power loss and displacement amplitude |
在竖直振动的容器中颗粒床的运动受约化加速度的影响(
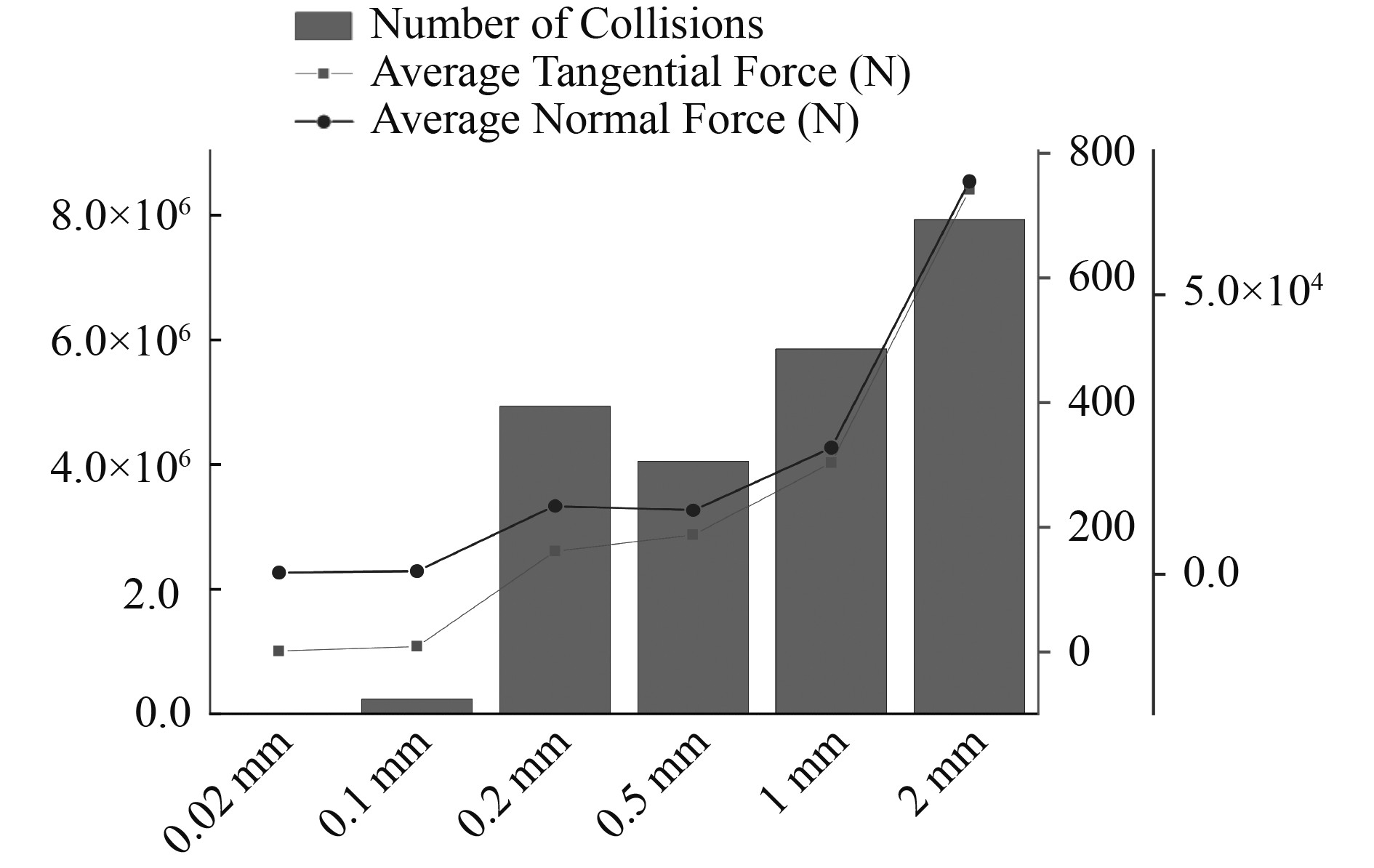
|
图 6 碰撞元素的属性随位移幅值变化图 Fig. 6 The properties of the collision element change with the displacement amplitude |
图7表示阻尼器简谐振动幅值1 mm,颗粒填充率90%时,损耗功率与振动频率的关系曲线。随着振动频率的升高损耗功率呈现先上升后下将的趋势,当振动频率约为300 Hz时,损耗功率达到最大值。由图8可以看出,随着振动频率的升高,在一个振动周期中颗粒间的总碰撞次数呈指数衰减并且趋于稳定,平均切向力与平均法向力的值有着先增大后减小的趋势,此时颗粒的碰撞最充分,一个振动周期内的总碰撞次数与碰撞平均程度共同决定了颗粒的耗能能力,并在振动频率约为300 Hz处达到最大值。颗粒阻尼器的损耗功率对振动频率的变化较为敏感,通过合理设计其减振频带可以将颗粒阻尼器的效果发挥到最大。
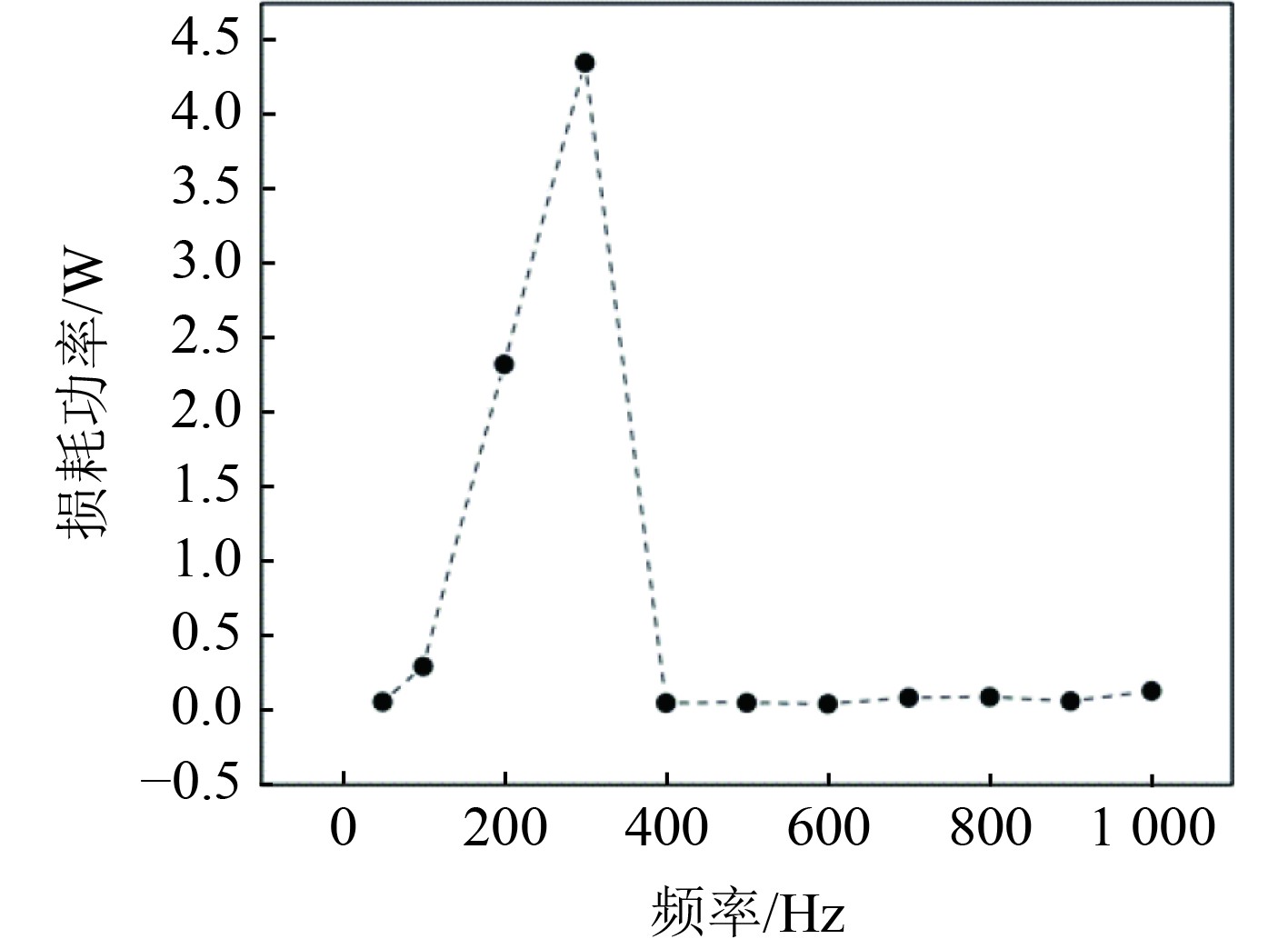
|
图 7 损耗功率随频率的变化 Fig. 7 Change of the loss power varing with the frequence |

|
图 8 碰撞元素的属性随频率变化图 Fig. 8 The properties of the collision element change with the frequence |
本文基于离散元法建立圆柱形颗粒阻尼的仿真模型,研究垂直振动边界条件驱动下由颗粒体产生的损耗功率。结果表明,颗粒的填充率、简谐振动的频率与幅值均会影响着颗粒阻尼器的损耗功率。针对具体的振动水平,发现在高填充率范围内存在一个填充率的最优值。当简谐振动的频率固定时,只有当简谐振动的幅值超过某个临界点后,颗粒阻尼器才体现出耗能能力,并且损耗功率随着位移幅值的增大而增大。损耗功率对频率的变化较为敏感,在100~400 Hz的频带范围内具有较强的耗能能力,在实际应用场景中应根据结构体的振动特点来合理设计其减振频带,将颗粒阻尼器的效果发挥到最大。
| [1] |
SAEKI M. Analytical study of multi-particle damping[J]. Journal of Sound and Vibration, 2005, 281(3-5): 1133-44. DOI:10.1016/j.jsv.2004.02.034 |
| [2] |
胡溧, 黄其柏, 许智生. 颗粒阻尼的回归分析研究[J]. 中国机械工程, 2008, 19(23): 2834-2837. DOI:10.3321/j.issn:1004-132X.2008.23.015 |
| [3] |
周天平. 颗粒阻尼器对悬臂梁结构受追振动的减震作用研究 [D]. 兰州: 兰州大学, 2012.
|
| [4] |
蒋华, 陈前. 恢复力曲面法在颗粒阻尼器研究中的应用[J]. 振动、测试与诊断, 2007(3): 228-31+59. DOI:10.3969/j.issn.1004-6801.2007.03.012 |
| [5] |
刘雁梅, 黄协清, 陈天宁. 非阻塞性颗粒阻尼加筋板振动功率流的研究[J]. 西安交通大学学报, 2001(1): 61-65. DOI:10.3321/j.issn:0253-987X.2001.01.014 |
| [6] |
TANRIKULU A H. Application of ANN techniques for estimating modal damping of impact-damped flexible beams[J]. Advances in Engineering Software, 2009, 40(10): 986-90. DOI:10.1016/j.advengsoft.2009.04.001 |
| [7] |
HERTZ H. On the contact of elastic solids [J]. Journal für die reine and Angewandte Mathematik (Crelles Journal), 1880, 92(156).
|
| [8] |
CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies [J]. Géotechnique, 1979, 29(1).
|
| [9] |
Y. T, T. T, T. I. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe [J]. Elsevier, 1992, 71(3).
|
| [10] |
D. M R. Compliance of elastic bodies in contact [J]. Journal of Applied Mechanias, 1949, 16(3).
|
| [11] |
胡国明. 颗粒系统的离散元素法分析仿真 [M]. 颗粒系统的离散元素法分析仿真, 2010.
|
| [12] |
姚冰. 颗粒阻尼建模仿真及工程应用 [D]. 南京: 南京航空航天大学, 2013.
|
| [13] |
周宏伟. 颗粒阻尼及其控制的研究与应用 [D]. 南京: 南京航空航天大学, 2008.
|
| [14] |
姜泽辉, 刘新影, 彭雅晶, 等. 竖直振动颗粒床中的倍周期运动[J]. 物理学报, 2005(12): 182-188. |
 2022, Vol. 44
2022, Vol. 44
