2. 浙江大学 海洋学院,浙江 舟山 316021;
3. 宁波大学 海运学院,浙江 宁波 315211
2. Ocean College Zhejiang University, Hangzhou 316021China;
3. Faculty of Maritime and Transportation, Ningbo University, Ningbo 315211
晃荡是工程领域中常见的流体运动现象,常发生于部分充满液体的容器内[1]。具体是指2种或2种以上互不相容的流体(通常是气体和液体)在有限空间内的运动。海洋工程领域中主要考虑晃荡问题的海洋工程装备包括液化天然气运输船、液化石油气船、大型原油货船以及浮式生产储卸油装置等[2-4]。这些运载装备在海洋环境中受到风浪流的联合作用时,储液舱内的液体会在外部激励的影响下产生晃荡运动[5]。当外界激励的频率接近液舱内液体的固有频率或者激励的振幅非常大时,很容易引起液舱内液体的剧烈晃荡,进而对舱壁或者舱顶产生强烈的冲击压力,从而造成结构的变形或破损[6]。与此同时,液体发生晃荡时也会伴随波面翻卷、破碎、气泡卷入等强非线性现象,进而破坏液舱的围栏系统,导致沉船事故[7]。
当前关于液舱晃荡的研究主要集中于内部液体本身或是外部载荷环境变化所导致的舱壁结构强度问题[8-10],对于液舱形状的变化对液舱晃荡的影响的相关研究比较缺乏。本文以2种典型的液舱结构为计算模型,采用自适应网格法捕捉液舱晃荡中的自由面,同时分析不同激励频率、不同液体装载率下舱内液体自由面的波高时历曲线,对液舱晃荡过程中的非线性动力学行为和自由面演化特征的研究有一定借鉴和参考价值。
1 自适应网格自适应网格加密(adaptive mesh refinement,AMR),是指计算中对于某些物理解变化特别剧烈的区域,如湍流区、激波面等,网格在迭代过程中不断细化,从而为重要区域的精确求解提供足够高的分辨率;而在物理解变化平缓区域网格相对稀疏,这样在保持计算高效率的同时可得到高精度的解[11]。自适应网格加密方法以块为基本操作单元,所有块单元的几何结构完全一致,所以该方法也容易实现高阶差分格式,如图1所示。同时自适应网格加密方法采用叉树结构进行数据管理,并通过守恒的块边界插值算法实现粗细网格之间的信息传递,通过自适应网格加密方法和动态负载平衡算法、数据收发技术等的结合,可对流场内的关键流动区域进行局部自适应加密,结合自适应步长调整。
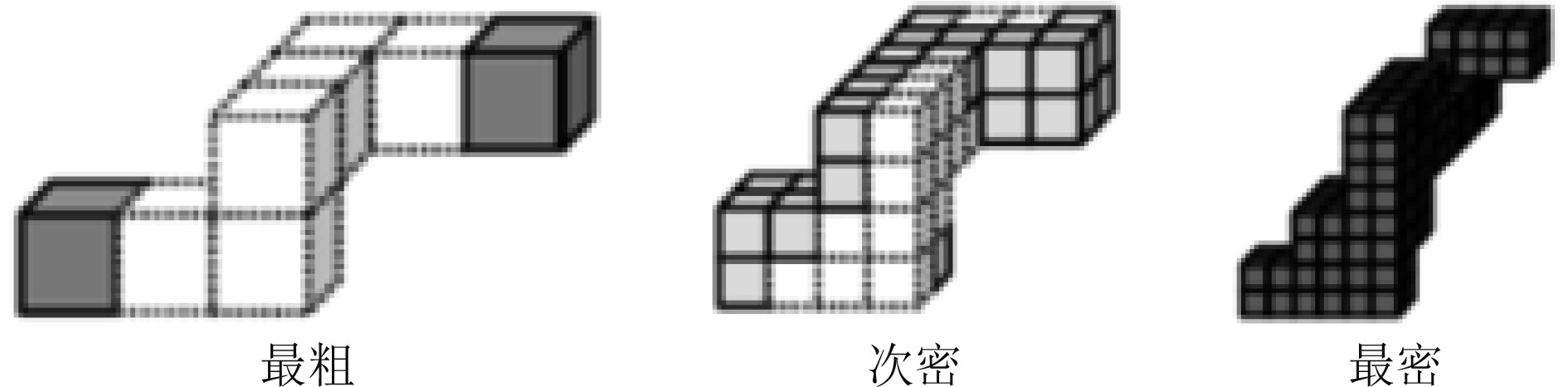
|
图 1 AMR中的不同加密等级 Fig. 1 Different levels of ARM |
基于模型驱动的AMR在海洋工程领域应用非常广泛,包括自由液面驱动的AMR、重叠网格驱动的AMR以及自定义场函数驱动的AMR等。VOF多相流驱动的AMR,通过设置一个稀疏的网格尺寸,在计算过程中智能加密自由液面上的网格,利用较少的网格捕捉VOF自由液面,同时配合自动化时间步长,大大加快了计算速度和效率[12]。本文液舱晃荡过程中的自由液面的网格加密通过自适应网格加密技术实现。
2 矩形液舱晃荡的数值模拟 2.1 计算模型与舱内液体晃荡固有频率分析考虑水平余弦激励下矩形液舱的横向运动,将其作为二维问题处理。矩形液舱长L=1 m,高H=1 m,液体装载率为50%,即水的高度h为0.5 m。矩形液舱模型如图2所示。
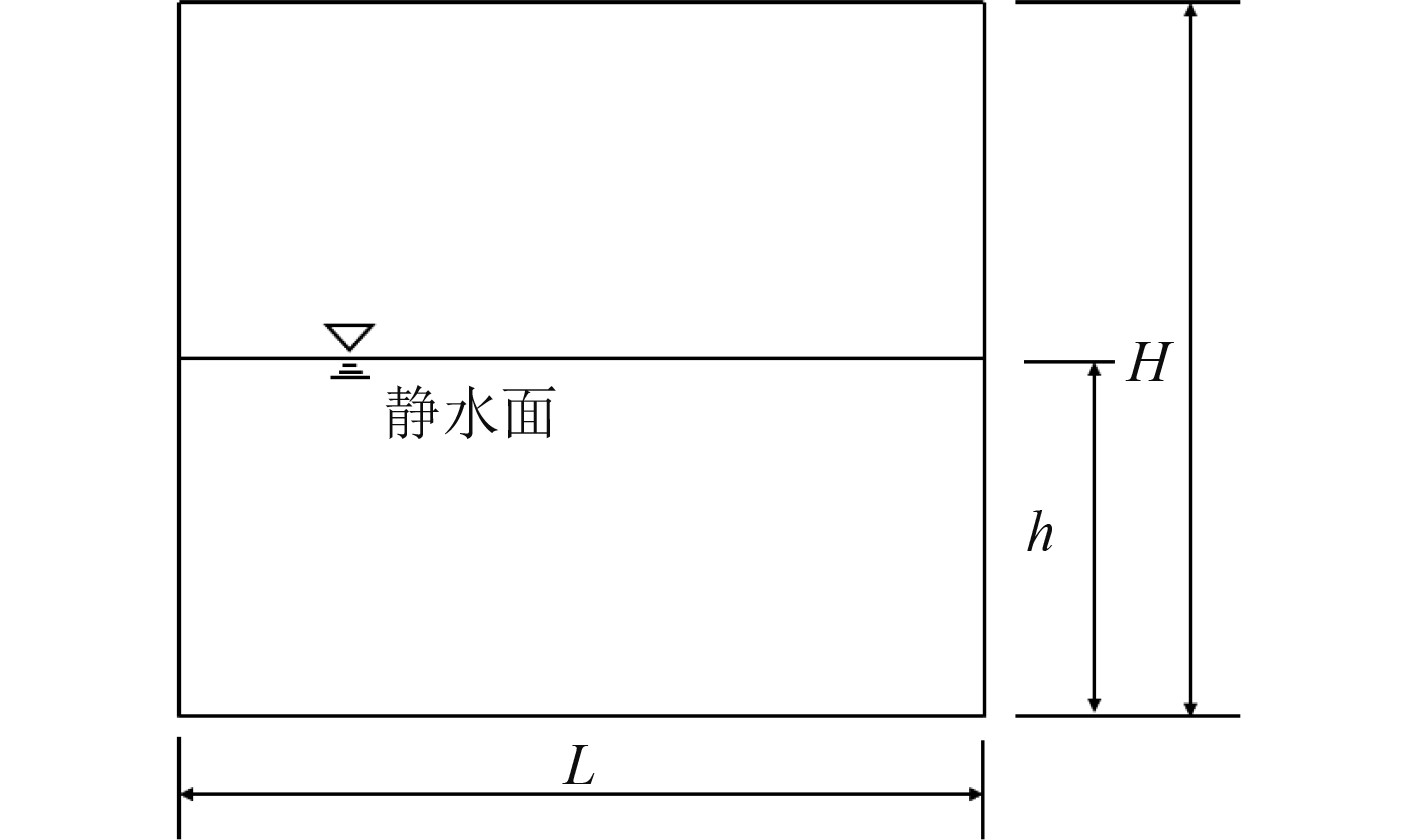
|
图 2 矩形液舱计算模型 Fig. 2 Numerical model of rectangular tank sloshing |
当液舱所受外部激励频率接近舱内晃荡液体的固有频率时,舱内液体将会出现大幅晃荡现象,产生共振。不同装载率情况下舱内晃荡液体的固有频率不同,因此,达到共振的频率也不相同。对于矩形液舱容器,舱内液体的固有频率与装载高度、晃荡方向的自由液面长度有关,其固有频率可由以下经验公式计算:
| $ {f_n} = \frac{1}{2}\sqrt {g\frac{{n\text{π} }}{L}\tanh \left(\frac{{n\text{π} }}{L}h\right)} 。$ | (1) |
式中:fn为液体的第n阶固有频率;h为装载高度;L为液舱宽度;g为重力加速度9.81 m/s2,原点位于液舱中心,静水面处。对于液深0.5 m的情况,舱内液体的一阶固有频率f1为0.846 Hz。
计算2种外部水平激励下的液舱晃荡模型,一种是远离共振频率的小振幅晃荡,其中f=0.5f1,b=0.01 m;另一种是靠近共振频率的大振幅晃荡,其中f=0.95f1,b=0.1 m。
2.2 网格划分与自适应网格准则目前AMR暂不支持二维分析,因此对于矩形液舱晃荡问题可以采用2.5D进行建模分析,计算域厚度方向生成1层网格。计算域长度和高度方向生成50层网格,初始网格(未进行自适应网格细化之前)数量为2500,如图3所示。

|
图 3 矩形液舱网格 Fig. 3 Mesh of rectangular tank |
在AMR的属性设置中,有2个比较重要的参数,一个是转换宽度,另一个是最高细化等级。最大加密等级控制最小的网格尺寸,转换宽度控制这些不同级别网格之间的过渡。通常情况下,最大加密等级视加密情况设置为2~3级,转换宽度设置为3~5,本文中的最大加密等级设置为3级,转换宽度为5。初始化后自由界面附近的网格被自动加密,如图4所示。

|
图 4 初始化后的自由界面网格细化 Fig. 4 Mesh refinement of free water surface |
Faltinsen[13]针对水平激励下矩形液舱的晃荡问题,提出了一个求解自由面波高的方程,适用于装载率大于20%H的二维矩形液舱,被广泛应用于数值模型有效性的验证。令液舱长L=2a,舱内液体静止时水深为h,当液舱遭遇水平激励为λ=bsinωt时(ω为外部激励的圆频率,b为水平激励幅值),水平周期性的液舱激励速度函数为ue=−Acosωt(A=bω为速度幅值),此时自由液面任意位置x的波高η为:
| $\begin{split} \eta = &\frac{1}{g}\sum\limits_{n = 0}^\infty {\sin \left[\frac{{(2n + 1)\text{π} }}{{2a}}x\right]} \cosh \sin \left[\frac{{(2n + 1)\text{π} }}{{2a}}x\right]\\ &( - {A_n}\sin{\omega _n} - {C_n}\omega \sin \omega t) - \frac{1}{g}A\omega x\sin \omega t。\end{split} $ | (2) |
式中:
图5为中等装载率、外部激励频率远离共振频率时液舱小幅度振动情况下的右侧围壁处波高时历曲线,虚线代表用式(2)计算的Faltinsen的理论值,实线代表本算例的计算值。由图5可知,对于中等装载率下远离共振频率的小振幅晃荡情况,计算值与理论值的周期性一致,且波峰波谷位置较为吻合,右侧围壁处的波高变化趋势一致,这说明基于自适应网格加密技术的液舱晃荡数值模拟方法具有相当高的可靠性和准确性。由于CFD计算考虑了流体的粘性作用,因此波高峰值比基于势流理论的解析值要有所增加,计算后期波高和波谷的值与解析值相比在时域上有所滞后。
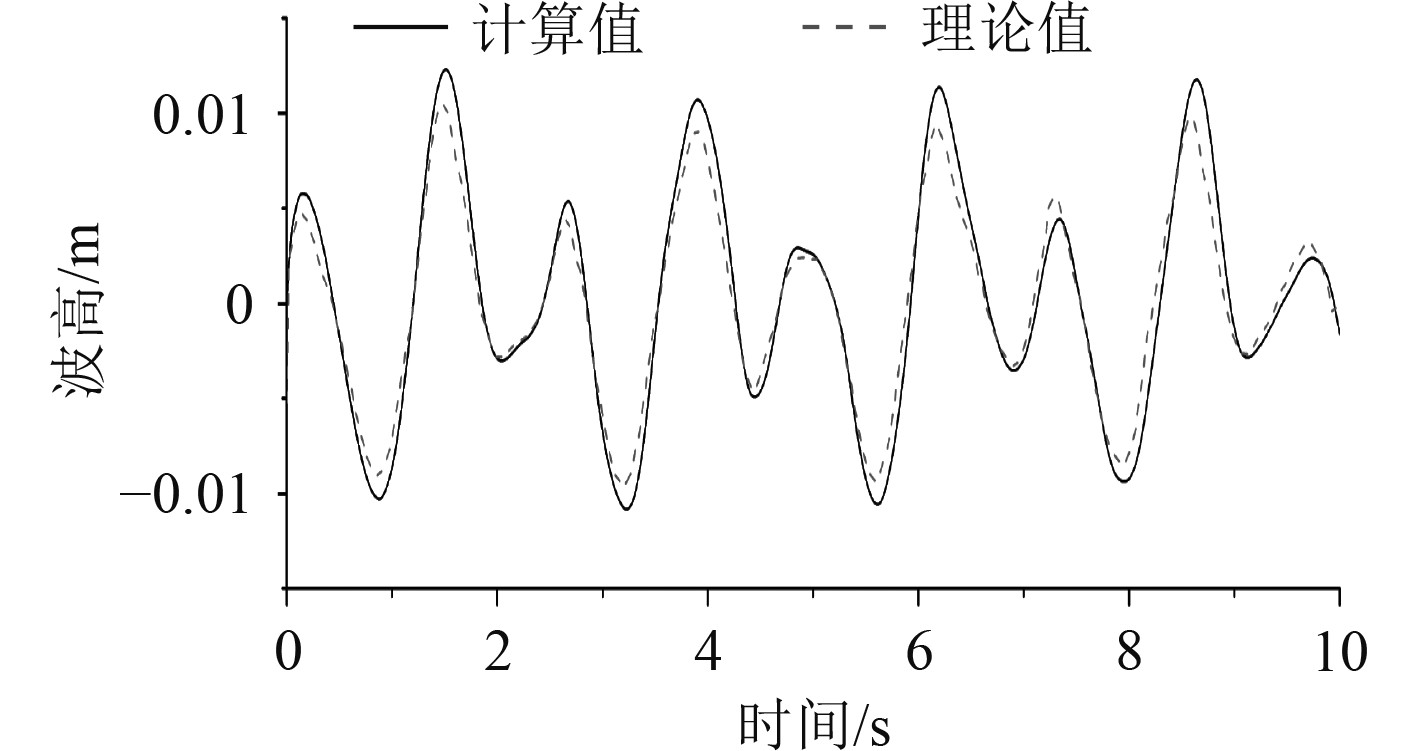
|
图 5 b=0.01 m,f=0.5f1时右侧围壁波高时历曲线 Fig. 5 Wave height duration curve of the right wall with b=0.01 m,f=0.5f1 |
图6为中等装载率、外部激励频率靠近共振频率时液舱大幅度振动情况下的右侧围壁处波高时历曲线,虚线代表右侧围壁的波高,实线代表左侧围壁的波高。可以看出,在8 s的晃荡时间内,左右两侧围壁的波峰和波谷基本上交错出现,但并不是对称分布。当外部激励作用到矩形液舱时,液舱向左侧作平移运动,此时舱内液体仍有保持原来静止不动的趋势,因此在计算前期的0.1 s左右,左侧围壁的自由面高度会有所下降,相应的,右侧围壁的波高会上升。液体摆脱掉自身的惯性后会跟随容器一起向左运动,反映到图6中为右侧围壁的波高曲线平缓下降(左侧围壁波高曲线平缓上升)。当时间t=0.6s左右时,矩形液舱运动到起始位置,两侧围壁的波高达到第1个极值,此后矩形液舱在向右运动的过程中,右侧围壁的波高快速上升,左侧围壁的波高则快速下降。右侧围壁的液体在液舱从右端返回到初始位置的过程中继续沿右侧围壁向顶部爬升,直到一个运动周期(约1.244 s)结束后达到液舱顶部,此时舱内液体沾满了整个右侧围壁。在t=1.5 s后相当长的一段时间内,舱内液体的自由面非线性程度不断增强。液体从左侧围壁攀升到液舱顶部后有极少数液滴从水流中脱离出来并飞溅到右侧围壁,导致右侧围壁的平缓的波高曲线在t=1.8 ~2.3 s的时间内发生剧烈激增。t=2.3 s后由于舱内液体已经具备了一定的速度,在动能和惯性力的共同作用下右侧围壁的波高增幅快速增加。t=2.6 s后舱内液体已经晃动到左侧围壁,然而此时矩形容器右半部分仍滞留了大量参杂气体和液体的混合物,且舱内液体还未完全从右侧围壁脱离,造成右侧围壁的波高曲线在较长的一段时间内维持在0.5 m的幅值上。前5 s的计算时间内,液体在晃荡的过程中不断冲击到液舱顶部,发生冲顶现象,5 s后,随着液体内部能量的不断积累,液体的速度和运动的频率逐渐向外部激励的速度和频率靠拢,两侧围壁的波高也随之降低,并呈现非周期性变化。
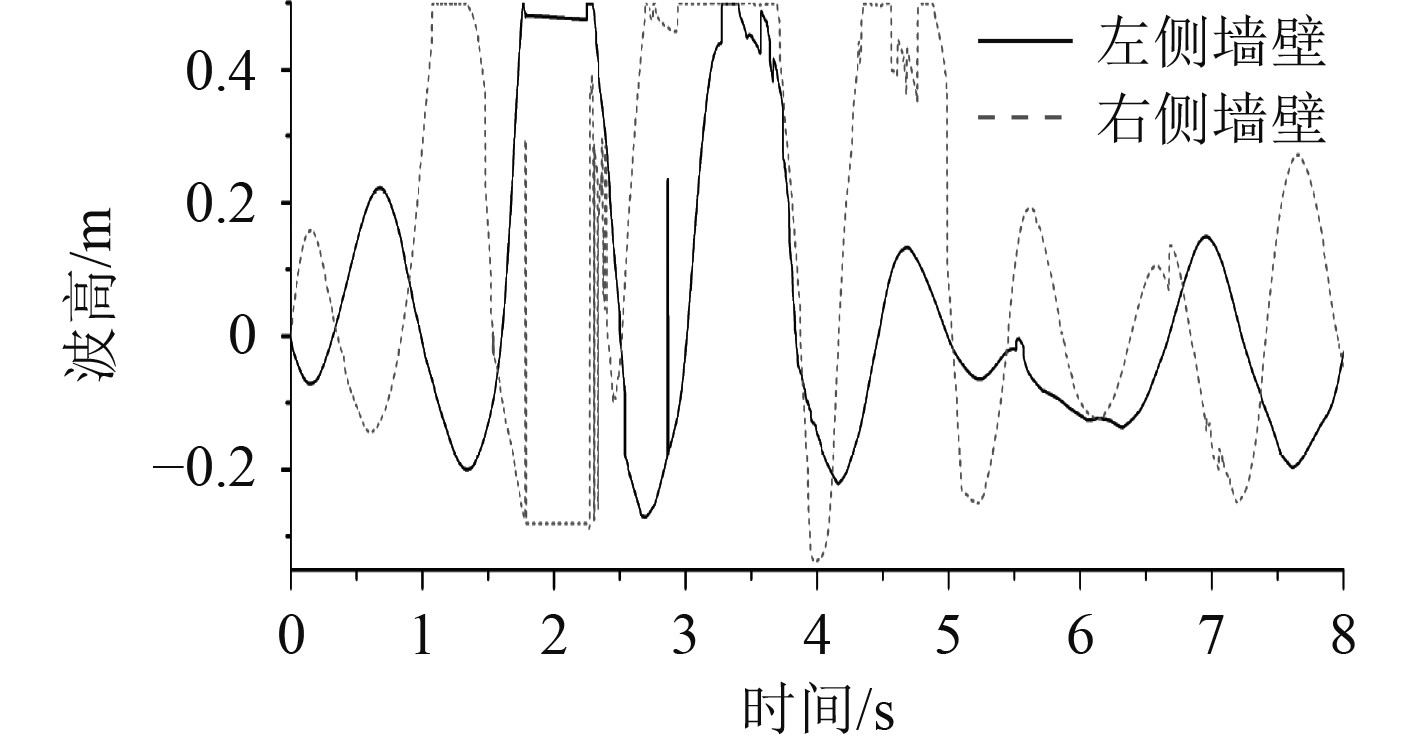
|
图 6 b=0.1 m,f=0.95f1时两侧围壁波高时历曲线 Fig. 6 Wave height duration curve of the two walls with b=0.1 m,f=0.95f1 |
由图7可以看出,VOF多相流驱动的AMR在计算过程中,自由液面处的网格密度并不是一成不变的,而是随着自由液面的流动自适应加密,计算域的网格数量也在计算过程中不停的改变,但网格总数不超过10万,采用AMR处理自由液面处的网格密度的方法大大提高了计算效率。
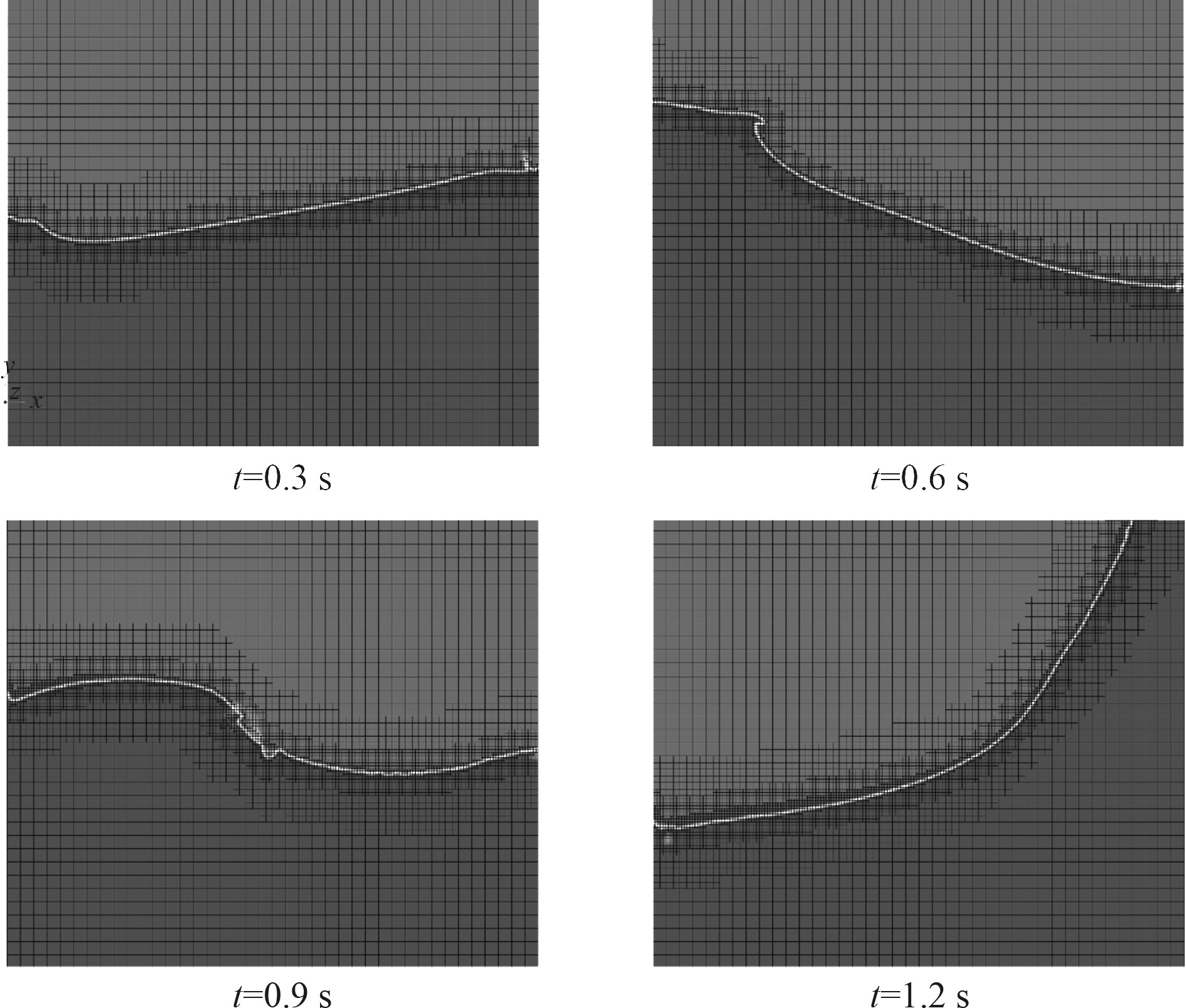
|
图 7 前1.2 s内液舱内的气液分布图 Fig. 7 Gas-liquid distribution of rectangular tank in 0~1.2 s |
图8为t=1.2~2.0 s内矩形液舱内的气液两相的分布情况。总的来看,在t=2 s之前舱内液体自由面的变化较为平缓。t=1.2 s时晃动的液体沿液舱右侧围壁攀升到顶部,随后在液舱顶部发生小范围冲顶现象。液舱向左侧横荡的过程中,左侧围壁的波高逐渐上升,右侧围壁波高下降的同时水体受到围壁的阻滞作用,少量水滴从水体中脱离出来后又迅速坠回水体,舱内的自由面逐渐展平。t=1.8 s时舱内液体在左侧围壁顶部发生一次范围和程度更大的冲顶现象,舱内液体和液舱顶部发生相互作用的同时在水流前端产生了少量的水气,该水气会不断的喷溅到右侧围壁上。与此同时,靠近右侧围壁的自由面在向下凹陷的同时掺入了大量的空气,使该处自由面的水体积分数有所降低。自由面越低,水气的量越大。

|
图 8 1.2~2.0 s内矩形液舱的气液两相图 Fig. 8 Gas-liquid distribution of rectangular tank in 1.2~2.0 s |
由图9可知,t=2.0 s后舱内液体晃荡行为的非线性成分明显增强,液体在晃荡的过程中不断与容器侧壁和顶部发生碰撞,期间产生大量的在壁面破碎的行波。围壁对舱内液体的冲击作用破坏了原本的自由面波形,无数个形状大小不一的液滴从冲击到围壁的自由面一端脱离出来,分散到自由面上方的空气中并与之融合,形成气液混合物。冲击过程中的气液混合和裹气冲击也是晃荡过程的物理作用机理之一。

|
图 9 2.1~3.0 s内矩形液舱的气液两相图 Fig. 9 Gas-liquid distribution of rectangular tank in 2.1~3.0 s |
由图10可知,液舱晃荡到t=3.7 s后,液体内部能量的不断积累,液体的速度和运动的频率逐渐向外部激励的速度和频率靠拢。由于外部激励的频率接近舱内一阶固有频率,液舱在发生共振的期间积累了大量的动能,使舱内液体有与液舱发生同向晃动的趋势,此时舱内液体自由面的波浪形态多是驻波和涌波的组合波。在一阶段的冲击过程中的产生的气液混合物聚集在自由面的上方,而矩形液舱的四周均为围壁,无法散出,从而改变了舱内原始的压强。自由面上方增的大压强作用到自由液面上使液体冲顶现象的发生频率降低,舱内两侧围壁的波高也随之降低。

|
图 10 3.7~6.4 s内矩形液舱的气液两相图 Fig. 10 Gas-liquid distribution of rectangular tank in 3.7~6.4 s |
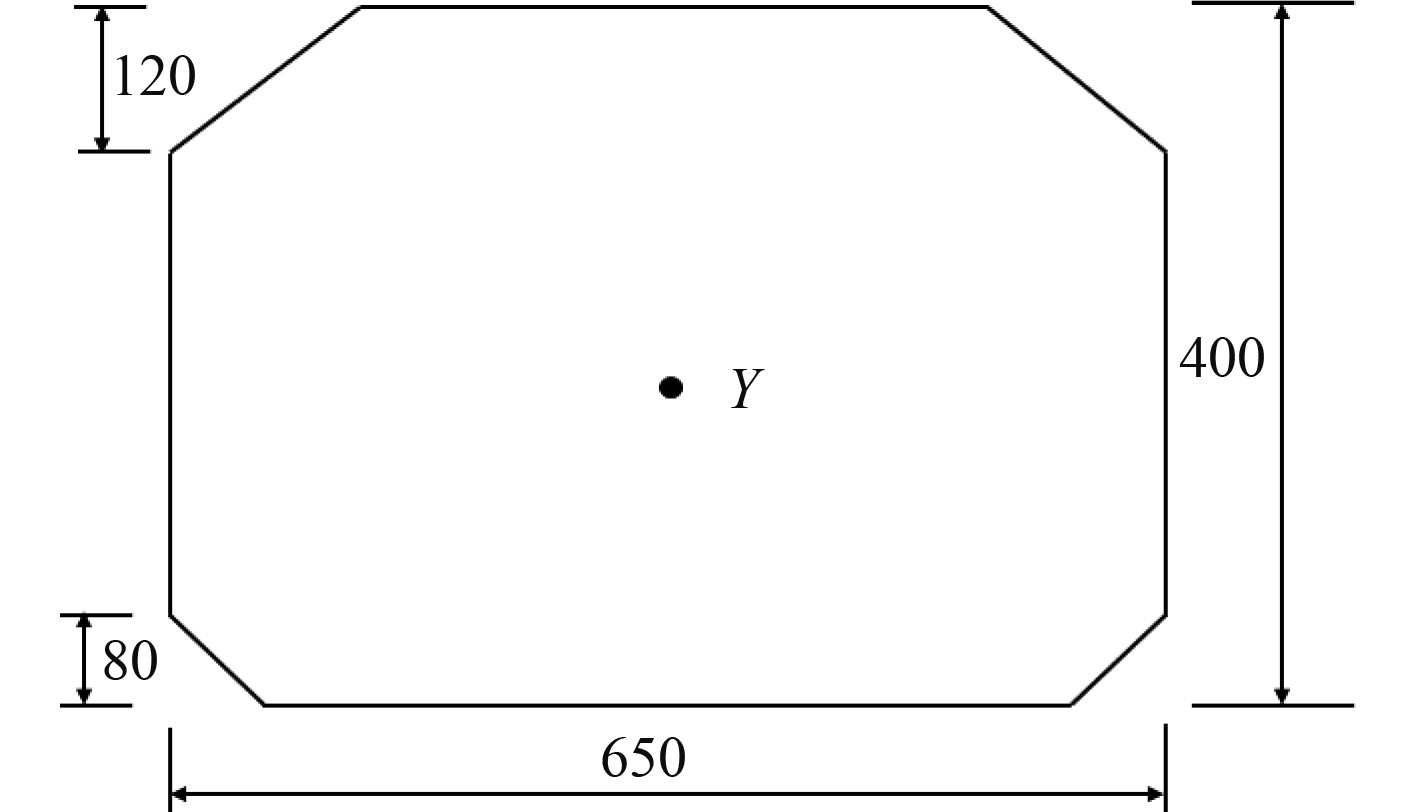
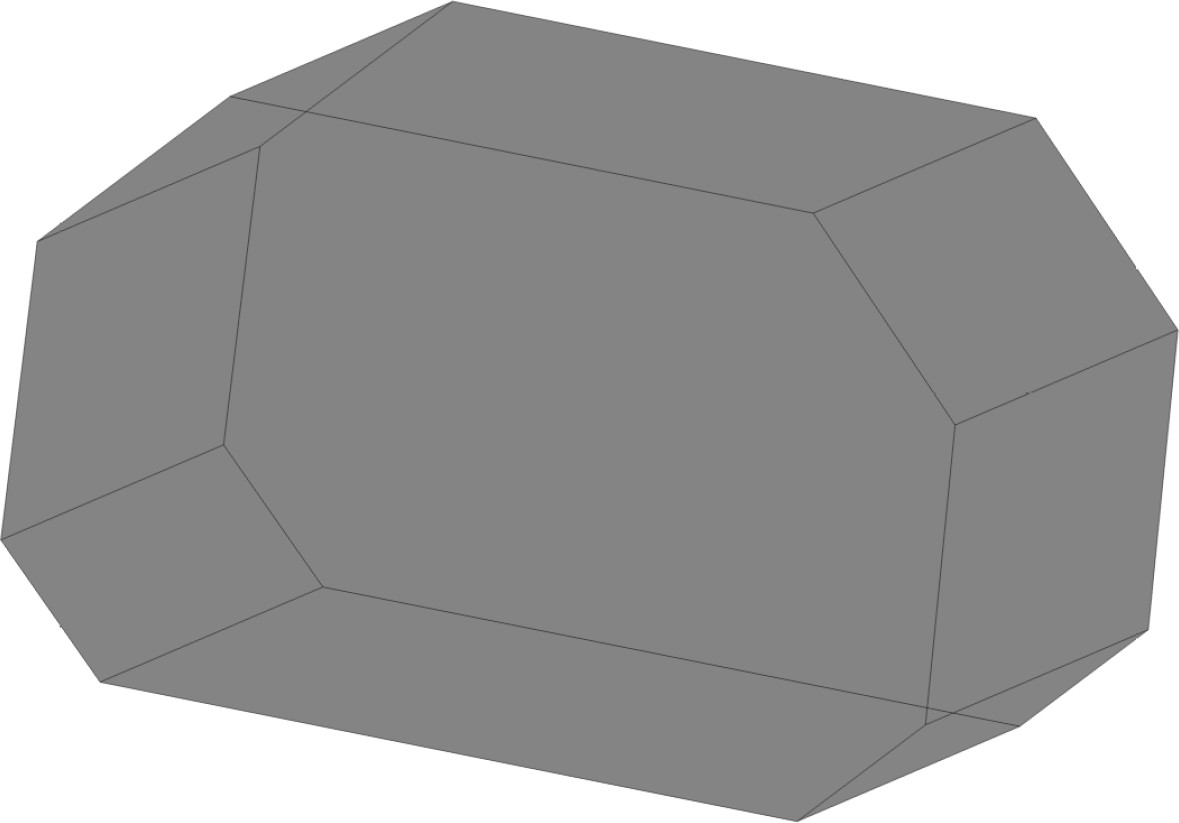
随着海洋运输的发展和能源需求的提高,带有顶边舱和底边舱的棱形液舱被广泛应用于大型载液货(油)船储液系统设计中。本文所采用的三维棱形液舱的尺寸和模型如图11和图12所示。
|
图 11 棱柱液舱的平面图(mm) Fig. 11 Prismatic tank plan |
|
图 12 三维棱形液舱模型 Fig. 12 Three-dimensional prismatic tank model |
三维棱形液舱的长为0.65 m,高0.4 m,宽0.4 m;顶边舱长为0.12 m,底边舱长0.08 m,上下边舱的坡度均为45°。液舱遭遇外部横摇激励,横摇中心Y位于几何模型的中心,距离底部0.2 m,距离侧边0.325 m。液舱横摇激励的运动描述为θ=θ0sinωt,其中,最大横摇角度θ0=10°,ω为横摇运动的圆频率。
计算2种装载率(水深分别为0.2 m和0.3 m)下对应的3个横摇频率(f分别的0.6 Hz,0.8 Hz和1.2 Hz),总计6个工况。
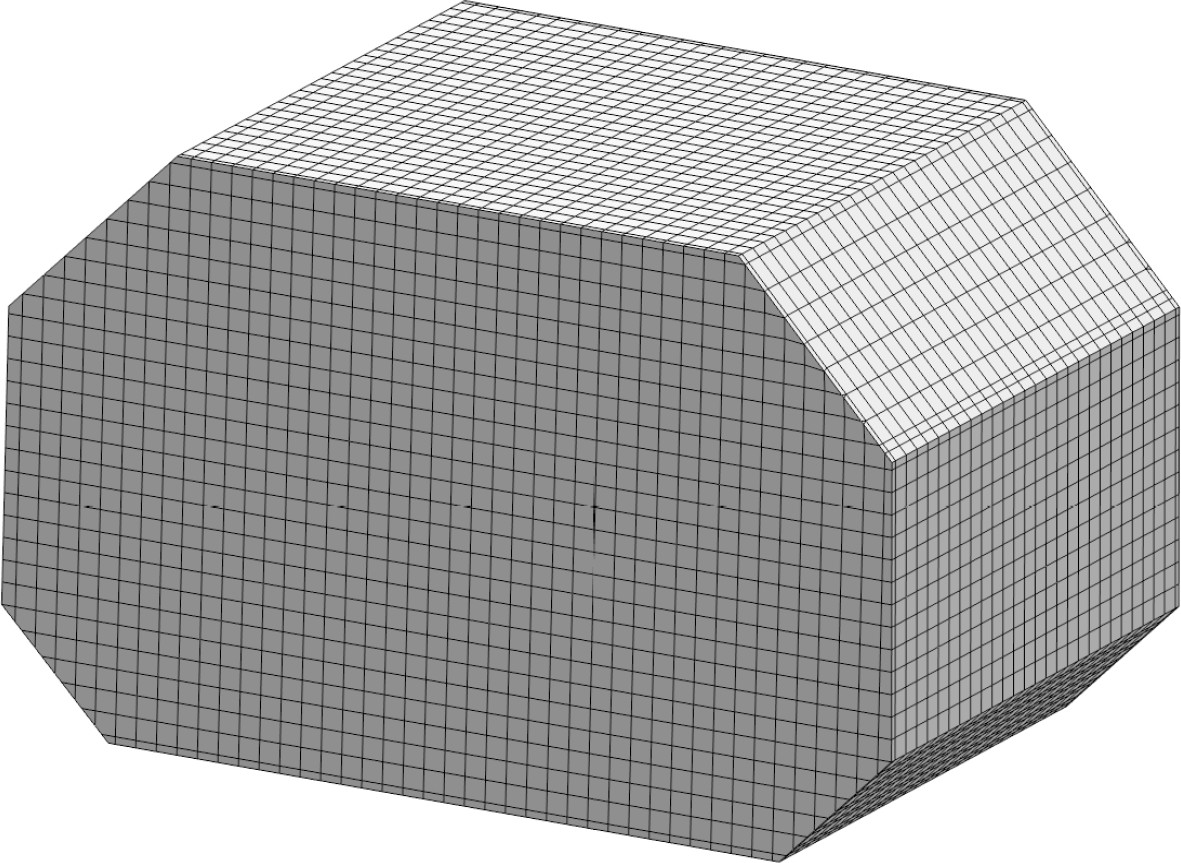
3.2 网格划分与自适应网格准则三维棱形液舱晃荡问题中生成的初始网格(未进行自适应网格细化之前)数量为31640。网格的相关细节如图13所示。
|
图 13 棱形液舱网格图 Fig. 13 Mesh of prismatic tank |
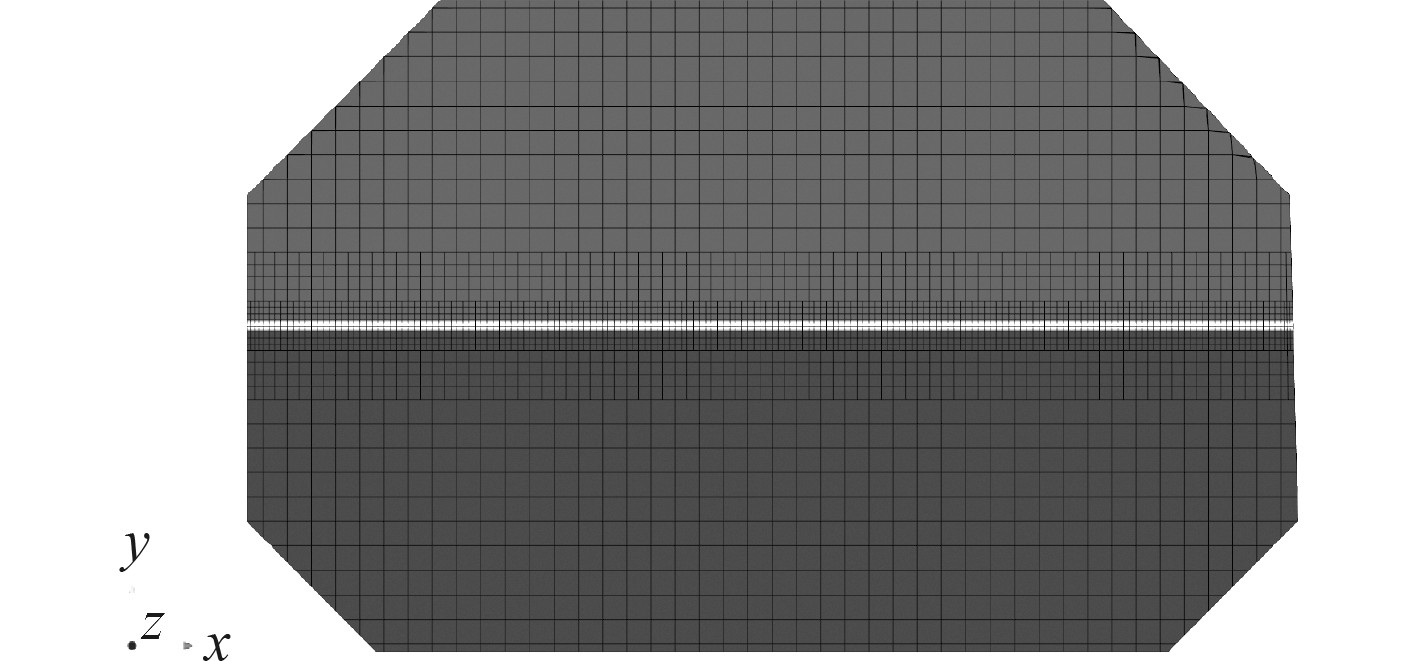
自由面网格细化遵循VOF相之间交界面驱动的非稳态的自适应网格准则,最大加密等级设置为2级,转换宽度为3。自适应时间步模型会在模拟运行期间自动确定时间步长,使用自由表面CFL条件时间步提供程序来控制时间步长,以使求解器保留尖锐的自由表面的交界面。该自适应时间步提供的程序基于按体积分数变化率加权的CFL数设置时间步。初始化后自由界面附近的网格被自动加密,如图14所示。
|
图 14 初始化后的自由界面网格细化 Fig. 14 Mesh refinement of free water surface |
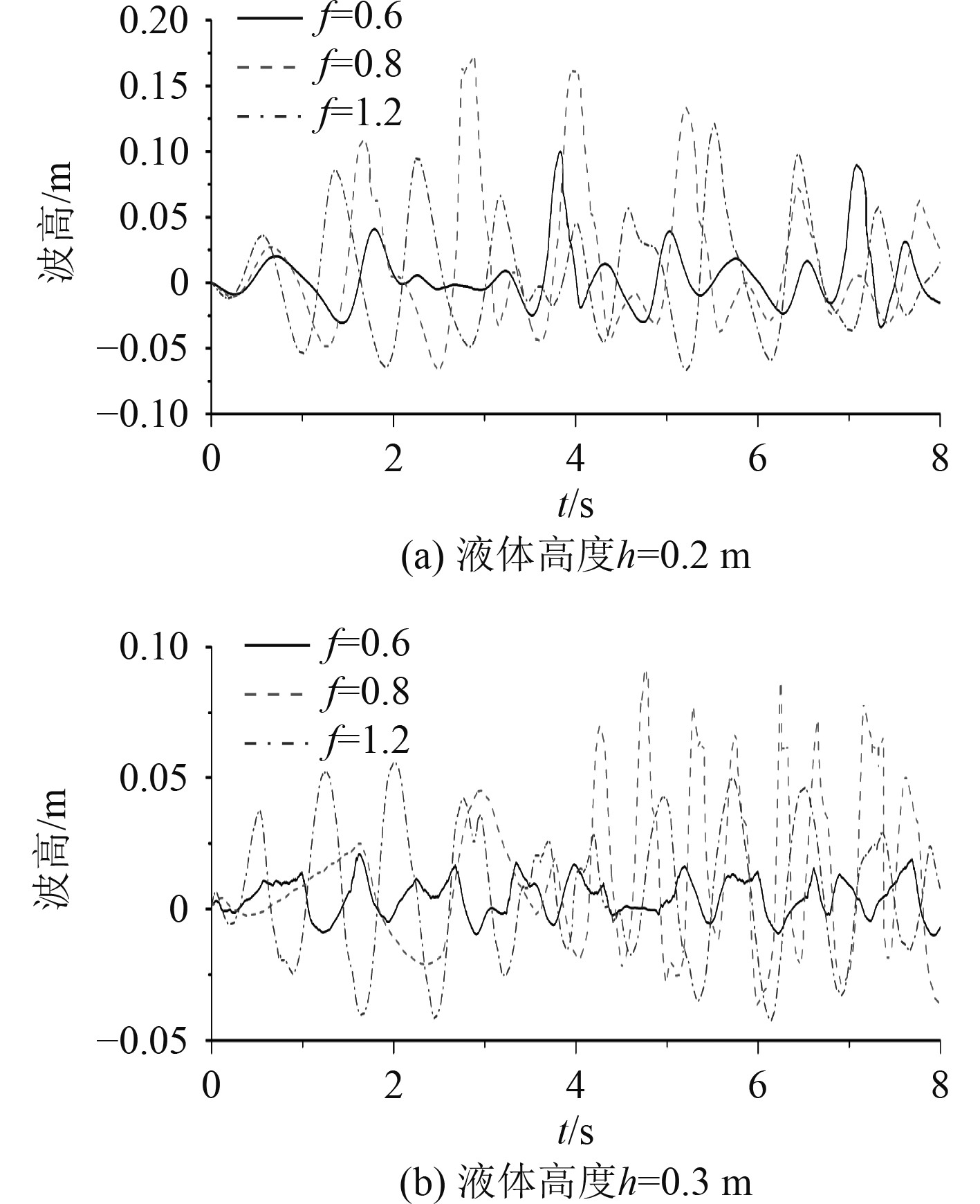
图15为三维棱形液舱在2种水深下不同横摇频率所对应的左侧围壁波高曲线。当装载液体的深度h=0.2 m时,3种频率的波高曲线均在0 m上下波动,其波峰的值约是波谷值的2~3倍。这说明在棱形液舱摇晃的过程中,左侧围壁处的波高大部分均处在初始的自由面高度之上。计算时间t=1 s之前,棱形液舱刚开始晃动,此时液舱晃荡的幅度较小,舱内液体从静止运动时需要克服自身的重力和惯性力,因此在t=1 s之前左侧围壁波高曲线变化比较平缓,线性程度较强,液体在左侧围壁的爬升高度也较小。t=1 s后,舱内液体积累的动能不断增加,随着液舱的晃动舱内液体的晃动变得更加剧烈,自由面的线性成分减小,非线性成分增加,同时波浪对左侧围壁的抨击作用加剧,因此t=1 s后的波高曲线变得不规则、不规律且无序。计算开始时,棱形液舱在外部横摇激励的作用下向左舷倾斜,左侧围壁的波高在小幅度下降后平缓上升。3种频率下的波高曲线在t=1 s前有一个微小的相位差,横摇频率f=1.2 Hz最先达到第1个峰值,f=0.8 Hz次之,f=0.6 Hz最后达到峰值,且3个频率的峰值高度也是依次降低。t=1 s后3种频率的波高曲线呈现较大的差异。f=0.6 Hz的波高曲线在时域上的波动较为平缓,只有t=3.5~4 s和t=6.8~7.3 s的区间内出现了2个较陡的波峰,其余时间波高曲线的幅值均比较小。在t=2.5~3.3 s的一段较长时间内,f=0.6 Hz的波高曲线在0 m上趋于一条直线,此时液舱处在横摇角度的最大值,横摇角加速度为0,自由面的波动较为平缓,与左侧围壁的相互作用力较小,反映到波高曲线上近似为一条直线。t=2 s后f=0.8的波高曲线出现了多个长波峰,其幅值远大于其余2种频率的波高曲线。这说明该横摇频率下舱内液体多次发生冲顶现象,左侧围壁的波浪会沿着顶边舱攀升到液舱顶部,而其余2种横摇频率均不会发生冲顶现象。
|
图 15 左侧围壁的波高分布 Fig. 15 Wave height duration curves of the left wall |
当装载液体的深度h=0.3 m时,自由面的初始位置在顶边舱上。不同于初始位置在直立侧壁的情况,液体晃荡时会持续受到倾斜顶边舱的挤压作用,因此,深度h=0.3 m的波高曲线在波动过程中的各个幅值明显小于h=0.2 m。当h=0.2 m时外部激励的横摇中心作用在静水面上,除了横摇中心附近的自由面波动较平缓之外,左侧围壁的波高变化较陡。当液体高度增加到h=0.3 m时,舱内液体晃动需克服的重力和惯性力增大,在两侧横摇力矩变化不大的情况下,液体开始晃荡的时间变长,左侧围壁波浪跃升的高度也降低。h=0.3 m下的波峰便尖,液体在顶边舱上的停滞时间变短。不同横摇频率所对应的波高曲线的变化趋势与h=0.2 m相比差别不大:f=0.8 Hz的波高曲线的幅值变化最剧烈,非线性程度最强,计算后期还会出现双波峰现象;f=0.6 Hz的波高曲线幅值变化最缓慢,自由面和顶边舱的相互作用比较微弱,在液舱晃荡的过程中自由面的波形更多的是以微幅波形式出现。
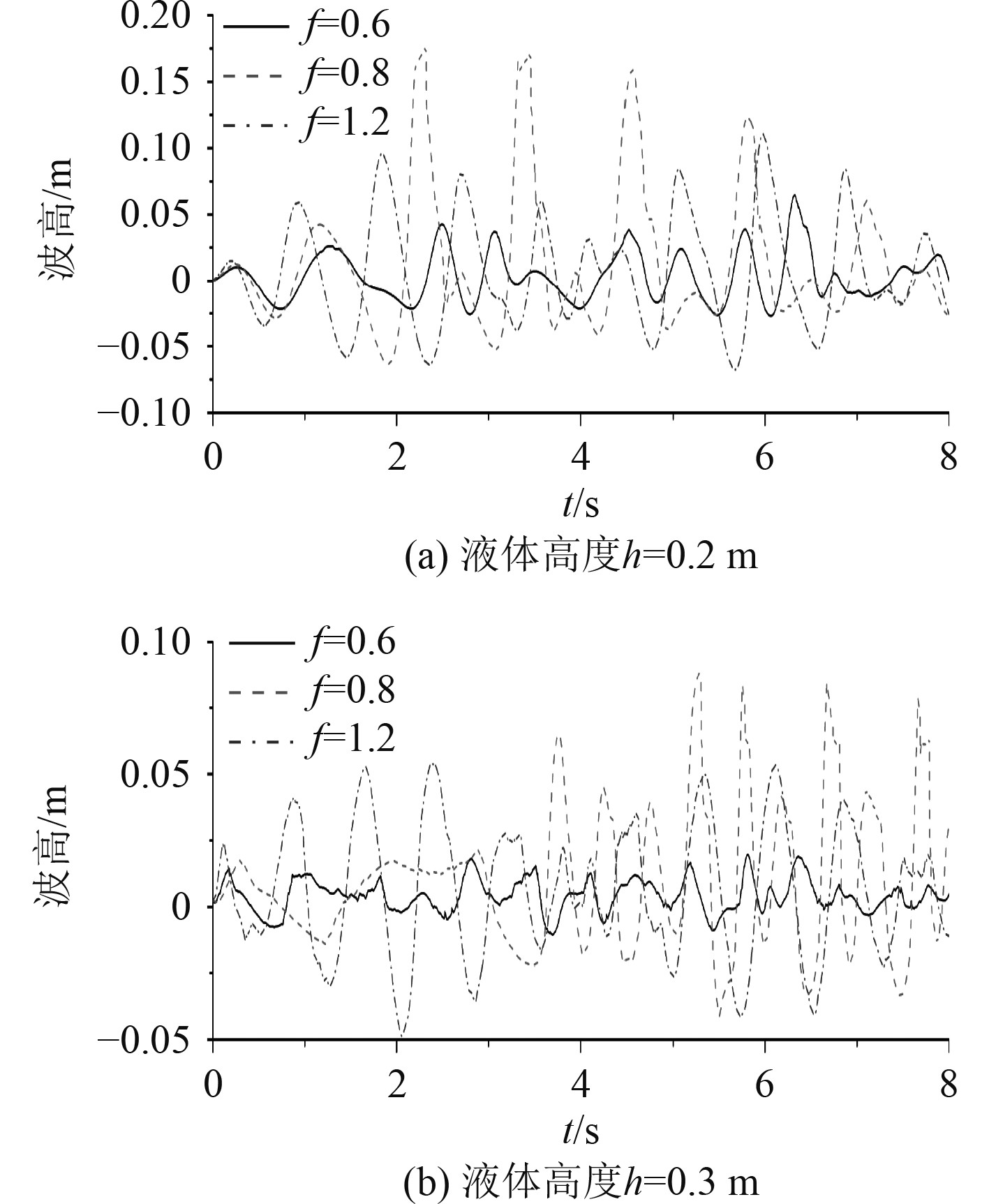
图16为三维棱形液舱在2种水深下不同横摇频率所对应的右侧围壁波高曲线。2种水深在t=1.5 s左右的计算前期,两侧围壁的波高曲线基本上可以视作是对称分布,即右侧围壁出现波峰的同时左侧围壁出现波谷。此时舱内液体刚开始晃动,自由面波动并不剧烈,线性程度较强,非线性程度较弱。t=1.5 s后右侧围壁的波高曲线呈现不规则的波动。
|
图 16 右侧围壁的波高分布 Fig. 16 Wave height duration curves of the right wall |
矩形液舱的固有频率可以由经验公式来确定。然而对于不规则形状的液舱(如棱形液舱),其固有频率很难通过经验公式或解析值得到。通过数值研究了不同水深下液舱激励频率与自由面波高及波形之间的关系可以初步确定共振频率的范围。很明显,横摇频率f=0.8 Hz对应的波高曲线与其余2种频率相比非线性程度更强,舱内液体多次发生冲顶现象,自由面波形更加无序,因此可以初步推断出,横摇频率f=0.8 Hz比其余2种横摇频率更接近本算例中的棱形液舱的固有频率。
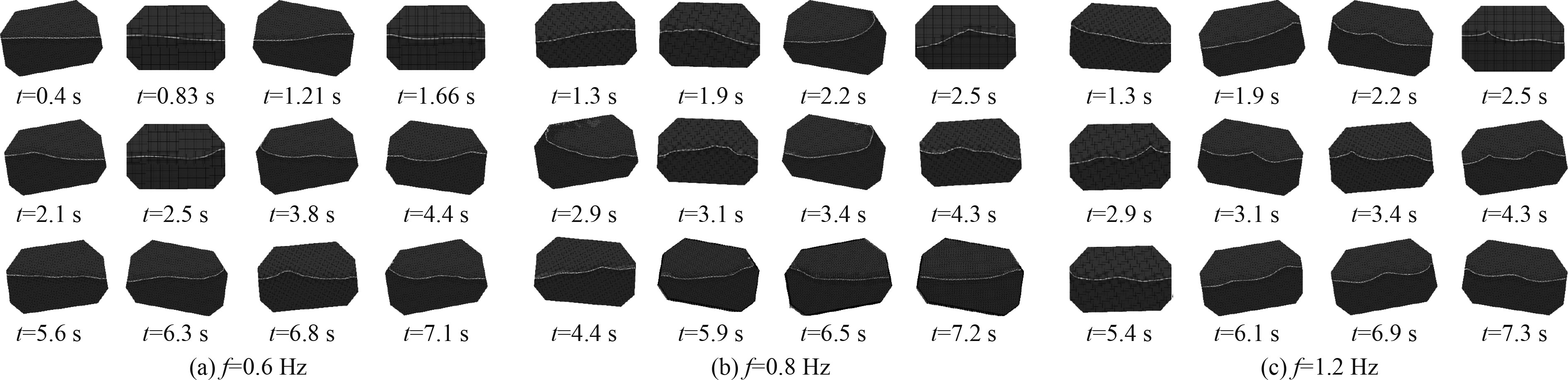
3.3.2 气液两相图图17为液体深度h=0.2 m下3种横摇频率对应的气液两相图。外部激励为横摇激励时,舱内液体自由面的波浪形态以驻波和行进波以及两者的叠加波为主。不同于矩形液舱遭受水平激励,行波在舱内往复运动的过程中不会发生波浪破碎,即使液体冲击到直立侧壁和顶边舱,自由面更多的是以反射波的形式回流。舱内液体作用到围壁形成的反射波与后部液体速度相反,碰撞后动能相互抵消,迅速形成一个峰值不大的孤立波。频率f=0.6时在液舱横摇的过程中有少量液体沿倾斜的顶边舱向上爬升一小段距离,随后又迅速跌落回液体中。频率f=0.8时液体沿顶边舱爬升到顶部,发生冲顶现象,同时伴有气液少量混合的现象发生。当频率f=1.2时,液体反而很少撞击到顶边舱,自由面的波峰变尖波谷变坦,同时行波在舱内往复运动的过程中伴有多个波峰出现。
|
图 17 h=0.2 m时各横摇频率下的气液两相图 Fig. 17 Gas-liquid distributions of prismatic tank with h=0.2 m under different roll frequencies |
观察图18可以发现,当液体深度h=0.3 m时,液体的重力和惯性力增大,同等横摇频率下液体跟随液舱一起晃荡所需的时间更长。在晃荡过程中,舱内液体的自由面的波高低于h=0.2 m,振荡频率比h=0.2 m时略高,波形大多是短促的微幅波。

|
图 18 h=0.3 m时各横摇频率下的气液两相图 Fig. 18 Gas-liquid distributions of prismatic tank with h=0.3 m under different roll frequencies |
本文以矩形和棱形液舱为研究对象,基于自适应网格加密技术(AMR)对液舱遭遇不同外部激励的情况进行数值模拟,得到结论如下:
1)自适应网格加密技术配合自适应时间步长,能够大幅度提高计算速度和效率。通过与理论值进行对比,本文验证了AMR具有良好的计算准确性。
2)当矩形液舱发生靠近共振频率的大振幅晃荡时,舱内液体晃荡行为的非线性成分明显增强。液体冲击围壁的过程中发生的气液混合和裹气冲击是晃荡过程的物理作用机理之一。
3)液舱遭遇横摇激励后,舱内自由面波高的非线性程度明显比遭遇水平余弦激励低;高装载率下,两侧围壁的波高幅值较中等装载率为低;舱内液体越多,抵抗外部激励的力矩越大,液体的晃荡程度越不明显。
4)不同于矩形液舱遭遇外部激励为水平激励的情况,棱形液舱遭遇横摇激励时,舱内液体晃荡的非线性程度较弱,自由面几乎不会发生大幅度波浪翻卷或破碎,波浪形态主要是行进波和驻波。
| [1] |
周博, 伍友军, 李曼, 等. 基于晃荡载荷的液舱结构强度研究[J]. 舰船科学技术, 2021, 43(1): 37-42. |
| [2] |
崔铭超, 王庆伟, 张彬. 纵摇运动下船载养殖水体流场特性数值分析[J]. 船舶工程, 2020, 42(10): 56-60+132. |
| [3] |
肖凯隆, 陈作钢, 代燚. 多液舱晃荡与船体运动耦合数值研究[J]. 船舶工程, 2020, 42(8): 50-54. |
| [4] |
胡泰安. 基于光滑粒子流体动力学与光滑点插值耦合方法模拟液舱晃荡问题[D]. 大连: 大连理工大学, 2020.
|
| [5] |
王庆丰, 徐刚, 王树齐, 等. 耦合激励下的液舱晃荡新型数值解法[J]. 船舶力学, 2019, 23(5): 523-530. DOI:10.3969/j.issn.1007-7294.2019.05.003 |
| [6] |
徐博. 随机激励下液舱晃荡及制荡效果研究[D]. 大连: 大连理工大学, 2020.
|
| [7] |
吴巧瑞, 张珍, 陈明辉, 等. 基于粒子法的水平挡板对液舱晃荡现象影响的分析[J]. 中国造船, 2021, 62(1): 50-61. DOI:10.3969/j.issn.1000-4882.2021.01.005 |
| [8] |
王瑾, 吴磊. 液舱晃荡与船体耦合运动的全非线性数值模拟与分析[J]. 船舶力学, 2020, 24(9): 1142-1150. DOI:10.3969/j.issn.1007-7294.2020.09.006 |
| [9] |
丁仕风, 周利, 周亚军. 液化天然气船晃荡与冰区运动的耦合分析[J]. 哈尔滨工程大学学报, 2020, 41(8): 1136-1142. |
| [10] |
程聪. 基于SPH方法的液舱晃荡和多相流问题的并行数值模拟[D]. 大连: 大连理工大学, 2020.
|
| [11] |
罗富强, 邓锐, 汪昱全, 等. 基于OpenFOAM的自适应网格计算策略研究[J]. 中国造船, 2020, 61(S2): 169-178. |
| [12] |
李金龙, 尤云祥, 陈科. 一种几何VOF方法在液舱晃荡流动模拟中的应用[J]. 上海交通大学学报, 2019, 53(8): 943-951. |
| [13] |
张秋艳, 任冰, 蒋梅荣. 二维矩形弹性液舱内液体晃荡数值模拟研究[J]. 船海工程, 2012, 41(4): 11-15+20. DOI:10.3963/j.issn.1671-7953.2012.04.003 |
 2022, Vol. 44
2022, Vol. 44

